Quantum Processors in Silicon Photonics

Abstract

Machines that can exploit their hardware to process quantum information can solve certain problems exponentially faster than purely classical (conventional) computers. To harness the potentially groundbreaking applications of quantum computers, these machines will be required to control and process quantum systems at a very large scale, potentially involving millions of high-quality quantum information carriers. While a number of challenges must be overcome before silicon photonics can support quantum computing at scale, the capabilities of mature semiconductor fabrication process to integrate large quantum photonic circuits on single devices, means this is a promising and emerging platform for quantum information processing. In this chapter, we will review recent results in developing key building blocks for chip-scale photonic quantum devices and discuss the progress towards useful large-scale quantum computers in the silicon quantum photonics platform.

1 Introduction

The field of quantum mechanics has provoked deep and philosophical questions about the nature of our universe: Are the outcomes of measurements truly random? Can a particle simultaneously occupy two different states? Can the uncertain states of two separated particles instantaneously become certain and correlated? The field of quantum technologies took hold when, rather than worrying about these questions, scientists instead began to explore how the counter intuitive features of quantum mechanics might be used as resources.

We now know how the combination of particle superpositions and uncertain measurement outcomes enables secret quantum communication. We have discovered how particular quantum states of light can enhance the measurement sensitivity when used as measurement probes. And, perhaps most excitingly, we know how entangled states of particles can be used to run quantum algorithms to solve problems exponentially faster than is possible with classical computers.

Silicon photonics is an appealing platform for quantum information processing. The mature fabrication tools from the microelectronics industry, together with cutting edge techniques from academia, allow the design and lithography of large and complex, yet stable photonic circuits. Reproducible photonic circuitry enables near-identical sources of photons and high-quality interferometers, key elements to the implementation of photonic entangling operations.

The scale of the circuitry required for general purpose photonic quantum computing might seem beyond the capabilities of today’s technology. Yet, here we discuss important proof-of-concept demonstrations for photonic quantum processors at significant leaps of complexity over what had been reported only a few years before.

2 Photonic Quantum Information Processing

We start with a brief background on photonic quantum information processing. The interested readers can find more details, for example, in  [1,2,3].

2.1 Quantum States of Light

In the second quantisation formalism, light in a single optical mode is described as an harmonic oscillator with Hamiltonian $\hat{H}=\hbar \omega (\hat{a}^\dagger \hat{a} + 1/2)$, where $\omega$ is the mode frequency and $\hat{a}^\dagger$ ($\hat{a}$) is the bosonic creation (annihilation) operator for the single quantum excitations of the electromagnetic field: photons. If k labels different optical modes, Fock states for photon configurations $\boldsymbol{n}$ describe states with fixed number of photons in the different modes:

$$\begin{aligned} \left| {\boldsymbol{n}} \right\rangle = \left| {n_1 n_2 \ldots n_m} \right\rangle = \left| {n_1} \right\rangle _1\otimes \left| {n_2} \right\rangle _2 \otimes \ldots \otimes \left| {n_m} \right\rangle _m, \end{aligned}$$

(11.1)

where the quantum states $\left| {n_k} \right\rangle$ represent $n_k$ photons in the k-th mode and are given by $\left| {n_k} \right\rangle _k= (\hat{a}_k^\dagger )^{n_k}/\sqrt{n_k!} \left| {\emptyset } \right\rangle _k$, with $\left| {\emptyset } \right\rangle _k$ the vacuum state on mode k. Quantum states can also contain a coherent superposition of different photon numbers, such as the single-mode squeezed vacuum (SMS) and two-mode squeezed vacuum (TMS) states, described in term of Fock states as

$$\begin{aligned} \left| {\text {SMS}(\xi )} \right\rangle&= \frac{1}{\sqrt{\cosh r}} \sum _{n=0}^\infty (-e^{i\varphi }\tanh r)^n \frac{\sqrt{(2n)!}}{2^n n!} \left| {2n} \right\rangle , \end{aligned}$$

(11.2)

$$\begin{aligned} \left| {\text {TMS}(\xi )} \right\rangle&= \frac{1}{\cosh r} \sum _{n=0}^\infty (e^{i\varphi } \tanh r)^n \left| {n} \right\rangle _1 \left| {n} \right\rangle _2, \end{aligned}$$

(11.3)

where $\xi =r e^{i\varphi }$ is the squeezing parameter [1].

2.2 Encoding Qubits and Qudits in Photons

While all quantum states of light introduced above can be used to encode and process quantum information [3], in this chapter we will focus on using single photons. A qubit, the quantum equivalent of a classical bit, is a two-level quantum system which can be encoded in the state of a single photon in two optical modes. Although these modes can represent many different photonics degrees of freedom (e.g. polarisation, wavelength, time, orbital angular momentum, etc.), the typical choice in integrated quantum photonics is to use the path of the photon, i.e. the different waveguides the photon can travel in. The qubit is then encoded in a single photon as pictured in Fig. 11.1, where the mapping between the computational state of the qubit and the Fock state is defined as follows: the qubit is in the computation state $\left| {k} \right\rangle$ if the single photon passes through the k-th waveguide, with $k\in \{0,1\}$. Furthermore, this definition can be straightforwardly generalised to go beyond qubits and encode d-dimensional quantum systems—qudits—by using d different paths, as also shown in Fig. 11.1 [4, 5].

Fig. 11.1

Encoding of a qubit (left) and a qudit (right) on the spatial modes of a single photon propagating through integrated waveguides

2.3 Processing Photons with Linear Optics

The typical approach to process photons in integrated quantum circuits is via the use of linear-optical interferometers: linear evolutions conserving the number of photons. Evolutions in a linear-optical system with m modes are described via $m\times m$ unitary matrices, where the unitarity ensures energy conservation (non-unitarity can appear in presence of losses). Linear-optical operations can be constructed using two building blocks: phase shifters and beam-splitters (see Fig. 11.2a), described via the unitaries

$$\begin{aligned} U_{\text {PS}}(\phi )= \begin{bmatrix} 1 &{} 0 \\ 0 &{} e^{i \phi } \end{bmatrix}, \qquad U_{\text {BS}}(\eta )= \begin{bmatrix} \sqrt{\eta } &{} i\sqrt{1-\eta } \\ i\sqrt{1-\eta } &{} \sqrt{\eta } \end{bmatrix}, \end{aligned}$$

(11.4)

where $\phi$ is the phase applied by the phase shifter, and $\eta$ is the beam-splitter reflectivity. While these components act on single and two modes, they can be combined into Mach–Zehnder interferometers (MZIs, see Fig. 11.2b) and networked to build m-mode circuits implementing an arbitrary unitary evolution U, known as universal linear-optical schemes. A variety of universal schemes has been developed [6, 7, 9], with two prominent examples by Reck et al. [6] and Clements et al. [7] shown in Figs. 11.2c, d, respectively. Reconfigurable circuits able to implement arbitrary unitary operations on six modes with high fidelity have been recently demonstrated on a silica chip (see Fig. 11.2e) [8]. Such circuits can be used to implement arbitrary single-qubit or single-qudit gates with high precision [5, 10,11,12].

Fig. 11.2

a Building blocks for linear-optical circuits: the beam-splitter mixes amplitudes of different modes, the phase shifter inserts an optical phase $\phi$ in the associated mode. b Beam-splitters and phase shifters are combined to form generalised beam-splitters via Mach–Zehnder interferometers and networked to build universal interferometers. Examples of universal linear-optical schemes are shown in (c) (Reck scheme [6]) and in (d) (Clements scheme [7]). e Implementation of a universal scheme via integrated quantum photonics. Image e is from  [8]

2.4 Scalable Photonic Quantum Computing Architectures

While single-photon operations can thus be performed deterministically and with high precision in linear optics, the main challenge for photonic quantum processors is to perform entangling operations between different photons. Such operations are required to perform two-qubit gates in universal quantum computing circuits [16]. This difficulty comes from the fact that photons do not directly interact, and therefore photon–photon nonlinearities are highly suppressed (although interesting integrated hybrid approaches are emerging to mediate photon-photon nonlinearities through interfaces with solid-state systems [17]). Nevertheless, universal quantum computing can be scalably implemented in photonics by inducing photon–photon entangling gates through measurements [14, 18]. Due to the probabilistic nature of quantum measurements, such entangling gates are inherently probabilistic, but their success can be heralded via the measurement of auxiliary photons. The heralding enables multiplexing schemes to boost the success probability of such probabilistic entangling operations to near-unity to make them scalable. [14, 18,19,20].

Fig. 11.3

a Optical interferometer for the generation of a three-photon heralded GHZ entangled state $( \left| {000} \right\rangle + \left| {111} \right\rangle )/\sqrt{2}$, with success probability 1/32 [13]. b Photonic circuit to perform type-II fusion gates (with success probability 1/2), fusing different photonic entangled states to form larger entanglement resources [14]. c Modular LOQC architecture for generating universal resource states for MBQC, e.g. states as shown in (d). Each module includes GHZ generators (black squares), type-II fusion gates (circles), delay lines and single-photon detectors. Image c is from  [15]

An example of an heralded entangling gate for the generation of three-photon entanglement, in particular the Greenberger–Horne–Zeilinger (GHZ) state $( \left| {000} \right\rangle + \left| {111} \right\rangle )/\sqrt{2}$, is shown in Fig. 11.3a [13]. Such states play an important role in modern linear-optical quantum computing (LOQC) architectures as they can be fused together to form larger entangled states via fusion gates [14, 19]. An example of a fusion gate (type-II) circuit is reported in Fig. 11.3b, which has a success probability of 1/2 [14]; this success probability can be boosted to 3/4 via the use of additional auxiliary photons [21].

Modular architectures for scalable universal quantum computing with linear optics can be built, for example, by fusing a large number of GHZ states to form entangled resource states for universal measurement-based quantum computing (MBQC), known as cluster states [14, 15, 19, 22, 23]. As shown in Fig. 11.3c, each module in such architecture fuses GHZ states to make a single computational photonic qubit and connects it to other qubits in the lattice of a universal cluster state [14, 19], such as the square lattice of entangled qubits shown in Fig. 11.3d. These types of universal LOQC architectures also enable fault-tolerant photonic quantum computation [15], which is crucial to suppress the exponential amplification of photon loss and computational errors that prevents scaling quantum computation on non-error-corrected quantum devices beyond few tens of qubits [24]. However, the resource costs for such architectures [25] mean that a hardware platform able to integrate millions to billions of components is required to reach a scale where useful fault-tolerant photonic quantum computing applications can become practical. Nearer-term special-purpose photonic quantum devices are possible and will be discussed in Sects. 11.4 and  11.5. Although the prefault-tolerant applications for such devices are significantly more limited, the hardware requirements are reduced to thousands of components [26]; a scale achievable with the current silicon quantum photonic technology.

3 Silicon Quantum Photonic Technology

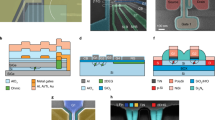
To reach the scale required for computationally interesting applications, photonic quantum processors must integrate at least thousands of high-quality components to generate, process and measure quantum states of light. Thanks to its compatibility with mature fabrication facilities, and together with more advanced components, silicon quantum photonics might reach such a scale. Silicon photonics circuits comprising thousands of components are in fact already routinely used for classical applications [27]. Quantum photonic circuits, however, need additional components and generally have stringent performance requirements (for example in term of losses) with respect to purely classical devices. As shown in Fig. 11.4, silicon photonics can integrate all such components into a single platform.

Fig. 11.4

Blueprint of a typical quantum photonic processor in the silicon platform, which includes waveguide (a) and ring (b) SFWM sources. Beam-splitters based on MMIs (c) or directional couplers (d), phase shifters (e) and delay lines (f) are networked to form reconfigurable linear-optical circuits. Filters (g) are used to suppress the pump light and on-chip detectors (h) are used to measure the processed single photons. Classical control electronics can be interfaced with the device via wire-bonding to a PCB (i) or via a homogeneous integration or direct chip-to-chip bonding with CMOS electronics (j)

3.1 Integrated Photon Sources

Quantum states of light can be generated via spontaneous nonlinear processes arising from the interaction of a pump light with a nonlinear-optical medium [1]. Although silicon does not naturally posses a $\chi ^{(2)}$ due to its centro-symmetric crystal structure, preventing the use of spontaneous parametric down-conversion (SPDC) processes for photon generation, it posses a strong $\chi ^{(3)}$ nonlinearity. Pairs of photons can thus be generated via the spontaneous four-wave mixing (SFWM) $\chi ^{(3)}$ process that naturally arise when a bright laser pump field propagates through silicon [28,29,30]. In order to be suitable for scalable quantum photonic architectures, the key qualities to be considered for spontaneous photon-pair sources are [30]:

• Indistinguishability: Photons emitted from different sources need to be indistinguishable in order to interfere.

• Purity: The state in each degree of freedom (frequency, polarisation, etc.) of the individual photons emitted needs to be pure in order to ensure high-quality quantum interference.

• Heralding efficiency: the intrinsic losses in the source have to be low to avoid photon loss. In other words, for a spontaneous photon-pair source, if one of the photons (the idler) is detected to herald the emission of the other photon (the signal), the probability that the signal photon is actually present needs to be high.

• Brightness: photon emission with low pump power requirements is desirable to limit the power consumption when scaling to large arrays of sources, as well as for facilitating pump-rejection filtering.

3.1.1 Waveguide Sources

In the bright-pump approximation, the SFWM process in a silicon waveguide can be described via the Hamiltonian [1]

$$\begin{aligned} \hat{H}=\int d\omega _{i} d\omega _{s}\ F(\omega _i,\omega _s) \hat{a}^\dagger (\omega _i) \hat{a}^\dagger (\omega _s) +h.c., \end{aligned}$$

(11.5)

where h.c. indicates the Hermitian conjugate, $\omega _{s}$ ($\omega _{i}$) represent the signal (idler) frequency and $\hat{a}^\dagger (\omega _s)$ ($\hat{a}^\dagger (\omega _i)$) the associated photon creation operation. $F(\omega _i,\omega _2)$ is the joint spectral amplitude (JSA) of the emitted pairs of signal and idler photons, given by

$$\begin{aligned} F(\omega _i,\omega _s) = \mathcal {N}&\int \limits _0^L dz \int d\omega _{p_1} d\omega _{p_2} \nonumber \\&\alpha _{p_1}(\omega _{p_1}) \alpha _{p_2}(\omega _{p_2}) \delta (\omega _i+\omega _s - \omega _{p_1} - \omega _{p_2}) \exp (-\text {i} \Delta k z). \end{aligned}$$

(11.6)

Here, $\mathcal {N}$ is a normalisation factor, L is the waveguide length, $\alpha _{p_1}$ and $\alpha _{p_2}$ are the spectral envelops for the two pump fields, and $\Delta k(\omega _i,\omega _s,\omega _{p_1},\omega _{p_2})$ is the phase mismatch between the four fields. The factor $\delta (\omega _i+\omega _s - \omega _{p_1} - \omega _{p_2})$ ensures energy conservation, while the phase-matching term $\exp (-\text {i} \Delta k z)$ ensures momentum conservation.

The Hamiltonian in  11.5 describes a squeezing process where two photons are absorbed from the pump light at frequencies $\omega _{p_1}$ and $\omega _{p_2}$, generating a photon pair at frequencies $\omega _{i}$ and $\omega _{s}$ [1]. Depending on the choice of frequencies for the pump field and for the emitted photons, SFWM can be operated in two different regimes, illustrated in Fig. 11.5a:

• Non-degenerate SFWM: $\omega _{p_1} = \omega _{p_2}$ and $\omega _{i} \ne \omega _{s}$. In this case, the photons are generated in two separate spectral modes, and two-mode squeezing is obtained (see  11.3).

• Degenerate SFWM: $\omega _{p_1} \ne \omega _{p_2}$ and $\omega _{i} = \omega _{s}$. In this case, photons are generated in the same spectral mode, and single-mode squeezing is obtained (see  11.2).

Fig. 11.5

a Spontaneous four-wave mixing schemes. Non-degenerate SFWM (top) generates TMS with photons at difference frequencies, while degenerate SFWM generates SMS with pairs of degenerate photons. b Exemplary joint spectra produced in waveguide sources via non-degenerate SFWM. Using spectral filters (shaded areas), the photon spectral purity is increased from 30 to $96\%$

In the low-squeezing regime (i.e. low pump energy), the TMS state generated with non-degerate SFWM approximates the state

$$\begin{aligned} \left| {\psi } \right\rangle _{i,s}\simeq \left| {0} \right\rangle _i \left| {0} \right\rangle _s - i \gamma L P \int d\omega _{i} d\omega _{s} F(\omega _i,\omega _s) \left| {1} \right\rangle _{i,\omega _i} \left| {1} \right\rangle _{s,\omega _s} \end{aligned}$$

(11.7)

which describes the probabilistic generation of a photon-pair with an approximate probability $p=\gamma ^2 L^2 P^2$, where $\gamma$ is the nonlinear parameter of the silicon waveguide and P is the pump power [31].

Both degenerate and non-degenerate SFWM regimes have been demonstrated in silicon single-mode waveguide sources [32, 33]. The typical length for standard single-mode 220 nm SOI waveguide sources is approximately 1  cm, usually wrapped in a spiral shape to reduce the component footprint, as shown in Fig. 11.4a. Being fully passive devices and easily reproducible with standard semiconductor fabrication facilities, waveguide sources are very practical and with high indistinguishability, resulting in a wide usage in silicon quantum photonic processors [5, 32,33,34]. The intrinsic heralding efficiency in waveguide sources is only limited by transmission losses in the waveguide. However, phase-matching conditions in waveguides imply very strong spectral correlations between the photons in each pair, as manifested in the typical JSA shown in Fig. 11.5b. Such spectral correlations imply that the spectral state of the individual photons is highly impure [35]. The single-photon purity can be improved to values $90\%$ via spectrally filtering the photons (see Fig. 11.5b), which comes at the cost of significantly reducing the heralding efficiency of the source [36].

3.1.2 Multimodal Waveguide Sources

Multimodal SFWM (mmSFWM) approaches have been recently demonstrated to be capable of solving the limitations of standard waveguide sources in silicon [37, 38]. As shown in the schematic in Fig. 11.5a, in mmSFWM the nonlinear interaction is performed between different transverse modes propagating through a multimode waveguide. Via the use of beam-splitters and mode converters, the pump light is injected into the multimode waveguide in a superposition between different transverse modes, e.g. the TM0 and TM1 modes in the device in Fig. 11.5, with the signal and idler photons also emitted in different transverse modes. By tailoring the group velocities dispersion of the different modes through the design of the multimode waveguide cross section, the phase-matching conditions can be engineered to reduce the spectral correlations between the emitted photons [38]. Moreover, a time delay can be inserted between the pump modes so that, due to the different group velocities of the modes, the temporal overlap between the pump modes gradually increases and decreases along the waveguide, as shown in Fig. 11.5a. This adiabatic switching of the nonlinear interaction further suppress the spectral correlations enabling a near-unit spectral purity [37, 39, 40]. Moreover, due to the lower losses in multimode waveguides, the heralding efficiency is also significantly improved compared to single-mode waveguide sources. Sources based on mmSFWM have been recently demonstrated on commercial silicon-on-insulator (SOI) photonic devices (see Fig. 11.5b), exhibiting a near-ideal spontaneous photon source performance: spectral purities of $99\%$ without any spectral filtering of the photons (see Fig. 11.5c), source indistinguishability $98\%$, and intrinsic heralding efficiency $90\%$. All such performances resulted in the demonstration of a record-high on-chip heralded quantum interference visibility of $96\%$ without spectral filtering of the photons, making this type of sources excellent candidates for photonic quantum information processing [37]. Moreover, mmSFWM has been also recently used to generate photonic entanglement between the transverse modes of photons in silicon multimode waveguides [41].

Fig. 11.6

a Schematic of a multimodal source in silicon, where the input pump is prepared in a superposition between the TM0 and TM1 transverse modes via a beam-splitter and a mode converter. A time delay $\tau$ is inserted to increase the source purity. Photons are emitted in the TM0 and TM1 modes via intermodal SFWM along the waveguide and separated at the output by a second mode converter. b Microscope image of a multimodal SFWM source in silicon. c Joint spectra of the emission from two different multimodal silicon sources show highly uncorrelated spectra (purity of $99\%$) and high overlap between the sources (indistinguishability $>98\%$). Images from  [37]

3.1.3 Ring Cavity Sources

Waveguide sources are cavity-free elements. To improve the source brightness, resonant structures such as ring resonators [42,43,44,45,46,47,48,49,50,51,52] or photonic crystal waveguides [53,54,55] can be used. Ring sources (see Fig. 11.4b) are particularly appealing due to their high miniaturisation and the capability to achieve high Q factors (up to the $10^4$–$10^5$ range for standard single-mode waveguides). Significant benefits to the source brightness are possible when operating SFWM in a cavity: in principle, the photon-pair emission probability is enhanced by a factor $F^6$, with F being the field enhancement in the cavity [56]. However, when using telecom wavelengths in silicon waveguides, the strong pump field inside the ring can induce large nonlinear losses due to effects such as two-photon absorption, which can significantly limit the ring source [57, 58]. These limitations can be avoided by moving to mid-infrared ($\ge$2$~\mu$m) wavelengths in silicon [59] or using wider band-gap materials, such as silicon nitride [60,61,62,63], where two-photon absorption is suppressed.

Because the photon emission, as well as the pump fields, need to be resonant with the ring cavity, the narrow-band photon emission reduces spectral correlations between the photons, and thus purities above 80% are readily achieved [49, 51, 56]. Although for standard Gaussian pump spectral envelopes the photon purity from ring resonator sources is limited to be below $93\%$ [64], approaches where more complex pump spectral shapes [65] or dispersive coupling to the resonator, via auxiliary rings or asymmetric MZI structures [64], can boost the purity to near-unity. Such schemes have been recently implemented in silicon devices [52]. The active control of ring resonances via thermal phase shifters has also been demonstrated to ensure a good indistinguishability between multiple ring sources [50, 51]. Moreover, ring structures have also been proposed and demonstrated to mitigate noises when operating SFWM in the degenerate regime for the generation of single-mode squeezed states [63, 66].

3.2 Linear-Optical Components

Identically to classical laser light, single photons can be guided in silicon photonic chips through waveguides and manipulated through linear-optical components such as multimode interference (MMI) couplers and evanescent directional couplers (DC) (see Fig. 11.4c, d). In the quantum regime, however, it is crucial to minimise the insertion loss of all linear-optical components in order to reduce the probability of losing single photons—one of the main sources of errors for photonic quantum computing. Linear losses in waveguides have been shown to reach values as low as 0.3 dB/cm at telecom wavelengths, with interesting prospects for building delay lines (see Fig. 11.4f) in silicon, required for multiplexing schemes in linear-optical quantum computing architectures [67, 68]. Beam-splitters implemented by evanescent coupling can offer minimal additional loss, but exhibit less robust splitting ratios, being more sensitive to waveguide fabrication variations. MMI structures are much more robust to fabrication imperfections, but with slightly higher losses (typically $\ge 0.1$ dB insertion loss) [69].

Phase shifters are commonly realised as thermal heaters (see Fig. 11.4e), which present extremely low losses but are limited to KHz bandwidths [70,71,72,73,74]. High-speed modulation of quantum states can be achieved with carrier-injection or carrier-depletion modulators, showing typical 10 GHz bandwidths [75]. However, their characteristic high and phase-dependent loss can severely reduce their functionality for quantum circuits. Moreover, they have limited functionality to operate at cryogenic temperatures due to carrier freeze-out. Recent developments in thin-film barium titanate on silicon show great potential for the development of on-chip fast modulators, with demonstrated losses below 0.5 dB, speed of tens of GHz [76], and compatible with cryogenic temperatures for full-system integration with superconducting single-photon detectors [77].

Beam-splitters with tunable reflectivities can be built by cascading MMIs and phase shifters into Mach–Zehnder-type structures [78]. Extremely high-precision control of such linear-optical two-mode operations has been demonstrated with extinctions exceeding 60 dB, corresponding to single-qubit computational errors below $10^{-5}$ [79, 80].

3.3 Detection Systems

The integration of high-efficiency photon detectors is important to reduce losses due to off-chip coupling, as well as for reducing the system latency (implying less losses in delay lines) and enabling scalable detection of large quantum systems. Superconducting nanowire single-photon detectors (SNSPDs, see Fig. 11.4h) can perform near-ideal single-photon detection with extremely low jitter, death time and dark counts [81,82,83] and have been integrated in a variety of integrated quantum photonic platforms [84]. The high-yield fabrication of SNSPDs in the NbN material in silicon photonic devices has been demonstrated [85], as well as arrays of up to 240 detectors suitable for the detection of large-scale circuits [86]. Furthermore, the integration of superconducting transition edge sensors (TES), capable of performing photon-number-resolving detection, has also been recently reported in Ti:LiNbO$_3$ waveguides [87], with prospects also for silicon integration. However, superconducting detection systems require the photonic device to operate at cryogenic temperature, typically at <2 K temperature for standard SNSPDs, and few tens of mK for TES detectors. Recent engineering efforts have also showed that few-photon number resolution, sufficient for a large part of LOQC applications, is achievable with impedance-matched single standard nanowire superconducting detectors [88].

Apart from single-photon detectors, integrated homodyne detectors have also been recently demonstrated in the silicon quantum photonic platform [89]. In contrast to SNSPDs, these systems can operate at room temperature. A record-high detection bandwidth of up to 9 GHz has been recently reported for on-chip homodyne measurements in silicon [90]. These systems are promising for on-chip continuous-variable photonic quantum applications such as on-chip quantum metrology, quantum random number generation and continuous-variable photonic quantum computing [89, 91, 92].

3.4 Single-Photon Filters

The simultaneous integration of single-photon sources and single-photon detectors necessarily requires the integration of filtering structures for high-extinction pump suppression. Such components must suppress the pump below the typical noise level of SNSPDs (less than kHz typical dark counts values), thus providing extinctions above 100 dB. While in most current silicon quantum photonic experiments pump rejection is performed off-chip using standard telecommunication components, devices showing on-chip pump filtering have been realised combining Bragg grating structures and add-drop filters (see Fig. 11.4g), or coherently cascaded unbalanced Mach–Zehnder interferometers. Currently, such filters can achieve up to 150 dB pump suppression when implemented between two silicon chips [44, 93]. For a monolithic integration of pump filters with sources and detectors on a single device, a challenge for filtering comes from the pump light scattered off the waveguides, which might limit the total extinction [93]. The full monolithic system integration of SFWM sources, filters and detectors would represent a major technological milestone for silicon quantum devices, but has yet to be demonstrated.

3.5 Optical and Electronic Packaging

When expanding the complexity of photonic quantum processors in microscale silicon devices, a scalable optical and electronic packaging of the system becomes increasingly important. Fortunately, chip packaging methods developed for classical applications can in principle be readily adapted to quantum photonic processors [94]. Optical access to silicon quantum photonic devices is typically achieved via coupling single-mode fibres and fibre arrays via edge-couplers or grating couplers, with sub-1dB coupling losses demonstrated in both approaches [95,96,97,98,99]. For the electronic packaging, most experiments in silicon quantum photonics currently use direct electrical probing [32, 48] or wire-bonding to an external PCB (see Fig. 11.4i) [5, 11, 33, 34, 51, 100, 101]. To decrease the latency of the electronic classical control and read-out systems, crucial to decrease photon losses in feed-forward operations, impressive improvements have been recently shown via direct wire-bonding of quantum photonic chips to microelectronics [90]. Hybrid integration of photonic and electronic CMOS systems [102] as well as flip-chip bonding techniques [103, 104] hold great promise for further speed and scalability enhancements for the classical control of quantum photonic devices (see Fig. j).

Fig. 11.7

Progress in the number of components (top) and number of photons and qubits (bottom) for silicon quantum photonic processors. Exemplary devices from some of the reported experiments are shown. Images are from the following references: a [48], b [11], c [5], d [100, 105, 106], e [33], f [34]

3.6 Scaling Silicon Quantum Photonic Circuits

The silicon photonics platform enables to scale quantum photonic circuits where the large number of the components described above can be interconnected on single silicon devices. As shown in Fig. 11.7, this has allowed a rapid scaling of quantum photonic experiments in silicon quantum photonics in recent years, both in terms of circuit complexity [5, 11, 34, 107] and number of photons and qubits generated and processed on-chip [33, 34, 101], which shows a good potential for developing large-scale quantum processors on this platform.

4 Silicon Photonic Quantum Processors

In the past five years, remarkable improvements for quantum photonic processors in silicon have been reported: starting from the first on-chip generation and processing of qubit entanglement using two photons and approximately 10 components in 2015 (see Fig. 11.7), we are now at the stage where experiments with ten or more photons and qubits processed via thousand of optical components are conceivable. While such experiments are still far from the scale required for general purpose quantum computers, they are a good indication of the potential scaling capability of the silicon quantum photonics platform. In this section, the aforementioned recent silicon quantum photonic results are reviewed.

Fig. 11.8

a Silicon quantum device for the generation and measurement of two-qubit path-encoded entanglement via ring resonators sources. b Characterisation of the generated on-chip two-qubit entanglement via Bell inequality violation. c Silicon device for the generation of two-qubit entanglement and the operation of a post-selected CNOT entangling gate. d Silicon device for the operation of arbitrary two-qubit controlled operations. e Implementation of a witness-assisted variational quantum simulation algorithm on the device. f Large-scale silicon quantum photonic processor for the implementation of arbitrary two-qubit gates. g Reconstruction of an exemplary two-qubit gate on the device using quantum process tomography, showing a fidelity of $95\%$. Images a and b are from  [48], c is from  [108], d is from  [106], e is from  [105] f and g are from  [107]

4.1 Entanglement Generation and Processing in Silicon Photonics

The first demonstration of path-encoded entanglement between two photonic qubits in silicon photonics was achieved in 2015 using the device shown in Fig. 11.7a. In this integrated photonic circuit, schematised in Fig. 11.8a, a pair of ring sources are coherently coupled to generate a photon pair in superposition between the two sources via non-degenerate SFWM. Such superposition corresponds to a maximally entangled path-encoded state of two qubits (i.e. a Bell pair), obtained after the two emitted photons, which possess different frequencies, are separated and grouped via ring-based filters and a crosser. The generated entanglement was characterised via the use of two integrated MZIs to perform arbitrary local measurements (detection was performed via off-chip SNSPDs) and verified through the violation of a Bell inequality (see Fig. 11.8b). Note that with this approach the two-photon entanglement is generated directly at the sources, where the nonlinearity of SFWM converts the coherent pumping of different sources to the correlated superposition of the photon pair, without the need of entangling gates. Similar ideas have also been used to obtain two-photon entanglement in other degrees of freedom using on-chip sources in silicon, such as frequency entanglement [45, 109,110,111,112,113], time-bin entanglement [46, 114], polarisation entanglement [115] and transverse-mode entanglement [41].

The increase in the complexity of linear-optical circuits has opened the possibility to perform on-chip probabilistic post-selected entangling gates in silicon quantum photonics. A six-mode circuit embedding a post-selected controlled-NOT entangling operation was demonstrated using the device in Fig. 11.8c to add arbitrary tunability to the two-photon entanglement generated and processed on-chip [108]. A more general circuit was reported in the silicon device used in  [100, 105, 106] (see Fig. 11.7a for a photo of the chip, and Fig. 11.8d for a circuit schematic), which was able to perform on-chip arbitrary and reconfigurable controlled operations between two qubits. Using such a circuit, a number of proof-of-principle implementations of novel quantum algorithms were demonstrated on this device, such as the quantum simulation of small chemical systems via witness-assisted variational quantum algorithms (see Fig. 11.8e) [105] and via Bayesian approaches to quantum phase estimation [100], and quantum Hamiltonian learning techniques for the efficient characterisation of quantum systems [106]. A fully programmable two-qubit silicon photonic quantum processor able to implement universal two-qubit quantum operations was demonstrated in 2018 using the large-scale circuit shown in Fig. 11.8f [107]. High-precision performance of arbitrary two-qubit operations was demonstrated with this device (see Fig. 11.8g), which was also used to perform some small-scale quantum algorithms, such as the quantum approximate optimisation algorithms [116] and the simulation of Szegedy quantum walks [117].

While the silicon photonic quantum processors described so far display a remarkable increase in the circuit complexity, they are limited to two-qubit generation and processing. Generating multiphoton entanglement adds important difficulties compared to the two-photon case due to the need of probabilistic multiphoton entangling gates, a significant decrease in the SFWM-based generation rate for four or more photons compared to the two-photon case, and the appearances of noise effects, such as single-photon spectral impurities, which are not significant in two-photon experiments. Thanks to the development of lower-loss silicon components, the last two years have seen a remarkable increase in the number of qubits and photons in silicon quantum photonics (see Fig. 11.7). The first multiphoton experiments with four photons generated and processed on silicon chips have been reported in 2018 [49, 101]. The current state of the art is silicon quantum photonics experiments with up to eight photons [33] (see Fig. 11.7e) and eight qubits (see Fig. 11.7f) [34], as described in the following sections.

Fig. 11.9

a Circuit schematic for the generation and measurement of high-dimensional photonic entanglement on a reconfigurable large-scale silicon quantum photonic device. b Entangled states of two qubits of local dimension 12 reconstructed on the silicon chip via quantum state tomography. Images from  [5]

4.2 High-Dimensional Quantum Entanglement in Silicon

Recent experiments have exploited the capability of silicon photonics to integrate extremely complex circuits to enlarge the quantum information processing capability for quantum devices with limited number of photons, via the use of high-dimensional quantum systems. In particular, the device in Fig. 11.7c was used to demonstrate the on-chip generation and processing of high-dimensional entanglement between a pair of photons [5]. Qudits, with local dimensionality up to 16, were encoded in the paths of each photon, as described in Fig. 11.1, and maximally entangled states were generated via the coherent pumping of multiple SFWM waveguide sources. The large-scale reconfigurable silicon circuit used, which embedded more than 500 optical components (see Fig. 11.9a), was demonstrated to be able to process the high-dimensional photonic entanglement with very high precision, with the reconstructed entangled states showing unprecedented quality for high-dimensional entangled systems. The reconstructed entangled state for a pair of two qudits in dimension 12 is shown Fig. 11.9b.

Although silicon quantum photonics can enhance the complexity of current photonic quantum processors, increasing the photon number is ultimately required to build up scalable quantum photonics devices. Nevertheless, the resource savings it enables are of potential interest for both near-term applications on prefault-tolerant quantum devices and more efficient large-scale architectures. In a recent silicon quantum photonic experiment, Vigliar et al. have demonstrated such resource savings for the generation of quantum states of up to eight qubits by using four photons, each one encoding two qubits in its four-dimensional Hilbert space [34]. The silicon device, shown in Fig. 11.10a, used a circuit where eight SFWM sources were pumped to generate four photons in two pairs of maximally entangled ququarts (four-dimensional qudits). Using the circuit schematised in Fig. 11.10b, post-selected fusion operations were used two perform entangling gates between the two pairs of qudits, generating a multiphoton high-dimensional entangled states (see Fig. 11.10c). Such four-photon state was able to encode the equivalent of up to eight qubits. By reconfiguring the photonic circuit, the device was able to explore a wide range of entanglement classes, so-called graph states, as shown in Fig. 11.10d.

Fig. 11.10

a Silicon chip embedding the photonic circuit in b for the generation and processing of eight-qubit entangled states via the use of multiphoton high-dimensional entanglement. c Reconstructed entangled state of the four photons, with each photon representing a four-dimensional qudit. d Fidelities for different classes of entangled graph states of up to eight qubits that can be generated reconfiguring the circuit in (b)

4.3 Measurement-Based Quantum Computing in Silicon Quantum Photonics

The generation of highly entangled multiphoton states represents the fundamental resource for measurement-based quantum computation (MBQC), the most relevant quantum computing paradigm for quantum photonics [14, 15, 23]. The scale reached with current silicon quantum photonic devices enables the implementation of simple MBQC protocols fully on-chip. A proof-of-principle MBQC implementation in integrated quantum photonics was firstly reported using a laser-written glass device passively operating a four-qubit state, demonstrating an MBQC implementation of the Grover search algorithm for a four-bin register [118, 119]. The eight-qubit silicon quantum processor shown in Fig. 11.10 demonstrated more complex MBQC protocols on-chip, demonstrating also the embedding of simple quantum error-correcting codes in the measurement-based quantum model [34]. In particular, MBQC operations were implemented using graph states formed of both logical (error-corrected) qubits as well as physical (non-error-corrected). For various single-qubit MBQC operations, increased fidelities were observed when adopting error-protected codes. Such improvements resulted in a significant performance enhancement in the MBQC implementation of the quantum phase estimation algorithm.

4.4 Networking Silicon Quantum Devices

One of the most important advantages of quantum photonics compared to other quantum platforms is the capability of photons to travel long distances and efficiently interconnect different and distant processors. In silicon quantum photonics, this capability has enabled a number of demonstrations for integrated systems for quantum key distribution with weak-coherent states of light, which can greatly leverage on silicon components developed for classical communications [120,121,122]. The chip-to-chip distribution of quantum entanglement is a key task in networking quantum processors, with prospects for the development of modular quantum computing architectures [123, 124] and the quantum internet [125]. The first entanglement distribution between two silicon quantum photonic devices was achieved in 2016, where a path-encoded qubit from an entangled pair was converted into a polarisation qubit via a two-dimensional grating coupler, and sent via a fibre to a second chip to convert it back to path and measure the entanglement [126]. Quantum teleportation between two silicon chips has also been recently demonstrated using the devices schematised in Fig. 11.11a [51]. A qubit from an entangled photon pair was distributed from a silicon Chip A to a second chip B via a path-polarisation interconversion and a fibre link. The state of a third heralded photon in chip A was then teleported to the photon in Chip B via a Bell measurement on the two photons left on Chip A. The teleported states, shown in Fig. 11.11b for few exemplary states, achieved fidelities of approximately $90\%$.

Fig. 11.11

a Schematic of silicon photonic devices used to perform chip-to-chip quantum teleportation. Two pairs of photons are generated on Chip A. A photon from an entangled pair is sent to Chip B via path-polarisation interconversion which allows to transmit the qubit via a 10m-long optical fibre. A post-selected Bell measurement between two photons on Chip A performs the single-qubit quantum state teleportation from Chip A to Chip B, and the circuit on chip is used to characterise the teleported state. b Reconstruction of the teleported states on Chip B for some exemplary one-qubit states. Images from  [51]

5 Applications for Near-Term Photonic Quantum Processors

In previous sections, we discussed how silicon quantum photonics enables a scalable approach to build large-scale photonic quantum processors, with hundreds of quantum optical components linked together in optically stable interferometers. However, a crucial challenge in photonics is to increase the number of quantum information carries, i.e. photons, that can be processed in such large circuits. In fact, the number of photons is a key parameter to determine the computational complexity of the photonic quantum computation performed. However, optical loss in integrated components, as well as non-deterministic photon generation and entangling operations, suppress the computation rate exponentially when increasing the photon number on preloss-tolerant devices. This renders the efficient scaling of photonic architectures challenging. Note that these errors are unique to quantum photonics, as in other quantum platforms (solid-state qubits, superconducting circuits, trapped ions, etc.) the possibility that a quantum information carrier disappears is typically negligible. Fault-tolerant architectures, as the ones mentioned in Sect. 11.2, are tolerant to photon loss and key to enable scalable photonic quantum hardware [15, 19]. However, the highly demanding overheads required for fault-tolerance will necessitate considerable technological progress before making such scalable and universal photonic quantum machines accessible.

A nearer-term goal is the development of non-universal machines that perform specialised algorithms on non-fault-tolerant quantum machines [24, 26]. We will here focus on boson sampling [26, 127], a promising approach for such special purpose quantum photonic devices, describing different boson sampling protocols and reviewing recent implementations in silicon photonics and possible applications.

5.1 Boson Sampling Machines

Fault-tolerant quantum computation is well beyond current quantum technologies. On the other hand, there are already quantum systems currently accessible, e.g. ultra-cold atomic systems, that allow some degree of control and whose behaviour seems to be intractable to simulate on classical machines [128,129,130]. It is, however, difficult to interpret these systems in terms of computational machines, i.e. with some well-specified inputs and outputs, as well as to theoretically assess the classical computational complexity for their simulation.

Boson sampling has been proposed by Aaronson and Arkiphov as an intermediate situation: a well-defined computational model that is provably intractable on classical machines but realistic using near-term experimental capabilities [26]. The use of sampling protocols inspired by boson sampling has recently enabled the groundbreaking demonstration of the first quantum computational advantage, obtained by Google in the superconducting qubits platform [130]. The boson sampling computational model is pictured in Fig. 11.12 and can be schematised as follows.

• Inputs: an initial multimode photonic state $\left| {\psi } \right\rangle$ and a linear-optical network with m input modes and m output modes, described by a $m \times m$ unitary transformation U randomly sampled from the Haar random distribution.

• Experiment: The input state $\left| {\psi } \right\rangle$ is propagated through the linear-optical circuit U and single-photon detection is performed on the evolved state, using m detectors on the output modes. (Here, we will focus on single-photon detection, although the protocol can be further generalised to include Gaussian measurements as well [131]).

• Outputs: the observed n-photon coincidence pattern at the single-photon detectors.

The computational model is a sampling problem: given the input state and the unitary transformation, the experimenter is required to sample measurement outcomes from the resulting output distribution of the detection patterns. Clearly, this model is quite simple from a technological point of view; no feed-forward, optical nonlinearity or adaptivity is required, making boson sampling machines much more realistic than fault-tolerant quantum hardware for near-term experiments. Still, it has been demonstrated to be intractable to simulate, even approximately, on classical computers if the number of photons is large enough ($n \gtrsim 50$ photons) [26, 132, 133]. The price to pay is universality: the boson sampling computational model is strongly believed to be non-universal.

In recent years, a range of boson sampling variants has been developed and implemented [8, 134,135,136,137,138,139,140,141,142,143] to enhance the scalability in practical devices and open a wider set of applications, with the main difference being the input photonic state $\left| {\psi } \right\rangle$. Here, we discuss three of the main protocols.

Fig. 11.12

Schematic representation of the boson sampling computational problem

Fig. 11.13

a Schematic representation of the standard boson sampling protocol, where n photons are prepared in the configuration $\boldsymbol{j}$ and injected into a $m\times m$ interferometer described by the unitary transformation U. The detection pattern $\boldsymbol{k}$ is recorded at the output of the interferometer. b Schematic of scattershot boson sampling. Weak TMS states are generated and separated. The n-photon configuration $\boldsymbol{j}$ injected into the interferometer is now random but heralded upon detection of the idlers modes (blue modes). c Schematic of Gaussian boson sampling, where the single photons at the input are replaced with SMS states

5.1.1 Standard Boson Sampling

In its original proposal [26], boson sampling assumed as input state $\left| {\psi } \right\rangle$ a Fock state of n photons in n different modes, as schematised in Fig. 11.13a. Considering the case where the n photons are injected in modes $\mathbf {j}=\{ j_1, j_2, \ldots , j_n\}$ of a $m \times m$ linear interferometer described by a transfer unitary matrix U, the probability of obtaining an n-photon detection pattern $\mathbf {k}=\{k_1,k_2,\ldots ,k_n\}$ is given by [144]

$$\begin{aligned} p_U (\mathbf {k}|\mathbf {j})= \frac{1}{\Big [\prod _{i=1}^m s(\boldsymbol{j})_i! \Big ] \Big [\prod _{i=1}^m s(\boldsymbol{k})_i! \Big ]} \big |\text {Perm}\left( U_{\boldsymbol{j},\boldsymbol{k}} \right) \big |^2. \end{aligned}$$

(11.8)

Here, $s(\boldsymbol{j})$ and $s(\boldsymbol{k})$ represent the mode occupancies for the two configurations, i.e. $s(\boldsymbol{k})_i$ indicated how many photons are present in the i-th mode for the configuration $\boldsymbol{k}$. The matrix $U_{\mathbf {j},\mathbf {k}}$ is the submatrix of U obtained by taking its rows and columns associated with $\mathbf {k}$ and $\mathbf {j}$, respectively [144], and $\text {Perm}(\cdot )$ is the matrix permanent function.

Aaronson and Arkiphov showed that, under mild conjectures, approximate sampling of output states $\mathbf {k}$ from the distribution $p_U (\mathbf {k}|\mathbf {j})$ is intractable on classical machines for large values of n [26]. Current estimates predict that $n\approx 50$ are required to enter a regime where a classical simulation of boson sampling would no longer be possible on supercomputers [132]. However, non-deterministic photon sources and losses limit the scalability of this approach. In fact, if n sources with an efficiency $\epsilon$ are used to produce the n-photon input Fock state in the standard boson sampling configuration, the probability of generating such state is thus $p_{\text{ B }S}(n)=\epsilon ^n$. Therefore, if the sources are non-deterministic ($0\le \epsilon <1$), the experimenter would need to wait an exponentially long time before observing an n-photon event. Although significant progress has been achieved in high-efficiency solid-state single-photon emitters, this issue has so far limited current implementations of standard boson sampling to systems with less than 15 photons [143].

5.1.2 Scattershot Boson Sampling

The scattershot approach to boson sampling, developed by Lund et al. few years after the original boson sampling proposal [145], represents a way to increase the complexity of photonic experiments with probabilistic sources based on spontaneous parametric processes, such as SFWM-based sources in silicon waveguides. The protocol is represented in Fig. 11.13b. To perform n-photon boson sampling, $m_0\ge n$ parametric sources are used, each generating a TMS state (see  11.3). The total state is then a product of TMS states produced from the array of sources:

$$\begin{aligned} \left| {\psi } \right\rangle =\bigotimes _{j=1}^{m_0} \left| {\text {TMS}(\xi )} \right\rangle _j, \end{aligned}$$

(11.9)

where the two-mode squeezing parameter $\xi$ is for simplicity considered uniform across the sources. Half of each TMS, i.e. the idler modes, are sent directly to a photon counter, while the other $m_0\le m$ signal modes are injected into an $m\times m$ interferometer described by U. Due to the perfect correlations of the photon number in TMS states, the photon state $\mathbf {j}$ injected into the interferometer corresponds directly to the pattern measured at the idler modes, and a standard boson sampling scenario is thus recovered. Note, however, that now the input state is random but, crucially, heralded. In particular, an n-photon input state is generated whenever n out of the $m_0$ probabilistic sources fire, which provides a combinatorial enhancement with respect to the standard boson sampling case. In fact, the probability to generate an n-photon input state is now given by [145]:

$$\begin{aligned} p_{\text{ S }BS}(n)=\left( {\begin{array}{c}m_0\\ n\end{array}}\right) \epsilon ^n (1-\epsilon )^{m_0} \end{aligned}$$

(11.10)

where $\epsilon = |\tanh (\xi )|^2$ is the photon-pair emission probabilities for each TMS source (in the low-squeezing regime). Considering $m_0=n^2$, such combinatorial enhancement can now provide a polynomial n-photon generation probability scaling as $p_{\text{ S }BS} \propto 1/ \sqrt{n}$, even if the efficiency $\epsilon$ of each source is very low. In contrast to standard boson sampling, the scattershot approach enables an efficient scaling also in presence of probabilistic sources, at the cost of increasing the number of sources and detectors used [138]. It is therefore well-suited for integrated photonics approaches, and in particular silicon quantum photonics, where large arrays of probabilistic sources and detectors are accessible [5, 86].

5.1.3 Gaussian Boson Sampling

In scattershot boson sampling, the squeezed states from the sources is collapsed to single-photon states before the interference by measuring the idler modes. Gaussian boson sampling is instead another variant of boson sampling where such collapse happens only after the interference [146, 147]. As schematised in Fig. 11.13c, $m_0$ SMS states, generated for example, via degenerate SFWM in silicon waveguides (see  11.2), are directly injected in the interferometer, followed by single-photon detection at the output. In this situation, the input photon configuration is a coherent superposition of many different possible Fock states, and the probability to detect an output pattern $\boldsymbol{k}$ is given by [147]:

$$\begin{aligned} p_{\boldsymbol{\xi }}(\mathbf {k})=\frac{1}{\Big [\prod _{i=1}^m s(\boldsymbol{k})_i! \Big ]\sqrt{\det (\boldsymbol{\sigma }_Q)}}\big |\text {Haf}\left[ B_\mathbf {k}(\boldsymbol{\xi })\right] \big |^2, \end{aligned}$$

(11.11)

where

$$\begin{aligned} B(\boldsymbol{\xi })=U \left( \bigoplus _{i=1}^m \tanh (\xi _i) \right) U^\top , \end{aligned}$$

(11.12)

with $\xi _i$ the SMS parameter of the ith source, and $B_\mathbf {k}$ the submatrix obtained from the rows and columns $\{k_1,k_2,\ldots ,k_n\}$ of B [147]. The functions $\det (\cdot )$ and $\text {Haf}(\cdot )$ are, respectively, the determinant and the Hafnian of a matrix [148], while ${\sigma }_Q = \sigma + {\mathbbm {1}}$ and $\sigma$ is the total covariance matrix of the input SMS states [149, 150]. Also, for Gaussian boson sampling, the probability to detect n photons at the output is combinatorially enhanced [147]:

$$\begin{aligned} p_{\text{ G }BS}(n)=\left( {\begin{array}{c}n + m_0/2 -1\\ n\end{array}}\right) \epsilon ^{n} (1-\epsilon )^{m_0/2}, \end{aligned}$$

(11.13)

which, for $m_0=n^2$ scales as $p_{\text{ G }BS}\propto 1/\sqrt{n}$ similarly to scattershot (with an asymptotic additional speed-up by a constant factor of $e\simeq 2.71$) [147]. In addition, Gaussian boson sampling is also more resource efficient compared to scattershot, for instance, because no auxiliary detectors are required for heralding. However, as the computation time for the calculation of a permanent and a Hafnian of a $n\times n$ matrix are $\mathcal {O}(n 2^n)$ and $\mathcal {O}(n2^{n/2})$ respectively [151], it is expected that 2n photons are required for a Gaussian boson sampling protocol to achieve a classical run time comparable with a n photon standard boson sampling experiment [146, 147].

5.2 Scaling Boson Sampling with Silicon Quantum Photonics

Achieving a regime of quantum computational advantage with boson sampling requires a photonic platform able to generate and process states with tens of photons in hundreds of modes. While significant improvements in quantum dot sources interfaced with low-loss passive interferometers (generally based on bulk optics) have enabled experiments with up to 14 detected photons [139,140,141, 143], reconfigurable integrated quantum photonics circuitry will be required for practical applications at scale. Although a number of the initial boson sampling demonstrations have been performed via integrated laser-written interferometers in glass chips, they relied on bulk photon sources and were limited to less than 6 photons, presenting significant scaling challenges [8, 135,136,137,138, 142, 152,153,154].

Fig. 11.14

a Schematic of the silicon boson sampling device. Four integrated SFWM sources are used for photon generation, and two layers of asymmetric MZI interferometers are used to filter out the pump light from the photons and to separate the idler and signal photons. A 12-mode unitary transformation is implemented via a low-loss random walk, obtained by coupling together 12 waveguides of length $\sim 110~\upmu {\text{ m }}$, to interfere the signal photons. Finally, photons are fibre-coupled off-chip via low-loss grating couplers [95] ($\sim 1$dB loss) and detected off-chip. b Optical microscope image of the silicon photonic circuit. c Pumping schemes used to generate SMS and TMS states via degenerate and non-degenerate SFWM, respectively. The generated TMS (SMS) states are used to implement scattershot (Gaussian) boson sampling within the same silicon quantum photonic device

5.2.1 Implementing Boson Sampling in Silicon Quantum Photonics

Silicon quantum photonics, enabling the integration of large arrays of high-quality sources [5, 37] and large-scale reconfigurable interferometers [5, 11, 34, 107], offers a promising photonic platform to scale up boson sampling experiments. Recently, the first boson sampling experiment with fully on-chip photon generation and processing (off-chip detection) was reported in a silicon quantum photonic device, where up to 8-photon states were operated to perform scattershot and Gaussian boson sampling [33]. The device used is schematised in Fig. 11.14a and the silicon circuit is shown in Fig. 11.14b. The device consisted of four SFWM sources, reconfigurable asymmetric-MZI-based filters to reject the pump and separate the idler and signal photons, a 12-mode low-loss random walk interferometer and low-loss grating couplers [95] to couple photons off-chip and send them to high-efficiency ( $90\%$) off-chip SNSPDs. To implement different boson sampling protocols, the sources were operated in two different regimes, as shown in Fig. 11.14b. In the first regime, they were pumped using a single-wavelength laser in order to generate weak TMS states via non-degenerate SFWM. In this case, signal and idler photons are emitted at different wavelengths. In the second regime, a dual-wavelength pumping scheme was used to generate weak SMS states via degenerate SFWM. In this second case, all photons are emitted at the signal frequency. The first pumping regime allows scattershot boson sampling, based on TMS states, while the second implements Gaussian boson sampling, based on SMS states. The switching between the two different regimes can be performed within the same chip, by reprogramming the nonlinear effect operated in the sources (degenerate or non-degenerate SFWM) via the choice of the pumping scheme.

Thanks to the low-loss silicon photonic components used in the device, up to 8 photons were generated and processed in the scattershot regime (4 heralded signal photons), the current record in integrated quantum photonics, although at low 8-photon event rates (few per hour). Experimental results for scattershot and Gaussian boson sampling implementations are reported in Fig. 11.15a, b, respectively, where the observed input/output probability distributions are shown to be consistent with the theoretical expectations.

Recently, another boson sampling experiment was reported in the silicon platform, where a bright off-chip source of squeezing was coupled into a passive silicon circuit to perform quantum interference of up to 5 photons [155].

Fig. 11.15

a Input/output scattershot boson sampling experimental and theoretical distributions for six-photon events (three heralded signal photons). b Output Gaussian boson sampling experimental and theoretical distributions for four-photon events. c Optimal event rate (top) and associated circuit size (bottom) estimated for different numbers of signal photons in the scattershot (red) and Gaussian (blue) boson sampling regimes. Shaded areas represent impractical experiments, where the threshold is set to be 1 event/week

5.2.2 Scaling with Near-Term Silicon Devices

While the device discussed above provides an architecture for implementing various boson sampling protocols in silicon quantum photonics, the scale of the protocols implemented is still small, meaning that they can be easily simulated on classical computers. However, we can investigate how the computational complexity of the protocols implementable with such architecture scale when increasing the size of the silicon photon circuits. To represent the capability of near-term silicon quantum photonic devices, we consider low-loss components as those implemented and characterised in the chip of Fig. 11.14a [33], high-quality SFWM sources as in Fig. 11.6 [37], and arrays of integrated SNSPDs [86]. The protocols we consider are scattershot and Gaussian boson sampling. In terms of N-photon event rates, the combinatorial enhancement obtained in both protocols when increasing the number of sources (and modes) is compensated by the additional losses obtained when increasing the depth of the interferometer [33]. A trade-off between these two effects is required to achieve high rates. The optimal circuit size and rates with the device parameters described above are shown in Fig. 11.15c for different photon numbers and for both scattershot and Gaussian boson sampling. It can be observed that experiments at a scale of up to $\approx$70 signal photons are estimated to be possible with Gaussian boson sampling, and of $\approx$50 signal photons for scattershot. These values are expected to be at the limit of what is tractable with classical supercomputers [132]. Note that the circuits require hundreds of sources, modes in the interferometer, and detectors; a scale impractical for bulk optical experiments.

To further increase the complexity, e.g. to target experiments with hundreds of photons, significant technological progress is required. A first improvement would be to develop materials with lower transmission losses and more efficient sources of squeezed light. In this direction, promising alternatives are being investigated in the SiN, LiN, LNOI and LiNbO$_3$ integrated photonic platforms [60,61,62,63, 66, 156, 157].

5.3 Quantum Simulation via Boson Sampling

While boson sampling is an interesting quantum computing model to reach quantum advantages with photonics, the task of sampling the output photons from a random interferometer is a specialised problem with no direct application. However, in recent years, a wide number of applications, from quantum chemistry to graph theory problems, have been shown to be solvable on boson sampling machines, with potential prospects to achieve quantum speed ups in industrially relevant applications with boson sampling. We describe some of these applications, with special focus on molecular quantum chemistry simulations.

Fig. 11.16

a Example of a molecular potential energy surface and its harmonic approximation. b Representation of the normal (top) and localised (bottom) vibrational modes in the H$_2$CS (Thioformaldehyde) molecule. The change of basis between the localised and normal modes is performed via the unitary matrix $U^L$. c Mapping of the quantum evolution of the localised vibrational modes into a reconfigurable boson sampling machines. Such a machine can be implemented and scaled up using universal integrated quantum photonics circuits. d Example of experimentally simulated quantum dynamics in the H$_2$CS (Thioformaldehyde) molecule, reported in  [158]

5.3.1 Simulation of Molecular Quantum Dynamics

The reason why complex quantum chemical systems are intractable on classical machines was described by Dirac already in the early days of quantum mechanics [159], namely he noted that the wavefunction of a quantum system grows exponentially with the number of particles, making classical computers unable to exactly simulate quantum systems in an efficient way. This problem led Feynman in 1982 to propose the development of controllable quantum hardware for efficient simulation of complex chemical systems [160]. Quantum chemistry can thus be considered as the original motivation that led to the field of quantum computing in the first place.

The particular system we here focus on are vibrational quantum molecular dynamics. Quantum vibrations in molecules, due to atomic oscillations perturbing a stable molecular configuration, are important, for example, in the study and design of efficient molecular dissociation pathways [161,162,163]. However, evolving a multiexcitation state across many vibrational modes is computationally inefficient on classical computers even for the basic models based on independent quantum harmonic oscillators. The general idea to map such systems into boson sampling machines is to map the evolution of the bosonic vibrational modes (phonons) to the evolution of bosonic excitations of the electromagnetic field (photons) in optical interferometers.

In more detail, vibrational dynamics in a molecule are essentially small oscillations of the nuclei around a local minimum in the potential energy surface of the molecule. The energy surface depends on the electronic structure of the molecule and the nuclear positions, but, in the Born–Oppenheimer approximation, it is independent from the vibrational state of the molecule. For a general molecule with N atoms the energy surface lives in a $3N - 6$ space ($3N-5$ for linear molecules), so that $3N-6$ vibrational modes are possible. In the harmonic approximation, a quadratic form is assumed for the potential energy surface near the stable configuration (see Fig. 11.16a), and $3N-6$ independent normal vibrational modes can be defined (see Fig. 11.16b, top panel), with associated bosonic creation operations $\hat{a}^\dagger _i$ and normal frequencies $\{ \omega _i\}$. Another set of vibrational modes that are of practical interest are the so-called localised modes, described by bosonic creation operations $\hat{b}^\dagger _i$. These are modes where the vibrational energy is spatially localised on single atoms of the molecule, as shown in Fig. 11.16b bottom panel. Localised modes are of practical importance for understanding many molecular phenomena, such as energy transport and dissociation, and single excitations of these modes can be prepared in quantum chemistry experiments [164]. We therefore focus on simulating quantum dynamics of molecules prepared and measured in localised modes. To describe the dynamics of localised modes, it is convenient to define the basis transformation between the normal and localised modes, given by unitary matrix $U_L$ such that

$$\begin{aligned} {\hat{a}_\ell }^\dagger \mapsto \sum _{k=1}^{3N-6} U_{L_{k,\ell }} {\hat{b}_k}^\dagger . \end{aligned}$$

(11.14)

The unitary evolution U(t) of the localised modes can then be obtained by converting them into the normal modes, which in the harmonic approximation are independent and evolve according to $\oplus _\ell e^{-i w_\ell t/ \hbar }$, and then convert back into the localised modes basis (see Fig. 11.16c):

$$\begin{aligned} U(t)={U_L} \left( \bigoplus _\ell e^{-i w_\ell t/ \hbar } \right) {U_L}^\dagger . \end{aligned}$$

(11.15)

Due to the analogy between bosonic vibrational modes and photons, the ingredients described so far can be mapped into a photonic scenario in the following way [158]:

• Vibrational modes $\leftrightarrow$ Optical modes.

• Vibrational mode $\ell$ initialised with n excitations $\leftrightarrow$ Optical mode $\ell$ initialised with n photons.

• Evolution of the molecular vibrations described by U(t) $\leftrightarrow$ Evolution of the photons in a linear interferometer described by U(t).

• Measurement of the final vibrational configuration $\leftrightarrow$ Photon number detection at the output of the interferometer.

The experimental scenarios described above can be directly mapped into boson sampling machines: photons need to be prepared in an input state that matches the initial vibrational state of the molecule, and output configurations are sampled after the evolution according to U(t) implemented via a reconfigurable integrated interferometer (see Fig. 11.16c). Standard boson sampling corresponds to the case where the molecular state is initialised in Fock vibrational states, i.e. with a fixed number of excitations, while if molecules are prepared in squeezed states (or other Gaussian states) the simulation is mapped into Gaussian boson sampling.

Integrated quantum photonics is a very promising platform to implement these simulations and scale them up into computationally interesting regimes. The first photonic quantum simulation of molecular quantum dynamics was implemented using a fully reconfigurable 6-mode integrated interferometer on a silica chip [8, 158]. In this experiment, the molecular quantum dynamics for a wide range of molecules were simulated with up to four photons (see Fig. 11.16d for an example), both in the harmonic approximation and in the anharmonic regime. A proof-of-principle demonstration of how these simulators could be used for the design of more efficient molecular dissociation processes was also reported [158]. The scalability of the silica photonic platform used was, however, limited due to the large footprint of the silica device and the use of bulk off-chip sources. As discussed above, silicon quantum photonics has huge potential to overcome such limitations.

Fig. 11.17

a Simplified schematic of a vibronic transition. The molecule is initially in an electronic configuration with normal vibrational modes (in the harmonic approximation) $\boldsymbol{q}$ associated with the energy surface. When a process, e.g. photon absorption, induces a change in the electronic structure, the energy surface is modified, defining a new set of normal vibrational modes $\boldsymbol{q}'$. In the Franck-Condon approximation, the transformation between the two sets of vibrational modes is given by a linear mapping $\mathcal {U}_\text {Dok}$. b Schematic of the photonic circuit required for the calculation of Franck-Condon profiles. c Reconstructed Franck-Condon profile for a synthetic molecule with the silicon quantum photonic boson sampling device in Fig. 11.14

5.3.2 Calculation of Molecular Franck-Condon Profiles

A different quantum chemistry problem that can be mapped to boson sampling is the calculation of molecular vibronic (vibrational and electronic) spectra, known as Franck–Condon profiles. While the molecular vibrations discussed in the previous section considered fixed potential energy surfaces, vibronic transitions represent the transition from an initial set of vibrational modes to a new set of vibrational modes that arise when the potential energy surface is modified following a modification in the electronic structure (see Fig. 11.17a). While the spectra for such transitions, i.e. the Franck–Condon profiles, are useful to investigate chemical properties of the molecules, such as their performance as solar cells [165] or as dyes [166], their prediction using classical approaches is computationally challenging already for molecules of modest size [167,168,169]. On the other hand, Huh et al. have shown how such calculations can be implemented on a variant of Gaussian boson sampling [170].

The mapping makes use of the Doktorov transformation to describe the transition of the molecular vibrational operators $\hat{a}^\dagger _i$ [171] in vibronic processes, given by the operator

$$\begin{aligned} \mathcal {U}_\text {Dok}=\mathcal {U}_\text {L}\left[ \otimes _{i=1}^m\mathcal {S}(\xi _i)\right] \mathcal {U}_\text {R}^\dagger \left[ \otimes _{i=1}^m\mathcal {D}(\alpha _i)\right] , \end{aligned}$$

(11.16)

where $\mathcal {D}(\alpha _{i})$ represents single-mode displacement operators with amplitudes $\alpha _i$, $\mathcal {S}(\xi _i)$ represents a single-mode squeezing operator with squeezing parameter $\xi _i$, and $\mathcal {U}_\text {R}$ and $\mathcal {U}_\text {L}$ are unitary evolutions. If we consider for simplicity the molecule to be initially at zero-temperature (i.e. the initial vibrational state of the molecule in the vacuum state), the Franck–Condon probability for a vibronic transition to a final vibrational configuration $|\boldsymbol{k}\rangle$ is then given by [172, 173]

$$\begin{aligned} p_\text {FC}(\boldsymbol{k})=|\langle \boldsymbol{k}|\mathcal {U}_\text {Dok}|{0 \ldots 0}\rangle |^2. \end{aligned}$$

(11.17)

Because, as for the simulation of molecular quantum dynamics, the vibrational operators $\hat{a}^\dagger _i$ have direct analogy to photonic operators, the vibronic transformation in  11.16 is analogous to the optical circuit shown in Fig. 11.17b, with the Franck–Condon probabilities $p_\text {FC}(\boldsymbol{k})$ corresponding to the probability to detect the photon configuration $\left| {\boldsymbol{k}} \right\rangle$ at the output.

Note that the circuit required to calculate Franck–Condon probabilities is a Gaussian boson sampling circuit (boxed in Fig. 11.17b), with the addition of coherent states and a first unitary transformation $U_{\text{ R }}$. In practice, such additional resource implies weak laser light injected in the signal modes of the interferometer, which is easy to implement. If the particular molecule under study does not require displacement, the quantum simulation circuit reduces exactly to a Gaussian boson sampling machine [174].

Proof-of-principle demonstrations of the quantum simulation of Franck–Condon profiles via Gaussian boson sampling have been recently reported in a variety of platforms, including fibre-optical set-ups [174], trapped ions [175], superconducting cavities [176], as well as in the silicon quantum photonic processor discussed in Sect. 11.5.2.1 [33]. A Franck–Condon profile experimentally reconstructed on the silicon quantum photonic processor is shown in Fig. 11.17c. In this case, because the interferometer in the chip is not reconfigurable (see schematic in Fig. 11.14a), the calculation was performed for a synthetic molecule associated with the passive circuit used, and with no displacement. Reconfigurable large-scale silicon quantum photonic circuits, such as those reported in Sect. 11.4, are promising to scale this implementation to larger applications, and recent ring-based schemes can be used to reduce computational errors arising from noises in the on-chip SFWM single-mode squeezers [63, 66].

5.3.3 Other Boson Sampling Applications

Apart from the quantum simulations applications already discussed, boson sampling has been recently mapped also to other types of problems, including the simulation of spin Hamiltonians [177], molecular docking [178], the enhancement of classical optimisation heuristics [179], certain graph theory calculations [180, 181] and quantum identification and cryptography protocols [182]. This wide portfolio of different near-term applications for reconfigurable photonic devices represents a valuable motivation for the development of large-scale integrated boson sampling photonic hardware.

6 Outlook

While the mature fabrication tools of the silicon industry have enabled a series of demonstrations of photonic quantum processors with successively more complex circuitry, a powerful general purpose quantum computer remains a highly ambitious goal. As with all current proposals for quantum computing hardware, a number of challenges must be overcome before silicon photonics can support quantum computing at scale. These challenges include filtering strong pump light and full system integration with SNSPDs, developing fast low-loss switches for photonic feed-forward operations, improving the quality of spontaneous photon sources, decreasing photon loss, and enhancing the success probability for probabilistic entangling gates.

The technological journey to general purpose quantum computing is perhaps foreshadowed by that of experimentally demonstrating a Bose–Einstein condensate. Also, a quantum state of matter, seventy years elapsed between its prediction, made in 1925, and its experimental demonstration in 1995. Feynman famously proposed quantum computers in 1982, and a similar 70 year development would mean we have just over thirty years to wait for a general purpose quantum computer, at time of writing.