Neuromorphic Silicon Photonics for Artificial Intelligence

Abstract

Recent investigations in neuromorphic photonics, i.e. neuromorphic architectures on photonics platforms, have garnered much interest to enable high-bandwidth, low-latency, low-energy applications of neural networks in machine learning and neuromorphic computing. Although electronics can match biological time scales and exceed them, they eventually reach bandwidth limitations. Neuromorphic photonics exploits the advantages of optical electronics, including the ease of analog processing, and fully parallelism achieved by busing multiple signals on a single waveguide at the speed of light. In this chapter, we summarize silicon photonic on-chip neural network architectures that have been widely investigated from different approaches that can be grouped into three categories: (1) reservoir computing; reconfigurable architectures based on (2) Mach-Zehnder interferometers, and (3) ring-resonators. Our scope is limited to their forward propagation, and includes potential on-chip machine learning tasks and efficiency analyses of the proposed architectures.

1 Introduction

In the past few years, analog computing has gained important attention due to hardware acceleration-related milestones. Analog hardware has been known as a way to perform efficient operations—since those operations are embedded in the hardware itself. Each analog system can only implement operations for which it has been built. Therefore, the design of analog machines for specialized task acceleration can be achieved if the task can be broken down into a physical model.

In the field of artificial intelligence (AI), analog computing has been considered as a potential venue to decrease energy and time requirements to run algorithms such as deep neural networks. Analog special-purpose hardware for artificial neural networks (ANNs) would require the construction of a machine that will physically model every single individual component of such networks. This expensive demand should be fulfilled if all neurons are expected to be used in parallel—which is indeed what is required. Considering that current deep networks sizes scale up to thousands or even billions of neurons to solve complex AI related tasks, such a requisite becomes a challenge. For instance, AlexNet requires 650,000 neurons to solve ImagNet [1].

Electronics and photonic platforms are currently the most promising technologies to tackle the expensive calculations performed by deep networks. The analog electronics approach is based on space-efficient topologies such as the resistive crossbar arrays [2]. Despite the fact that passive resistive arrays have been associated with low power consumption, crossbar arrays show fundamental performance flaws when used to model large neural networks. Large crossbar arrays are associated with high energy costs and low bandwidth. Overall, the power consumption, scalability and speed can be greatly affected when working with large networks [3].

The optical platform based on silicon photonics offers high scalability, great bandwidth and less energy consumption for longer distances than its electrical counterpart. This recent expanse in the demonstration of silicon photonic structures for photonic processing belongs to the second wave of optical computing. The first wave occurred in the early 1990s, where photonic processing of optical neural networks were consider slow and bulky. In fact, optical computing never reached the market due to the bulky size of free-space optical systems and to the intensive, low-bandwidth optoelectronic processing of the time. The rejuvenation of the field was possible due to the many advances in optical processing, higher bandwidth achieved and accessible fabrication facilities. As the second wave of analog optical computing comes with important advances for hardware acceleration, this chapter will be focused on the most relevant photonic processing demonstrations. Due to their speed and energy efficiency, photonic neural networks have been widely investigated from different approaches that can be grouped into three categories: (1) reservoir computing [4,5,6,7]; reconfigurable architectures based on (2) Mach-Zehnder interferometers [8, 9], and (3) ring-resonators [10,11,12,13].

Reservoir computing successfully implements neural networks for fast information processing. Such an advantageous concept is found to be simple and implementable in hardware, however the predefined random weights of their hidden layers cannot be modified [7]. We will describe how to build and utilize a silicon photonic reservoir computer for machine learning applications. This on-chip reservoir will be trained off-line to solve an on-line classification task of isolated spoken digits based on the TI46 corpus [14].

The first reconfigurable architecture that we explore is based on meshes of tunable silicon Mach-Zehnder interferometers (MZIs) that can implement fully connected neural networks. Such architectures are known to demonstrate their versatility to perform unitary matrix operations. In particular, some arrangements of MZIs can be used to implement singular value decomposition on a given layer of an ANN. Such a process is known as a method to reduce the dimensionality of data. Therefore, if applied on each layer of any given ANN, the most computationally expensive parts of AI processing would be alleviated. Here, we will show how to use a $4\times 4$ MZI-based network to recognize 11 vowel phonemes spoken by 90 different speakers. The training of the network will be performed off-line via backpropagation and the inference stage on-line [15].

Finally, we present an architecture that can implement photonic convolutional neural networks (CNN) for image recognition. The competitive MNIST handwriting dataset [16] is used as a benchmark test for our photonic CNN. We will describe a scalable photonic architecture for parallel processing that can be achieved by using on-chip wavelength division multiplexed (WDM) techniques [11, 17], in conjunction with banks of tunable filters, i.e. photonic synapses, that implement weights on signals encoded onto multiple wavelengths. Silicon microring resonators (MRRs) cascaded in series have demonstrated fan-in and indefinite cascadability [18, 19] which make them ideal as on-chip synaptic weights with small footprint. At first, we train a standard two-layer CNN off-line, after which network parameters are uploaded to the photonic CNN. Then, the on-line inference stage is set to recognize handwritten numbers.

2 Background: Neuroscience and Computation

Digital computers are typically computing systems that perform logical and mathematical operations with high accuracy. Nowadays, such complex systems significantly outweigh human capabilities for calculation and memory. However, no-one could have imagined the extent that computers were going to reach when they were first envisioned. In 1822, the British mathematician Charles Babbage created the first mechanical computer that could work as an automatic computing machine. At the time, this architecture was known as an analytic engine which could compute several sets of numbers and made hard copies of the results. The core of this first general-purpose computer contained an arithmetic logic unit (ALU), a flow control, punch cards and integrated memory. Unfortunately, many adverse events occurred before the machine could be physically built.

It was not until mid 1930s that a general-purpose computer reached its physical form. Between 1936 and 1938, the German civil engineer Konrad Zuse created the first electromechanical binary programmable computer named Z1. Z1 was capable of executing instructions that were inputted through a punched tape that it could read. This computer also contained a control unit, integrated memory and an ALU that used floating-point logic.

During the same period of time, the British mathematician Alan Turing envisioned an architecture which followed similar principles. However, Turing went further and laid the groundwork for computational science. He defined a computing system as a machine for matching human computing capabilities. He proposed a machine that emulated a human agent following a series of logical instructions. The Turing machine manipulates symbols much as a person manipulates pencil marks on paper during arithmetical operations [20]. Turing motivated his approach by reflecting on how an ideal human computer agent would process information. He argues that human being’s information processing principles can be replicated as they are based on symbolic algorithms that are being executed by the brain. Symbolic configurations are executable mechanical procedures that can be mimicked.

Fig. 10.1

Turing machine

In fact, when Turing posed the question “can machines think?” [21], he stated that at least digital computers can follow the same fixed rules that we find in human agents. Digital computers are intended to carry out any operations which could be done by a human computer. Such rules are supplied in a book written following a well defined finite alphabet that consists in discrete strings of elements (digits), see Fig. 10.1. Although the alphabet is fixed, the book is not. The supplied book can be altered whenever it is put on to a new job. As for the previous models of computers, the Turing’s digital computer was composed of: a memory component, an executive unit that carries out all the operations involved in calculations, and a control unit to see that those instructions are obeyed correctly in the right order.

If we are to compare a human agent with a Turing machine, we would see that there are many abstractions that should be made to perform one-to-one comparisons. Such abstractions disclose that human cognitive processes are completely procedural and follow any standard logic. Assumptions of this kind attempted to be human-inspired, but in fact they ended up influencing our previous understanding of human cognitive processes. In psychology, the computational theory of intelligence was mainly based on the procedural type of abstraction introduced below. The logic theorists Newell and Simon defined intelligence as the process of specifying a goal, assessing the current situation to see how it differs from the goal, and applying a set of operations that reduce the difference [22, 23]. However, this theory has important flaws. The cognitive scientist Steven Pinker pointed out that the vast majority of human acts may not need to crank through a mathematical model or a set of well defined instructions. For instance, cognitive phenomena that include intuition and beliefs cannot be explained and these are frequently used by human agents to forecast and classify [24]. Therefore, a one-to-one mapping between human and digital computers might be a delusion. If so, what can be done from our side to match them?

Fig. 10.2

a Illustration of a brain and a biological neuron model, b action potential and c spiking waveform

2.1 Digital Versus Analog

Neuromorphic computing approaches that do not use alphabets might be more suited to mimic brain processes. The human brain is one of the most fascinating organic machines in our body composition. The human brain contains around 100 billion neurons, which interact with each other to analyze data coming from an external stimulus. Its 100 trillion set of synaptic interconnections makes the processing of large amounts of information a task that turns out to be fast and well performed. A biological neuron is a cell composed of dendrites, body, axon and synaptic terminals, see the schematic illustration in Fig. 10.2a. The dendrites carry input signals into the cell body, where this incoming information is summed to produce a single reaction. In most cases, the transmission of signals between neurons are represented by action potentials at the axon of the cell, which are changes of polarization potential of the cell membrane. The anatomic structure where the neurons communicate with each other is known as a synapse [25]. The cell membrane has a polarization potential of −70 mV at resting state, produced by an imbalanced concentration inside and outside of its charged molecules. This change of the polarization happens when several pulses arrive almost simultaneously at the cell. Then, the potential increases from −70 mV to approximately +40 mV. Some time after the perturbation, the membrane potential becomes negative again but it falls to −80 mV [2, 3]. The cell recovers gradually, and at some point the cell membrane returns to its initial potential (−70 mV), as schematically illustrated in Fig. 10.2b.

The binary nature of digital computers can also be used to mimic neural processes. The digital logic can be compared with the all-or-nothing (“1” or “0”) process of the action potential transmission. Nevertheless, the whole story is not being said. This model does not include information about the times between action potential transmissions. The frequency at which neurons spike have functional significance that cannot be dismissed. Therefore, a complete model of neural dynamics would specify the waveform that a series of spikes perform in time (see Fig. 10.2c). This phenomenon has an impact in neural information encoding. For example, the strength of a given stimulus is coded as a frequency value. The stronger the stimulus (information) to the neuron, the smaller the time between spikes [26].

If our nervous system encodes information in such a way, then a digital only representation of the neural functions is inherently incomplete. If we were forced to use it, we would find out that a waveform could be described as well using a binary alphabet, where each spike is a “1”, and each resting state is a “0” in time. For this to work, each of the waveforms constituted by a series of spikes and resting states should be identifiable and separable. This will ensure that they can be standardized and used in a “reference book” of operations that describe human cognition. A task of this kind would need an extremely large book which includes each waveform that we detect. Then, each waveform has to be connected to others in a meaningful manner in order to describe different human cognitive processes. This method could be difficult and inefficient to follow if we take into account that some neurons can also spike randomly and create random waveforms that have no meaning.

A more realistic interpretation incorporates a continuous-type model that is typically described by analog systems. This process will create a one-to-one map between the neural system and the analog machine. For this to come true, each biological quantity would be modeled by an analog quantity, i.e. a biological neuron would have its equivalent analog artificial model. For an architecture such as the brain this could be a demanding requirement. As previously introduced, the human brain contains around 100 billion neurons and 100 trillion synaptic interconnections that need to be represented in an artificial machine.

An equivalent analog machine to the brain can possibly be achieved, but we wonder at what cost. The average human brain burns 1300 calories per day in the resting state (54.16 kcal/h = 62.94 watts), which accounts for $20\%$ of the body’s energy use. For all the incommensurable amount of operations that the brain needs to perform per day, this amount of energy looks really low. Interestingly, when the brain is thinking, it can burn around 300 calories (12.5 kcal/h = 14.527 watts). As human thoughts can be used for training purposes, a brain that has training activity during e.g. four days can burn around 120 watts in total—for training only. In contrast, a digital machine playing Go such as AlphaGo (which simulates brain training process using binary logic and alphabet) can do the same while burning 50,000 times more energy in one task only [27]. A dedicated (special-purpose) analog machine per task should resolve this problem.

Fig. 10.3

a Schematic diagram of a perceptron and b ReLU function

2.2 Artificial Neural Networks

Towards the utilization of analog machines to map some of the brain circuitry, we need to define how to model the biological neurons and synapses. Among many others, the most commonly used neural models are spiking artificial neurons and perceptrons. While spiking artificial neurons are significantly more biologically realistic, the field of artificial intelligence (AI) is currently perceptron-based. Nowadays, most significant advances in AI have been achieved using a perceptron as an artificial model of the neuron, therefore in this chapter we will assume that all our artificial neuron models are perceptron-based. A perceptron is shown in its general model by Fig. 10.3a. The output y of the neuron represents the signals coming from the axon of a biological neuron, and it is mathematically described by

$$\begin{aligned} y = f(\mathbf {W} \cdot \mathbf {x} + b). \end{aligned}$$

(10.1)

The $x_{i}$ inputs transmit the information to the neuron through the weights $W_i$, which correspond to the strength of the synapses. The summation of all weighted inputs, and their transformation via activation function f, are associated with the physiological role of the neuron’s cell body. The bias b represents an extra variable that remains in the system even if the rest of the inputs are absent. The activation function can be linear or nonlinear, and it mimics the firing feature of biological neurons. A nonlinear activation function can be used to set a threshold from which to define activated and deactivated behaviors in artificial neurons. For instance, a ReLU function f (see Fig. 10.3b) mimics a spiking neuron when its weighted addition $(\mathbf {W} \cdot \mathbf {x} + b) > 0$, otherwise the neuron is considered to be in a resting state.

Indeed, a perceptron can be seen as a compact model of a spiking neuron when data is injected in its input terminals, as the neural response has a one-to-one correspondence with the provided input. It means that different inputs will have different and unique (identifiable and separable) neural responses. Such compact responses have the same functionality of waveforms in biological neural responses.

Fig. 10.4

Schematic diagrams of a a recurrent neural network, b one layer feedforward neural network and c deep network or multilayer neural network

ANNs are built using perceptrons as neural primitives and the synaptic connections are typically defined as real-valued numbers. Such numbers can be either positive or negative to mimic excitatory and inhibitory neural behavior. Among many other categorization, ANNs can be categorized in the following two main branches: feed forward and recurrent neural networks. Recurrent neural networks (RNNs) are made up of three layers of neurons: input, hidden and output. A RNN has a particular architecture in which outputs of its individual neurons serve as inputs to other neurons on the same hidden layer, see Fig. 10.4a. These feedback connections allow networks’ input information to be recycled, transformed and reused. Consequently, RNNs are able to generate internal dynamics that could be advantageous for the development and maintenance of patterns in the networks’ high dimensional space (defined by the neurons) [28].

The second branch is led by feed forward neural networks (FFNNs) that represent a conceptually similar configuration to RNNs. FFNNs are also composed from input, internal and output layers. But, different from RNNs, they do not involve any internal feedback between neurons as part of their architectures, see Fig. 10.4b. These networks usually build models that perform smooth function fits to input information. In many cases, FFNNs are designed with more than one layer of neurons to enhance their information processing competencies. Such larger architectures are known as deep networks (Fig. 10.4c), and they are used to solve highly complex problems previously deemed unsolvable by classical methods in an efficient manner, such as pattern classification [1] or human-level control [29].

3 Electronics and Photonic Platforms

Attempts to build efficient perceptron-based neural networks have been reported through out recent years. Efficiency is expected on any machine that attempts to match or outweigh human computing capabilities. An interesting computing acceleration technique consists in the use of hardware units that perform multiply-accumulate (MAC) operations very fast. A MAC unit performs multiplications and accumulation processes: $a+(w \times x)$. Multiple MAC operations can be run in parallel to perform complex operations such as convolutions and digital filters. By comparing a MAC unit with the concept of a perceptron, we realize that they have a similar mathematical model. A neuron made of M inputs and synapses, one output and a bias term can be therefore written as an array of M MAC operations $(a_{i} = a_{i-1}+w_{i}x_{i})$ [3]. For instance, the weighted addition $(w_{1}x_{1} + w_{2}x_{2} + \cdots + w_{M}x_{M} + b)$ of the neuron:

$$\begin{aligned} y = f(w_{1}x_{1} + w_{2}x_{2} + \cdots + w_{M}x_{M} + b), \end{aligned}$$

(10.2)

can be performed in M blocks as follows: if $a_{0} = b$, then the first MAC operation is $a_{1}=a_{0}+w_{1}x_{1}$. The second MAC operation would be $a_{2}=a_{1}+w_{2}x_{2}$; and the last one $a_{M}=a_{M-1}+w_{M}x_{M}$. The activation function f can be applied to all the weighted summations at the end of the process. Consequently, a neural network of size N requires $M\times N$ MAC operations per time step. In a fully connected network where $M=N$, the number of MAC operations per time step is $N^{2}$. MAC operations are typically used in implementations of neural networks in digital electronics. Nevertheless, the serialization of the summands to perform weighted addition makes this process inefficient. As such operations follow a serial processing, the overall computation efficiency will depend on the clock speed of the digital machine. Since 2014, clock rates have saturated at around 8 GHz, and chip designers are looking for alternative solutions such as full parallelism. The most promising technologies used for this purpose are based on specialized analog electronic and photonic platforms.

Fig. 10.5

a Electronic crossbar array and b schematic diagram of the cross-section of a rib waveguide

3.1 Electronics

The analog electronics approach is based on space-efficient topologies such as resistive crossbar arrays. In Fig. 10.5a we show the layout of these devices, that consists of tunable resistive elements at each junction that could represent a synaptic weight element. They are typically built as a metal-insulator-metal sandwich, where the insulator can be made of SiO$_x$, with $x<2$. Tuning is typically performed through the application of input voltages (or currents) to the device in order to change its resistance value. In this case, each column from such a mesh can represent the weighted addition of any neuron. Input values that are injected through voltages $V_{i}$ are distributed through all the N synaptic weights, which are represented by resistors of conductance $G_{j}$. The output of the neuron is represented by the resultant current $I_{i}$ at each column of N elements. Such currents are obtained by the Kirchhoff’s current law, where the multiplications and summations ($I_{j} = \sum _{i} V_{i}\cdot G_{i,j}$) are performed.

This architecture is advantageous as the $N^2$ MAC operations can be executed in parallel. If we are to use passive arrays of resistive elements to perform MAC operations, we need to determine how many analog weight values can be represented per resistive device. This decision should be taken for the sake of the entire machine efficiency. It has been shown in [3] that for a maximum of 16 analog values (4 bits) such devices consume fairly low energy. The total energy consumption of an electronic crossbar array is 4.0 aJ/MAC. This number stays almost unchangeable for 8 bits. However, crossbar arrays show fundamental performance flaws when used to model large neural networks. Large crossbar arrays ($L > 100~\upmu$m) are associated with high energy costs and low bandwidth. Overall, the power consumption, scalability and speed can be greatly affected when working with large networks. Nowadays, ANNs have been doubling in size every 3.5 months, therefore platforms with strong limitations to model large neural networks will add to the problem. Accordingly, we continue exploring different platforms in the following.

3.2 Photonics

The photonic platform comes as an ideal candidate due to its high scalability, great bandwidth and less energy consumption for longer distances than its electrical counterpart. In particular, silicon photonics can offer analog processing on integrated circuits with high-speed and low power consumption. The silicon material for integrated photonics offers a manufacturable, low-cost and versatile platform for photonics. In fact, silicon photonic devices can be manufactured with standard silicon foundries and some modified versions of their processing capabilities [30, 31]. Additionally, silicon is well-known for its high refractive index contrast, which allows for submicrometer waveguide dimensions and dense packing of optical functions on the surface of the chip, i.e. small footprint.

In order to make the light propagate in a small micrometer area, a slab waveguide made of three layers can be designed. As shown in Fig. 10.5b, the core layer of the slab waveguide is made of a high index material (silicon, index = 3.48) and the two cladding layers with lower index (air, index = 1.0). In particular, the photonic waveguide illustrated in the same figure is also known as a rib waveguide, which allows for electrical connections to be made to the waveguide [32]. Such a waveguide typically sits on silicon dioxide SiO$_2$ whose refractive index is 1.54. Each on-chip waveguide is designed with a width of 500 nm and a thickness of 220 nm—associated with single mode operation. An outstanding feature of rib waveguides is their capability for signal parallelization, in which hundreds of high speed, multiplexed channels can be independently modulated and detected. Optical channels are defined by different wavelengths, and can be used to transmit independent information with small optical crosstalk.

We introduce a first photonic device which implements weights on signals encoded onto multiple wavelengths. Tuning a given filter on and off resonance changes the transmission of each signal through that filter, effectively multiplying the signal with a desired weight in parallel. Silicon microring resonators (MRRs) have demonstrated to be ideal as on-chip synaptic weights with small footprint [10], see Fig. 10.6a. MRRs can be designed with a ring and one (all-pass) or two (add-drop) adjacent bus waveguides. MRRs are devices capable of trapping light at certain frequencies at which they resonate, according to their physical characteristics. The resonance frequency can be obtained from the wavelength equation $\lambda _{R} = 2\pi Rn_{\mathrm{eff}}/m$, where R is the radius of the ring and $n_{\mathrm{eff}}$ is the effective refractive index. A wide variety of synaptic weights can be represented by an MRR through the tuning of the waveguide refractive index or (as we will see later) by tuning the amount of light that gets trapped in the waveguide. An array of N MRRs can emulate the weighted addition of a single neuron if add-drop MRRs and a photodetector are added to the model as shown in Fig. 10.6b. Each MRR implements a weight value $w_i$, the input values $x_i$ are injected into the neuron through a modulator (a microring [33] or a Mach-Zehnder [34]), and the photodetector adds up all optical signals [$\sum _{i} w_{i}\cdot x_{i}$].

A second design implements weights encoded onto different phases of Mach Zehnder interferometers (MZI). As shown by Fig. 10.6c, a MZI is designed with a splitter that splits the incoming light into two branches (the upper and lower waveguide), and then a coupler recombines them again. Splitters and couplers are designed with Y-branches or directional couplers [10, 32]. By tuning the amount of phase delay on one of a MZI’s arms, a specific weight value can be set. This causes an array of input optical signals $\mathbf {x}$ to be multiplied by a weight matrix $\mathbf {W}$, as $\mathbf {W} \cdot \mathbf {x}$, see Fig. 10.6d. Therefore, each row of the matrix $\mathbf {W}$ represents the weighted addition part of a neuron.

Fig. 10.6

a all-pass and add-drop MRRs, b add-drop MRR weightbank with a balance photodetector, c the model of a MZI and d $2\times 2$-MZIs with phase shifters and directional couplers

Meshes composed of $N^2$ MRRs (plus N photodetectors) or $N^2$ MZIs can accomplish $N^2$ MAC operations of the kind $[w_{i,j}\cdot x_{i}]$ each. Furthermore, both methods can be tuned via the thermo-optic effect, where a voltage (or current) is applied to optimize their weight values. For a maximum of 16 values (4 bits), such devices consume way less energy than their electronic counterparts. The total energy consumption of optical meshes is estimated to be around 2.0 aJ/MAC. However, as reported in [3], the energy required to represent 256 values (8 bits) is 40 times bigger than the 4-bits case. Thankfully, many ANNs still work well when computational precision is low [35, 36].

The total energy consumption estimated in this section does not take into account the amount of energy required to tune these devices to specific weight values. These passive calculations are agnostic to the tuning technology that is used to set the weights, the type of activation function, the control unit and the memory unit used to build a system capable of modeling ANNs. Each of those modules will add to the overall power consumption and speed constrains. Nevertheless, MAC operations have been found to be the most burdensome hardware bottlenecks in ANNs as N grows large [3]. Therefore, such afore mentioned modules should be optimized for the sake of the machine efficiency maintenance. In the following sections, we will describe how to build potentially efficient analog photonic ANNs.

4 Silicon Photonic Neural Networks

As introduced above, the high speed and parallelism property of the light allows for optical information processing at a high data rate [37]. Furthermore, the high scalability, submicrometer and dense packing of optical functions of silicon integrated photonics makes this a promising technology not only for accelerating AI, but also for ultra fast special-purpose computing. In silicon photonic platforms, there are two main approaches that leverage some (or all) of those afore mentioned features. The first approach harnesses the coherent properties of the light. Under the coherent approach, we present two different experiments. The first experiment is based on MZI-based silicon integrated circuits. This circuit has the property of being fully reconfigurable through thermo-optic tuning. The second coherent experiment differes from the MZI-based circuit in that it consists of a passive non-reconfigurable (non-tunable) circuit for reservoir computing applications only. Finally, we introduce an experiment under the incoherent approach that harnesses the parallelism feature of light and is fully-reconfigurable.

4.1 MZI-based Processing Unit

As commented in the previous section, weighted additions (MAC operations) are one of the most computationally expensive parts of AI processing. In order to accelerate these operations, a dimensionality reduction method can be applied on any ANN weight matrix W. One of the most used methods for this purpose is known as singular value decomposition (SVD). SVD could automatically decompose W as $W = U \Sigma V^{\dag }$, where U is a unitary matrix, $\Sigma$ is a rectangular diagonal matrix and $V^{\dag }$ is the complex conjugate of the unitary matrix V. Additionally, if we also leverage the high speed property of optical integrated circuits, we can accomplish ultra fast accelerators for AI. Nevertheless, we would need to know how to implement unitary and diagonal matrices in optics.

In fact, theoretical and experimental models have shown that certain arrangements of beam splitter devices can be used to represent unitary matrices [38]. For silicon integrated photonics, MZI have been tested to be equivalent replacements of beam splitters [39]. In Fig. 10.7, we illustrate a MZI-based mesh that can implement W decomposed in $U, \Sigma$ and $V^{\dag }$ [15]. Each $2\times 2$-MZI (Fig. 10.6(d)) is built with two phase shifters that can be tuned to program the nanophotonic circuit to solve a task. In this case, the Phase term 1, defined as $\theta$, controls the power at the MZI outputs, and the Phase term 2, defined as $\phi$, determines the relative phases of those outputs [40].

A $2\times 2$-MZI implements the following transformation [40]:

$$\begin{aligned} R(\theta ,\phi )_{MZI} = {\mathrm{e}}^{j\left( \frac{\theta +\pi }{2}\right) } \begin{pmatrix} {\mathrm{e}}^{j\phi }\sin \frac{\theta }{2} &{} {\mathrm{e}}^{j\phi }\cos \frac{\theta }{2} \\ \cos \frac{\theta }{2} &{} -\sin \frac{\theta }{2} \end{pmatrix}. \end{aligned}$$

(10.3)

Such a transformation is associated with the SU(2) rotation group. Unitary matrices U and V are therefore represented by sets of SU(2) transformations that can perform all rotations on the two MZI input signals. For this purpose, the implementation of U and V matrices requires the MZIs’ phases $\theta$ and $\phi$ to be tuned. The diagonal matrix $\Sigma$ can be implemented as the change of power to the input signals, then only $\theta$ should be optimized. The resulting chip will apply a weight matrix W to the amplitude of the input signals [15].

Fig. 10.7

Illustration of a MZI mesh that performs singular value decomposition

To program the chip, an $N\times N$ unitary matrix U(N) is multiplied by a succession of unitary matrices $R(\theta ,\phi )_{i}$ of the same dimensionality until all its off-diagonal elements are set to zero. This process can be viewed as the result of a rotation of each column of the matrix U(N). In total, $m=N(N-1)/2$ rotations will be performed with $2\times 2$-MZIs. The resultant diagonal matrix is equal to the identity:

$$\begin{aligned} U(N)R(\theta _{1},\phi _{1})_{1}R(\theta _{2},\phi _{2})_{2}\ldots R(\theta _{m},\phi _{m})_{m} = I, \end{aligned}$$

(10.4)

such that U(N) can be expressed as a succession of multiplications of the $R(\theta ,\phi )_{i}$ inverses:

$$\begin{aligned} U(N) = R(\theta _{m},\phi _{m})^{-1}_{m}\ldots R(\theta _{2},\phi _{2})^{-1}_{2}R(\theta _{1},\phi _{1})^{-1}_{1}. \end{aligned}$$

(10.5)

This representation of U(N) allows for its implementation as a set of phases $\theta$’s and $\phi$’s that will be determined by adjusting the voltage on each internal thermo-optic phase shifter of MZIs from $m=1$ to $m=N(N-1)/2$. This process is repeated for the unitary matrix $V^{\dag }$. The diagonal matrix $\Sigma$ contains the effects of photodetection on the uncertainty of the system output [15], and it is implemented by tuning the voltage on each internal thermo-optic phase shifter of a different set of N MZIs.

Fig. 10.8

a The model of a deep network with four hidden layers, and b a $4\times 4$ weight matrix represented with sets of $2\times 2$-MZIs

4.1.1 MZI-based Deep Neural Networks

This method can be extended to model large deep neural networks where each layer will be represented by an optical inference unit, followed by a non-linear function that can also be implemented with MZI-based circuits [41], see Fig. 10.8a. As a proof of concept, a $4\times 4$ weight matrix W (also $4\times 4$ MAC operations) was implemented on-chip [15], see Fig. 10.8b. This circuit represents matrices U and $\Sigma$. The matrices U is composed of $m=6$ sets of $2\times 2$-MZIs, and the matrix $\Sigma$ is composed of $N=4$ sets of $2\times 2$-MZIs. U and $\Sigma$ are implemented on a single pass through the chip, and $V^{\dag }$ is implemented separately in this experiment. The authors of this work suggest that a larger circuit would be required to perform the full matrix decomposition on a single pass. As the unitary matrices U and V are represented by SU(2) transformations that basically perform all rotations of the two MZI input signals, the phases $\theta$ and $\phi$ have to be tuned on MZIs from (1) to (6). The diagonal matrix $\Sigma$ can be implemented as the change of power to the input signals, then only $\theta$ should be optimized on MZIs from (7) to (10).

The first step of this experiment consists in the determination of the weight matrix W for a specific task. The proposed task is called vowel recognition, where 11 vowel phonemes spoken by 90 different speakers have to be recognized. The training of the network was perform via backpropagation off-line (not on-chip but on a computer), and the inference stage was perform on-line (on-chip). Once W is obtained, this matrix is decomposed in $U,\Sigma$ and $V^{\dag }$. The unitary matrix U could be programmed by successively multiplying it by the following array of rotation matrices until all off-diagonal elements are set to zero [40]:

$$\begin{aligned} U(4)R(\theta ,\phi )_{1}R(\theta ,\phi )_{2}R(\theta ,\phi )_{4}R(\theta ,\phi )_{3}R(\theta ,\phi )_{5}R(\theta ,\phi )_{6} = I(4), \end{aligned}$$

(10.6)

where,

$$\begin{aligned} U(4) = \begin{pmatrix} U_{1,1} &{} U_{1,2} &{} U_{1,3} &{} U_{1,4} \\ U_{2,1} &{} U_{2,2} &{} U_{2,3} &{} U_{2,4} \\ U_{3,1} &{} U_{3,2} &{} U_{3,3} &{} U_{3,4} \\ U_{4,1} &{} U_{4,2} &{} U_{4,3} &{} U_{4,4} \end{pmatrix}; \end{aligned}$$

(10.7)

and

$$\begin{aligned} R(\theta _{i},\phi _{i})_{i} = e^{j\left( \frac{\theta _{i} +\pi }{2}\right) } \begin{pmatrix} e^{j\phi _{i}}\sin \frac{\theta _{i}}{2} &{} e^{j\phi _{i}}\cos \frac{\theta _{i}}{2} &{} 0 &{} 0 \\ \cos \frac{\theta _{i}}{2} &{} -\sin \frac{\theta _{i}}{2} &{} 0 &{} 0 \\ 0 &{} 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 0 &{} 1 \end{pmatrix}. \end{aligned}$$

(10.8)

For instance, when the operation $U(4)R(\theta _{1},\phi _{1})_{1} = A(\theta _{1},\phi _{1})$ is performed, the element $A_{4,1}$ resultant matrix can be set to zero. Therefore, $\theta _{1}$ is calculated from:

$$\begin{aligned} \theta _{1} = 2\tan ^{-1}\left( -\frac{U_{4,2}}{U_{4,1}}\right) . \end{aligned}$$

(10.9)

We incorporate $A_{4,1}=0$ to the resultant matrix $A(\theta _{1},\phi _{1})$, and multiply it by the second rotation $R(\theta ,\phi )_{2}$ to obtain a new matrix $B(\theta _{2},\phi _{2})$. If the element $B_{4,2}$ is set to zero, then $\theta _{2}$ can be obtained as well. After we incorporate the element $B_{4,2}=0$ to the resultant matrix B, we proceed to multiply it by $R(\theta ,\phi )_{4}$. This operation allows us to obtain $\theta _{4}$ once the element $C_{4,3}$ of the resultant matrix $C(\theta _{4},\phi _{4})$ is set to zero. Once all elements of the last row except the one on the diagonal in $C(\theta _{4},\phi _{4})$ are set to zero, the next step consists in setting all the elements of its last column to zero—except the diagonal. Since all applied transformations are unitary, the last column will contain only zeros, and the diagonal element will be set to one:

$$\begin{aligned} C(\theta _{4},\phi _{4}) = U(4)R(\theta ,\phi )_{1}R(\theta ,\phi )_{2}R(\theta ,\phi )_{4} = \begin{pmatrix} U(3) &{} 0 \\ 0 &{} 1 \end{pmatrix}, \end{aligned}$$

(10.10)

where the last step already reduced the effective dimension of U to 3.

We repeat this process with the rest of the rotation matrices until the resultant matrix is equal to the identity. This process will provide the remaining phases to fully program the chip that implement W. The inference stage of this experiment was successfully performed on-chip and the recognition task achieved an accuracy of $76.7\%$. According to the energy calculations performed by the authors of this experiment, a four neuron system would dissipate approximately 8 mW. In the inference stage, this system can perform such calculations quite efficiently, but the heaters used to program each individual MZI burns an important amount of power.

4.2 Photonic Reservoir Computing

Reservoir computing is a term that encompasses some types of RNNs that can solve complex tasks with a simplified training methodology. This trend started with echo state networks (ESNs) [42] and Liquid State Machines (LSMs) [43]. These two network architectures come from the fields of machine learning and computational neuroscience, respectively. More recently, a delay echo state network appeared as a novel computational machine. Such an advantageous concept is found to be simple and implementable in hardware [7].

Reservoir computers can also be seen as a random RNN, where the synaptic weights are Gaussian or uniformly [44] distributed. Although the brain’s connectivity cannot be assumed to be fully random, there is experimental evidence supporting the assumption that some parts of the brain are described by stochastic architectures. For example, in insects’ olfactory systems the odour recognition process is performed by olfactory receptor neurons with structureless (random) synaptic connections [45, 46]. Therefore, reservoir computers might be useful to model a few random (non-trainable) neural dynamics, but it is limited to that.

Reservoirs consist of reservoirs of m neurons in state $\mathbf{x} _{n}$, internally connected in this case through uniformly randomly distributed internal weights that are defined in a matrix W of dimensionality $m\times m$. The resulting randomly connected network is injected with input data $\{ b, y^{in}_{n+1} \}$ according to random offset and teacher/input weights $W^{off}$ and $W^{in}$, respectively. We normalize the largest eigenvalue of W to one. The time-discrete equation that governs the network is [42]

$$\begin{aligned} \mathbf{x} _{n+1}=f_{NL}(W\cdot \mathbf{x} _{n} + W^{\mathrm{off}}\cdot b + W^{in}\cdot y^{in}_{n+1}), \end{aligned}$$

(10.11)

$$\begin{aligned} y^{\mathrm{out}}_{n+1} =W^{\mathrm{out}} \cdot \mathbf{x} _{n+1} \end{aligned}$$

(10.12)

where $f_{NL}(\cdot )$ is a nonlinear sigmoid-like activation function and b a constant value which has the role of an offset. The network is trained via a supervised learning rule, where we estimate the output weights $W^{out}$ through which we obtain the network’s output $y^{\mathrm{out}}$, see Fig. 10.9a.

The supervised learning rule used to estimate the output weights $W^{out}$ is based on regression. The ridge regression is commonly employed to train reservoirs, and it is executed according to

$$\begin{aligned} W^{\mathrm{out}}_{\mathrm{op}}=M_{y^{T}}\cdot M^{\dagger }_{x}(M_{x}\cdot M^{\dagger }_{x}-\lambda \mathbf {I}_{m})^{-1}, \end{aligned}$$

(10.13)

where $M_{y^{T}}$ and $M_{x}$ are matrices containing information about target and node responses, respectively. $\lambda$ is the regression parameter.

Fig. 10.9

a A schematic diagram of a reservoir computer, and b a swirl on chip silicon reservoir

4.2.1 Swirl On-Chip Silicon Reservoir Computer

A $6\times 6$ reservoir computer that can perform speech recognition is shown by Fig. 10.9b [14]. The interconnections between neurons follow a swirl topology, because the connections are oriented as if they were in a whirling motion. Each neuron was designed with 2 cm long waveguides with a square roll shape. The 36 neurons are arranged in a rectangular grid, allowing for nearest neighbor interconnections only. Coupling and splitting between the nodes is done by multimode interferometers with low insertion loss. In order to leverage the full advantages of the maturity of silicon processing technology, this reservoir design does not contain any active element.

The classification task of isolated spoken digits (from 0 to 9) was based on the TI46 speech corpus. This dataset contains 500 samples, where each digit is spoken 10 times by five female speakers. The ridge regression was used to train the network using $75\%$ of the TI46 dataset. Each trained output returns the value $+1$ whenever the corresponding digit is spoken and −1 otherwise. The testing stage used the remaining $25\%$ set of digits. This circuit was simulated only with all the parameters of the designed chip and it achieved near $100\%$ performance.

Reservoir computing has demonstrated to be a simple and powerful tool for analog AI. Reservoirs are well suited for hardware implementations as the synaptic weights of each neuron can be set as random—they do not need to be configured to specific values. Nevertheless, its lack of full reconfigurability makes it unable to tackle complex machine learning problems that are being solved by reconfigurable deep feedforward architectures.

4.3 Broadcast-and-Weight Architecture

A scalable photonic architecture for parallel processing can be achieved by using on-chip wavelength division multiplexed (WDM) techniques (see Fig. 10.10), in conjunction with MRRs, i.e. photonic synapses, that implement weights on signals encoded onto multiple wavelengths. Tuning a given MRR on and off resonance changes the transmission of each signal through that filter, effectively multiplying the signal with a desired weight in parallel. Silicon microring resonators (MRRs) cascaded in series have demonstrated fan-in and indefinite cascadability which make them ideal as on-chip synaptic weights with small footprint.

Fig. 10.10

Illustration of the wave division multiplexing process

Fig. 10.11

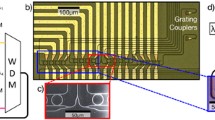
a Illustration of an experiment showing how to test add-drop MRRs that have index or absorption tuners that can be optimized through the application of a voltage. A laser feeds the MRRs and an OSA receives the transmission at the drop port. b Transmissions at the drop (dashed line) and the through port (solid curve)

The big advantage of using MRRs to represent weights is that they can be tuned with a wide variety of methods: thermally, electro-optically or through light absorption (phase-change [18] or graphene [47] materials). Those tuning methods can be categorized into two different groups: index and absorption-tuning. In order to illustrate the action of each tuning method, we introduce a simple experiment shown in Fig. 10.11a. In this experiment, an add-drop MRR is fed by a laser at certain wavelength $\lambda$ at which this MRR resonates. Under this condition, the MRR begins trapping the incoming light that eventually partially escapes through the drop port via evanescent waves. The output light is captured by an optical spectrum analyzer (OSA). The MRR can perform index or absorption tuning when a certain voltage value is applied. In Fig. 10.11b we show the transmissions at the drop port (dashed curve) and at the through port (solid curve) without any tuning, where the MRR is on resonance at wavelength $\lambda _{R}$. The transfer function of the through port light intensity with respect to the input light is:

$$\begin{aligned} T_{p}(\phi ) = \frac{(ar)^2 - 2r^2\cos \phi + r^2}{1 - 2r^2\cos \phi + (r^2a)^2}; \end{aligned}$$

(10.14)

and the transfer function of the drop port light intensity with respect to the input light is:

$$\begin{aligned} T_{d}(\phi ) = \frac{(1-r)^2a}{1 - 2r^2\cos \phi + (r^2a)^2}. \end{aligned}$$

(10.15)

The parameter r is the self-coupling coefficient, and a defines the propagation loss from the ring and the directional coupler. The phase $\phi$ depends on the wavelength $\lambda$ of the light and radius R of the MRR [48]:

$$\begin{aligned} \phi = \frac{4\pi ^2 R n_{\mathrm{eff}}}{\lambda }. \end{aligned}$$

(10.16)

In the case where the coupling losses are negligible, $a\approx 1$, the relationship between the add-drop through and drop transfer functions is $T_p = 1 - T_d$.

Fig. 10.12

Transmission versus wavelength for the graphene-based MRR (a) and the n-doped MRR, b collected from their drop port when different voltage values are applied

In Fig. 10.12 we show the behavior of optical signals detected by the OSA when the voltage is varied. By applying a positive voltage to the index-tuning device, we tune the refractive index of the waveguide, leading to drifts of the natural resonance frequency. As shown in Fig. 10.12a, we define this type of behavior as a photonic synaptic weight that can be tuned horizontally on the transmission profile, since the drive voltage causes $\lambda _{R}$ to shift from 1.6250 to $1.6350 \upmu$ m and beyond. A different weighting-type of methodology is shown in Fig. 10.12b, where we show how weight values can be defined as transmission values that decrease with incrementing negative voltage. We define this type of behavior as a photonic synaptic weight that can be tuned vertically on the transmission profile. The index-tuning approach is so far the most employed tuning method due to the fabrication of index-tuning devices (heaters or NP-modulators) being compatible with standard silicon foundries. Absorption-tuning devices based on graphene have to be manufactured with isolated processes that are not yet standardized by any nanophotonic foundry.

4.3.1 Multiwavelength Weighted Additions

The broadcast and weight architecture can perform weighed additions based on WDM techniques as shown by Fig. 10.13. In this illustration we show how to multiply in parallel four vectors contained in set $\mathcal {A}$:

$$\begin{aligned} \mathcal {A} = {\left\{ \begin{array}{ll} (A_{11}, A_{12}, A_{13},A_{14}), \\ (A_{21}, A_{22}, A_{23},A_{24}), \\ (A_{31}, A_{32}, A_{33},A_{34}), \\ (A_{41}, A_{42}, A_{43},A_{44}); \\ \end{array}\right. } \end{aligned}$$

(10.17)

with four vectors contained in set set $\mathcal {B}$:

$$\begin{aligned} \mathcal {B} = {\left\{ \begin{array}{ll} (B_{11}, B_{12}, B_{13},B_{14}), \\ (B_{21}, B_{22}, B_{23},B_{24}), \\ (B_{31}, B_{32}, B_{33},B_{34}), \\ (B_{41}, B_{42}, B_{43},B_{44}). \\ \end{array}\right. } \end{aligned}$$

(10.18)

All vectors are composed of positive real-valued numbers. Vectors from sets $\mathcal {A}$ and $\mathcal {B}$ are implemented as arrays of 8 MRRs cascaded in series. For this implementation we use input and through ports only of add-drop MRRs.

Fig. 10.13

Photonic architecture for $4\times 4$ vector-to-vector multiplications between sets of vectors $\mathcal {A}$ and $\mathcal {B}$, containing 4 vectors each

Fig. 10.14

a Transmission versus wavelength curves of two different MRRs [RR($A_{11}$), MRR($B_{11}$)] performing element-to-element optical multiplications, and b the product of such multiplication

The elements of a given set $\mathcal {A}$ can be mapped to voltage values $Va_{ij}$ that tune each individual MRR($A_{ij}$). Each voltage value has a one-to-one correspondence with a MRR transmission profile $T_{ij}$. The same principle holds for matrix $\mathcal {B}$ with voltage values $Vb_{ij}$. The experimental implementation of this method requires the use of four lasers with different wavelengths $\lambda _{i}$ (with $i=1,2,3,4$) that represent four channels. Each channel will represent a vector element from each set through an on resonance MRR. For instance, channel $\lambda _{1}$ represents $A_{11}$ from $\mathcal {A}$ and $B_{11}$ from $\mathcal {B}$ at the same time. This property allows for optical interactions between the two MRRs that result in the product of the two of them. In Fig. 10.14 we show an illustration of the multiplication between two vector elements $A_{11}$ and $B_{11}$, and how the result R is obtained. Let’s suppose that the element $A_{11}$ was tuned to have the maximum optical transmission whereas $B_{11}$ was tuned to have half of it. In order to implement $A_{11}$, we leave the MRR($A_{11}$) on-resonance with $\lambda _{1}$, and we tune MRR($B_{11}$) to be half off-resonance with the same wavelength. They represent real-valued numbers 1 and 0.5, respectively. The result of such multiplication is $R = 0.5$. Two MRRs with different on and off resonance configurations at the same wavelength $\lambda _{i}$ will therefore perform element-to-element multiplications. A similar process is followed with all other vector elements of sets $\mathcal {A}$ and $\mathcal {B}$.

Furthermore, to perform a full vector-to-vector multiplication of the form:

$$\begin{aligned} C_{1} = \begin{pmatrix} A_{11}&{} A_{12}&{} A_{13}&{} A_{14} \\ \end{pmatrix} \cdot \begin{pmatrix} B_{11}\\ B_{12}\\ B_{13}\\ B_{14}\\ \end{pmatrix}, \end{aligned}$$

(10.19)

all the sets of multiplications $A_{ij}B_{ij}$, performed per array of eight MRRs, are all summed up by a photodetector located in the end of the array. The photonic circuit shown in Fig. 10.13 performs four weighted additions in parallel by leveraging the signal parallelization property of the light in which hundreds of high speed, multiplexed channels can be independently modulated and detected. Therefore, this architecture can perform four MAC operations in parallel consuming 23.956 Watts of energy—taking into account the tuning process.

4.3.2 Convolutions and Convolutional Neural Networks

The efficient parallelism of broadcast and weight architectures for matrix multiplication can be leveraged to perform operatons such as convolutions. A convolution is a weighted summation of two discrete domain functions f and g:

$$\begin{aligned} (f*g)[t]=\sum _{t=-\infty }^{\infty }f[\tau ]g[t-\tau ], \end{aligned}$$

(10.20)

where $(f*g)$ represents a weighted average of the function $f[\tau ]$ when it is weighting by $g[-\tau ]$ shifted by t. The weighting function $g[-\tau ]$ emphasizes different parts of the input function $f[\tau ]$ as t changes.

In this subsection we will learn how to utilize convolutions to do operations on images. Convolutions are well known to perform a highly efficient and parallel matrix multiplication using kernels [49]. Let us introduce the convolution of an image $\mathbb {A}$ with a kernel $\mathbb {B}$ that produces a convolved image $\mathbb {O}$, see Fig. 10.15(a). An image is represented as a matrix of numbers with dimensionality $H\times W\times D$, where H and W are the height and width of the image, respectively; and D refers to the number of channels within the input image. Each element of a matrix $\mathbb {A}$ represents the intensity of a pixel at that particular spatial location. A kernel is a matrix $\mathbb {B}$ of real numbers with dimensionality $R\times R\times D$. The value of a particular convolved pixel is defined by:

$$\begin{aligned} O_{i,j}=\sum _{h=1}^{D}\sum _{q=0}^{iS+R}\sum _{p=0}^{js+R}B_{q,p,h}A_{iS+q,jS+p,h}. \end{aligned}$$

(10.21)

The additional parameter S is referred to as the “stride” of the convolution. The dimensionality of the output feature is:

$$\begin{aligned} \left\lceil \frac{H-R}{S}+1\right\rceil \times \left\lceil \frac{W-R}{S}+1\right\rceil \times K, \end{aligned}$$

(10.22)

where K is the number of different kernels of dimensionality $R\times R\times D$ applied to an image, and $\lceil \cdot \rceil$ is the ceiling function.

The efficiency of convolutions for image processing is based on the fact that they lower the dimensions of the outputted convolved features. Since kernels are typically smaller than the input images, the feature extraction operation allows efficient edge detection, therefore reducing the amount of memory required to store those features.

Fig. 10.15

a Illustration of a convolution between and image $\mathbb {A}$ and $\mathbb {B}$, that generates output $\mathbb {O}$, and b the block diagram that describes a typical CNN, which contains convolutions, activation functions, pooling and fully connected layers

As efficiency and parallelism are properties that can be expected from convolution operations, let us incorporate such operations in ANNs for image processing. In particular, we will build convolutional neural networks (CNNs) for image recognition tasks. A CNN consists of some combination of convolutional, nonlinear, pooling and fully connected layers [50]. CNNs are networks suitable to be implemented in photonic hardware since they demand fewer resources to do matrix multiplication and memory usage. The linear operation performed by convolutions allows single feature extraction per kernel. Hence, many kernels are required to extract as many features as possible. For this reason, kernels are usually applied in blocks, allowing the network to extract many different features all at once and in parallel.

In feed-forward networks, it is typical to use a rectified linear unit (ReLU) activation function. Since ReLUs are linear piecewise functions that model an overall nonlinearity, they allow CNNs to be easily optimized during training. The pooling layer introduces a stage where a set of neighbor pixels are encompassed in a single operation. Typically, such an operation consists of the application of a function that determines the maximum value among neighboring values. An average operation can be implemented likewise. Both approaches describe max and average pools, respectively. This statistical operation allows for a direct down-sampling of the image, since the dimensions of the object are reduced by a factor of two. From this step, we aim to make our network invariant and robust to small translations of the detected features.

The triplet, convolution-activation-pooling, is usually repeated several times for different kernels, keeping invariant the pooling and activation functions. Once all possible features are detected, the addition of a fully connected layer is required for the classification stage. This layer prepares and shows the solutions of the task.

CNNs are trained by changing the values of the kernels, analogous to how feed-forward neural networks are trained by changing the weighted connections [51]. The estimated kernel weight values are required in the testing stage. In this work, we trained the CNN to perform image recognition on the MNIST dataset, see Fig. 10.15b. The training stage uses the ADAM optimizer and back-propagation algorithm to compute the gradient function. The optimized parameters to solve MNIST can be categorized in two groups: (i) two $5\times 5\times 8$ different kernels and (ii) two fully connected layers of dimensions $800\times 1$ and $10\times 1$; and their respective bias terms. These kernels are then defined by eight $5\times 5$ different filters. In the following we use our photonic CNN simulator to recognize new input images, obtained from a set of 500 images, which are intended to be used for the test step. Our simulator only works at the transfer level and does not simulate noise or distortion from analog components. As it can be seen in the illustration (Fig. 10.15b), a $28\times 28$ input image from the test dataset is filtered by a first $5\times 5\times 8$ kernel, using stride one. The output of this process is a $24\times 24\times 8$ convolved feature, with a ReLU activation function already applied. Following the same process, the second group of filters is applied to the convolved feature to generate the second output, i.e. a $20\times 20\times 8$ convolved feature.

Fig. 10.16

a Add-drop configuration and O/E conversion and amplification. b Transmissions of the drop and though ports and c output of the balance photodiode

4.3.3 Photonic Deep Convolutional Neural Networks

In general, the elements of the kernel matrix are defined as real-valued numbers, and the elements of the input matrix are typically integer positive numbers. In order to map convolutions onto photonics we need to consider how to represent negative numbers in our photonic circuits. This can be done by using the through and drop ports of the MRRs at once connected to a balance photodetector (BPD). In Fig. 10.16a we show how to represent a single negative number in a photonic circuit. The through and drop ports of the MRR($B_{i}$) are connected to the BPD, and then linked to a TIA with gain equal to one. The transmissions of those ports can be seen in Fig. 10.16b, and the output of the BPD can be represented as a waveform shown by Fig. 10.16c. The result of the subtraction of the two optical signals performed by the BPD results in an electrical signal whose range is in $[-1,1]$. Therefore, any weight value among $[-1,1]$ can be represented on-chip. The addition of the TIA will allow for the representation of numbers out of this range.

This stage can be performed by an on-chip photonic version of the simulated CNN. Figure 10.17 shows a high-level overview of the proposed testing on-chip architecture. First, we consider an architecture that can produce one convolved pixel at a time. To handle convolutions for kernels with dimensionality up to $R \times R \times D$, we will require $R^2$ lasers with unique wavelengths since a particular convolved pixel can be represented as the dot product of two $1\times R^2$ vectors. To represent the values of each pixel, we require $DR^2$ add-drop modulators (one per kernel value) where each modulator keeps the intensity of the corresponding carrier wave proportional to the normalized input pixel value. The $R^2$ lasers are multiplexed together using WDM, which is then split into D separate lines. On every line, there are $R^2$ add-drop MRRs (where only input and through ports are being used), resulting in $DR^2$ MRRs in total. Each WDM line will modulate the signals corresponding to a subset of $R^2$ pixels on channel k, meaning that the modulated wavelengths on a particular line correspond to the pixel inputs $(A_{m, n, k})\begin{array}{c} m\in [i, i+R] n\in [j,j+R] \end{array}$ where $k\in [1,D]$, and $S=1$.

The D WDM lines will then be fed into an array of D photonic weight banks (PWB). Each PWB will contain $R^2$ MRRs with the weights corresponding to the kernel values at a particular channel. Each MRR within a PWB should be tuned to a unique wavelength within the multiplexed signal. The outputs of the weight bank array are electrical signals, each proportional to the dot product $(B_{m,n,k})\begin{array}{c} m\in [1,R^2] n\in [1,R^2] \end{array}\cdot (A_{p, q, k})\begin{array}{c} p\in [i,i+R^2] q\in [j,j+R^2] \end{array}$, where $k\in [1,D]$, and $S=1$. Finally, the signals from the weight banks need to be added together. This can be achieved using a passive voltage adder. The output from this adder will therefore be the value of a single convolved pixel.

Fig. 10.17

Photonic architecture for producing a single convolved pixel. We use an array of $R^{2}$ lasers with different wavelengths $\lambda _{i}$ to feed the MRRs. The input and kernel values modulate the MRRs via electrical currents proportional to those values. Once the matrix parallel multiplications are performed, the voltage adder has the function to add all signals from weight banks. Here, $\textit{R}$ are resistance values. Then the output is the convolved feature

Here, the testing input images modulate the intensities of a group of lasers with identical powers but unique wavelengths. These modulated inputs would be sent into an array of PWBs, which would then perform the convolution for each channel. The kernels obtained in the training step are used to modulate these weight banks. Finally, the outputs of the weight banks would be summed using a voltage adder, which produces the convolved feature. This simulator works using the transfer function of the MRRs, through port and drop port summing equations at the BPDs, and the TIA gain term to simulate a convolution. The simulator assumes that MRRs transfer functions design is based on the averaged transfer function behavior validated experimentally in prior work [34]. The control accuracy of the MRRs is 6-bits as that has been empirically observed [52]. The MRR self-coupling coefficient is equal to the loss, $r=a=0.99$ [53] in  (10.14) and (10.15).

The interfacing of optical components with electronics would be facilitated by the use of digital-to-analog converters (DACs) and analog-to-digital converters (ADCs). The storage of output and retrieving of inputs would be achieved by using memories GDDR SDRAM. The SDRAM is connected to a computer, where the information is already in a digital representation. Then, the implementation of the ReLU nonlinearity and the reuse of the convolved feature to perform the next convolution can be performed. The idea is to use the same architecture to implement the triplet convolution-activation-pooling on hardware.

The results of the MNIST task solved by our simulated photonic CNN, for a test set of 500 images, obtained an overall accuracy of $97.6\%$. This result was found to be $1\%$ better than on-chip MZIs-based theoretical CNNs [54]. These results were obtained with 7 bits of precision. As described in [33], assuming that a maximum of 1024 MRRs can be manufactured in the modulator array, a convolutional unit can support a large kernel size with a limited number of channels, R = 10, D = 12, or a small kernel size with a large number of channels, R = 3, D = 113. We will consider both edge cases to get a range of energy consumption values. For the smaller convolution size, we will have $R^2$ lasers, $R^2$ MRRs and DACs in the modulator array, $R^2D$ MRRs and D TIAs in the weight bank array and one ADC to convert back into digital signal. With 100 mW per laser, 19.5 mW per MRR, 26 mW per DAC, 17 mW per TIA [55] and 76 mW per ADC, we get an energy usage of 112 W for the large kernel size and 95 W for the smaller kernel size.

5 Summary and Concluding Remarks

We have outlined the architectures and motivations behind the use of three photonic integrated circuits that can implement ANNs on-chip. Despite the fact that reservoir computers are simple hardware solutions for machine learning problems that cannot be efficiently solved with classical methods, reconfigurable approaches such as MZI-based meshes and broadcast-and-weight circuits have demonstrated even more versatility. Reconfigurable architectures can be used not only for special-purpose analog tasks, but potentially for general-purpose analog computing as they can be utilized for matrix multiplications, SVD and convolutions. Therefore, it will not come as a surprise if in the future we find a way to create a general-purpose analog machine that is highly optimized for machine learning and neuromorphic computing, but also tackles other more simpler classical tasks.

The reconfigurability of such photonic processing units promise many exciting developments in AI, but there are many challenges that remain with the future implementations of those machines. Such challenges are related to control of the whole processing unit and efficient memory access to the data that needs to be processed. Just like in digital computers, the control unit shall ensure that those data sets are uploaded correctly and in the right order to the processing unit. Since we are working with analog machines, the control unit is particularly important because accurate real-valued numbers only should be inputted to the photonic circuit. The first challenge would be focused on the accurate representation of analog values in photonic processors.

The second critical element is the memory unit. The processes of reading from and writing to memory should not constitute a bottleneck to the processing and control units. This unit has to be optimized in order to receive and deliver information accurately, fast and with low power consumption. Currently, the memory unit is accessed through DACs and ADCs, which slow down the processor considerably. Therefore, the development of analog memories is a crucial step that we need to pursue. For instance, crossbar arrays can be a good solution to this. Crossbar array modules that do not exceed the length limit $L = 100$ $\mu$m should help to create an optimized photonic processor. By adding a crossbar-based memory to our machine, we could store analog voltage values on it and tune our MZIs or MRRs with them. The only flaw of this solution is that the cost of transferring information through electric paths has been considered as a bottleneck for power efficiency. In practice, most of the system-energy is lost in data movement between the processor and the memory [56]. However, photonics has been found to efficiently reduce such data movement problems. In fact, optical loss is nearly negligible for intrachip distances [3]. The development of optical memories [57] are a potential solution in the case where analog optical information can be used to tune a device. Such a device should be tuned with light instead of electrons. Unfortunately, this technology has not been developed yet for neuromorphic computing.

In general, the overall system-speed and power remain as challenge points. Many groups and companies have targeted research directions on some of the afore mentioned issues, but it is currently unknown how these problems will be overcome and how a fully working special (or general) purpose photonic processor can be successfully built.