One-Sided Discrete Terrain Guarding and Chordal Graphs

Abstract

The Terrain Guarding problem, a variant of the famous Art Gallery problem, has garnered significant attention over the last two decades in Computational Geometry from the viewpoint of complexity and approximability. Both the continuous and discrete versions of the problem were shown to be NP-Hard in [14] and to admit a PTAS [8, 15]. The biggest unsolved question regarding this problem is if it is fixed-parameter tractable with respect to the size of the guard set. In this paper, we present two theorems that establish a relationship between a restricted case of the Annotated Terrain Guarding problem and the Clique Cover problem in chordal graphs. These theorems were proved in [11] for a special class of terrains called orthogonal terrains and were used to present a FPT algorithm with respect to the parameter that we require for Discrete Orthogonal Terrain Guarding in [2]. We hope that the results obtained in this paper can, in future work, be used to produce such an algorithm for Discrete Terrain Guarding.

1 Introduction

Let $V =\{v_1,\dots ,v_n\}$ be a finite sequence of three or more points in $\mathbb {R}^2$. The polygonal chain defined by V is the curve specified by the line segments connecting $v_i$ and $v_{i+1}$ for all $1 \le i <n$. In this paper, we additionally assume that polygonal chains are simple curves. For a point v in $\mathbb {R}^2$, we use x(v) and y(v) to denote the x and y coordinates of v. A 1.5-dimensional terrain (which we will refer to as a terrain) is a polygonal chain defined by V where $x(v_i) \le x(v_j)$ for all i and j such that $1 \le i < j \le n$. We also view a terrain T as an undirected graph with vertices V and edges $E= \{(v_i,v_{i+1}) \mid 1 \le i <n \}$. We say that two points a and b on a terrain T see or guard each other if no point in the line segment joining these two points lies strictly below the terrain. An example of a terrain is shown in Fig. 1a. Let U be a set of points on the terrain. The visibility region of U is defined to be the collection of all points on the terrain which is seen by at least one point of U. We let $\textsc {Vis}\; U$ denote this set. The encircled vertices in Fig. 1a are precisely the ones that are present in $\textsc {Vis}\; U$ when $U = \{v_2,v_9\}$. When U contains a single element, say u, we abuse this notation and write $\textsc {Vis}\; u$ instead of $\textsc {Vis}\; U$.

These definitions naturally lead us to the three major versions of the terrain guarding problem. They revolve around finding k-many points (called guards) on the terrain to guard a chosen set of points of the terrain. In the Continuous Terrain Guarding problem, we are required to guard the vertex set of the graph by placing guards anywhere on the terrain. In the Discrete Terrain Guarding version, while we are still to guard the vertex set, we can only place guards on the vertices themselves. Annotated Terrain Guarding generalizes the discrete version by restricting the vertices where the guards can be placed to a subset of V while requiring us to guard a given subset of vertices. We will focus on the annotated version of the terrain guarding problem in this paper and define it formally below. This is referenced from [2]. Hereafter, we assume that the number of vertices of a terrain is n.

Problem

Annotated Terrain Guarding: Given a terrain T(V, E), $k \in \mathbb {N}$ and $\mathcal {G},\mathcal {C}\subseteq V$ decide if there exists a $S \subseteq \mathcal {G}$ with $|S| \le k$ such that $\textsc {Vis}\; S \supseteq \mathcal {C}$.

Fig. 1.

Examples of terrains where the vertices and edges are marked by small discs and straight lines respectively. In (a), the vertices that are seen by $U=\{v_2,v_9\}$ are encircled. The second figure is an example of an orthogonal terrain.

Note that if $\mathcal {G}= \mathcal {C}= V$ in the annotated version of the problem, then it is exactly the Discrete Terrain Guarding problem. We use $(T(V,E),n,k,\mathcal {G},\mathcal {C})$ to denote an instance of the Annotated Terrain Guarding problem. The visibility graph of such an instance, $G_T$, is defined to be the undirected graph $G_T=(\mathcal {C},E')$, where $E' = \{(u,v) \in \mathcal {C}^2 \mid \text {there is a } g \in \mathcal {G}\text { that sees } u \text { and } v\}$. In some variants of the Art Gallery problem, vertices in the visibility graph are connected by an edge if those two vertices see each other [16]. Here, however, there exists an edge between two vertices of $G_T$ if there exists an element in the guard set which can see both these vertices.

A subclass of terrains which are of particular interest are orthogonal terrains. In an orthogonal (or rectilinear) terrain, each edge is either parallel to the x-axis or parallel to the y-axis. Furthermore, each vertex is incident to at most one edge of each type. An example of an orthogonal terrain is given in Fig. 1b.

A graph G(V, E) is chordal if for any $V' \subseteq V$, where $|V'| \ge 4$, the subgraph induced by $V'$ is not a cycle. Equivalently, G is chordal if the graph induced by any cycle of length at least 4 is not a cycle. Chordal graphs have been well studied in literature since a lot of the typical NP-Hard graph problems can be solved quickly for this graph class [10]. In particular, there exists a simple polynomial time algorithm which solves the Clique Cover problem in chordal graphs [9]. The Clique Cover problem is defined as follows: given a graph G(V, E) and a $k \in \mathbb {N}$, decide if there exists a collection of k-many cliques of G that covers V. An instance of this problem is denoted by $(G(V,E),n,k)$ where $|V|=n$.

1.1 Motivation

Optimal guarding of terrains arises in the placement of antennas for communication networks. We study this problem in two dimensions to understand better the considerably more difficult problem of guarding terrains in three dimensions. Moreover, 1.5-dimensional terrains arise directly in applications of coverage along a highway as well as in security lamp and camera placement along walls and streets [3, 11, 14].

1.2 Related Work

The Terrain Guarding problem was stated in 1995 by Chen et al. in [4]. In the same paper, the authors hypothesized that both the continuous and discrete versions of the problem are NP-Hard, but did not provide a concrete proof in support of their claim. It was only in 2010 that King and Krohn finally showed that both the Continuous Terrain Guarding and Discrete Terrain Guarding problems are NP-Hard [14]. Meanwhile, the problem continued to be studied from the viewpoint of approximation algorithms and Ben-Moshe et al. [3] proposed the first constant-factor approximation for the discrete version of the problem. The factor of approximation was improved over the course of several papers [5, 6, 13] and finally a PTAS for the discrete version of the problem was given by Krohn et al. in 2014 [15]. A PTAS for Continuous Terrain Guarding was obtained a couple of years later by Friedrichs et al. [8].

Thus, we have a satisfactory understanding of the approximability of the terrain guarding problem. In the paper that they proved the NP-Hardness of the terrain guarding problems, King and Krohn stated that the biggest remaining question regarding this problem was its fixed-parameter tractability. Terrain guarding has been shown to have a FPT algorithm with respect to few parameters [1, 12] but it is still not known if the problem is fixed-parameter tractable with respect to the number of guards that are required to guard the terrain. In 2018, Ashok et al. showed that this is indeed true for the Discrete Orthogonal Terrain Guarding problem in [2]. Their algorithm exploited a connection between guarding orthogonal terrains and covering chordal graphs with cliques that was established by Katz and Roisman in Lemmas 3.6 and 3.7 of their paper [11]. In these lemmas, they considered the visibility graph of the Annotated Orthogonal Terrain Guarding instance $(T(V,E),n,k,\mathscr {R},\mathscr {C}_l)$ and proved that it is chordal. They then showed that any clique of the visibility graph can been seen by a single guard. In this paper, we will show that these lemmas can be stated and proved for a special case of the annotated version of the terrain guarding problem called the Left-Sided Terrain Guarding problem (we define the problem formally in the next section).

1.3 Results

This paper presents two theorems which prove the equivalence between a restricted case of the Left-Sided Terrain Guarding problem and the Clique Cover problem in chordal graphs. Theorem 3.1 proves that the visibility graph corresponding to an instance of this problem is chordal. Theorem 3.2 builds on top of this and proves that there exists a clique in the visibility graph, if, and only if, there exists a guard that sees all the vertices of that clique. Collating these two theorems gives us the main result of this paper. Lemmas 3.4 and 3.5 show that this paper indeed generalizes results that are known for orthogonal terrains.

Main Result. Let $(T(V,E),n,k,\mathcal {G},\mathcal {C})$ be a Left-Sided Terrain Guarding instance where $\mathcal {G}\cap \mathcal {C}= \emptyset$ and $\textsc {Vis}\; \mathcal {G}\supseteq \mathcal {C}$. Then, this is a true instance of the problem if, and only if, $(G_T(\mathcal {C}, E'),|\mathcal {C}|,k)$ is a true instance of the Clique Cover problem where $G_T$, the visibility graph of T, is a chordal graph.

2 Preliminaries

For points a and b on T, we say a precedes b, denoted by $a \prec b$, if a appears on the terrain before b does (the terrain is scanned from left to right). The Order Claim, which was originally stated in [3] and later slightly generalized in [1], lays the foundation for the theorems that follow in the next section.

Lemma 2.1

(Order Claim). Let a, b, c and d be four points on a terrain T(V, E) such that $a \prec b \prec c \prec d$. If a sees c and b sees d, then, a sees d.

In an orthogonal terrain T(V, E), a vertex $v_i$, where $1<i<n$, is convex if $x(v_i)=x(v_{i+1})$ and $y(v_i)<y(v_{i+1})$ or $x(v_i)=x(v_{i-1})$ and $y(v_i)<y(v_{i-1})$ and is reflex otherwise. Equivalently, $v_i$ is a convex vertex if the angle formed by the vertices $v_{i-1}$, ${v_i}$ and $v_{i+1}$ (measured above the terrain) is convex and is a reflex vertex otherwise. It is a left vertex if $x(v_{i-1})=x(v_{i})$ and a right vertex if $x(v_{i})=x(v_{i+1})$. The set of convex vertices is denoted by $\mathscr {C}$ and the set of reflex vertices is denoted by $\mathscr {R}$. In Fig. 1b, the convex vertices are encircled and the reflex vertices are marked using squares. The set of vertices which are both convex and left are called left convex vertices and is denoted by $\mathscr {C}_l$. Right convex, left reflex and right reflex vertices are defined similarly and are denoted by $\mathscr {C}_r$, $\mathscr {R}_l$, and $\mathscr {R}_r$ respectively. Vertices $a \in \mathscr {C}_l$ and $b \in \mathscr {R}_r$ are said to be of the opposite type as are vertices $c \in \mathscr {C}_r$ and $d \in \mathscr {R}_l$. $v_1$ is defined to be of the opposite type as $v_2$ and $v_n$ is defined to be that of $v_{n-1}$. In Fig. 1b, $\mathscr {R}_l = \{v_7\}$, $\mathscr {R}_r = \{v_2,v_4,v_8\}$, $\mathscr {C}_l = \{v_1,v_3,v_5,v_9\}$ and $\mathscr {C}_r = \{v_6\}$. Finally, we define a restriction of the annotated version of the terrain guarding problem where we allow the guards to only see in one direction.

Problem

Left-Sided Terrain Guarding: Given a terrain T(V, E), $k \in \mathbb {N}$ and $\mathcal {G},\mathcal {C}\subseteq V$ decide if there exists a $S \subseteq \mathcal {G}$ with $|S| \le k$ such that for all $v \in \mathcal {C}$, there is a $g \in \mathcal {G}$ such that $x(v) \le x(g)$ and g sees v.

Equivalently, in this version of the problem we enforce that the guards of $\mathcal {G}$ can only see to their left. In this case, we say that $\mathcal {G}$ is a set of left guards. Right-Sided Terrain Guarding and right guards are defined symmetrically. In the paper that they introduced the terrain guarding problem [4], Chen et al. also described the left and right-guarding versions of the problem. They produced an algorithm, which they called Army-Withdraw, which ran in linear time to solve these versions. Elbassioni et al. [6] constructed a bipartite graph G from a Left-Sided Terrain Guarding instance $(T(V,E),n,k,\mathcal {G},\mathcal {C})$ where $\mathcal {G}\cap \mathcal {C}= \emptyset$ with the bipartition $(\mathcal {G}, \mathcal {C})$. An element $(g,c) \in \mathcal {G}\times \mathcal {C}$ was an edge of this graph if $x(c) \le x(g)$ and g sees c. They then proved that the vertex-vertex incidence matrix corresponding to this graph is totally balanced an used the properties of such matrices to produce a 4-approximation algorithm for the Annotated Terrain Guarding problem where $\mathcal {G}\cap \mathcal {C}= \emptyset$. The author refers the reader to [7] and [10] for a detailed discussion on totally balanced matrices.

3 Terrains and Chordal Graphs

In this section, we will prove two theorems which will lead us to the main result of this paper. Even though this section deals exclusively with the Left-Sided Terrain Guarding problem, the claims and their proofs apply, by symmetry, to the Right-Sided Terrain Guarding problem. The first theorem proves that the visibility graph of an Left-Sided Terrain Guarding instance $(T(V,E),n,k,\mathcal {G},\mathcal {C})$ is chordal. The proof of this theorem considers a cycle C of length k, where $k \ge 4$, in $G_T$ and proves that the subgraph induced by C, denoted by $G_T[C]$, is not a cycle. This is done by an extensive use of Lemma 2.1 on the various cases that arise depending on the positions of the vertices of C and the guards that see them on the terrain.

The second theorem considers a Left-Sided Terrain Guarding instance $(T(V,E),n,k,\mathcal {G},\mathcal {C})$ where $\mathcal {G}$ and $\mathcal {C}$ are disjoint and $\textsc {Vis}\; \mathcal {G}\supseteq \mathcal {C}$. It proves that the vertices of any clique of $G_T$ can be seen by a single guard. This proves that k-many guards can see all of $\mathcal {C}$ if, and only if, there exists k-many cliques that cover $G_T$. This along with the previous theorem directly proves our main result. We prove this theorem using induction over the number of vertices in the clique. In Fig. 8, we provide an example of a terrain where this claim fails if $\mathcal {G}\cap \mathcal {C}$ is non-empty.

Finally, we prove two corollaries of our main result. The first one states that if a Left-Sided Terrain Guarding instance is false, then there exists a small subset of $\mathcal {C}$ (with $k+1$ vertices) that cannot be seen by k-many guards. We prove this by producing an independent set U of size $k+1$ in $G_T$ and observing that if k guards did see all the vertices of U, then U would fail to be an independent set. The second corollary proves that for an orthogonal terrain T, $(T(V,E),n,k,\mathscr {R},\mathscr {C}_l)$ is a true instance if, and only if, $(G_l(\mathscr {C}_l,E'),|\mathscr {C}_l|,k)$ is a true instance of the Clique Cover problem. This was the result obtained in [11] by Katz and Roisman. This is done by observing that left convex vertices can only see to one side.

Theorem 3.1

Let $(T(V,E),n,k,\mathcal {G},\mathcal {C})$ be a Left-Sided Terrain Guarding instance. Then, the visibility graph of this instance, say $G_T$, is chordal.

Proof

Let $C \subseteq \mathcal {C}$ where $|C| =p \ge 4$ be a cycle in $G_T$. We prove that $G_T[C]$ is not a cycle. Let $C = \{c_1,c_2 \dots c_p\}$ be the order of the vertices as they appear on the cycle. Also, we assume, without loss in generality, that $c_i \preceq c_1$ for all $c_i \in C$ and that $c_p \prec c_2$. As $c_1$ and $c_p$ are neighbours in $G_T$, there is a left guard $g_{1,p}$ which sees both these vertices. Similarly, we have $g_{1,2}$, a left guard, which sees both $c_1$ and $c_2$. Note that $c_1 \preceq g_{1,p}$ and $c_1 \preceq g_{1,2}$. If $g_{1,2} = g_{1,p}=g$, then g sees both $c_2$ and $c_p$. This implies that $c_2$ and $c_p$ share an edge in $G_T[C]$. Since $p \ge 4$, $(c_2,c_p)$ is a chord of the cycle. Thus, $G_T[C]$ is not a cycle. We are now left with two cases:

Case 1

($g_{1,p} \prec g_{1,2}$). This is illustrated in Fig. 2. Here, $c_p \prec c_2 \prec g_{1,p} \prec g_{1,2}$ and $c_p$ sees $g_{1,p}$ while $c_2$ sees $g_{1,2}$. Thus, by Lemma 2.1, $g_{1,2}$ sees $c_p$. Since $g_{1,2}$ sees $c_2$ by construction, there is an edge between $c_2$ and $c_p$ in $G_T$. As observed previously, this implies that $G_T[C]$ is not a cycle. Note that $g_{1,p}$ could be $c_1$.

Fig. 2.

This figure illustrates Case 1 of Theorem 3.1 where $g_{1,p} \prec g_{1,2}$. Two vertices that see each other are connected by a dashed line. If we substitute a, b, c and d with $c_p$, $c_2$, $g_{1,p}$ and $g_{1,2}$ respectively in Lemma 2.1, we get that $c_p$ sees $g_{1,2}$ in this case.

Case 2

($g_{1,2} \prec g_{1,p}$). In this case, we have two possibilities. The first one is when $c_1 \prec g_{1,2}$ while the second one is where $g_{1,2}$ is $c_1$. Figure 3a illustrates the first case. Here, $c_2 \prec c_1 \prec g_{1,2} \prec g_{1,p}$ and $c_2$ sees $g_{1,2}$ while $c_1$ sees $g_{1,p}$. We infer that $g_{1,p}$ sees $c_2$ by applying Lemma 2.1 on these vertices. Thus, there is an edge between $c_2$ and $c_p$ in $G_T[C]$ proving that $G_T[C]$ is not a cycle. Now, assume that $c_1 = g_{1,2}$. This is considered in Fig. 3b. Unfortunately, in this situation, we cannot use Lemma 2.1 directly.

We now consider $c_3$, the other neighbour of $c_2$, in C. Note that $c_3$ exists as $|C| \ge 4$. Since $c_2$ and $c_3$ are neighbours in C, and thus in $G_T$, there exists a left guard, say $g_{2,3}$, which sees both these vertices. If $g_{2,3} = g_{1,p}=g$, then $c_3$ has an edge with $c_1$ in $G_T$. Since the neighbours of $c_1$ in C are $c_2$ and $c_p$, where $p>3$, $(c_1,c_3)$ is chord of C. This proves that $G_T[C]$ is not a cycle. Thus, we will focus on the situations where $g_{2,3} \ne g_{1,p}$ in the cases that follow.

We will show that if $c_3 \prec c_2$, then $G_T[C]$ is not a cycle. We will then prove that if $c_{j+1} \prec c_2 \prec c_j \prec c_1$ for any $3 \le j < p$, then $G_T[C]$ is not a cycle. Finally, we prove that these two claims jointly imply that $G_T[C]$ is never a cycle and complete our proof.

Fig. 3.

This figure depicts Case 2 of Theorem 3.1 where $g_{1,2} \prec g_{1,p}$. In (a) $c_1 \prec g_{1,2}$, while in (b) $c_1=g_{1,2}$. In the first possibility, we can apply Lemma 2.1 on the encircled vertices. Doing so, we get that $c_2$ sees $g_{1,p}$. We are unable to apply the Lemma 2.1 on (b). The dashed line between $c_1$ and $c_2$ in (b) is curved for illustrative purposes.

Claim 1

If $c_3 \prec c_2$, then $G_T[C]$ is not a cycle.

We consider the following two cases depending on the position of $c_3$: it precedes $c_p$ or it lies between $c_p$ and $c_2$.

Subcase 2.1

($c_3 \prec c_p$). We have two possibilities: $g_{2,3} \prec g_{1,p}$ or $g_{1,p} \prec g_{2,3}$. These are shown in Fig. 4a and 4b respectively. Lemma 2.1 guarantees an edge between $c_1$ and $c_3$ in the former case and between $c_2$ and $c_p$ in the latter case in $G_T[C]$ (apply the lemma on $c_3$, $c_p$, $g_{2,3}$ and $g_{1,p}$ in the first case and on $c_p$, $c_2$, $g_{1,p}$ and $g_{2,3}$ in the second case). As noted previously, $G_T[C]$ is not a cycle in both these cases. Note that $g_{2,3}$ could be $c_1$ or $c_2$ in the first case and $g_{1,p}$ could be $c_1$ in the second.

Fig. 4.

This figure illustrates Subcase 2.1 of Theorem 3.1 where $c_3 \prec c_p$. In (a) $g_{2,3}$ precedes $g_{1,p}$, while in (b) $g_{1,p}$ precedes $g_{2,3}$. On applying Lemma 2.1 to the marked vertices, we get that $c_3$ is seen by $g_{1,p}$ in (a) and $c_p$ is seen by $g_{2,3}$ in (b).

Fig. 5.

$c_3$ lies between $c_2$ and $c_p$ in both these figures which illustrate Subcase 2.2 of Theorem 3.1. In (a) $g_{2,3} \prec c_1$, while in (b) $c_1 \prec g_{2,3} \prec g_{1,p}$. On applying Lemma 2.1 on the encircled vertices we infer that $c_3$ is seen by $c_1$ in (a) and by $g_{1,p}$ in (b).

Subcase 2.2

($c_p \prec c_3 \prec c_2$). Depending on the position of $g_{2,3}$, we have three possibilities: $g_{2,3}$ precedes $c_1$, or it lies between $c_1$ and $g_{1,p}$, or it lies after $g_{1,p}$. Note that the third case is equivalent to the one in Fig. 4b since the position of $c_3$ was not used in the proof of the existence of the $(c_2,c_p)$ edge. If $g_{2,3}$ is equal to $c_1$, then $c_1$ has an edge with $c_3$ in $G_T[C]$ since it sees itself as well as $c_3$. Thus, $G_T[C]$ is not a cycle. This leaves two cases: $g_{2,3} \prec c_1$ and $c_1 \prec g_{2,3} \prec g_{1,p}$. These are shown in Figs. 5a and 5b. On applying Lemma 2.1 on the four encircled vertices in the order they appear on the terrain, we infer that the $(c_1,c_3)$ edge exists in $G_T[C]$ in both these cases proving that it is not a cycle.

Thus, we have proven that if $c_3$ precedes $c_2$, $G_T[C]$ is not a cycle. We will complete the proof by proving the following claim.

Claim 2

If $c_{j+1} \prec c_2 \prec c_j \prec c_1$ for some j where $3 \le j < p$, then $G_T[C]$ is not a cycle.

We have three cases depending on the position of the left guard, called $g_{j,j+1}$, which sees $c_j$ and $c_{j+1}$. If $g_{j,j+1} = c_1$, then there exists a $(c_2, c_{j+1})$ edge in $G_T[C]$ since $c_1$ sees $c_2$. As $c_{j+1}$ is neither $c_1$ nor $c_3$, $G_T[C]$ is not a cycle. The other two cases: $g_{j,j+1} \prec c_1$ and $c_1 \prec g_{j,j+1}$ are shown in Figs. 6a and 6b respectively. In both these cases, on applying Lemma 2.1 on the marked vertices, we get that $c_2$ and $c_{j+1}$ share an edge in $G_T[C]$. From the argument that we just stated, $G_T[C]$ is not a cycle. Note that $g_{j,j+1}$ could be $c_j$ in Fig. 6a. This proves our claim.

Fig. 6.

This figure corresponds to cases that are discussed in Claim 2 of Theorem 3.1. Here, $c_j$ lies between $c_2$ and $c_1$. In (a) $g_{j,j+1} \prec c_1$, while in (b) $g_{j,j+1}$ lies after $c_1$. On applying Lemma 2.1, we get that $c_1$ sees $c_{j+1}$ in (a) and $c_2$ sees $g_{j,j+1}$ in (b).

Now, let $D = \{i \mid c_2 \prec c_i \prec c_1\}$. If D is empty, then $c_3 \prec c_2$. By our first claim, $G_T[C]$ is not a cycle. Since we assumed that $c_p \prec c_2$, $j:= \max \{ i \mid i \in D\}<p$. Thus, $c_{j+1}$ exists and is not in D. This implies that $c_{j+1} \prec c_2 \prec c_j \prec c_1$ and will prove that $G_T[C]$ is not a cycle by the second claim. This completes the proof of this theorem since C was arbitrary cycle of length at least 4.   $\square$

Theorem 3.2

Let $(T(V,E),n,k,\mathcal {G},\mathcal {C})$ be a Left-Sided Terrain Guarding instance where $\mathcal {G}\cap \mathcal {C}= \emptyset$ and $\textsc {Vis}\; \mathcal {G}\supseteq \mathcal {C}$. Then, for $K \subseteq \mathcal {C}$, $G_T[K]$ is a clique if, and only if, there is a $g \in \mathcal {G}$ such that $\textsc {Vis}\; g \supseteq K$.

Proof

Let K be a set such that there is a $g \in \mathcal {G}$ such that $\textsc {Vis}\; g \supseteq K$. Then, for any pair of vertices in K there is an edge between them in $G_T[K]$ since there is a guard (g itself) seeing them both. Thus, $G_T[K]$ is a clique. Now, we prove the forward direction of the claim. Assume that $K \subseteq \mathcal {C}$ such that $G_T[K]$ is a clique. We prove that there exists a guard seeing all of K by induction on the number of vertices in K. If $|K| = 1$ or $|K| = 2$, then our claim follows trivially. Assume that our supposition holds for all cliques of size at most p, where $p \ge 2$.

Let $K = \{k_1, k_2, \dots k_p,k_{p+1}\}$ be a subset of $\mathcal {C}$ such that $G_T[K]$ is a clique. The vertices of K are ordered according to how they appear on the terrain. Let $K' = \{k_2 \dots k_p,k_{p+1}\}$. Since $G_T[K']$ is a clique of size p, by the induction hypothesis, there is a left guard $g_1$ such that $\textsc {Vis}\; g_1 \supseteq K'$. Since there is a $(k_1,k_{p+1})$ edge in $G_T[K]$, there is a left guard, say $g_2$, which sees them both. If $g_1=g_2 = g$, then we have $\textsc {Vis}\; g \supseteq K$ proving the supposition. We are now left with two cases:

Case 1

($g_2 \prec g_1$). This case is shown in Fig. 7a. Here, we observe that $k_1 \prec k_j \prec g_2 \prec g_1$ where $k_1$ sees $g_2$ and $k_j$ sees $g_1$. By Lemma 2.1, $g_1$ guards $k_1$ as well. Thus, $\textsc {Vis}\; g_1 \supseteq K$.

Case 2

($g_1 \prec g_2$). This is illustrated in Fig. 7b. Here, on applying Lemma 2.1 on the marked vertices, we get that $g_2$ sees $k_j$ for all j where $2 \le j \le p$. Thus, $\textsc {Vis}\; g_2 \supseteq K$. Note that we can apply Lemma 2.1 on these four vertices only because $g_1 \ne k_{p+1}$.

Fig. 7.

This figure corresponds to the cases that arise in Theorem 3.2. In (a) $g_2 \prec g_1$, while in (b) $g_1 \prec g_2$. By Lemma 2.1, $g_1$ also sees $k_1$ in (a) and $g_2$ guards all the vertices from $k_2$ through to $k_{p+1}$ in (b).

This proves our supposition and completes the proof by induction. Note that the situations illustrated in Figs. 7a and 7b are similar to the ones in Figs. 2 and 3a. They are presented in this proof again for clarity.   $\square$

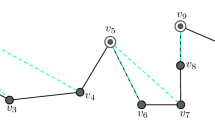
This theorem’s claim is not true if $\mathcal {G}\cap \mathcal {C}\ne \emptyset$. A non-example is presented in Fig. 8. In the terrain illustrated by that figure, we let $\mathcal {C}= \{v_1, v_3, v_4\}$ and $\mathcal {G}= \{v_4, v_5, v_7\}$ be a set of left guards. $v_1$ shares an edge with both $v_3$ and $v_4$ in $G_T$ since $v_7$ sees both $v_1$ and $v_3$ while $v_5$ sees both $v_1$ and $v_4$. Furthermore, since $v_4$ sees itself as well as $v_3$, there is an edge between $v_3$ and $v_4$ in $G_T$. Thus, $G_T[\mathcal {C}]$ is a clique. However, none of the three guards in $\mathcal {G}$ guard all the vertices of $\mathcal {C}$: $v_4$ does not see $v_1$, $v_5$ does not see $v_3$, and $v_7$ does not see $v_4$. It is also clear that Theorem 3.2 fails to hold if $\textsc {Vis}\; \mathcal {G}\supseteq \mathcal {C}$. For example, if $\mathcal {C}=\{v_3\}$ and $\mathcal {G}= \{v_5\}$ in the terrain illustrated in Fig. 8, then the isolated vertex $v_3$ is a clique but no guard in $\mathcal {G}$ sees it.

Theorem 3.1 and 3.2 are, to the best of the author’s knowledge, an addition to existing literature. Combining these two theorems gives us the main result of this paper.

Theorem 3.3

Let $(T(V,E),n,k,\mathcal {G},\mathcal {C})$ be a Left-Sided Terrain Guarding instance where $\mathcal {G}\cap \mathcal {C}= \emptyset$ and $\textsc {Vis}\; \mathcal {G}\supseteq \mathcal {C}$. Then, this is a true instance of the problem if, and only if, $(G_T(\mathcal {C}, E'),|\mathcal {C}|,k)$ is a true instance of the Clique Cover problem where $G_T$, the visibility graph of T, is a chordal graph.

As stated in the beginning of this section, the above result also holds for the Right-Sided Terrain Guarding problem. It is well known that in a chordal graph G(V, E), the minimum number of cliques required to cover V, denoted by $\overline{\chi }(G)$, is equal to the size of a maximum sized independent set of G, denoted by $\alpha (G)$ [10]. The algorithm that solves the Clique Cover problem can be modified slightly to solve the Independent Set problem in polynomial time [9]. We use these two properties of chordal graphs in the proof of the lemma that follows.

Fig. 8.

This terrain presents an example where a clique in $G_T$ is not seen by a single left guard if $\mathcal {G}\cap \mathcal {C}\ne \emptyset$. The vertices of $\mathcal {C}$ and $\mathcal {G}$ have been encircled and marked by squares respectively.

Lemma 3.4

Let $(T(V,E),n,k,\mathcal {G},\mathcal {C})$ be a Left-Sided Terrain Guarding instance where $\mathcal {G}\cap \mathcal {C}= \emptyset$ and $\textsc {Vis}\; \mathcal {G}\supseteq \mathcal {C}$. One can decide, in polynomial time, if this is a true instance of the problem. If this instance is false, then one can find $U \subseteq \mathcal {C}$ in polynomial time such that $|U| = k+1$ and $(T(V,E),n,k,\mathcal {G},U)$ is a false instance.

Proof

By Theorem 3.3, we know that the visibility graph, say $G_T$, corresponding to $(T(V,E),n,k,\mathcal {G},\mathcal {C})$ is chordal and that it is a true instance if, and only if, $(G_T(\mathcal {C}, E'),|\mathcal {C}|,k)$ is a true instance of the Clique Cover problem. Since the Clique Cover problem can be solved in polynomial time in chordal graphs, we can decide if $(T(V,E),n,k,\mathcal {G},\mathcal {C})$ is a true instance of the Left-Sided Terrain Guarding problem in polynomial time.

Now, if $(T(V,E),n,k,\mathcal {G},\mathcal {C})$ is false, then $G_T$ cannot be covered by k many cliques. Thus, $\overline{\chi }(G_T) > k$. This implies that $\alpha (G_T) > k$. We compute a maximum sized independent set of $G_T$ and let U be a subset of size $k+1$ of this independent set. Since $G_T$ is chordal, this can be done in polynomial time. Clearly, U is an independent set of $G_T$. If there exists k many guards in $\mathcal {G}$ which guards U, then there must exist one guard which sees at least two vertices of U. By construction of $G_T$, there must exist an edge between them. This contradicts the fact that U is an independent set of $G_T$ and thus completes the proof of this lemma.    $\square$

We note that the above lemma holds for the right-sided version of the terrain guarding problem as well. The lemma stated and proved above generalizes Lemmas 4.8 and 4.9 of [2]. These were used to present a FPT algorithm with respect to the solution size for the Discrete Orthogonal Terrain Guarding problem in that paper. We conclude this paper by proving that the following result by Katz and Roisman [11] follows from Theorem 3.3.

Lemma 3.5

Consider the Annotated Orthogonal Terrain Guarding instance $(T(V,E),n,k,\mathscr {R},\mathscr {C}_l)$ and let $G_l$ be the visibility graph corresponding to this instance. Then, $G_l$ is chordal. Furthermore, $(T(V,E),n,k,\mathscr {R},\mathscr {C}_l)$ is a true instance of the problem if, and only if, $(G_l(\mathscr {C}_l,E'),|\mathscr {C}_l|,k)$ is a true instance of the Clique Cover problem. The symmetric claim holds for the set of right convex vertices.

Proof

Note that a vertex $v \in \mathscr {C}_l$ can only see to its right (referring back to Fig. 1b will make this observation straightforward) [11]. Equivalently, a vertex $g \in \mathscr {R}$ which is to guard v needs to look only to its left. Thus, we can consider the guards which are required to guard $\mathscr {C}_l$ to be a set of left guards. Using a symmetric argument, we see that the guard set that is to guard the right convex vertices can be considered to be a set of right guards. Also, we note that $\textsc {Vis}\; \mathscr {R}\supseteq V$. This implies that $\mathscr {R}$ sees all of $\mathscr {C}_l$ and $\mathscr {C}_r$. Since $\mathscr {C}\cap \mathscr {R}= \emptyset$, we can apply Theorem 3.3 to the Left-Sided Terrain Guarding instance $(T(V,E),n,k,\mathscr {R},\mathscr {C}_l)$. By a symmetric argument, our claim is also true for the Right-Sided Terrain Guarding instance $(T(V,E),n,k,\mathscr {R},\mathscr {C}_r)$. This completes the proof of the lemma.    $\square$