Keywords

1 Introduction

Mathematical modelling is a major subject among the activities associated with mathematical thinking and has received more attention in recent years, including in the Netherlands. Mathematical modelling became a new component of the examination programmes for the five-year stream (HAVO) and the six-year stream (VWO) in 2015. However, mathematical modelling is absent in the greater part of lower secondary education in the Netherlands.

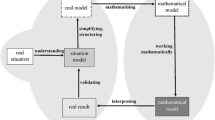
In the field of mathematical modelling, various representations of the modelling cycle exist. According to Blum and Leiß (2005), the modelling process begins with understanding the real situation and problem, resulting in a situation model. Then, the given situation has to be simplified, structured and made more precise, which results in a real model (Blum and Leiß 2005; Blum and Borromeo Ferri 2009). In the modelling cycle of Perrenet and Zwaneveld (2012), these first two parts of the process are taken together as the conceptualization phase, followed by mathematizing, solving, interpreting and validating. Plath and Leiß (2018) emphasize the importance of the conceptualization phase and use this as the basis for all subsequent decisions (see also Blum and Leiβ 2005; Borromeo Ferri 2006; Leiβ et al. 2019). Therefore, in this chapter, we will focus especially on the difficulties that students encounter in the conceptualization phase.

Assumption making is one of the modelling competencies used to understand a real problem and to set up a model (Maaβ 2006). Galbraith and Stillman (2001) emphasized the role of assumption making as an underrated aspect of successful modelling activity. Seino (2005) argued that assumptions are “the bridge” that connects the real world and the mathematical world. While the ability of novice modellers to make assumptions is rather weak (Chan et al. 2012), it hardly receives attention in the Dutch mathematics curriculum. Therefore, it is important to examine students’ difficulties related to assumption making, especially in lower secondary education.

Usually, modelling problems in context-rich assignments are offered to learners through texts. One of the first obstacles students may encounter is reading and interpreting text. In secondary school, being able to read a problem is a decisive factor in solving a problem (Korhonen et al. 2012). The language used at school often forms an obstacle to learning mathematics (Van Eerde and Hajer 2009). Language proficiency may play a different role in every phase of the modelling cycle. In the conceptualization phase, the student has to be able to understand the text in which the problem is posed to translate it into a conceptual model. Plath and Leiβ (2018) pointed out that the linguistic features of understanding and solving mathematical modelling tasks have not been thoroughly examined. Therefore, this study will also investigate the role of language comprehension in the conceptualization phase.

To improve vertical coherence in the curriculum, more insight is needed into the modelling ability of students in lower secondary education and the difficulties they encounter while solving modelling tasks. Therefore, this study explores two research questions: How do Dutch lower secondary students perform on context-rich mathematical modelling tasks? Which problems do they encounter in the conceptualization phase?

2 Method

To answer these questions, we developed two modelling tasks and two mathematical core assignments for three age groups and conducted task-based interviews.

2.1 Participants

The participants in the study were 73 students from Grade 6 (age 11–12), 116 students from Grade 8 (age 13–14) and 59 students from Grade 10 (age 15–16). In the Netherlands, Grade 6 is the final year of primary school, Grade 8 is part of lower secondary education and Grade 10 is part of upper secondary education. In total, four primary schools and four secondary schools with seven classes located in an urban environment participated in this research (see Table 19.1).

Table 19.1 Number of students per task, grade and school
Full size table

Schools A, B and C were primary schools and schools D, E, F and G were secondary schools. All schools were located in an urban environment. In schools B, D and E, most students were raised bilingually with different parental languages. School G had a more mixed population. The other schools, A, C and F, have more homogeneous populations whose first language is mainly Dutch.

The teacher of each class selected two students, one with strong language proficiency and one with weak language proficiency, with whom we performed task-based interviews. These teachers had taught these students for over a year. Task-based interviews were performed with 26 learners (see Table 19.2).

Table 19.2 Number of interviewees per task and grade
Full size table

2.2 Modelling Tasks

We designed two paper-and-pencil mathematical modelling tasks in a rich context with three difficulty levels. The first level was Grade 6, the second level Grade 8 and the third level Grade 10. The complexity increased with each level, such as by adding more data to the process (Task 1) or by providing a context that is further from students’ daily experiences (Task 2). Furthermore, the modelling tasks were developed according to the design principles of Galbraith (2006) and were improved using feedback from two primary school teachers, three secondary school teachers and an independent mathematics education researcher.

Task 1

You want an iPad for your birthday. That is why your mother asks you to investigate the prices of iPad Pros. Figure 1 shows the two different sizes of the iPad Pro in inches. In many English-speaking countries, an inch is used as a measure of length.

Imagine that your mother travels the world for her work. She is able to buy an iPad for you in one of the countries she is visiting. She only does this if it is cheaper than in the Netherlands. Next week she has to go to San Francisco. That is in the USA, where they use the American dollar. Then, she travels to Singapore. That is in Asia. In Singapore, they use the Singapore dollar. The values of the various currencies against the euro can be found in Table 1. The prices of the various iPads are shown in Table 2.

Advise your mother where the best place is to buy the iPad. It is important that you also explain which format you choose and why. Explain to your mother how you came to your decision.

Task 2

Just before the holiday you organize a dance party in this classroom for the children in your grade. There will be 32 children at the party. There are a few tables and chairs and a few more closets.

  1. 1.

    Try to calculate if there is enough space to dance.

  2. 2.

    Make a map of the classroom during the party and give the dimensions.

The first modelling task consisted of an algebraic problem. In this task, all the information needed for the student to solve the task was given. Consequently, this task contained a longer text to read. The student had to discern the information relevant to construct a model. We used a single best answer question format, which is comparable to problems in mathematics textbooks and the Dutch national examinations. The task concerned a pupil who needs an iPad for school. Her mother travels the world for her work and would be able to buy an iPad in one of the countries she is visiting. The question for Grade 6 students was to calculate where the iPad is the least expensive. Task 1 shows the shortened version of the task for Grade 6. We left out the tables showing the currencies from different countries, the iPad prices in the different countries and an image of an iPad. Grade 8 students also had to account for the Value-Added Tax, and Grade 10 students also had to calculate the import taxes.

The second task concerned geometry. The problem description was stated as an open-ended question. The task concerned the organization of a dance party. Grade 6 students had to organize a dance party in the classroom for the students in their grade, as shown in Task 2. The original version of this task also contained a picture of dancing children in a classroom. Grade 8 students had to organize a dance party in the school canteen and Grade 10 students had to complete the same assignment for the music hall. Students needed to calculate the dancing space for the appropriate number of party-goers and make a map of the party, including the dimensions. This second task had missing information that required students to make spatial and numerical assumptions.

2.3 Mathematical Core Assignment

We designed a mathematical core assignment focusing on the mathematical content without any context to identify pure mathematical problems. The mathematical core assignment of the first task focused on currency calculations, percentages and reading abilities. The students in Grades 8 and 10 had to solve an additional question with a percentage calculation. For all grades, the table showing the currencies in the different countries was given. The core assignment of task two asked for the meaning of the word area, applications of the metric system and the area calculation. The students in Grades 8 and 10 had to solve a second question regarding calculating an area and a third question for which they had to draw a 0.5 dm2 area.

2.4 Task-Based Interview

We conducted semi-structured interviews with 26 students. We prepared ten main questions and, depending on the given answers, the interviewer asked clarification questions. The questions that were posed focused on the understanding of the task, text comprehension, word problems, problems the students encountered, outcomes and the approach taken, focusing on the different ways of solving the task. Examples of the questions asked include the following: Can you explain in your own words what you had to do? Are there words that you did not know, or are there sentences that you did not understand? How did you perform the task?

2.5 Procedure

The students had to construct their answers individually. After the modelling task was handed in, the core assignment was given. Most of the students finished both assignments in 30 min. The interviews were conducted at school directly after the assignments.

2.6 Analysis

2.6.1 Analysis of Student Work

All student answers were scored using an answer model. In addition, we highlighted (parts of) the answers that could inform us of the problems that the students encountered. Because all tasks had different total scores, we calculated the percentages of the points obtained for each student and task. A portion of the student answers were scored by a second rater (n = 37). A Cohen’s kappa of κ = 0.73 indicated sufficient inter-rater agreement. Linear mixed model analyses were conducted in SPSS to account for the hierarchical structure of the data. In the first step of the analysis, a three-level null model (model 0) was estimated without explanatory variables. This baseline model was used to determine the variance within and between Task 1 and Task 2. In the next step (model 1), the explanatory variables, the mathematical core assignment scores, were added and the interaction between the task and mathematical core assignment (MCA). In the second step of the analysis (model 2), we included grade and the interaction between the task and grade. We ultimately excluded the school level due to the small numbers. The correlations between the scores for the modelling task and the mathematical core assignment were calculated.

2.6.2 Analysis of Task-Based Interviews

The interviews with each student lasted from 6 to 20 min. The audio recordings of the interviews were transcribed. We used the modelling cycle of Perrenet and Zwaneveld (2012) as a tool to analyse the students’ answers (see also Kaiser et al. 2006). First, we coded the data in terms of the modelling activities of conceptualization, mathematization and solving, interpretation, validation, reflection (on the modelling process) and iteration (to improve the model). Assumption making was also added to this coding scheme. Second, we coded the problems that students encountered. Next to difficulties with understanding words and sentences (which we asked about during the interview), we used open coding with an ongoing formulation and refinement of the categories.

3 Results

In this section, we report the results of the paper-and-pencil modelling tasks and the results of the task-based interviews.

3.1 Results of the Modelling Tasks

Table 19.3 reports the average percentages of the correct answers given for Task 1, Task2 and the respective mathematical core assignments (MCA 1 and MCA 2). The students generally did not perform well on the modelling tasks, although the standard deviations indicated some variation. In Grade 6, students failed to earn half the number of points possible on Task 1 and the corresponding mathematical core assignment (MCA 1), while students from Grades 8 and 10 performed better on these tasks. In contrast, the multilevel analysis showed that Grade 6 students performed better on Task 2 than Grade 8 students (p = 0.02). The same effect could not be shown for Grade 6 students versus Grade 10 students (p = 0.07).

Table 19.3 Means and standard deviation on the tasks per Grade
Full size table

In each grade, the learners who performed well at the mathematical core assignment also performed better at the modelling task (p < 0.005). For each additional point on the mathematical core assignment, the score on the modelling task was 0.277 points higher (p < 0.002).

A remarkable finding is the better performance on Task 2 of Grade 6 students compared with the performance of students in Grades 8 and 10. It is possible that this group’s surprisingly better performance on the second task can be attributed to the physical surrounding in which the problem of the Grade 6 students was situated (the classroom) while the problem of the Grade 8 students was the canteen of their school. Galbraith and Stillman (2001) have mentioned the significant importance of students’ physical experience with the context. Therefore, we more closely examined students’ drawings and noticed differences in the quality and detail of the drawings that students created during Task 2. As in Rellensman et al. (2017), we found situational and mathematical drawings but also drawings where learners experienced problems with reducing three-dimensional objects to a two-dimensional map, as well as drawings that were too abstract and have lost too much detail for the student to successfully continue with the modelling problem. The latter type of drawings occurred more often in the higher grades. The students in Grade 6 focused more on the details than the students in Grades 8 and 10.

Furthermore, we asked in MCA 2 for the meaning of the word area. Remarkably, most of the students simply provided the formula of length multiplied by the width instead of offering an explanation. Finally, in Task 1, a frequently occurring mistake was that students multiplied instead of divided in currency calculations. This mistake is related to students’ understanding of the context and mathematical knowledge. In Task 2, most of the students encountered difficulties with calculating the dancing space, and in the mathematical core assignment, it appears that they had difficulty using the metric system.

3.2 Results of the Task-Based Interviews

The task-based interviews showed that most of the interviewed students enjoyed solving the given tasks, but they also found it difficult to make assumptions and solve the task. In addition, they indicated that they had not performed a similar task before.

Contrary to our expectations, the data did not show a substantial difference between the students with a strong language proficiency and those with a weak language proficiency. The interviews, however, illustrated that for some students, language was an important obstacle. In those cases, the learners failed to construct a meaningful representation of the described situation. The transition from reality, presented by the text, to a conceptual model stopped halfway. In all grades, most of the students repeatedly re-read the text of the modelling task and learners at each level encountered difficulties in constructing a meaningful representation of the described modelling problem, sometimes even failing to understand the problem. These representation problems were partially related to language problems. Most of the students were sufficiently able to restate the problem in their own words. They mostly agreed that the text did not contain any difficult words or sentences. Nevertheless, they still had their own interpretations and associations of the context. For example, there were students who drew a map of a classroom party for Task 2 in which the tables were in groups in the middle of the classroom instead of creating an empty dance floor. The following conversation between the researcher and a student shows how the student construed the meaning of a dance party.

Researcher::

Why have you drawn the classroom in this way?

Student::

Because it has to be, right?

Researcher::

Have you ever been to a class party?

Student::

No, not really a class party.

Researcher::

What was it then?

Student::

Just to a Christmas dinner in class, but not really a class party.

According to Dewolf et al. (2011) and Galbraith and Stillman (2001), the context provided in the task exerts an important effect on the interpretation and, thus, also on the solution. This student associated the context with something he recognized (a Christmas party). Although his knowledge of mathematics was sufficient, the student nonetheless failed.

These problems with students’ interpretation of the context occurred in the conceptualization phase. Although some students did not reach a solution, we found that most of them were sufficiently able to explain what the task asked for. They became stuck when they had to formulate this concept mathematically. For this group of students, there seemed to be a barrier between the conceptual model and the mathematical model.

4 Conclusion and Discussion

In this chapter, we examined the performance of Dutch lower secondary students on context-rich mathematical modelling tasks. We compared their performance with the performance of Grade 6 (primary school) and Grade 10 (upper secondary school) students. We found that overall, students did not perform well. In Grade 8, on average, students earned 57% of the total points for task 1 and 40% of the total points for task 2. Although the tasks were assessed by different teachers, the tasks may have been too difficult. The mathematical core assignments showed that mathematical knowledge is indispensable for solving modelling tasks. Moreover, these students had not received any education focused on mathematical modelling or on making assumptions. The standard deviations indicated substantial variation in student performance. When introducing mathematical modelling in lower secondary education, it is important that teachers cater to students’ different learning needs or use collaborative learning tasks in which students can learn from one another.

Our second research question focused on the problems that students encounter, particularly during the conceptualization phase. From the data, we found four types of problems: the inability to simplify, structure and make the problem story more precise; problems of context; the inability to make correct interpretations; and the lack of mathematical direction shown by making overly abstract drawings.

Many of the students encountered problems in translating the real problem to the conceptual model, in the conceptualization phase of the modelling cycle. These findings are in line with previous studies showing that students experience difficulties with reading the problem (Korhonen et al. 2012) and making assumptions (Chan et al. 2012). In all grades, most of the students repeatedly re-read the text of the modelling task, and students encountered difficulties when constructing a meaningful representation of the described modelling problem.

We found that most of the students were able to retell the problem in their own words but were unable to sufficiently solve the problem. The problem for most students seemed to arise at the end of the conceptualization phase. The conceptualization phase (Perrenet and Zwaneveld 2012) consists of the first two steps (from real situation to situation model and then from situation model to real model) of the modelling cycle of Blum and Leiβ (2005). Understanding the problem is the first step, and most of the students were successful at that stage. The second step is to simplify, structure and make the problem more precise, which is where most students became stuck. Assumption making was also a part of this difficulty.

Every student interpreted the given problem in his or her own way. In some cases, these interpretations, caused by a limited or incorrect understanding of the keywords in the problem description (e.g. dance party), led to difficulties in making correct assumptions and affected their solution of the problem. Thinking aloud would be a good addition to gain more insight into students’ difficulties and interpretations. In Task 1, all the needed information was given, unlike in Task 2. For Task 2, we found that Grade 8 students experienced more problems than Grade 6 students, and we also found differences in their assumption making and drawings. This study supports the findings for students aged 13–14 years old from Kaiser and Maaβ (2007), that “strong students choose more challenging models while weaker students prefer simpler ways to achieve their final solutions” (p. 104). Students from Grades 8 and 10 tended more towards abstract drawings and models, so they experienced more difficulties in solving the problems than the Grade 6 students who kept their drawings and models fairly simple. We found that the transition from reality, presented by the text, towards a conceptual model often stopped halfway.