Keywords

1 Introduction

In modern military information wars, Satellite monitoring plays an important role because satellites have important mechanics and advantages. At present, in the information reconnaissance of communication, S-band (USB) monitoring system is widely used, so it is a prominent problem to extract multiple subcarriers from a monitoring frequency band. In the identification of satellite monitoring subcarrier signals, unknown bandwidth and uncorrelated, the manual detection method is mainly used. However, this method has the disadvantages of complex operation, high cost and high false detection rate, which can not meet the needs of satellite monitoring information reconnaissance and can not adapt to the environment of information war.

The time-frequency analysis technique of signal processing is a powerful tool when it is used to analyze non-stationary signals. The number is called time-frequency distribution. Using time-frequency distribution to analyze the signal can give the instantaneous of each moment frequency and its amplitude, and can be used for time-frequency filtering and time-varying signal research.

The so-called joint time-frequency analysis refers to mapping the time-domain signal s(t) to the time-frequency plane (phase plane), so as to analyze the local spectrum characteristics of the signal at a certain time. This method overcomes the shortcoming that the traditional Fourier transform can’t describe the local characteristics of signals, so it has been widely used in signal and image analysis, seismic signal processing, speech analysis and synthesis, nondestructive testing and other non-stationary signal processing, and has achieved great success.

The advantage of independent component analysis is that it does not need instantaneous mixing parameters, and only needs a small amount of statistical information (mutual independence and Gaussian distribution) to recover the source signal from the observed signal. The signal can be extracted without statistical information.

In signal detection, this algorithm can effectively divide the signals with overlapping spectrum. ICA algorithm based on negative entropy maximization and time-frequency analysis is applied to satellite signal recognition algorithm. The analysis shows that it has a great application prospect in military communication.

1.1 Independent Component Analysis

$$ \left[ \begin{gathered} x_{1} \\ x_{2} \\ \vdots \\ x_{n} \\ \end{gathered} \right] = \left( {\begin{array}{*{20}c} {a_{11} } & \ldots & {a_{1n} } \\ \vdots & \ddots & \vdots \\ {a_{m1} } & \cdots & {a_{mn} } \\ \end{array} } \right)\left[ \begin{gathered} s_{1} \\ s_{2} \\ \vdots \\ s_{m} \\ \end{gathered} \right] \Leftrightarrow {\rm{X = AS}} $$
(1)

ICA is based on the assumption that the source signals are independent of each other. Based on this premise, the algorithm can use a linear transformation matrix to transform the variables in the case of unknown source signal and mixed matrix, so that the output variables and source signals are independent.

$$ {\rm{Y = W}}^{{\rm{T}}} {\rm{X = W}}^{{\rm{T}}} {\rm{AS =\, }}\widehat{{\rm{S}}} $$
(2)

In this paper,a fast ICA algorithm based on negative entropy maximization combined with time-frequency analysis is adopted. The algorithm will be introduced step by step.

1.2 Algorithm Theory

The central limit theorem states that: when \(X_{i} (i = 1,2, \cdots )\) are independently identically distributed, \(Y_{n} = \sum\limits_{i = 1}^{n} {\left( {X_{i} - n\mu_{s} } \right)/\sqrt n \sigma_{x} } (n = 1,2, \cdots )\); when \(n \to \infty\), \(Y_{n} \sim N(0,1)\).

Before this separation and extraction algorithm for satellite monitoring signals, we make the following assumptions:

  1. (a)

    The influence of noise is not considered;

  2. (b)

    Satellite signal is a typical stationary independent random signal.

(1) Preprocessing

Firstly, we need to preprocess the signal, including centralized processing and whitening. Hypothesis is to delete the average value of x from it, so that x becomes the zero mean vector. The meaning of whitening is to make the components independent of each other through linear transformation Q of observation vector, and they also have a unit covariance matrix (for example), whitening is realized through PCA network. \({\rm{v = Qx = \ddot{\rm{E}}}}^{{ - 1/2}} {\rm{U}}^{{\rm{T}}} {\rm{x}}\), where \({\ddot{\rm{E}}}\,{ = }\,diag(d_{1,} \cdots ,d_{n} )\) is diagonal matrix of N maxima of correlation matrix \({\rm{R}}_{{\rm{x}}} = {\rm{E\{ xx}}^{{\rm{T}}} {\rm{\} }}\) on its diagonal line, and \({\rm{U}} \in C^{m \times n}\) is a matrix consists of corresponding eigenvectors.

(2) ICA Algorithm Based on the Maximization of Negentropy

In information theory, the negative entropy of Gaussian variable is the largest among all random variables with the same variance. We can use this theory to measure the degree of non Gaussian of a variable. Negative entropy is a kind of modified entropy.. Let \({\rm{y}}_{{\rm{G}}}\) is the combination vector of \(n\) Gauss random variables, with the same mean and variance matrix of y, then \(J({\rm{y}}) = H_{G} ({\rm{y}}) - H({\rm{y}}).\)

$$ \begin{aligned} J({\rm{y}}) & = \int {p({\rm{y}})} \log p({\rm{y}})d{\rm{y - }}\int {p_{G} ({\rm{y}})} \log p_{G} ({\rm{y}})d{\rm{y}} \\ & { = }\int {p({\rm{y}})} \log (\frac{{p({\rm{y}})}}{{p_{G} ({\rm{y}})}})d{\rm{y + }}\int {(p({\rm{y}}) - p_{G} ({\rm{y}}))} \log p_{G} ({\rm{y}})d{\rm{y}} \\ \end{aligned} $$
(3)

The parameters of the output signal can be expressed as Negentropy: \(I({\rm{y}}) = J({\rm{y}}) - \sum\limits_{i = 1}^{n} {J({\rm{y}}_{i} )}\). So the cost function based on maximization of Negentropy is \(\Phi_{NM} ({\rm{W}}) = - \log \left| {\det {\rm{W}}} \right| - \sum\limits_{i = 1}^{n} {J({\rm{y}}_{i} )} + H_{G} ({\rm{y}}) - H({\rm{x}})\)

$$ \Delta {\rm{W}} \propto [({\rm{W}}^{{\rm{T}}} )^{ - 1} - \xi ({\rm{y}}){\rm{x}}^{{\rm{T}}} ]{\rm{W}}^{{\rm{T}}} {\rm{W = (I - }}\xi ({\rm{y}}){\rm{y}}^{{\rm{T}}} {\rm{)W,}}\,\xi ({\rm{Y}}) = - \frac{\partial }{{\partial {\rm{W}}}}\sum\limits_{i = 1}^{n} {J({\rm{y}}_{i} )} $$

The measurement of the independence between different signals can be accomplished by the calculation of negative entropy. However, the calculation of negative entropy needs to estimate the probability density function of random variables. It is very complex to estimate the probability density function. The effectiveness of the estimation depends on the selected parameters, and the amount of calculation will become larger.

(3) The Algorithm Step

The formula of Negentropy calculation is as follows \(J({\rm{y}}) \approx \sum\limits_{i = 1}^{p} {k_{i} \{ E[G_{i} ({\rm{y}})] - E[G_{i} ({\rm{v}})]\}^{2} }\). \(G_{i}\) is a non-quadratic function,

$$\begin{array}{*{20}l} {G_{1} (u) = (1/a_{1} )\log \cos a_{1} u,(1 \le a_{1} \le 2);} \hfill \\ {G_{2} (u) = - (1/a_{2} )\exp ( - a_{2} u^{2} /2),(a_{2} \approx 1);G_{3} (u) = 0.25u^{4} } \hfill \\ \end{array}$$
$$ J_{G} ({\rm{W}}) \propto \{ E[G({\rm{w}}^{{\rm{T}}} {\rm{X}})] - E[G({\rm{v}})]\}^{2} $$
(4)

Maximizing this expression respect to \(E[G({\rm{y}})]\) = \(E[G({\rm{w}}^{{\rm{T}}} {\rm{X}})]\), namely \(E^{\prime}[G({\rm{w}}^{{\rm{T}}} {\rm{X}})] = E[{\rm{Xg(w}}^{{\rm{T}}} {\rm{X)}}] = 0\), where \(g(x)\) is the derivative of \(G(x)\).

Multiply both sides of the equation by \(E[{\rm{g^{\prime}(w}}^{{\rm{T}}} {\rm{X)}}]\), we get \({\rm{W^{\prime}}}E[{\rm{g^{\prime}(w}}^{{\rm{T}}} {\rm{X)}}]{\rm{ = W}}E[{\rm{g^{\prime}(w}}^{{\rm{T}}} {\rm{X)}}] - E[{\rm{Xg(w}}^{{\rm{T}}} {\rm{X)}}]\).

Let \({\rm{W}}^{ + } = - {\rm{W^{\prime}}}E[{\rm{g^{\prime}(w}}^{{\rm{T}}} {\rm{X)}}]\), after transformation we get \({\rm{W}}^{ + } = E[{\rm{Xg(w}}^{{\rm{T}}} {\rm{X)}}] - E[{\rm{g^{\prime}(w}}^{{\rm{T}}} {\rm{X)}}]{\rm{W}}\).

Let \({\rm{W}}^{*} = {\rm{W}}^{ + } /\left\| {{\rm{W}}^{ + } } \right\|\). If the result does not converge, continue to repeat the above steps until it converges. This algorithm can be divided into five steps.

  1. (1)

    Set \(n = 0\), initializing the weighting vector \({\rm{W(0)}}\);

  2. (2)

    Set \(n = n + 1\), computing \(y(t) = {\rm{w}}^{{\rm{T}}} (n)x(t)\);

  3. (3)

    Computing \({\rm{w}}(n + 1)\), and de-correlated \({\rm{w}}(n + 1)\) from \({\rm{w}}_{{1}} {\rm{,w}}_{{2}} {,} \cdots {\rm{w}}_{{\rm{n}}}\).\({\rm{W(n + 1)}} = E[{\rm{Xg(w}}^{{\rm{T}}} {\rm{(n)X)}}] - E[{\rm{g^{\prime}(w}}^{{\rm{T}}} {\rm{(n)X)}}]{\rm{W(n)}}\);

  4. (4)

    Normalizing \({\rm{W(n + 1)}} = {\rm{W(n + 1)}}/\left\| {\rm{W(n + 1)}} \right\|\);

    When the result of the algorithm is not convergent, jump to the second step, continue the iteration;

  5. (5)

    When \(\left| {\rm{W(n + 1) - W(n)}} \right| < \varepsilon\), the algorithm converges, we can get an independent component \(y_{1} = \hat{s}_{1} = {\rm{WX}}\).

When \({\rm{W}}_{i + 1}\) is computed, we use Gram-Schmidt de-correlating algorithm, \({\rm{w}}^{{\rm{T}}}_{{1}} {\rm{x,w}}^{{\rm{T}}}_{{2}} {\rm{x,}} \cdots {\rm{w}}^{{\rm{T}}}_{{\rm{n}}} {\rm{x}}\) will be de-correlated. \({\rm{W}}_{i + 1} {(}n + 1{)}\) will be After each iteration, the following formula is reused to decorrelate.

$$ {\rm{W}}_{i + 1} {(}n + 1{\rm{) = W}}_{i + 1} {(}n + 1{) - }\sum\limits_{j = 1}^{i} {{\rm{W}}^{{\rm{T}}}_{i + 1} {(}n + 1{)}} {\rm{w}}_{j} {\rm{w}}_{j} $$
(5)
$$ {\rm{W}}_{i + 1} {(}n + 1{\rm{) = W}}_{i + 1} {(}n + 1{)/}\sqrt {{\rm{W}}^{{\rm{T}}}_{i + 1} {(}n + 1{\rm{)W}}_{i + 1} {(}n + 1{)}} $$
(6)

2 Short Time-Fourier Transform

STFT(Short Time-Fourier Transform) is one solution of JTFA. The basic idea is to use window function to intercept the signal. Assuming that the signal in the window is stationary, the local frequency domain information can be obtained by Fourier transform. Corresponding to a certain moment t, STFT only analyzes the signal near the window and can roughly reflect the local spectrum information of the signal near the window. Then moving the window function along the signal, we can get the time-frequency distribution of the signal. It is defined as

$$ {\rm{STFT}}({\rm{t}},\omega ) = \int {{\rm{x(}}\tau {)}} \gamma^{*} (\tau - {\rm{t}}){\rm{e}}^{{ - {\rm{j}}\omega \tau }} {\rm{d}}\tau $$
(7)

  • Where: x(t)-signal.

  • \(\gamma (\tau - {\rm{t}}){\rm{e}}^{{ - {\rm{j}}\omega \tau }}\)-basic function.

  • t-time.

  • \(\omega\)-frequency.

2.1 Simulation Results and Analysis

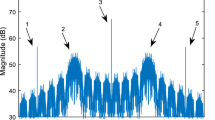
In this paper, a large number of simulation experiments are carried out to solve the problem of extracting and identifying satellite monitoring signals. In this paper, two signals randomly monitored by two satellites are selected randomly. Taking the signal of satellite downlink channel as an example, the two monitoring signals are generated by cortex monitoring terminal. Next, the two signals are extracted and separated, and the test results are verified. Firstly, the time-frequency analysis method is combined with fast ICA algorithm to separate the mixed signals. After three iterations, the first independent component is extracted. It can be seen from the figure that although there are some changes in the amplitude of the source signal, from the point of view of the signal waveform, the separation result is to achieve the desired goal (Figs. 1 and 2).

Fig. 1.
figure 1

Mixed signals with different parameters observed

Full size image
Fig. 2.
figure 2

Extracted signals

Full size image

Simulation results show that:

  1. (a)

    This method analyzes the statistical independence of the signal. Firstly, it avoids the limitation of signal complexity in the previous signal extraction algorithm, and can also identify the signal with wrong parameters, which greatly improves the recognition accuracy.

  2. (b)

    Because the number of sampling points has an impact on the effect of extraction and separation, the parameters of different signals are different, so the extraction effect depends on the total number of sampling points. Generally speaking, with the increase of the number of sampling points, the higher the extraction accuracy; the greater the difference of parameters between signals, the higher the extraction accuracy. When the parameters of the signal are close, if the same number of sampling points can not be used to extract the signal properly, it can be solved by increasing the number of sampling points.

3 Conclusions

This paper presents an algorithm that combines time-frequency analysis with independent variables. As the objective function of non Gaussian random variables, this function can maximize the non Gaussian property of random variables and make the output parts independent of each other. The algorithm is applied to the extraction of satellite signals, which solves the problem of signal recognition without prior knowledge, unknown number of signals and unknown bandwidth of subcarrier signals. In this paper, the algorithm of sub carrier signal detection and acquisition is studied, and each step of the algorithm is discussed in detail. The test and simulation results show that the proposed algorithm can effectively identify the satellite signal subcarriers, and has the advantages of high extraction accuracy and fast convergence speed.