1 Introduction

As a new kind of ship navigation system, AIS can be used for data transmission between ships and shore units [4]. Satellite-based AIS receives the signals through the satellite and feedbacks the information to the test center of the shore [3]. Then a global monitoring of the ship can be realized. Usually, satellite-based AIS communication range is more than 1500 nautical mile (radius), and a satellite view contains a plurality of AIS subnets. And this will cause the signal collision phenomenon which can reduce ship detection rate; thus, how to separate signal accurately is an important issue.

Since the source signal (i.e., a signal transmitted by AIS subnet) is statistically independent, the method of ICA [5] to separate the AIS mixed signal is general. ICA algorithm has been widely used in various subjects, such as speech signal processing, medical signal processing, image enhancement, pattern recognition. For example, Budiharto proposed blind speech separation system using FastICA for audio filtering and separation that can be used in education or entertainment [2]. En et al. [7] used the FastICA to denoise the voice signal having strong noises, which successfully achieves the goal of conditional continuous speech signal transmission and improves to some extent the quality of the voice transmission. ICA algorithm includes information maximization (Informax) algorithm [1] and extended Informax [10], the natural gradient algorithm [9] and FastICA algorithm [14]. Among these, Informax algorithm is only used in the situation with super-Gaussian distribution. Then the extended Informax algorithm can separate super-Gaussian and sub-Gaussian mixed signal, but its convergence rate is slow. The natural gradient algorithm is only applicable to the case that the number of observed signals is equal to the number of source signals. FastICA algorithm, also known as the fixed point algorithm, can estimate independent components only through a nonlinear function. However, its robustness is not good and it is sensitive to the initial value of the weight vector. To solve this problem, Douglas and Chao put forward an improved FastICA algorithm [6], using Huber M estimation function as a nonlinear function. And Yang et al. proposed a FastICA algorithm, which combines the Newton iterative method with gradient descent method. In this paper, an improved algorithm is proposed based on the constant model of AIS signal.

2 The Original FastICA Algorithm

2.1 Signal Separation Model

ICA technique separates mixed signals blindly without any information of mixing system. Depending on the mixing process, the blind separation can be divided into linear instantaneous mixing, linear convolution mixing and nonlinear mixing. For satellite-based AIS, received signal is linear instantaneous mixing way, and the separation model is illustrated in Fig. 1.

Fig. 1
figure 1

Separation model

Full size image

In Fig. 1, \(s(t)=[s_1 (t),s_2 (t),\ldots ,s_N (t)]^{T}\) shows N-dimensional statistically independent unknown signal sources, \(x(t)=[x_1 (t),x_2 (t),\ldots ,x_M (t)]^{T}\) denotes M-dimensional observed signals, \(y(t)=[y_1 (t),y_2 (t),\ldots ,y_N (t)]^{T}\) means separation signals. So mathematical model of the ICA can be expressed by matrix:

$$\begin{aligned} \mathbf{X}=\mathbf{AS}. \end{aligned}$$
(1)

In the formula, \(\mathbf{A}\) is a \(M\times N\)-dimensional mixing matrix and it represents unknown transmission channel. The number of independent signal sources here is assumed to be equal to that of observed signal, which is \(M=N\). The task of blind source separation is to identify the signal sources by estimating the separation matrix \(\mathbf{W}\). Therefore, the separation signal is expressed as:

$$\begin{aligned} \mathbf{Y}=\mathbf{WX}=\mathbf{WAS}. \end{aligned}$$
(2)

2.2 Signal Preprocessing

When conducting the signal separation in FastICA algorithm, preprocessing for the observed signal is necessary. Preprocessing includes signal centering and pre-whitening. The centering process is to use time average to replace statistic average and use the arithmetic mean value to replace mathematical expectation. For the convenience of discussion, it is considered that \(\mathbf{X}\) is random variable with mean value of zero. In the separation question, conduct whitening for \(\mathbf{X}\) through a linear transformation \(\mathbf{B}\), so \(\mathbf{Z}=\mathbf{BX}\) can satisfy:

$$\begin{aligned} \mathbf{R}_\mathbf{Z} =E[\mathbf{ZZ}^{T}]=\mathbf{I}. \end{aligned}$$
(3)

In the formula, \(\mathbf{I}\) is a unit matrix, \(\mathbf{B}\) means the whitening matrix and \(\mathbf{Z}\) expresses the whiten signal. So:

$$\begin{aligned} \mathbf{R}_\mathbf{Z} =E[(\mathbf{BX})(\mathbf{BX})^{T}]=\mathbf{BR}_\mathbf{X} \mathbf{B}^{T}=\mathbf{I}. \end{aligned}$$
(4)

Because \(\mathbf{R}_\mathbf{X} \) is generally symmetrical and nonnegative definite, it can be calculated by the principal component analysis as follows:

$$\begin{aligned} \mathbf{B}=\mathbf{D}^{-1/2}{} \mathbf{U}^{T} \end{aligned}$$
(5)

where \(\mathbf{U}\) is the characteristic vector matrix of \(\mathbf{R}_\mathbf{X} \), \(\mathbf{D}\) is the diagonal matrix of corresponding characteristic value. Above all, signal preprocessing makes the observed signal into unrelated components, and this can reduce the workload of the algorithm.

2.3 Component Extraction Processing

FastICA algorithm includes data processing and component extraction processing. Among them, the independent component extraction is realized by constructing and optimizing the objective function. In this paper, the objective function is based on negative entropy and its form is as follows [8]:

$$\begin{aligned} J_G (w)= & {} E\{G(w^{T}{} \mathbf{Z})\}-\beta (E\{(w^{T}{} \mathbf{Z})^{2}\}-1)\nonumber \\ \beta= & {} E\{w_0^H \mathbf{Z}\cdot g(w_0^H \mathbf{Z})\}. \end{aligned}$$
(6)

Here \(G(\cdot )\) is a nonlinear function, and it is desirable as \(G(y)=\ln \cdot \cosh (y)\) combined with the AIS signal non-Gaussian characteristics, \(g(\cdot )\) is the differential coefficient of \(G(\cdot )\), \(w_0 \) is the initial value of w. Using Newton iterative method with a locally quadratic convergence rate optimizes the objective function. The Newton iterative formula is given as follows:

$$\begin{aligned} w_{k+1} =w_k -\frac{F(w_k )}{F^{\prime }(w_k )} \end{aligned}$$
(7)

where k is the number of iterations, and \(F(w)=J_G ^{\prime }(w)\), and there are:

$$\begin{aligned} F(w)= & {} E\{\mathbf{Z}\cdot g(w^{T}{} \mathbf{Z})\}-\beta w \end{aligned}$$
(8)
$$\begin{aligned} F^{\prime }(w)= & {} E\{g^{\prime }(w^{T}{} \mathbf{Z})\}-\beta \mathbf{I}. \end{aligned}$$
(9)

Put Eqs. (8) and (9) into Eq. (7), the iterative formula is shown as follows:

$$\begin{aligned} w_{k+1} =E\{\mathbf{Z}g(w_k^T \mathbf{Z})\}-E\{g^{\prime }(w_k^T \mathbf{Z})\}w_k. \end{aligned}$$
(10)

When the convergence condition \(|w_{k+1} -w_k |\le \delta (\delta \) is the convergence threshold) is fulfilled, make \(w=w_{k+1} \) and extract the signal \(y_i =w_i^T \mathbf{Z}\).

3 The Improved FastICA Algorithm

The performance of FastICA algorithm is determined by the initial condition \(w_0 \) and the nonlinear function \(G(\cdot )\). At the same time, the convergence speed is affected by the Newton iteration algorithm. Therefore, the FastICA algorithm is improved based on these three areas.

3.1 The Initial Condition \(w_0\)

AIS signal is a GMSK modulation signal with constant module feature; hence, constant modulus character can be used to blind source separation to improve the FastICA algorithm. So stochastic gradient constant modulus algorithm can be used to calculate the initial weight vector. Define the cost function as follows [12]:

$$\begin{aligned} J\left( {\hat{{w}}\left( k \right) } \right) =E\left\{ {\left| {\left| {\hat{{w}}^{H}\left( k \right) x\left( k \right) } \right| ^{p}-\left| \alpha \right| ^{p}} \right| ^{q}} \right\} \end{aligned}$$
(11)

where \(\alpha \) is the amplitude of a desired signal, p and q are positive integers, which can affect the convergence property and complexity. Because the source signal amplitude is 1 in this simulation, let \(\alpha =1\). p and q determine the convergence characteristics and complexity of the most steep decline constant modulus algorithm. Take different p and q; the error function of the calculation formula e(n) is, respectively, given in Table 1.

Table 1 Different error functions for p and q
Full size table

This paper chooses \(p=1\) and \(q=2\); iterative formula can be deduced:

$$\begin{aligned} \hat{{w}}\left( {k+1} \right) =\hat{{w}}\left( k \right) -\mu x\left( k \right) e^{*}\left( k \right) \; \end{aligned}$$
(12)

where \(e\left( k \right) =2\left[ {\hat{{w}}^{H}\left( k \right) x\left( k \right) -\frac{\hat{{w}}^{H}\left( k \right) x\left( k \right) }{\left| {\hat{{w}}^{H}\left( k \right) x\left( k \right) } \right| }} \right] \), \(\mu =\frac{1}{2\lambda _1^2 }\) is the step factor, \(\lambda _1 \) is the biggest nonzero singular value of receiving data matrix.

3.2 The Nonlinear Function \(G(\cdot )\)

In the second step of the improved algorithm, select Modified-M estimation function as a nonlinear function of the objective function, which is expressed as [11]:

$$\begin{aligned} G\left( u \right) =\left\{ {{\begin{array}{ll} \frac{1}{2}u^{2},&{}\quad \left| u \right| \le a \\ a\left| u \right| -\frac{1}{2}a^{2},&{}\quad a<\left| u \right| \le b \\ \frac{a}{b}\frac{1-e^{c\left( {-\left| u \right| +b} \right) }\left( {1+c\left| u \right| } \right) }{c^{2}}+ab-\frac{1}{2}a^{2}+\frac{a}{c}&{}\quad \left| u \right| >b \\ \end{array} }} \right. \end{aligned}$$
(13)

where c is the impact factor, and a and b are the boarders.

Fig. 2
figure 2

Objective function of the cost function, the influence function and the weight function

Full size image

In Fig. 2, u represents the residual. As shown in the weight function: First, the middle part of the data is very small residual data, and this part of the data is the most consistent with the fitting of the data which deserve a sufficient proportion of weight, so the weight of the residual value near 0 in the area should be assigned to 1; then, on both sides of the weight reduction area, the data can reflect the data distribution law in a certain degree, but the range of residual is relatively large and the weight of convergence speed should be faster; finally, when the data difference is large, retaining each observation value, the weight of the data should be assigned to a value rather than 0, which should be given much faster convergence.

3.3 The Third-Order Newton Iterative Algorithm

Finally, amend the second-order Newton iterative algorithm for the third-order Newton iterative algorithm so as to improve the convergence speed. The specific form is shown as follows [15]:

$$\begin{aligned} \;\;\;\;\;\tilde{w}_{k+1}= & {} w_k -\frac{F\left( {w_k } \right) }{F^{{\prime }}\left( {w_k } \right) }\nonumber \\ w_{k+1}= & {} w_k -\frac{2F\left( {w_k } \right) }{F^{{\prime }}\left( {w_k } \right) +F^{{\prime }}\left( {\tilde{w}_{k+1} } \right) }. \end{aligned}$$
(14)

After calculation, the iterative formula of improved algorithm can be simplified to:

$$\begin{aligned} \;\;\;\;\;\;\;\tilde{w}_{k+1}= & {} E\{\mathbf{Z}g(w_k^T \mathbf{Z})\}-E\{g^{{\prime }}(w_k^T \mathbf{Z})\}w_k \nonumber \\ w_{k+1}= & {} 2E\{\mathbf{Z}g(w_k^T \mathbf{Z})\}-\left\{ {E\{g^{{\prime }}(w_k^T \mathbf{Z})\}+E\{g^{{\prime }}(\tilde{w}_k^T \mathbf{Z})\}} \right\} w_k. \end{aligned}$$
(15)

3.4 The Entire Improved FastICA Algorithm Process

In summary, the entire improved FastICA algorithm is described as follows:

  1. (1)

    Preprocessing for the observed signals;

  2. (2)

    Calculating the initial weight vector by stochastic gradient constant modulus algorithm;

  3. (3)

    Constructing the objective function combined with the initial weight vector and Modified-M estimate function;

  4. (4)

    Optimizing the objective function by the third-order Newton iteration algorithm so that the signal \(y_i \) can be separated;

  5. (5)

    If i is less than N, remove the correlation of separating vector. Then repeat step (2) until \(i=N\) (Fig. 3).

Fig. 3
figure 3

Entire improved FastICA algorithm process

Full size image

4 Experimental Results

4.1 Parameter Selection [11]

In the thesis of Dr. Wang, it is explained that when a is 1.345 and b is 3 and c is 0.3, the improved Huber function can achieve the best estimation effect. Combining with the improved algorithm in this paper, when the parameters take these values, the separation effect can be optimized best, and the robust performance of the algorithm can achieve the best.

4.2 Simulation Experiment

In order to show the performance of separation method more accurately, many papers choose mean square error SMSE as the evaluation criteria. Assume that N is the number of the signal sources, and SMSE can be obtained as:

$$\begin{aligned} {SMSE}=\frac{1}{N}\sum _{i=1}^N {E\left\{ {|s_i -y_j |^{2}} \right\} }. \; \end{aligned}$$
(16)

The smaller the value of SMSE means the better separation effect of the algorithm. When SMSE is equal to zero, estimated signal is no difference in full with the source signal.

This paper performs some signal simulation experiments under the environment of MATLAB. Here, AIS source signal is GMSK modulation, bit rate is 9600 bit/s, and carrier frequency is 40 kHz. Mix 4 source signals through a mixing matrix \(\mathbf{A}\); then, adopt the improved algorithm to estimate source signal. The simulation results as follows:

Fig. 4
figure 4

Mean square error curves of four algorithms

Full size image

In Fig. 4, the improved algorithm of this paper and the two improved algorithms in the references are compared. The improved algorithm in the reference 10 is based on the classical FastICA, and the Newton iteration method and the steepest descent method are used to improve the convergence performance of the algorithm [13]. In the reference 9, the Huber function is used as the nonlinear function in the optimization objective function to improve the robust performance of the algorithm [6]. From the experimental results, the improved algorithm of this paper is superior to the classical FastICA algorithm and the improved algorithms in references, and the convergence rate increases and robustness has been improved obviously.

Fig. 5
figure 5

Separation effects of PCA and FastICA. a is the source signals, b shows the signals separated by FastICA, c shows the signals separated by PCA

Full size image

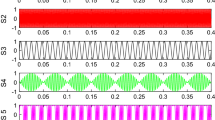
As shown in Fig. 5, the FastICA algorithm can basically separate the mixed signals, except for the order of the signals, and the signals separated by PCA cannot represent any characteristics of the source signals. Similarly, the MCA algorithm cannot separate the mixed signal,which is essentially the same as PCA. It can be seen that the FastICA algorithm is superior to PCA and MCA.

Table 2 shows the iteration times of four algorithms. It can be seen that when the number of source signals is 2, the iteration times are so little difference between the four algorithms. With the increase in the number of source signals, the iteration time of the improved algorithm is much smaller than that of the other three algorithms. Hence, the method in this paper can speed up the convergence rate and reduce the number of iterations.

Table 2 Iteration times of four algorithms
Full size table

5 Conclusion

FastICA algorithm is the most commonly used method of blind source separation, and many new improvements have been put forward. A new and reliable algorithm based on the latest mathematical theory is proposed in this paper. First, the initial value of the separation matrix affects the convergence performance of the algorithm. Therefore, the stochastic gradient constant modulus algorithm is used to calculate the initial value to ensure the convergence performance of the algorithm. Secondly, the Modified-M estimation function is adopted as the nonlinear function of the objective function to improve the algorithm. And then using the third-order Newton iteration algorithm speeds up the convergence rate of the improved algorithm. Finally, though comparing the improved algorithm and the improved algorithm of the previous algorithm, it shows that the improved algorithm can effectively separate the useful signal and enhance the convergence and robustness.