Optimal Majority Rule Versus Simple Majority Rule

Abstract

We consider social dynamics determined by voting in a stochastic environment with qualified majority rules for homogeneous society consisting of classically rational economic agents. Proposals are generated by means of random variables in accordance with the ViSE model. In this case, there is an optimal, in terms of maximizing the agents’ expected utility, majority threshold for any specific environment parameters. We obtain analytical expression for this optimal threshold as a function of the parameters of the environment and specialize this expression for several distributions. Furthermore, we compare the relative effectiveness of the optimal and simple (with the threshold of 0.5) majority rule.

1 Introduction

Collective decisions are often made based on a simple majority rule or qualified majority rules. A certain proportion of voters (more than 0.5 in case of the simple majority rule) must support an alternative for its approval. Society chooses from two alternatives (status quo and reform) in the simplest case. We focus on the iterated game where reforms may be beneficial for some participants and disadvantageous for others in order to reveal whether qualified majority rules surpass the simple one in dynamics. The study may be applicable to optimize the work of local governments, senates, councils, etc.

1.1 The Model

We use the ViSE (Voting in a Stochastic Environment) model proposed in [5]. It describes a society that consists of n economic agents. Each agent is characterized by the current value of individual utility. A proposal of the environment is a vector of proposed utility increments of the agents. It is stochastically generated by independent identically distributed random variables. The society can accept or reject each proposal by voting. If the proportion of the society supporting this proposal is greater than a strict relative voting threshold $\alpha \in [0,1]$, then the proposal is accepted and the participants’ utilities are incremented in accordance with this proposal. Otherwise, all utilities remain unchanged¹. The voting threshold (quota) $\alpha$ can also be called the majority threshold or the acceptance threshold, since $\alpha < 0.5$ (minority) is allowed and sometimes more effective. After accepting/rejecting the proposal, the environment generates a next one and puts it to a general vote over and over again.

Each agent chooses some cooperative or non-cooperative strategy. An agent that maximizes his/her individual utility in every act of choice will be called an egoist. Each egoist votes for those and only those proposals that increase their individual utility. Cooperative strategies where each member of a group votes “for” if and only if the group gains from the realization of this proposal (the so-called group strategies) are considered in [5]. The key theorems showing how the utility increment of an agent depends on the mentioned strategies and environmental parameters are obtained in [6]. The case of gradual dissemination of group strategy to all egoists is presented in [7]. In [13], a modification of the group strategy by introducing a “claims threshold,” i.e., the minimum profitability of proposals the group considers acceptable for it, is examined. The agents that support the poorest strata of society or the whole society are called altruists (they were considered in [9]).

1.2 Related Work and Contribution

The subject of the study is the dynamics of the agents’ utilities as a result of repeated voting.

There are several comparable voting models. Firsts, a similar dynamic model with individual utilities and majority voting has been proposed by A. Malishevski and presented in [14], Subsection 1.3 of Chap. 2. It allows one to show that a series of democratic decisions may (counterintuitively) systematically lead the society to the states unacceptable to all the voters.

Another model with randomly generated proposals and voting was presented in [10]. The main specificity of this model is in a discount factor that reduces utility increment for every rejection. This factor makes the optimal quota lower to speed up decision-making.

Unanimity and simple majority rule (which are special cases of majority rule) are considered in [3]. In this paper agents are characterized by competence (the likelihood of choosing a proposal that is beneficial to all agents). Earlier in [2] the validity of the optimal qualified majority rule under subjective probabilities was studied within the same model.

An interesting model with voting and random agent types was studied in [1]. If we consider environment proposals (in the ViSE model) as agent types in the model of [1] and are limited to qualified majority rules, then we get the same models.

Another model whose simplest version is very close to the simplest version of the ViSE model was studied in [4]. The “countries” of n agents with representatives and two-stage voting (a representative aggregates agents’ opinions and representatives’ choices are aggregated on the second stage) is considered. If each country consists of 1 agent, the agent’s strategy is the first voting, and the second voting is “$\alpha$-majority”, then the models coincide.

On other connections between the ViSE model and comparable models, we refer to [9].

In this paper, we show that when all agents are classically rational, then there is an optimal, in terms of maximizing the agents’ expected utility, acceptance threshold (quota) for any specific stochastic environment. Furthermore, we focus on four families of distributions: continuous uniform distributions, normal distributions (cf. [8]), symmetrized Pareto distributions (see [9]), and Laplace distributions.

Each distribution is characterized by its mathematical expectation, $\mu$, and standard deviation, $\sigma$. The ratio $\sigma /\mu$ is called the coefficient of variation of a random variable. The inverse coefficient of variation $\rho = \mu /\sigma$, which we call the adjusted mean of the environment, measures the relative favorability of the environment. If $\rho > 0$, then the environment is favorable on average; if $\rho < 0$, then the environment is unfavorable. We investigate the dependence of the optimal acceptance threshold on $\rho$ for several types of distributions and compare the expected utility increase of an agent when society uses the simple majority rule and the optimal one.

2 Optimal Acceptance Threshold

2.1 A General Result

The optimal acceptance threshold solves one serious problem of simple majority rule that can be revealed from the dependence of the expected utility increment of an agent on the adjusted mean $\rho$ of the environment [8].

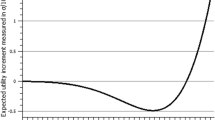
Consider an example. The dependence of the expected utility increment on $\rho =\mu /\sigma$ for 21 participants and $\alpha =0.5$ is presented in Fig. 1, where proposals are generated by the normal distribution.

Fig. 1.

Expected utility increment of an agent: 21 agents; $\alpha = 0.5$; normal distribution.

Figure 1 shows that for $\rho \in (-0.85,-0.266),$ the expected utility increment is a negative value, i.e., proposals approved by the majority are unprofitable for the society on average. This part of the curve is called a “pit of losses.” For $\rho < -0.85,$ the negative mean increment is very close to zero, since the proposals are extremely rarely accepted.

Let $\varvec{\zeta }=(\zeta _1,\ldots ,\zeta _n)$ denote a random proposal on some step. Its component $\zeta _i$ is the proposed utility increment of agent i. The components $\zeta _1,\ldots ,\zeta _n$ are independent identically distributed random variables. $\zeta$ will denote a similar scalar variable without reference to a specific agent. Similarly, let $\varvec{\eta }=(\eta _1,\ldots ,\eta _n)$ be the random vector of actual increments of the agents on the same step. If $\varvec{\zeta }$ is adopted, then $\varvec{\eta }=\varvec{\zeta }$; otherwise $\varvec{\eta }=(0,\ldots ,0)$. Consequently,

$$\begin{aligned} \varvec{\eta }=\varvec{\zeta }I(\varvec{\zeta }, \alpha n), \end{aligned}$$

(1)

where²

$$\begin{aligned} I(\varvec{\zeta }, \alpha n) = {\left\{ \begin{array}{ll} 1, &{}\#\{k:\zeta _k> 0, k = 1,...,n\} > \alpha n \\ 0, &{}\text {otherwise.} \end{array}\right. } \end{aligned}$$

(2)

Equation (1) follows from the assumption that each agent votes for those and only those proposals that increase his/her individual utility.

Let $\eta$ be a random variable similar to every $\eta _i,$ but having no reference to a specific agent. We are interested in the expected utility increment of an agent, i.e. $\mathrm{E}(\eta ),$ where $\mathrm{E}(\cdot )$ is the mathematical expectation.

For each specific environment, there is an optimal acceptance threshold³ $\alpha _0$ that provides the highest possible expected utility increment $\mathrm{E}(\eta )$ of an agent.

The optimal acceptance threshold for the normal distribution as a function of the environment parameters has been studied in [8]. This threshold turns out to be independent of the size of the society n.

The following theorem, proved in [12], provides a general expression for the optimal voting threshold, which holds for any distribution that has a mathematical expectation.

Theorem 1

In a society consisting of egoists, the optimal acceptance threshold is

$$\begin{aligned} \alpha _0 = \left( 1+\frac{E^+}{E^-}\right) ^{-1}, \end{aligned}$$

(3)

where $E^- = \big |\mathrm{E}(\zeta \; | \; \zeta \le 0)\big |, E^+ = \mathrm{E}(\zeta \; | \; \zeta > 0),$ and $\zeta$ is the random variable that determines the utility increment of any agent in a random proposal.

Voting with the optimal acceptance thresholds always yields positive expected utility increments and so it is devoid of “pits of losses.”

Let $\bar{\alpha }_0$ be the center of the half-interval of optimal acceptance thresholds for fixed $n,\sigma$, and $\mu$. Then this half-interval is $[\bar{\alpha }_0-\tfrac{1}{2n}, \bar{\alpha }_0+\tfrac{1}{2n})$. Figures 2 and 3 show the dependence of $\bar{\alpha }_0$ on $\rho =\mu /\sigma$ for normal and symmetrized Pareto distributions used for the generation of proposals.

For various distributions, outside the segment $\rho \in [-0.7,\, 0.7]$, if an acceptance threshold is close to the optimal one and the number of participants is appreciable, then the proposals are almost always accepted (to the right of the segment) or almost always rejected (to the left of this segment). Therefore, in these cases, the issue of determining the exact optimal threshold loses its practical value.

2.2 Proposals Generated by Continuous Uniform Distributions

Let $-a < 0$ and $b > 0$ be the minimum and maximum values of a continuous uniformly distributed random variable, respectively.

Corollary 1

The optimal majority/acceptance threshold in the case of proposals generated by the continuous uniform distribution on the segment $[-a, b]$ with $-a<0$ and $b>0$ is

$$\begin{aligned} \alpha _0 = \left( 1+\frac{b}{a}\right) ^{-1}. \end{aligned}$$

(4)

Indeed, in this case, $E^- = \frac{a}{2}, E^+ = \frac{b}{2},$ and $R = \frac{b}{a},$ hence, (3) provides (4).

If b approaches 0 from above, then $\alpha _0$ approaches 1 from below, and the optimal voting procedure is unanimity. Indeed, positive proposed utility increments become much smaller in absolute value than negative ones, therefore, each participant should be able to reject a proposal.

As $-a$ approaches 0 from below, negative proposed utility increments become much smaller in absolute value than positive ones. Therefore, a “coalition” consisting of any single voter should be able to accept a proposal. In accordance with this, the optimal relative threshold $\alpha _0$ decreases to 0.

Corollary 2

In terms of the adjusted mean of the environment $\rho =\mu /\sigma ,$ it holds that for the continuous uniform distribution,

$$\begin{aligned} \alpha _0 = {\left\{ \begin{array}{ll} 1, &{}\rho \le -\sqrt{3},\\ \frac{1}{2} \left( 1 - \frac{\rho }{\sqrt{3}} \right) , &{}-\sqrt{3}< \rho < \sqrt{3},\\ 0, &{}\rho \ge \sqrt{3}. \end{array}\right. } \end{aligned}$$

(5)

This follows from (4) and the expressions $\mu = \frac{-a+b}{2}$ and $\sigma = \frac{b+a}{2\sqrt{3}}.$ It is worth mentioning that the dependence of $\alpha _0$ on $\rho$ is linear, as distinct from (4).

2.3 Proposals Generated by Normal Distributions

Fig. 2.

The center $\bar{a}_0$ of the half-interval of optimal majority/acceptance thresholds (a “ladder”) for $n=21$ and the optimal threshold (6) as functions of $\rho$ for normal distributions.

For normal distributions, the following corollary holds.

Corollary 3

The optimal majority/acceptance threshold in the case of proposals generated by the normal distribution with parameters $\mu$ and $\sigma$ is

$$\begin{aligned} \alpha _0 = F(\rho ) \left( 1 - \frac{\rho F(-\rho )}{f(\rho )} \right) , \end{aligned}$$

(6)

where $\,\rho = \mu /\sigma ,$ while $\,F(\cdot )$ and $f(\cdot )\,$ are the standard normal cumulative distribution function and density, respectively.

Corollary 3 follows from Theorem 1 and the facts that $E^- = -\sigma \left( \rho - \frac{f(\rho )}{F(-\rho )}\right)$ and $E^+ = \sigma \left( \rho + \frac{f(\rho )}{F(\rho )}\right) ,$ which can be easily found by integration. Note that Corollary 3 strengthens the first statement of Theorem 1 in [8].

Figure 2 illustrates the dependence of the center of the half-interval of optimal majority/acceptance thresholds versus $\rho =\mu /\sigma$ for normal distributions in the segment $\rho \in [-2.5,\, 2.5]$.

We refer to [8] for some additional properties (e.g., the rate of change of the optimal voting threshold as a function of $\rho$).

2.4 Proposals Generated by Symmetrized Pareto Distributions

Fig. 3.

The center $\bar{a}_0$ of the half-interval of optimal majority/acceptance thresholds (a “ladder”) for $n=131$ (odd) and the optimal threshold (7) as functions of $\rho$ for symmetrized Pareto distributions with k = 8.

Pareto distributions are widely used for modeling social, linguistic, geophysical, financial, and some other types of data. The Pareto distribution with positive parameters k and a can be defined by means of the function $P\{\xi > x\} = \left( \frac{a}{x}\right) ^{k},$ where $\xi \in [a,\infty )$ is a random variable.

The ViSE model normally involves distributions that allow both positive and negative values. Consider the symmetrized Pareto distributions (see [9] for more details). For its construction, the density function $f(x) = \frac{k}{x} \left( \frac{a}{x}\right) ^{k}$ of the Pareto distribution is divided by 2 and combined with its reflection w.r.t. the line $x = a$.

The density of the resulting distribution with mode (and median) $\mu$ is

$$\begin{aligned} f(x) = \frac{k}{2a} \left( \frac{|x-\mu |}{a} + 1\right) ^{-(k+1)}. \end{aligned}$$

For symmetrized Pareto distributions with $k>2,$ the following result holds true.

Corollary 4

The optimal majority/acceptance threshold in the case of proposals generated by the symmetrized Pareto distribution with parameters $\mu ,$ $\sigma ,$ and $k>2$ is

$$\begin{aligned} \alpha _0 = \frac{1}{2}\left( 1+\mathrm{sign}(\rho )\frac{1-(k-2)\hat{\rho }-(1+\hat{\rho })^{-k+1}}{1+k\hat{\rho }}\right) \end{aligned}$$

(7)

where $\,\rho = \frac{\mu }{\sigma }$, $C = \sqrt{\frac{(k-1)(k-2)}{2}} = \frac{a}{\sigma }$, and $\hat{\rho }=|\rho /C|=|\mu /a|$.

Corollary 4 follows from Theorem 1 and the facts (their proof is given below) that:

$E^- = \sigma \left( \frac{C + \rho }{k-1}\right) ,$ $E^+ = \frac{\sigma }{1 - \frac{1}{2}\left( \frac{C}{C + \rho } \right) ^k} \left( \rho + \left( \frac{C}{C + \rho } \right) ^k \frac{C + \rho }{2(k-1)}\right)$ whenever $\mu > 0;$

$E^- = -\frac{\sigma }{1 - \frac{1}{2}\left( \frac{C}{C - \rho } \right) ^k} \left( \rho - \left( \frac{C}{C - \rho } \right) ^k \frac{C - \rho }{2(k-1)}\right) ,$ $E^+ \; = \; \sigma \left( \frac{C - \rho }{k-1}\right)$ whenever $\mu \le 0.$

The “ladder” and the optimal acceptance threshold curve for symmetrized Pareto distributions are fundamentally different from the corresponding graphs for the normal and continuous uniform distributions. Namely, $\alpha _0(\rho )$ increases in some neighborhood of $\rho = 0$.

As a result, $\alpha _0(\rho )$ has two extremes. This is caused by the following peculiarities of the symmetrized Pareto distribution: an increase of $\rho$ from negative to positive values decreases $E^+$ and increases $E^-$. By virtue of (3), this causes an increase of $\alpha _0.$

This means that the plausible hypothesis about the profitability of the voting threshold raising when the environment becomes less favorable (while the type of distribution and $\sigma$ are preserved) is not generally true. In contrast, for symmetrized Pareto distributions, it is advantageous to lower the threshold whenever a decreasing $\rho$ remains close to zero (an abnormal part of the graph).

Figure 3 illustrate the dependence of the center of the half-interval of optimal voting thresholds versus $\rho =\mu /\sigma$ for symmetrized Pareto distributions with $k=8.$

2.5 Proposals Generated by Laplace Distributions

The density of the Laplace distribution with parameters $\mu$ (location parameter) and $\lambda > 0$ (rate parameter) is

$$\begin{aligned} f(x) = \frac{\lambda }{2} \exp {\left( -\lambda |x-\mu |\right) }. \end{aligned}$$

For Laplace distributions, the following corollary holds.

Corollary 5

The optimal majority/acceptance threshold in the case of proposals generated by the Laplace distribution with parameters $\mu$ and $\lambda$ is

$$\begin{aligned} \alpha _0=\frac{1}{2}\left( 1+\mathrm{sign}(\rho )\frac{1-\beta -\exp {\left( -\beta \right) }}{1+\beta }\right) , \end{aligned}$$

(8)

where $\beta =|\lambda \mu |=|\lambda \sigma \rho | = |\sqrt{2}\rho |.$

Corollary 5 follows from Theorem 1 and the facts (their proof is similar to the proof of Corollary 4) that:

$E^- = \frac{1}{\lambda },$ $E^+ = \frac{2\mu + \frac{e^{-\lambda \mu }}{\lambda }}{2-e^{-\lambda \mu }}$ whenever $\mu > 0;$

$E^- = -\frac{2\mu - \frac{e^{\lambda \mu }}{\lambda }}{2-e^{\lambda \mu }},$ $E^+ = \frac{1}{\lambda }$ whenever $\mu \le 0.$

In Lemma 3 of [9] , it was proved that the symmetrized Pareto distribution with parameters k, $\mu$, and $\sigma$ tends, as $k \rightarrow \infty$, to the Laplace distribution with the same mean and standard deviation.

2.6 Proposals Generated by Logistic Distributions

The density of the logistic distribution with parameters $\mu$ (location parameter) and $s > 0$ (scale parameter) is

$$\begin{aligned} f(x) = \frac{1}{4s} \mathrm{sech}^2\left( \frac{x-\mu }{2s}\right) . \end{aligned}$$

For logistic distributions, the following corollary holds.

Corollary 6

The optimal majority/acceptance threshold in the case of proposals generated by the logistic distribution with parameters $\mu$ and s is

$$\begin{aligned} \alpha _0=\frac{\left( \frac{1}{2} +\frac{1}{2}\tanh {\left( \frac{\mu }{2s}\right) }\right) \left( s \ln {2} + s \ln {\left( \cosh {\left( \frac{\mu }{2s}\right) }\right) } -\frac{\mu }{2}\right) }{s \ln {2} + s \ln {\left( \cosh {\left( \frac{\mu }{2s}\right) }\right) } -\frac{\mu }{2}\tanh {\left( \frac{\mu }{2s}\right) }}. \end{aligned}$$

(9)

Corollary 6 follows from Theorem 1 and the facts, which can be easily found by integration, that:

We summarize the results of the above corollaries in Tables 1 and 2.

Table 1. Probabilities of positive and negative proposals for several distributions.

Table 2. Expected win and loss for several distributions.

3 Comparison of the Expected Utility Increments

By a “voting sample” of size n with absolute voting threshold $n_0$ we mean the vector of random variables $(\zeta _1 I(\varvec{\zeta }, n_0),\ldots ,\zeta _n I(\varvec{\zeta }, n_0))$, where $\varvec{\zeta }=(\zeta _1,\ldots ,\zeta _n)$ is a sample from some distribution and $I(\varvec{\zeta }, n_0)$ is defined by (2).

According to this definition, a voting sample vanishes whenever the number of positive elements of sample $\varvec{\zeta }$ does not exceed the threshold $n_0$.

The lemma on “normal voting samples” obtained in [6] can be generalized as follows.

Lemma 1

Let $\varvec{\eta }=(\eta _1,\ldots ,\eta _n)$ be a voting sample from some distribution with an absolute voting threshold $n_0$. Then, for any $k=1,...,n,$

$$\begin{aligned} \mathrm{E}(\eta _k) = \sum \limits _{x=n_0+1}^{n} \left( (E^+ + E^-)\frac{x}{n} - E^-\right) \begin{pmatrix} n \\ x \end{pmatrix} p^x q^{n-x}, \end{aligned}$$

(10)

where $E^- = \big |\mathrm{E}(\zeta \; | \; \zeta \le 0)\big |, E^+ = \mathrm{E}(\zeta \; | \; \zeta > 0),$ $p = P\{\zeta > 0\} = 1 - F(0), q = P\{\zeta \le 0\} = F(0),$ $\zeta$ is the random variable that determines the utility increment of any agent in a random proposal, and $F(\cdot )$ is the cumulative distribution function of $\zeta .$

In [9], the issue of correct location-and-scale standardization of distributions for the analysis of the ViSE model has been discussed. An alternative (compared to using the same mean and variance) approach to standardizing continuous symmetric distributions was proposed. Namely, distributions similar in position and scale must have the same $\mu$ and the same interval (centered at $\mu$) containing a certain essential proportion of probability. Such a standardization provides more similarity in the central region and the same weight of tails outside this region.

In what follows, we apply this approach for the comparison of the expected utility for several distributions. Namely, for each distribution, we find the variance such that the first quartiles (and thus, all quartiles because the distributions are symmetric) coincide for zero mean distributions, where the first quartile, $Q_1$, splits off the “left” 25% of probability from the “right” 75%.

For the normal distribution, $Q_1 \approx -0.6745 \sigma _N$, where $\sigma _N$ is the standard deviation.

For the continuous uniform distribution, $Q_1 = -\frac{\sqrt{3}}{2} \sigma _U$, where $\sigma _U$ is its standard deviation.

For the symmetrized Pareto distribution, $Q_1 = C(1-2^\frac{1}{k})\sigma _P$, where $\sigma _P$ is the standard deviation and $C = \sqrt{\frac{(k-1)(k-2)}{2}}$. This follows from the equation

$$\begin{aligned} F_P(Q_1) = \frac{1}{2}\left( \frac{C}{C-\frac{Q_1}{\sigma _P}}\right) ^{k} = \frac{1}{4}, \end{aligned}$$

where $F_P(\cdot )$ is the corresponding cumulative distribution function.

Fig. 4.

Expected utility increment of an agent as a function of $\mu$ with a majority/acceptance threshold of $\alpha = \frac{1}{2}$ for several distributions: black line denotes the symmetrized Pareto distribution, black dotted line the normal distribution (with $\sigma _N=1$), black dashed line the logistic distribution, gray line the continuous uniform distribution, and gray dotted line the Laplace distribution.

Fig. 5.

Difference in expected utility increment of an agent as a function of $\mu$ between the optimal majority/acceptance thresholds and $\alpha = \frac{1}{2}$ cases for several distributions: black line denotes the symmetrized Pareto distribution, black dotted line the normal distribution (with $\sigma _N=1$), black dashed line the logistic distribution, gray line the continuous uniform distribution, and gray dotted line the Laplace distribution.

For the Laplace distribution, $Q_1 = \frac{-\ln {2}}{\lambda } = -\sigma _L\frac{\ln {2}}{\sqrt{2}}$, where $\sigma _L$ is the standard deviation.

For the logistic distribution, $Q_1 = \frac{-2\sqrt{3}}{\pi } \tanh ^{-1}{\left( \frac{1}{2}\right) }\sigma _{Log}$, where $\sigma _{Log}$ is the standard deviation.

Consequently, $\sigma _U \approx 0.7788\sigma _N$, $\sigma _P \approx 1.6262\sigma _N$ for $k = 8$,

$\sigma _L \approx 1.3762\sigma _N$ and $\sigma _{Log} \approx 1.1136\sigma _N$.

Figures 4 and 5 show the dependence of the expected utility increment of an agent on the mean $\mu$ of the proposal distribution for several distributions (normal, continuous uniform, symmetrized Pareto, Laplace and logistic) for the majority threshold $\alpha = \frac{1}{2}$ and difference in expected utility increment of an agent as a function of $\mu$ between the optimal majority/acceptance thresholds and $\alpha = \frac{1}{2}$ cases for several distributions, respectively. They are obtained by substituting the parameters of the environments into (10), (5), (6), (7), and (8). Obviously, the optimal acceptance threshold excludes “pits of losses” because the society has the option to take insuperable threshold of 1 and reject all proposals.

Fig. 6.

The optimal majority/acceptance threshold as function of $\mu$ for several distributions: black line denotes the symmetrized Pareto distribution, black dotted line the normal distribution, black dashed line the logistic distribution, gray line the continuous uniform distribution, and gray dotted line the Laplace distribution.

Figure 6 illustrates the dependence of the optimal majority threshold on $\mu$ for the same list of distributions. It helps to explain why for $\alpha = \frac{1}{2},$ the continuous uniform distribution has the deepest pit of losses (because of the biggest difference between the actual and optimal thresholds), and why the symmetrized Pareto and Laplace distributions have no discernible pit of losses (because those differences are the smallest).

4 Conclusion

In this paper, we used closed-form expressions for the expected utility increase and the optimal voting threshold (i.e., the threshold that maximizes social and individual welfare), as functions of the parameters of the stochastic proposal generator in the assumptions of the ViSE model, to calculate difference in expected utility increment of an agent between the optimal majority/acceptance thresholds and simple majority voting rule cases for several distributions. These expressions were given more specific forms for several types of distributions.

Estimation of the optimal acceptance threshold seems to be a solvable problem. If the model is at least approximately adequate and one can estimate the type of distribution and $\rho =\mu /\sigma$ by means of experiments, then it is possible to obtain an estimate for the optimal acceptance threshold using the formulas provided in this paper.

We found that for some distributions of proposals, the plausible hypothesis that it is beneficial to increase the voting threshold when the environment becomes less favorable is not generally true. A deeper study of this issue should be the subject of future research.