Hypoplastic Model for Clays with Stiffness Anisotropy

Abstract

The Intergranular Strain Anisotropy (ISA) model by Fuentes and Triantafyllidis (2015) corresponds to an extension for the conventional hypoplastic models to account for the effects observed under cyclic loading. Similar to the Intergranular Strain (IS) theory proposed by Niemunis and Herle (1997), this extension enhance the hypoplastic models in many aspects as increasing the stiffness and reducing the plastic strain rate on cyclic loading. The present work is devoted to extend and evaluate a constitutive model for anisotropic clays under cyclic loading. The reference model corresponds to the anisotropic hypoplasticity for clays by Mašín (2014), which accounts for an elastic tensor depending on the bedding plane’s orientation. The proposed model results from extending the hypoplastic model with ISA. For validation purposes, different simulations under monotonic and cyclic loading were performed with an anisotropic kaolin clay. It was found that the proposed model accurately predict the experimental results under a wide range of strain amplitudes.

1 Introduction

Anisotropy plays an important role on the mechanical behavior of clays, which can not be neglected in the simulation of boundary value problems (Lings et al. 2000; Wichtmann and Triantafyllidis 2018). There are two different sources of clay anisotropy: inherent and induced. The first type is caused by the prevalent orientation of platy clay particles and generates different mechanical responses depending on the bedding plane, while the second type results from subsequent deformations (Arthur et al. 1977; Arthur and Menzies 1972; Fuentes et al. 2018). Inherent anisotropy generates different stiffnesses and ultimate shear strengths on monotonic loading depending on the loading direction relative to the sedimentation axis (Mitchell and Wong 1973; Saada et al. 1994). These effects has been considered in the formulation of some constitutive models, which successfully predict different experimental results under monotonic loading (e.g. Wheeler et al. 2003; Whittle and Kavvadas 1994). On the other hand, under cyclic loading it has been found that the inherent anisotropy generates a strong influence on the small strain stiffness and its degradation curve depending on the loading direction (Bellotti et al. 1996; Likitlersuang et al. 2013). However, these effects under cyclic loading are complex to simulate.

The present work introduces an extension of the anisotropic hypoplastic model for clays proposed by Mašín (2014), with the ISA model to account for small strain effects. The ISA model is based on the Intergranular Strain (IS) concept previously proposed by Niemunis and Herle (1997), which enhance the capabilities of the hypoplastic models under cyclic loading. However, in contrast to the conventional IS, the ISA model is based on a simple bounding surface approach and considers some important changes compared to the former one: a) the evolution of the intergranular strain is now elastoplastic, and b) ISA implements an elastic locus related to a specific strain amplitude which can be adjusted to the elastic threshold strain amplitude and simulates a smooth transition between the elastic and plastic behavior. The experimental results of an anisotropic kaolin clay reported by Wichtmann and Triantafyllidis (2018) were implemented for the calibration and validation of the proposed model. The element test simulation results show that the proposed model accurately predict the experiments under monotonic and cyclic loading.

2 Brief Description of the ISA Model

The hypoplasticity alone can be considered as a family of constitutive models capable to simulate the mechanical behavior of soils under monotonic loading. Different hypoplastic models has been developed to simulate the behavior of sands (e.g. Bauer (1996); Wolffersdorff (1996); Wu and Bauer (1994)) and clays (e.g. Herle and Kolymbas (2004); Mašín (2005; 2014)). However, this type of models delivers an excessive plastic accumulation (ratcheting) upon cyclic loading (Fuentes and Triantafyllidis 2015; Niemunis and Herle 1997). In order to encompass this shortcoming, the IS and ISA theories were developed to account for small strain effects. The proposed model combines some concepts of the hypoplastic model by Mašín (2014) (for medium and large strains amplitudes) and the recently developed ISA model (for small strain effects). The general form of the model is presented in Eq. (1):

$$ \dot{\varvec{\sigma }} = {\mathbf{L}}^{{{\mathbf{hyp}}}} :{\dot{\mathbf{\upvarepsilon }}} + {\mathbf{N}}^{{{\mathbf{hyp}}}} :\left\| {{\dot{\mathbf{\upvarepsilon }}}} \right\| $$

(1)

where $\dot{\varvec{\sigma }}$ is the stress rate tensor, ${\dot{\mathbf{\varepsilon }}}$ is the strain rate tensor, and ${\mathbf{L}}^{{{\mathbf{hyp}}}}$ and ${\mathbf{N}}^{{{\mathbf{hyp}}}}$ are the (fourth rank) linear stiffness tensor and (second rank) state-dependent tensor, respectively. These tensors are adjusted to simulate the soil behavior under medium and large strain amplitudes (e.g. under monotonic loading). An important feature of Eq. (1) is that it can be rewritten in terms of its continuum tangent modulus ${\mathbf{\rm M}}$ as:

$$ \dot{\varvec{\sigma }} = \left( {{\mathbf{L}}^{{{\mathbf{hyp}}}} + {\mathbf{N}}^{{{\mathbf{hyp}}}} \overrightarrow {{{\dot{\mathbf{\upvarepsilon }}}}} } \right):{\dot{\mathbf{\upvarepsilon }}} = {\mathbf{\rm M}}:{\dot{\mathbf{\upvarepsilon }}} $$

(2)

According to the ISA model, the tangent modulus is defined as:

$$ {\mathbf{\rm M}} = \left\{ {\begin{array}{*{20}l} {m\left( {{\mathbf{L}}^{{{\mathbf{hyp}}}} + \rho^{\chi } {\mathbf{N}}^{{{\mathbf{hyp}}}} {\mathbf{N}}} \right)} \hfill & {\text{for}\,F_{H} \, = \,0 \left( {\text{plastic}} \right)} \hfill \\ {m_{R} {\mathbf{L}}^{{{\mathbf{hyp}}}} } \hfill & {\text{for}\,F_{H} \, < \,0 \left( {\text{elastic}} \right)} \hfill \\ \end{array} } \right. $$

(3)

where ${\mathbf{N}} = ({\mathbf{h}} - \overrightarrow {{\mathbf{c}}} )$ is the intergranular strain flow rule, $m_{R}$ is a parameter and $\rho ,m, \chi , F_{H}$ are scalar functions defined in the following lines:

$$ F_{H} = \left\| {{\mathbf{h}} - {\mathbf{c}}} \right\| - R/2\quad \left( {\text{yield surface}} \right) $$

(4)

where ${\mathbf{h}}$ is the IS tensor, ${\mathbf{c}}$ is the back-IS tensor, and $R$ is a parameter. Factors $m, y_{h}$ and $\rho$ are defined as:

$$ m = m_{R} + \left( {1 - m_{R} } \right)y_{h} $$

(5)

$$ y_{h} = \rho^{\chi } \left\langle {{\mathbf{N}}:{\dot{\mathbf{\varepsilon }}}} \right\rangle $$

(6)

$$ \rho \, = \,1 - \frac{{\left\| {{\mathbf{d}}_{{\mathbf{b}}} } \right\|}}{2R}, \,{\text{with }}\,{\mathbf{d}}_{{\mathbf{b}}} \, = \,{\mathbf{h}}_{{\mathbf{b}}} - {\mathbf{h}},\,{\text{and}}\,{\mathbf{h}}_{{\mathbf{b}}} \, = \,R{\mathbf{N}} $$

(7)

On the other hand, the bounding surface function $F_{b}$ is defined as:

$$ F_{b} = \left\| {\mathbf{h}} \right\| - R\quad \left( {\text{bounding surface}} \right) $$

(8)

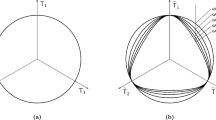
The shape of the yield and bounding surface of the intergranular strain h are schematized in Fig. 1:

Fig. 1.

Sketch of the yield and bounding surface of the intergranular strain h.

The evolution of the intergranular strain tensor h follows:

$$ {\dot{\mathbf{h}}} = {\dot{\mathbf{\upvarepsilon }}} - \dot{\lambda }_{H} {\mathbf{N}},\,\varvec{ }{\text{with }}\,{\mathbf{N}} = \frac{{{\mathbf{h}} - {\mathbf{c}}}}{R/2},\varvec{ }\,{\text{and}}\,\varvec{ }\dot{\lambda }_{H} = \frac{{\left\langle {{\mathbf{N}}:{\dot{\mathbf{\upvarepsilon }}}} \right\rangle }}{{1 + {\mathbf{N}}:{\mathbf{c}}}} $$

(9)

where $\dot{\lambda }_{H}$ is the plastic multiplier of the IS model. The evolution equation of the tensor ${\mathbf{c}}$ is:

$$ {\dot{\mathbf{c}}} = \dot{\lambda }_{H} \overline{{\mathbf{c}}} ,\,{\text{with }}\,\overline{{\mathbf{c}}} \, = \,\beta_{h} \left( {{\mathbf{c}}_{{\mathbf{b}}} - {\mathbf{c}}} \right)/R,\,{\text{and}}\,{\mathbf{c}}_{{\mathbf{b}}} \, = \,\left( {R/2} \right)\overrightarrow {{{\dot{\mathbf{\upvarepsilon }}}}} $$

(10)

$$ \beta_{h} = \beta_{hmax} + \left( {\beta_{h0} - \beta_{hmax} } \right)\left| {\overrightarrow {{{\mathbf{h}}_{{\mathbf{b}}} }} :\overrightarrow {{{\mathbf{d}}_{{\mathbf{b}}} }} } \right| $$

(11)

The internal variable $\dot{\varepsilon }_{acc}$ evolves according to:

$$ \dot{\varepsilon }_{acc} = \frac{{c_{a} }}{R}\left( {1 - y_{h} - \varepsilon_{acc} } \right)\left\| {{\dot{\mathbf{\upvarepsilon }}}} \right\| $$

(12)

Function $\chi$ is defined as:

$$ \chi = \chi_{0} + \varepsilon_{acc} \left( {\chi_{max} - \chi_{0} } \right) $$

(13)

The proposed model predicts an elastic response for small strain amplitudes (${\varvec{\Delta}}\varvec{\varepsilon}\le 10^{ - 4}$) and delivers $\dot{\varvec{\sigma }} = m_{R} {\mathbf{L}}^{{{\mathbf{hyp}}}} :{\dot{\mathbf{\upvarepsilon }}}$. Under medium strain amplitudes ($10^{ - 2} \le {\varvec{\Delta}}\varvec{\varepsilon}< 10^{ - 4}$), the transitional equation $\dot{\varvec{\sigma }} = m\left( {{\mathbf{L}}^{{{\mathbf{hyp}}}} + \rho^{\chi } {\mathbf{N}}^{{{\mathbf{hyp}}}} {\mathbf{N}}} \right):{\dot{\mathbf{\upvarepsilon }}}$ is achieved providing a smooth response. Finally, under large strain amplitudes (${\varvec{\Delta}}\varvec{\varepsilon}> 10^{ - 2}$), the proposed model coincides with the hypoplastic equation $\dot{\varvec{\sigma }} = \left( {{\mathbf{L}}^{{{\mathbf{hyp}}}} + {\mathbf{N}}^{{{\mathbf{hyp}}}} {\mathbf{N}}} \right):{\dot{\mathbf{\varepsilon }}}$ for the simulation of monotonic loading. The parameters of the ISA model (without the parameters of the hypoplastic model) are $R, \chi_{0} , \chi_{max} , \beta_{h0}$ and $\beta_{hmax}$. The state variables are ${\mathbf{h}},\varvec{ }{\mathbf{c}}$ and $\varepsilon_{acc}$. The tensors ${\mathbf{L}}^{{{\mathbf{hyp}}}}$ and ${\mathbf{N}}^{{{\mathbf{hyp}}}}$ were taken from Mašín (2014).

3 Description of Test Material and Experiments

The present work implemented the kaolin clay reported by Wichtmann and Triantafyllidis (2018) as test material for the calibration and validation of the proposed model. The analyzed tests are presented in Table 1. They include an oedometric compression test (OC) with 3 unloading-reloading cycles, four monotonic undrained triaxial tests (UT) and five cyclic undrained triaxial tests with constant deviator stress amplitudes $q^{amp}$ (CUT). The table includes test name, test type, confining pressure $p_{0}$ (for triaxial tests only), deviator stress amplitude $q^{amp}$, overconsolidation ratio (OCR), the initial experimental void ratio $e_{0}$ and the cutting direction after the consolidation process.

Table 1. Testing program with the kaolin clay reported by Wichtmann and Triantafyllidis (2018)

4 Model Calibration and Numerical Implementation

Simulations of experiments assuming element test conditions are shown in the next section to analyze the performance of the proposed model. The parameters of the proposed model are divided in two main groups: a) parameters of the hypoplastic model alone, which are $\varphi_{c}$, $\xi$, $\lambda$, $\kappa$, $N$, $\nu$ and $\alpha_{G}$ b) parameters of the ISA model, which corresponds to $A_{g}$, $n_{g}$, $R$, $\beta_{h0}$, $\beta_{hmax}$, $\chi_{0}$, $\chi_{max}$ and $c_{a}$. The proposed model has been implemented in a Fortran subroutine with a standard user interface which can be used to simulate Boundary Value Problems in the software Abaqus Standard. An explicit algorithm with a substepping scheme was considered for its numerical implementation. Its numerical integration was performed by the open-code software Incremental Driver. The parameters of the proposed model for the kaolin clay are summarized in Table 2.

Table 2. Parameters of the proposed model for the kaolin clay

5 Simulation of Element Tests

In this section, the capabilities of the proposed model are evaluated through the simulation of the experimental tests listed in Table 1. For triaxial tests, the initial void ratios $e_{0}$ were determined through the equation $\ln \left( {1 + e_{0} } \right) = N - \lambda \ln \left( {p_{0} /p_{r} } \right)$, with $p_{r}$ = 1 kPa the reference stress, and $p_{0}$ the confining pressure. Vector ${\mathbf{n}}$ describing the bedding plane orientation was adjusted depending on the orientation of the bedding plane of the samples, see Table 1. For all tests except test C41, vector ${\mathbf{n}}$ was set to ${\mathbf{n}} = \left\{ {1, 0, 0} \right\}$, which indicates a horizontal bedding plane (vertically cut samples). For the special case of test C41, vector n was set to ${\mathbf{n}} = \left\{ {0, 1, 0} \right\}$, indicating a vertical bedding plane (horizontally cut samples). The first test is an oedometric compression with 3 unloading-reloading cycles, see Fig. 2(a). The element test simulation result shows that the proposed model presents a good agreement with the experiment. However, the model delivered a lightly stiffer response than the experiment. On the other hand, the

Fig. 2.

Element test simulation results: (a) Oedometer test with 3 unloading-reloading cycles (b,c) Monotonic undrained triaxial test in the $q - p$ and $q - \varepsilon_{1}$ spaces, respectively

simulation of the monotonic tests with different confining pressure, $p_{0} = \left\{ {100, 200, 300, 400} \right\}$ kPa, are shown in Fig. 2(b,c). Simulations of the undrained shearing stage showed satisfactory assessments by the proposed model.

The performance on the proposed model under cyclic loading is now analyzed. The triaxial tests C1, C4, C5 and C7 were performed with different deviator stress amplitudes $q^{amp} = \left\{ {30, 45, 50, 60} \right\}$ kPa, and consequently, they presented a very different pore pressure accumulation. For all the simulations, identical number of cycles as by the experiments were considered. An example of one of the simulation results (test C1) with the proposed model in the $q - p$ and $q - \varepsilon_{1}$ spaces is presented in Fig. 3(a,b). The simulation results show that the “inclined slopes” in the $q - p$ space presented by the experiment were successfully captured by the proposed model. This behavior was achieved by the selection of parameter $\alpha_{G} = 1.9$, which controls the stiffness anisotropy and affects the initial inclination of the undrained stress path. Also, the number of cycles required to reach failure conditions, or equivalently, to develop large strains $(\varepsilon_{1} > 5 \% )$, was precisely captured by the proposed model. Finally, the proposed model accurately predict he accumulated pore water pressure p_w for tests with different deviator stress, see Fig. 3(c).

Fig. 3.

Element test simulation results: (a,b) Cyclic undrained triaxial test C1 in the $q - p$ and $q - \varepsilon_{1}$ spaces, respectively (c) Accumulation of pore water pressure on cyclic undrained triaxial test C1–C7

The last test corresponds to a cyclic undrained triaxial with a deviator stress amplitude of $q^{amp} = 45$ kPa. However, in contrast to the previous tests, the tested sample has a vertical bedding plane (horizontally cut). The element test simulation results are presented in Fig. 4(a,b). In this test, the slopes of the $q - p$ cycles are different than the ones exhibited by samples with horizontal bedding plane, see Fig. 3(a). This effect is accurately predicted by the proposed model due to the anisotropic nature of the tensor ${\mathbf{L}}^{{{\mathbf{hyp}}}}$. The pore pressure accumulation presented by this sample is completely different to the one exhibited by sample C4, which have the same deviator stress amplitude, but different bedding plane orientation. This suggest that there is a remarkable influence of the bedding plane on the pore water pressure accumulation, which was successfully captured by the proposed model, see Fig. 4(c).

Fig. 4.

Element test simulation results: (a,b) Cyclic undrained triaxial test C41 in the $q - p$ and $q - \varepsilon_{1}$ spaces, respectively (c) Accumulation of pore water pressure on cyclic undrained triaxial test C41

6 Conclusions

In the present work, a constitutive model for anisotropic clays is proposed by gathering some aspects of the hypoplastic model clays by Mašín (2014) and the ISA constitutive model proposed by Fuentes and Triantafyllidis (2015) and Poblete et al. (2016). The proposed model is able to capture some of the observed effects of the anisotropy in the experiments, as for example, the observed inclination of the $q - p$ paths under undrained cyclic conditions for different bedding planes. Also, the proposed model showed that it is able to capture with accuracy the number of cycles required to reach failure conditions under undrained cyclic loading, and the behavior of the accumulated pore water pressure on samples with vertical and horizontal bedding planes.