Keywords

1 Introduction

Clustering for computer vision and subspace learning is a challenging work. Many clustering methods were proposed for image retrieval [1], image indexing [2] and image classification [3]. To achieve image clustering effectively, a widely used approach is to discover an effective low-dimensional representation for the original data. Therefore, a lot of researches were presented to dig out the geometrical structure information of the original data, which can lead to a more discriminative representation.

In the past decades, many dimensionality reduction techniques were proposed including principal components analysis (PCA) [4] and non-negative matrix factorization (NMF) [5]. Among these methods, the non-negative property of the learned representation leads to be more meaningful in image representation. NMF decomposes the original data matrix into two low-dimensional matrices (i.e. a basis matrix and an encoding matrix), whose product can be best approximate to the original data matrix. Due to the excellent property of NMF, some variants [6,7,8,9,10,11,12,13,14,15,16,17,18,19] were proposed to improve the clustering accuracy from different views.

Although traditional NMF performs very well in learning a parts-based representation for clustering, it fails to achieve clustering while the original data is heavily corrupted. In the view of recent researches, the loss function of traditional NMF are very sensitive to outliers. In other words, the Frobenius norm enlarges the approximation error between the original data matrix and the product of the decomposed matrices. To address this issue, some studies [6,7,8,9,10,11,12] proposed some robust loss functions to minimize the reconstruction error. These proposed methods can reduce outliers of the representation, but they cannot remove outliers. Moreover, the learned representation cannot respect the geometrical structure of the original data contaminated by outliers and noise.

To address above-mentioned problems, we present a robust graph regularized non-negative matrix factorization (RGRNMF) for image clustering. Firstly, we propose a robust framework to measure the approximation error. Secondly, we construct a weighted graph to encode the geometrical information of the original data. Our achievements are as follows:

  • We propose a robust non-negative matrix factorization framework to remove outliers, and we incorporate the geometrical information of the original data into the learned representation.

  • Extensive experiments demonstrate that our proposed framework can achieve image clustering from the original data corrupted by Salt and Pepper noise or Contiguous Occlusion.

2 Related Works

Supposed that there are n sample images \(\{x_i\}_{i=1}^n\) and any image \(x_i\) has m features. Thus, we denote the original data matrix by \(V\in R^{m \times n}\). Due to the high-dimensional property of V, it is a challenging task to achieve image clustering. Generally, NMF is utilized to find two low-dimensional matrices \(W \in R^{m \times r}\) and \(H \in R^{r \times n}\) such that the product of W and H can be approximately equal to V. There, we have

$$\begin{aligned} V \approx WH, \end{aligned}$$
(1)

where r is a factorization rank and \(r<<\min \{m,n\}\). Generally, problem (1) can be transformed into a non-convex optimization problem as follows:

$$\begin{aligned} \begin{aligned}&\min _{W,H} \quad Error(V,WH)\\&s{.}t. \quad W \ge 0, H \ge 0. \end{aligned} \end{aligned}$$
(2)

where the loss function Error can be the Frobenius norm, \(L_1\) norm, \(L_{2,1}\) norm or Huber. Recently, Guan et al. [12] proposed a Truncated Cauchy loss (CauchyNMF) to reduce outliers, which can be summarized as follows:

$$\begin{aligned} \min _{W \ge 0,H \ge 0} F(W,H)=\sum _{i=1}^m\sum _{j=1}^n g(\frac{(V-WH)_{ij}}{\gamma }), \end{aligned}$$
(3)

where \(g(x)= {\left\{ \begin{array}{ll} ln(1+x), &{}0 \le x \le \sigma \\ ln(1+\sigma ) , &{} x>\sigma \end{array}\right. }\); \(\sigma \) and \(\gamma \) denote the scale parameter and the truncation parameter. \(\sigma \) can be obtained by three-sigma-rule, and \(\gamma \) is given by the Nagy algorithm [12]. Traditional NMF utilizes the different loss functions to reduce outliers, but they cannot remove outliers. Therefore, a robust NMF framework was proposed to eliminate outliers as follows:

$$\begin{aligned} \begin{aligned}&\min _{W,H,E} \quad loss(M,WH,E)+\lambda \varOmega (E,W,H)\\&s{.}t. \quad W \ge 0, H \ge 0, \end{aligned} \end{aligned}$$
(4)

where M is the original data matrix corrupted by noises, E is an error matrix, \(\lambda \) is a hyper-parameter, and the function \(\varOmega \) is the constraint term. Zhang et al. [11] proposed the Frobenius norm as the loss function and the \(L_1\) norm as the constraint on E, which can be described as follows:

$$\begin{aligned} \begin{aligned}&\min _{W,H,E} \parallel M-WH-E\parallel _F^2+\lambda \parallel E \parallel _M\\&s{.}t. \quad W \ge 0, H \ge 0, \end{aligned} \end{aligned}$$
(5)

where \(\parallel E \parallel _M=\sum _{ij}|e_{ij}|\).

3 Robust Graph Regularized Non-negative Matrix Factorization

3.1 Model Formulation

Previous NMF models have some defects: 1) They cannot remove outliers from the dataset corrupted by Salt and Pepper noise or Contiguous Occlusion. 2) While the dataset is corrupted by noises, the learned representation H cannot preserve the geometrical structure information.

In (5), Zhang et al. [11] supposed that the error matrix E is sparse, but the outliers in E are neglected. If the error matrix contains some outliers, then the constraint \(\parallel E \parallel _M\) is not inappropriate for outliers. Supposed that all outliers of the corrupted image matrix \(M \in R^{m \times n}\) produced by Salt and Pepper noise or Contiguous Occlusion are detected. A weight graph S can be utilized to label these outliers as follows:

(6)

Thus, we propose the constraint on E by the following form:

$$\begin{aligned} \parallel E\otimes S \parallel _M \end{aligned}$$
(7)

To learn the geometrical structure information of the original data, manifold regularization is proposed to construct the relation between the original data and the low-dimensional representation. A widely used manifold regularization term [20] can be described as follows:

$$\begin{aligned} tr(H(D-U)H^T), \end{aligned}$$
(8)

where \(U_{jl}=e^{-\frac{\parallel x_j-x_l\parallel ^2}{\sigma }}\) and \(D_{ii}=\sum _j W_{ij}\). In summary, combining (7), (8) and (5) results in our robust graph regularized non-negative matrix factorization (RGRNMF), which can be summarized into the following optimization problem

$$\begin{aligned} \begin{aligned}&\min _{W,H,E} F(W,H,E) \\ =&\parallel M-WH-E\parallel _F^2+\lambda \parallel E \otimes S \parallel _F^2 \\&+\,\gamma tr(H(D-U)H^T)\\&s{.}t. \quad W \ge 0, H \ge 0, \end{aligned} \end{aligned}$$
(9)

where \(\lambda \) and \(\gamma \) are hyper-parameters.

4 Optimization Scheme

It is obvious that problem (9) is non-convex. Therefore, the global optimal solution cannot be searched. Supposed that the \(k-\)th solution of problem (9) is obtained. We can have the \(k+1-\)th solution by optimizing the following problems

$$\begin{aligned} \begin{aligned} E^{k+1}&={\arg \min }_E \parallel M-W^kH^k-E\parallel _F^2\\&+\,\lambda \parallel E \otimes S \parallel _F^2 \end{aligned} \end{aligned}$$
(10)

and

$$\begin{aligned} \begin{aligned}&W^{k+1}={\arg \min }_W \parallel M-WH^k-E^{k+1}\parallel _F^2\\&s.t. \quad W \ge 0 \end{aligned} \end{aligned}$$
(11)

and

$$\begin{aligned} \begin{aligned}&H^{k+1}={\arg \min }_H \parallel M-W^{k+1}H-E^{k+1}\parallel _F^2\\&+\,\gamma tr(H(D-U)H^T)\\&s{.}t. \quad H \ge 0. \end{aligned} \end{aligned}$$
(12)

It is easy to obtain the solution of problems (10), (11) and (12) as follows:

$$\begin{aligned} e_{ij} \leftarrow \frac{m_{ij}-(WH)_{ij}}{1+\lambda s_{ij}}. \end{aligned}$$
(13)
$$\begin{aligned} w_{il} \leftarrow w_{il} \frac{(M{H}^T)_{il}-{(EH^T)}_{il}}{(WHH^T)_{il}}, \end{aligned}$$
(14)
$$\begin{aligned} \begin{aligned}&h_{lj} \leftarrow h_{lj} \frac{(W^TM)_{lj}-{(W^TE)}_{lj}+\gamma HU_{lj}}{(W^TWH)_{lj}+\gamma HD_{lj}}. \end{aligned} \end{aligned}$$
(15)

5 Experimental Results

We compare our proposed method (RGRNMF) with NMF [5], RNMF [9], MahNMF [8] and CauchyNMF [12] on the clustering performances of the ORL dataset. To verify the clustering ability on the corrupted data, we propose two corruptions including Salt and Pepper noise and Contiguous Occlusion. For Salt and Pepper noise, there are several percentages of corrupted pixels from 1% to 25%. Similarly, we vary the corrupted block size for Contiguous Occlusion from 1 to 16.

Fig. 1.
figure 1

The clustering performances on the ORL dataset corrupted by Salt and Pepper noise.

Full size image
Fig. 2.
figure 2

The clustering performances on the ORL dataset corrupted by Contiguous Occlusion.

Full size image

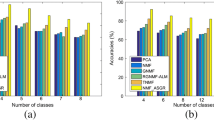
To evaluate the clustering effect of all methods, we propose Accuracy (AC) and Normalized Mutual Information (NMI) [21]. Let \(\lambda =100\) and \(\gamma =100\). Figure 1 and 2 show the clustering performances on the ORL dataset contaminated by Salt and Pepper noise and Contiguous Occlusion. From these figures, we observe that:

  • CauthyNMF achieves satisfactory clustering ACs and NMIs from the ORL dataset corrupted by Salt and Pepper noise and Contiguous Occlusion in the beginning, however, it obtains the poor clustering effect finally. This phenomenon indicates that CauthyNMF cannot handle heavy outliers.

  • NMF, PCA Kmeans and GNMF fail to achieve clustering. This means that They cannot handle outliers.

  • RGRNMF has relatively stable clustering performances on the Salt and Pepper noise and Contiguous Occlusion, that is to say, RGRNMF is more robust to outliers.

6 Conclusion

This paper proposed robust graph regularized non-negative matrix factorization (RGRNMF) to handle Salt and Pepper noise and Contiguous Occlusion. Clustering results demonstrate that our proposed NMF framework has the following properties. Firstly, RGRNMF can learn a more effective and discriminative parts-based representation from the ORL dataset corrupted by handle Salt and Pepper noise or Contiguous Occlusion. Secondly, RGRNMF is more robust to outliers than existing NMF methods.