Keywords

1 Introduction

Deep learning models have achieved remarkable performance on many supervised learning problems by leveraging large labeled datasets [12]. Creating large datasets with high-quality labels, however, is usually very labor-intensive and time-consuming [21, 24]. Semi-supervised learning [3] (SSL) provides an attractive way to improve the performance of deep learning models by also utilizing easily obtainable unlabeled data, so as to mitigate the reliance on large labeled datasets. Algorithms for SSL mainly include the following core ideas: consistency regularization [11, 14, 19], entropy minimization [7, 13], and traditional regularization [23]. Recent holistic approaches, Mixmatch [2] and UDA [20] achieve the state-of-the-art performance by combining these ideas above.

Existing SSL algorithms usually demonstrate their successes using fully-labeled classification datasets (e.g., CIFAR-10 [10], SVHN [15] and Imagenet [5]) by treating most samples of each dataset as unlabeled. Therefore, those evaluation results are based on an implicit assumption that all unlabeled samples come from the same classes as labeled samples. In real world, however, it is very likely that a large portion of the unlabeled samples do not belong to any classes of the labeled data, i.e., there exist a mismatch between class distributions of labeled and unlabeled data. As an example, if you intend to train a model to distinguish between ten classes of animals with only a small amount of labeled images at hand, you may want to employ a large collection of unlabeled animal images to improve the model performance. The unlabeled dataset may contain many images of other animal classes than the ten target classes. Most existing SSL algorithms use a combined loss of a supervised term and an auxiliary (unsupervised) term to achieve high test accuracy as well as generalize better to unseen data. As reported in some recent work, the class mismatch issue can make it difficult to minimize the auxiliary loss term [22], furthermore, drastically degrade the performances of SSL algorithms compared to not using any unlabeled data at all [16]. Though class mismatch can actually hurt the applicability of SSL algorithms, it has not received much attention until recently. [11] and [22] consider to evaluate SSL algorithms in class-mismatch cases. Two techniques, Split Batch normalization (Split-BN) [22] and ROI regularization, have been proposed to improve the robustness of existing SSL methods against class mismatch.

In this work, we focus on reducing the performance degradation caused by class mismatch problems so as to improve the applicability of existing SSL algorithms. We propose a novel entropy repulsion technique for mismatch (ERCM) to restrict potentially mismatched unlabeled samples from participating in the training process. Specifically, we introduce a new entropy repulsion loss term, which is gradually relaxed to prevent the model from premature overfitting on mismatched unlabelled data. We also design a batch annealing and reloading mechanism to work together with the loss, which dump samples with low-confidence pseudo labels and reload samples with highest-confidence pseudo labels from a temporal pool to make the training more stable. Our contributions are summarized as follows:

  • We propose a novel technique ERCM, including an entropy repulsion loss together with a batch annealing and reloading mechanism, which can empower existing SSL algorithms to achieve a significant performance improvement over the state of the art even when there is a significant class mismatch between labeled and unlabeled data. For example, with 250 labeled data and 20000 unlabeled data (mismatched data accounts for 20%) on CIFAR-10, as shown in Table 1, our method achieved 11.3% test error, which is 5.9% lower compared to 17.2% test error of the next-best method (Mix*). Specially, our analysis and ablation experiments show that ERCM can effectively alleviate the difficulty to minimize the auxiliary loss term in class-mismatch cases, which is a challenging issue reported by previous work [22].

  • Our design is orthogonal to traditional SSL algorithms and can be effectively adopted by existing SSL methods to improve their performance in class-mismatch cases. Our ERCM technique is highly portable, requiring no change to network structures and only introducing minor extra computational overhead.

Fig. 1.
figure 1

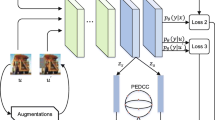
Workflow of our proposed ERCM technique (details in Sect. 3).

Full size image

2 Related Work

In this section, we mainly review state-of-the-art SSL techniques and recent efforts to address the class mismatch issue. A more comprehensive survey of SSL is provided in [3]. A common underlying assumption of SSL algorithms is that the decision boundary should pass through the low-density regions of data. One core idea to enforce this is entropy minimization. EntMin [7] makes low-entropy predictions for all unlabeled samples by adding an explicit loss term. Pseudo Label [13] gives pseudo labels for unlabeled data with high-confidence outputs for entropy minimization. Another core idea is consistency regularization that encourages the model to output the same class distribution for various augmentations of an unlabeled sample. \(\varPi \)-Model [11] and Temporal Ensembling [17] generalize ensemble predictions of unlabeled samples by networks with dropout regularization [18]. Mean Teacher [19] averages model weights instead of label predictions in which teacher model is an average of consecutive student models. VAT [14] involves consistency by applying a perturbation to the input. Recently, holistic methods Mixmatch [2] and UDA [20] achieve state-of-the-art performance on benchmark datasets by incorporating several recent advanced techniques. When it comes to a more realistic setting where class mismatch exists, those methods, however, may suffer a significant performance degradation.

The class-mismatch problem has not drawn much attention from traditional SSL methods. It is first considered in [11], which only appears in partial experiments and has not been discussed in depth. Recently, class distribution mismatch is formally discussed in [16], which shows clear performance degradation of various SSL methods in class-mismatch cases. Moreover, class mismatch shares some characteristics with domain adaptation [1, 6] in which there are differences between distributions of training data and test data. [9] designs ROI regularization to help VAT perform better against class mismatch. Split-BN [22] uses split batch normalization to improve the performance of Mean Teacher and VAT. And a SSL method named UASD [4] is proposed to mitigate the impact of class mismatch. In this paper, we aim to further enhance existing SSL methods by restricting potentially mismatched unlabeled samples from participating in the training process. Moreover, ERCM can also effectively improve the performance of the holistic method, Mixmatch.

3 Our Method

3.1 Problem Formulation

In SSL, we are given a labeled dataset \(\mathcal {D}_L\) and an unlabeled dataset \(\mathcal {D}_U\). Let \(\mathcal {D}_\mathcal {Y}=\{0,1..K-1\}\) be the set of labels. For each labeled sample \(x \in \mathcal {D}_L\), we have \(label(x) \in \mathcal {D}_\mathcal {Y}\). SSL algorithms aim to leverage unlabeled samples from \(\mathcal {D}_U\) to train a model with better performance than what would have been obtained by using \(\mathcal {D}_L\) alone. In this work, we consider a situation that is very common in real-world settings, named class mismatch. \(\mathcal {D}_U\) is very likely to have extra “dirty” data called mismatched samples that do not belong to any of these K classes. As reported in [16], class mismatch can actually hurt the performance of SSL methods. Our goal is to improve the performance of SSL in class-mismatch cases by mitigating the negative impact of mismatched unlabeled samples during the training process.

3.2 Design Overview

In a typical training process of SSL, a minibatch is composed of a labeled batch \(\mathcal {X}\) (a set of size \(\mathcal {C}\) randomly sampled from \(\mathcal {D}_L\)), an unlabeled batch \(\mathcal {U}\) (a set of size \(\mathcal {C}\) randomly sampled from \(\mathcal {D}_U\)), and corresponding labels \(\mathcal {Y}\) of \(\mathcal {X}\). Many recent SSL approaches use a combined loss function \(\mathcal {L}\) consisting of a supervised part and an auxiliary part:

$$\begin{aligned} \mathcal {L} = \lambda _\mathcal {X}\mathcal {L}_\mathcal {X}+\lambda _\mathcal {U}\mathcal {L}_\mathcal {U}, \end{aligned}$$
(1)

where \(\lambda _\mathcal {X}\) and \(\lambda _\mathcal {U}\) are weights of loss terms. The supervised part \(\mathcal {L}_\mathcal {X}\) is a loss function of labeled samples like cross-entropy:

$$\begin{aligned} \mathcal {L}_\mathcal {X}=\frac{1}{|\mathcal {X}|} \sum _{x \in \mathcal {X}, \hat{y} \in \mathcal {Y}} \,\hat{y}\,log(\frac{1}{p(\,y|x,\theta )\,)}. \end{aligned}$$
(2)

The auxiliary loss \(\mathcal {L}_\mathcal {U}\) is designed to explore the decision boundary by unlabeled data. For example, in Mixmatch, \(\mathcal {L}_\mathcal {U}\) is a consistency regularization loss term defined as \(||\,\hat{g}-p(\,y|u,\theta )\,||_{2}^2, u \in \mathcal {U}\), where \(\hat{g}\) represents “guessing label” of unlabeled samples after sharpening.

Entropy Repulsion Loss. In traditional SSL algorithms, combining a cross-entropy loss and a consistency regularization loss leads to a decrease of the entropy of labeled and unlabeled samples, which achieves good performance on standard datasets. In class-mismatch cases, however, blindly reducing the entropy of unlabeled data is not always beneficial and can even hurt the performance. Once the model is over-trained or over-fitted on mismatched unlabeled samples, it will introduce great errors to the model. To address this problem, we propose an entropy repulsion loss term \(\mathcal {L}_\mathcal {M}\) (shown in Eq. (3)), which encourages output entropy of labeled samples relatively smaller than that of unlabeled ones during the training process. \(\mathcal {L}_\mathcal {M}\) encourages the entropy of \(p(\,y|x',\theta ), x' \in \mathcal {X}^{d}\) to be relatively smaller than the entropy of \(p(\,y|u',\theta ), u' \in \mathcal {U}^{d}\), where \(\mathcal {X}^{d}\) and \(\mathcal {U}^{d}\) are randomly sampled from batch \(\mathcal {X}\) and \(\mathcal {U}\).

$$\begin{aligned} \mathcal {L}_\mathcal {M}=\,E[\mathcal {H}(p(\,y|x',\theta ))]-&E[\mathcal {H}(p(\,y|u',\theta ))] \nonumber \\ = \frac{1}{\alpha \,|\mathcal {U}|} (\sum _{x' \in \mathcal {X}^{d}}\mathcal {H}(p(\,y|x',\theta ))-&\sum _{u' \in \mathcal {U}^{d}}\mathcal {H}(p(\, y|u',\theta ))) \end{aligned}$$
(3)

Here the conditional entropy \(\mathcal {H}(\mathcal {Y}|\mathcal {X})\) is defined as

$$\begin{aligned} \mathcal {H}(p(\,y|x,\theta )) = -\sum _{i=1}^n p(\,y|x,\theta )^{i}\, log\,p(\,y|x,\theta )^{i} \end{aligned}$$
(4)

The conditional entropy is a measure of class overlap, which is invariant to the parameterization of the model. It is related to the usefulness of unlabeled samples where labeling is indeed ambiguous [7, 8].

Batch Annealing and Reloading with Temporal Pool. To further reduce the negative impact of mismatched unlabeled samples, we design a batch annealing mechanism to discard those high-entropy unlabeled samples from batch \(\mathcal {U}\) and reserve only low-entropy unlabeled samples in batch \(\mathcal {U}^{r}\) for training. The standard for reserved samples is strict in the early stages and is gradually relaxed as the model gets more accurate. Inspired by [11] and [19] which utilize the temporal information of training process, we propose a reloading mechanism with a temporal pool to refill \(\mathcal {U}^{r}\) with low-entropy unlabeled samples. The temporal pool is a size limited buffer to store the temporal samples with lowest entropy in the training process. The reloading mechanism increases the degree of fitting on low-entropy unlabeled samples as well as enhances training stability. The details of batch annealing and reloading will be presented in Sect. 3.3 and Sect. 3.4.

figure a

Based on our batch annealing and reloading mechanism, we redefine the consistency regularization loss term \(\mathcal {L}_\mathcal {U}\) in a class mismatch case as

$$\begin{aligned} \mathcal {L}_\mathcal {U}=\frac{1}{(1-\alpha )\,|\mathcal {U}|} \,||\,\hat{g}-p(\,y|u,\theta )\,||_{2}^2 \quad u \in \mathcal {U}^{r} \end{aligned}$$
(5)

where \(\mathcal {U}^{r}\) represents unlabeled samples after batch annealing and reloading.

Loss Function in ERCM. By adding our proposed entropy repulsion loss term to supervised loss and consistency regularization loss, the loss function in our method is presented in Eq. (6), which is a weighted combination of \(\mathcal {L}_\mathcal {X}\), \(\mathcal {L}_\mathcal {U}\), and \(\mathcal {L}_\mathcal {M}\). Here, \(\lambda _\mathcal {X}\), \(\lambda _\mathcal {U}\) and \(\lambda _\mathcal {M}\) are weights of loss terms.

$$\begin{aligned} \,\mathcal {L} = \lambda _\mathcal {X}\mathcal {L}_\mathcal {X}+\lambda _\mathcal {U}\mathcal {L}_\mathcal {U}+\lambda _\mathcal {M}\mathcal {L}_\mathcal {M} \end{aligned}$$
(6)

Workflow of ERCM. We illustrate the workflow of ERCM in Fig. 1 and give the detailed algorithm in Algorithm 1. First, we conduct stochastic augmentation (line.1, like random horizontal flips or crops) on the input batch \(\mathcal {X}\) and \(\mathcal {U}\). At the beginning of training, there will be a warming up process of weights for stability as usually done in traditional SSL approaches (line.3). During training the batch s, batch annealing discards high-entropy parts of \(\mathcal {U}\) and reserves \(\mathcal {U}^{r}\) (line.5). We uniformly sample \(\mathcal {X}^{d}\) and \(\mathcal {U}^{d}\) from \(\mathcal {X}\) and \(\mathcal {U}\). Then, we refill \(\mathcal {U}^{r}\) by reloading low-entropy samples from the temporal pool \(\mathcal {T}\) (line.6). Finally, we calculate the supervised loss term \(\mathcal {L}_\mathcal {X}\) by labeled batch \(\mathcal {X}\) and corresponding labels \(\mathcal {Y}\), auxiliary loss term \(\mathcal {L}_\mathcal {U}\) by \(U^{r}\), and entropy repulsion loss term \(\mathcal {L}_\mathcal {M}\) by \(\mathcal {U}^{d}\) and \(\mathcal {X}^{d}\) (line.8–10). We update the model by minimizing the total loss \(\mathcal {L}\) (line.11).

3.3 Batch Annealing

As shown in Algorithm 2, we first calculate the conditional entropy \(\mathcal {H}(p(\,y|u,\theta ))\) of unlabeled samples in \(\mathcal {U}\). Then, we reserve the first \(\alpha \times \mathcal {C}\) lowest-entropy (most confident) samples from \(\mathcal {U}\) to compose \(\mathcal {U}^{r}\) for training. Here, the \(\alpha \) is the annealing rate, which is obtained by the following increment function:

$$\begin{aligned} \alpha = \beta + log(\gamma \frac{s}{t}+1). \end{aligned}$$
(7)

t is the total training step number and s is the current training step. \(\beta \) and \(\gamma \) are hyperparameters. With steps of training, the model becomes more accurate and robust, meanwhile \(\alpha \) increases so as to gradually relax the standard for selecting reserved samples. In this way, our mechanism improves the model training by restricting potential mismatched unlabeled samples from participating in the training.

For each round of training, to calculate \(\mathcal {L}_\mathcal {M}\), we uniformly select \((1 - \alpha ) \times \mathcal {C}\) samples from \(\mathcal {U}\) to compose \(\mathcal {U}^{d}\) and uniformly select \((1 - \alpha ) \times \mathcal {C}\) samples from \(\mathcal {X}\) to compose \(\mathcal {X}^{d}\). We note that the limitation of \(\mathcal {L}_\mathcal {M}\) will gradually decrease due to the increase of \(\alpha \). The batch annealing mechanism anneals both the loss term \(\mathcal {L}_\mathcal {M}\) and unlabeled samples \(\mathcal {U}^{r}\) which will participate in the calculation of \(\mathcal {L}_\mathcal {U}\).

figure b

3.4 Reloading with Temporal Pool

Before training, we initialize a temporal pool of size \(\mathcal {M}\) to store “very likely matched” unlabeled samples in \(\mathcal {D}_U\). We first get the union set \(\mathcal {B}\) of current \(\mathcal {U}^{r}\) (output of the batch annealing) and the temporal pool \(\mathcal {T}\). Then, top \((1-\alpha ) \times \,\mathcal {C}\) samples with lowest entropy in \(\mathcal {B}\) will be reloaded into \(\mathcal {U}^{r}\) to calculate of the auxiliary loss. The top \(\mathcal {M}\) samples with lowest entropy in \(\mathcal {B}\) will compose the updated temporal pool. A sample will be reloaded if it keeps high confident pseudo label in several continuous temporal training models. The reloading mechanism improves the model to achieve better fitting on high-confidence unlabeled samples as well as more stable training process.

4 Evaluation

4.1 Experiment Configuration

We use Wide ResNet-28 [16] for all models in experiments. Because traditional SSL methods will be badly hurt by class-mismatch problems in the late training period, for fair comparison, we run \(3 \times 2^{23}\) training steps and report the test error rate of a model with highest valid accuracy.

4.2 Supervised with Mixup

Mixup [23] is a widely adopted data augmentation method. In our experiments, we obtain the performance of supervised learning with Mixup using only labeled data, which is denoted as Supervised-only.

4.3 ERCM-SSL Implementations

We combine our design with three state-of-the-art SSL approaches MeanTeacher, VAT, and Mixmatch to obtain ERCM-MT, ERCM-VAT, ERCM-Mix. \(\lambda _{\mathcal {X}}\) and \(\lambda _{\mathcal {U}}\) in SSL methods refer to the implementation in [2] which achieve good performance. Unless otherwise noted, we use constant ERCM hyperparameters with \(k=100 \mathbf{k} \), \( \mathcal {M}=64\), and \(\gamma =0.5\) in our experiments.

ERCM-MT & ERCM-VAT: We use consistency regularization in [19] as the auxiliary loss function. Before feeding the unlabeled data into the model, we add a “guessing label” operation to obtain \(p(y|u,\theta )\). In our experiments, we set hyperparameters for all class-mismatch cases, where \(\lambda _{\mathcal {X}}=1\), \(\lambda _{\mathcal {U}}=50\), \(\lambda _{\mathcal {M}}=0.001\), and \(\beta =0.65\). We adopt the loss function of VAT to implement ERCM-VAT with the same \(p(y|u,\theta )\) as ERCM-MT. In our experiments, we set hyperparameters for all class-mismatch cases, where \(\lambda _{\mathcal {X}}=1\), \(\lambda _{\mathcal {U}}=0.3\), \(\lambda _{\mathcal {M}}=0.05\), and \(\beta =0.75\).

ERCM-Mix: We adopt square difference between guessing label and output for \(\mathcal {L}_{\mathcal {U}}\) as shown in Eq. (5). Moreover, original Mixmatch mixes labeled data with unlabeled data by Mixup for better performance with no mismatched samples. However, in class-mismatch cases, we find that it makes the supervised loss hurt by mismatched samples, especially when the quantity of labeled samples is small as shown in Fig. 2 and Table 1. We adjust Mixmatch to Mix* by mixing labeled data and unlabeled data separately. In ERCM-Mix, we set hyperparameters for all class-mismatch cases, where \(\lambda _{\mathcal {C}}=1\), \(\lambda _{\mathcal {U}}=100\), \(\lambda _{\mathcal {M}}=0.5\), and \(\beta =0.75\).

4.4 Results

Table 1. Test error (%) ± standard deviation of methods against different class mismatch rate on CIFAR-10 with 250 label samples and 20k unlabeled samples on different random splits.
Full size table
Table 2. Test error (%) ± standard deviation of methods against different class mismatch rate on SVHN with 250 label samples and 20k unlabeled samples on different random splits.
Full size table
Table 3. Ablation study results on CIFAR-10 with 250 labeled samples and 20k unlabeled samples when mismatch rate is 60%. Average test error ± standard deviation with different entropy repulsion loss weights (\(\lambda _{\mathcal {M}}=0.1, 0.25, 0.5\)).
Full size table
Fig. 2.
figure 2

Test error on various numbers of labeled samples with mismatch rate 60% on splits of CIFAR-10 (6 classes, 400 labels each class). Shaded regions indicate standard deviation over five trials.

Full size image

In this section, we compare the performances of various methods in class-mismatch cases on different datasets. Mismatch rate represents the proportion of mismatched data among unlabeled data. For example, given 20000 unlabeled samples, 60% mismatch rate means 12000 unlabeled samples are mismatched (Table 3).

CIFAR-10: We first discuss the situation with only a small number of labeled samples. We selected 250 labeled samples, 20k unlabeled samples and 5000 valid samples from CIFAR-10 [10] to train a 5-classes classifier with random splits. We report the average test errors and standard deviations in Table 1. The performances of all three SSL methods decrease gradually as the mismatch rate rises. With the help of our design, ERCM-MT clearly outperforms traditional MT and Supervised-only. ERCM-Mix performs best among all algorithms on CIFAR-10. Compared to the standard Mixmatch, ERCM-Mix achieves up to 6.7% improvement when the mismatch rate is 20%. Compared to Mix*, ERCM-Mix reduces the error rate by 5.9% when the mismatch rate is 20%. The results prove that ERCM significantly improves the performance of SSL methods in class-mismatch cases.

We vary the number of labeled samples (250–2000) when the mismatch rate is 60%. The test errors of different methods are presented in Fig. 2. ERCM-Mix still outperforms other methods. We note that the performance of Mix gradually approaches and slightly exceeds Mix* as the number of labeled samples increases. Imbalance between the quantities of labeled and unlabeled samples will introduce uncertainty to training. With smaller quantity of labeled samples, the improvement introduced by ERCM is more significant. Compared to Mix*, the improvement of ERCM-Mix decreases from 3.4% to 0.8% as the number of labeled samples rises.

Table 4. Test error (%) ± standard deviation comparison of 6 classes (400 per class) on CIFAR-10 with mismatch rate of 25% and 75%.
Full size table
Table 5. Test error (%) ± standard deviation comparison on 8A8O-Imagenet with mismatch rate of 25% and 75%. Details of 8A8O-Imagenet are described in [22].
Full size table

To compare with the recent work Split-BN [22] and ROIreg [9], which aims to address the class mismatch issue, we conduct experiments on 6 classes (400 per class) of CIFAR-10 according to [16] and [22]. As shown in Table 4, ERCM-MT and ERCM-VAT significantly outperform Split-BN+MT, Split-BN+VAT and ROIreg+VAT when mismatch rates are 25% and 75%.Footnote 1. Moreover, ERCM-Mix performs best among these methods and achieves 11.8% test error when mismatch rate is 75%.

SVHN: On SVHN [15], we evaluate traditional VAT and Mixmatch in various class-mismatch cases (0% –100%). We implement ERCM-SSL methods with \(\gamma =0.2\). Table 2 reports the average test error on 250 labeled samples and 20k unlabeled samples over random splits. With no class-mismatch problems, ERCM-SSL methods perform slightly worse than traditional SSL methods. ERCM-SSL methods, however, achieve better performance in all class-mismatch cases. For example, when the mismatch rate is 100%, ERCM-Mix achieves 11.2% test error which is 3.4% lower than Mix*.

8A8O-Imagenet: We conduct evaluations on 8A8O-Imagenet (8 animals and 8 others), a subset of Imagenet [5] described in [22]. We select 600 labeled samples per class for an 8-animals classifier. As shown in Table 5, the performances of ERCM-MT, ERCM-VAT and ERCM-Mixmatch are better than Split-BN+MT and Split-BN+VAT.

4.5 Auxiliary Loss

We explore the impact of our design on auxiliary loss (unsupervised loss). We use 250 labeled samples and 20k unlabeled samples on CIFAR-10 when the mismatch rates is 60%. As shown in Fig. 3, we select uniform batches to observe the auxiliary loss term produced by the unlabeled samples of MT, Mix*, ERCM-MT and ERCM-Mix every \(2^{16}\) steps during training. However, auxiliary loss terms of ERCM-SSL methods are becoming lower than those of traditional SSL methods. ERCM mitigates the harm caused by mismatched data and makes it easier for auxiliary terms to be minimized.

Fig. 3.
figure 3

Auxiliary loss term of SSL methods with and without ERCM when the mismatch rate is 60%. The smoothing rate is 0.95.

Full size image

4.6 Ablation Study

We conduct ablation study on ERCM-Mix to figure out the importance of each part by removing each part of ERCM separately. We carry out our experiments on CIFAR-10 with 250 labeled and 20k unlabeled samples mentioned in Sect. 4.4 when the mismatch rate is 60% (\(\lambda _{\mathcal {M}}=0.1,0.25,0.5\)). We measure the impact of using original mixup mode, removing entropy repulsion loss, removing batch annealing operation (i.e. setting \(\alpha =1\) and \(\mathcal {L}_{\mathcal {M}}=0\), equal to Mix*), and removing temporal pool.

5 Conclusion

In this work, we propose ERCM, a new technique that involves a novel entropy repulsion loss together with a batch annealing and reloading mechanism to empower traditional SSL approaches against class-mismatch problems. Compared with the original SSL methods, ERCM-SSL methods can reduce the performance degradation caused by class mismatch samples. Extensive experiments demonstrate a clear performance improvement and strong portability of ERCM. We believe that ERCM has the potential to be combined with more advanced SSL approaches in the future.