Keywords

1 Introduction

Referring to geometric structures could be a way to a systematic design approach in art, design and architecture. The Dutch artist Gerard Caris put the question “How to imagine something from nothing?” at the beginning of his art work.

Intuitively received forms and structures can be related to geometry which has to be seen as the science to capture, develop and generate structures and forms. In this way geometry is part of the understanding of mathematics as a general structural science according the project Bourbaki in the 1930s. The idea to use those geometric considerations for aesthetic creations has a long history, but especially structural approaches had been part of the concept of Ulm School of Design (1953–1968) with a mathematical-geometric visual methodology. The philosopher Elisabeth Walther, professor at University Stuttgart and lecturer at Ulm School of Design, described the aesthetics, developed by the philosopher Max Bense [1] as fundamental for techniques as well as architecture and art:

Aesthetics, as Bense brings it into play, is the principle of order par excellence. Aesthetics is order, and order on the other hand is describable by mathematics. Therefore, aesthetics is important as structuring the world for techniques as well as architecture, literature, etc., for all what will be created. Whenever we take something out of the chaos of existing und assemble it new, we need an aesthetic foundation. [2], translated from German to English by the author

Digital design techniques provoke such a shift to thinking in geometric structures as a fundament in creative processes. Toni Kotnik [3] analyzed the relationship between actual digital design techniques and the necessarily changing way of thinking in structures. He speaks of a new form of structuralism based on mathematics as the science of structures. The described aesthetic approach of Bense had already anticipated the actual requirements and is of actual relevance. Such principles of order as an aesthetic foundation of art, design, and architecture can be found for example in the geometry of tessellations, patterns, transformations, and forms. Therefore, we will have a look at those geometric order principles before we will analyze works of art and architecture according those fundamentals of geometry.

2 Geometric Structures

Fundamental geometric structures can be seen for instance in plane and spatial tessellations. The regular and semiregular plane tessellations build the background for paintings and patterns. A next step could be looking for the principle of duality of these tessellations. The duals of the semiregular tessellations form tessellations out of congruent non-regular polygons. The number of lines in one vertex produces the number of vertexes of the resulted polygon. The duality principle of projective geometry is a mighty tool for creative steps from one structure to another. The counterpart in three-dimensional space are polyhedra and their duals. the Platonian solids are the fundament for developing the Archimedean solids and the dual Catalan solids. Approaches filling the space with solids give the basis for building structures. Tessellations, grids, and lattice structures can be found as the background for floor plans, connectivity of spaces as well as supporting structures in architecture.

Another point of view offers the symmetry considerations based on the notion of transformations. Patterns can be described and classified as symmetry groups. The symmetry concept gets expanded to more general transformations by this conception, which offers a process-oriented approach from single elements to complex structures, from one form to another. Transformations can be classified according March and Steadman [4] in identity, isometry, similarity, affinity, perspectivity, and topology transformations. These offer additional rich tools for designing, which are essential in digital design processes.

More sophisticated geometric structures like aperiodic tiling, fractals or Voronoi diagrams and its dual Delaunay triangulation supplement the repertoire of geometric structures which are effective for fundamental design processes. Further examples are described in Leopold, 2015 [5].

3 Examples of Geometric Structures in Works of Art

The work of the Dutch artist Gerard Caris shows a strong approach on the basis of tessellations with regular pentagons and in the sculptural spatial work on dodecahedra. Caris wrote in a statement of 2018 about his work:

Geometric as well as non-algorithmic elements involved in the creation of these new works evoke a sense of unity in the viewing process in which aesthetics and mathematical logic merge together as one. The regular pentagon and the dodecahedron being the principal building blocks of this oeuvre …. [6]

After some explorations in tiling the plane with variations of irregular pentagons and hexagons, Caris had been fascinated by the universe of the regular pentagon with its systematical consequences. While trying to tile the plane with regular pentagons, he explored the different positions of the remaining rhombuses between them. Series of his works discover aesthetic results from variations, which suggest spatial interpretations by using bright-dark colors. The result of his explorations had been his Pentagrid which contains the manifold relationships and configurations resulting from the regular pentagon. It can be seen therefore as the repertoire for all possible derivable art works. Caris uses his Pentagrid in his creation processes. Figure 1 illustrates the resulted grid and figures from the tiling approaches by regular pentagons.

Fig. 1
figure 1

Five-dimensional grid of the pentagon and figures in the Pentagrid

Full size image

A detailed analysis of his work also correspondingly of his sculptural and relief work on the basis of the dodecahedron is published by the author in the Handbook of the Mathematics of the Arts and Sciences [7].

A work of the Danish-Islandic artist Olafur Eliasson with his studio in Berlin [8] might serve as a second example for art based on geometric structures. Some examples of his works are strongly related to the relationships of polyhedra, some of them evolved in co-operation with the Icelandic architect Einar Thorsteinn [9]. The work “Your sound galaxy” of 2012 (Fig. 2), exhibited for example in the Red Brick Art Museum in Beijing, 2014, gives the chance to explore characteristics and relationships of polyhedra in an exceptional way. Eliasson described the work with its elements, relationships and materials as follows:

Fig. 2
figure 2

Photo: Xing Yu (left), Anders Sune Berg (right). © Studio Olafur Eliasson GmbH [10]

“Your sound galaxy”, 2012 by Olafur Eliasson, Red Brick Art Museum, Beijing 2018.

Full size image

Your sound galaxy suspends a group of twenty-seven polyhedrons from the ceiling in two horizontally concentric circles. Each polyhedron is made of a stainless steel frame clad in mirrored glass that has been turned inward so that the blue-grey backs of the mirrors act as the faces of the solid. A single halogen light mounted inside each polyhedron is multiplied by the reflective interior into a twinkling glow that escapes through the gaps in the frames. The polyhedrons are organizable into nine ‘families’ of three related forms. [10]

Our student Rahaf Nader analyzed and studied the relationships between the used polyhedra by remodeling this work in a seminar on polyhedral structures in 2020. Starting with two tetrahedra, because the tetrahedron is self-dual, the dual solids follow in the outer circle and get more complex and multi-faceted. In some parts she found additional geometric orders in the sequence of the polyhedra which led her to a deep research on the relationships between them. In her analysis in Fig. 3 the Platonic solids and their compound are shown in yellow, the Archimedean solids in red and their dual Catalan solids in blue. In the first four groups and in the sixth and seventh group the transition between the groups arises from the inner circle to the outer by forming the convex hull of the compound star polyhedron, marked with a green bent arrow. In this way we come from the star tetrahedron to the cube in the outer circle as its convex hull, from the compound of cube and octahedron to the Catalan solid rhombic dodecahedron and its dual Archimedean cuboctahedron, from their compound star solid by the convex hull to the Catalan solid deltoidal icositetrahedron and its dual Archimedean rhombicuboctahedron. These relationships explain why we step in the sequence first to the Catalan solid and then to the dual Archimedean solid, only with one exception in the last group. From the sixth group we have the transition from the convex hull of the icosahedron-dodecadron-star to the Catalan solid rhombic triacontahedron and it Archimedean dual icosidodecahedron, and one more transition from the compound of these two to the Catalan solid deltoidal hexecontahedron as their convex hull and from there again to the dual Archimedean rhombicosidodecahedron.

Fig. 3
figure 3

Remodeling and study of Eliassons’s galaxy by student Rahaf Nader

Full size image

There remain artistic free decisions for selecting the solids and their sequence, but these studies on the relationships between the solids had been fascinating results in this research. It is interesting to see how geometric research can inspire artwork in Olafur Eliasson’s studio. In the advanced geometry video of the livestream collection Anna Engberg-Pedersen, co-director of Studio Olafur Eliasson, says:

What we are hoping to do, is demystify a little bit what it takes to do art works, where do the ideas come from …. [11]

It gets obvious that the art work had been a result of an intensive research on the characteristics and relationships between polyhedra.

4 Examples of Geometric Structures in Works of Architecture

Geometric structures can be used in many ways when designing and realizing architecture. We want to focus here on four examples related to architectural structures based on polyhedra.

The work of Richard Buckminster Fuller offers a lot to discover related to geometric structures. One of his most renowned inventions is the geodesic sphere, which resulted in built examples like the biosphere in Montreal, 1967. The idea for the geodesic sphere had been developed out of the icosahedron, the most spherical Platonic solid by subdividing and projecting onto the circumscribed sphere. Figure 4 shows the design and realization of a level 1 geodesic dome made from cardboard tubes, a waste product of A0 plots, and knots from laser cut MDF by our student Simon Kunzler in 2014.

Fig. 4
figure 4

Concept drawing, 3D-printed model and realized cardboard dome by Simon Kunzler

Full size image

By studying the various polyhedra it stands to reason taking another polyhedron with more faces for creating a dome. A suitable solid could be one of the Catalan solids. The faces are not regular, but they are congruent. The rhombic triacontahedron with 30 faces can be a suitable starting point. Our student Moritz Brucker had this idea and found a similar approach by Fuller in the Egg-Crate Basic Assembly Dome of 1950, realized in the University of Oregon Dome in 1953 with his students. Those explorations of Fuller and his students are well documented in the new published book by Daniel López-Pérez [12]. Moritz Brucker worked in 2020 with the rhombic triacontahedron, divided the rhombus in triangles, these in smaller rhombuses by connecting the midpoints of the triangles. By subdividing again, we get two different rhombuses, shown in green and red in Fig. 5. The faces with the rhombic pattern are then put on the faces of the rhombic triacontahedron, then projected onto the inscribed sphere. A Catalan solid has an inscribed sphere, not a circumscribed one. The rhombic sphere pattern is shown in Fig. 6 with the created 3D model.

Fig. 5
figure 5

Developing the sphere approximation from the rhombic triacontahedron by subdividing the rhombuses and projecting onto the inscribed sphere by Moritz Brucker

Full size image
Fig. 6
figure 6

Rhombic sphere pattern with the rhombic triacontahedron as starting solid and final 3D-model by Moritz Brucker

Full size image

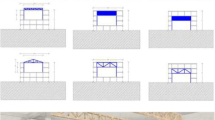
A third example started with analyzing works of Konrad Wachsmann, especially the structure of the USAF Aircraft Hangar, 1951 [13]. Our student Arutiun Papikian created a triangular structure with irregular tetrahedra in 2020, stimulated by his research on Wachsmann’s works, which should be usable for horizontal as well as vertical structures, therefore applicable for support structures and facade designs (Fig. 7).

Fig. 7
figure 7

Triangular structure based on irregular tetrahedra by Arutiun Papikian, digital and physical models

Full size image

The fourth example picks up the work of Anne Tyng [14]. She worked 1944 in the New York office of Konrad Wachsmann before joining Louis I. Kahn’s office 1945 in Philadelphia. She had been fascinated by the work of Buckminster Fuller when she listened to his lecture in 1949. Her work, too, together with Louis I. Kahn, is permeated with the application of polyhedral structures, especially as space frame architecture. In her design of an Elementary School (1950–1951) for example she designed a structure out of octahedra and tetrahedra in several space layers that converge finally in a point and become a pillar. The article by Cristina Càndito includes a description of this work [15]. We can find similarities to Wachsmann’s USAF Aircraft Hangar.

The space frame structure is variegated in the Philadelphia City Tower (1952–1957), designed together with Kahn. One layer is formed by three joined hexagons, packed with 18 tetrahedra, seven octahedra and four half octahedra. From level to level this structure is moved in six possible directions. Figure 8 shows the analysis of our student Benedikt Blumenröder in 2017 with physical models of the structure. Anne Tyng assigned an important role to the Platonic solids in architectural design processes. She described them as a three-dimensional probability matrix.

Fig. 8
figure 8

Photo right ©Bernhard Friese

Geometric structure of a layer and model of the Philadelphia City Tower by Benedikt Blumenröder, designed by Anne Tyng and L. I. Kahn, 1952–1957.

Full size image

An icosahedron may be nested within the octahedron, and the dodecahedron may be built-out from a cube. It’s a very elegant family of forms that expresses probability. It’s a three-dimensional probability matrix …. [16, p. 130]

5 Conclusions

The shown examples can only give an idea of the power of geometric structures for creation processes in art and architecture. Digital design techniques provoke a new actuality of geometric structural attempts in designing and creating. The described background should be taken into account when forming curricula of such creative disciplines. Geometry has its place in design and should not be reduced to representation techniques. Those structural approaches facilitate design methodologies instead of intuitive throws of the genius and offer therefore ways for developing ideas.