Keywords

1 Introduction

Communicating Sequential Processes (CSP) is a language to specify and verify patterns of interaction of concurrent systems. Together with CCS and LOTOS, it belongs to the family of process algebras. CSP’s rich theory comprises denotational, operational and algebraic semantic facets and has influenced programming languages such as Limbo, Crystal, Clojure and most notably Golang [15]. CSP has been applied in industry as a tool for specifying and verifying the concurrent aspects of hardware systems, such as the T9000 transputer [6].

The theory of CSP was first described in 1978 in a book by Tony Hoare [20], but has since evolved substantially [9, 10, 29]. CSP describes the most common communication and synchronization mechanisms with one single language primitive: synchronous communication written \({\text {-}}{[\![}{\text {-}}{]\!]}{\text {-}}\). CSP semantics is described by a fully abstract model of behaviour designed to be compositional: the denotational semantics of a process \(P\) encompasses all possible behaviours of this process in the context of all possible environments \(P\ {[\![}S{]\!]}\ Env\) (where \(S\) is the set of \(atomic\ events\) both \(P\) and \(Env\) must synchronize on). This design objective has the consequence that two kinds of choice have to be distinguished:

  1. 1.

    the external choice, written \({\text {-}}{\Box }{\text {-}}\), which forces a process “to follow” whatever the environment offers, and

  2. 2.

    the internal choice, written \({\text {-}}{\sqcap }{\text {-}}\), which imposes on the environment of a process “to follow” the non-deterministic choices made.

Generalizations of these two operators \({\Box }x\,{\,\in \,}\,A{.}\ P{(}x{)}\) and \({\sqcap \,}x\,{\,\in \,}\,A{.}\ P{(}x{)}\) allow for modeling the concepts of input and output: Based on the prefix operator \(a{\rightarrow }P\) (event \(a\) happens, then the process proceeds with \(P\)), receiving input is modeled by \({\Box }x\,{\,\in \,}\,A{.}\ x{\rightarrow }P{(}x{)}\) while sending output is represented by \({\sqcap \,}x{\,\in \,}A{.}\ x{\rightarrow }P{(}x{)}\). Setting choice in the center of the language semantics implies that deadlock-freeness becomes a vital property for the well-formedness of a process, nearly as vital as type-checking: Consider two events \(a\) and \(b\) not involved in a process \(P\), then \({(}a{\rightarrow }P\ {\Box }\ b{\rightarrow }P{)}\ {[\![}{\{}a{,}b{\}}{]\!]}\ {(}a{\rightarrow }P\ {\sqcap }\ b{\rightarrow }P{)}\) is deadlock free provided \(P\) is, while \({(}a{\rightarrow }P\ {\sqcap }\ b{\rightarrow }P{)}\ {[\![}{\{}a{,}b{\}}{]\!]}\ {(}a{\rightarrow }P\ {\sqcap }\ b{\rightarrow }P{)}\) deadlocks (both processes can make “ruthlessly” an opposite choice, but are required to synchronize).

Verification of CSP properties has been centered around the notion of process refinement orderings, most notably \({\text {-}}{\sqsubseteq }_{FD}{\text {-}}\) and \({\text {-}}{\sqsubseteq }{\text {-}}\). The latter turns the denotational domain of CSP into a Scott cpo [33], which yields semantics for the fixed point operator \({\mu }x{.}\ f{(}x{)}\) provided that \(f\) is continuous with respect to \({\text {-}}{\sqsubseteq }{\text {-}}\). Since it is possible to express deadlock-freeness and livelock-freeness as a refinement problem, the verification of properties has been reduced traditionally to a model-checking problem for finite set of events \(A\).

We are interested in verification techniques for arbitrary event sets \(A\) or arbitrarily parameterized processes. Such processes can be used to model dense-timed processes, processes with dynamic thread creation, and processes with unbounded thread-local variables and buffers. However, this adds substantial complexity to the process theory: when it comes to study the interplay of different denotational models, refinement-orderings, and side-conditions for continuity, paper-and-pencil proofs easily reach their limits of precision.

Several attempts have been undertaken to develop a formal theory in an interactive proof system, mostly in Isabelle/HOL [12, 23, 28, 37]. This paper is based on [37], which has been the most comprehensive attempt to formalize denotational CSP semantics covering a part of Bill Roscoe’s Book [29]. Our contributions are as follows:

  • we ported [37] from Isabelle93-7 and ancient ML-written proof scripts to a modern Isabelle/HOL version and structured Isar proofs, and extended it substantially,

  • we introduced new refinement notions allowing a deeper understanding of the CSP Failure/Divergence model, providing some meta-theoretic clarifications,

  • we used our framework to derive new types of decomposition rules and stronger induction principles based on the new refinement notions, and

  • we integrate this machinery into a number of advanced verification techniques, which we apply to two generalized paradigmatic examples in the CSP literature, the CopyBuffer and Dining PhilosophersFootnote 1.

2 Preliminaries

2.1 Denotational CSP Semantics

The denotational semantics of CSP (following [29]) comes in three layers: the trace model, the (stable) failures model and the failure/divergence model.

In the trace semantics model, a process \(P\) is denoted by a set of communication traces, built from atomic events. A trace here represents a partial history of the communication sequence occurring when a process interacts with its environment. For the two basic CSP processes \(Skip\) (successful termination) and \(Stop\) (just deadlock), the semantic function \({\mathcal {T}}\) of the trace model just gives the same denotation, i.e.the empty trace: \({\mathcal {T}}{(}Skip{)}\ {=}\ {\mathcal {T}}{(}Stop{)}\ {=}\ {\{}{[}{]}{\}}\). Note that the trace sets, representing all partial history, is in general prefix closed.

Example 1

Let two processes be defined as follows:

  1. 1.

    \(P_{det}\ {=}\ {(}a\ {\rightarrow }\ Stop{)}\ {\Box }\ {(}b\ {\rightarrow }\ Stop{)}\)

  2. 2.

    \(P_{ndet}\ {=}\ {(}a\ {\rightarrow }\ Stop{)}\ {\sqcap }\ {(}b\ {\rightarrow }\ Stop{)}\)

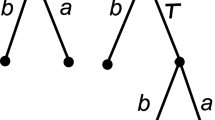
These two processes \(P_{det}\) and \(P_{ndet}\) cannot be distinguished by using the trace semantics: \({\mathcal {T}}{(}P_{det}{)}\ {=}\ {\mathcal {T}}{(}P_{ndet}{)}\ {=}\ {\{}{[}{]}{,}{[}a{]}{,}{[}b{]}{\}}\). To resolve this problem, Brookes [9] proposed the failures model, where communication traces were augmented with the constraint information for further communication that is represented negatively as a refusal set. A failure \({(}t{,}\ X{)}\) is a pair of a trace \(t\) and a set of events \(X\), called refusal set, that a process can refuse if any of the events in \(X\) were offered to him by the environment after performing the trace \(t\). The semantic function \({\mathcal {F}}\) in the failures model maps a process to a set of refusals. Let \({\varSigma }\) be the set of events. Then, \({\{}{(}{[}{]}{,}{\varSigma }{)}{\}}\ {\,\subseteq \,}\ {\mathcal {F}}\ Stop\) as the process \(Stop\) refuses all events. For Example 1, we have \({\{}{(}{[}{]}{,}{\varSigma }{\backslash }{\{}a{,}b{\}}{)}{,}{(}{[}a{]}{,}{\varSigma }{)}{,}{(}{[}b{]}{,}{\varSigma }{)}{\}}\ {\,\subseteq \,}\ {\mathcal {F}}\ P_{det}\), while \({\{}{(}{[}{]}{,}{\varSigma }{\backslash }{\{}a{\}}{)}{,}{(}{[}{]}{,}{\varSigma }{\backslash }{\{}b{\}}{)}{,}{(}{[}a{]}{,}{\varSigma }{)}{,}{(}{[}b{]}{,}{\varSigma }{)}{\}}\ {\,\subseteq \,}\ {\mathcal {F}}\ P_{ndet}\) (the \({\text {-}}{\,\subseteq \,}{\text {-}}\) refers to the fact that the refusals must be downward closed; we show only the maximal refusal sets here). Thus, internal and external choice, also called nondeterministic and deterministic choice, can be distinguished in the failures semantics.

However, it turns out that the failures model suffers from another deficiency with respect to the phenomenon called infinite internal chatter or divergence.

Example 2

The following process \(P_{inf}\) is an infinite process that performs \(a\) infinitely many times. However, using the CSP hiding operator \({\text {-}}{\backslash }{\text {-}}\), this activity is concealed:

  1. 1.

    \(P_{inf}\ {=}\ {(}{\mu }\ X{.}\ a\ {\rightarrow }\ X{)}\ {\backslash }\ {\{}a{\}}\)

where \(P_{inf}\) will correspond to \({\bot }\) in the process cpo ordering. To distinguish divergences from the deadlock process, Brookes and Roscoe proposed failure/divergence model to incorporate divergence traces [10]. A divergence trace is the one leading to a possible divergent behavior. A well behaved process should be able to respond to its environment in a finite amount of time. Hence, divergences are considered as a kind of a catastrophe in this model. Thus, a process is represented by a failure set \({\mathcal {F}}\), together with a set of divergence traces \({\mathcal {D}}\); in our example, the empty trace \({[}{]}\) belongs to \({\mathcal {D}}\ P_{inf}\).

The failure/divergence model has become the standard semantics for an enormous range of CSP research and the implementations of [1, 34]. Note, that the work of [23] is restricted to a variant of the failures model only.

2.2 Isabelle/HOL

Nowadays, Isabelle/HOL is one of the major interactive theory development environments [27]. HOL stands for Higher-Order Logic, a logic based on simply-typed \({\lambda }\)-calculus extended by parametric polymorphism and Haskell-like type-classes. Besides interactive and integrated automated proof procedures, it offers code and documentation generators. Its structured proof language Isar is intensively used in the plethora of work done and has been a key factor for the success of the Archive of Formal Proofs (https://www.isa-afp.org).

For the work presented here, one relevant construction is:

  • \(\mathbf {typedef}\ \ {(}{\alpha }_{\textit{1}}{,}\,\mathbf {.} {} \mathbf {.} {} \mathbf {.} {,}\,{\alpha }_{n}{)}t\ {=}\ E\)

It creates a fresh type that is isomorphic to a set \(E\) involving \({\alpha }_{\textit{1}}{,}\,{.}{.}{.}{,}\,{\alpha }_{n}\) types. Isabelle/HOL performs a number of syntactic checks for these constructions that guarantee the logical consistency of the defined constants or types relative to the axiomatic basis of HOL. The system distribution comes with rich libraries comprising Sets, Numbers, Lists, etc. which are built in this “conservative” way.

For this work, a particular library called \(HOLCF\) is intensively used. It provides classical domain theory for a particular type-class \({\alpha }\,{:}{:}\,pcpo\), i.e.the class of types \({\alpha }\) for which

  1. 1.

    a complete partial order \({\text {-}}{\sqsubseteq }{\text {-}}\) is defined, and

  2. 2.

    a least element \({\bot }\) is defined.

For these types, \(HOLCF\) provides a fixed-point operator \({\mu }X{.}\ f\ X\), fixed-point induction and other (automated) proof infrastructure. Isabelle’s type-inference can automatically infer, for example, that if \({\alpha }\,{:}{:}\,pcpo\), then \({(}{\beta }\ {\Rightarrow }\ {\alpha }{)}\,{:}{:}\,pcpo\).

3 Formalising Denotational CSP Semantics in HOL

3.1 Process Invariant and Process Type

First, we need a slight revision of the concept of trace: if \({\varSigma }\) is the type of the atomic events (represented by a type variable), then we need to extend this type by a special event \({\surd }\) (called “tick”) signaling termination. Thus, traces have the type \({(}{\varSigma }{+}{\surd }{)}^{*}\), written \({\varSigma }^{\surd *}\); since \({\surd }\) may only occur at the end of a trace, we need to define a predicate \(front\_tickFree\ t\) that requires from traces that \({\surd }\) can only occur at the end.

Second, in the traditional literature, the semantic domain is implicitly described by 9 “axioms” over the three semantic functions \({\mathcal {T}}\), \({\mathcal {F}}\) and \({\mathcal {D}}\). Informally:

  • the initial trace of a process must be empty;

  • any allowed trace must be \(front\_tickFree\);

  • traces of a process are prefix-closed;

  • a process can refuse all subsets of a refusal set;

  • any event refused by a process after a trace \(s\) must be in a refusal set associated to \(s\);

  • the tick accepted after a trace \(s\) implies that all other events are refused;

  • a divergence trace with any suffix is itself a divergence one

  • once a process has diverged, it can engage in or refuse any sequence of events.

  • a trace ending with \({\surd }\) belonging to divergence set implies that its maximum prefix without \({\surd }\) is also a divergent trace.

Formally, a process \(P\) of the type \({\varSigma }\ process\) should have the following properties:

$$\begin{aligned} \begin{array}{l} {(}{[}{]}{,}{\{}{\}}{)}\ {\,\in \,}\ {\mathcal {F}}\ P\ {\wedge }\\ {(}{\forall \,}\ s\ X{.}\ \ {(}s{,}X{)}\ {\,\in \,}\ {\mathcal {F}}\ P\ {\longrightarrow }\ front{\text {-}}tickFree\ s{)}\ {\wedge }\\ {(}{\forall \,}\ s\ t\ {.}\ {(}s{@}t{,}{\{}{\}}{)}\ {\,\in \,}\ {\mathcal {F}}\ P\ {\longrightarrow }\ {(}s{,}{\{}{\}}{)}\ {\,\in \,}\ {\mathcal {F}}\ P{)}\ {\wedge }\\ {(}{\forall \,}\ s\ X\ Y{.}\ {(}s{,}Y{)}\ {\,\in \,}\ {\mathcal {F}}\ P\ {\wedge }\ X\,{\,\subseteq \,}\,Y\ {\longrightarrow }\ {(}s{,}X{)}\ {\,\in \,}\ {\mathcal {F}}\ P{)}\ {\wedge }\ \\ {(}{\forall \,}\ s\ X\ Y{.}\ {(}s{,}X{)}\ {\,\in \,}\ {\mathcal {F}}\ P\ {\wedge }\ {(}{\forall \,}c\ {\,\in \,}\ Y{.}\ {(}{(}s{@}{[}c{]}{,}{\{}{\}}{)}\ {\notin }\ {\mathcal {F}}\ P{)}{)}\ {\longrightarrow }\ {(}s{,}X\ {\,\cup \,}\ Y{)}\ {\,\in \,}\ {\mathcal {F}}\ P{)}\ {\wedge }\\ {(}{\forall \,}\ s\ X{.}\ \ {(}s{@}{[}{\surd }{]}{,}{\{}{\}}{)}\ {\,\in \,}\ {\mathcal {F}}\ P\ {\longrightarrow }\ {(}s{,}X{-}{\{}{\surd }{\}}{)}\ {\,\in \,}\ {\mathcal {F}}\ P{)}\ {\wedge }\\ {(}{\forall \,}\ s\ t{.}\ s\ {\,\in \,}\ {\mathcal {D}}\ P\ {\wedge }\ tickFree\ s\ {\wedge }\ front{\text {-}}tickFree\ t\ {\longrightarrow }\ s{@}t\ {\,\in \,}\ {\mathcal {D}}\ P{)}\ \ {\wedge }\\ {(}{\forall \,}\ s\ X{.}\ s\ {\,\in \,}\ {\mathcal {D}}\ P\ {\longrightarrow }\ {(}s{,}X{)}\ {\,\in \,}\ {\mathcal {F}}\ P{)}\ {\wedge }\\ {(}{\forall \,}\ s{.}\ s{@}{[}{\surd }{]}\ {\,\in \,}\ {\mathcal {D}}\ P\ {\longrightarrow }\ s\ {\,\in \,}\ {\mathcal {D}}\ P{)} \end{array} \end{aligned}$$

Our objective is to encapsulate this wishlist into a type constructed as a conservative theory extension in our theory HOL-CSP. Therefore third, we define a pre-type for processes \({\varSigma }\ process_{\textit{0}}\) by \({\mathcal {P}}{(}{\varSigma }^{\surd *}\,{\times }\,{\mathcal {P}}{(}{\varSigma }^{\surd }{)}{)}\,{\times }\,{\mathcal {P}}{(}{\varSigma }^{\surd *}{)}\). Fourth, we turn our wishlist of “axioms” above into the definition of a predicate \(is{\text {-}}process\ P\) of type \({\varSigma }\ process_{\textit{0}}\ {\Rightarrow }\ bool\) deciding if its conditions are fulfilled. Since \(P\) is a pre-process, we replace \({\mathcal {F}}\) by \(fst\) and \({\mathcal {D}}\) by \(snd\) (the HOL projections into a pair). And last not least fifth, we use the following type definition:

  • \(\mathbf {typedef}\ {^\prime }{\alpha }\ process\ {=}\ {\{}P\,{:}{:}\,{^\prime }{\alpha }\ process_{\textit{0}}\ {.}\ is{\text {-}}process\ P{\}}\)

Isabelle requires a proof for the existence of a witness for this set, but this can be constructed in a straight-forward manner. Suitable definitions for \({\mathcal {T}}\), \({\mathcal {F}}\) and \({\mathcal {D}}\) lifting \(fst\) and \(snd\) on the new \({^\prime }{\alpha }\ process\)-type allows to derive the above properties for any \(P\,{:}{:}\,{^\prime }{\alpha }\ process\).

3.2 CSP Operators over the Process Type

Now, the operators of CSP \(Skip\), \(Stop\), \({\text {-}}{\sqcap }{\text {-}}\), \({\text {-}}{\Box }{\text {-}}\), \({\text {-}}{\rightarrow }{\text {-}}\), \({\text {-}}{[\![}{\text {-}}{]\!]}{\text {-}}\) etc. for internal choice, external choice, prefix and parallel composition, can be defined indirectly on the process-type. For example, for the simple case of the internal choice, we construct it such that \({\text {-}}{\sqcap }{\text {-}}\) has type \({^\prime }{\alpha }\ process\ {\Rightarrow }\ {^\prime }{\alpha }\ process\ {\Rightarrow }\ {^\prime }{\alpha }\ process\) and such that its projection laws satisfy the properties \({\mathcal {F}}\ {(}P\ {\sqcap }\ Q{)}\ {=}\ {\mathcal {F}}\ P\ {\,\cup \,}\ {\mathcal {F}}\ Q\) and \({\mathcal {D}}\ {(}P\ {\sqcap }\ Q{)}\ {=}\ {\mathcal {D}}\ P\ {\,\cup \,}\ {\mathcal {D}}\ Q\) required from [29]. This boils down to a proof that an equivalent definition on the pre-process type \({\varSigma }\ process_{\textit{0}}\) maintains \(is{\text {-}}process\), i.e.this predicate remains invariant on the elements of the semantic domain. For example, we define \({\text {-}}{\sqcap }{\text {-}}\) on the pre-process type as follows:

  • \(\mathbf {definition}\ P\ {\sqcap }\ Q\ {\equiv }\ Abs{\text {-}}process{(}{\mathcal {F}}\ P\ {\,\cup \,}\ {\mathcal {F}}\ Q\ {,}\ {\mathcal {D}}\ P\ {\,\cup \,}\ {\mathcal {D}}\ Q{)}\)

where \({\mathcal {F}}\ {=}\ fst\ {\circ }\ Rep{\text {-}}process\) and \({\mathcal {D}}\ {=}\ snd\ {\circ }\ Rep{\text {-}}process\) and where \(Rep{\text {-}}process\) and \(Abs{\text {-}}process\) are the representation and abstraction morphisms resulting from the type definition linking \({^\prime }{\alpha }\ process\) isomorphically to \({^\prime }{\alpha }\ process_{\textit{0}}\). Proving the above properties for \({\mathcal {F}}\ {(}P\ {\sqcap }\ Q{)}\) and \({\mathcal {D}}\ {(}P\ {\sqcap }\ Q{)}\) requires a proof that \({(}{\mathcal {F}}\ P\ {\,\cup \,}\ {\mathcal {F}}\ Q\ {,}\ {\mathcal {D}}\ P\ {\,\cup \,}\ {\mathcal {D}}\ Q{)}\) satisfies the 9 “axioms”, which is fairly simple in this case.

The definitional presentation of the CSP process operators according to [29] follows always this scheme. This part of the theory comprises around 2000 loc.

3.3 Refinement Orderings

CSP is centered around the idea of process refinement; many critical properties, even ones typically considered as “liveness properties”, can be expressed in terms of these, and a conversion of processes in terms of (finite) labelled transition systems leads to effective model-checking techniques based on graph-exploration. Essentially, a process \(P\) refines another process \(Q\) if and only if it is more deterministic and more defined (has less divergences). Consequently, each of the three semantics models (trace, failure and failure/divergence) has its corresponding refinement orderings. What we are interested in this paper is the following refinement orderings for the failure/divergence model.

  1. 1.

    \(P\ {\sqsubseteq }_{\mathcal {F}\mathcal {D}}\ Q\ {\equiv }\ {\mathcal {F}}\ P\ {\supseteq }\ {\mathcal {F}}\ Q\ {\wedge }\ {\mathcal {D}}\ P\ {\supseteq }\ {\mathcal {D}}\ Q\)

  2. 2.

    \(P\ {\sqsubseteq }_{\mathcal {T}\mathcal {D}}\ Q\ {\equiv }\ {\mathcal {T}}\ P\ {\supseteq }\ {\mathcal {T}}\ Q\ {\wedge }\ {\mathcal {D}}\ P\ {\supseteq }\ {\mathcal {D}}\ Q\)

  3. 3.

    \(P\ {\sqsubseteq }_{\mathfrak {F}}\ Q\ {\equiv }\ \ {\mathfrak {F}}\ P\ {\supseteq }\ {\mathfrak {F}}\ Q{,}\ {\mathfrak {F}}{\,\in \,}{\{}{\mathcal {T}}{,}{\mathcal {F}}{,}{\mathcal {D}}{\}}\)

Notice that in the CSP literature, only \({\sqsubseteq }_{\mathcal {F}\mathcal {D}}\) is well studied for failure/divergence model. Our formal analysis of different granularities on the refinement orderings allows deeper understanding of the same semantics model. For example, \({\sqsubseteq }_{\mathcal {T}\mathcal {D}}\) turns out to have in some cases better monotonicity properties and therefore allow for stronger proof principles in CSP. Furthermore, the refinement ordering \({\sqsubseteq }_{\mathcal {F}}\) analyzed here is different from the classical failure refinement in the literature that is studied for the stable failure model [29], where failures are only defined for stable states, from which no internal progress is possible.

3.4 Process Ordering and HOLCF

For any denotational semantics, the fixed point theory giving semantics to systems of recursive equations is considered as keystone. Its prerequisite is a complete partial ordering \({\text {-}}{\sqsubseteq }{\text {-}}\). The natural candidate \({\text {-}}{\sqsubseteq }_{\mathcal {F}\mathcal {D}}{\text {-}}\) is unfortunately not complete for infinite \({\varSigma }\) for the generalized deterministic choice, and thus for the building block of the read-operations.

Roscoe and Brooks [31] finally proposed another ordering, called the process ordering, and restricted the generalized deterministic choice in a particular way such that completeness could at least be assured for read-operations. This more complex ordering is based on the concept refusals after a trace \(s\) and defined by \({\mathcal {R}}\ P\ s\ {\equiv }\ {\{}X\ {\mid }\ {(}s{,}\ X{)}\ {\,\in \,}\ {\mathcal {F}}\ P{\}}\).

Definition 1 (process ordering)

We define \(P\ {\sqsubseteq }\ Q\ {\equiv }\ {\psi }_{\mathcal {D}}\ {\wedge }\ {\psi }_{\mathcal {R}}\ {\wedge }\ {\psi }_{\mathcal {M}}\), where

  1. 1.

    \({\psi }_{\mathcal {D}}\ {=}\ {\mathcal {D}}\ P\ {\supseteq }\ {\mathcal {D}}\ Q\)

  2. 2.

    \({\psi }_{\mathcal {R}}\ {=}\ s\ {\notin }\ {\mathcal {D}}\ P\ {\Rightarrow }\ {\mathcal {R}}\ P\ s\ {=}\ {\mathcal {R}}\ Q\ s\)

  3. 3.

    \({\psi }_{\mathcal {M}}\ {=}\ Mins{(}{\mathcal {D}}\ P{)}\ {\,\subseteq \,}\ {\mathcal {T}}\ Q\)

Note that the third condition \({\psi }_{\mathcal {M}}\) implies that the set of minimal divergent traces (ones with no proper prefix that is also a divergence) in \(P\), denoted by \(Mins{(}{\mathcal {D}}\ P{)}\), should be a subset of the trace set of \(Q\). It is straight-forward to define the least element \({\bot }\) in this ordering by \({\mathcal {F}}{(}{\bot }{)}\,{=}\,{\{}{(}s{,}X{)}{.}\ front{\text {-}}tickFree\ s{\}}\) and \({\mathcal {D}}{(}{\bot }{)}\ {=}\ {\{}s{.}\ front{\text {-}}tickFree\ s{\}}\)

While the original work [37] was based on an own—and different—fixed-point theory, we decided to base HOL-CSP 2 on HOLCF (initiated by [26] and substantially extended in [21]). HOLCF is based on parametric polymorphism with type classes. A type class is actually a constraint on a type variable by respecting certain syntactic and semantic requirements. For example, a type class of partial ordering, denoted by \({\alpha }\,{:}{:}\,po\), is restricted to all types \({\alpha }\) possessing a relation \({\le }{:}{\alpha }\,{\times }\,{\alpha }\,{\rightarrow }\,bool\) that is reflexive, anti-symmetric, and transitive. Isabelle possesses a construct that allows to establish, that the type \(nat\) belongs to this class, with the consequence that all lemmas derived abstractly on \({\alpha }\,{:}{:}\,po\) are in particular applicable on \(nat\). The type class of \(po\) can be extended to the class of complete partial ordering \(cpo\). A \(po\) is said to be complete if all non-empty directed sets have a least upper bound (\(lub\)). Finally the class of \(pcpo\) (Pointed cpo) is a \(cpo\) ordering that has a least element, denoted by \({\bot }\). For \(pcpo\) ordering, two crucial notions for continuity (\(cont\)) and fixed-point operator (\({\mu }X{.}\ f{(}X{)}\)) are defined in the usual way. A function from one \(cpo\) to another one is said to be continuous if it distributes over the \(lub\) of all directed sets (or chains). One key result of the fixed-point theory is the proof of the fixed-point theorem:

$$\begin{aligned} cont\ f\ {\Longrightarrow }\ \ {\mu }X{.}\ f{(}X{)}\ {=}\ f{(}{\mu }X{.}\ f{(}X{)}{)} \end{aligned}$$

For most CSP operators \({\otimes }\) we derived rules of the form:

$$\begin{aligned} cont\ P\ {\Longrightarrow }\ cont\ Q\ {\Longrightarrow }\ cont{(}{\lambda }x{.}\ {(}P\ x{)}\ {\otimes }\ {(}Q\ x{)}{)} \end{aligned}$$

These rules allow to automatically infer for any process term if it is continuous or not. The port of HOL-CSP 2 on HOLCF implied that the derivation of the entire continuity rules had to be completely re-done (3000 loc).

HOL-CSP provides an important proof principle, the fixed-point induction:

$$\begin{aligned} cont\ f\ {\Longrightarrow }\ adm\ Pr\ {\Longrightarrow }\ Pr\ {\bot }\ {\Longrightarrow }\ {(}{\bigwedge }X{.}\ \ X\ {\Longrightarrow }\ Pr{(}f\ X{)}{)}\ {\Longrightarrow }\ Pr{(}{\mu }X{.}\ f\ X{)} \end{aligned}$$

Fixed-point induction requires a small side-calculus for establishing the admissibility of a predicate; basically, predicates are admissible if they are valid for any least upper bound of a chain \(x_{\textit{1}}\ {\sqsubseteq }\ x_{\textit{2}}\ {\sqsubseteq }\ x_{\textit{3}}\ {.}{.}{.}\) provided that \({\forall \,}i{.}\ Pr{(}x_{i}{)}\). It turns out that \({\text {-}}{\sqsubseteq }{\text {-}}\) and \({\text {-}}{\sqsubseteq }_{F\,D}{\text {-}}\) as well as all other refinement orderings that we introduce in this paper are admissible. Fixed-point inductions are the main proof weapon in verifications, together with monotonicities and the CSP laws. Denotational arguments can be hidden as they are not needed in practical verifications.

3.5 CSP Rules: Improved Proofs and New Results

The CSP operators enjoy a number of algebraic properties: commutativity, associativities, and idempotence in some cases. Moreover, there is a rich body of distribution laws between these operators. Our new version HOL-CSP 2 not only shortens and restructures the proofs of [37]; the code reduces to 8000 loc from 25000 loc. Some illustrative examples of new established rules are:

  • \({\Box }x{\,\in \,}A{\,\cup \,}B{\rightarrow }P{(}x{)}\ {=}\ {(}{\Box }x{\,\in \,}A{\rightarrow }P\ x{)}\ {\Box }\ {(}{\Box }x{\,\in \,}B{\rightarrow }P\ x{)}\)

  • \(A{\,\cup \,}B{\,\subseteq \,}C\ {\Longrightarrow }\ {(}{\Box }x{\,\in \,}A{\rightarrow }P\ x\ {[\![}C{]\!]}\ {\Box }x{\,\in \,}B{\rightarrow }Q\ x{)}\ {=}\ {\Box }x{\,\in \,}A{\,\cap \,}B{\rightarrow }{(}P\ x\ {[\![}C{]\!]}\ Q\ x{)}\)

  • \(\begin{aligned} A{\,\subseteq \,}C\ {\Longrightarrow }&B{\,\cap \,}C{=}{\{}{\}}\ {\Longrightarrow }\ {(}{\Box }x{\,\in \,}A{\rightarrow }P\ x\ {[\![}C{]\!]}\ {\Box }x{\,\in \,}B{\rightarrow }Q\ x{)}\ {=}\ {\Box }x{\,\in \,}B{\rightarrow }{(}{\Box }x{\,\in \,}A{\rightarrow }P\ x\ {[\![}C{]\!]}\ Q\ x{)} \end{aligned}\)

  • \(finite\ A\ {\Longrightarrow }\ A{\,\cap \,}C\ {=}\ {\{}{\}}\ {\Longrightarrow }\ {(}{(}P\ {[\![}C{]\!]}\ Q{)}\ {\backslash }\ A{)}\ {=}\ {(}{(}P\ {\backslash }\ A{)}\ {[\![}C{]\!]}\ {(}Q\ {\backslash }\ A{)}{)}\ {.}{.}{.}\)

The continuity proof of the hiding operator is notorious. The proof is known to involve the classical König’s lemma stating that every infinite tree with finite branching reference processes are

has an infinite path. We adapt this lemma to our context as follows:

$$\begin{aligned} infinite\ tr\;&{\Longrightarrow }\ {\forall \,}i{.}\ finite{\{}t{.}\ {\exists \,}t{^\prime }{\,\in \,}tr{.}\ t\ {=}\ take\ i\ t{^\prime }{\}}\ \\&{\Longrightarrow }\ {\exists \,}\ f{.}\ strict{\text {-}}mono\ f\ {\wedge }\ range\ f\ {\,\subseteq \,}\ {\{}t{.}\ {\exists \,}t{^\prime }{\,\in \,}tr{.}\ t\ {\le }\ t{^\prime }{\}} \end{aligned}$$

in order to come up with the continuity rule: \(finite\ S\ {\Longrightarrow }\ cont\ P\ {\Longrightarrow }\) \(cont{(}{\lambda }X{.}\ P\ X\ {\backslash }\ S{)}\). Our current proof was drastically shortened by a factor 10 compared to the original one and important immediate steps generalized: monotonicity, for example, could be generalized to the infinite case.

As for new laws, consider the case of \({(}P\ {\backslash }\ A{)}\ {\backslash }\ B\ {=}\ P\ {\backslash }\ {(}A\ {\,\cup \,}\ B{)}\) which is stated in [30] without proof. In the new version, we managed to establish this law which still need 450 lines of complex Isar code. However, it turned out that the original claim is not fully true: it can only be established again by König’s lemma to build a divergent trace of \(P\ {\backslash }\ {(}A\ {\,\cup \,}\ B{)}\) which requires \(A\) to be finite (\(B\) can be arbitrary) in order to use it from a divergent trace of \({(}P\ {\backslash }\ A{)}\ {\backslash }\ B\)Footnote 2. Again, we want to argue that the intricate number of cases to be considered as well as their complexity makes pen and paper proofs practically infeasible.

4 Theoretical Results on Refinement

4.1 Decomposition Rules

In our framework, we implemented the pcpo process refinement together with the five refinement orderings introduced in Sect. 3.3. To enable fixed-point induction, we first have the admissibility of the refinements.

$$\begin{aligned} cont\ u\ {\Longrightarrow }\ mono\ v\ {\Longrightarrow }\ adm{(}{\lambda }x{.}\ u\ x\ {\sqsubseteq }_{\mathfrak {F}}\ v\ x{)}\ where\ {\mathfrak {F}}{\,\in \,}{\{}{\mathcal {T}}{,}{\mathcal {F}}{,}{\mathcal {D}}{,}{\mathcal {T}}{\mathcal {D}}{,}{\mathcal {F}}{\mathcal {D}}{\}} \end{aligned}$$

Next we analyzed the monotonicity of these refinement orderings, whose results are then used as decomposition rules in our framework. Some CSP operators, such as multi-prefix and non-deterministic choice, are monotonic under all refinement orderings, while others are not.

  • External choice is not monotonic only under \({\sqsubseteq }_{\mathcal {F}}\), with the following monotonicities proved:

    $$\begin{aligned} P\ {\sqsubseteq }_{\mathfrak {F}}\ P{^\prime }\ {\Longrightarrow }\ Q\ {\sqsubseteq }_{\mathfrak {F}}\ Q{^\prime }\ {\Longrightarrow }\ {(}P\ {\Box }\ Q{)}\ {\sqsubseteq }_{\mathfrak {F}}\ {(}P{^\prime }\ {\Box }\ Q{^\prime }{)}\ where\ {\mathfrak {F}}{\,\in \,}{\{}{\mathcal {T}}{,}{\mathcal {D}}{,}{\mathcal {T}}{\mathcal {D}}{,}{\mathcal {F}}{\mathcal {D}}{\}} \end{aligned}$$

  • Sequence operator is not monotonic under \({\sqsubseteq }_{\mathcal {F}}\), \({\sqsubseteq }_{\mathcal {D}}\) or \({\sqsubseteq }_{\mathcal {T}}\):

    $$\begin{aligned} P\ {\sqsubseteq }_{\mathfrak {F}}\ P{^\prime }{\Longrightarrow }\ Q\ {\sqsubseteq }_{\mathfrak {F}}\ Q{^\prime }\ {\Longrightarrow }\ {(}P\ {;}\ Q{)}\ {\sqsubseteq }_{\mathfrak {F}}\ {(}P{^\prime }\ {;}\ Q{^\prime }{)}\ where\ {\mathfrak {F}}{\,\in \,}{\{}{\mathcal {T}}{\mathcal {D}}{,}{\mathcal {F}}{\mathcal {D}}{\}} \end{aligned}$$

  • Hiding operator is not monotonic under \({\sqsubseteq }_{\mathcal {D}}\):

    $$\begin{aligned} P\ {\sqsubseteq }_{\mathfrak {F}}\ Q\ {\Longrightarrow }\ P\ {\backslash }\ A\ \ {\sqsubseteq }_{\mathfrak {F}}\ Q\ {\backslash }\ A\ where\ {\mathfrak {F}}{\,\in \,}{\{}{\mathcal {T}}{,}{\mathcal {F}}{,}{\mathcal {T}}{\mathcal {D}}{,}{\mathcal {F}}{\mathcal {D}}{\}} \end{aligned}$$

  • Parallel composition is not monotonic under \({\sqsubseteq }_{\mathcal {F}}\), \({\sqsubseteq }_{\mathcal {D}}\) or \({\sqsubseteq }_{\mathcal {T}}\):

    $$\begin{aligned} P\ {\sqsubseteq }_{\mathfrak {F}}\ P{^\prime }\ {\Longrightarrow }\ Q\ {\sqsubseteq }_{\mathfrak {F}}\ Q{^\prime }\ {\Longrightarrow }\ {(}P\ {[\![}A{]\!]}\ Q{)}\ {\sqsubseteq }_{\mathfrak {F}}\ {(}P{^\prime }\ {[\![}A{]\!]}\ Q{^\prime }{)}\ where\ {\mathfrak {F}}{\,\in \,}{\{}{\mathcal {T}}{\mathcal {D}}{,}{\mathcal {F}}{\mathcal {D}}{\}} \end{aligned}$$

4.2 Reference Processes and Their Properties

We now present reference processes that exhibit basic behaviors, introduced in fundamental CSP works [30]. The process \(RUN\ A\) always accepts events from \(A\) offered by the environment. The process \(CHAOS\ A\) can always choose to accept or reject any event of \(A\). The process \(DF\ A\) is the most non-deterministic deadlock-free process on \(A\), i.e., it can never refuse all events of \(A\). To handle termination better, we added two new processes \(CHAOS_{SKIP}\) and \(DF_{SKIP}\).

Definition 2

\(RUN\ A\ {\equiv }\ {\mu }\ X{.}\ {\Box }\ x\ {\,\in \,}\ A\ {\rightarrow }\ X\)

Definition 3

\(CHAOS\ A\ {\equiv }\ {\mu }\ X{.}\ {(}STOP\ {\sqcap }\ {(}{\Box }\ x\ {\,\in \,}\ A\ {\rightarrow }\ X{)}{)}\)

Definition 4

\(CHAOS_{SKIP}\ A\ {\equiv }\ {\mu }\ X{.}\ {(}SKIP\ {\sqcap }\ STOP\ {\sqcap }\ {(}{\Box }\ x\ {\,\in \,}\ A\ {\rightarrow }\ X{)}{)}\)

Definition 5

\(DF\ A\ {\equiv }\ {\mu }\ X{.}\ {(}{\sqcap }\ x\ {\,\in \,}\ A\ {\rightarrow }\ X{)}\)

Definition 6

\(DF_{SKIP}\ A\ {\equiv }\ {\mu }\ X{.}\ {(}{(}{\sqcap }\ x\ {\,\in \,}\ A\ {\rightarrow }\ X{)}\ {\sqcap }\ SKIP{)}\)

In the following, we denote \({\mathcal {R}}{\mathcal {P}}\ {=}\ {\{}DF_{SKIP}{,} DF{,}\ RUN{,}\ CHAOS{,}\) \( CHAOS_{SKIP}{\}}\). All five reference processes are divergence-free.

$$\begin{aligned} D\ {(}{\mathfrak {P}}\ UNIV{)}\ {=}\ {\{}{\}}\ where\ {\mathfrak {P}}\ {\,\in \,}\ {\mathcal {R}}{\mathcal {P}}\ and\ UNIV\ is\ the\ set\ of\ all\ events \end{aligned}$$

Regarding the failure refinement ordering, the set of failures \({\mathcal {F}}\ P\) for any process \(P\) is a subset of \({\mathcal {F}}\ {(}CHAOS_{SKIP}\ UNIV{)}\).

$$\begin{aligned} CHAOS_{SKIP}\ UNIV\ {\sqsubseteq }_{\mathcal {F}}\ P \end{aligned}$$

The following 5 relationships were demonstrated from monotonicity results and a denotational proof. Thanks to transitivity, we can derive other relationships.

  1. 1.

    \(CHAOS_{SKIP}\ A\ {\sqsubseteq }_{\mathcal {F}}\ CHAOS\ A\)

  2. 2.

    \(CHAOS_{SKIP}\ A\ {\sqsubseteq }_{\mathcal {F}}\ DF_{SKIP}\ A\)

  3. 3.

    \(CHAOS\ A\ {\sqsubseteq }_{\mathcal {F}}\ DF\ A\)

  4. 4.

    \(DF_{SKIP}\ A\ {\sqsubseteq }_{\mathcal {F}}\ DF\ A\)

  5. 5.

    \(DF\ A\ {\sqsubseteq }_{\mathcal {F}}\ RUN\ A\)

Last, regarding trace refinement, for any process P, its set of traces \({\mathcal {T}}\ P\) is a subset of \({\mathcal {T}}\ {(}CHAOS_{SKIP}\ UNIV{)}\) and of \({\mathcal {T}}\ {(}DF_{SKIP}\ UNIV{)}\) as well.

  1. 1.

    \(CHAOS_{SKIP}\ UNIV\ {\sqsubseteq }_{\mathcal {T}}\ P\)

  2. 2.

    \(DF_{SKIP}\ UNIV\ {\sqsubseteq }_{\mathcal {T}}\ P\)

Recall that a concurrent system is considered as being deadlocked if no component can make any progress, caused for example by the competition for resources. In opposition to deadlock, processes can enter infinite loops inside a sub-component without ever interact with their environment again (“infinite internal chatter”); this situation called divergence or livelock. Both properties are not just a sanity condition; in CSP, they play a central role for verification. For example, if one wants to establish that a protocol implementation \(IMPL\) satisfies a non-deterministic specification \(SPEC\) it suffices to ask if \(IMPL\ {\mid }{\mid }\ SPEC\) is deadlock-free. In this setting, \(SPEC\) becomes a kind of observer that signals non-conformance of \(IMPL\) by deadlock.

In the literature, deadlock and livelock are phenomena that are often handled separately. One contribution of our work is establish their precise relationship inside the Failure/Divergence Semantics of CSP.

Definition 7

\(deadlock\_free\ P\ {\equiv }\ \ DF_{SKIP}\ UNIV\ {\sqsubseteq }_{\mathcal {F}}\ P\)

A process \(P\) is deadlock-free if and only if after any trace \(s\) without \({\surd }\), the union of \({\surd }\) and all events of \(P\) can never be a refusal set associated to \(s\), which means that \(P\) cannot be deadlocked after any non-terminating trace.

Theorem 1 (DF definition captures deadlock-freeness)

\(deadlock{\text {-}}free{} P\ {\longleftrightarrow }\ {(}{\forall \,}s{\,\in \,}{\mathcal {T}}\ P{.}\ tickFree\ s\ {\longrightarrow }\ {(}s{,}\ {\{}{\surd }{\}}{\,\cup \,}events{\text {-}}of\ P{)}\ {\notin }\ {\mathcal {F}}\ P{)}\)

Definition 8

\(livelock\_free\ P\ {\equiv }\ {\mathcal {D}}\ P\ {=}\ {\{}{\}}\)

Recall that all five reference processes are livelock-free. We also have the following lemmas about the livelock-freeness of processes:

  1. 1.

    \(livelock\_free\ P\ {\longleftrightarrow }\ {\mathfrak {P}}\ UNIV\ {\sqsubseteq }_{\mathcal {D}}\ P\ where\ {\mathfrak {P}}\ {\,\in \,}\ {\mathcal {R}}{\mathcal {P}}\)

  2. 2.

    \(\begin{aligned} livelock\_free\ P\ {\longleftrightarrow }\ DF_{SKIP}\ UNIV\ {\sqsubseteq }_{\mathcal {T}\mathcal {D}}\ P\ {\longleftrightarrow }\ CHAOS_{SKIP}\ UNIV\ {\sqsubseteq }_{\mathcal {T}\mathcal {D}}\ P\end{aligned}\)

  3. 3.

    \(livelock\_free\ P\ {\longleftrightarrow }\ CHAOS_{SKIP}\ UNIV\ {\sqsubseteq }_{\mathcal {F}\mathcal {D}}\ P\)

Finally, we proved the following theorem.

Theorem 2 (DF implies LF)

\(deadlock{\text {-}}free\ P\ {\longrightarrow }\ livelock{\text {-}}free\ P\)

This is totally natural, at a first glance, but surprising as the proof of deadlock-freeness only requires failure refinement \({\sqsubseteq }_{\mathcal {F}}\) (see Definition 7) where divergence traces are mixed within the failures set. Note that the existing tools in the literature normally detect these two phenomena separately, such as FDR for which checking livelock-freeness is very costly. In our framework, deadlock-freeness of a given system implies its livelock-freeness. However, if a system is not deadlock-free, then it may still be livelock-free.

5 Advanced Verification Techniques

Based on the refinement framework discussed in Sect. 4, we will now turn to some more advanced proof principles, tactics and verification techniques. We will demonstrate them on two paradigmatic examples well-known in the CSP literature: The CopyBuffer and Dijkstra’s Dining Philosophers. In both cases, we will exploit the fact that HOL-CSP 2 allows for reasoning over infinite CSP; in the first case, we reason over infinite alphabets approaching an old research objective: exploiting data-independence [2, 25] in process verification. In the latter case, we present an approach to a verification of a parameterized architecture, in this case a ring-structure of arbitrary size.

5.1 The General CopyBuffer Example

We consider the paradigmatic copy buffer example [20, 30] that is characteristic for a specification of a prototypical process and its implementation. It is used extensively in the CSP literature to illustrate the interplay of communication, component concealment and fixed-point operators. The process \(COPY\), defined as follows, is a specification of a one size buffer, that receives elements from the channel \(left\) of arbitrary type \({\alpha }\) (\(left{?}x\)) and outputs them on the channel \(right\) (\(right{!}x\)):

$$\begin{aligned}&\mathbf {datatype}\ \ {\alpha }\ events\ {=}\ left\ {\alpha }\ {\mid }\ right\ {\alpha }\ {\mid }\ mid\ {\alpha }\ {\mid }\ ack \\&\mathbf {definition}\ COPY\ {\equiv }\ {(}{\mu }\ X\mathbf {{.}}\ left{?}x\ {\rightarrow }\ {(}right{!}x\ {\rightarrow }\ X{)}{)} \end{aligned}$$

From our HOL-CSP 2 theory that establishes the continuity of all CSP operators, we deduce that such a fixed-point process \(COPY\) exists and follows the unrolling rule below:

$$\begin{aligned} \mathbf {lemma}\ COPY\ {=}\ {(}left{?}x\ {\rightarrow }\ {(}right{!}x\ {\rightarrow }\ COPY{)}{)} \end{aligned}$$

We set \(SEND\) and \(REC\) in parallel but in a row sharing a middle channel \(mid\) and synchronizing with an \(ack\) event. Then, we hide all exchanged events between these two processes and we call the resulting process \(SYSTEM\):

$$\begin{aligned}&\mathbf {definition}\ SEND\ {\equiv }\ {(}{\mu }\ X\mathbf {{.}}\ left{?}x\ {\rightarrow }\ {(}mid{!}x\ {\rightarrow }\ {(}ack\ {\rightarrow }\ X{)}{)}{)}\\&\mathbf {definition}\ REC\ {\equiv }\ {(}{\mu }\ X\mathbf {{.}}\ mid{?}x\ {\rightarrow }\ {(}right{!}x\ {\rightarrow }\ {(}ack\ {\rightarrow }\ X{)}{)}{)}\\&\mathbf {definition}\ SYN\ \ {\equiv }\ {(}range\ mid{)}\ {\,\cup \,}\ \mathbf {{\{}}ack\mathbf {{\}}}\\&\mathbf {definition}\ SY\!STEM\ {\equiv }\ {(}SEND\ {[\![}SYN{]\!]}\ REC{)}\ {\backslash }\ SYN \end{aligned}$$

We want to verify that \(SYSTEM\) implements \(COPY\). As shown below, we apply fixed-point induction to prove that \(SYSTEM\) refines \(COPY\) using the \(pcpo\) process ordering \({\sqsubseteq }\) that implies all other refinement orderings. We state:

$$\begin{aligned} \mathbf {lemma}{:}\ COPY\ {\sqsubseteq }\ SY\!STEM \end{aligned}$$

and apply fixed-point induction over \(COPY\) that generates three subgoals:

  1. 1.

    \(adm\ {(}{\lambda }a{.}\ a\ {\sqsubseteq }\ SY\!STEM\)

  2. 2.

    \({\bot }\ {\sqsubseteq }\ SY\!STEM\)

  3. 3.

    \(P\ {\sqsubseteq }\ SY\!STEM\ {\Longrightarrow }\ left{?}x\ {\rightarrow }\ right{!}x\ {\rightarrow }\ P\ {\sqsubseteq }\ SY\!STEM\)

The first two sub-proofs are automatic simplification proofs; the third requires unfolding \(SEND\) and \(REC\) one step and applying the algebraic laws. No denotational semantics reasoning is necessary here; it is just an induct-simplify proof consisting of 2 lines proof-script involving the derived algebraic laws of CSP.

After proving that \(SY\!STEM\) implements \(COPY\) for arbitrary alphabets, we aim to profit from this first established result to check which relations \(SY\!STEM\) has wrt. to the reference processes of Sect. 4.2. Thus, we prove that \(COPY\) is deadlock-free which implies livelock-free, (proof by fixed-point induction similar to \(lemma{:}\ COPY\ {\sqsubseteq }\ SY\!STEM\)), from which we can immediately infer from transitivity that \(SYSTEM\) is. Using refinement relations, we killed four birds with one stone as we proved the deadlock-freeness and the livelock-freeness for both \(COPY\) and \(SYSTEM\) processes. These properties hold for arbitrary alphabets and for infinite ones in particular.

$$\begin{aligned} \begin{array}{l} \begin{array}{l} \mathbf {lemma}\ DF\ UNIV\ {\sqsubseteq }\ COPY \end{array}\\ \\ \begin{array}{l} \mathbf {corollary}\ deadlock{\text {-}}free\ COPY\\ \mathbf {and}\ livelock{\text {-}}free\ COPY\\ \mathbf {and}\ deadlock{\text {-}}free\ SY\!STEM\\ \mathbf {and}\ livelock{\text {-}}free\ SY\!STEM \end{array} \end{array} \end{aligned}$$

5.2 New Fixed-Point Inductions

The copy buffer refinement proof \(DF\ UNIV\ {\sqsubseteq }\ COPY\) is a typical one step induction proof with two goals: \(base{:}\ {\bot }\ {\sqsubseteq }\ Q\) and \({\textit{1}}{-}ind{:}\ X\ {\sqsubseteq }\ Q\ {\Longrightarrow }\ {(}{\text {-}}\ {\rightarrow }\ X{)}\ {\sqsubseteq }\ Q\). Now, if unfolding the fixed-point process \(Q\) reveals two steps, the second goal becomes \(X\ {\sqsubseteq }\ Q\ {\Longrightarrow }\ {\text {-}}\ {\rightarrow }\ X\ {\sqsubseteq }\ {\text {-}}\ {\rightarrow }\ {\text {-}}\ {\rightarrow }\ Q\). Unfortunately, this way, it becomes improvable using monotonicities rules. We need here a two-step induction of the form \(base{\textit{0}}{:}\ {\bot }\ {\sqsubseteq }\ Q\), \(base{\textit{1}}{:}\ {\text {-}}\ {\rightarrow }\ {\bot }\ {\sqsubseteq }\ Q\) and \({\textit{2}}{-}ind{:}\ X\ {\sqsubseteq }\ Q\ {\Longrightarrow }\ {\text {-}}\ {\rightarrow }\ \ {\text {-}}\ {\rightarrow }\ X\ {\sqsubseteq }\ {\text {-}}\ {\rightarrow }\ {\text {-}}\ {\rightarrow }\ Q\) to have a sufficiently powerful induction scheme.

For this reason, we derived a number of alternative induction schemes (which are not available in the HOLCF library), which are also relevant for our final Dining Philosophers example. These are essentially adaptions of k-induction schemes applied to domain-theoretic setting (so: requiring \(f\) continuous and \(P\) admissible; these preconditions are skipped here):

  • \(\begin{aligned}&{.}{.}{.}\ {\Longrightarrow }\ {\forall \,}i{<}k{.}\ P\ {(}f^{i}\ {\bot }{)}\ {\Longrightarrow }\ {(}{\forall \,}X{.}\ {(}{\forall \,}i{<}k{.}\ P\ {(}f^{i}\ X{)}{)}\ {\longrightarrow }\ P\ {(}f^{k}\ X{)}{)}\ {\Longrightarrow }\ P\ {(}{\mu }X{.}\ f\ X{)}\end{aligned}\)

  • \({.}{.}{.}\ {\Longrightarrow }\ {\forall \,}i{<}k{.}\ P\ {(}f^{i}\ {\bot }{)}\ {\Longrightarrow }\ {(}{\forall \,}X{.}\ P\ X\ {\longrightarrow }\ P\ {(}f^{k}\ X{)}{)}\ {\Longrightarrow }\ P\ {(}{\mu }X{.}\ f\ X{)}\)

In the latter variant, the induction hypothesis is weakened to skip \(k\) steps. When possible, it reduces the goal size.

Another problem occasionally occurring in refinement proofs happens when the left side term involves more than one fixed-point process (e.g.\(P\ {[\![}{\{}A{\}}{]\!]}\ Q\ {\sqsubseteq }\ S\)). In this situation, we need parallel fixed-point inductions. The HOLCF library offers only a basic one:

  • \(\begin{aligned}{.}{.}{.}&{\Longrightarrow }\ P\ {\bot }\ {\bot }\ {\Longrightarrow }\ {(}{\forall \,}X\ Y{.}\ P\ X\ Y\ {\Longrightarrow }\ P\ {(}f\ X{)}\ {(}g\ Y{)}{)} {\Longrightarrow }\ P\ {(}{\mu }X{.}\ f\ X{)}\ {(}{\mu }X{.}\ g\ X{)}\end{aligned}\)

This form does not help in cases like in \(P\ {[\![}{\emptyset }{]\!]}\ Q\ {\sqsubseteq }\ S\) with the interleaving operator on the left-hand side. The simplifying law is:

$$\begin{aligned} {(}{\Box }x{\,\in \,}A{\rightarrow }P\ x\ {[\![}{\emptyset }{]\!]}\ {\Box }x{\,\in \,}B{\rightarrow }Q\ x{)}\ {=}&\quad \,{(}{\Box }x{\,\in \,}A\ {\rightarrow }\ {(}\ \ \ \ \ \ \ \ \ \ \ \ P\ x\ {[\![}{\emptyset }{]\!]}\ {\Box }x{\,\in \,}B\ {\rightarrow }\ Q\ x{)}\ \\&{\Box }\ {(}{\Box }x{\,\in \,}B\ {\rightarrow }\ {(}{\Box }x{\,\in \,}A\ {\rightarrow }\ P\ x\ {[\![}{\emptyset }{]\!]}\ \ \ \ \ \ \ \ \ \ Q\ x{)}{)} \end{aligned}$$

Here, \({(}f\ X\ {[\![}{\emptyset }{]\!]}\ g\ Y{)}\) does not reduce to the \({(}X\ {[\![}{\emptyset }{]\!]}\ Y{)}\) term but to two terms \({(}f\ X\ {[\![}{\emptyset }{]\!]}\ Y{)}\) and \({(}X\ {[\![}{\emptyset }{]\!]}\ g\ Y{)}\). To handle these cases, we developed an advanced parallel induction scheme and we proved its correctness:

  • \(\begin{aligned}&{.}{.}{.}\ {\Longrightarrow }\ {(}{\forall \,}Y{.}\ P\ {\bot }\ Y{)}\ {\Longrightarrow }\ {(}{\forall \,}X{.}\ P\ X\ {\bot }{)}\\&\qquad \!{\Longrightarrow }\ {\forall \,}X\ Y{.}\ {(}P\ X\ Y\ {\wedge }\ P\ {(}f\ X{)}\ Y\ {\wedge }\ P\ X\ {(}g\ Y{)}{)}\ {\longrightarrow }\ P\ {(}f\ X{)}\ {(}g\ Y{)}\ \\&\qquad \;{\Longrightarrow }\ P\ {(}{\mu }X{.}\ f\ X{)}\ {(}{\mu }X{.}\ g\ X{)} \end{aligned}\)

which allows for a “independent unrolling” of the fixed-points in these proofs. The astute reader may notice here that if the induction step is weakened (having more hypotheses), the base steps require enforcement.

5.3 Normalization

Our framework can reason not only over infinite alphabets, but also over processes parameterized over states with an arbitrarily rich structure. This paves the way for the following technique, that trades potentially complex process structure against equivalent simple processes with potentially rich state.

Roughly similar to labelled transition systems, we provide for deterministic CSP processes a normal form that is based on an explicit state. The general schema of normalized processes is defined as follows:

$$\begin{aligned} P_{norm}{[\![}{\tau }{,}{\upsilon }{]\!]}\ {\equiv }\ {\mu }\ X{.}\ {(}{\lambda }{\sigma }{.}\ {\Box }e{\,\in \,}{(}{\tau }\ {\sigma }{)}\ {\rightarrow }\ X\ {(}{\upsilon }\ {\sigma }\ e{)}{)} \end{aligned}$$

where \({\tau }\) is a transition function which returns the set of events that can be triggered from the current state \({\sigma }\) given as parameter. The update function \({\upsilon }\) takes two parameters \({\sigma }\) and an event \(e\) and returns the new state. This normal form is closed under deterministic and communication operators.

The advantage of this format is that we can mimick the well-known product automata construction for an arbitrary number of synchronized processes under normal form. We only show the case of the synchronous product of two processes:

Theorem 3 (Product Construction)

Parallel composition translates to normal form:

$$\begin{aligned}&{(}P_{norm}{[\![}{\tau }_{\textit{1}}{,}{\upsilon }_{\textit{1}}{]\!]}\ {\sigma }_{\textit{1}}{)}\ {\mid }{\mid }\ {(}P_{norm}{[\![}{\tau }_{\textit{2}}{,}{\upsilon }_{\textit{2}}{]\!]}\ {\sigma }_{\textit{2}}{)}\ {=}\ \\&\quad \, P_{norm}{[\![}{\lambda }{(}{\sigma }_{\textit{1}}{,}{\sigma }_{\textit{2}}{)}{.}\ {\tau }_{\textit{1}}\ {\sigma }_{\textit{1}}\ {\,\cap \,}\ {\tau }_{\textit{2}}\ {\sigma }_{\textit{2}}\ {,}\ {\lambda }{(}{\sigma }_{\textit{1}}{,}{\sigma }_{\textit{2}}{)}{.}{\lambda }e{.}{(}{\upsilon }_{\textit{1}}\ {\sigma }_{\textit{1}}\ e{,}\ {\upsilon }_{\textit{2}}\ {\sigma }_{\textit{2}}\ e{)}{]\!]}\ {(}{\sigma }_{\textit{1}}{,}{\sigma }_{\textit{2}}{)} \end{aligned}$$

The generalization of this rule for a list of \({(}{\tau }{,}{\upsilon }{)}\)-pairs is straight-forward, albeit the formal proof is not. The application of the generalized form is a corner-stone of the proof of the general dining philosophers problem illustrated in the subsequent section.

Another advantage of normalized processes is the possibility to argue over the reachability of states via the closure \({\mathfrak {R}}\), which is defined inductively over:

  • \({\sigma }\ {\,\in \,}\ {\mathfrak {R}}\ {\tau }\ {\upsilon }\ {\sigma }\)

  • \({\sigma }\ {\,\in \,}\ {\mathfrak {R}}\ {\tau }\ {\upsilon }\ {\sigma }_{\textit{0}}\ {\Longrightarrow }\ e\ {\,\in \,}\ {\tau }\ {\sigma }\ {\Longrightarrow }\ {\upsilon }\ {\sigma }\ e\ {\,\in \,}\ {\mathfrak {R}}\ {\tau }\ {\upsilon }\ {\sigma }_{\textit{0}}\)

Thus, normalization leads to a new characterization of deadlock-freeness inspired from automata theory. We formally proved the following theorem:

Theorem 4 (DF vs. Reachability)

If each reachable state \(s\ {\,\in \,}\ {(}{\mathfrak {R}}\ {\tau }\ {\upsilon }{)}\) has outgoing transitions, the CSP process is deadlock-free:

$$\begin{aligned} {\forall \,}{\sigma }\ {\,\in \,}\ {(}{\mathfrak {R}}\ {\tau }\ {\upsilon }\ {\sigma }_{\textit{0}}{)}{.}\ {\tau }\ {\sigma }\ {\not =}\ {\{}{\}}\ {\Longrightarrow }\ deadlock{\text {-}}free\ {(}P_{norm}{[\![}{\tau }{,}{\upsilon }{]\!]}\ {\sigma }_{\textit{0}}{)} \end{aligned}$$

This theorem allows for establishing properties such as deadlock-freeness by completely abstracting from CSP theory; these are arguments that only involve inductive reasoning over the transition function.

Summing up, our method consists of four stages:

  1. 1.

    we construct normalized versions of component processes and prove them equivalent to their counterparts,

  2. 2.

    we state an invariant over the states/variables,

  3. 3.

    we prove by induction over \({\mathfrak {R}}\) that it holds on all reachable states, and finally

  4. 4.

    we prove that this invariant guarantees the existence of outgoing transitions.

5.4 Generalized Dining Philosophers

The dining philosophers problem is another paradigmatic example in the CSP literature often used to illustrate synchronization problems between an arbitrary number of concurrent systems. It is an example of a process scheme for which general properties such as deadlock-freeness are desirable in order to inherit them for specific instances. The general dining philosopher problem for an arbitrary \(N\) is presented in HOL-CSP 2 as follows

Note that both philosophers and forks are pairwise independent but both synchronize on \(picks\) and \(putsdown\) events. The philosopher of index 0 is left-handed whereas the other \(N{-}{\textit{1}}\) philosophers are right-handed. We want to prove that any configuration is deadlock-free for an arbitrary number N.

First, we put the fork process into normal form. It has three states: (0) on the table, (2) picked by the right philosopher or (1) picked by the left one:

To validate our choice for the states, transition function \(trans_{f}\) and update function \(upd_{f}\), we prove that they are equivalent to the original process components: \(FORK_{norm}\ i\ {=}\ FORK\ i\). The anti-symmetry of refinement breaks this down to the two refinement proofs \(FORK_{norm}\ i\ {\sqsubseteq }\ FORK\ i\) and \(FORK\ i\ {\sqsubseteq }\ FORK_{norm}\ i\), which are similar to the CopyBuffer example shown in Sect. 5.1. Note, again, that this fairly automatic induct-simplify-proof just involves reasoning on the derived algebraic rules, not any reasoning on the level of the denotational semantics.

From the generalization of “Theorem 3, we obtain normalized processes for \(FORKs\), \(PHILs\) and \(DINING\):

$$\begin{aligned} \begin{array}{l} \begin{array}{l} \mathbf {definition}\ trans_{F}\ {\equiv }\ {\lambda }fs{.}\ {(}{\,\bigcap \,}_{i<_{N}}{.}\ trans_{f}\ i\ {(}fs{!}i{)}{)}\\ \mathbf {definition}\ upd_{F}\ \ \ {\equiv }\ {\lambda }fs\ e\mathbf {.} \ \mathbf {let}\ i{=}{(}fork\ e{)}\ \mathbf {in}\ fs{[}i{:}{=}{(}upd_{f}\ i\ {(}fs{!}i{)}\ e{)}{]} \end{array} \\ \\ \begin{array}{l} \mathbf {lemma}\ FORKs\ {=}\ P_{norm}{[\![}trans_{F}{,}\ upd_{F}{]\!]}\ \mathbf {.} {} \mathbf {.} {} \mathbf {.} \\ \mathbf {lemma}\ PHILS\ {=}\ P_{norm}{[\![}trans_{P}{,}\ upd_{P}{]\!]}\ \mathbf {.} {} \mathbf {.} {} \mathbf {.} \end{array}\\ \\ \begin{array}{l} \mathbf {definition}\ trans_{D}\ {\equiv }\ {\lambda }{(}ps{,}fs{)}{} \mathbf {.} \ {(}trans_{P}\ ps{)}\ {\,\cap \,}\ {(}trans_{F}\ fs{)}\\ \mathbf {definition}\ upd_{D}\ \ \ {\equiv }\ {\lambda }{(}ps{,}fs{)}\ e\mathbf {.} \ {(}upd_{P}\ ps\ e{,}\ upd_{F}\ fs\ e{)} \end{array}\\ \\ \begin{array}{l} \mathbf {lemma}\ DINING\ {=}\ P_{norm}{[\![}trans_{D}{,}\ upd_{D}{]\!]} \end{array} \end{array} \end{aligned}$$

The variable \(ps\) stands for the list of philosophers states and \(fs\) for the list of forks states, both are of size \(N\). The pair \({(}ps{,}\ fs{)}\) encodes the whole dining table state over which we need to define an invariant to ensure that no blocking state is reachable and thus the dining philosophers problem is deadlock-free. As explained before, the proof is based on abstract reasoning over relations independent from the CSP context.

The last steps towards our goal are the following definitions and lemmas:

$$\begin{aligned} \begin{array}{l} \begin{array}{l} \mathbf {definition}\ INV_{DINING}\ ps\ fs\ {\equiv }\ {(}{\forall \,}i\mathbf {.} \ {(}{(}fs{!}i{=}{\textit{1}}{)}\ {\leftrightarrow }\ ps{!}i\ {\not =}\ {\textit{0}}{)}\ {\wedge }\ \mathbf {.} {} \mathbf {.} {} \mathbf {.} \ {)}\\ \mathbf {lemma}\ {(}ps{,}fs{)}\ {\,\in \,}\ {\mathfrak {R}}\ trans_{D}\ upd_{D}\ \ {\Longrightarrow }\ INV_{D I N I N G}\ ps\ fs\ \mathbf {.} {} \mathbf {.} {} \mathbf {.} \\ \mathbf {lemma}\ INV_{D I N I N G}\ ps\ fs\ {\Longrightarrow }\ trans_{D}\ {(}ps{,}\ fs{)}\ {\not =}\ \mathbf {\{} {} \mathbf {\}} \ \mathbf {.} {} \mathbf {.} {} \mathbf {.} \end{array} \\ \\ \begin{array}{l} \mathbf {corollary}\ deadlock{\text {-}}free\ DINING\ \end{array} \end{array} \end{aligned}$$

To sum up, we proved once and for all that the dining philosophers problem is deadlock free for an arbitrary number \(N\ {\ge }\ {\textit{2}}\). Common model-checkers like PAT and FDR fail to answer for a dozen of philosophers (on a usual machine) due to the exponential combinatorial explosion. Furthermore, our proof is fairly stable against modifications like adding non synchronized events like thinking or sitting down in contrast to model-checking techniques.

6 Related Work

The theory of CSP has attracted a lot of interest from the eighties on, and is still a fairly active research area, both as a theoretical device as well as a modelling language to analyze complex concurrent systems. It is therefore not surprising that attempts to its formalisation had been undertaken early with the advent of interactive theorem proving systems supporting higher-order logic [12, 16, 17, 22, 37], where especially the latter allows for some automated support for refinement proofs based on induction. However, HOL-CSP2 is based on a failure/divergence model, while [22] is based on stable failures, which can infer deadlock-freeness only under the assumption that no livelock occurred; In our view, this is a too strong assumption for both the theory as well as the tool.

In the 90ies, research focused on automated verification tools for CSP, most notably on FDR  [1]. It relies on an operational CSP semantics, allowing for a conversion of processes into labelled transition systems, where the states are normalized by the “laws” derived from the denotational semantics. For finite event sets, refinement proofs can be reduced to graph inclusion problems. With efficient compression techniques, such as bisimulation, elimination and factorization by semantic equivalence [32], FDR was used to analyze some industrial applications. However, such a model checker cannot handle infinite cases and does not scale to large systems.

The fundamental limits of automated decision procedures for data and processes has been known very early on: Undecidability of parameterized model checking was proven by reduction to non-halting of Turing machines [35]. However, some forms of well-structured transitions systems, could be demonstrated to be decidable [8, 18]. HOL-CSP2 is a fully abstract model for the failure/divergence model; as a HOL theory, it is therefore a “relative complete proof theory” both for infinite data as well as number of components. (see [3] for relative completeness).

Encouraged by the progress of SMT solvers which support some infinite types, notably (fixed arrays of) integers or reals, and limited forms of formulas over these types, SMT-based model-checkers represent the current main-stream to parametric model-checking. This extends both to LTL-style model-checkers for Promela-like languages [14, 24] as well as process-algebra alikes [4, 5, 7]. However, the usual limitations persist: the translation to SMT is hardly certifiable and the solvers are still not able to handle non-linear computations; moreover, they fail to elaborate inductive proofs on data if necessary in refinement proofs.

Some systems involve approximation techniques in order to make the formal verification of concurrent systems scalable; results are sometimes inherently imprecise and require meta-level arguments assuring their truth in a specific application context. For example, in [5], the synchronization analysis techniques try to prove the unreachability of a system state by showing that components cannot agree on the order or on the number of times they participate on system rules. Even with such over-approximation, the finiteness restriction on the number of components persists.

Last but not least, SMT-based tools only focusing on bounded model-checking like [13, 19] use k-induction and quite powerful invariant generation techniques but are still far from scalable techniques. While it is difficult to make any precise argument on the scalability for HOL-CSP 2, we argue that we have no data-type restrictions (events may have realvector-, function- or even process type) as well as restrictions on the structure of components. None of our paradigmatic examples can be automatically proven with any of the discussed SMT techniques without restrictions.

7 Conclusion

We presented a formalisation of the most comprehensive semantic model for CSP, a ‘classical’ language for the specification and analysis of concurrent systems studied in a rich body of literature. For this purpose, we ported [37] to a modern version of Isabelle, restructured the proofs, and extended the resulting theory of the language substantially. The result HOL-CSP 2 has been submitted to the Isabelle AFP [36], thus a fairly sustainable format accessible to other researchers and tools.

We developed a novel set of deadlock - and livelock inference proof principles based on classical and denotational characterizations. In particular, we formally investigated the relations between different refinement notions in the presence of deadlock - and livelock; an area where traditional CSP literature skates over the nitty-gritty details. Finally, we demonstrated how to exploit these results for deadlock/livelock analysis of protocols.

We put a large body of abstract CSP laws and induction principles together to form concrete verification technologies for generalized classical problems, which have been considered so far from the perspective of data-independence or structural parametricity. The underlying novel principle of “trading rich structure against rich state” allows to convert processes into classical transition systems for which established invariant techniques become applicable.

Future applications of HOL-CSP 2 could comprise a combination to model checkers, where our theory with its derived rules is used to certify the output of a model-checker over CSP. In our experience, generated labelled transition systems may be used to steer inductions or to construct the normalized processes \(P_{norm}{[\![}{\tau }{,}{\upsilon }{]\!]}\) automatically, thus combining efficient finite reasoning over finite sub-systems with globally infinite systems in a logically safe way.