The Unsuitable Neighbourhood Inequalities for the Fixed Cardinality Stable Set Polytope

Abstract

Given an undirected graph G = (V, E) and an integer $k \in \left \lbrace 1, \ldots , |V|\right \rbrace$, we initiate the combinatorial study of stable sets of cardinality exactly k in G. Our aim is to instigate the polyhedral investigation of the convex hull of fixed cardinality stable sets, and we begin by introducing a large class of valid inequalities to the natural integer programming formulation of the problem.

1 From Conflict-Free Trees to Fixed Cardinality Stable Sets

We investigate a problem that is appealing to different research directions around algorithms, combinatorics and optimization. Let G = (V, E) be a finite, simple, undirected graph, and denote n = |V |, and m = |E|. A stable set (or independent set, or co-clique) in G is a subset of pairwise non-adjacent vertices. Given k ∈{1, …, n} and a vertex-weighting function $w: V \rightarrow \mathbb {Q}_{+}$, the k stable set problem consists in finding a minimum weight stable set of cardinality k in G, or deciding that none exists. Note that k is also part of the input to this problem; if it were an arbitrary fixed integer, the enumeration and optimization problems over stable sets of that cardinality could be solved in time polynomially bounded by a function of n.

Our original motivation for considering fixed cardinality stable sets stems from the NP-hard problem of determining minimum spanning trees under conflict constraints (MSTCC). Given a graph G = (V, E) and a set of conflicting edge pairs C ⊆ E × E, a conflict-free spanning tree in G is a set of edges T ⊆ E inducing a spanning tree in G, such that for each (e, f) ∈ C, at most one of the edges e and f is in T. The MSTCC problem, introduced by Darmann et al. [5], asks for such a conflict-free spanning tree of minimum weight.

Different combinatorial and algorithmic results about the MSTCC problem explore the associated conflict graph H = (E, C), which has a vertex corresponding to each edge in the original graph G, and we represent each conflict constraint by an (undirected) edge connecting the corresponding vertices in H. Note that each conflict-free spanning tree in G is a subset of E which corresponds both to a spanning tree in G and to a stable set in H. Therefore, one can equivalently search for stable sets in H of cardinality exactly |V |− 1 which do not induce cycles in the original graph G.

It is not hard to devise different approaches for studying the MSTCC problem exploring the connection with fixed cardinality stable sets. Therefore, results of different nature from research on the k stable set problem (e.g. integer programming formulations and valid inequalities, well-solved particular cases, primal and dual bounds) could provide fundamental components to advance knowledge on the MSTCC problem as well.

It is surprising that the combinatorics and optimization literature has not addressed the kstable set problem problem in depth before. The convex hull of stable sets of cardinality at most k was studied by Janssen and Kilakos [8], but only for k ∈{2, 3}. Apart from that article, it has also appeared as part of an algorithm for a variant of the survivable network design problem [3, Chapter 2], where only an alternative proof of one of the original results on [8] is given. We remark that the thorough survey on fixed cardinality versions of combinatorial optimization problems by Bruglieri et al. [4] does not mention stable sets, in spite of the major role played by that structure throughout the development of polyhedral combinatorics.

Our contribution with this work is twofold. First, we draw attention to the fixed cardinality version of a classical structure in combinatorial optimization and graph theory, motivated by its application in the MSTCC problem. Second, we introduce an exponential class of valid inequalities to the fixed cardinality stable set polytope, whose separation problem is interesting in its own right.

2 Polyhedral Results

For any graph G, we denote by V (G) and E(G) the sets of vertices and edges of G, respectively. For conciseness, we abbreviate ‘stable set of cardinality k’ as k-stab. The family of all k-stabs in G is denoted $\mathscr {F}(G,k)$. Recall that the incidence vector of any S ⊂ V  is $\chi ^{S} \in \left \lbrace 0,1 \right \rbrace ^{V}$ defined by $\chi ^{S}_i = 1$ if i ∈ S, and $\chi ^{S}_i = 0$ if i ∈ V ∖S; so the central object of our interest is , i.e. the convex hull of incidence vectors of all the k-stabs in G.

The natural integer programming (IP) formulation for minimum-weight k-stabs in G is

$$\displaystyle \begin{aligned} \min \left\lbrace \sum_{v \in V}{w(v) x_v} : \mathbf{x} \in \mathscr{P}(G,k) \cap \left\lbrace 0,1 \right\rbrace^{n} \right\rbrace, {} \end{aligned} $$

(1)

where $\mathscr {P}(G,k)$ denotes the polyhedral region defined by:

$$\displaystyle \begin{aligned}\begin{array}{r*{20}l} \sum_{v \in V}{x_v} & = k & {} \end{array}\end{aligned} $$

(2)

(3)

(4)

Constraints (3) are known as edge inequalities, imposing that no two adjacent vertices belong to the selection in x. Together with bounds (4), they determine the fractional stable set polytope [14, Section 64.5].

Remark 1

Recall that a vector z is half-integer if 2z is integer. A classical result of Nemhauser and Trotter [11] shows that the fractional stable set polytope is half-integer, i.e. all its vertices are $\left \lbrace 0, \frac {1}{2}, 1 \right \rbrace$-valued. Since that is the starting point for a series of both polyhedral and algorithmic advances, one could be interested in extending that result for $\mathscr {P}(G,k)$ as well. Unfortunately, we could verify that is not the case. While no small counterexample is found, we report a computational finding using benchmark instances from the minimum spanning tree under conflict constraints problem [13]. When $\hat {G}$ corresponds to the conflict graph associated with instance z100-300-1344 in that paper, which has 300 vertices and 1344 edges, and k = 60, the primal simplex method implemented in Gurobi Optimizer 8.1 (with all presolve, heuristics and cut options disabled) terminates with a solution corresponding to a vertex of $\mathscr {P}(\hat {G},k)$ which is not half-integer.

We introduce next a class of valid inequalities for , exploring the relationship between k, the size of the neighbourhood

$$\displaystyle \begin{aligned} N(S) = \left\lbrace u \in V\backslash S : \exists \left\lbrace u,v \right\rbrace \in E \text{ for some } v \in S \right\rbrace \end{aligned}$$

of any set S ⊂ V , and how many vertices from S can appear in any k-stab. First, denoting the set of neighbours of a vertex v ∈ V  by δ(v), that is $\delta (v) = N(\left \lbrace v \right \rbrace )$, one can immediately observe that no vertex which has too many neighbours to still build a k-stab can be chosen. This gives the following simple reduction rule.

Proposition 1

If x is the incidence vector of any k-stab, and v ∈ V  is such that |δ(v)| > n − k, then x _v = 0.

In an attempt to enforce an algebraic expression that enough vertices are left upon choosing a set S ⊂ V  towards building a k-stab, we introduce a class of exponentially-many constraints, which we refer to as unsuitable neighbourhood inequalities (UNI).

Theorem 1

The inequality ∑_{v ∈ S} x _v ≤|S|− 1 is valid for , for each S ⊂ V  such that 1 ≤|S| < k and |N(S)| > n − k.

Proof

From |S| < k, it follows that S is not a k-stab in itself. If S were a subset of any k-stab, there should be at least k −|S| vertices left to choose from, while no neighbour in N(S) can be selected towards building a stable set. That is

Since |N(S)| > n − k by hypothesis, S cannot be part of a k-stab. Therefore no incidence vector x of a k-stab induces the selection of all the vertices in S, and the result follows. □

While Proposition 1 is clearly a special case of Theorem 1, one could ask whether the UNI indeed give a stronger condition. The positive answer follows next.

Theorem 2

For any graph G and k > 1, the UNI imply the condition enforced by Proposition 1 in the description of , but the converse does not hold.

Proof

Let x be a vector satisfying all UNI. The inequalities in Proposition 1 are implied by the UNI with |S| = 1. Suppose that $S = \left \lbrace u \right \rbrace$ and |N(S)| = |δ(u)| > n − k. Then u cannot be extended to a k-stab and the UNI include x _u =∑_{v ∈ S} x _v ≤|S|− 1 = 0, which is the condition on the former proposition.

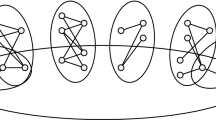
Now the converse does not hold, i.e. even if |δ(v)|≤ n − k for each v ∈ V , the UNI need not be automatically satisfied, as the following counterexample shows (see Fig. 1). Consider the graph G = 2P ₃, which consists of two copies of the path graph on 3 vertices put together, so that n = 6, and suppose that k = 3. Since all vertices have degree 1 or 2, it follows that |δ(u)|≤ n − k = 3 for each vertex u. On the other hand, with a test set S consisting of the two vertices of degree 2 in the middle of the paths, we have 1 ≤|S| < k and |N(S)| = 4 > n − k, thus yielding the unsuitable neighbourhood inequality given by ∑_{v ∈ S} x _v ≤|S|− 1 = 1 which separates from the convex hull any vector selecting those two vertices. □

Fig. 1

The graph 2P ₃ and the selection of its two central vertices

Proposition 2

In either of the following two conditions, the corresponding unsuitable neighbourhood inequality is redundant in : (i) if S ⊂ V  is not independent, or (ii) if S ⊂ V  is not minimal with respect to the condition |N(S)| > n − k.

Proof

If u, v ∈ S are adjacent vertices, the edge inequality x _u + x _v ≤ 1 implies ∑_{v ∈ S} x _v ≤|S|− 1.

Otherwise, let S ⊂ V  with 1 ≤|S| < k and N(S) > n − k be a given independent set, and suppose that $T \subsetneq S$ is such that |N(T)| > n − k. The UNI corresponding to T is ∑_{v ∈ T} x _v ≤|T|− 1. Combined with x _v ≤ 1 for each v ∈ S∖T , it implies the UNI corresponding to S, i.e. ∑_{v ∈ S} x _v ≤|S|− 1, which is thus redundant in the description of . □

Recall that the domination number γ(G) gives the least cardinality of a dominating set in G = (V, E), i.e. a subset D ⊂ V  such that every vertex u ∈ V ∖D has a neighbour in D. If a lower bound on the domination number of G is known, the following result might be useful.

Proposition 3

If γ(G) ≥ k, then there exists no UNI for .

Proof

Suppose there were S ⊂ V  with 1 ≤|S| < k and |N(S)| > n − k, and denote ${T = V \backslash \left \lbrace S \cup N(S) \right \rbrace }$. Note that any vertex belongs to exactly one among S, N(S), or T; then

$$\displaystyle \begin{aligned} |S| + |N(S)| + |T| = n \ \implies \ |S| + |T| = n - |N(S)| \ \implies \ |S| + |T| < n - [n-k] = k, \end{aligned}$$

since |N(S)| > n − k. Now, S ∪ T would be a dominating set of cardinality strictly less than k, contradicting the hypothesis that γ(G) ≥ k. □

On the algorithmic side, it is in general impractical to include a priori all minimal UNI in an IP formulation for a black-box solver, since the number of those inequalities may grow exponentially with the size of the input (n, k). The natural approach in this case is to try to cut off successive solutions x ^∗ to a linear programming (LP) relaxation, by finding cutting planes corresponding to UNI violated at x ^∗, i.e. separating x ^∗ from , or deciding that none exists. Answering that question is known as the separation problem for a class of valid inequalities.

Definition 1 (Separation Problem for UNI)

Given a graph G = (V, E), with $n= |V|,\ k \in \left \lbrace 2, \dots, n-1 \right \rbrace$, and x ^∗∈ [0, 1]ⁿ satisfying the conditions that $\sum _{v\in V} x^*_v = k$ and that $x^*_u + x^*_v \leq 1$ for each $\left \lbrace u,v \right \rbrace \in E$, determine

• i. either a set S ⊂ V , with 1 ≤|S|≤ k − 1 and |N(S)|≥ n − (k − 1), such that $\sum _{v\in S} x^*_v > |S|-1$, in which case the unsuitable neighbourhood inequality corresponding to S separates x ^∗ from ,

• ii. or that no such set exists, in which case all UNI are satisfied at x ^∗.

We give next a slight reformulation of the separation problem which might be useful in future work. Given the input [G, k, x ^∗] corresponding to Definition 1, define y ^∗∈ [0, 1]ⁿ such that $y^*_v = 1 - x^*_v$. Note now that $\sum _{v\in S} x^*_v > |S|-1$ if and only if $\sum _{v\in S} y^*_v < 1$. We thus have the following equivalent statement of the problem.

Definition 2 (Equivalent Formulation of the Separation Problem for UNI)

Given a graph G = (V, E), with $n= |V|,\ k \in \left \lbrace 2, \dots, n-1 \right \rbrace$, and y ^∗∈ [0, 1]ⁿ satisfying the conditions that $\sum _{v\in V} y^*_v = n-k$ and that $y^*_u + y^*_v \geq 1$ for each $\left \lbrace u,v \right \rbrace \in E$, determine

• i. either a set S ⊂ V , with |N(S)|≥ n − (k − 1) and $\sum _{v\in S} y^*_v < 1$, in which case the unsuitable neighbourhood inequality corresponding to S separates x ^∗ = 1 − y ^∗ from ,

• ii. or that no such set exists, in which case all UNI are satisfied at x ^∗ = 1 − y ^∗.

We consider this statement of the problem to be particularly appealing. Note that if S has size exactly k − 1, then |N(S)|≥ n − (k − 1) implies that it would be a dominating set. Given the condition that adjacent vertices have y ^∗ values summing up to at least 1, and that we require $\sum _{v\in S} y^*_v < 1$, we would actually have an independent dominating set if |S| = k − 1, i.e. a subset of vertices which is both dominating and independent (stable). Now, allowing |S|≤ k − 1 means that there might be $q\in \left \lbrace 0, 1, \dots, k-2 \right \rbrace$ vertices neither in S nor dominated by it. If we define a q-quasi dominating set in a graph G = (V, E) to be a subset of vertices which is dominating in G[V ∖X], for some X ⊂ V, |X|≤ q, our separation problem corresponds to finding an independent (k − 2)-quasi dominating set of weight at most 1, or deciding that none exists. (Recall that, for any graph G and U ⊂ V (G), the induced subgraph $G\left [U\right ]$ is a graph with vertex set U and all of the edges in E(G) which have both endpoints in U.)

We leave the open question of establishing the complexity of that problem.

Conjecture 1

The separation problem for UNI is NP-hard.

3 Concluding Remarks and Directions Towards a Branch-and-Cut Algorithm

We investigate in this work the fixed cardinality version of the classical stable set problem, highlighting an interesting gap in the combinatorial optimization literature. Generalizing the remark that vertices of too high degree cannot be in a stable set of cardinality k, we derive a large class of valid inequalities for the k-stab polytope. The corresponding separation problem asks for optimizing over subgraphs with a domination-like property and an additional budget constraint.

We are interested in a deeper polyhedral investigation, the starting point of which is to shed light on the relevance of the inequalities we introduce here, and how they relate to other families of valid inequalities for the classical stable set polytope. Moreover, progress in this direction could lead to an interesting algorithm for solving the MSTCC problem, as we indicate in Sect. 1. The remaining ingredient to find conflict-free spanning trees in the original graph G, from a cardinality k = |V (G)|− 1 stable set in the conflict-graph H, is to enforce an acyclic solution in the original graph. That could be attained by using a relax-and-cut approach (see [6, 9], for instance), separating subtour elimination constraints and immediately dualizing them in a Lagrangean fashion. In fact, Lucena [9] introduced an effective relax-and-cut algorithm for the fixed cardinality set partitioning problem.

We conclude by indicating selected insights on the practical issue of leveraging a modern branch-and-cut solver for the classical stable set problem (referring the reader to the eminently readable tutorial of Rebennack et al. [12]) towards one for the fixed cardinality version.

3.1 UNI Separation with MIP Heuristics

Besides the natural strategies of designing separation heuristics or including a priori some UNI corresponding to sets S of small cardinality, it might prove useful to explore an IP formulation of the separation problem. One can actually use good but not necessarily optimal solutions to that auxiliary IP, which give very effective cutting planes, for instance, in the context of an example of optimizing over the first Chvátal closure [2, Section 5.4]. Most MIP solvers include a collection of general purpose heuristics to accelerate the availability of integer feasible solutions, like local branching, feasibility pump and neighbourhood diving methods; see [7] for a recent survey.

The following is described in light of Definition 2, with input [G, k, y ^∗]. We suppose further that the input is preprocessed by the reduction rules:

• (i) Remove any vertex v such that $y^*_v = 1$

• (ii) Remove isolated vertices

Those operations do not change the problem answer, since a UNI is automatically satisfied if it contains a vertex with $y^*_v = 1$, and since isolated vertices are not contained in a minimal set S corresponding to a UNI.

For each v ∈ V , let variables $z_v \in \left \lbrace 0,1 \right \rbrace$ be such that z _v = 1 if and only if v ∈ S, and $w_v \in \left \lbrace 0,1 \right \rbrace$ be such that w _v = 1 if and only if v ∈ N[S] = S ∪ N(S), the closed neighbourhood of S ⊂ V . Then, we have to determine

$$\displaystyle \begin{aligned} \rho = \min \left\lbrace \sum_{v \in V}{y^*_v \cdot z_v} : (\mathbf{z},\mathbf{w}) \in \mathscr{P}_{\text{UNI}}(G,{\mathbf{y}}^*) \cap \left\lbrace 0,1 \right\rbrace^{2n} \right\rbrace, {} \end{aligned} $$

(5)

where $\mathscr {P}_{\text{UNI}}(G,{\mathbf {y}}^*)$ denotes the polyhedral region:

(6)

$$\displaystyle \begin{aligned}\begin{array}{r*{20}l} z_u & \leq w_v && \forall u \in V, \forall v \in N[u] {} \end{array}\end{aligned} $$

(7)

$$\displaystyle \begin{aligned}\begin{array}{r*{20}l} \sum_{u \in N[v]}{z_u} & \geq w_v && \forall v \in V {} \end{array}\end{aligned} $$

(8)

$$\displaystyle \begin{aligned}\begin{array}{r*{20}l} z_u + z_v & \leq 1 && \forall \left\lbrace u,v \right\rbrace \in E {} \end{array}\end{aligned} $$

(9)

$$\displaystyle \begin{aligned}\begin{array}{r*{20}l} 0 \leq z_{v} & \leq 1 && \forall v \in V {} \end{array}\end{aligned} $$

(10)

$$\displaystyle \begin{aligned}\begin{array}{r*{20}l} 0 \leq w_{v} & \leq 1 && \forall v \in V {} \end{array}\end{aligned} $$

(11)

The objective function in (5) accounts for the used y ^∗ budget, as prescribed in Definition 2. Inequality (6) guarantees the minimum number of vertices dominated by S (excluding those which are in S). Inequalities (7) and (8) bind the binary variables w and z, to enforce the domination condition that w _v = 1 if and only if z _u = 1 for some u ∈ N[v].

Inequalities (9) are redundant, being implied at integer points in $\mathscr {P}_{\text{UNI}}(G,{\mathbf {y}}^*)$ by (6) and the fact the input parameter satisfies $y^*_u + y^*_v \geq 1$ for each $\left \lbrace u,v \right \rbrace \in E$. Still, adding those inequalities is likely to tighten the LP relaxation bounds, and hence speed up the overall optimization procedure.

The exact separation problem thus reduces to deciding if ρ < 1. The MIP heuristic, on the other hand, consists of searching (e.g. allowing a MIP solver to run with a prescribed time limit) for any integer feasible solution (z ^′, w ^′) with an objective value less than 1, which determines the UNI $\sum _{v \in S^\prime } x_v \leq |S^\prime |-1$, with $S^\prime = \left \lbrace v \in V: z^\prime _v=1 \right \rbrace$, violated at x ^∗ = 1 − y ^∗.

3.2 Balanced Branching

A fundamental component for the performance of branch-and-cut algorithms for the classical stable set problem is the balanced branching rule of Balas and Yu [1]; see also [12] and [10]. Its original motivation also applies to the fixed cardinality setting: avoiding unbalanced branch-and-bound trees when branching on a fractional variable x _v, since fixing x _v = 1 has the larger impact of implying x _u = 0 for each u ∈ N(v), while fixing x _v = 0 has no impact on the neighbourhood.

The general branching scheme can be adapted to find minimum weight k-stabs with little effort. Suppose that, on a given node of the enumeration tree, G ^′ = (V ^′, E ^′) denotes the subgraph induced by vertices not fixed in this subproblem, and that $\overline {z}$ is the best primal bound available. Let W ⊆ V ^′ be such that we can determine efficiently that the minimum weight of a k-stab in the subgraph induced by W, denoted z(W), is such that $z(W) \geq \overline {z}$. Note that, if W = V ^′, the subproblem is fathomed and the whole subtree rooted on this node can be pruned. Otherwise, if the search on this subtree is to eventually find that $z(V^\prime ) < \ \overline {z}$, any bound-improving solution must intersect $V^\prime \backslash W = \left \lbrace v_1, \dots, v_p \right \rbrace$. That is, we can partition the search space into the sets

$$\displaystyle \begin{aligned} V^\prime_i = \left\lbrace v_i \right\rbrace \ \bigcup \ V^\prime \backslash \left( N(v_i) \cup \left\lbrace v_{i+1}, \dots, v_p \right\rbrace \right) \end{aligned}$$

for 1 ≤ i ≤ p. The enumeration can therefore branch on p subproblems, each fixing $x_{v_i}=1$, and fixing at 0 those variables corresponding to $N(v_i) \cup \left \lbrace v_{i+1}, \dots, v_p \right \rbrace$.

Now, there are different strategies to determine subgraph W. The standard one is to find a collection of cliques in G ^′, e.g. with as many cliques as the currently available lower bound, when searching for maximum cardinality stable sets. For minimum-weight k-stabs, the natural idea would be to greedily find k cliques, such that the combined weight of the cheapest vertices in each exceed $\overline {z}$. We describe next an alternative approach tailored for optimizing over k-stabs, leaving for future work the task of comparing those two strategies, whether theoretically or according to computational experience.

Recall that a matching in a graph is a subset of pairwise non-adjacent edges, that is, a subset of edges without common vertices. Since each k-stab contains at most one vertex from each edge in a matching, a lower bound on z(W) can be derived by simply picking the k vertices of lowest weight among: (i) the cheapest vertex in each matched edge, and (ii) the remaining vertices not covered by the matching. We thus have the following result, which we state in the general form of a combinatorial dual bound for the minimum weight of k-stab in an arbitrary graph.

Theorem 3

Suppose that $\mathscr {P}(G,k) \cap \left \lbrace 0,1 \right \rbrace ^{n} \neq \varnothing$ , so that problem (1) is well-defined. Let M ⊂ E be any matching in G. Define $c_e = \min \left \lbrace w(v_i), w(v_j) \right \rbrace$ for each edge $e = \left \lbrace v_i, v_j \right \rbrace \in M$ . Also define c _u = w(v _u) for any vertex v _u not covered by the matching M. Then, the sum of the k lowest values in the image of c(⋅) is a lower bound on (1). That is, given an order c ₁ ≤ c ₂⋯ ≤ c _(n−|M|) on $\left \lbrace c_e \right \rbrace _{e\in M} \cup \left \lbrace c_u \right \rbrace _{u \in V\backslash V_M}$ , where V _M corresponds to the set of vertices covered by M, we have that $\sum _{i=1}^{k} c_i$ is a lower bound on the weight of a k-stab in G.

Therefore, using the weight function corresponding to c(⋅) in the above theorem, we can determine candidate subgraphs W by inspecting, for each $l \in \left \lbrace 1, \dots, k \right \rbrace$:

• 1. A minimum-weight matching in G ^′ with cardinality l

• 2. A suitable choice of k − l vertices not covered by the matching

Finally, note that finding a minimum-weight matching of a specified cardinality in a graph is a well-solved problem. More generally, for any $l,u \in \mathbb {Z}_{+},\ l \leq u$, the convex hull of incidence vectors of matchings M ⊂ E(G) such that l ≤|M|≤ u is equal to the set of those vectors in the matching polytope of G satisfying l ≤1 ^⊤ x ≤ u, that is, l ≤∑_{e ∈ E(G)} x(e) ≤ u; see [14, Section 18.5f].