Finite Element Nonlocal Integral Elasticity Approach

Abstract

In the current chapter, a finite element theory has been developed based on the nonlocal integral elasticity using Hamilton’s principle. Formulations have been derived using Euler-Bernoulli beam theory and classical plate theory in order to study the bending, buckling and vibration behavior of nanostructures. The current method is capable of modelling complex geometries and boundary conditions. Besides, effects of nonlocal parameter, geometrical parameters, boundary conditions and viscoelastic parameter on the mechanical behavior of nano-scaled beams and plates have been studied.

1 Introduction

There are several fields, which cannot be examined thoroughly using classical theories. Solid fracture, stress field on the dislocation core and crack tip, singularities at points where loads are applied, sharp corners and discontinuities in the body, elastic short-wavelength behavior prediction, and viscosity increase of fluid flows in microscopic channels are some weaknesses of the classical theories. Besides, polaritons, gyrotropic effects and superconductivity cannot be investigated using the classical field theories. Also, classical continuum field theories are unable to predict the correct behavior of materials in micro and nano-scale. So, for studying the mechanical behavior of materials in small-scale and phenomena that inherently happens in small-scale, atomic or nonlocal theories, which can consider the long-range interatomic force effects, should be employed. Atomic theories have relatively higher computational cost than nonlocal theories.

In summary, in nonlocal theories, the behavior of the material at one point is a function of the state of all points. One of the most popular non-local theories for studying nano-scale structures is Eringen’s nonlocal theory [1]. In Eringen’s nonlocal theory, stress at a point is a function of strains at all points of the material [1]. Under certain conditions, the nonlocal differential form could be extracted from the more general nonlocal integral theory. Despite the relative simplicity of nonlocal differential elasticity theory, it has some restrictions, e.g., some individual kernels must be considered for nonlocal differential elasticity to be derived, applying the natural boundary conditions for nano-plates are somehow ambiguous, investigating the complex geometries are intricate. Therefore, it is more reasonable to use the nonlocal integral theory for the accuracy of some applications and problems. Some researchers have conducted some investigations using the nonlocal integral elasticity theory. Finite element nonlocal integral elasticity theory, which first have been prepared by Polizzotto [2], is one of the best-known methods, that have advantages of both the nonlocal integral theory and finite element method. Also, Marotti de Sciarra [3, 4] has proved the complete family of variational principles, developed a consistent nonlocal finite element procedure based on a suitable definition of weight function and provided some numerical applications for a bar in tension. The nonlocal FE method has been then further developed by Pisano et al. [5] (for analyzing a nano-plates under tension), Taghizadeh et al. [6, 7] (for analyzing the bending and buckling of nano-beams and nano-plates), Koutsoumaris et al. [8,9,10] (for investigating the bending and dynamic response of nano-beams considering the modified kernel type), Norouzzadeh and Ansari [11] (for Bending of nanobeams), Tuna and Kirca [12] (for analyzing the bending, buckling and vibration of nano-beams) and Naghinejad and Ovesy [13,14,15,16] (for considering the viscoelastic effects and studying the vibrations and buckling of nano-beams and nano-plates).

For accuracy of analyzing the nanostructures in some applications, the viscoelastic properties have been taken into account, in some studies. For example, the proper functioning of oscillators depends on considering their damping characteristics [17]. Also, by assuming the viscoelastic characteristics in the nano-scale mass sensors, which works by measuring the shift in the vibration frequency, more accurate detections can be achievable. Also, considering these properties leads to the excellent image quality of atomic force microscopes (AFM) [18]. Knowing the importance of considering viscoelasticity in some applications of nanostructures, recently some researchers have combined the nonlocal theory with viscoelastic properties. For instance, Ghavanloo and Fazalzadeh [19] have studied the flexural vibration of viscoelastic carbon nanotubes conveying fluid and embedded in viscous fluid. They considered the nonlocal Timoshenko beam model and used Hamilton’s principle to derive the formulations. Lei et al. [20, 21] have investigated the free vibration of nano-beams based on nonlocal differential elasticity theory by considering viscoelastic properties. They obtained complex frequencies by the transfer function method. Pouresmaeeli et al. [22] have investigated the vibration behavior of viscoelastic orthotropic nano-plates using the nonlocal differential theory and the Kelvin-Voigt viscoelastic model. They have studied the effects of nonlocal parameter, structural damping, stiffness and damping coefficient of the foundation on the vibration frequency. Free vibration of multi-nanoplate system embedded in viscoelastic medium have been studied by Karlicic et al. [23] using nonlocal differential theory. Governing equations have been derived using D’Alamberts principle and Kirchhoff-Love plate theory. Naghinejad and Ovesy [15] have developed a non-local integral finite element method to investigate the free vibration of viscoelastic Euler-Bernoulli nano-scaled beam. The formulations have been obtained using Hamilton’s principle, and effects of different parameters and boundary conditions on the free vibration behavior have been discussed. They have also studied the viscoelastic buckling of nano-scaled beams using the nonlocal differential theory and the Kelvin-Voigt viscoelastic model [14].

In the current chapter, firstly, the constitutive equations of nonlocal elasticity and viscoelasticity theories are derived, then the aforementioned finite element nonlocal integral elasticity theory is developed using Hamilton’s principle and the formulations are explained. Besides, applying the boundary conditions for beams and plates in the current method and the governing formulations of bending, buckling, and vibration are discussed. Finally, bending, buckling, and vibration of nano-scaled beams and plates are investigated through numerical examples, and the effects of different parameters on the mechanical behavior are studied.

2 Nonlocal Integral Theory

2.1 Elastic Constitutive Equations

In classical elasticity theory, the stress-strain relations are stated only for a single material point. Whereas, weighted averages of a material state-variable over a region should be taken into account for defining the constitutive law at a point, in an integral-type nonlocal theory. Eringen and Edelen [24, 25] developed the theories of nonlocal elasticity in which the nonlocal characteristics have been attached to many fields, including mass, entropy, internal energy, and body forces. Because of their ambiguity, yet to be verified and be used in real problems, simplifications have been considered later. After that, equilibrium and kinematic equations have been used as a standard form, and only the nonlocal form of the constitutive equations have been considered [26, 27]. Thus, in mentioned non-local theory, stress at any point of the material is a function of all strains at the vicinity. For a linear isotropic elastic continuum, the constitutive equation is given by Eq. (1)

$$\begin{aligned} \mathbf {t}\left( \mathbf {x} \right) =\underset{V}{\mathop \int }\,\alpha \left( \left| \mathbf {{x}'}-\mathbf {x} \right| ,~\tau \right) \varvec{\sigma }\left( {\mathbf {{x}'}} \right) dV,~~~\forall \mathbf {x}\in V \end{aligned}$$

(1)

in which $\mathbf {t}$, $\alpha$ and $\varvec{\sigma }$ are nonlocal stress tensor, nonlocal kernel function, and local stress tensor respectively. The local stress tensor is written as $\varvec{\sigma }\left( \mathbf {x} \right) =\mathbf {D}:\varvec{\varepsilon }\left( \mathbf {x} \right)$ in which $\mathbf {D}$ is the fourth-order elastic moduli tensor, and $\varepsilon$ is a strain tensor. The nonlocal kernel is a function of distance, between any point in the domain and reference point, and $\tau ={{e}_{0}}a/l$ in which a and l are the internal (e.g. lattice parameter or granular distance) and external (e.g. wavelength or crack length) characteristic lengths. $e_0$ is a constant for any material which can be calibrated by comparing the results with different methods such as molecular dynamics or lattice dynamics according to various parameters, e.g. geometry, mode shapes and boundary conditions [13]. As a result, the nonlocal stress is expressed as a weighted value of the strain field:

$$\begin{aligned} \mathbf {t}\left( \mathbf {x} \right) =\underset{V}{\mathop \int }\,\alpha \left( \left| \mathbf {{x}'}-\mathbf {x} \right| ,~\tau \right) \mathbf {D}: \varvec{\varepsilon }\left( {\mathbf {{x}'}} \right) dV',~~~\forall \mathbf {x}\in V \end{aligned}$$

(2)

It is known that, if the nonlocal kernel was taken as the Dirac delta function, the nonlocal constitutive equation reduces to that of the local theory. It is worth noting that the nonlocal constitutive equation can be considered as two-phase [2, 5]. The first phase corresponds to the local part (local fraction ${{\zeta }_{1}}$) and the second phase to the nonlocal part (non-local fraction ${{\zeta }_{2}}$). It is evident that ${{\zeta }_{1}}+{{\zeta }_{2}}=1$ and ${{\zeta }_{1}},~~{{\zeta }_{2}}>0$. ${{\zeta }_{1}}$ and ${{\zeta }_{2}}$ can be obtained using different methods. An approach to calculate values of ${{\zeta }_{1}}$ and ${{\zeta }_{2}}$ can be determining the contribution of reference point and all points in the region (except the reference point) on the stiffness [13, 15, 28, 29]. For example, in the current study, for determining the values of ${{\zeta }_{1}}$ and ${{\zeta }_{2}}$ on each element, nonlocal kernel is integrated on the whole domain (the value is called ${{I}_{1}}$). Then kernel is integrated on the element containing the reference point (namely ${{I}_{2}}$). Obviously the remaining portion is named ${{I}_{3}}={{I}_{1}}-{{I}_{2}}$. So, the ratio of $I_2$ to $I_1$ corresponds to ${{\zeta }_{1}}$ and the ratio of $I_3$ to $I_1$ corresponds to ${{\zeta }_{2}}$. The two-phase model mathematically handles the constitutive equation. In particular, the two-phase model transforms the first kind Fredholm integral equation into a second kind one. In applications in a finite domain, the first kind Fredholm integral equation leads to an ill-posed problem, which is difficult to deal with [30]. Assuming the kernel function as follows:

$$\begin{aligned} \alpha \left( \left| \mathbf {{x}'}-\mathbf {x} \right| ,\tau \right) ={{\zeta }_{1}}\delta \left( \mathbf {{x}'}-\mathbf {x} \right) +{{\zeta }_{2}}\bar{\alpha }\left( \left| \mathbf {{x}'}-\mathbf {x} \right| ,\tau \right) \end{aligned}$$

(3)

in which, $\bar{\alpha }$ is the typical nonlocal kernel function, Eq. (2) could be written as the two-phase nonlocal constitutive equation:

$$\begin{aligned} \mathbf {t}\left( \mathbf {x} \right) ={{\zeta }_{1}}\varvec{\sigma }\left( \mathbf {x} \right) +{{\zeta }_{2}}\underset{V}{\mathop \int }\,\bar{\alpha }\left( \left| \mathbf {{x}'}-\mathbf {x} \right| ,~\tau \right) \mathbf{D} :\varvec{\varepsilon }\left( {\mathbf {{x}'}} \right) dV~~~~~\forall \mathbf {x}\in V \end{aligned}$$

(4)

The better performance of the latter form in some applications has led to the usage of this form over the original form in some recent articles [13, 15, 16, 31].

2.2 Viscoelastic Constitutive Equations

For a nonlocal viscoelastic material, Eq. (1) can be written as follows [15, 20]

$$\begin{aligned} {\mathbf {t}^{ve}}\left( \mathbf {x} \right) =\underset{V}{\mathop \int }\,\alpha \left( \left| \mathbf {{x}'}-\mathbf {x} \right| ,~\tau \right) {{\varvec{\sigma }}^{ve}}\left( {\mathbf {{x}'}} \right) dV~~~~~\forall \mathbf {x}\in V \end{aligned}$$

(5)

in which, $\mathbf {t}^{ve}$ and ${\varvec{\sigma }}^{ve}$ are the nonlocal and local viscoelastic stress tensors, respectively [15, 20]. It is known that the viscoelastic constitutive equation for a linear homogeneous solid is as follows.

$$\begin{aligned} {{\varvec{\sigma }}^{ve}}=\mathbf {G}\left( t \right) \varvec{\varepsilon }\left( 0 \right) +\underset{0}{\overset{t}{\mathop \int }}\,\mathbf {G}\left( t-T \right) \frac{\partial \varvec{\varepsilon }\left( T \right) }{\partial T}dT \end{aligned}$$

(6)

where $\mathbf {G}$ is the stress relaxation tensor and $\varvec{\varepsilon }$ is the strain tensor. Substituting Eq. (6) into Eq. (5) gives

$$\begin{aligned}&{\mathbf {t}^{ve}}\left( \mathbf {x} \right) =\underset{V}{\mathop \int }\,\alpha \left( \left| \mathbf {{x}'}-\mathbf {x} \right| ,~\tau \right) \mathbf {G}\left( t \right) \varvec{\varepsilon }\left( \mathbf {{x}'},~0 \right) dV \nonumber \\&+\underset{V}{\mathop \int }\,\alpha \left( \left| \mathbf {{x}'}-\mathbf {x} \right| ,~\tau \right) \left( \underset{0}{\overset{t}{\mathop \int }}\,\mathbf {G}\left( t-T \right) \frac{\partial \varvec{\varepsilon }\left( \mathbf {{x}'},~T \right) }{\partial T}dT \right) dV~~~\forall \mathbf {x}\in V \end{aligned}$$

(7)

Equation (7) is the constitutive equation of a nano-material considering nonlocal integral theory and viscoelastic properties. The relaxation tensor of a general viscoelastic model (see Fig. 1) could be stated as

$$\begin{aligned} \mathbf {G}\left( t \right) ={\mathbf {{G}}_{0}}-\underset{n=1}{\overset{N}{\mathop \sum }}\,{\mathbf {G}_{n}}\left( 1-{{e}^{-t{\mathbf {T}_{n}}^{-1}}} \right) ={\mathbf {G}_{\infty }}+\underset{n=1}{\overset{N}{\mathop \sum }}\,{\mathbf {G}_{n}}{{e}^{-t{\mathbf {T}_{n}}^{-1}~}} \end{aligned}$$

(8)

in which, ${{\mathbf {G}}_{0}}={{\mathbf {G}}_{\infty }}+\text { }\!\!\Sigma \!\!\text { }{{\mathbf {G}}_{n}}$ is the initial relaxation tensor and ${\mathbf {T}_{n}}={\mathbf {G}_{n}}^{-1}{{\varvec{\eta }}_{n}}$ are the relaxation times (in which $\mathbf {{T}}_{n}$ and ${{{\varvec{\eta }}}_{n}}$ are diagonal). Using the Boltzmann superposition principle and substituting Eq. (8) into Eq. (7), the nonlocal viscoelastic constitutive equation is obtained as (due to the fact that, as time passes the values of $t{{\mathbf {T}}_{n}}^{-1}$ and strain increases, and the value of ${{\mathbf {T}}_{n}}$ is relatively small, we can neglect $\sum {{\mathbf {G}}_{n}}{{e}^{-t\mathbf {T}_{n}^{-1}}}\varvec{\varepsilon }\left( 0 \right)$ compared to other terms)

Fig. 1

General viscoelastic model schematic according to relaxation modulus

$$\begin{aligned}&{\mathbf{t }^{ve}}\left( \mathbf {x} \right) =\underset{V}{\mathop \int }\,\alpha \left( \left| \mathbf {{x}'}-\mathbf {x} \right| ,~\tau \right) {{\mathbf {G}}_{\infty }}\varvec{\varepsilon }\left( \mathbf {{x}'},~t \right) dV \nonumber \\&+\underset{V}{\mathop \int }\,\alpha \left( \left| \mathbf {{x}'}-\mathbf {x} \right| ,~\tau \right) \left( \underset{0}{\overset{t}{\mathop \int }}\,\underset{n=1}{\overset{N}{\mathop \sum }}\,{{\mathbf {G}}_{n}}{{e}^{-\left( t-T \right) {{\mathbf {T}}_{n}}^{-1}}}\frac{\partial \varvec{\varepsilon }\left( \mathbf {{x}'},~T \right) }{\partial T}dT \right) dV \end{aligned}$$

(9)

Different viscoelastic models are assumed by considering different values for parameters of Eq. (9). For example, by taking $N=1$ and ${{\mathbf {G}}_{1}}\rightarrow \infty$ Kelvin-Voigt model is given, and by considering $N=1$, the three-parameter standard viscoelastic model can be yielded [20]. By considering the above parameters the Kelvin-Voigt and the three-parameter standard model are respectively obtained as follows. For the Kelvin-Voigt model the derivation process is as follows

$$\begin{aligned}&{{\mathbf {t}}^{ve}}\left( \mathbf {x} \right) =\underset{V}{\mathop \int }\,\alpha \left( \left| \mathbf {{x}'}-\mathbf {x} \right| ,~\tau \right) {{\mathbf {G}}_{\infty }}\varvec{\varepsilon }\left( \mathbf {{x}'},~t \right) dV \nonumber \\&+\underset{V}{\mathop \int }\,\alpha \left( \left| \mathbf {{x}'}-\mathbf {x} \right| ,~\tau \right) \left( {\mathbf{G }_{1}}{{e}^{-\left( t-T \right) {{\mathbf {T}}_{1}}^{-1}}}\frac{\partial \varvec{\varepsilon }\left( \mathbf {{x}'},~T \right) }{\partial T}dT \right) dV \end{aligned}$$

(10)

By carrying out the integration, considering the Kelvin-Voigt assumptions,

$$\begin{aligned} {{\mathbf {t}}^{ve}}\left( \mathbf {x} \right) =\underset{V}{\mathop \int }\,\alpha \left( \left| \mathbf {{x}'}-\mathbf {x} \right| ,~\tau \right) \left( {{\mathbf {G}}_{\infty }}\varvec{\varepsilon }\left( \mathbf {{x}'},~t \right) +\frac{\partial \varvec{\varepsilon }\left( \mathbf {{x}'},~t \right) }{\partial t}{{\mathbf {G}}_{1}}{{\mathbf {T}}_{1}} \right) dV \end{aligned}$$

(11)

So,

$$\begin{aligned} {{\mathbf {t}}^{ve}}\left( \mathbf {x} \right) =\underset{V}{\mathop \int }\,\alpha \left( \left| \mathbf {{x}'}-\mathbf {x} \right| ,~\tau \right) \left( {{\mathbf {G}}_{\infty }}\varvec{\varepsilon }\left( \mathbf {{x}'},~t \right) +\frac{\partial \varvec{\varepsilon }\left( \mathbf {{x}'},~t \right) }{\partial t}{{\varvec{\eta }}_{1}} \right) dV \end{aligned}$$

(12)

and by introducing ${{\mathbf {T}}_{d}}={{\mathbf {G}}_{\infty }}^{-1}{{\varvec{\eta }}_{1}}$, finally we have

$$\begin{aligned} {{\mathbf {t}}^{ve}}\left( \mathbf {x} \right) =\underset{V}{\mathop \int }\,\alpha \left( \left| \mathbf {{x}'}-\mathbf {x} \right| ,~\tau \right) {{\mathbf {G}}_{\infty }}\left( \varvec{\varepsilon }\left( \mathbf {{x}'},~t \right) +{{\mathbf {T}}_{d}}\frac{\partial \varvec{\varepsilon }\left( \mathbf {{x}'},t \right) }{\partial t} \right) dV \end{aligned}$$

(13)

It is noted that the classical form of the above constitutive equation is as follows:

$$\begin{aligned} {{\varvec{\sigma }}^{ve}}={{\mathbf {G}}_{\infty }}\left( \varvec{\varepsilon }+{{\mathbf {T}}_{d}}\frac{\partial \varvec{\varepsilon }}{\partial t} \right) \end{aligned}$$

(14)

Also considering the three-parameter viscoelastic model, Eq. (9) can be simply written as

$$\begin{aligned}&{{\mathbf {t}}^{ve}}\left( \mathbf {x} \right) =\underset{V}{\mathop \int }\,\alpha \left( \left| \mathbf {{x}'}-\mathbf {x} \right| ,~\tau \right) {{\mathbf {G}}_{\infty }}\varvec{\varepsilon }\left( \mathbf {{x}'},~t \right) dV \nonumber \\&+\underset{V}{\mathop \int }\,\alpha \left( \left| \mathbf {{x}'}-\mathbf {x} \right| ,~\tau \right) \left( {{\mathbf {G}}_{1}}{{e}^{-\left( t-T \right) {{\mathbf {T}}_{1}}^{-1}}}\frac{\partial \varvec{\varepsilon }\left( \mathbf {{x}'},~T \right) }{\partial T}dT \right) dV \end{aligned}$$

(15)

For a two-phase nonlocal theory, using Eqs. (4) and (9) the constitutive equation will be obtained as

$$\begin{aligned}&{{\mathbf {t}}^{ve}}\left( \mathbf {x} \right) ={{\zeta }_{1}}\left( {{\mathbf {G}}_{\infty }}\varvec{\varepsilon }\left( \mathbf {x},~t \right) +\underset{0}{\overset{t}{\mathop \int }}\,\underset{n=1}{\overset{N}{\mathop \sum }}\,{{\mathbf {G}}_{n}}{{e}^{-(t-T)\mathbf {T}_{n}^{-1}}}\frac{\partial \varvec{\varepsilon }\left( \mathbf {x},~T \right) }{\partial T}dT \right) \nonumber \\&+{{\zeta }_{2}}\underset{V}{\mathop \int }\,\bar{\alpha }\left( \left| \mathbf {{x}'}-\mathbf {x} \right| ,~\tau \right) {{\mathbf {G}}_{\infty }}\varvec{\varepsilon }\left( \mathbf {{x}'},~t \right) dV \nonumber \\&+{{\zeta }_{2}}\underset{V}{\mathop \int }\,\bar{\alpha }\left( \left| \mathbf {{x}'}-\mathbf {x} \right| ,~\tau \right) \left( \underset{0}{\overset{t}{\mathop \int }}\,\underset{n=1}{\overset{N}{\mathop \sum }}\,{{\mathbf {G}}_{n}}{{e}^{-(t-T)\mathbf {T}_{n}^{-1}}}\frac{\partial \varvec{\varepsilon }\left( \mathbf {{x}'},~T \right) }{\partial T}dT \right) dV \end{aligned}$$

(16)

2.3 Notes on the Kernel Type

Looking at the constitutive Eq. (1), the three dimensional nonlocal kernel $\bar{\alpha }\left( \left| \mathbf {{x}'}-\mathbf {x} \right| ,\tau \right)$ has the (length)$^{-3}$ dimension. Besides, it is known that $\bar{\alpha }$ is a function of the characteristic length ratio (a/l). Also, the nonlocal kernel has some notable specifications. For example, as it has been expressed by Eringen [1]:

• (i) Nonlocal kernels maximum value happens at the reference point (i.e., $\mathbf {{x}'}=\mathbf {x}$).

• (ii) $\bar{\alpha }$ converts to Dirac-delta whenever $\tau \rightarrow 0$, i.e., the classical theory must be extracted when $\tau \rightarrow 0$.

• (iii) $\bar{\alpha }$ can be determined for a certain material by curve-fitting the plane waves dispersion-curves with those of experiments or atomic lattice dynamics.

It is noted that because of defining the kernel function on the infinite domain, for using it in the finite domain it must be normalized and, in the current approach, truncated at the boundaries [5, 7, 13] (e.g., see Fig. 2). The normalization process is carried out since the nonlocal kernel should satisfy the following condition

$$\begin{aligned} \underset{{{V}_{\infty }}}{\mathop \int }\,\alpha \left( \left| \mathbf {{x}'}-\mathbf {x} \right| ,\tau \right) dV=1 \end{aligned}$$

(17)

where $V_{\infty }$ is an infinite domain, in which the working domain is embedded [2, 5]. The condition (17) also guarantees that for an infinite domain, when the strain is uniform, the related stress will also be uniform [2]. For this purpose in the current study the kernel function, which may violate the condition (17) considering a finite length or truncating near the boundaries, is normalized by dividing it by the normalization parameter. The normalization parameter is obtained by integrating the kernel value in the finite domain of the problem.

Fig. 2

Modifications of kernel function near the boundaries

Some examples of kernel function are [1]:

$\bullet$ One-dimensional form:

$$\begin{aligned} \alpha \left( \left| {x}'-x \right| ,\frac{{{e}_{0}}a}{l} \right) =\left\{ \begin{array}{*{35}{l}} \frac{1}{{{e}_{0}}a}\left( 1-\frac{\left| {x}'-x \right| }{{{e}_{0}}a} \right) ~~~\left| {x}'-x \right| \le {{e}_{0}}a \\ 0~~~~~~~~~~~~~~~~~~~~~~~~~~~\left| {x}'-x \right| >{{e}_{0}}a \\ \end{array} \right. \end{aligned}$$

(18)

$$\begin{aligned} \alpha \left( \left| {x}'-x \right| ,\frac{{{e}_{0}}a}{l} \right) =\frac{1}{2{{e}_{0}}a}\exp \left( -\left| {x}'-x \right| /{{e}_{0}}a \right) \end{aligned}$$

(19)

$$\begin{aligned} \alpha \left( \left| {x}'-x \right| ,\frac{{{e}_{0}}a}{l} \right) =\frac{1}{\sqrt{\pi {{e}_{0}}al}}\exp \left( -{{\left( {x}'-x \right) }^{2}}/{{e}_{0}}al~ \right) \end{aligned}$$

(20)

$\bullet$ Two-dimensional form:

$$\begin{aligned} \alpha \left( \left| \mathbf {{x}'}-\mathbf {x} \right| ,\frac{{{e}_{0}}a}{l} \right) =\frac{1}{2\pi {{\left( {{e}_{0}}a \right) }^{2}}}{{K}_{0}}(\left| \mathbf {{x}'}-\mathbf {x} \right| /{{e}_{0}}a) \end{aligned}$$

(21)

in which ${K}_{0}$ is the modified Bessel function of the second kind.

$$\begin{aligned} \alpha \left( \left| \mathbf {{x}'}-\mathbf {x} \right| ,\frac{{{e}_{0}}a}{l} \right) =\frac{1}{\pi {{e}_{0}}al}\exp \left( -\left( \mathbf {{x}'}-\mathbf {x} \right) .\left( \mathbf {{x}'}-\mathbf {x} \right) /{{e}_{0}}al \right) \end{aligned}$$

(22)

$\bullet$ Three-dimensional form

$$\begin{aligned} \alpha \left( \left| \mathbf {{x}'}-\mathbf {x} \right| ,t \right) =\frac{1}{8{{\left( \pi t \right) }^{\frac{3}{2}}}}\exp \left( -\frac{\left( \mathbf {{x}'}-\mathbf {x} \right) .\left( \mathbf {{x}'}-\mathbf {x} \right) }{4t} \right) \end{aligned}$$

(23)

where $~~~t={{e}_{0}}al/4$.

$$\begin{aligned}&\alpha \left( \left| \mathbf {{x}'}-\mathbf {x} \right| ,\frac{{{e}_{0}}a}{l} \right) =\frac{1}{4\pi {{\left( {{e}_{0}}a \right) }^{2}}} \nonumber \\&\times \frac{1}{\sqrt{\left( \mathbf {{x}'}-\mathbf {x} \right) .\left( \mathbf {{x}'}-\mathbf {x} \right) }}\exp \left( -\frac{\sqrt{\left( \mathbf {{x}'}-\mathbf {x} \right) .\left( \mathbf {{x}'}-\mathbf {x} \right) }}{{{e}_{0}}a} \right) \end{aligned}$$

(24)

In addition to the above solution to deal with the normalization problem, Koutsoumaris et al. [9, 30] have used the so-called modified kernel which has been defined by Bazant and Jirasek [32]. This modified kernel preserves symmetry with respect to $\mathbf {x}$, satisfies the normalization condition at each point of a finite domain V and satisfies all the properties of a nonlocal kernel [9]. In addition it is seen that the modified kernel recalls the locality only when the normalization condition is violated [9] (i.e. near the boundaries).

$$\begin{aligned} {{\alpha }_{mod}}\left( \left| \mathbf {x}-\mathbf {{x}'} \right| ,~\tau \right)= & {} \left( 1-\mathop {\int }_{V}\alpha \left( \left| \mathbf {{x}'}-\mathbf {x} \right| ,\tau \right) dV \right) \delta \left( \left| \mathbf {x}-\mathbf {{x}'} \right| \right) \nonumber \\+ & {} \alpha \left( \left| \mathbf {x}-\mathbf {{x}'} \right| ,\tau \right) \end{aligned}$$

(25)

3 Nonlocal Integral Finite Element Method

3.1 Variational Equations

In this section, the finite element nonlocal integral method is developed considering viscoelastic properties as it has been proposed by Polizzotto [2] for elastic materials. The finite element formulations are derived using Hamilton’s principle based on nonlocal integral theory. These formulations are then extended in the following sections to study the bending, buckling, and vibration of nanostructures. Considering the two-phase non-local theory using Eqs. (4) and (5), and taking into account the inertia effects, the total potential energy can be written as follows

$$\begin{aligned} \Pi= & {} \frac{1}{2}{{\zeta }_{1}}\mathop {\int }_{V}\varvec{\varepsilon }\left( \mathbf {x} \right) :{{\varvec{\sigma }}^{ve}}\left( \mathbf {x} \right) dV \nonumber \\+ & {} \frac{1}{2}{{\zeta }_{2}}\mathop {\int }_{V}\mathop {\int }_{{{V}'}}\alpha \left( \left| \mathbf {{x}'}-\mathbf {x} \right| ,~\tau \right) \varvec{\varepsilon }\left( \mathbf {x} \right) :{{\varvec{\sigma }}^{ve}}\left( \mathbf {x}' \right) d{V}'dV \nonumber \\- & {} {{W}_{inrt}}-{{W}_{ext}}-{{W}_{g}} \end{aligned}$$

(26)

where ${W}_{inrt}$ is the work done by inertia forces, ${W}_{ext}$ is the work done by external forces, and ${W}_{g}$ shows the energy due to geometric stiffness. Considering the Kelvin-Voigt model (Eqs. (13)), (26) can be written as [15]

$$\begin{aligned} \Pi= & {} \frac{1}{2}{{\zeta }_{1}}\mathop {\int }_{V}\varvec{\varepsilon }\left( \mathbf {x} \right) :D:\left( \varvec{\varepsilon }\left( \mathbf {x},t \right) +{{\mathbf {T}}_{d}}\frac{\partial \varepsilon \left( \mathbf {x},t \right) }{\partial t} \right) dV \nonumber \\+ & {} \frac{1}{2}{{\zeta }_{2}}\mathop {\int }_{V}\mathop {\int }_{{{V}'}}\alpha \left( \left| \mathbf {{x}'}-\mathbf {x} \right| ,~\tau \right) \varvec{\varepsilon }\left( \mathbf {x} \right) :\mathbf {D}:\varvec{\varepsilon }\left( {\mathbf {{x}'}} \right) d{V}'dV \nonumber \\+ & {} \frac{1}{2}{{\zeta }_{2}}\mathop {\int }_{V}\mathop {\int }_{{{V}'}}\alpha \left( \left| \mathbf {{x}'}-\mathbf {x} \right| ,~\tau \right) \varvec{\varepsilon }\left( \mathbf {x} \right) :\mathbf {D}:\left( {{\mathbf {T}}_{d}}\frac{\partial \varvec{\varepsilon }\left( \mathbf {{x}'},t \right) }{\partial t} \right) d{V}'dV \nonumber \\- & {} {{W}_{inrt}}-{{W}_{ext}}-{{W}_{g}} \end{aligned}$$

(27)

in which $\mathbf {D}={{\mathbf {G}}_{\infty }}$ is the fourth rank elastic moduli tensor. It is noted that the above statement can be extended for other viscoelastic models by using the explained procedure. Now, applying the variations, the total potential energy (Eq. (27)) is minimized as

$$\begin{aligned} \delta \Pi= & {} {{\zeta }_{1}}\mathop {\int }_{V}\delta \varvec{\varepsilon }\left( \mathbf {x} \right) :\mathbf {D}:\left( \varvec{\varepsilon }\left( \mathbf {x},t \right) +{{\mathbf {T}}_{d}}\frac{\partial \varepsilon \left( \mathbf {x},t \right) }{\partial t} \right) dV \nonumber \\+ & {} {{\zeta }_{2}}\mathop {\int }_{V}\mathop {\int }_{{{V}'}}\alpha \left( \left| \mathbf {{x}'}-\mathbf {x} \right| ,~\tau \right) \delta \varvec{\varepsilon }\left( \mathbf {x} \right) :\mathbf {D}:\varvec{\varepsilon }\left( {\mathbf {{x}'}} \right) d{V}'dV \nonumber \\+ & {} {{\zeta }_{2}}\mathop {\int }_{V}\mathop {\int }_{{{V}'}}\alpha \left( \left| \mathbf {{x}'}-\mathbf {x} \right| ,~\tau \right) \delta \varvec{\varepsilon }\left( \mathbf {x} \right) :\mathbf {D}:\left( {{\mathbf {T}}_{d}}\frac{\partial \varvec{\varepsilon }\left( \mathbf {{x}'},t \right) }{\partial t} \right) d{V}'dV \nonumber \\- & {} \delta {{W}_{inrt}}-\delta {{W}_{ext}}-\delta {{W}_{g}}=0 \end{aligned}$$

(28)

By substituting the corresponding terms of ${W}_{inrt}$, ${W}_{ext}$ and ${W}_{g}$, we have

$$\begin{aligned} \delta \Pi= & {} {{\zeta }_{1}}\mathop {\int }_{V}\delta \varvec{\varepsilon }\left( \mathbf {x} \right) :\mathbf {D}:\left( \varvec{\varepsilon }\left( \mathbf {x},t \right) +{{\mathbf {T}}_{d}}\frac{\partial \varvec{\varepsilon }\left( \mathbf {x},t \right) }{\partial t} \right) dV \nonumber \\+ & {} {{\zeta }_{2}}\mathop {\int }_{V}\mathop {\int }_{{{V}'}}\alpha \left( \left| \mathbf {{x}'}-\mathbf {x} \right| ,~\tau \right) \delta \varvec{\varepsilon }\left( \mathbf {x} \right) :\mathbf {D}: \varvec{\varepsilon }\left( {\mathbf {{x}'}} \right) d{V}'dV \nonumber \\+ & {} {{\zeta }_{2}}\mathop {\int }_{V}\mathop {\int }_{{{V}'}}\alpha \left( \left| \mathbf {{x}'}-\mathbf {x} \right| ,~\tau \right) \delta \varvec{\varepsilon }\left( \mathbf {x} \right) :\mathbf {D}:\left( {{\mathbf {T}}_{d}}\frac{\partial \varvec{\varepsilon }\left( \mathbf {{x}'},t \right) }{\partial t} \right) d{V}'dV \nonumber \\- & {} \mathop {\int }_{V}\delta \mathbf {u}\cdot \left( -\rho {\ddot{\mathbf {u}}} \right) dV-\mathop {\int }_{V}\bar{\mathbf {b}}\cdot \delta \mathbf {u}dV \nonumber \\- & {} \mathop {\int }_{{{S}_{t}}}\bar{\mathbf {t}}\cdot \delta \mathbf {u}~dS-\mathop {\int }_{V}{{\varvec{\sigma }}_{0m}}\delta {{\varvec{\varepsilon }}_{nl}}\left( \mathbf {x} \right) dV=0 \end{aligned}$$

(29)

where ${{\varvec{\varepsilon }}_{nl}}$ is the nonlinear strain tensor, ${{\varvec{\sigma }}_{0m}}$ is the external compressive stress, $\rho$ is the mass density, $\bar{\mathbf {t}}$ and $\bar{\mathbf {b}}$ are respectively the surface force on the surface $S_t$ and body force in volume V and $\mathbf {u}$ is the displacement field. It is seen that Eq. (29) is of a general form that can be used for analyzing the various mechanical behavior of nanostructures. For example, it can be used for extracting the formulations for studying the bending, buckling, and vibration.

3.2 Finite Element Formulations

In this section, the foundation of finite element formulation is to be established. For developing the finite element nonlocal integral theory Eq. (29) should be discretized. So, domain V will be partitioned to N subdomains, and displacement field $\mathbf {u(x)}$ and strain tensor $\varvec{\varepsilon }(\mathbf {x})$ of the n-th element can be written as

$$\begin{aligned} \mathbf {u}\left( \mathbf {x} \right) ={{\mathbf {N}}_{\text {n}}}\left( \mathbf {x} \right) {{\mathbf {d}}_{n}},~~~~~~n=1,\ldots ,~N \end{aligned}$$

(30)

$$\begin{aligned} \varvec{\varepsilon }\left( \mathbf {x} \right) ={{\mathbf {B}}_{\text {n}}}\left( \mathbf {x} \right) {{\mathbf {d}}_{n}},~~~~~~n=1,\ldots ,~N \end{aligned}$$

(31)

Matrices ${{\mathbf {N}}_{n}}\left( \mathbf {x} \right)$, ${{\mathbf {B}}_{n}}\left( \mathbf {x} \right)$ and ${{\mathbf {d}}_{n}}\left( \mathbf {x} \right)$ include the shape functions, corresponding partial derivatives, and node degrees of freedom, respectively. Applying the discretizing process and using Eqs. (30) and (31), then Eq. (29) can be written as

$$\begin{aligned}&\delta \Pi ={{\zeta }_{1}}\underset{n=1}{\overset{N}{\mathop \sum }}\,\delta \mathbf {d}_{n}^{T}\left( \mathop {\int }_{{{V}_{n}}}\mathbf {B}_{n}^{T}:\mathbf {D}:{{\mathbf {B }}_{n}}dV \right) {{\mathbf {d}}_{n}}\nonumber \\&+{{\zeta }_{1}}\underset{n=1}{\overset{N}{\mathop \sum }}\,\delta \mathbf {d}_{n}^{T}\left( \mathop {\int }_{{{V}_{n}}}{{\mathbf {T}}_{d}}\mathbf {B}_{n}^{T}:\mathbf {D}:{{\mathbf {B}}_{n}}dV \right) {{\dot{\mathbf {d}}}_{n}}\nonumber \\&+{{\zeta }_{2}}\underset{n=1}{\overset{N}{\mathop \sum }}\,\underset{m=1}{\overset{N}{\mathop \sum }}\,\delta \mathbf {d}_{n}^{T}\left( \mathop {\int }_{{{V}_{n}}}\mathop {\int }_{{{V}_{m}}}\alpha \left( \left| \mathbf {{x}'}-\mathbf {x} \right| ,\tau \right) \mathbf {B}_{n}^{T}:\mathbf {D}:\mathbf {B}_{m}^{'}d{V}'dV \right) {{\mathbf {d}}_{m}} \nonumber \\&+{{\zeta }_{2}}\underset{n=1}{\overset{N}{\mathop \sum }}\,\underset{m=1}{\overset{N}{\mathop \sum }}\,\delta \mathbf {d}_{n}^{T}\left( \mathop {\int }_{{{V}_{n}}}\mathop {\int }_{{{V}_{m}}}{{\mathbf {T}}_{\mathbf {d}}}\alpha \left( \left| \mathbf {{x}'}-\mathbf {x} \right| ,\tau \right) \mathbf {B}_{n}^{T}:\mathbf {D}:\mathbf {B}_{m}^{'}d{V}'dV \right) {{\dot{\mathbf {d}}}_{m}}\nonumber \\&-\underset{n=1}{\overset{N}{\mathop \sum }}\,\left( \delta \mathbf {d}_{n}^{T}\mathop {\int }_{{{V}_{n}}}\mathbf {N}_{n}^{T}.\bar{\mathbf {b}}~dV \right) -\underset{n=1}{\overset{N}{\mathop \sum }}\,\left( \delta \mathbf {d}_{n}^{T}\mathop {\int }_{{{S}_{{{\mathbf {t}}_{n}}}}}\mathbf {N}_{n}^{T}.\bar{\mathbf {t}}~dS \right) \nonumber \\&-\underset{n=1}{\overset{N}{\mathop \sum }}\,\left( \delta \mathbf {d}_{n}^{T}\left( \mathop {\int }_{{{V}_{n}}}\mathbf {N}_{n}^{T}.\left( -\rho {{\mathbf {N}}_{n}} \right) dV \right) \overset{{\ }}{{{\ddot{\mathbf {d}}_{n}}}}\, \right) \nonumber \\&-\underset{n=1}{\overset{N}{\mathop \sum }}\,\left( \begin{matrix} \delta \mathbf {d}_{n}^{T}\left( \mathop {\int }_{{{V}_{n}}}\mathbf {B}{{_{n}^{g}}^{T}}:{{\varvec{\sigma }}_{0}}:\mathbf {B}_{n}^{g}dV \right) {{\mathbf {d}}_{n}} \\ \end{matrix} \right) =0 \end{aligned}$$

(32)

It is noted that matrix $\mathbf {B}_{n}^{g}$ is related to nonlinear strains and ${{\dot{\mathbf {d}}}_{n}}=\partial {{\mathbf {d}}_{n}}/\partial t$. Moreover, as it has been defined ${{\zeta }_{1}}$ and ${{\zeta }_{2}}$ correspond to the local and nonlocal fractions (${{\zeta }_{1}}+{{\zeta }_{2}}=1$, ${{\zeta }_{1}},~{{\zeta }_{2}}>0$). Using the Boolean matrix ${{\mathbf {Q}}_{n}}$ the degrees of freedom of the n-th element (${\mathbf {d}_{n}}$) is connected to the structural DOF matrix ($\mathbf {U}$)

$$\begin{aligned} {{\mathbf {d}}_{n}}={{\mathbf {Q}}_{n}}\mathbf {U} \end{aligned}$$

(33)

Substituting Eq. (33) into Eq. (32) gives

$$\begin{aligned}&\delta \Pi ={{\zeta }_{1}}\underset{n=1}{\overset{N}{\mathop \sum }}\,\delta {{\mathbf {U}}^{T}}\mathbf {Q}_{n}^{T}\left( \mathop {\int }_{{{V}_{n}}}\mathbf {B}_{n}^{T}:\mathbf {D}:{{\mathbf {B}}_{n}}dV \right) {{\mathbf {Q}}_{n}}\mathbf {U} \nonumber \\&+{{\zeta }_{1}}\underset{n=1}{\overset{N}{\mathop \sum }}\,\delta {{\mathbf {U}}^{T}}\mathbf {Q}_{n}^{T}\left( \mathop {\int }_{{{V}_{n}}}{{\mathbf {T}}_{d}}\mathbf {B}_{n}^{T}:\mathbf {D}:{{\mathbf {B}}_{n}}dV \right) {{\mathbf {Q}}_{n}}{\dot{\mathbf {U}}} \nonumber \\&+{{\zeta }_{2}}\underset{n=1}{\overset{N}{\mathop \sum }}\,\underset{m=1}{\overset{N}{\mathop \sum }}\,\delta {{\mathbf {U}}^{T}}\mathbf {Q}_{n}^{T}\left( \mathop {\int }_{{{V}_{n}}}\mathop {\int }_{{{V}_{m}}}\alpha \left( \left| \mathbf {{x}'}-\mathbf {x} \right| ,\tau \right) \mathbf {B}_{n}^{T}:\mathbf {D}:\mathbf {B}_{m}^{'}d{V}'dV \right) {{\mathbf {Q}}_{m}}\mathbf {U} \nonumber \\&+{{\zeta }_{2}}\underset{n=1}{\overset{N}{\mathop \sum }}\,\underset{m=1}{\overset{N}{\mathop \sum }}\,\delta {{\mathbf {U}}^{T}}\mathbf {Q}_{n}^{T}\left( \mathop {\int }_{{{V}_{n}}}\mathop {\int }_{{{V}_{m}}}{{\mathbf {T}}_{d}}\alpha \left( \left| \mathbf {{x}'}-\mathbf {x} \right| ,\tau \right) \mathbf {B}_{n}^{T}:\mathbf {D}:\mathbf {B}_{m}^{'}d{V}'dV \right) {{\mathbf {Q}}_{m}}{\dot{\mathbf {U}}}\nonumber \\&-\underset{n=1}{\overset{N}{\mathop \sum }}\,\left( \delta {{\mathbf {U}}^{T}}\mathbf {Q}_{n}^{T}\mathop {\int }_{{{V}_{n}}}\mathbf {N}_{n}^{T}.b~dV \right) -\underset{n=1}{\overset{N}{\mathop \sum }}\,\left( \delta {{\mathbf {U}}^{T}}\mathbf {Q}_{n}^{T}\mathop {\int }_{{{S}_{{{t}_{n}}}}}\mathbf {N}_{n}^{T}.t~dS \right) \nonumber \\&-\underset{n=1}{\overset{N}{\mathop \sum }}\,\left( \delta {{\mathbf {U}}^{T}}\mathbf {Q}_{n}^{T}\left( \mathop {\int }_{{{V}_{n}}}\mathbf {N}_{n}^{T}.\left( -\rho {{\mathbf {N}}_{n}} \right) dV \right) {{\mathbf {Q}}_{n}}{\ddot{\mathbf {U}}} \right) \nonumber \\&-\underset{n=1}{\overset{N}{\mathop \sum }}\,\left( \begin{matrix} \delta {{\mathbf {U}}^{T}}\mathbf {Q}_{n}^{T}\left( \mathop {\int }_{{{V}_{n}}}{{\mathbf {B}}^{g}}_{n}^{T}:{{\varvec{\sigma }}_{0}}:\mathbf {B}_{n}^{g}dV \right) {{\mathbf {Q}}_{n}}\mathbf {U} \\ \end{matrix} \right) =0 \end{aligned}$$

(34)

Equation (34) is the governing finite element equation based on the nonlocal integral theory considering the Kelvin-Voigt viscoelastic model. Mechanical behavior of nanostructures (e.g., bending, vibration, and buckling) can be analyzed by considering the related terms of the current equation.

3.3 Element Types

Noting that the proposed method has a finite element base, various types of elements can be used for analyzing different problems. For example, to analyze the simple tension problem of a plate (for axial behavior), elements of the $C^0$ continuity class will suffice, however, for analyzing the bending, buckling or vibration assuming the classical beam theory elements of the $C^1$ continuity class is usually needed. $C^0$ continuity means that the displacements between the elements are continuous, but their first derivatives are not (Lagrange elements). However, in $C^1$ continuity, both the displacements and their first derivatives are continuous (Hermite elements). In this section, some of the sample elements that have relatively more applications are introduced.

Fig. 3

Hermite beam element

Hermite beam element (Fig. 3) is used later in this chapter for analyzing the mechanical behavior of Euler-Bernoulli beam elements. These elements include two nodes with two degrees of freedom for each node, i.e. displacement and rotation. The displacement matrix and shape functions of Hermite beam elements in the local coordinate system are considered as

$$\begin{aligned} {{\mathbf {d}}_{n}}=\left\{ \begin{matrix} {{w}_{1}} \\ {{\left( \frac{\partial w}{\partial x} \right) }_{1}} \\ {{w}_{2}} \\ {{\left( \frac{\partial w}{\partial x} \right) }_{2}} \\ \end{matrix} \right\} \end{aligned}$$

(35)

$$\begin{aligned} \mathbf {N}_{n}^{T}\left( \xi \right) =\frac{1}{8}\left\{ \begin{matrix} 2{{\left( 1-\xi \right) }^{2}}\left( 2+\xi \right) \\ {{l}_{e}}{{\left( 1-\xi \right) }^{2}}\left( 1+\xi \right) \\ \begin{matrix} 2{{\left( 1+\xi \right) }^{2}}\left( 2-\xi \right) \\ {{l}_{e}}{{\left( 1+\xi \right) }^{2}}\left( \xi -1 \right) \\ \end{matrix} \\ \end{matrix} \right\} \end{aligned}$$

(36)

The general coordinates can be converted to local ones using (see Fig. 4)

$$\begin{aligned} \xi =\frac{\text {2}x}{{{l}_{e}}}-\text {1};~~~~\text {0}\le x\le {{l}_{e}},~~~~-\text {1}\le \xi \le \text {1} \end{aligned}$$

(37)

in which ${l}_{e}$ is the element length.

Fig. 4

Local and general coordinates of the beam

Conforming elements (displacements are always continuous between adjacent elements) are mostly based on higher degree polynomials and need relatively high computational cost for producing the corresponding matrices. Moreover, the nonlocal integral finite element method has more computational cost in comparison to the local method. Therefore, it is more efficient to use elements with polynomials of lower degree (e.g. non-conforming elements) for modelling the nonlocal plate problems. If the assumed elements pass the “patch test”, the results will converge [33]. The original patch test, developed by Irons et al. [34] is a check that determines whether a patch of elements subject to a constant strain reproduced the constitutive behavior of the material and resulted in correct stresses when it became infinitesimally small [35]. In other words, patch test is a sufficient requirement for convergence.

The Adini-Clough quadrilateral element (Fig. 5) is a non-conforming element, which despite being unable to pass the patch test, is known to give good convergent results for bending and buckling of thin plates, i.e. it is a generalized conforming element [36]. These elements consist of four nodes with three degrees of freedom for each. Matrix ${{\mathbf {d}}_{n}}$ for the n-th element is expressed as

$$\begin{aligned} {{\mathbf {d}}_{n}}=&[\begin{matrix} {{w}_{1}} &{} {{w}_{1,x}} &{} {{w}_{1,y}} &{} {{w}_{2}} &{} {{w}_{2,x}} &{} {{w}_{2,y}} &{} \ldots \\ \end{matrix} \nonumber \\&\begin{matrix} \ldots &{} {{w}_{3}} &{} {{w}_{3,x}} &{} {{w}_{3,y}} &{} {{w}_{4}} &{} {{w}_{4,x}} &{} {{w}_{4,y}} \\ \end{matrix}{{]}^{T}} \end{aligned}$$

(38)

Also, the shape functions of the Adini-Clough elements are as ($-1<\xi<1,~-1<\eta <1$)

$$\begin{aligned} \mathbf {N}_{n}^{T}\left( \xi ,\eta \right) =\frac{1}{8}\left\{ \begin{matrix} e\left( a-\xi -\eta \right) \\ e\left( 1-{{\xi }^{2}} \right) \\ e\left( 1-{{\eta }^{2}} \right) \\ \begin{matrix} f\left( a+\xi -\eta \right) \\ -f\left( 1-{{\xi }^{2}} \right) \\ f\left( 1-{{\eta }^{2}} \right) \\ \begin{matrix} g\left( a+\xi +\eta \right) \\ -g\left( 1-{{\xi }^{2}} \right) \\ -g\left( 1-{{\eta }^{2}} \right) \\ \begin{matrix} h\left( a-\xi +\eta \right) \\ h\left( 1-{{\xi }^{2}} \right) \\ -h\left( 1-{{\eta }^{2}} \right) \\ \end{matrix} \\ \end{matrix} \\ \end{matrix} \\ \end{matrix} \right\} \end{aligned}$$

(39)

where

$$\begin{aligned} a= & {} 2-{{\xi }^{2}}-{{\eta }^{2}}, ~~~~e=\left( 1-\xi \right) \left( 1-\eta \right) ,~~~~f=\left( 1+\xi \right) \left( 1-\eta \right) , \nonumber \\ g= & {} \left( 1+\xi \right) \left( 1+\eta \right) ,~~~~h=\left( 1-\xi \right) \left( 1+\eta \right) \end{aligned}$$

(40)

Fig. 5

Adini-Clough quadrilateral plate element

The 8-node $C^0$-quadratic isoparametric Serendipity elements with 2 degrees of freedom per node can be used for analyzing the beam in 3-dimensions [6] or tension of a plate [5]. ${{\mathbf {d}}_{n}}$ and ${{\mathbf {N}}_{n}}$ matrices are as

$$\begin{aligned} {{\mathbf {d}}_{n}}=&[\begin{matrix} {{u}_{1}} &{} {{v}_{1}} &{} {{u}_{2}} &{} {{v}_{2}} &{} {{u}_{3}} &{} {{v}_{3}} &{} {{u}_{4}} &{} {{v}_{4}} &{} \ldots \\ \end{matrix} \nonumber \\&\begin{matrix} \ldots &{} {{u}_{5}} &{} {{v}_{5}} &{} {{u}_{6}} &{} {{v}_{6}} &{} {{u}_{7}} &{} {{v}_{7}} &{} {{u}_{8}} &{} {{v}_{8}} \\ \end{matrix}{{]}^{T}} \end{aligned}$$

(41)

$$\begin{aligned} \mathbf {N}_{n}^{{{T}^{u~\left( or \right) ~v}}}\left( \xi ,\eta \right) =\frac{1}{4}\left\{ \begin{matrix} -~\left( \xi +\eta +1 \right) \left( \xi -1 \right) \left( \eta -1 \right) \\ 2\left( \xi -1 \right) \left( \xi +1 \right) \left( \eta -1 \right) \\ \left( -\xi +\eta +1 \right) \left( \xi +1 \right) \left( \eta -1 \right) \\ \begin{matrix} -~2\left( \eta -1 \right) \left( \xi +1 \right) \left( \eta +1 \right) \\ \left( \xi +\eta -1 \right) \left( \xi +1 \right) \left( \eta +1 \right) \\ -2\left( \xi -1 \right) \left( \xi +1 \right) \left( \eta +1 \right) \\ \begin{matrix} -\left( -\xi +\eta -1 \right) \left( \xi -1 \right) \left( \eta +1 \right) \\ 2\left( \xi -1 \right) \left( \eta +1 \right) \left( \eta -1 \right) \\ \end{matrix} \\ \end{matrix} \\ \end{matrix} \right\} \end{aligned}$$

(42)

where $\mathbf {N}_{n}^{{{T}^{u~\left( or \right) ~v}}}$ includes the shape functions of the element corresponding to both u and v degrees of freedom.

3.4 Notes on the Boundary Conditions

In this section, by considering a sample case, it is attempted to demonstrate the incapability of nonlocal differential elasticity theory for efficiently applying the natural boundary conditions on a plate. Consider a plate of length and width $l_x$ and $l_y$, respectively. The boundary conditions of the mentioned plate are simply-supported on all four edges. Using the nonlocal differential constitutive equation, the following set of equations can be obtained [37]

$$\begin{aligned} {{M}_{xx}}-{{l}^{2}}{{\tau }^{2}}{{\nabla }^{2}}{{M}_{xx}}=-{{D}_{11}}\frac{{{\partial }^{2}}w}{\partial {{x}^{2}}}-{{D}_{12}}\frac{{{\partial }^{2}}w}{\partial {{y}^{2}}} \end{aligned}$$

(43a)

$$\begin{aligned} {{M}_{yy}}-{{l}^{2}}{{\tau }^{2}}{{\nabla }^{2}}{{M}_{yy}}=-{{D}_{12}}\frac{{{\partial }^{2}}w}{\partial {{x}^{2}}}-{{D}_{22}}\frac{{{\partial }^{2}}w}{\partial {{y}^{2}}} \end{aligned}$$

(43b)

$$\begin{aligned} {{M}_{xy}}-{{l}^{2}}{{\tau }^{2}}{{\nabla }^{2}}{{M}_{xy}}=-2{{D}_{66}}\frac{{{\partial }^{2}}w}{\partial x\partial y} \end{aligned}$$

(43c)

Assuming the bottom left corner of the plate as the center of the coordinate system, the boundary condition at $x=0$ would be like ${{M}_{xx}}=0$. So the Eq. (43) becomes

$$\begin{aligned} \frac{{{\partial }^{2}}w}{\partial {{x}^{2}}}=\frac{{{l}^{2}}{{\tau }^{2}}}{{{D}_{11}}}\frac{{{\partial }^{2}}{{M}_{xx}}}{\partial {{x}^{2}}}-\frac{{{D}_{12}}}{{{D}_{11}}}\frac{{{\partial }^{2}}w}{\partial {{y}^{2}}} \end{aligned}$$

(44)

It is noted that the equilibrium equations for a plate are as [37]

$$\begin{aligned} \frac{{{\partial }^{2}}{{M}_{xx}}}{\partial {{x}^{2}}}+2\frac{{{\partial }^{2}}{{M}_{xy}}}{\partial x\partial y}+\frac{{{\partial }^{2}}{{M}_{yy}}}{\partial {{y}^{2}}}+\frac{\partial }{\partial x}\left( N_{0}^{x}\frac{\partial w}{\partial x} \right) +\frac{\partial }{\partial y}~\left( N_{0}^{y}\frac{\partial w}{\partial y} \right) \nonumber \\ +\frac{\partial }{\partial x}\left( N_{0}^{xy}\frac{\partial w}{\partial y} \right) +\frac{\partial }{\partial y}\left( N_{0}^{xy}\frac{\partial w}{\partial x} \right) -{{m}_{0}}\frac{{{\partial }^{2}}w}{\partial {{t}^{2}}}+q=0 \end{aligned}$$

(45a)

$$\begin{aligned} {{Q}_{x}}-\frac{\partial {{M}_{xx}}}{\partial x}-\frac{\partial {{M}_{xy}}}{\partial y}-N_{0}^{x}\frac{\partial w}{\partial x}-N_{0}^{xy}\frac{\partial w}{\partial y}=0 \end{aligned}$$

(45b)

$$\begin{aligned} {{Q}_{y}}-\frac{\partial {{M}_{xy}}}{\partial x}-\frac{\partial {{M}_{yy}}}{\partial y}-N_{0}^{y}\frac{\partial w}{\partial y}-N_{0}^{xy}\frac{\partial w}{\partial x}=0 \end{aligned}$$

(45c)

Now the Navier solution can only be applied when ${{{\partial }^{2}}w}/{\partial {{n}^{2}}}\;$ is zero across the boundary of the plate. It means that, for considering the Navier solution, according to Eq. (44) $({{{l}^{2}}{{\tau }^{2}}}/{{{D}_{11}}}\;)[({{\partial }^{2}}{{M}_{xx}}/\partial {{x}^{2}})-({{D}_{12}}/{{D}_{11}})({{\partial }^{2}}w/\partial {{y}^{2}})]$ should be zero at $x=0$, but it is not. Even for a free boundary condition, the mentioned problem arises for a plate. It is where the finite element nonlocal integral method comes in and makes things easier! No such complexity is seen in the FEM based method, and various kinds of rather complex boundary conditions can be dealt with.

4 Nano-Scaled Beams

The finite element formulations for bending, vibration, and buckling of nano-scaled beams are prepared in the following sections. It is noted that various beam theories can be included in the formulation, but for the sake of brevity only Euler-Bernoulli beam theory is assumed here.

4.1 Applying Boundary Conditions for Nano-Scaled Beams

The boundary conditions can be applied rather quickly in the currently proposed method. For instance, some of the common boundary conditions are as follow (see Fig. 6)

Both-ends simply supported beam:

$$\begin{aligned} w\left( x \right)= & {} 0~~~~~~\text {at}~~~~~~x=0 \nonumber \\ w\left( x \right)= & {} 0~~~~~~\text {at}~~~~~~x=l \end{aligned}$$

(46)

Both-ends clamped beam:

$$\begin{aligned} w\left( x \right)= & {} {{w}_{,x}}\left( x \right) =0~~~~~~\text {at}~~~~~~x=0 \nonumber \\ w\left( x \right)= & {} {{w}_{,x}}\left( x \right) =0~~~~~~\text {at}~~~~~~x=l \end{aligned}$$

(47)

Clamped-free beam:

$$\begin{aligned} w\left( x \right)= & {} {{w}_{,x}}\left( x \right) =0~~~~~~\text {at}~~~~~~x=0 \end{aligned}$$

(48)

Simply supported-clamped beam:

$$\begin{aligned} w\left( x \right)= & {} 0~~~~~~\text {at}~~~~~~x=0 \nonumber \\ w\left( x \right)= & {} {{w}_{,x}}\left( x \right) =0~~~~~~\text {at}~~~~~~x=l \end{aligned}$$

(49)

Fig. 6

The geometry of a beam

4.2 Bending of Elastic Nano-Scaled Beams

The bending formulations are given for an Euler-Bernoulli nano-scaled beam. It is noted that this method can be extended for other beam theories. Considering the classical beam theory, the displacement field is given as

$$\begin{aligned} u\left( x,z \right) ={{u}_{0}}\left( x \right) -z\frac{\partial {{w}_{0}}}{\partial x} \end{aligned}$$

(50)

$$\begin{aligned} w\left( x,z \right) ={{w}_{0}}\left( x \right) \end{aligned}$$

(51)

in which u and w are longitudinal and transverse displacements of the beam, respectively. Also, $u_0$ and $w_0$ are the displacement components at the mid-axis. Also, neglecting the higher-order terms, the strain can be expressed as

$$\begin{aligned} \varepsilon ={{\varepsilon }_{x}}=\frac{\partial u}{\partial x}=\frac{\partial {{u}_{0}}}{\partial x}-z\frac{{{\partial }^{2}}{{w}_{0}}}{\partial {{x}^{2}}} \end{aligned}$$

(52)

For an Euler-Bernoulli beam, if the pure bending condition is assumed, Eq. (52) might be written as

$$\begin{aligned} \varepsilon ={{\varepsilon }_{x}}=-z\frac{{{\partial }^{2}}{{w}_{0}}}{\partial {{x}^{2}}}={{\mathbf {B}}_{n}}{{\mathbf {d}}_{n}}=z\mathbf {B}_{n}^{b}{{\mathbf {d}}_{n}} \end{aligned}$$

(53)

where $\mathbf {B}_{n}^{b}$ consists of the partial derivatives of the shape functions of the subject beam. Substituting Eq. (53) into Eq. (34) and only considering the terms corresponding to elastic bending, the local and nonlocal stiffness matrices and external force matrix can be obtained as

$$\begin{aligned} \mathbf {K} _{n}^{L}={{\zeta }_{1}}\left( {{I}_{yy}}\mathop {\int }_{-1}^{1}\mathbf {B}{{_{n}^{b}}^{T}}\left( \xi \right) E\mathbf {B}_{n}^{b}\left( \xi \right) \det \left( \mathbf {J}\left( \xi \right) \right) d\xi \right) \end{aligned}$$

(54)

$$\begin{aligned} \mathbf {K}_{nm}^{NL}= & {} {{\zeta }_{2}}[bh~{{I}_{yy}}\mathop {\int }_{-1}^{1}\mathop {\int }_{-1}^{1}\alpha \left( \left| {x}'\left( \xi \right) -x\left( \xi \right) \right| ,\tau \right) ~\mathbf {B}{{_{n}^{b}}^{T}}\left( \xi \right) E\mathbf {B}_{m}^{b}\left( \xi ' \right) \nonumber \\\times & {} \det (\mathbf {J}\left( \xi ' \right) )\det \left( \mathbf {J}\left( \xi \right) \right) d\xi 'd\xi ] \end{aligned}$$

(55)

$$\begin{aligned} {{\mathbf {F}}_{n}}=bh\mathop {\int }_{-1}^{1}\mathbf {N}_{n}^{T}.\bar{\mathbf {b}}~\text {det}\left( \mathbf {J}\left( \xi \right) \right) d\xi +b\mathop {\int }_{-1}^{1}\mathbf {N}_{n}^{T}.\bar{\mathbf {t}}~\text {det}\left( \mathbf {J}\left( \xi \right) \right) d\xi \end{aligned}$$

(56)

where $\mathbf {K}_{nm}^{NL}$ shows the nonlocal effect of the m-th element on the n-th one. $\mathbf {J}$ is the Jacobian matrix, and $I_{yy}$ is the second moment of area. Also, total matrices can be written as

$$\begin{aligned} \mathbf {K}_{total}^{L}=\underset{n=1}{\overset{N}{\mathop \sum }}\,\mathbf {Q}_{n}^{T}~\left( \mathbf {K}_{n}^{L} \right) ~{{\mathbf {Q}}_{n}} \end{aligned}$$

(57)

$$\begin{aligned} \mathbf {K}_{total}^{NL}=\underset{n=1}{\overset{N}{\mathop \sum }}\,\underset{m=1}{\overset{N}{\mathop \sum }}\,\mathbf {Q}_{n}^{T}~\left( \mathbf {K}_{nm}^{NL} \right) ~{{\mathbf {Q}}_{m}} \end{aligned}$$

(58)

$$\begin{aligned} {{\mathbf {F}}_{total}}=\underset{n=1}{\overset{N}{\mathop \sum }}\,\mathbf {Q}_{n}^{T}~\left( {{\mathbf {F}}_{n}} \right) ~{{\mathbf {Q}}_{n}} \end{aligned}$$

(59)

It is noted that for carrying out the corresponding integration, numerical integration schemes can be used. Substituting Eqs. (54)–(58) into Eq. (34) and assuming bending related terms, the corresponding governing bending equation of the elastic beam is developed as follows

$$\begin{aligned} \left( \mathbf {K}_{total}^{L}+\mathbf {K}_{total}^{NL} \right) \mathbf {U}={{\mathbf {F}}_{total}} \end{aligned}$$

(60)

By solving Eq. (60), displacement matrix $\mathbf {U}$ can be calculated as

$$\begin{aligned} \mathbf {U}={{\left( \mathbf {K}_{total}^{L}+\mathbf {K}_{total}^{NL} \right) }^{-1}}{{\mathbf {F}}_{total}} \end{aligned}$$

(61)

4.3 Vibration of Nano-Scaled Beams

For analyzing the vibration of the beam, mass (inertia effects) and stiffness of the beam should be considered. It is noted that for a viscoelastic beam, the damping matrix should also be taken into account. So, Eq. (34) can be written as

$$\begin{aligned}&\delta \Pi ={{\zeta }_{1}}\underset{n=1}{\overset{N}{\mathop \sum }}\,\delta {{\mathbf {U}}^{T}}\mathbf {Q}_{n}^{T}\left( \mathop {\int }_{{{V}_{n}}}\mathbf {B}_{n}^{T}:\mathbf {D}:{{\mathbf {B}}_{n}}dV \right) {{\mathbf {Q}}_{n}}\mathbf {U} \nonumber \\&+{{\zeta }_{1}}\underset{n=1}{\overset{N}{\mathop \sum }}\,\delta {{\mathbf {U}}^{T}}\mathbf {Q}_{n}^{T}\left( \mathop {\int }_{{{V}_{n}}}{{\mathbf {T}}_{d}}\mathbf {B}_{n}^{T}:\mathbf {D}:{{\mathbf {B}}_{n}}dV \right) {{\mathbf {Q}}_{n}}{\dot{\mathbf {U}}} \nonumber \\&+{{\zeta }_{2}}\underset{n=1}{\overset{N}{\mathop \sum }}\,\underset{m=1}{\overset{N}{\mathop \sum }}\,\delta {{\mathbf {U}}^{T}}\mathbf {Q}_{n}^{T}\left( \mathop {\int }_{{{V}_{n}}}\mathop {\int }_{{{V}_{m}}}\alpha \left( \left| \mathbf {{x}'}-\mathbf {x} \right| ,\tau \right) \mathbf {B}_{n}^{T}:\mathbf {D}:\mathbf {B}_{m}^{'}d{V}'dV \right) {{\mathbf {Q}}_{m}}\mathbf {U} \nonumber \\&+{{\zeta }_{2}}\underset{n=1}{\overset{N}{\mathop \sum }}\,\underset{m=1}{\overset{N}{\mathop \sum }}\,\delta {{\mathbf {U}}^{T}}\mathbf {Q}_{n}^{T}\left( \mathop {\int }_{{{V}_{n}}}\mathop {\int }_{{{V}_{m}}}{{\mathbf {T}}_{d}}\alpha \left( \left| \mathbf {{x}'}-\mathbf {x} \right| ,\tau \right) \mathbf {B}_{n}^{T}:\mathbf {D}:\mathbf {B}_{m}^{'}d{V}'dV \right) {{\mathbf {Q}}_{m}}{\dot{\mathbf {U}}}\nonumber \\&-\underset{n=1}{\overset{N}{\mathop \sum }}\,\left( \delta {{\mathbf {U}}^{T}}\mathbf {Q}_{n}^{T}\mathop {\int }_{{{V}_{n}}}\mathbf {N}_{n}^{T}.b~dV \right) -\underset{n=1}{\overset{N}{\mathop \sum }}\,\left( \delta {{\mathbf {U}}^{T}}\mathbf {Q}_{n}^{T}\mathop {\int }_{{{S}_{{{t}_{n}}}}}\mathbf {N}_{n}^{T}.t~dS \right) \nonumber \\&-\underset{n=1}{\overset{N}{\mathop \sum }}\,\left( \delta {{\mathbf {U}}^{T}}\mathbf {Q}_{n}^{T}\left( \mathop {\int }_{{{V}_{n}}}\mathbf {N}_{n}^{T}.\left( -\rho {{\mathbf {N}}_{n}} \right) dV \right) {{\mathbf {Q}}_{n}}{\ddot{\mathbf {U}}} \right) =0 \end{aligned}$$

(62)

Local and nonlocal stiffness matrices are expressed as Eqs. (54)–(58). Mass matrix (${{\mathbf {M}}_{n}}$) and damping matrices ($\mathbf {C}_{n}^{L}$ and $\mathbf {C}_{nm}^{NL}$) might be extracted for elements by substituting Eqs. (50)–(53) into Eq. (62).

$$\begin{aligned} {{\mathbf {M}}_{n}}=\left( bh\mathop {\int }_{-1}^{1}\mathbf {N}_{n}^{T}\left( \xi \right) \rho {{\mathbf {N}}_{n}}\left( \xi \right) \det \left( \mathbf {J}\left( \xi \right) \right) d\xi \right) \end{aligned}$$

(63)

$$\begin{aligned} \mathbf {C}_{n}^{L}={{\zeta }_{1}}\left( {{I}_{yy}}\mathop {\int }_{-1}^{1}{{\mathbf {B}}^{b}}_{n}^{T}\left( \xi \right) E{{T}_{d}}\mathbf {B}_{n}^{b}\left( \xi \right) \det \left( \mathbf {J}\left( \xi \right) \right) d\xi \right) \end{aligned}$$

(64)

$$\begin{aligned} \mathbf {C}_{nm}^{NL}= & {} {{\zeta }_{2}}[bh~{{I}_{yy}}\mathop {\int }_{-1}^{1}\mathop {\int }_{-1}^{1}\alpha \left( \left| {x}'\left( \xi \right) -x\left( \xi \right) \right| ,\tau \right) ~\mathbf {B}{{_{n}^{b}}^{T}}\left( \xi \right) E{{T}_{d}}\mathbf {B}_{m}^{b}\left( \xi ' \right) \nonumber \\\times & {} \det \left( \mathbf {J}\left( {{\xi }'} \right) \right) \det \left( \mathbf {J}\left( \xi \right) \right) d\xi 'd\xi ] \end{aligned}$$

(65)

Besides, the total mass and damping matrices are as follows

$$\begin{aligned} {{\mathbf {M}}_{total}}=\underset{n=1}{\overset{N}{\mathop \sum }}\,\mathbf {Q}_{n}^{T}~\left( {{\mathbf {M}}_{n}} \right) ~{{\mathbf {Q}}_{n}} \end{aligned}$$

(66)

$$\begin{aligned} \mathbf {C}_{total}^{L}=\underset{n=1}{\overset{N}{\mathop \sum }}\,\mathbf {Q}_{n}^{T}~\left( \mathbf {C}_{n}^{L} \right) ~{{\mathbf {Q}}_{n}} \end{aligned}$$

(67)

$$\begin{aligned} \mathbf {C}_{total}^{NL}=\underset{n=1}{\overset{N}{\mathop \sum }}\,\underset{m=1}{\overset{N}{\mathop \sum }}\,\mathbf {Q}_{n}^{T}~\left( \mathbf {C}_{nm}^{NL} \right) ~{{\mathbf {Q}}_{m}} \end{aligned}$$

(68)

Substituting Eqs. (54)–(58) and (63)–(68) into Eq. (62), the following equation is obtained for viscoelastic vibration of nonlocal Euler-Bernoulli nano-scaled beam.

$$\begin{aligned} {{\mathbf {M}}_{total}}{\ddot{\mathbf {U}}}+\left( \mathbf {C}_{total}^{L}+\mathbf {C}_{total}^{NL} \right) {\dot{\mathbf {U}}}+\left( \mathbf {K}_{total}^{L}+\mathbf {K}_{total}^{NL} \right) \mathbf {U}=0 \end{aligned}$$

(69)

Free vibration frequencies and mode shapes are the eigenvalues and eigenfunctions of Eq. (69), respectively. For solving the eigenvalue problem of Eq. (69), the following parameters are first defined.

$$\begin{aligned} \mathbf {V}=\left[ \begin{matrix} {\dot{\mathbf {U}}} \\ \mathbf {U} \\ \end{matrix} \right] \end{aligned}$$

(70)

$$\begin{aligned} {{\mathbf {M}}^{\mathbf {*}}}\mathbf {=}\left[ \begin{matrix} {{\mathbf {M}}_{{total}}} &{} \mathbf {0} \\ \mathbf {0} &{} \mathbf {I} \\ \end{matrix} \right] \end{aligned}$$

(71)

$$\begin{aligned} {{\mathbf {C}}^{\mathbf {*}}}\mathbf {=}\left[ \begin{matrix} {\mathbf {C}_{{total}}^{{L}}}{\mathbf {+C}_{{total}}^{{NL}}} &{} {\mathbf {K}_{{total}}^{{L}}}{\mathbf {+K}_{{total}}^{{NL}}} \\ \mathbf {-I} &{} \mathbf {0} \\ \end{matrix} \right] \end{aligned}$$

(72)

Assuming Eqs. (70)–(72), (69) becomes

$$\begin{aligned} {{\mathbf {M}}^{\mathbf {*}}}\dot{\mathbf {V}}+{{\mathbf {C}}^{\mathbf {*}}}\mathbf {V=0} \end{aligned}$$

(73)

For calculating the complex eigenvalues of the free vibration, the solution of the following form is assumed

$$\begin{aligned} \mathbf {V}=\varvec{\phi }\left( x \right) ~{{e}^{i\omega t}} \end{aligned}$$

(74)

Now substituting Eq. (74) in Eq. (73), the following relation has resulted.

$$\begin{aligned} \left( i\omega {{\mathbf {M}}^{*}}+{{\mathbf {C}}^{*}} \right) \varvec{\phi }=0 \end{aligned}$$

(75)

For obtaining the eigenvalues of Eq. (75), the determinant of the coefficient matrix should be set to zero as

$$\begin{aligned} \left| i\omega {{\mathbf {M}}^{*}}+{{\mathbf {C}}^{*}} \right| =0 \end{aligned}$$

(76)

By solving Eq. (76), the values of $\omega$ are calculated and by substituting them into Eq. (75) mode shapes can be obtained. It is noted that for an elastic beam, Eq. (69) becomes

$$\begin{aligned} {{\mathbf {M}}_{total}}{\ddot{\mathbf {U}}}+\left( \mathbf {K}_{total}^{L}+\mathbf {K}_{total}^{NL} \right) \mathbf {U}=0 \end{aligned}$$

(77)

By considering matrix $\mathbf {U}$ as

$$\begin{aligned} \mathbf {U}=\varvec{\phi }\left( x \right) ~{{e}^{i\omega t}} \end{aligned}$$

(78)

Equation (77) can be written as

$$\begin{aligned} \left( \left( \mathbf {K}_{total}^{L}+\mathbf {K}_{total}^{NL} \right) -{{\omega }^{2}}{{\mathbf {M}}_{total}} \right) {\varvec{\phi }} \left( x \right) =0 \end{aligned}$$

(79)

By equating the determinant of coefficient matrix of Eq. (79)to zero, natural frequencies and mode shapes can be calculated.

$$\begin{aligned} \left| \left( \mathbf {K}_{total}^{L}+\mathbf {K}_{total}^{NL} \right) -{{\omega }^{2}}{{\mathbf {M}}_{total}} \right| =0 \end{aligned}$$

(80)

4.4 Buckling of Nano-Scaled Beams

For analyzing the viscoelastic buckling of structures (relaxation or creep model), an imperfection (initial displacement) is needed to be assumed. So, for deriving more general relations, imperfection effects are taken into account. Retaining the buckling related terms and the imperfection effects, Eq. (34) takes the form

$$\begin{aligned}&\delta \Pi ={{\zeta }_{1}}\underset{n=1}{\overset{N}{\mathop \sum }}\,\delta {{\mathbf {U}}^{T}}\mathbf {Q}_{n}^{T}\left( \mathop {\int }_{{{V}_{n}}}\mathbf {B}_{n}^{T}:\mathbf {D}:{{\mathbf {B}}_{n}}dV \right) {{\mathbf {Q}}_{n}}\mathbf {U} \nonumber \\&+{{\zeta }_{1}}\underset{n=1}{\overset{N}{\mathop \sum }}\,\delta {{\mathbf {U}}^{T}}\mathbf {Q}_{n}^{T}\left( \mathop {\int }_{{{V}_{n}}}{{\mathbf {T}}_{d}}\mathbf {B}_{n}^{T}:\mathbf {D}:{{\mathbf {B}}_{n}}dV \right) {{\mathbf {Q}}_{n}}{\dot{\mathbf {U}}} \nonumber \\&-{{\zeta }_{1}}\underset{n=1}{\overset{N}{\mathop \sum }}\,\left( \begin{matrix} \delta {{\mathbf {U}}^{T}}\mathbf {Q}_{n}^{T}\left( \mathop {\int }_{{{V}_{n}}}{{\mathbf {B}}^{0}}_{n}^{T}:\mathbf {D}:\mathbf {B}_{n}^{0}dV \right) {{\mathbf {Q}}_{n}}{{\mathbf {U}}_{0}} \\ \end{matrix} \right) \nonumber \\&+{{\zeta }_{2}}\underset{n=1}{\overset{N}{\mathop \sum }}\,\underset{m=1}{\overset{N}{\mathop \sum }}\,\delta {{\mathbf {U}}^{T}}\mathbf {Q}_{n}^{T}\left( \mathop {\int }_{{{V}_{n}}}\mathop {\int }_{{{V}_{m}}}\alpha \left( \left| \mathbf {{x}'}-\mathbf {x} \right| ,\tau \right) \mathbf {B}_{n}^{T}:\mathbf {D}:\mathbf {B}_{m}^{'}d{V}'dV \right) {{\mathbf {Q}}_{m}}\mathbf {U} \nonumber \\&+{{\zeta }_{2}}\underset{n=1}{\overset{N}{\mathop \sum }}\,\underset{m=1}{\overset{N}{\mathop \sum }}\,\delta {{\mathbf {U}}^{T}}\mathbf {Q}_{n}^{T}\left( \mathop {\int }_{{{V}_{n}}}\mathop {\int }_{{{V}_{m}}}{{\mathbf {T}}_{d}}\alpha \left( \left| \mathbf {{x}'}-\mathbf {x} \right| ,\tau \right) \mathbf {B}_{n}^{T}:\mathbf {D}:\mathbf {B}_{m}^{'}d{V}'dV \right) {{\mathbf {Q}}_{m}}{\dot{\mathbf {U}}}\nonumber \\&-{{\zeta }_{2}}\underset{n=1}{\overset{N}{\mathop \sum }}\,\underset{m=1}{\overset{N}{\mathop \sum }}\,\left( \begin{matrix} \delta {{\mathbf {U}}^{T}}\mathbf {Q}_{n}^{T}\left( \mathop {\int }_{{{V}_{n}}}\mathop {\int }_{{{V}_{m}}}\alpha \left( \left| \mathbf {{x}'}-\mathbf {x} \right| ,\tau \right) {{\mathbf {B}}^{0T}}_{n}:\mathbf {D}:{\mathbf {B}_{m}^{0}}'d{V}'dV \right) {{\mathbf {Q}}_{m}}{{\mathbf {U}}_{0}} \\ \end{matrix} \right) \nonumber \\&-\underset{n=1}{\overset{N}{\mathop \sum }}\,\left( \begin{matrix} \delta {{\mathbf {U}}^{T}}\mathbf {Q}_{n}^{T}\left( \mathop {\int }_{{{V}_{n}}}{{\mathbf {B}}^{g}}_{n}^{T}:{{\varvec{\sigma }}_{0}}:\mathbf {B}_{n}^{g}dV \right) {{\mathbf {Q}}_{n}}\mathbf {U} \\ \end{matrix} \right) =0 \end{aligned}$$

(81)

In addition to Eqs. (54)–(58) and (64), (65), (67) and (68), initial stiffness matrix and geometric stiffness matrix are defined as follows

$$\begin{aligned} \mathbf {K}_{n}^{{{L}^{0}}}={{\zeta }_{1}}\left( {{I}_{yy}}\mathop {\int }_{-1}^{1}{{\mathbf {B}}^{0}}{{_{n}^{b}}^{T}}\left( \xi \right) E{{\mathbf {B}}^{0}}_{n}^{b}\left( \xi \right) \det \mathbf {J}\left( \xi \right) d\xi \right) \end{aligned}$$

(82)

$$\begin{aligned} \mathbf {K}_{nm}^{N{{L}^{0}}}= & {} {{\zeta }_{2}}[ bh~{{I}_{yy}}\mathop {\int }_{-1}^{1}\mathop {\int }_{-1}^{1}\alpha \left( \left| {x}'\left( \xi \right) -x\left( \xi \right) \right| ,\tau \right) ~{{\mathbf {B}}^{0bT}}{{_{n}}}\left( \xi \right) E{{\mathbf {B}}^{0b}}_{m}\left( \xi ' \right) \nonumber \\\times & {} \det \left( \mathbf {J}\left( {{\xi }'} \right) \right) \det \left( \mathbf {J}\left( \xi \right) \right) d\xi ' d\xi \ \end{aligned}$$

(83)

$$\begin{aligned} \mathbf {K}_{n}^{g}=\left( bh\mathop {\int }_{-1}^{1}{\mathbf {B}{_{n}^{g}}}^{T}\left( \xi \right) {{\sigma }_{0}}\mathbf {B}_{n}^{g}\left( \xi \right) \det \left( \mathbf {J}\left( \xi \right) \right) d\xi \right) \end{aligned}$$

(84)

It is known that, for an Euler-Bernoulli beam, the nonlinear strain can be assumed as

$$\begin{aligned} {{\varepsilon }_{nl}}=\frac{1}{2}{{\left( \frac{\partial w}{\partial x} \right) }^{2}} \end{aligned}$$

(85)

$B_{n}^{g}$ is consistent with the nonlinear strain form. Taking into account the defined parameters, the governing viscoelastic buckling equation becomes

$$\begin{aligned}&\left( \mathbf {C}_{total}^{L}+\mathbf {C}_{total}^{NL} \right) \dot{\mathbf {U}}+\left( \mathbf {K}_{total}^{L}+\mathbf {K}_{total}^{NL} \right) \mathbf {U} \nonumber \\&-\left( \mathbf {K}_{total}^{{{L}^{0}}}+\mathbf {K}_{total}^{N{{L}^{0}}} \right) {{\mathbf {U}}_{0}}-\mathbf {K}_{total}^{g}\mathbf {U}=0 \end{aligned}$$

(86)

By numerically solving Eq. (86), the viscoelastic buckling solutions can be acquired. By viscoelastic buckling solution, we mean the condition in which the compressive load is kept constant and as time passes, the displacements increase. There comes a time in which the displacements exceed the assumed buckling condition. This time is called the viscoelastic buckling time. Also, by keeping out the time-related terms and imperfections in Eq. (86) the eigenvalue problem for the elastic buckling of perfect beam would result.

$$\begin{aligned} \left( \mathbf {K}_{total}^{L}+\mathbf {K}_{total}^{NL} \right) \mathbf {U}-\mathbf {K}_{total}^{g}\mathbf {U}=0 \end{aligned}$$

(87)

5 Nano-Scaled Plates

The appropriate formulations are to be introduced for analyzing the bending, vibration, and buckling of nano-scaled plates. As it has been assumed with respect to the beams, in the plate case also the classical plate theory is only taken into account, and other theories can be added to the formulation by following a similar procedure.

Fig. 7

Plate dimensions

5.1 Applying Boundary Conditions for Nano-Scaled Plates

One of the main advantages of finite element integral elasticity approach is the straightforwardness of applying the boundary conditions for a plate (Fig. 7). It is noted that the boundary conditions are applied as they are imposed in conventional finite element methods of classical elasticity. For example, the following commonly used boundary conditions are outlined.

All-sides simply supported plate:

$$\begin{aligned} w(x,y)=0~~~~\text {at}~~~~x=0,l_x \nonumber \\ w(x,y)=0~~~~\text {at}~~~~x=0,l_y \end{aligned}$$

(88)

All-sides clamped plate:

$$\begin{aligned} w\left( x,y \right) ={{w}_{,x}}\left( x,y \right) =0~~~~\text {at}~~~~x=0,l_x \nonumber \\ w\left( x,y \right) ={{w}_{,x}}\left( x,y \right) =0~~~~\text {at}~~~~x=0,l_y \end{aligned}$$

(89)

Two-sides clamped, two-sides free (opposite sides):

$$\begin{aligned} w\left( x,y \right) ={{w}_{,x}}\left( x,y \right) =0~~~~\text {at}~~~~x=0,l_x \end{aligned}$$

(90)

Two-sides simply supported, two-sides clamped (opposite sides):

$$\begin{aligned} w\left( x,y \right) ==0~~~~\text {at}~~~~x=0,l_x \nonumber \\ w\left( x,y \right) ={{w}_{,x}}\left( x,y \right) =0~~~~\text {at}~~~~x=0,l_y \end{aligned}$$

(91)

Interestingly enough, the partial boundary conditions can also be applied fairly easily and with little effort using the current method, for instance, some partial boundary conditions are expressed below.

Two-sides clamped, the other two sides each partially simply supported:

$$\begin{aligned} w\left( x,y \right) ={{w}_{,x}}\left( x,y \right) =0~~~~\text {at}~~~~x=0,l_x \nonumber \\ w\left( x,y \right) =0~~~~\text {at}~~~~y=0,~x=0-l_{x1} \nonumber \\ w\left( x,y \right) =0~~~~\text {at}~~~~y=l_y,~x=0-l_{x2} \end{aligned}$$

(92)

Two-sides simply supported, the other two sides each partially clamped:

$$\begin{aligned} w\left( x,y \right) =0~~~~\text {at}~~~~x=0,l_x \nonumber \\ w\left( x,y \right) ={{w}_{,x}}\left( x,y \right) =0~~~~\text {at}~~~~y=0,~x=0-l_{x1} \nonumber \\ w\left( x,y \right) ={{w}_{,x}}\left( x,y \right) =0~~~~\text {at}~~~~y=l_y,~x=0-l_{x2} \end{aligned}$$

(93)

5.2 Bending of Nano-Scaled Plates

Bending formulations considering the nonlocal integral theory and classical plate theory are presented in the current section. Through the classical plate theory, the following relation is assumed for the strain field of a plate.

$$\begin{aligned} \varvec{\varepsilon }\left( \mathbf {x} \right) =\left\{ \begin{matrix} {{\varepsilon }_{x}} \\ {{\varepsilon }_{y}} \\ {{\gamma }_{xy}} \\ \end{matrix} \right\} =\left\{ \begin{matrix} {{u}_{0,x}} \\ {{v}_{0,y}} \\ {{u}_{0,x}}+{{v}_{0,y}} \\ \end{matrix} \right\} -z\left\{ \begin{matrix} {{w}_{,xx}} \\ {{w}_{,yy}} \\ 2{{w}_{,xy}} \\ \end{matrix} \right\} \end{aligned}$$

(94)

in which, $\varepsilon _x$, $\varepsilon _y$, and $\gamma _{xy}$ are the longitudinal strain, transverse strain, and in-plane shear strain, respectively. Also, $u_0$, $v_0$, and w are the displacements of mid-plane in the x-, y-, and z-directions. By considering the pure bending condition, Eq. (94) becomes

$$\begin{aligned} \varvec{\varepsilon }\left( \mathbf {x} \right) =\left\{ \begin{matrix} {{\varepsilon }_{x}} \\ {{\varepsilon }_{y}} \\ {{\gamma }_{xy}} \\ \end{matrix} \right\} =-z\left\{ \begin{matrix} {{w}_{,xx}} \\ {{w}_{,yy}} \\ 2{{w}_{,xy}} \\ \end{matrix} \right\} ={{\mathbf {B}}_{n}}\left( \mathbf {x} \right) {{\mathbf {d}}_{n}}=z\mathbf {B}_{n}^{p}\left( \mathbf {x} \right) {{\mathbf {d}}_{n}} \end{aligned}$$

(95)

Substituting Eq. (95) into Eq. (34), using Eq. (33) and considering the bending-related terms, for an elastic case, Eq. (34) becomes

$$\begin{aligned}&\delta \Pi ={{\zeta }_{1}}\underset{n=1}{\overset{N}{\mathop \sum }}\,\delta {{\mathbf {U}}^{T}}\mathbf {Q}_{n}^{T}\left( \mathop {\int }_{{{V}_{n}}}\mathbf {B}_{n}^{T}:\mathbf {D}:{{\mathbf {B}}_{n}}dV \right) {{\mathbf {Q}}_{n}}\mathbf {U} \nonumber \\&+{{\zeta }_{2}}\underset{n=1}{\overset{N}{\mathop \sum }}\,\underset{m=1}{\overset{N}{\mathop \sum }}\,\delta {{\mathbf {U}}^{T}}\mathbf {Q}_{n}^{T}\left( \mathop {\int }_{{{V}_{n}}}\mathop {\int }_{{{V}_{m}}}\alpha \left( \left| \mathbf {{x}'}-\mathbf {x} \right| ,\tau \right) \mathbf {B}_{n}^{T}:\mathbf {D}:\mathbf {B}_{m}^{'}d{V}'dV \right) {{\mathbf {Q}}_{m}}\mathbf {U} \nonumber \\&-\underset{n=1}{\overset{N}{\mathop \sum }}\,\left( \delta {{\mathbf {U}}^{T}}\mathbf {Q}_{n}^{T}\mathop {\int }_{{{V}_{n}}}\mathbf {N}_{n}^{T}.\bar{\mathbf {b}}~dV \right) -\underset{n=1}{\overset{N}{\mathop \sum }}\,\left( \delta {{\mathbf {U}}^{T}}\mathbf {Q}_{n}^{T}\mathop {\int }_{{{S}_{{{t}_{n}}}}}\mathbf {N}_{n}^{T}.\bar{\mathbf {t}}~dS \right) =0 \end{aligned}$$

(96)

Substituting the last term of Eq. (95) into Eq. (96) the following relations are defined for local and nonlocal stiffness matrices of the n-th element.

$$\begin{aligned} \mathbf {K}_{n}^{L}={{\zeta }_{1}}\left( \mathop {\int }_{{{A}_{elem}}}\mathop {\int }_{h}\mathbf {B}{{_{n}^{p}}^{T}}:\mathbf {D}:\mathbf {B}_{n}^{p}\det \left( \mathbf {J} \right) {{z}^{2}}dz~d{{A}_{elem}} \right) \end{aligned}$$

(97)

$$\begin{aligned} \mathbf {K}_{nm}^{NL}= & {} {{\zeta }_{2}} [\mathop {\int }_{{{A}_{elem}}}\mathop {\int }_{h}\mathop {\int }_{A_{elem}^{'}}\mathop {\int }_{{{h}'}}\alpha \left( \left| \mathbf {{x}'}\left( \xi ,\eta \right) -\mathbf {x}\left( \xi ,\eta \right) \right| ,\tau \right) z{{'}^{2}}~\mathbf {B}{{_{n}^{p}}^{T}}:\mathbf {D}:\mathbf {B}_{m}^{{{p}'}}\nonumber \\\times & {} \det \left( \mathbf {J} \right) \det \left( {\mathbf {{J}'}} \right) d{z}'~dA_{elem}^{'}dz~d{{A}_{elem}}] \end{aligned}$$

(98)

The total stiffness matrices are also given as Eqs. (57) and (58). Also, the bending governing equations (similar to Eq. (60)) can be solved by the same procedure as that explained in Sect. 4.2.

5.3 Vibration of Nano-Scaled Plates

For analyzing the vibration of nano-scaled plates, the general form of Eq. (62) could be used. For a nano-scaled plate, the local and nonlocal stiffness matrices can be expressed as Eqs. (97) and (98). Also, noting Eq. (62) the element mass matrix and damping matrices can be obtained as

$$\begin{aligned} {{\mathbf {M}}_{n}}=\mathop {\int }_{{{A}_{elem}}}\mathop {\int }_{h}\mathbf {N}_{n}^{T}.\left( \rho {{\mathbf {N}}_{n}} \right) \det \left( \mathbf {J} \right) dzd{{A}_{elem}} \end{aligned}$$

(99)

$$\begin{aligned} \mathbf {C}_{n}^{L}={{\zeta }_{1}}\left( \mathop {\int }_{{{A}_{elem}}}\mathop {\int }_{h}{{\mathbf {T}}_{d}}\mathbf {B}{{_{n}^{p}}^{T}}:\mathbf {D}:\mathbf {B}_{n}^{p}\det \left( \mathbf {J} \right) {{z}^{2}}dz~d{{A}_{elem}} \right) \end{aligned}$$

(100)

$$\begin{aligned} \mathbf {C}_{nm}^{NL}= & {} {{\zeta }_{2}}[ \mathop {\int }_{{{A}_{elem}}}\mathop {\int }_{h}\mathop {\int }_{A_{elem}^{'}}\mathop {\int }_{{{h}'}}\alpha \left( \left| \mathbf {{x}'}\left( \xi ,\eta \right) -\mathbf {x}\left( \xi ,\eta \right) \right| ,\tau \right) {{\mathbf {T}}_{d}}~z{{'}^{2}}\mathbf {B}{{_{n}^{p}}^{T}}:\mathbf {D}:\mathbf {B}_{m}^{{{p}'}} \nonumber \\\times & {} \det \left( \mathbf {J} \right) \det \left( {\mathbf {{J}'}} \right) d{z}'~dA_{elem}^{'}dz~d{{A}_{elem}}] \end{aligned}$$

(101)

The total structural matrices can also be calculated by Eqs. (66)–(68). Also, the eigenvalues and eigenfunctions of vibration might also be given by applying the same procedure as that explained in Sect. 4.3.

5.4 Buckling of Nano-Scaled Plates

Buckling analysis of nano-scaled plates can also be carried out by considering the buckling form of general variational Eq. (34) as Eq. (81). The nonlinear strain for a plate is assumed as

$$\begin{aligned} {{\varepsilon }_{nl}}=\frac{1}{2}\left\{ \begin{matrix} w_{,x}^{2} \\ w_{,y}^{2} \\ 2{{w}_{,x}}{{w}_{,y}} \\ \end{matrix} \right\} \end{aligned}$$

(102)

It is seen that the stiffness matrices are given by Eqs. (97) and (98), and geometric stiffness matrix and initial stiffness matrices are given as follow

$$\begin{aligned} \mathbf {K}_{n}^{{{L}^{0}}}={{\zeta }_{1}}\left( \mathop {\int }_{{{A}_{elem}}}\mathop {\int }_{h}{{\mathbf {B}}^{0}}{{_{n}^{p}}^{T}}:\mathbf {D}:{{\mathbf {B}}^{0}}_{n}^{p}\det \left( \mathbf {J} \right) {{z}^{2}}dz~d{{A}_{elem}} \right) \end{aligned}$$

(103)

$$\begin{aligned} K_{nm}^{N{{L}^{0}}}= & {} {{\zeta }_{2}}[\mathop {\int }_{{{A}_{elem}}}\mathop {\int }_{h}\mathop {\int }_{A_{elem}^{'}}\mathop {\int }_{{{h}'}}\alpha \left( \left| \mathbf {{x}'}\left( \xi ,\eta \right) -\mathbf {x}\left( \xi ,\eta \right) \right| ,\tau \right) z{{'}^{2}}~{{\mathbf {B}}^{0}}{{_{n}^{p}}^{T}}:\mathbf {D}:{{\mathbf {B}}^{0}}_{m}^{{{p}'}} \nonumber \\\times & {} \det \left( \mathbf {J} \right) \det \left( {\mathbf {{J}'}} \right) d{z}'~dA_{elem}^{'}dz~d{{A}_{elem}}] \end{aligned}$$

(104)

$$\begin{aligned} \mathbf {K}_{n}^{g}=\mathop {\int }_{{{A}_{elem}}}\mathop {\int }_{h}{{\mathbf {B}}^{g}}_{n}^{T}:{{\varvec{\sigma }}_{0}}:\mathbf {B}_{n}^{g}dz~d{{A}_{elem}} \end{aligned}$$

(105)

in which, ${{\varvec{\sigma }}_{0}}$ is the initial stress which has the following form

$$\begin{aligned} {{\varvec{\sigma }}_{0}}=\left[ \begin{matrix} \sigma _{xx}^{0} &{} \sigma _{xy}^{0} \\ \sigma _{yx}^{0} &{} \sigma _{yy}^{0} \\ \end{matrix} \right] \end{aligned}$$

(106)

Considering the mentioned equations, Eqs. (86) and/or (87) are used for nano-scaled plates to solve the viscoelastic/elastic buckling problems.

6 Numerical Examples and Discussions

In this section, the bending, buckling, and vibration of nano-scaled beams and plates are studied using the presented finite element nonlocal integral method. Due to a better correlation between current results with those of nonlocal differential elasticity, the Bessel kernel is used in the following analysis. The assumed kernel is [6, 13]

$$\begin{aligned} \bar{\alpha }\left( \left| \mathbf {x}-\mathbf {{x}'} \right| ,~\tau \right) =2\pi {{\left( {{e}_{0}}a \right) }^{2}}{{K}_{0}}\left( \frac{\left| \mathbf {x}-\mathbf {{x}'} \right| }{{{e}_{0}}a} \right) \end{aligned}$$

(107)

6.1 Elastic Beam and Plate Bending

In this section, the bending of nano-beams and nano-plates are analyzed using some examples. It is noted that in the current section, the constitutive equation (2) (one-phase nonlocal integral elasticity theory) has been adopted for implementing the finite element nonlocal integral elasticity method.

6.1.1 Bending of Nano-Scaled Beams

The bending of nonlocal Euler-Bernoulli nano-scaled beams is investigated. Results are obtained using the approach explained in Sect. 4.2. The Hermite element (see Sect. 3.3) is assumed in the analysis, and for the numerical integration, the Gauss-Legendre quadrature rule is used by considering three Gauss points.

Fig. 8

Variations of non-dimensional deflection with the nonlocal parameter for both-sides simply supported Euler-Bernoulli nano-scale beam [6] ($l=$ 10 nm and $h=$0.1 nm)

Figure 8 shows the non-dimensional maximum deflection ($w/w_L$) for two-sides simply supported beam, under $\bar{k}=1$ and $\bar{q}=1$ loading. $\bar{k}=F{{l}^{2}}/EI~$ is the non-dimensional central point load parameter, and $\bar{q}=q{{l}^{3}}/EI$ is the non-dimensional uniformly-distributed load parameter. The results of the finite element nonlocal integral elasticity (nonlocal integral elasticity theory NLIET) are compared with those of Wang et al. [38] (for distributed load) and Wang and Liew [39] (for point load) based on the nonlocal differential elasticity theory (NLDET). It is observed that for a beam with simply supported boundary conditions subjected to a point load, the nonlocal differential elasticity theory could not predict the bending deflection properly. However, both the differential and integral theories show a rise in deflection by increasing the nonlocal parameter for uniformly-distributed load case.

Figure 9 shows the variation of maximum deflection with the nonlocal parameter for two-sides clamped boundary condition ($\bar{k}=1$, $\bar{q}=1$). It is seen that in this case the nonlocal differential elasticity has not captured the effect of nonlocality by considering distributed load. However, the nonlocal integral theory shows an increase in deflection by considering the nonlocal parameter, for both loading conditions.

Fig. 9

Variations of non-dimensional deflection with the nonlocal parameter for both-sides clamped Euler-Bernoulli nano-scale beam [6] ($l=$ 10 nm and $h=$0.1 nm)

6.1.2 Bending of Nano-Scaled Plates

Figure 10 show the variations of deflection for the midpoint of a nano-scaled simply supported plate under the uniformly-distributed loading ${{q}_{0}}=1$ nN/nm. The assumed plate have properties of $l=$ 10 nm, $E=30\times {{10}^{3}}$ nN/nm$^{2}$, and $\nu =0.3$. The Adini-clough element type is used for modeling the plate and for numerical integration, the Gauss-Legendre quadrature method assuming three integration points in each direction is considered. Also, the results of the current study have been compared with those of Aghababaei and Reddy [40] based on the nonlocal differential elasticity theory. As it is seen, by increasing the nonlocal parameter, both the integral and differential theories predict the decrease in the stiffness of the plate. However, the increase in deflection is more pronounced for the nonlocal integral elasticity method. It might have occurred because the nonlocal differential elasticity theory has been extracted from the general integral form and cannot satisfy the force boundary conditions properly [6].

Fig. 10

Variations of non-dimensional deflection with the nonlocal parameter for all-sides simply supported nano-scale plate ($l/b=1$) under distributed load

Figure 11 shows the variation of midpoint deflection of the all-sides simply supported nano-scaled plate with nonlocal parameter under point load ${{F}_{0}}=1$ nN. It is seen that the increase in deflection is more pronounced for nonlocal differential elasticity case in comparison with the nonlocal integral elasticity.

Fig. 11

Variations of non-dimensional deflection with the nonlocal parameter for all-sides simply supported nano-scale plate under point load

6.2 Elastic Beam and Plate Vibration

Free vibration of nano-beams and nano-plates are studied using the finite element nonlocal integral elasticity method and considering the two-phase nonlocal constitutive equation (Eq. (4)). The convergence study is carried out for obtaining the optimum number of elements. The results are then compared with those available in the literature, and finally, the effects of various parameters are investigated on free vibration behavior. For the subject beam $E=1$ TPa and $\rho =2000$ kg/m$^3$, and for the plate $E=1$ TPa, $\nu =0.16$ and $\rho =2250$ kg/m$^3$.

6.2.1 Free Vibration of Nano-Scaled Beams

The free vibration of nano-scaled beams is investigated through the assumption of Euler-Bernoulli beam theory. Thus, the procedure of Sect. 4.3 has been adopted for elastic beams, and Hermite beam elements have been considered (see Sect. 3.3). For the numerical integration, three integration points are used for Gauss-Legendre quadrature method. Dimensions of the beam are as $l=10$ nm, $h=1$ nm and $b=0.5$ nm.

Table 1 shows the convergence study for free vibration of nano-scaled Euler-Bernoulli beam considering two types of boundary conditions. It is seen that the convergence rate for the local case ($\tau =0$) is faster than the nonlocal case. This behavior can be explained by further investigation of the nonlocal kernel function characteristics. For a given reference point, the value of kernel function is maximum, i.e.g.oes to infinity, on that point and it decreases by moving further from it. So, for accurately capturing the nonlocal effects near the reference point, several elements are needed. Besides, by decreasing the size of elements the accuracy of numerical integrations increases.

Table 1 Convergence study of natural frequency ($\bar{\omega }=l\sqrt{\omega /{{C}_{0}}}$, ${{C}_{0}}=\sqrt{EI/\rho A}$) by nonlocal Euler-Bernoulli beam theory [13]

Table 2 shows the comparison of the natural frequencies based on the nonlocal integral theory with those of differential elasticity theory which have been reported by Lu et al. [41], Reddy [42] and Ghannadpour [43]. It is seen that the nonlocal differential theory cannot predict the softening effect of the nonlocal parameter for the cantilever beam (considering the fundamental natural frequency). As it has been said, the current discrepancy might have been caused by the fact that the nonlocal differential theory is extracted from the integral one under certain assumptions and in the region far from the boundaries. However, there has been a generally good agreement between the results.

Table 2 Comparison of non-dimensional natural frequencies ($\bar{\omega }=l\sqrt{\omega /{{C}_{0}}}$, ${{C}_{0}}=\sqrt{EI/\rho A}$) for nonlocal Euler-Bernoulli beam

Figure 12 shows the variations of the fundamental natural frequency with the nonlocal parameter considering different length to thickness ratio for cantilever boundary conditions. It is seen that, by increasing the nonlocal parameter value, natural frequency decreases. Also, it is observed that for larger values of l/h, the sensitivity of frequency to $e_{0}a$ decreases. This might be due to the fact that, the effects of nonlocality are more pronounced near the boundaries, so for shorter beams these effects can increase.

Fig. 12

Fundamental frequency variations with the nonlocal parameter considering different length to thickness ratios for cantilever nano-scaled beam [13]

Figure 13 shows the effect of length to thickness ratio on the natural frequency considering different nonlocal parameters and various boundary conditions. It is seen that regardless of local/nonlocal effects, the increase in l/h has led to the reduction of natural frequencies. The highest reduction belongs to both-sides clamped boundary condition and the lowest to cantilever.

Fig. 13

Variations of the fundamental natural frequency with length to thickness ratio for nano-scaled beams [13]

6.2.2 Free Vibration of Nano-Scaled Plates

The classical plate theory is used to investigate the free vibration of nano-scaled plates [16]. The procedure of Sect. 5.3, in conjunction with Adini-Clough element types (3.3), have been adopted. Three points in each direction have been assumed for numerical integration. It is noted that the length and thickness of the square plate are 10 nm and 0.34 nm, respectively.

Convergence study of a square plate considering ${{e}_{0}}a=1$ nm and all-sides simply supported boundary condition are shown in Table 3. Equal size square elements have been used for mesh allocation. It is seen that the results converge for 45 $\times$ 45 elements.

Table 3 Convergence study of free vibration considering a simply-supported square nano-scaled plate (${{e}_{0}}a=1$ nm)

Table 4 shows the comparison of non-dimensional fundamental natural frequency based on finite element integral nonlocal elasticity with those of nonlocal differential theory. Results of Pradhan and Phadikar [44] are obtained by using the Navier solution and nonlocal classical plate theory. Murmu and Pradhan [45] have also used nonlocal classical plate theory whereas Ansari et al. [46] have implemented nonlocal first-order shear deformation theory. Besides, the results of molecular dynamics have been included in the table. As it is predictable, considering the non-locality leads to some discrepancies between the results which are relatively more pronounced for all-sides simply supported boundary condition. By comparing the results of current study with those of molecular dynamics, it can be concluded that for the subject case the value of nonlocal parameter lies between 0 and 1 nm.

Table 4 Comparison of the results for free vibration of a square nano-scaled plate (${{\omega }_{ND}}=\omega {{l}^{2}}\sqrt{\rho h/D}$)

Figure 14 shows the effect of nonlocal parameter on the natural frequency of square nano-scaled plate considering different length to thickness ratios. As observed, by increasing the nonlocal parameter natural frequency decrease. This softening effect is more pronounced for the lower values of the plate length to thickness ratio, i.e., the variation of natural frequency with l/h is less noticeable for larger plates. This might be due to the importance of nonlocal effects near the boundaries, that is to say, for the smaller plates, the boundary conditions play an important role in nonlocal characteristics of the structure. It is noted that by increasing the length of the structure the $e_{0}a/l$ value diminishes for a given value of $e_{0}a$.

Fig. 14

Effect of the nonlocal parameter on the natural frequency of square plate with all-sides simply supported, all-sides clamped and cantilever boundary condition ($h=$ 0.34 nm) [16]

Figure 15 shows the variations of the natural frequency with the length of the square plate for different boundary conditions considering $e_{0}a=1$ nm. It is seen that, by increasing the length the natural frequency decreases. Also, decrease in natural frequency is more steep for all-sides clamped boundary condition in comparison with all-sides simply supported and clamped free conditions.

Fig. 15

Effect of the length of the square plate on the natural frequency for $e_{0}a=1$ nm and $h=0.34$ nm

Figure 16 shows the effect of aspect ratio on free vibration of rectangular nano-scaled plate considering all-sides simply supported boundary condition. As it is seen, by increasing the aspect ratio, the natural frequencies decrease.

Fig. 16

Effect of the aspect ratio of the rectangular plate on the natural frequency considering all-sides simply supported boundary condition [16]

6.3 Elastic Beam and Plate Buckling

The buckling of nano-beams and nano-plates are investigated employing the finite element nonlocal integral elasticity method and considering the single-phase nonlocal constitutive equation (Eq. (2)).

6.3.1 Buckling of Nano-Scaled Beams

The procedure of Sect. 4.4 has been employed for the buckling analysis of Euler-Bernoulli nano-scaled beams. Hermite beam elements (see Sect. 3.3 ) are used and the beam properties are $E=1$ TPa, $l=20$ nm, $b=t=1$ nm. Table 5 shows the convergence study for a two-sides clamped beam considering ${{e}_{0}}a=1$ nm and 2 nm.

Table 5 Convergence study for buckling of nonlocal Euler-Bernoulli beam considering two-sides clamped boundary condition

Figures 17 and 18 show the variations of buckling load ratio with the nonlocal parameter for both-sides simply supported and clamped boundary conditions, respectively. Also, the results of the current study have been compared with those based on the nonlocal differential elasticity [7] considering the Timoshenko beam theory. It is seen that, by increasing the nonlocal parameter buckling load decreases.

Fig. 17

Variations of buckling load ratio with the nonlocal parameter for both sides simply supported Euler-Bernoulli beam [7]

Fig. 18

Variations of buckling load ratio with the nonlocal parameter for both sides clamped Euler-Bernoulli beam [7]

Figures 19 and 20 show the variations of buckling load with length to thickness ratio for different boundary conditions considering ${{e}_{0}}a=1$ nm. It is observed that, by increasing the length to thickness ratio, the discrepancy between the results of the current method with those of local elasticity and differential elasticity theory decreases. Also, it is seen that the effect of the nonlocal parameter is more pronounced for shorter beams.

Fig. 19

Variations of buckling load with length to thickness ratio for ${{e}_{0}}a=1$ nm considering both sides simply supported beam [7]

Fig. 20

Variations of buckling load with length to thickness ratio for ${{e}_{0}}a=1$ nm considering both sides clamped beam [7]

6.3.2 Buckling of Nano-Scaled Plates

The buckling of classical plates are analyzed using the finite element nonlocal integral method, and the results are compared with those of nonlocal differential elasticity theory. The Adini-Clough element has been used for the analysis (see Sect. 3.3).

Figure 21 shows the variations of buckling load ratio with the length of square plate for all-sides simply supported boundary condition considering ${{e}_{0}}a=1$ nm and ${{e}_{0}}a=2$ nm. The results of the current study have been compared with those obtained by Levy method based on nonlocal differential elasticity theory [47]. It is seen that by increasing the length of the plate, the nonlocal effects decrease. These effects in smaller dimensions result in more reduction of buckling loads. In other hands, by increasing the ${{e}_{0}}a$ discrepancy between the results of the current study with those of nonlocal differential elasticity increase. This might be due to the fact that by increasing the value of ${{e}_{0}}a$, the effects of boundary conditions can play a more important part.

Fig. 21

Variations of non-dimensional buckling load with the length of the square plate considering all-sides simply supported boundary conditions

Figure 22 shows the variations of buckling load ratio with the length of the plate for ${{l}_{x}}/{{l}_{y}}=1$ and ${{l}_{x}}/{{l}_{y}}=2$ considering ${{e}_{0}}a=1$ nm and all-sides simply supported boundary conditions.

Fig. 22

Variations of non-dimensional buckling load with the length of the plate for different values of aspect ratio considering all-sides simply supported boundary condition

Figure 23 shows the effect of nonlocal parameter on the buckling ratio of nano-scaled plate considering all sides simply supported, and all sides clamped boundary conditions. It is seen that for all sides clamped boundary condition, the reduction in buckling load is more pronounced in comparison with the all sides simply supported boundary conditions. It is due to the fact that, stronger boundary conditions lead to more pronounced nonlocal effects near the boundaries.

Fig. 23

Effect of the nonlocal parameter on the buckling load ratio for all-sides clamped and all-sides simply supported nano-scaled plate (${{l}_{x}}={{l}_{y}}=1.5$ nm)

6.4 Viscoelastic Free Vibration

The free vibration of nano-scaled beams and plates are studied using the finite element nonlocal integral elasticity approach considering the Kelvin-Voigt viscoelastic model. Properties of the beam are $E=1$ TPa and $\rho =2000$ kg/m$^3$, and for the plate $E=1$ TPa, $\nu =0.16$ and $\rho =2250$ kg/m$^3$.

6.4.1 Free Vibration of Viscoelastic Nano-Scaled Beams

For obtaining the results of the viscoelastic free vibration of nano-scaled beams, the procedure explained in Sect. 4.3 have been adopted. Hermite type elements have been used for meshing the beam (see Sect. 3.3). The complex eigenvalues of the current study based on the finite element nonlocal integral method are compared with those of Lu et al. [41] and Lei et al. [20] based on the nonlocal differential elasticity theory and those obtained by Abaqus/CAE commercial software (local viscoelasticity) in Table 6 [15]. The results have been extracted for different values of nonlocal and viscoelastic parameters considering various boundary conditions. The complex eigenvalues obtained by the finite element integral nonlocal method is lower than those of the nonlocal differential theory. Also, both the real and imaginary parts of the eigenvalue decrease by increasing the nonlocal parameter for both methods, except in the case of cantilever boundary condition for the nonlocal differential theory.

Table 6 Comparison of the complex eigenvalues ($\bar{\omega }=l\sqrt{\omega /{{C}_{0}}}$, ${{C}_{0}}=\sqrt{EI/\rho A}$) for free vibration of nonlocal viscoelastic Euler-Bernoulli beam [15]

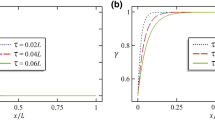
Figures 24 and 25 show the variations of real and imaginary parts of non-dimensional eigenvalues, (non-dimensionalized by local elastic natural frequency ${{\omega }_{LE}}$) with the viscoelastic parameter considering different values of nonlocal parameter and various boundary conditions. It is seen that by increasing the viscoelastic parameter the real part of complex eigenvalues decreases and the imaginary part increases. Also, it is observed that for the both-sides clamped boundary condition, in comparison with other boundary conditions, the effect of the viscoelastic parameter is more noticeable. However, by increasing the nonlocal parameter the change in eigenvalues due to viscoelastic parameter decreases.

Fig. 24

Variations of the real part of the frequency with viscoelastic parameter for Euler-Bernoulli nano-scaled beam for ${{e}_{0}}a=0$ nm and ${{e}_{0}}a=1$ nm [15]

Fig. 25

Variations of the imaginary part of the frequency with viscoelastic parameter for Euler-Bernoulli nano-scaled beam for ${{e}_{0}}a=0$ nm and ${{e}_{0}}a=1$ nm [15]

Fig. 26

Effects of the nonlocal parameter on the complex eigenvalues for both sides simply supported Euler-Bernoulli beam [15]

Figure 26 shows the effect of nonlocal parameter on the real and imaginary parts of eigenvalues for viscoelastic nonlocal Euler-Bernoulli beam considering both sides simply supported boundary condition and various viscoelastic parameters and beam lengths. It is seen that by increasing the value both the real and imaginary parts of frequency decrease. For shorter beams, the variations of the eigenvalues are relatively more pronounced, because by decreasing the length of the beam, the effects of boundary conditions become more important and nonlocality effects are stronger near the boundaries. Besides, for shorter beams, the effects of viscoelastic parameter on the imaginary part become more noticeable.

6.4.2 Free Vibration of Viscoelastic Nano-Scaled Plates

For analyzing the free vibration behavior of viscoelastic square nano-scaled plates, the procedure explained in Sect. 5.3 is followed. The plate has been meshed by Adini-Clough type elements (see Sect.3.3), and it has length and thickness of 10 and 0.34 nm, respectively. Also, in the current section terms of diagonal matrix ${{\mathbf {T}}_{d}}$ (viscoelastic parameters) are assumed to be equal and shown by $T_d$.

Comparison between the fundamental eigenvalues based on the nonlocal integral theory with those of nonlocal differential theory [48] considering all sides simply supported boundary condition is shown in Table 7. It is seen that for a local case ($\tau =0$), the agreement between the results is excellent. By increasing the nonlocal parameter, the results start to differentiate.

Table 7 Comparison between the fundamental natural frequency (GHz) of nano-scaled plates based on nonlocal integral theory and nonlocal differential theory considering all sides simply supported boundary condition

Figure 27 shows the effect of nonlocal parameter on the free vibration behavior of viscoelastic classical nano-scaled plate for different viscoelastic and length parameters considering all sides simply supported boundary condition. It is seen that by increasing the value of $e_{0}a$, both the real and imaginary parts of eigenvalues decrease and this effect is more pronounced for smaller plates. Also, the decrease in the imaginary part due to increase in nonlocal parameter is more pronounced for larger values of $T_d$.

Fig. 27

Variations of the complex eigenvalues with nonlocal parameter for all-sides simply supported plate considering different viscoelastic parameters

Figure 28 shows the variations of real and imaginary parts of non-dimensional eigenvalues (non-dimensionalized by the natural frequency of local elastic plate) with the viscoelastic parameter considering different boundary conditions for ${{e}_{0}}a=1$ nm. It is observed that by increasing the value of $T_d$, the real part of eigenvalues decrease and imaginary part increase. Besides, this variation is more pronounced for all-sides clamped boundary condition.

Fig. 28

Variations of the complex eigenvalues for a nano-scaled plate with the viscoelastic parameter for different boundary conditions

7 Conclusions

In this chapter, a finite element method based on the nonlocal integral theory has been developed to study the mechanical behavior of nano-scaled beams and plates. The constitutive equation has been obtained considering the nonlocal integral theory and viscoelastic properties. Then, Hamilton’s principle has been adopted for deriving the formulations and preparing the finite element foundation. Despite the simplicity of non-local differential theory in some aspects, it has been extracted from the more general nonlocal integral theory under certain conditions, thus it can only manage some limited problems (e.g. simple geometries, boundary conditions, and certain kernel types). However, the method presented in the current chapter can be used for modeling a broad range of problems, including complex geometries, various boundary conditions, and different kernel types. For instance, by using the finite element nonlocal theory the force boundary conditions can be analyzed properly for nano-scaled plates. In addition, the paradox, which has been seen in some cases considering the nonlocal differential theory, does not arise in the current method.

In previous sections, the formulations for studying bending, buckling, and vibration of nano-scaled beams and plates have been presented, and some examples have been discussed for understanding the effects of non-local parameters, geometrical parameters, boundary conditions and viscoelastic effects on the corresponding mechanical behavior.