The Importance of Factorial Design of Experiments in Functional Nanomaterials Preparation and Performance

Abstract

The experimental planning and design are important parts for successful performance and result analysis in a project. Both for industry and academic settings, there is the constant need to analyze the influence of many variables in the different types of responses. Traditionally, the influence of different variables in the experimental outcome has been analyzed by changing “one factor at a time”, which is usually described as univariate or OFAT approach. However, unless all variables are close to their optimum value, there is no guarantee that this approach will lead to the best optimized outcome. Additionally, the OFAT approach can lead to the implementation of an excessive number of experiments, which usually increases the expenses related to the project. Pursuing to analyze how the synergy between different variables can influence the experimental outcomes, there is the multivariate approach, where two or more variables are changed simultaneously enabling the experimentalist to analyze the beneficial or antagonistic effect of this combination of variables in the experimental outcome. Moreover, the multivariate approach may improve the chances to find the best outcome possible with the conduction of a fewer number of experiments. In this sense, this chapter introduces the concept of factorial design of experiments, a multivariate approach based on choosing two or more levels for multiple variables, calculating the effects of each variable individually and of each possible combination of variables, obtaining a model from these results, applying this model to predict untested conditions and judge the statistic significance of the model. The examples presented in the chapter will all be focused on the preparation and performance of nanomaterials. For instance, how the concentrations of different precursors can influence the particle size of colloidal silica nanoparticles. Or how different variables, such as, time, temperature and reagents concentration can influence the thickness of manganese sulfide (MnS) thin films. The chapter begins providing the definition of the basic terms underlying the factorial design, then, it presents examples from literature applying factorial designs starting with the simpler ones, such as 2³. Then, the chapter evolves presenting optimization and response surface methodologies factorial designs, for instance, central composite, Box-Behken, and Doehlert designs. Finally, the chapter presents tables with references from papers published in the period from 2015 to 2020. In each one of them, the factorial design of experiments was used for the development of functional materials applied in nanoparticles preparation, drug delivery and encapsulation, wastewater remediation, and solar cells development. With this chapter, the author hopes to introduce a powerful and underexplored statistical tool to scientists, engineers, and all practitioners of nanomaterials science. Focus will be placed on how they can benefit from the concepts and examples presented, and possibly adapt them for their own projects, instead of relying on heavy mathematical notations and calculations.

1 Introduction

The development of functional materials requires accurate control of each step in their production. In this sense, to be able to test a broader range of experimental conditions by performing a lower number of experiments is desirable. So, the factorial design of experiments is a set of statistical concepts intended to optimize specific properties by taking advantage of a multivariate approach. In this approach, the interaction between different factors is interpreted holistically. The design of experiments allows the research to judge which factors are statistically significant by calculating their effects on the property to be optimized. Moreover, empirical models can be obtained, allowing the researcher to predict how that specific property will behave in untested conditions.

The ability to predict results based on an empirical model opens up an array of opportunities and saves time and resources from the researcher. So, this chapter aims to show from the scientific literature examples how the factorial design of experiments has widely been applied to the development and performance of functional materials.

This chapter is intended to fulfill the needs of readers with different knowledge levels about the design of experiments, from the beginner to the experienced reader.

That being said, readers from different familiarity levels have the opportunity to focus their attention on different parts of the chapter. For the beginner ones, it is recommended to start reading the chapter from Sect. 2. Since in this part, the essential concepts and terminology of factorial design are introduced. Then, a step by step 2³ factorial design is performed. This 2³ factorial design is developed very comprehensively, aiming that even a beginner reader can try to adapt the design to their own experimental situation, without using black-box programs. This part appreciates the statistical formalism whenever it is necessary. In such a way, it can sound intimidating at first sight. However, with attention and persistence, the reader can benefit from the knowledge.

Since Sect. 2 is very comprehensive. Consequently, it is also extensive. So, if a reader is already familiar with all the terminology, structure, and calculations related to factorial designs, he/she is welcome to skip this full part and start straight on Sect. 3. There, the reader will find analyses of literature examples where the factorial design of experiments and response surface methodologies were applied to the context of materials preparation and performance. This part appreciates a critical analysis of each research paper by remarking the steps followed by the authors.

Finally, in Sect. 4, readers will find references from papers published in the period from 2015 to 2020. In each one of them, the factorial design of experiments was applied to the development of four types of functional materials. They are nanoparticles preparation, drug encapsulation and delivery, wastewater remediation, and solar cell development.

2 The Fundamentals and Statistical Basis of the Factorial Design of Experiments

2.1 Factorial Design of Experiments: Initial Concepts and Terminology

The experimental planning and design are essential parts for successful performance and analysis of results in a project. Both for industry and academic settings, there is a constant need to analyze the influence of many factors in the different types of responses. Traditionally, the impact of different factors in the experimental outcome has been analyzed by changing “one factor at a time,” which is usually described as a univariate or OFAT approach.

For instance, suppose that a research group is aiming to maximize the yield of a certain chemical reaction, and they know that the yield can be affected by factors such as pH, temperature, and catalyst concentration. From previous literature knowledge, the scientists figured out that this reaction has been described to occur in the following ranges for each factor, as presented in Table 1.

Table 1 Matrix of experiments showing the factors and their respective lower and upper limits

According to the OFAT approach, they would perform a series of experiments varying the pH and keeping temperature and catalyst concentration constant. For instance, by fixing the temperature at 85 $^\circ{\rm C}$, the catalyst concentration at 5 × 10^–4 mol L⁻¹, and making the pH equal to 8, 10, 12, and 14 units.

Next, they would vary the temperature and keep the pH and catalyst concentration constant. For instance, by fixing pH equal to 14, catalyst concentration at 5 × 10^–4 mol L⁻¹, and making the temperature equal to 25, 50, 70, and 85 $^\circ{\rm C}$.

Then, they would vary catalyst concentration and keep pH and temperature constant. For instance, by fixing pH equal to 14, temperature at 85 $^\circ{\rm C}$, and making catalyst concentration equal to 1 × 10^–4, 2.5 × 10^–4, 3.5 × 10^–4, and 5 × 10^–4 mol L⁻¹.

There are potential flaws associated with this OFAT approach. The first one is related to choosing the values for the factors that will remain fixed [1]. Notice that, whenever fixing the pH and catalyst concentration, the researchers always chose to fix them at the uppermost level possible. This choice could have been determined by a preconceived idea that maximizing factor values always are going to lead to a yield maximization, which is not always true.

Second, this OFAT approach could ignore potential effects related to the interaction of two or more factors being varied at the same time [1]. For instance, the yield could be maximized at pH 11, 30 $^\circ{\rm C}$, and catalyst concentration equal to 1.5 × 10^–4 mol L⁻¹. This condition was not performed in the OFAT approach adopted, so the researchers would not be aware of the yield maximization at this set of conditions.

A third potential flaw could be related to the large number of experiments performed [1]. In general, a higher number of experiments represent higher consumption of chemicals, analysis time, production of waste, and, consequently, a higher total cost. In this sense, an approach that offers useful trends and conclusions with a lower amount of experiments is always preferred. So, in the next section, we will see how this experimental approach could be redesigned according to the factorial design of experiments. And how the factorial design could potentially decrease the chance of each of these flaws to occur.

2.2 Planning According to the Factorial Design of Experiments

Pursuing to analyze how the interaction between different variables can influence the experimental outcomes, there is the multivariate approach. Where two or more variables are changed simultaneously, enabling the researcher to analyze the beneficial or antagonistic effect of this interaction of variables in the experimental outcome. Moreover, the multivariate approach may improve the chances to find the best result possible with the conduction of a fewer number of experiments.

Before we start redesigning the series of experiments shown in the previous section, we should define the terms commonly related to the factorial design of experiments. The first term is factor. Factors, as seen in the previous section, are the variables that would be varied across the experimental design. So, according to the situation we are analyzing, three factors have been studied, they are pH, temperature, and catalyst concentration.

The second term is the response variable, which is the response the researchers are aiming to observe by performing the experiments. In the example presented, the yield is the response variable. It is important to say that experimental designs can have more than one response variable.

The values each factor will adopt will be called levels. For instance, let's suppose that the temperature will be fixed in their lowest and highest values, so, respectively, 25 and 85 $^\circ{\rm C}$. In this case, 25 and 85 $^\circ{\rm C}$ are called the levels of the temperature factor. If only two levels are adopted for each factor, then the factorial design is called a two-level factorial design. Now, supposing that the scientist had chosen three levels for each variable, in that case, the factorial design would be called three-level factorial design. The levels could either be quantitative or qualitative. In case qualitative levels are chosen, it is necessary to consistently order them in such a way that a certain level is defined as the lower level, and the other one is the upper level, taking the two-level factorial design as an example.

The effects are how single factors or the interaction of two or more factors would influence the value obtained for the response variable. For instance, among the three factors studied, one of them, for instance, temperature, may have a higher influence on the response variable. Whereas, other factors may be concluded to be insignificant to change the response variable. The total number of possible effects will be dependent on how many factors the experimental design has.

In the studied example, as there are three factors, each factor will have its individual effect. Then, the design can have secondary effects, which will arise from the interaction of two factors at a time. So, the secondary factors would be pH-Temperature, pH-Catalyst Concentration, and Temperature-Catalyst Concentration. Finally, in models having three or more factors, tertiary effects are predicted, which are obtained by the combination of three variables at a time. In the studied example, the only tertiary effect would be pH-Temperature-Catalyst Concentration. If the design had four factors, it would have more tertiary effects and one quaternary effect. In conclusion, this three-factor, two-level experimental design has three primary effects, three secondary effects, and one tertiary effect.

A factorial design is the experimental design comprising all levels of each factor studied varied in a multivariate manner, in such a way that allows the interaction effects to be calculated. In general, the factorial designs are named according to how many factors they have and how many levels each factor has. A common representation for the factorial design name is s^k, where k is equal to the number of factors, and s is how many levels each factor has. In the studied example, which has three factors, and two levels for each one of them, this can be called to be a 2³ factorial design.

The s^k representation also indicates the minimum number of experiments without replicas to be performed to be considered a full s^k factorial design. To figure out the number of experiments it is necessary to solve the exponential equation shown in the s^k representation, for instance, a 2³ factorial design would require a minimum of 2³ = 8 different experimental conditions to be considered complete.

Another important concept is the coded levels. For calculating the effects and their statistical significance, matrix calculations will be necessary. In this sense, each level, whether it is quantitative or qualitative, should be normalized according to a common scale. In general, this scale ranges from −1 to +1. In the case of two-level factorial design, the lower limit is normalized as −1, and thus, the upper limit is normalized as +1. So, Table 1 could be improved to include the coded values between parenthesis, as shown in Table 2.

Table 2 The factors with their respective limits represented as coded (in parenthesis) and uncoded values

Matrix of experiments is the matrix that describes each experiment to be performed, according to the combination of the coded values for each factor. For instance, for the example given, as shown in Table 3.

Table 3 Matrix of experiments

Translating the matrix of experiments from the coded values to the original values, one can say that the experiment number 1 is performed with pH = 8, Temperature = 25 $\mathrm{^\circ{\rm C} }$, and catalyst concentration = 1 × 10^–4 mol L⁻¹. Taking another example, experiment 7 is performed at pH = 8, Temperature = 85 $\mathrm{^\circ{\rm C} }$, and catalyst concentration = 5 × 10^–4 mol L⁻¹.

The matrix of results is the one that summarizes the values observed for the response variable for each one of the experiments performed, as shown in Table 4.

Table 4 Matrix of results

After being introduced to the essential vocabulary and concepts about factorial design, we are ready to start seeing how the factorial design is structured.

2.3 The Structure of the Factorial Design

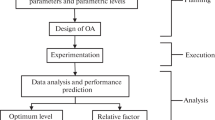
Factorial Design starts with its planning. In the planning stage, the factors and response variables to be studied should be defined. Then, within each factor is necessary to identify the upper and lower levels.

When planning a factorial design, it is essential to understand that there is no “one-size fits all” solution for all the scientific problems. However, there are some steps that the researcher can follow to better planning the design. For instance, the factors, their respective levels, and the response variables could be defined according to the need of the process that the researcher is aiming to optimize. Scientific or technical literature about the problem to be solved is a reasonable starting point. Also, the levels can be defined according to the capabilities of the pieces of equipment available for that experiment performance. The cost of using a specific piece of equipment or technique could be another decisive factor while planning the design [2].

In summary, to plan a factorial design accordingly, it is necessary: (a) to be familiar to the system to de studied, (b) to know the technical resources available, (c) to have clear goals about what is the response variable to be optimized, and (d) how the researcher is aiming to optimize this response variable, for instance, either maximizing or minimizing its value [3].

The second step in the factorial design is the factor screening. Due to the prior knowledge of the system, the researcher can identify variables that influence the response variable he/she is interested in optimizing. So, at this point, the researcher will perform a factor screening step. During factor screening, experiments will be performed according to some 2^k factorial design or some 2^k−p fractional factorial design. In either case, k is the number of factors to be studied. Then, all the experiments necessary to complete the selected factorial design will be performed. These experiments can be achieved with or without replicas, depending on the time and resources available to the researcher.

After the experiments conclusion, the researcher will analyze the data and determine which factors have significant effects and which factors do not have significant effects regarding influencing the response variable. At this point, the researcher will be able to obtain a linear polynomial equation describing how the significant factors quantitatively influence the response variable. For some situations, the model described by this equation can be enough to answer satisfactorily the question asked by the researcher. And the design can even be concluded on this point [3].

However, for other situations, the linear polynomial model obtained may not accurately describe the situation faced by the researcher. In this case, the factorial design will proceed to an optimization step. In this step, the insignificant factors will be disregarded, and additional experiments will be performed, considering only the significant factors. Also, in this step, in general, more than two levels will need to be considered for every factor [3, 4].

As more than two levels will be considered for each factor, the optimization step will allow the research to obtain a model described by a polynomial equation of order higher than one, for instance, a quadratic polynomial equation. Also, as the optimization is a refinement step, some factors may prove to be insignificant under the new design conditions. Consequently, they will be excluded from the definite model equation [4].

Most of the time, after one or a few optimization steps, the researcher will have a model that describes with satisfactory precision the behavior of the system in the study. Then, the next step is the conclusion of the design. In this step, the researcher will interpret how the empirical model obtained translates in the context of the studied situation. Additionally, the researcher will be able to apply the model to experimental conditions initially untested and verify how the experimental result agrees with the result predicted by the model.

The successful accomplishment of the four steps shown in Fig. 1 describes what is required to complete a factorial design. In the next two sections, we will discuss how the screening and optimization steps can be performed by using different types of factorial designs and their particularities.

Fig. 1

The four general steps of a factorial design of experiments

2.4 Screening the Factors

Depending on the complexity of the experimental problem to be solved, many factors can influence the response variable. In this sense, it is necessary to have a screening step, which will start with most of the factors that can hypothetically change the response variable. Then, the significance of the effects of these factors will be judged according to appropriate statistical tests, and the insignificant factors will be excluded from the optimization step. Besides deciding the significance of the effects, another goal from the screening step is to obtain a first-order polynomial equation, describing how the response variable varies according to changing the coded values of the significant factors.

The main differences between 2 and 2^k−p factorial designs are shown in Table 5, as adapted from Candioti et al. [5].

Table 5 Comparison of the features of the full factorial design (2^k) and fractional factorial design (2^k−p)

The fractional factorial designs 2^k−p are beyond the scope of this chapter. For readers interested in learning more regarding this type of design, references number [3] and [6] are good references to learn the essential concepts of fractional factorial designs.

2.5 2^k Factorial Designs

In Sect. 2.2, we first defined what 2^k factorial designs are and how many experiments are necessary to complete the design according to the k value. A feature of a 2^k factorial design is that for each factor, only two levels are defined, a lower and an upper level. This feature holds for 2^k factorial designs used in the factors screening steps. For more comprehensive steps, like the ones used for optimization steps, more levels will be needed. In this section, we will see the particularities of a 2^k factorial design. For instance, we will discuss how to calculate the effects and the coefficients of the equation describing the design model, and how to judge the significance of these effects.

Before we start, it is important to say that to perform all the calculations and graphs presented in this section does not require any specialized software. Any software able to program matrix multiplication and graphical plotting, for instance, Microsoft Excel, is enough to perform all the calculations. However, there are software packets specialized to perform all of the design of experiments calculations, most of them are paid packages. The readers more interested to know the names and capabilities of these software packages are encouraged to read the review paper by Hibbert [7], which contains a table listing the main commercial softwares used in design of experiment calculations.

As shown in Table 6, the number of effects possible for a 2^k factorial design is equal to 2^k − 1. In this sense, Table 6 explains how many and which are the effects, according to the k value.

Table 6 Number and type of effects according to the number of factors (k value) in a 2^k factorial design

Each one of the effects can be calculated according to the Eq. 1, as exemplified for Effect A [8]:

$${Effect}_{A}= \frac{\sum {Y}_{(+)}^{A}}{n/2}-\frac{\sum {Y}_{(-)}^{A}}{n/2}$$

(1)

where ${Y}_{(+)}^{A}$ are the values of the response variable for which A has coded value =  +1, ${Y}_{(-)}^{A}$ are the values of the response variable for which A has coded value = −1. n is defined as the total number of experiments in the factorial design, for instance, n = 8 for a 2³ or n = 16 for a 2⁴. Notice that the n value does not change if replicas are performed. The only thing that changes in case replicas were performed is the fact that each ${Y}_{(+)}^{A}$ and ${Y}_{(-)}^{A}$ should be taken as the average of the replicas.

A good way to understand the Eq. 1 is to think that the effect is the difference between the average of the response variable when A has coded value = +1 and the average of the response variable when A has coded value = −1.

To minimize the chances to be mistaken during the calculation of the effects, an alternative to Eq. 1, is to use matrix multiplication for each one of the effects. In Table 3, in Sect. 2.2, we introduced the concept of the matrix of experiments. Here, we will expand that matrix to include the coded values for each one of the possible interactions.

The coded value for each interaction was obtained by simply multiplying the coded values of the factors giving rise to that respective interaction. We can convert Table 7 in a square matrix (a matrix having the same number of columns and rows) by adding a column where all entries will be +1, as the first column of the matrix. We can call this matrix as matrix (M1):

Table 7 Matrix of experiments for the primary effects and interactions in a 2³ factorial design

$$X=\left[\begin{array}{cccccccc}+1& -1& -1& -1& +1& +1& +1& -1\\ +1& +1& -1& -1& -1& -1& +1& +1\\ +1& -1& +1& -1& -1& +1& -1& +1\\ +1& +1& +1& -1& +1& -1& -1& -1\\ +1& -1& -1& +1& +1& -1& -1& +1\\ +1& +1& -1& +1& -1& +1& -1& -1\\ +1& -1& +1& +1& -1& -1& +1& -1\\ +1& +1& +1& +1& +1& +1& +1& +1\end{array}\right]\quad(M1)$$

The transpose matrix (X^t) of the matrix 1 can be written as matrix (M2)

$${X}^{t}=\left[\begin{array}{cccccccc}+1& +1& +1& +1& +1& +1& +1& +1\\ -1& +1& -1& +1& -1& +1& -1& +1\\ -1& -1& +1& +1& -1& -1& +1& +1\\ -1& -1& -1& -1& +1& +1& +1& +1\\ +1& -1& -1& +1& +1& -1& -1& +1\\ +1& -1& +1& -1& -1& +1& -1& +1\\ +1& +1& -1& -1& -1& -1& +1& +1\\ -1& +1& +1& -1& +1& -1& -1& +1\end{array}\right]\quad(M2)$$

The matrix of results, shown in Table 4 can be written as matrix Y (M3):

$$Y=\left[\begin{array}{c}25\\ 42\\ 76\\ 45\\ 81\\ 5\\ 66\\ 15\end{array}\right]\quad(M3)$$

Multiplying the matrixes X^t and Y, as shown in Eq. 2, will be useful both for calculating the effects and the coefficients:

$$\left({X}^{t}\right)Y=\left[\begin{array}{c}355\\ -141\\ 49\\ -21\\ -23\\ -113\\ -59\\ 73\end{array}\right]$$

(2)

The effects can be calculated by the Eq. 3:

$$Effect(i)=\frac{\left({X}^{t}\right)Y}{n/2}$$

(3)

The effects calculated are shown in Fig. 2.

Fig. 2

Graph showing the effect value for each one of the primary effects and interactions possible for the 2³ factorial design. The effects were calculated according to Eq. 3

From Fig. 2, one can notice that except for the effect of the of the factor B, and the tertiary interaction ABC, all other effects had negative values. For the primary effects A, B, and C a negative value means that moving from the lower to the upper level of these factors, leads to a decrease in the response variable, in this case, the yield. Similarly, a positive effect means that switching from the lower to upper level leads to an increase in the response variable.

For the secondary effects, such as AB, AC, and BC, an increase in the effect means that the response variable increases when the product between the levels of the two factors switch from negative to positive. The interpretation is similar to the tertiary effect, such as ABC.

2.5.1 The Empirical Model

As previously told, a 2 ^k factorial model can produce a polynomial equation where all the terms are linear; in general, the empirical model can be described by the Eq. 4:

$$y={b}_{0}+\sum_{i=1}^{k}{b}_{i}{X}_{i}+\sum_{1\le i\le j}^{k}{b}_{ii}{X}_{i}{X}_{j}+ \xi$$

(4)

where: b₀ the independent term related to the average of the response of all experiments, b_i or b_ii are the coefficients for each term, the X_i or X_j are the coded values of each factor, and $\xi$ is the residual associated to the experiment.

For a factorial 2^k, the empirical model contains 2^k terms, being one term for each one of the effects plus the independent term. The residual term $\xi$ is not explicitly written in the equation. In this sense, the empirical model equations for 2², 2³, and 2⁴ designs are shown, respectively, in the equations varying from 5 to 7:

$$y={b}_{0}+{b}_{A}{X}_{A}+{b}_{B}{X}_{B}+{b}_{AB}{X}_{A}{X}_{B}$$

(5)

$$\begin{aligned}y&={b}_{0}+{b}_{A}{X}_{A}+{b}_{B}{X}_{B}+{b}_{C}{X}_{C}+{b}_{AB}{X}_{A}{X}_{B}\\ & \quad +{b}_{AC}{X}_{A}{X}_{C}+{b}_{BC}{X}_{B}{X}_{C}+{b}_{ABC}{X}_{A}{X}_{B}{X}_{C}\end{aligned}$$

(6)

$$\begin{aligned}y&={b}_{0}+{b}_{A}{X}_{A}+{b}_{B}{X}_{B}+{b}_{C}{X}_{C}+{b}_{D}{X}_{D}+{b}_{AB}{X}_{A}{X}_{B}+{b}_{AC}{X}_{A}{X}_{C} \\&\quad+{b}_{AD}{X}_{A}{X}_{D}{+{ b}_{BC}{X}_{B}{X}_{C} +{ b}_{BD}{X}_{B}{X}_{D}+{ b}_{CD}{X}_{C}{X}_{D}}\\ & \quad +{b}_{ABC}{X}_{A}{X}_{B}{X}_{C}+{{b}_{ABD}X}_{A}{X}_{B}{X}_{D}+ {{b}_{ADC}X}_{A}{X}_{D}{X}_{C}\\ & \quad +{{b}_{BDC}X}_{B}{X}_{D}{X}_{C}+ {{b}_{ABCD}X}_{A}{X}_{B}{X}_{C}{X}_{D}\end{aligned}$$

(7)

Each one of the b_i or b_ii coefficients can be calculated by dividing the Eq. 2 by the number of experiments; in other words, the coefficients can be calculated according to Eq. 8:

$$b(i)=\frac{\left({X}^{t}\right)Y}{n}$$

(8)

So, for the 2³ factorial design, we are working on, the empirical model is shown in Eq. 9:

$$\begin{aligned}Yield \left(\%\right)&=44.4-17.6{X}_{A}+6.1{X}_{B}-2.6{X}_{C}-2.9{X}_{A}{X}_{B}\\& \quad-14.1{X}_{A}{X}_{C}-7.4{X}_{B}{X}_{C}+9.1{X}_{A}{X}_{B}{X}_{C}\end{aligned}$$

(9)

2.5.2 Judging the Significance of the Effects to Refine the Empirical Model

Equation 9 presents all the eight possible terms for the empirical model. However, not all the terms will be significant. To judge which terms will be significant we have to decide which effects are significant using statistical tests. The coefficients related to the insignificant effects will be discarded from the model.

To have a rough estimate about which effects might be significant, the effects can be squared, and then, divided by the summation of all values, and multiplying by 100%, as shown in the Fig. 3.

Fig. 3

Graph showing the percentage of effects absolute value for each one of the primary effects and interactions possible for the 2³ factorial design

Figure 3 shows that effects A, AC, and ABC are the three bigger ones. The summation of these three effects accounts for about 85% of all the effects. We can affirm, almost unequivocally, that these three effects are significant. Contrastingly, we can also claim that the effect C, which is smaller than 1%, is insignificant. But how about the other four effects? Are they significant or not?

To answer this question, we need some statistical tests. One of the most popular tests is critical t-student, which is shown in Eq. 10:

$$critical-t= {s}_{Effect} \times t(DoF;p)$$

(10)

where ${s}_{Effect}$ is defined as the standard deviation of the effects and $t(DoF;p)$ is the value obtained from a t-Student table with the number of degrees of freedom (DoF) from which ${s}_{Effect}$ was calculated, and p is the probability. For instance, if the desired probability is 95%, the researcher should look for the t-student value with p = 0.05 in the t-Student table.

The ${s}_{Effect}$ can in principle be simply calculated as the square root of the variance of the effects (${{s}_{Effect}}^{2}$), from Eq. 11 [9]:

$${{s}_{Effect}}^{2}=\frac{4 {s}_{e}^{2}}{\sum_{i=1}^{n}{r}_{i}}$$

(11)

where ${s}_{e}^{2}$ is an estimative of the variances, which can be calculated from Eq. 12, and ${r}_{i}$ is the number of replicas. For instance, if each experiment was done twice, ${r}_{i }=2$

$${s}_{e}^{2}=\frac{\sum_{i=1}^{n}\left[{\left({r}_{i}-1\right)s}^{2}\right]}{\sum_{i=1}^{n}\left[\left({r}_{i}-1\right)\right]}$$

(12)

In fact, in Eq. 12 the term $\left({r}_{i}-1\right)$ is particularly the degrees of freedom used in order to calculate the estimative of the variances, and ${s}^{2}$ is the variance for each experimental condition, as shown in Eq. 13:

$${s}^{2}=\frac{\sum_{i=1}^{r}{\left({y}_{i}-\stackrel{-}{y}\right)}^{2}}{\left({r}_{i}-1\right)}$$

(13)

where ${y}_{i}$ is each individual result of the replica, $\stackrel{-}{y}$ is the average of each individual result from the replicas, and $r$ is the number of replicas.

After calculating critical-t using Eq. 10, the critical-t value is compared to the absolute value of each effect, and only the effects having absolute values higher than the critical-t will be considered significant, in that probability level p.

The best way to obtain all the variances necessary to calculate the critical-t is by performing all the experiments with replicas since it allows to calculate sequentially ${s}^{2}$, ${s}_{e}^{2}$, ${{s}_{Effect}}^{2}$, from Eqs. 11, 12, and 13, respectively.

However, if no replicas were made for any of the experiments, it is still possible to obtain the variances necessary to calculate t-value. Yet, there are distinct ways to accomplish this task, a popular and prudent one is to perform additional experimental with all the factors fixed at the central point.

For quantitative factors, the central point is defined as the average between the lower and upper levels, and it has the coded value equal to zero. Table 8 is an adaptation of Table 2, including the central point for each factor.

Table 8 The factors with their respective limits and central points represented as coded (in parenthesis) and uncoded values

As such, the experiment at the central point was then performed in triplicate, and the following results were obtained for the yield, as shown in Table 9.

Table 9 Yield obtained for the experiments performed in the central point using triplicates

The values for average, degrees of freedom, and variance (s² and s_e²), S_effect², S_effect, t-student (2; 0.05), and critical-t are shown in Table 10.

Table 10 Average yield, degrees of freedom, variances, standard deviation of the effect, tabled t-student value and, the critical-t value with 95% confidence obtained for the experiments performed in the central point using triplicates

The graph shown in Fig. 4 is called Pareto chart, it is a bar graph where in the Y-axis all the effects are categorized, and in the X-axis the absolute value of the effects are presented. Then, a vertical line is fixed on the X-axis over the critical-t value. From the Pareto chart we can see that the effects higher than the critical-t are the pH (A), the secondary interaction between pH and catalyst concentration (AC), and between temperature and catalyst concentration (BC), and the tertiary interaction among the three factors (ABC). Notice that the Pareto chart confirmed the initial guess based on Fig. 3 that the effects A, AC, and ABC are significant. Also, the Pareto chart was essential to confirm that BC is significant, whereas the effect B is insignificant, although it is very close to the critical-t value.

Fig. 4

Pareto chart showing which effects are higher (if so, significant) than the critical-t

Now that we decided which effects are significant, based on a statistical test. We can exclude from the model (Eq. 9) the coefficients related to the insignificant values. So, the model describing the factorial design is given by Eq. 14:

$$Yield \left(\%\right)=44.4-17.6{X}_{A}-14.1{X}_{A}{X}_{C}-7.4{X}_{B}{X}_{C}+9.1{X}_{A}{X}_{B}{X}_{C}$$

(14)

2.5.3 Assessing the Quality of the Model Using Analysis of Variance (ANOVA) Table

Replacing the coded values for X_A, X_B, and X_C on Eq. 14, it was possible to calculate the yield (%) predicted by the model for each one of the experiments performed, as shown in Table 11.

Table 11 Comparison between the yield (%) obtained experimentally and predicted by the model represented by Eq. 14

A standard method to assess the quality of the model by using three parameters called the sum of squares (SS), they are: the sum of square (SS) for the mean, for the regression, and for the residuals, and they are defined according to Eqs. 15–17:

$${SS}_{mean}=\sum {\left({y}_{i}-\stackrel{-}{y}\right)}^{2}$$

(15)

$${SS}_{regression}=\sum {\left(\widehat{{y}_{i}}-\stackrel{-}{y}\right)}^{2}$$

(16)

$${SS}_{residual}=\sum {\left({y}_{i}-\widehat{{y}_{i}}\right)}^{2}$$

(17)

where: ${y}_{i}$ is the value obtained experimentally, $\widehat{{y}_{i}}$ being value predicted according to the model, and the $\stackrel{-}{y}$ is the average of all experimental values.

Note that each sum of squares has a certain number of degrees of freedom which can be associated with them. It is known that for SS_residual the number of degrees of freedom is found to be equal to the difference of the number of independent experiments (8, in this example) and the number of parameters contained in the equation describing the model (5, in this example), so SS_residual has 3 degrees of freedom. For the SS_regression the number of degrees of freedom is equal to the number of parameters (5, in this example) minus 1, so the SS_regression has 4 degrees of freedom. Finally, the number of degrees of freedom of SS_mean is equal to the number of degrees of freedom for SS_residual plus SS_regression, so 7 degrees of freedom.

Hence, the mean square (MS) for regression, residual, and mean was then calculated by dividing each sum of squares by its respective number of degrees of freedom. So, Table 12 presents the complete ANOVA table for the example analyzed.

Table 12 Analysis of variance (ANOVA) Table for the 2³ factorial design

There are two criteria used to assess the model quality through the ANOVA table. The first one is based on the coefficient of determination (R²), which is the ratio between the SS_regression and SS_mean. An R² as close as to 1 represents a better quality of the model. In this example, an R² equal to 0.9224 means that 92.24% of the variation is explained by the model, whereas only 7.76% is explained by the residuals.

The second parameter is the ratio between MS_regression and MS_residual. This value is in general compared to the F-test value with 95% of confidence, and the number of degrees of freedom in the numerator as the same number of degrees of freedom as MS_regression. And the number of degrees of freedom in the denominator as the same number of degrees of freedom as MS_residual. As the ratio MS_regression/MS_residual (9.20) is higher than the F-test with 95% confidence, and 4/3 degrees of freedom (5.39), we can conclude that the model is appropriately fitted to the data.

For most of the researchers, the model described by Eq. 14 would have enough quality, which eliminates the need to perform additional experiments for optimization to obtain a model with quadratic terms, as the ones to be discussed in Sect. 2.6.

2.6 Optimization Steps

Depending on the situation studied, an empirical model where all the terms in the polynomial are linear may not be satisfying. In this sense, the researcher will have to use experimental designs able to produce polynomials containing quadratic terms, such as the one generically represented by Eq. 18:

$$y={b}_{0}+\sum_{i=1}^{k}{b}_{i}{X}_{i}+\sum_{i=1}^{k}{b}_{ii}{{X}_{i}}^{2}+ \sum_{1\le i\le j}^{k}{b}_{ii}{X}_{i}{X}_{j}+ \xi$$

(18)

Compare Eq. 18 with Eq. 4, and notice that there are no quadratic terms in the Eq. 4.

In this section, we will be introduced to the basics of four designs able to produce polynomial models containing quadratic terms. The four designs to be studied are 3^k Factorial Design, Central Composite Design (CCD), Box-Behnken Design, and Doehlert Design. In all these designs, all the factors are studied in more than two levels.

The group formed by these designs is called Response Surface Methodology (RSM), as the equations described by each model can be converted in a tri-dimensional graph called response surface. In none of these models there will be a detailed example, like the one we presented for 2^k factorial design. Readers interested to have a more in-depth knowledge about any one of these designs are encouraged read the references cited in this section or the ones in Sects. 3 and 4.

Also, specifically about RSM, the books: A Comprehensive Guide to Factorial Two-level Experimentation by Mee [6], and Design and Analysis of Experiments by Dean et al. [10] are good resources for readers avid for learning more about each one of the RSMs.

2.6.1 Three Level Factorial Design (3^k Design)

In the 3 ^k factorial design, all the factors have three levels (−1, 0, +1). Although the 3^k design implementation is not so complicated due to its similarity to 2^k designs, it requires a relatively large number of experiments. For this reason, the 3^k design is used to study a few factors, generally, two or three [11].

2.6.2 Central Composite Design (CCD)

The Central Composite Design (CCD) is made up by the combination of the following features [3, 9]:

• (i) A full 2^k factorial design or a fractional factorial design 2^k−p.

• (ii) Central point experiments, where all the factors have coded values equal to zero.

• (iii) Experiments in the axial points. In these experiments, one factor will have coded value equal to ±α. These ±α values are located in the axes of the coordinated system, and in distance ±α from the origin of the system.

Tables 13 and 14 show the matrix of experiments for a CCD design having a 2² and 2³ factorial as screening designs [3].

Table 13 Matrix of experiments for a 2² CCD factorial design

Table 14 Matrix of experiments for a 2³ CCD factorial design

From the matrix of experiments, one can conclude that the total number of experiments for a CCD, disregarding any replicas, is equal to the Eq. 19:

$$\mathrm{Number of Experiments}= {2}^{\mathrm{k}}+\mathrm{Central Point}+2\mathrm{k}$$

(19)

where the 2^k is the number of experiments related to the 2^k factorial, the Central Point is the experiment carried out in the central point, and 2k is the number of the experiments related to the axial points ±α.

The coded values ±α can be figured out according to Eq. 20 [9].

$$\upalpha = \sqrt[4]{{{2^{\rm k}}}}$$

(20)

In the CCD, any coded value can be decoded according to Eq. 21. This equation is also valid to convert the ±α to their respective decoded values [9]:

$${x}_{i}= \frac{{z}_{i}-\stackrel{-}{z}}{\Delta z/2}$$

(21)

where ${x}_{i}$ is the coded value for the factor i, ${z}_{i}$ is the decoded value for the factor i, $\stackrel{-}{z}$ is the decoded value for the central point for the factor i, and the $\Delta z$ is the difference between the upper (+) and lower (−) levels for the factor i.

Table 15 summarizes how many experiments should be made in the axial levels ±α, the value of α, and the total number of experiments according to the k value in 2^k−p.

Table 15 Number of experiments at axial level, axial levels, and total number of experiments for CCD factorial designs according to the number of factors

2.6.3 Box-Behken Designs

Similarly to the three levels factorial design the Box-Behken Desing (BBD) is a three levels (−1, 0, +1) for all factors. The number of experiments to be performed, disregarding replicas, according to the number of factors (k) is given by the Eq. 22 [12]:

$$\mathrm{Number of Experiments}= 2\mathrm{k}\left(\mathrm{k}-1\right) +\mathrm{ Central Point}$$

(22)

The conversion between the coded and uncoded values in a BBD is given by Eq. 23 [13]:

$${x}_{i}= \left(\frac{{z}_{i}-\stackrel{-}{z}}{\Delta z}\right)$$

(23)

where ${x}_{i}$ is the coded value for the factor i, ${z}_{i}$ is the decoded value for the factor i, $\stackrel{-}{z}$ is the decoded value for the central point for the factor i, and the $\Delta z$ is the difference between the upper (+) and lower (−) levels for the factor i.

One advantage of the BBD is that there is no experiment where the factors are taken all of them at the same time in the lower limit nor the upper limit. This fact avoids that experiments are carried out at extreme conditions and may avoid unsatisfactory or abnormal results to happen [14].

For more details about BDD matrix, readers are encouraged to read the review paper by Ferreira et al. [14].

2.6.4 Doehlert Designs

A feature differing Doehlert Designs (DD) from CCD and BBD is that DD does not have the same number of levels for all the factors. For instance, in a DD with k = 2, one factor has three levels (with coded values equal to −8.666, 0, +8.666), and the other has five levels (with coded values equal to −1, −0.5, 0, +0.5, +1). For a DD with k = 3, one factor has five levels (with coded values equal to −1, −0.5, 0, +0.5, +1), the second one has seven levels (with coded values equal to −0.866, −0.577, −0.289, 0, +0.289, +0.577, +0.866), and the third factor has `three levels (with coded values equal to −0.866, 0, +0.866) [11, 12]. In this sense, we can conclude that DD requires the following number of experiments, disregarding replicas, according to k value as shown in Eq. 24:

$$\mathrm{Number of Experiments}= {k}^{2}+\mathrm{k }+\mathrm{ Central Point}$$

(24)

The conversion between the coded and uncoded values in a DD is given by Eq. 25 [12]:

$${x}_{i}= \left(\frac{{z}_{i}-\stackrel{-}{z}}{\Delta z}\right)\alpha$$

(25)

where ${x}_{i}$ is the coded value for the factor i, ${z}_{i}$ is the decoded value for the factor i, $\stackrel{-}{z}$ is the decoded value for the central point for the factor i, the $\Delta z$ is the difference between the upper (+) and lower (−) levels for the factor i, and α is the coded value limit for the factor i.

For verifying examples about DD matrix, readers are encouraged to read the review paper by Ferreira et al. [12].

2.6.5 Comparison Between the Different Response Surface Methodologies

To compare the four RSMs presented in this section, we take advantage of the efficiency parameter, which is defined by the ratio between the number of coefficients present in the model of the RSM and the number of experiments necessary to accomplish that RSM [8]. Table 16 presents the number of coefficients, the number of experiments, the efficiency, according to the number of factors for the four RSMs presented.

Table 16 Comparison among the four RSMs presented regarding the number of experiments and efficiency

From Table 16, regardless of the number of factors, the DD presents a lower number of experiments and higher efficiency. Also notice that the 3^k design is not practical for n ≥ 4 [15].

3 Factorial Design of Experiments Applied to Nanomaterials Production and Performance

Nanomaterials are recognized for presenting outstanding properties when compared with their bulk-like versions. In this sense, it is necessary to develop synthetic methods able to precisely tune properties such as nanoparticle size, surface area, bandgap, and photoluminescent emission. To be able to obtain a fine control over these properties, usually, many factors need to be considered. Most of the time, a comprehensive study would require a massive number of experiments. For making the production process more efficient, the factorial design can be used to sort the significant factors. Then, it can be used to derive models for predicting how much that response property could be in a previously untested condition. In this section, we will see five examples where the factorial design was applied to obtain as the response variables different properties of nanomaterials.

3.1 Optimization of Copper (Cu) Nanoparticle Size Using 2² Factorial Design

The first paper of this section deals with the synthesis of copper (Cu) nanoparticles. Granata and co-workers studied how different capping agents, such as cetyl trimethyl ammonium bromide (CTAB), sodium dodecyl sulfate (SDS), and polyvinylpyrrolidone (PVP). And also, how different reducing agents, such as hydrazine and glucose, can influence the mean particle size and the stability against oxidation of the Cu nanoparticles [16].

By combining the three available capping agents with the two available reducing agents, the authors designed six different 2² factorial designs. The response variables analyzed were the mean and standard deviation of the particle size of the Cu nanoparticles as estimated by histograms counting 500 particles from scanning electron microscopy images. The authors were aiming to minimize the mean particle size and standard deviation since smaller Cu particles are more likely to present the surface plasmon resonance (SPR) phenomenon.

For all the designs, the temperature and initial pH were fixed at 85 ℃ and pH equal to 10. The levels for the surfactant and reducing agent factor for each one of the six 2² factorial designs are shown in Table 17 [16].

Table 17 The six 2² factorial designs used to analyze the interactions between capping and reducing agents—data by Granata et al. [16]

When glucose is used as the reducing agent, for design 1, only the glucose had a significant effect, and this effect was around +11.6 nm. As this effect is positive, it means that increasing glucose concentration from 0.2 to 0.5 mol L⁻¹ led to an increase of 11.6 nm in the size of Cu nanocrystals. For design 2, both the capping agent and reducing agent had significant effects. The glucose had a negative effect, whereas the CTAB had a positive effect. These results mean that the Cu mean particle size increased when the glucose concentration decreased or CTAB concentration increased. Finally, for design 3, not only glucose and PVP presented significant effect, but, the interaction between these two factors was significant as well. For all cases, the effects presented were negative, which means that by increasing the level of all variables from lower to the upper limit led to a decrease in the Cu mean particle size.

When hydrazine is used as the reducing agent, for design 4, only hydrazine and SDS had significant effects, being the hydrazine positive and the SDS negative. So, the Cu particle size increased with increasing hydrazine concentration a decreasing the SDS concentration. For design 5, both hydrazine and CTAB had significant effects, both of them positive. These results mean that the Cu mean particle size increased when the hydrazine or CTAB concentrations increased. Finally, for design 6, hydrazine and PVP presented a significant effect, following the same trend observed in design 4. Interestingly, for none of the designs, the interaction between capping and reducing agents showed significant effects.

After calculating the significant effects for each factorial design, the authors did not advance on using the factorial design to estimate a model for the mean particle size or standard deviation for the nanoparticles. From effects estimation the authors concluded that the PVP was probably the best capping agent for their purpose, as it is the capping agent that, for either reducing agents, had the highest effect on changing the nanoparticle size.

To subdivide all the data in six smaller 2² factorial designs was a wise decision, and it simplified a lot of the data analysis. Although this simplification eliminated, to some extent, the holistic character of the factorial design. To obtain a more comprehensive model would require that each factor to have a different number of levels.

3.2 Optimization of Silica Microspheres Size Using a 2³ Factorial Design a Linear Response Surface Model

Silica (SiO₂) microspheres are multifunctional materials, having applications in colloidal templating, photonic crystals, polymer encapsulation, to cite a few of them [17]. SiO₂ microspheres are prepared through the alkaline hydrolysis of silicon alkoxides in a water–ethanol solvent mixture. A common source of silicon is the tetraethyl orthosilicate (TEOS), whereas the reaction is usually catalyzed by water. The diameter of microspheres depends on an accurate control of the quantities of the reactants, catalysts, and solvents, for instance, TEOS, NH₃, and water. Considering that the diameter of the microspheres can determine its possible applications, to be able to control this feature systematically in a predictable way is a characteristic necessary for the synthetic method [18].

Aiming to obtain precise control over the diameter of SiO₂ microspheres, Arantes et al. used a 2³ factorial design to study the effect of the factors number of moles of ammonia, tetraethyl orthosilicate (TEOS), and water in the particle size of SiO₂ microspheres [19]. As such, the levels of each factor are shown in Table 18.

Table 18 The three factors and their levels in the 2³ factorial designs used to control the size of SiO₂ microspheres—data by Arantes et al. [19]

Only NH₃ and H₂O presented significant primary effects. The other significant effect was the interaction between TEOS and H₂O. After having concluded the significant effects, the authors calculated the coefficients related to each one of them and obtained a linear polynomial model to predict the SiO₂ particle size out of the initially performed experimental conditions, as shown in Eq. 26:

$$Y=158.82+97.52{X}_{1}+47.97{X}_{3}+29.092{X}_{2}{X}_{3}$$

(26)

where X₁ is the coded values for the number of moles of NH₃, X₂ is the number of moles of TEOS, and X₃ is the number of moles of water.

This model equation allowed the authors to plot a response surface graph by fixing NH₃ either in its lower (0.3 mol) or higher (0.6 mol) levels and varying the other two factors, as shown in Fig. 5.

Fig. 5

Adapted from reference number [19], with permission from Elsevier

Surface responses a by fixing the NH₃ molar amount in the level +1 (0.06 mol) and b by fixing the NH₃ molar amount in the level −1 (0.03 mol).

From Fig. 5, we notice that both graphs presented a similar behavior. In other words, by increasing the amount of H₂O and TEOS led to a maximization of the particle size of the SiO₂ microspheres. However, when NH₃ is fixed on its upper level, the SiO₂ particle size predicted is much higher than ones predicted by fixing NH₃ on its lower level and varying H₂O and TEOS.

To confirm the quality of the model, the authors calculated the analysis of variance (ANOVA) table, and it revealed a coefficient of determination (R²) equal to 95%, which means that 95% of the variation observed can in principle be explained by the obtained model. Finally, to experimentally confirm the applicability of the model, the authors performed an experiment where the coded values for NH₃, TEOS, and H₂O were, respectively, equal to -1, 0, and 0.5. By plugging these values into Eq. 26, it was predicted that the particle size should be around 85 nm. And in practice, the result of the experiment performed revealed that the SiO₂ particle size was very close 85 nm. This result showed a nice agreement in relation to the experimental data and the values predicted by the model.

3.3 Optimization of Manganese Sulfide (MnS) Thin-Films Thickness Using a 2⁴ Factorial Design and Dohelert Approach for Quadratic Response Surface

To be able to control thin film thickness is an essential property of a proper deposition procedure. In this sense, Hannachi and co-workers used a 2⁴ factorial to study the effects of time, temperature, initial concentrations of manganese acetate and thioacetamide on the thickness of manganese sulfide (MnS) deposited via chemical bath deposition onto glass substrates [20].

The levels were studied for each one of the factors, as shown in Table 19.

Table 19 The four factors and their levels in the 2⁴ factorial designs used to control the MnS thin-film thickness—data by Hannachi et al. [20]

The authors found that the deposition time, temperature, and manganese acetate initial concentration had significant primary effects. All these three factors had positive effects, which means that increasing either one of them from their lower to the upper levels would lead to an increase in the film thickness. On the other hand, the thioacetamide concentration effect was not significant. The secondary interactions involving the deposition time, temperature, and manganese acetate initial concentration when taken at two by two at a time also were significant. Endly, the tertiary interaction combining the three significant factors was significant as well. After judging the significance of the effects, the authors obtained the eight terms linear-polynomial model describing the thin-film thickness:

$$\begin{aligned}Y&=483+204.3{X}_{1}+159.5{X}_{2}+189.4{X}_{3}+98.3{X}_{1}{X}_{2}\\ & \quad +106.6{X}_{1}{X}_{3} + 159.1{X}_{2}{X}_{3}+71.4{X}_{1}{X}_{2}{X}_{3}\end{aligned}$$

(27)

where X₁ is the coded values for the deposition time, X₂ is deposition temperature, and X₃ is the concentration of manganese acetate.

The conclusions obtained in the 2⁴ factorial design served as the foundation to further optimize the model using a Doehlert approach, studying only the three factors that were significant in the 2⁴ screening factorial design. This Doehlert design allowed the authors to obtain a quadratic model (Eq. 28), and a set of response surface graphs.

$$\begin{aligned}Y&=349.0+136.5{X}_{2}+119.2{X}_{3}-129.0{X}_{1}^{2}-187.0{X}_{2}^{2}\\ & \quad - 124.0{X}_{3}^{2}+98.2{X}_{1}{X}_{2}+148.5{X}_{2}{X}_{3}\end{aligned}$$

(28)

where X₁ is the coded values for the deposition time, X₂ is deposition temperature, and X₃ is the concentration of manganese acetate.

The first response surface graph was plot fixing the thioacetamide concentration at 0.5 mol L⁻¹ and varying the deposition temperature and time. The second response surface graph was plot fixing the thioacetamide concentration at 0.5 mol L⁻¹ and varying the manganese acetate initial concentration and deposition time. Finally, the third surface was plot fixing the thioacetamide concentration at 0.5 mol L⁻¹ and varying the manganese acetate initial concentration and deposition temperature. The three response surfaces are shown in Fig. 6.

Fig. 6

Adapted from reference number [20], with permission from Elsevier

Surface responses (left) varying time and temperature (middle) varying time and Mn acetate conc. (right) varying temperature and Mn acetate conc.

By analyzing the three response surface plots, it was concluded that the MnS thin-film thickness was maximized (thickness around 330–400 nm), when the deposition temperature was 60 ℃, time was 20 h, manganese acetate concentration around 1.6 mol L⁻¹, and thioacetamide concentration equal to 0.5 mol L⁻¹.

To be able to indicate a narrow range of conditions that would lead to maximization of the thin-film thickness demonstrates how resourceful factorial design and response surface methodologies are. This affirmation comes from the fact that none of the conditions indicated as optimum were the same as the ones the authors initially used as levels in the 2⁴ factorial.

The authors deposited a thin-film under the conditions deemed to produce the highest thickness. The structural characterization techniques indicated the MnS was satisfactorily deposited onto the glass substrate. However, the authors failed to inform the thin-film thickness, which makes the readers unable to infer if the model used to produce the response surface graphs has a good agreement to the experimental data or not.

3.4 Optimization of Cellulose and Sugarcane Bagasse Oxidation Using a 2³ Factorial Design with Full Central Composite Design (FCCD)

The use of functional materials derived from natural sources or obtained from wastes is a procedure aligned with the Green Chemistry Principles, as long as the obtaining of these materials does not cause any environmental harm [21]. In this sense, Martins et al. studied the oxidation of cellulose and sugarcane bagasse by a simple procedure [22]. The oxidation procedure is based on stirring either the cellulose (Cel) or the sugarcane bagasse (SB) with phosphoric acid (H₃PO₄) and sodium nitrite (NaNO₂) for different time intervals.

To accomplish this goal, initially, the authors designed a 2³ factorial design, where the factors studied were the duration of the oxidation procedure (in hours), the volume of H₃PO₄ (in mL), and the mass of NaNO₂ (in g). The response variable was the number of carboxyl groups per gram of material, represented by the symbol n_COOH (in mmol/g), which can be taken as an indication of the successful oxidation of the initial material.

The Pareto plot revealed that for Cel, all the primary effects were significant, with the secondary effect between the volume of H₃PO₄ and the mass of NaNO₂ also being significant. For the SB, the Pareto plot revealed that only the primary effect related to the mass of NaNO₂ was significant. Additionally, the secondary effect between the volume of H₃PO₄ and the mass of NaNO₂ also was significant (Fig. 7).

Fig. 7

Adapted from reference number [22], with permission from Elsevier

Pareto charts for Cel (top) and SB (bottom).

Having concluded the significant factors for the oxidation of each one of the materials studied, the authors started to optimize the model by doing a full central composite design. This design was accomplished by a full central composite design (FCCD). For each one of the materials studied, this FCCD was carried out by performing the eight experiments predicted by the 2³ design, without replicas. Plus, the experiment in the central point, in triplicates, and six more experiments. Where, each one of these six, one of the factors assumed a + α or −α, whereas the two other factors were kept in the central point.

From the FCCD, the authors could obtain empirical models containing quadratic terms. These empirical models were used to plot the response surface graphs by fixing the reaction duration in 5 h, and varying the H₃PO₄ volume and NaNO₂ mass, as shown in Fig. 8.

Fig. 8

Adapted from reference number [22], with permission from Elsevier

Response surface graphs for Cel (top) and SB (bottom), by varying H₃PO₄ volume and NaNO₂ weight, the reaction duration was fixed at 5 h.

The response surface graphs showed that, when the reaction duration is equal to 5 h, the n_COOH is maximized for H₃PO₄ volume between 11 and 19 mL, and NaNO₂ volume between 500 and 970 mg. This conclusion agrees with the results initially obtained during the performance of the central point experiments.

After completing the full factorial design regarding the n_COOH, the authors used the products of Cel and SB oxidation to remove the dyes auramine O and crystal violet from simulated wastewater by adsorption. In general, the oxidated Cel presented better performance than the oxidated SB, for the removal of either of the dyes.

3.5 2^5-1 Fractional Factorial Design with Box-Behnken Optimization—Improving Reproducibility Between Batches of Silver Nanoparticles Using an Experimental Design Approach

Silver nanoparticles (Ag NPs) are very versatile materials since they can be applied in many different fields, such as catalysis, biological sensors, antimicrobial activities, DNA sequencing, surface-enhanced Raman spectroscopy, and information storage [23].

Ag NPs can be produced by the reduction of Ag⁺ with gallic acid (GA, C₇H₆O₅) in alkaline pH, by stirring the reaction mixture in the dark, at room temperature. However, this procedure lacks reproducibility since the Ag NPs tend to have different size distributions according to the reaction batch [24]. With the goal to decrease this lack of reproducibility, Núñez et al. performed a two-level factorial design to study the effects of NaOH, AgNO₃, and GA molar concentrations, also the effects of the reaction time and stirring speed [24]. So, the study had a total of five factors, with two-levels each. The response variable studied was a parameter called ψ, which was defined according to Eq. 29:

$$\psi =\frac{{A}_{max}}{{\lambda }_{max}\times FWHM}$$

(29)

In Eq. 29, A_max is the absorption intensity of the band corresponding to the surface plasmon resonance (SPR), λ_max is the wavelength of SPR band, and FWHM is the full-width at half-maximum of SPR band. The best ψ values are obtained when A_max is maximized, and λ_max and FWHM are both minimized, in other words, the ψ is better as it gets higher. And higher ψ means that Ag NPs were smaller and with a narrower size distribution [25].

As five factors were studied, a full two-level factorial design would lead to the performance of 32 experiments. To minimize the number of experiments to be done, the authors opted to do a fractional factorial design (FFD). In general, an FFD is symbolized as 2^(k−p). Where k is the number of factors, and p is the number of design generators. More specifically, in this paper, the authors carried out a 2^5–1 factorial design. The number 5 represents the five factors ([NaOH] = A, [AgNO₃] = B, [GA] = C, time = D, and speed = E), and 1 represents the generator I = ABCDE.

The FFD was made up of sixteen experiments plus five experiments with all the factors in the central point. All experiments were performed with replicas. The lower and upper levels of each variable were defined, as shown in Table 20.

Table 20 The five factors and their levels in the 2^5–1 factorial designs used to control the ψ in Ag NPs preparation—data by Núñez et al. [24]

The Pareto chart indicated that the significant primary effects were the [GA], the reaction time, and [AgNO₃]. As shown in Fig. 9.

Fig. 9

Adapted from reference number [24], with permission from Elsevier

Pareto chart showing the effects of ψ in Ag NPs synthesis.

After concluding the significant effects, the factorial designed continued by performing an optimization using the Box-Behnken design (BBD). The BBD is an incomplete three-level design to obtain a quadratic polynomial model. According to the number of experiments conducted is equal to 2k(k − 1) + C₀. Where k is the number of factors, in this case, k = 3, and C₀ is the number of experiments in the central point, in this case, C₀ = 5. In summary, 17 experiments were performed on this BBD. For the BBD, instead of using ψ as the response variable, the authors used A_max, λ_max, and FWHM separately.

For each one of the response variables (A_max, λ_max, and FWHM), quadratic polynomial equations were obtained, and response surface graphs were plotted by fixing either one of the factors ([AgNO₃], [GA] and reaction time). For the A_max, it is maximized as [AgNO₃], [GA], and reaction time increase. The λ_max is minimized when [AgNO₃] increases, and [GA] decreases. And the FWHM became narrower when [AgNO₃] increased, and [GA] decreased. The response surface graphs are shown for the λ_max in Fig. 10.

Fig. 10

Adapted from reference number [24], with permission from Elsevier

Response surface graphs of λ_max by varying a [AgNO₃] and [GA], b [AgNO₃] and time, c [GA] and time.

4 Factorial Design of Experiments Applied to Nanomaterials Production and Performance

The fields of Materials Science, Materials Chemistry, and Nanotechnology are all very broad. That being said, it would be impossible to cover every single possible application in a book chapter. In this sense, this part is intended to present some references related to four areas of application in Materials Science and Nanotechnology. They are nanoparticles preparation and characterization, drug encapsulation and delivery, wastewater remediation, and solar cell development.

For each one of these areas, around ten to twenty references, are presented classified according to the Factorial Design and Response Surface Methodology used on each paper, and the goal set by the papers. Unlike Sect. 3, there will not be any further detail about any paper. Instead, the readers are encouraged to read the tables and figure out if they get interested in the statistical methods or the theme of the paper. Then, they should feel free to consult these references independently. In order to show the relevance and the insertion of the factorial design of experiments in the current scientific literature, all examples presented were published between 2015 and 2020.

4.1 Design of Experiments Applied to Materials Synthesis and Characterization

See Table 21.

Table 21 List of papers related to materials synthesis and characterization

4.2 Design of Experiments Applied to Drug Encapsulation and Delivery

See Table 22.

Table 22 List of papers related to drug encapsulation and delivery

4.3 Wastewater Remediation

See Table 23.

Table 23 List of papers related to wastewater remediation

4.4 Design of Experiments Applied to Solar Cells Design and Performance

See Table 24.

Table 24 List of papers related to solar cells design and performance

5 Concluding Remarks

This chapter presented the theoretical bases of the factorial design and applications of the design of experiments in different areas of Materials Science and Nanotechnology. The depth and extent of the technique open up the possibility for the optimization of many experimental situations.

Hopefully, the knowledge brought by this chapter can motivate the readers to see the usefulness of the factorial design of experiments and encourage them to apply this knowledge to their own experimental situations.