A New Volume-Based Convexity Measure for 3D Shapes

Abstract

Convexity, as a global and learning-free shape descriptor, has been widely applied to shape classification, retrieval and decomposition. Unlike its extensively addressed 2D counterpart, 3D shape convexity measurement attracting insufficient attention has yet to be studied. In this paper, we put forward a new volume-based convexity measure for 3D shapes, which builds on a conventional volume-based convexity measure but excels it by resolving its problems. By turning the convexity measurement into a problem of influence evaluation through Distance-weighted Volume Integration, the new convexity measure can resolve the major problems of the existing ones and accelerate the overall computational time.

1 Introduction

Shape analysis has been playing a fundamental role in computer graphics, computer vision and pattern recognition. In shape analysis, research on how to quantify a shape with holistic descriptors such as convexity [5, 6, 8, 19], circularity [15], concavity [17], ellipticity [1], rectilinearity [9], rectangularity [18] and symmetry [4, 14] has been booming, because these descriptors can offer a global and efficient way for applications where shape representation is required. Among these holistic descriptors convexity has been most commonly used in shape decomposition [2, 10, 11], classification [6, 12], and retrieval [5, 6, 8], etc.. In general a planar shape $s$ $(s \subset \mathbf{R} ^{2})$ is regarded as convex if and only if the whole line segment between two arbitrary points in s belongs to s. When it comes to three-dimensional(3D) shapes, this definition can readily be generalised as: A 3D shape $S$ $(S \subset \mathbf{R} ^{3})$ is said to be convex if and only if all points on the line segment between two arbitrary points in S belong to S. Generally speaking, every convexity measure have to meet four desirable conditions:

• 1. The value of the convexity measure is a real number between (0,1].

• 2. The measured convexity value of a given shape equals 1 if and only if this shape is convex.

• 3. There are shapes whose measured convexity is arbitrary close to 0.

• 4. The value of the convexity measure should remain invariant under similarity transformation of the shape.

Next, we will review some state-of-the-art convexity measures for 3D shapes and analyse their pros and cons. Note that all the 3D shapes mentioned in this paper are topologically closed.

Definition 1

For a given 3D shape S with CH(S) denoting its convex hull, its convexity is measured as

$$\begin{aligned} {C_1}\left( S \right) = \frac{Volume \left( S \right) }{Volume \left( CH \left( S \right) \right) } \end{aligned}$$

(1)

$C_1$, a volume-based measure, cannot distinguish two shapes with the same ratio of shape to convex hull volumes, as shown in Fig. 3 (a) and (b).

To resolve the above problem, Lian et al. [8] proposed a projection-based convexity measure for 3D shapes, which was generalised from a 2D projection-based convexity measure reported by Zunic et al. [19].

Definition 2

For a given 3D shape S, its convexity is measured as

$$\begin{aligned} {C_2}\left( S \right) =\mathop {\min }\limits _{\alpha ,\beta ,\gamma \in [0,2\pi ]} \frac{Pview \left( S,\alpha ,\beta ,\gamma \right) }{Pface \left( S,\alpha ,\beta ,\gamma \right) } \end{aligned}$$

(2)

where Pface is the summed area of surface mesh faces of a 3D shape projected onto the three orthogonal planes, YOZ, ZOX and XOY, with $Pface={Pface_x}+{Pface_y}+{Pface_z}$, while Pview is the summed area of shape silhouette images projected onto six faces of its bounding box parallel to the orthogonal planes, with $Pview=2(Pview_x+Pview_y+Pview_z)$. $Pview\left( S,\alpha ,\beta ,\gamma \right)$ and $Pface\left( S,\alpha ,\beta ,\gamma \right)$ are Pview and Pface of S after rotating $\alpha$, $\beta$ and $\gamma$ with respect to x, y and z axes, respectively. Figure 1 illustrates examples of Pface and Pview. It is noticeable that there exists an inequality $Pface\ge Pview$ for any 3D shape and that they are equal only if a 3D shape is convex. Therefore, convexity is measured as a minimum value sought by rotating the shape at variant angles.

Fig. 1.

Projections of a triangular face and a whole shape on the coordinate planes.

Since the calculation of $C_2$ is a nonlinear optimisation problem that traditional methods cannot deal with, a genetic algorithm is used to help seek the minimum value of $C_2$. However, the genetic algorithm is computationally expensive and requires a plethora of iterations to reach an optimum. To avoid the heavy calculation of $C_2$, Li et al. proposed a heuristic convexity measure for 3D shape, which is still projection-based but computes the summed area ratio of projected shape silhouette images and surface mesh faces only once, just along principal directions of the shape, followed by a correction process based on shape slicing [5] rather than optimizing the ratio with the genetic algorithm in iterations.

Definition 3

For a given 3D shape S, its convexity is measured as

$$\begin{aligned} {C_3}\left( S \right) =Cor \left( \frac{Pview\left( S\cdot R \right) }{Pface\left( S\cdot R\right) }\right) \end{aligned}$$

(3)

where R represents the rotation matrix of the initial estimation achieved by principal component analysis (PCA) and $Cor \left( \cdot \right)$ indicates the subsequently applied correction process. Compared to $C_2$, $C_3$ can accelarate the overall computation by some an order of magnitude.

During the correction process of $C_3$, Li et al. sliced the 3D shape into a sequence of cross sections in equal interval along the principal directions of the shape, then 2D convexity measurement of the cross sections was performed in order to offset the precision loss introduced by the initial estimation of PCA. However, $C_3$ may introduce some error during the correction process.

In order to resolve the above problems of the existing convexity measures, in this paper we present a new volume-based convexity measure, which builds on the original volume-based $C_1$ but excels it by resolving its extant problems. The basic idea behind the new convexity is generalised from its 2D counterpart [6].

2 Our Volume-Based Convexity Measure

Fig. 2.

We can regard both of Shape (a) and (b), with the left and middle columes being their solid and wireframe views, as collapsed from their convex hulls (in the right colume) towards the geometric centres of the convex hulls, with the black arrows implying the collapsing directions.

Our new convexity measure is generalised from a 2D area-based measure [6] and shares the similar philosophy that any nonconvex 3D shape, no matter with protrusions (Fig. 2(b)) or dents (Fig. 2(a)), is formed by its convex hull collapsing towards the geometric centre of the convex hull. We assume that the convexity of an arbitrary 3D shape is associated with the total influence of dents collapsed from the shape convex hull, and consider that dent attributes, such as position and volume with respect to the shape convex hull, directly determine the dent influence.

Fig. 3.

The position and volume of dents determine the convexity calculation of 3D shapes. There are four cubes with dents in different positions and volumes. The corresponding convexity values computed by variant measures are listed beneath the shapes.

Some intuitional examples are given in Fig. 3, where four cubes have dents in different positions and volumes. For example, the dents of Shape (a) and (b) are identical in volume but different in position, and Shape (a) is visually more concave than Shape (b) as the dent of Shape (a) is centrally positioned. This distinction cannot be sensed by $C_1$ and $C_3$. $C_2$ considers that Shape (a) is even more convex than Shape (b) which is, however, not the case. Moreover, the dents of both Shape (a) and (c) are centrally positioned but different in volume, while dents of Shape (a) and (d) are the same in volume but different in position. Therefore, the new convexity measure should be able to distinguish all the above differences.

In light of the above analysis the new convexity measure should be defined by taking account of dent position and volume with respect to the shape convex hull. Note that dents here not only mean dents contained in the 3D shape but dents collapsed from the shape convex hull. This semantic nuance can be articulated by Fig. 2, where the former dents can be exemplified by (a) while the latter dents involve both (a) and (b).

To associate our convexity measure with dent position and volume, we consider that the convex hull of a given 3D shape S is made up of infinitely small cubes, and assign each small cube a weight associated with the Euclidean distance from the cube to the geometric centre of the convex hull in order to evaluate the influence of the cube on the convexity measurement. The closer a cube to the geometric centre of the convex hull, the more it influences the calculation of convexity. If the dent volume is symbolised as $D$ $(D \subset \mathbf{R} ^{3})$, the influence of D on the convexity measurement of S can be calculated by $\iiint _D W(r)dv$, where W(r) represents a weight function. Likewise, the total influence of the convex hull of S can be formulated as $\iiint _{CH(S)} W(r)dv$, and thus the influence of the 3D shape on the convexity measurement can be expressed as

$$\begin{aligned} \iiint _S W(r)dv=\iiint _{CH(S)}W(r)dv-\iiint _D W(r)dv \end{aligned}$$

(4)

Definition 4

For a given 3D shape S, its convexity is measured as

$$\begin{aligned} {C_\alpha }\left( S \right) = \frac{\iiint _S W(r)dv}{\iiint _{CH(S)} W(r)dv} \end{aligned}$$

(5)

and

$$\begin{aligned} W(r)=1-\alpha \frac{r}{r_{max}}=\frac{r_{max}-\alpha \cdot r}{r_{max}} \end{aligned}$$

(6)

where $\alpha$, $0 \le \alpha \le 1$, represents an influence factor of the weight function; r denotes the Euclidean distance variable between small cubes and the geometric centre of the convex hull of S; $r_{max}$ represents the maximum r.

Equations (5) and (6) define our notion of Distance-weighted Volume Integration. When $r=r_{max}$, W(r) reaches its minimum $1-\alpha$; when $r=0$, W(r) has a maximum 1. This distance-weighted strategy emphasises the influence of dents close to the geometric centre of the convex hull and downplays the impact of dents distant from the geometric centre. Moreover, by adjusting $\alpha$ we can control the influence of different attributes. For example, if we want to emphasise the contribution of dent position, we can increase $\alpha$ to lower the influence of distant cubes. If we want to emphasise the contribution of dent volume, we can degrade the weight influence of each cube by decreasing the value of $\alpha$. When we decrease $\alpha$ to 0, every cube will have an identical weight, and the new measure will degenerate into the traditional volume-based convexity measure $C_1$, only related to dent volume.

Fig. 4.

A hollow cube model. $l_1$ and $l_2$ indicate the outer and inner edge lengths of the cube, respectively.

3 Proof of the New Measure

In this section, we verify that the new convexity satisfies the four necessary conditions stated in Sect. 1.

Proof

For a given 3D shape S, assume that it has m dents denoted as ${D_1},{D_2}\cdots {D_m} \subset \mathbf{R} ^{3}$. The corresponding influences of dents ${D_1},{D_2}, \cdots ,{D_m}$ can be calculated by $\iiint _{D_1} {W(r)dv }$, $\iiint _{D_2} {W(r)dv }, \cdots ,\iiint _{D_m} {W(r)dv }$, respectively. Thus, ${C_\alpha }(S)$ can be rewritten as

$$\begin{aligned} {C_\alpha }(S) = \frac{\iiint _{S} {W(r)dv}}{{\iiint _{S} {W(r)dv} + \sum \limits _{i = 1}^m {\iiint _{D_i} {W(r)dv } }}}. \end{aligned}$$

(7)

It is easy to show that $0<{C_\alpha }(S)<1$. If there is no dent, that is $\sum \limits _{i = 1}^m {\iiint _{D_i} {W(r)dv } } = 0$, then ${C_\alpha }(S) = 1$. This means that S coincides with its convex hull. To this end, S is convex.

To prove Condition 3 we construct a hollow cube, as shown in Fig. 4. When we keep increasing $l_2$ making it infinitely close to $l_1$, we have

$$\begin{aligned} \lim \limits _{\begin{array}{c} l_2\rightarrow l_1 \end{array}}{C_\alpha }\left( S \right) =0 \end{aligned}$$

(8)

Under translation and rotation of a 3D shape, since the relevant distance between each small cube and the geometric centre of the convex hull remains the same, and the volume of the 3D shape and its convex hull also keeps unchanged, the convexity measured by $C_\alpha$ remains the same.

Taking the geometric centre of the convex hull as the origin to establish the coordinate system, we assume that S is scaled by a coefficient k. The convexity of the scaled shape is written as

$$\begin{aligned} \begin{aligned} {C_\alpha }(S')&= \frac{{\iiint _{S'} {(1 - \alpha \cdot r'/r{'_{\max }})}dx'dy'dz'}}{{\iiint _{CH(S')}} {(1 - \alpha \cdot r'/r{'_{\max }})dx'dy'dz'}}\\&= \frac{{\iiint _{S} {(1 - \alpha \cdot kr/k{r_{\max }})}{k^3}dxdydz}}{{\iiint _{CH(S)} {(1 - \alpha \cdot kr/k{r_{\max }}){k^3}dxdydz}}}\\&= {C_\alpha }(S), \end{aligned} \end{aligned}$$

(9)

where the prime symbol indicates those corresponding parameters after scaling. Hence Condition 4 of Theorem 1 is proved.

4 Algorithm Implementation

To implement $C_\alpha$ we need a discrete version of Definition 4 for calculation. A straightforward thought similar to its 2D counterpart [6] is to replace the integral symbols by summations and the infinitely small cubes by voxels. Thus we can rewrite $C_\alpha$ into its discrete form as

$$\begin{aligned} C_\alpha = \frac{N_{S}-\alpha \frac{{\sum \limits _{j = 1}^{N_{S}}}{r_j}}{r_{max}}}{N_{CH}-\alpha \frac{{\sum \limits _{k = 1}^{N_{CH}}}{r_k}}{r_{max}}} \end{aligned}$$

(10)

where $N_{S}$ and $N_{CH}$ represent the numbers of voxels in S and CH(S), respectively.

Fig. 5.

A $3*3*3$ illustration of the 3D Distance Dictionary.

Fig. 6.

3D shapes measured in different 3D grid sizes.

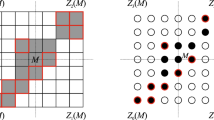
Prior to convexity measurement we need to voxelise the measured 3D shape and its convex hull. We first find the minimum bounding box of the shape convex hull with all the faces of the bounding box perpendicular to the x, y and z axes, and tessellate the minimum bounding box into a 3D grid of $n_1*n_2*n_3$ $(n_1, n_2, n_3\in \mathbf{Z} ^{+})$ voxels. Then the calculation of shape convexity is carried out in terms of evaluation of the influence of each voxel in the shape convex hull within the $n_1*n_2*n_3$ volume grid. We observe that all the 3D shapes can share the same volume grid, and the distances and weights of their voxels will be calculated repeatedly under the same grid during convexity measurement. Hence instead of calculating voxel distances for every 3D shape, we compute them only once by constructing an $N*N*N (N,n_m\in \mathbf{Z} ^{+}$ with $N >= 2n_{m}$ and $n_{m}=max(n_1,n_2,n_3))$ Distance Dictionary to pre-store all the Euclidean distances from the voxels to the grid centre of the Distance Dictionary. When computing the convexity of a specific 3D shape, we just need to align the geometric centre of its convex hull to the grid centre of the Distance Dictionary, scale the 3D grid of the shape convex hull to fit the 3D Distance Dictionary in voxel, and then look up Euclidean distances of the corresponding voxels of the 3D shape and its convex hull in the Distance Dictionary.

The 3D Distance Dictionary is an $N*N*N$ tensor, elements of which store values of the Euclidean distances from the voxels of the dictionary to its grid centre. Figure 5 illustrates a $3*3*3$ example of such a 3D Distance Dictionary. However, the value of the 3D Distance Dictionary N must be larger than two times $n_m$, and thus the resolution of 3D grid of the minimum bounding box for 3D shapes influenes the convexity measurement. General speaking, the larger the grid resolution, the more accurate the measured convexity, but the more time the computation consumes. In order to choose an appropriate resolution for the 3D minimum bounding box grid, we compare the performances when in turn setting $n_m=80,100,150,250,500$. As shown in Fig. 6, convexities measured with different grid resolutions for the same 3D shape are not much different. Therefore, for the sake of computational simplicity, the value of $n_m$ in the rest of this paper is set to 80. Note that in this paper without specification $\alpha$ is set to 1 by default, and the computer configuration is specified in Sect. 5.3. The pseudocode of the new measure is shown in Algorithm 1.

5 Experimental Results

5.1 Quantitative Evaluation

Fig. 7.

The quantitative convexity measurement of ten 3D shapes.

We carry out the convexity measurement to ten 3D shapes shown in Fig. 7, with eight of them picked from two commonly used 3D shape databases, the McGill Articulated 3D Shape Benchmark [16] and Princeton Benchmark [3], and the other two, the 1st and 6th, being two synthetic 3D shapes. These shapes are ordered in $C_\alpha$. It can be seen that for those shapes whose dents embrace the geometric centre of the shape convex hull, such as the 1st, 2nd, 3rd and 6th, their convexity values evaluated by $C_\alpha$ are lower than those by $C_1$. It can also be noticed from the results of Fig. 7 that the convexities measured by $C_2$ are relatively larger with all the values greater than 0.5, which cannot reflect the reality. As $C_3$ is a heuristic method that comes with a correction process at the end, $C_3$ more or less introduces some error into the convexity estimated. For example, the convexity of the sphere measured by $C_3$ in Fig. 7 is only 0.9744, while the results of $C_1$, $C_2$ and $C_\alpha$ on the sphere are either 1 or very close to 1.

5.2 3D Shape Retrieval

Fig. 8.

Samples of the 10 categories of watertight shapes for 3D shape retrieval.

Fig. 9.

Canonical forms of the shapes. The first row shows the original non-rigid models, while the second row shows their feature-preserved 3D canonical forms.

We also apply $C_1$, $C_2$, $C_3$ and $C_\alpha$ to non-rigid 3D shape retrieval on the McGill articulated 3D shape benchmark [16], which consists of 10 categories of 255 watertight shapes. Some classified samples are shown in Fig. 8. In this dateset shapes in the same categories such as the glasses and hand gestures shown in Fig. 9 may appear in quite different poses but have similar canonical forms. For this reason we apply a method introduced in [7] to construct the feature-preserved canonical forms of the 3D shapes. We compute convexities of the 3D shapes by $C_1$, $C_2$, $C_3$ and $C_\alpha$ and employ the $L_1$ norm to calculate the dissimilarity between two signatures. The retrieval performance is evaluated by four quantitative measures (NN, 1-Tier, 2-Tier, DCG) [13]. The results in Fig. 10 show that $C_3$ achieves the best retrieval rates as a solo convexity measure. Note that the smaller the value of $\alpha$, the higher the retrieval rate. This is because with $\alpha$ increasing, the distribution of the values of $C_\alpha$ for the same category is broadening, making the retrieval less precise. Representing 3D shapes by a solo convexity measure may result in relatively poor retrieval rates. In order to improve the accuracy of retrieval, we employ a shape descriptor, called CS (Convexity Statistics) [6], by taking advantage of our new convexity measure by setting $\alpha$ to 0.0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0. We collect the 11 convexities of every 3D shape as a set and calculate the mean, variance, skewness and kurtosis of each set to construct the four-dimensional shape descriptor CS. As can be seen from Fig. 10, the CS outperforms the competitors in all the retrieval measures.

Fig. 10.

Retrieval performance of the convexity measures on the McGill dataset.

Fig. 11.

Comparison of time consumptions.

5.3 Computational Efficiency

In this section we compare computational efficiencies of three convexity measures, as shown in Fig. 11, where some typical shapes are ordered in vertex number. $C_2$ is computationally expensive due to the adopted genetic algorithm with 50 individuals and 200 evolution generations [8], especially when the number of vertices in the shape is large. $C_3$ also needs to capture silhouette images from the frame buffer and the convexity measurement of 2D slides also takes time. The whole experiment is carried out with a laptop configured with Intel Core i5 CPU and 6G RAM. Note that $C_2$ and $C_3$ are computed using Visual Studio 2010 because the codes for calculating silhouette images from the frame buffer were written in C++. Even though $C_\alpha$ is coded and computed using MATLAB, which is normally considered slower than C++, $C_\alpha$ with the Distance Dictionary still accelerates the overall computational time by several orders of magnitude.

6 Limitations

Although $C_\alpha$ can overcome the shortcoming of $C_1$, $C_\alpha$ shares the same problem with $C_1$, as it is derived from $C_1$. If 3D shapes with a long and narrow dent inside or outside, the volume-based convexity measures $C_\alpha$ and $C_1$ will get unreasonable values. The grid resolution is artificially set, which is decided by $n_m$. If the dent is infinitesimally small, say smaller than a voxel, it may be missed out.

7 Conclusions

In this paper we proposed a new convexity measure based on Distance-weighted Volume Integration by turning the convexity measurement into a problem of influence evaluation. To facilitate the computation of the new convexity measure for 3D shapes we also introduced the use of a pre-calculated Distance Dictionary so as to avoid the repeated calculation of voxel distances for every 3D shape. The experimental results demonstrated the advantage of the new convexity measure, and the new convexity measure performed several orders of magnitude faster than those competitors. In respect of its application to 3D shape retrieval, we construct a variety of convexity measures by varying the value of $\alpha$ and form a new multi-dimensional shape descriptor with these different convexity measures.