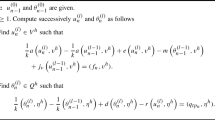A Frictional Dynamic Thermal Contact Problem with Normal Compliance and Damage

Abstract

We study a class of non-clamped dynamical problems for visco-elastic materials, the contact condition is modeled by a normal compliance, with friction, damage and heat exchange. The weak formulation leads to a general system defined by a second-order quasi-variational evolution inequality on the displacement field coupled with a nonlinear evolutional inequality on temperature field and a parabolic variational inequality on the damage field. We present and establish an existence and uniqueness result of different fields, by using general results on evolution variational inequalities, with monotone operators and fixed point methods. Then, we present a fully discrete numerical scheme of approximation and derive an error estimate. Finally, various numerical computations are developed.

1 Introduction

Problems involving contact between deformable bodies abound in industry and everyday life. For this reason, a considerable engineering and mathematical literature is devoted to dynamic and quasi-static frictional contact problems, including mathematical modeling, mathematical analysis, numerical analysis and numerical simulations. The study of contact problems for elastic–visco-elastic materials within the mathematical analysis framework was introduced in the early reference works [5, 8,9,10]. In these works, numerous types of frictional contact models with nonlinear visco-elastic or elasto-plastic materials were widely studied, in the framework of linearized infinitesimal deformations, using abstract variational inequalities, with monotonicity and convexity.

Further extensions to non-convex contact conditions with non-monotone and possible multi-valued constitutive laws led to the active domain of non-smooth mechanic within the framework of the so-called hemivariational inequalities, for a mathematical as well as mechanical treatment, we refer to [11].

This paper is a continuation work of the results obtained in [3], p. 251. In [3], the authors studied a problem for the quasi-static contact between an elastic–visco-plastic body and an obstacle, the contact was clamped on some part of the boundary and was frictionless, and it was defined by a normal compliance condition with damage. An existence and uniqueness result on displacement and damage fields has been established, and also some numerical approximations and simulations have been presented.

In this work, we study a class of dynamic contact problems with normal compliance condition and damage, with Coulomb’s friction and thermal effects, for visco-elastic material. The novelty here is that we investigate a general long memory material law, depending on time, on the temperature and the damage. Moreover, the evolution of the temperature is described by a general nonlinear equation, involving the gradient of temperature and the velocity of deformation, and the associated boundary condition is defined by an inclusion of sub-differential type in a non-convex framework. Also, the usual clamped condition has been deleted, so that Korn’s inequality cannot be applied any more. The problem appears then semi-coercive and strongly nonlinear due to the frictions. Semi-coercive problems were first studied in [5] for Coulomb’s friction models, where the inertial term of the dynamic process has been used in order to compensate the loss of coerciveness in the a priori estimates. The variational formulation of the mechanical problem leads to a new non-standard model of system defined by a second-order quasi-variational inequality on the displacement field, coupled with one nonlinear inequality for the temperature field and with a variational inequality on the damage field. Then, by using classical results on evolution variational inequalities, with monotone operators and adopting fixed point methods frequently used in [2], we prove an existence and uniqueness of solution on the displacement, damage, and temperature fields.

The paper is organized as follows. In Section 2, we describe the mechanical problem and specify the assumptions on the data to derive the variational formulation, and then we state our main existence and uniqueness result. In Section 3, we give the proof of the claimed result. In Section 4, we introduce a fully discrete approximation scheme and derive an order error estimate under solution regularity assumptions. In Section 5, we present some numerical simulations in order to show the evolution of deformation, of the Von Mise’s norm, of the temperature and the damage in the body.

2 The Contact Problem

In this section, we study a class of thermal contact problems with non-clamped frictional normal compliance condition, for visco-elastic materials. We describe the mechanical problems, list the assumptions on the data, and derive the corresponding variational formulations. Then, we state an existence and uniqueness result on displacement and temperature fields, which we will prove in the next section.

The physical setting is as follows. A visco-elastic body occupies a bounded domain $\varOmega \subset \mathbb {R}^d$ (d = 2, 3) with a Lipschitz boundary Γ that is partitioned into two disjoint measurable parts, Γ _F and Γ _c. Let [0, T] be the time interval of interest, where T > 0. We assume that a volume force of density f ₀ acts in Ω × (0, T) and that surface tractions of density f _F apply on Γ _F × (0, T). The body may come in contact with an obstacle, the foundation, over the potential contact surface Γ _C. The model of the contact is specified by a general sub-differential boundary condition, where thermal effects may occur in the frictional contact with the foundation. Our aim is to describe the dynamic evolution of the body.

Let us recall now some classical notations, see e.g. [5] for further details. We denote by S _d the space of second-order symmetric tensors on $\mathbb {R}^{d}$, while “⋅” and |⋅| will represent the inner product and the Euclidean norm on S _d and $\mathbb {R}^d$. Let ν denote the unit outer normal on Γ. Everywhere in the sequel, the indices i and j run from 1 to d, summation over repeated indices is implied, and the index that follows a comma represents the partial derivative with respect to the corresponding component of the independent variable. We also use the following notation:

$$\displaystyle \begin{aligned} H= \Big(L^{2}(\varOmega)\Big)^d,\qquad \mathcal{H}=\{\boldsymbol{\sigma}=(\sigma_{ij})\,\, |\,\, \sigma_{ij}=\sigma_{ji} \in L^{2}(\varOmega), \ 1\leq i,j \leq d \}, \end{aligned}$$

$$\displaystyle \begin{aligned} H_{1}=\{\boldsymbol{u} \in H\,\, |\,\, \boldsymbol{\varepsilon}(\boldsymbol{u}) \in \mathcal{H}\},\qquad \mathcal{H}_{1} = \{ \boldsymbol{\sigma} \in \mathcal{H} \,\, |\,\, \mathrm{Div}\,\,\boldsymbol{\sigma} \in H\}. \end{aligned}$$

Here, $\boldsymbol {\varepsilon } : H_{1} \longrightarrow \mathcal {H}$ and $\mathrm {Div}\, : \mathcal {H}_{1} \longrightarrow H$ are the deformation and the divergence operators, respectively, defined by

$$\displaystyle \begin{aligned} \boldsymbol{\varepsilon}({\boldsymbol{u}}) = (\varepsilon_{ij}({\boldsymbol{u}})),\quad \varepsilon_{ij}({\boldsymbol{u}}) = \frac{1}{2}( u_{i,j} + u_{j,i} ),\quad \mathrm{Div}\,\,\boldsymbol{\sigma} = (\sigma_{ij,j} ). \end{aligned}$$

The spaces H, $\mathcal {H}$, H ₁, and $\mathcal {H}_{1}$ are real Hilbert spaces endowed with the canonical inner products given by

$$\displaystyle \begin{aligned} ( {\boldsymbol{u}},\boldsymbol{v} )_H = \int_{\varOmega}{u_{i}v_{i}\,dx},\qquad ( \boldsymbol{\sigma}, \boldsymbol{\tau} )_{\mathcal{H}} = \int_{\varOmega}{\sigma_{ij}\tau_{ij}\,dx }, \end{aligned}$$

$$\displaystyle \begin{aligned} ( {\boldsymbol{u}},\boldsymbol{v} )_{H_{1}}= ( {\boldsymbol{u}},\boldsymbol{v} )_H + ( \boldsymbol{\varepsilon}({\boldsymbol{u}}),\boldsymbol{\varepsilon}(\boldsymbol{v}) )_{\cal{H}},\qquad ( \boldsymbol{\sigma},\boldsymbol{\tau} )_{\mathcal{H}_1} = (\boldsymbol{\sigma},\boldsymbol{\tau} )_{\mathcal{H}} + ( \mathrm{Div}\,\,\boldsymbol{\sigma},\mathrm{Div}\,\,\boldsymbol{\tau} )_{H}. \end{aligned}$$

We recall that C denotes the class of continuous functions; C ^m, $m\in \mathbb {N}^*$ the set of m times continuously differentiable functions; and W ^{m, p}, $m\in \mathbb {N}$, 1 ≤ p ≤ +∞ the classical Sobolev spaces.

Now, we consider a visco-elastic body which occupies a bounded domain Ω ⊂R ^d (d = 1, 2, 3) with a Lipschitz boundary Γ that is partitioned into two disjoint measurable parts, Γ _F and Γ _C. Let [0, T] be the time interval of interest, where T > 0. We assume that a volume force of density f ₀ acts in Ω × (0, T) and that surface tractions of density f _F apply on Γ _F × (0, T). The body may come in contact with an obstacle, the foundation, over the potential contact surface Γ _C, see figure below.

To continue, the mechanical problem is then formulated as follows.

Problem Q: Find a displacement field $\boldsymbol {u} :(0,T) \times \varOmega \longrightarrow \mathbb {R}^{d}$, a stress field σ :  (0, T) × Ω→S _d, a temperature field $\theta :\,(0,T) \times \varOmega \longrightarrow \mathbb {R}_+$, and a damage field $\alpha : (0,T) \times \varOmega \rightarrow \mathbb {R}$ such that for a.e. t ∈ (0, T):

$$\displaystyle \begin{aligned} \left\{ \begin{array}{l} \boldsymbol{\sigma}(t) = \mathcal{A}(t)\boldsymbol{\varepsilon}(\dot{\boldsymbol{u}}(t))+ \mathcal{G}(t)(\boldsymbol{\varepsilon}(\boldsymbol{u}(t)), \alpha(t)) + \int_0^t\,\mathcal{B}(t-s)\,(\boldsymbol{\varepsilon}(\boldsymbol{u}(s)), \alpha(s))\,ds \\ {} \qquad + C_e(t, \theta(t)) \quad \mbox{in} \quad \varOmega; \end{array} \right. \end{aligned} $$

(1)

$$\displaystyle \begin{aligned} \ddot{\boldsymbol{u}}(t) = \mathrm{Div}\,\boldsymbol{\sigma}(t) + \boldsymbol{f}_0(t) \quad \mbox{in} \quad \varOmega; \end{aligned} $$

(2)

$$\displaystyle \begin{aligned} \boldsymbol{\sigma}(t) \nu = \boldsymbol{f}_F(t) \quad \mbox{on} \quad \varGamma_{F}; \end{aligned} $$

(3)

$$\displaystyle \begin{aligned} \sigma_{\nu}(t) = -p_{\nu}(t,u_{\nu}(t) - g(t)) \quad \mathrm{on} \ \varGamma_{C}; \end{aligned} $$

(4)

$$\displaystyle \begin{aligned} \left\{ \begin{array}{l} |{\boldsymbol{\sigma}}_{\tau}(t)|\leq p_{\tau}(t,u_{\nu}(t) - g(t)):\\ {} |{\boldsymbol{\sigma}}_{\tau}(t)| < p_{\tau}(t,u_{\nu}(t)-g(t))\, \Longrightarrow \, \dot{\boldsymbol{u}}_{\tau}(t)=0; \\ {} |{\boldsymbol{\sigma}}_{\tau}(t)| = p_{\tau}(t,u_{\nu}(t)-g(t))\,\Longrightarrow\, \dot {\boldsymbol{u}}_{\tau}(t) = -\lambda\,{\boldsymbol{\sigma}}_{\tau}(t),\\ {} \qquad \qquad \qquad \qquad \qquad \qquad \qquad \mbox{ for some } \lambda\geq 0; \end{array} \right.\quad \mbox{ on } \varGamma_{C}; \end{aligned} $$

(5)

(6)

$$\displaystyle \begin{aligned} 0 \leq \alpha(t) \leq 1 \quad \mbox{in}\ \varOmega; \end{aligned} $$

(7)

$$\displaystyle \begin{aligned} \frac{\partial\alpha}{\partial\nu}(t) = 0 \quad \mbox{on}\ \varGamma; \end{aligned} $$

(8)

$$\displaystyle \begin{aligned} \dot{\theta}(t) - \mathrm{div}(\mathcal{K}_c(t,\nabla \theta(t))) = D_e(t, \varepsilon(\dot{\boldsymbol{u}}(t)), \theta(t)) + q(t) \quad \mbox{in}\quad \varOmega; \end{aligned} $$

(9)

$$\displaystyle \begin{aligned} -\mathcal{K}_c(t,\boldsymbol{x}, \nabla \theta(t,\boldsymbol{x})) \,\nu := \varXi(t,\boldsymbol{x}, \theta(t,\boldsymbol{x})) \in \partial \varphi(t, \boldsymbol{x}, \theta(t,\boldsymbol{x})) \quad \mbox{a.e.}\quad \boldsymbol{x} \in \varGamma_{C}; \end{aligned} $$

(10)

$$\displaystyle \begin{aligned} \theta(t) = 0 \quad \mbox{on} \quad \varGamma_F; \end{aligned} $$

(11)

$$\displaystyle \begin{aligned} \boldsymbol{u}(0) = \boldsymbol{u}_0;\quad \dot{\boldsymbol{u}}(0)=\boldsymbol{v}_0; \quad \alpha(0) = \alpha_0; \quad \theta(0) = \theta_0 \quad \mbox{in} \quad \varOmega. \end{aligned} $$

(12)

Equation (1) is the Kelving Voigt’s long memory thermo-visco-elastic constitutive law of the body including the influence of the damage variable. Here, σ is the stress tensor, $\mathcal {A}$ denotes the viscosity operator with, $\mathcal {A}(t)\boldsymbol {\tau } = \mathcal {A}(t,\cdot ,\boldsymbol {\tau })$ is some function defined on Ω, and $\mathcal {G}$ is the elastic operator depending on the linearized strain tensor ε(u) of infinitesimal deformations and on the damage α, with $\mathcal {G}(t)(\boldsymbol {\tau }, \alpha ) = \mathcal {G}(t,\cdot ,\boldsymbol {\tau }, \alpha )$ is some function defined on Ω. For example,

$$\displaystyle \begin{aligned} \mathcal{G}(t)(\boldsymbol{\tau}, \alpha) = \mathcal{G}^0(t)\boldsymbol{\tau} - \alpha\,C_{da}(t) \quad \mbox{in} \ \varOmega, \end{aligned}$$

where $\mathcal {G}^0(t)\boldsymbol {\tau } = \mathcal {G}^0(t,\cdot ,\boldsymbol {\tau })$ is some time-depending elastic tensor function independent on the damage, defined on Ω, and C _da(t) is some time-depending damage tensor. The term $\mathcal {B}(t)(\boldsymbol {\tau }, \alpha ) = \mathcal {B}(t,\cdot ,\boldsymbol {\tau }, \alpha )$ represents the relaxation tensor time depending on the linearized strain tensor and the damage, defined on Ω. And the last tensor C _e(t, θ) := C _e(t, ⋅, θ) denotes the thermal expansion tensor depending on time and temperature, defined on Ω. For example,

$$\displaystyle \begin{aligned} {C}_e(t, \theta) := - \theta\, C_{exp}(t) \quad \mbox{in} \ \varOmega, \end{aligned}$$

where

$$\displaystyle \begin{aligned} C_{exp}(t) := (c_{ij}(t,\cdot)) \end{aligned}$$

is some time-depending expansion tensor defined on Ω, with c _ij ∈ L ^∞((0, T) × Ω).

The model in (2) is the dynamic equation of motion where the mass density ϱ ≡ 1. Equation (3) is the traction boundary condition.

On the contact surface, the general relation (4) represents the normal compliance contact condition, where σ _ν denotes the normal stress, u _ν is the normal displacement, g is the gap between the contact surface and the foundation, and p _ν is some normal compliance function defined on $(0,T)\times \varGamma _{C} \times \mathbb {R}$ with the convention that p _ν(t, r) = p _ν(t, ⋅, r) denotes some function defined on Γ _C, for a.e. t ∈ (0, T), for all $r\in \mathbb {R}$. The term u _ν − g represents, when it is positive, the penetration of the surface asperities into the foundation.

For example, for a.e. t ∈ (0, T),

$$\displaystyle \begin{aligned} p_\nu(t,\cdot,r) = c_{\nu}(t,\cdot)\,r_+ \quad \mbox{on} \ \varGamma_{C},\ \forall r \in \mathbb{R}.\end{aligned}$$

In this formula, the normal stress is proportional to the penetration, with some positive coefficient c _ν defined on (0, T) × Γ _C, which is related to the hardness of the foundation.

Equation (5) represents a general version of Coulomb’s dry friction law, where σ _τ is the tangential stress, p _τ is the friction bound measuring the maximal frictional resistance defined on $(0,T)\times \varGamma _{C} \times \mathbb {R}$, and $\dot {\boldsymbol {u}}_{\tau }$ is the tangential velocity. Recall that p _τ(t, r) = p _τ(t, ⋅, r) is some function defined on Γ _C, for a.e. t ∈ (0, T), for all $r\in \mathbb {R}$.

For example, for a.e. t ∈ (0, T),

$$\displaystyle \begin{aligned} p_\tau(t,\cdot,r) = \mu_\tau(t,\cdot)\,c_{\nu}(t,\cdot)\,r_+ \quad \mbox{on} \ \varGamma_{C},\ \forall r \in \mathbb{R},\end{aligned}$$

where the friction bound is proportional to the normal stress with some positive coefficient of friction μ _τ defined on (0, T) × Γ _C.

Following Frémond [6, 7], the damage function α represents the percentage of the safe part or undamaged part, α = 1 means that the body is undamaged, and α = 0 says that the body is completely damaged. The evolution of the microscopic cracks responsible for the damage is described by the parabolic differential inclusion (6) of the damage function α satisfying 0 ≤ α ≤ 1, where γ is a positive constant and ϕ _d is a given constitutive function which describes damage source in the system. The inequality (6) means

and

and

Equation (8) represents the homogeneous Neumann boundary condition for the damage field, see e.g. [3], p. 241.

The differential equation (9) provides the evolution of the temperature field. There $\mathcal {K}_c(t,\nabla \theta ) := \mathcal {K}_c(t,\cdot ,\nabla \theta )$ is some nonlinear time-depending function of the temperature gradient ∇θ, which is defined on Ω. For example, denote by

$$\displaystyle \begin{aligned} K_c(t,\cdot) := (k_{ij}(t,\cdot)) \end{aligned}$$

the thermal conductivity tensor defined on Ω, we could consider

$$\displaystyle \begin{aligned} \mathcal{K}_c(t,\cdot,\nabla \theta) = K_c(t,\cdot)\,\nabla \theta. \end{aligned}$$

In the second member, q(t) denotes the density of volume heat sources, whereas

$$\displaystyle \begin{aligned} D_{e}(t, \boldsymbol{\varepsilon}(\dot{\boldsymbol{u}}(t)), \theta(t) ) := D_{e}(t, \cdot, \boldsymbol{\varepsilon}(\dot{\boldsymbol{u}}(t)), \theta(t) ) \end{aligned}$$

is the deformation-viscosity heat, which is a nonlinear function defined on Ω and which represents the heat generated by the velocity of deformation (viscosity) and may depend on the temperature.

Example 1

$$\displaystyle \begin{aligned} D_e(t, \varepsilon(\dot{\boldsymbol{u}}(t)), \theta(t) )= -C_{exp}(t):\varepsilon(\dot{\boldsymbol{u}}(t)) = -c_{ij}(t,\cdot)\,\varepsilon_{ij}(\dot{\boldsymbol{u}}(t)). \end{aligned} $$

(13)

Example 2

$$\displaystyle \begin{aligned} D_e(t, \varepsilon(\dot{\boldsymbol{u}}(t)), \theta(t) )= - \theta(t,\cdot) \, d_{e}(t,\cdot), \end{aligned} $$

(14)

with some coefficient $d_{e} \in L^\infty ((0,T)\times \varOmega . \mathbb {R}^+)$;

Example 3

$$\displaystyle \begin{aligned} D_e(t, \varepsilon(\dot{\boldsymbol{u}}(t)), \theta(t) )= -C_{exp}(t):\varepsilon(\dot{\boldsymbol{u}}(t)) - \theta(t,\cdot) \, d_{e}(t,\cdot). \end{aligned} $$

(15)

By assuming the variation of θ(t) small enough, then the heat function $D_{e}(t, \boldsymbol {\varepsilon }(\dot {\boldsymbol {u}}(t)), \theta (t) )$ may be considered as a formula which is independent of the temperature.

The associated temperature boundary condition is given by (10) and (11), where Ξ and φ are some functions defined on $(0,T) \times \varGamma _{C} \times \mathbb {R}$. Here,

$$\displaystyle \begin{aligned} \partial \varphi(t, \boldsymbol{x}, r) := \partial \varphi(t, \boldsymbol{x},\cdot) (r),\ \forall (t, \boldsymbol{x}, r) \in (0,T) \times \varGamma_{C} \times \mathbb{R} \end{aligned}$$

denotes the sub-differential on the third variable of φ in the locally Lipschitz framework.

We recall that for a locally Lipschitz function $G\,:\, \mathbb {R} \longrightarrow \mathbb {R}$, at any point $a \in \mathbb {R}$ and for any vector $d \in \mathbb {R}$, we can define the following directional derivative with respect to d:

$$\displaystyle \begin{aligned} \overline{\lim}_{\tau\rightarrow 0+} \frac{G(a+\tau d)-G(a)}{\tau}:= G^0(a;d). \end{aligned} $$

(16)

We have for all $a,\, d \in \mathbb {R}$, for all ξ ∈ ∂G(a):

$$\displaystyle \begin{aligned} G^0(a;d) \geq \xi\,d \end{aligned}$$

and

$$\displaystyle \begin{aligned} |G^0(a;d) | \leq |G^0(a)|\times |d|,\quad |\xi | \leq |G^0(a)|, \end{aligned}$$

where

$$\displaystyle \begin{aligned} \overline{\lim}_{h\rightarrow 0,\, h\neq 0} \frac{G(a+ h)-G(a)}{h}:= G^0(a).\end{aligned}$$

In the case where G is convex on $\mathbb {R}$, we have

$$\displaystyle \begin{aligned} G^0(a;d) = \left\{ \begin{array}{ll} G^{\prime}_r(a) d \quad \mbox{if} \quad d > 0 \\ {} G^{\prime}_l(a) d \quad \mbox{if} \quad d < 0 \\ {} 0 \qquad \quad \ \mbox{if} \quad d = 0, \end{array} \ \right. \end{aligned}$$

and

$$\displaystyle \begin{aligned} G^0(a) = \max\{ G^{\prime}_r(a), G^{\prime}_l(a) \}, \end{aligned}$$

where $G^{\prime }_r$ and $G^{\prime }_l$ denote the right side and left side derivatives, respectively.

In the sequel, for a.e. (t, x) ∈ (0, T) × Γ _c, for all $(r,s)\in \mathbb {R}^2$, we use the notation

$$\displaystyle \begin{aligned} \varphi^0(t,\boldsymbol{x},r;s) := [\varphi(t,\boldsymbol{x},\cdot)]^0(r;s), \end{aligned}$$

and

$$\displaystyle \begin{aligned} \varphi^0(t,\boldsymbol{x},r) := [\varphi(t,\boldsymbol{x},\cdot)]^0(r). \end{aligned}$$

Taking the previous example for $\mathcal {K}_c$, we have

$$\displaystyle \begin{aligned} \mathcal{K}_c(t,\boldsymbol{x}, \nabla \theta) \,\nu = k_{ij}(t,\boldsymbol{x})\, \frac{\partial\,\theta}{\partial\,x_j}\,\nu_i. \end{aligned}$$

Let us consider, for example,

$$\displaystyle \begin{aligned} \varphi(t, \boldsymbol{x}, r) := \frac{1}{2} k_e(t,\boldsymbol{x}) (r- \theta_R(t,\boldsymbol{x}))^2, \ \forall (t, \boldsymbol{x}, r) \in (0,T) \times \varGamma_{C} \times \mathbb{R}, \end{aligned} $$

(17)

where θ _R is the temperature of the foundation, and k _e is the heat exchange coefficient between the body and the obstacle. We obtain

$$\displaystyle \begin{aligned} \varXi(t, \boldsymbol{x}, r) = \partial \varphi(t, \boldsymbol{x}, r) = k_e(t,\boldsymbol{x})\,(r -\theta_R(t,\boldsymbol{x})), \ (t, \boldsymbol{x}, r) \in (0,T) \times \varGamma_{C} \times \mathbb{R}. \end{aligned}$$

Finally, the data in u ₀, v ₀, α ₀, and θ ₀ in (12) represent the initial displacement, velocity, damage, and temperature, respectively.

In view to derive the variational formulation of the mechanical problems (1)–(12), let us first precise the functional framework. Let

$$\displaystyle \begin{aligned} V = H_1 \end{aligned}$$

be the admissible displacement space, endowed with the inner product given by

$$\displaystyle \begin{aligned} ( \boldsymbol{u},\boldsymbol{v} )_{V} = ( \boldsymbol{\varepsilon}(\boldsymbol{u}),\boldsymbol{\varepsilon}(\boldsymbol{v}) )_{\mathcal{H}} + (\boldsymbol{u}, \boldsymbol{v})_H \qquad \forall\,\boldsymbol{u},\,\boldsymbol{v}\,\in V, \end{aligned}$$

and let ∥⋅∥_V be the associated norm, i.e.

$$\displaystyle \begin{aligned} \|\boldsymbol{v}\|{}_{V}^2 = \|\boldsymbol{\varepsilon}(\boldsymbol{v})\|{}_{\mathcal{H}}^2 + \|\boldsymbol{v}\|{}_H^2 \qquad \forall\,\boldsymbol{v} \in V. \end{aligned}$$

Therefore, (V, ∥⋅∥_V) is a real Hilbert space, where the norm ∥⋅∥_V is equivalent to $\|\cdot \|{ }_{(H^{1}(\varOmega ))^d}$.

Let

$$\displaystyle \begin{aligned} E=\{\eta\in H^{1}(\varOmega),\ \eta = 0 \quad \mbox{on } \quad \varGamma_F\} \end{aligned}$$

be the admissible temperature space, endowed with the canonical inner product of H ¹(Ω).

By the Sobolev’s trace theorem, there exists a constant c ₀  >  0 depending only on Ω, and Γ _C such that

$$\displaystyle \begin{aligned} \|\boldsymbol{v}\|{}_{ ( L^{2}(\varGamma_{C}) )^d}\ \leq\ c_0\,\|\boldsymbol{v}\|{}_{V}, \ \forall\,\boldsymbol{v} \in V; \quad \mbox{and}\quad \| \eta \|{}_{ L^{2}(\varGamma_{C}) }\ \leq\ c_0\,\|\ \eta \|{}_{E}, \ \forall\,\eta \in E. \end{aligned} $$

(18)

Next, we denote the set of admissible damage fields by

$$\displaystyle \begin{aligned} \mathcal{K}_{da} = \{ \xi \in H^1(\varOmega), \frac{\partial \xi}{\partial\nu} = 0 \ \mbox{on}\ \varGamma, \ 0 \leq \xi \leq 1 \ \mbox{a.e. in} \ \varOmega \}.\end{aligned}$$

We use here two Gelfand evolution triples (see e.g. [12], pp. 416) given by

$$\displaystyle \begin{aligned} V\subset H \equiv H'\subset V', \quad E\subset L^{2}(\varOmega) \equiv (L^{2}(\varOmega))'\subset E',\end{aligned}$$

where the inclusions are dense and continuous.

In the study of the mechanical problems (1)–(12), we assume that the viscosity operator ${\mathcal A} \,:\, (0,T)\times \varOmega \times S_d\longrightarrow S_d$ satisfies

$$\displaystyle \begin{aligned} \left\{ \begin{array}{l} \mathrm{(i)} \; \mathcal{A}(\cdot, \cdot, \boldsymbol{\tau}) \mbox{ is measurable on } (0,T)\times \varOmega,\ \forall \boldsymbol{\tau} \in S_d;\\ {} \mathrm{(ii)} \; {\mathcal A}(t, \boldsymbol{x}, \cdot) \mbox{ is continuous on } S_d \mbox{ for a.e. } (t, \boldsymbol{x}) \in(0,T)\times \varOmega;\\ {} [2mm] \mathrm{(iii)} \; \mbox{there exists } m_{\mathcal A} > 0\ \mbox{ such that } \\ \qquad ({\mathcal A}(t, \boldsymbol{x}, \boldsymbol{\tau}_1) - {\mathcal A}(t, \boldsymbol{x}, \boldsymbol{\tau}_2) ) \cdot (\boldsymbol{\tau}_1 - \boldsymbol{\tau}_2) \geq m_{\mathcal A}\,|\boldsymbol{\tau}_1-\boldsymbol{\tau}_2|{}^2,\\ {} \qquad \qquad \forall \boldsymbol{\tau}_1,\, \boldsymbol{\tau}_2 \in S_d, \mbox{ for a.e. } (t, \boldsymbol{x}) \in(0,T)\times \varOmega; \\ {} \mathrm{(iv)} \; \mbox{there exists } c_0^{\mathcal A} \in L^2((0,T)\times \varOmega; \mathbb{R}^+),\ c_1^{\mathcal A} > 0 \mbox{ such that } \\ {} \qquad |{\mathcal A}(t, \boldsymbol{x}, \boldsymbol{\tau}) | \leq c_0^{\mathcal A}(t,\boldsymbol{x}) + c_1^{\mathcal A}\,|\boldsymbol{\tau}|, \\ {} \qquad \forall \boldsymbol{\tau} \in S_d, \mbox{ for a.e. } (t, \boldsymbol{x}) \in(0,T)\times \varOmega. \end{array} \right. \end{aligned} $$

(19)

Here, recall that for every t ∈ (0, T) and τ ∈ S _d, we write by ${\mathcal A}(t) = {\mathcal A}(t,\cdot ,\cdot )$ a functional which is defined on Ω × S _d and ${\mathcal A}(t) \, \boldsymbol {\tau } = {\mathcal A}(t,\cdot ,\boldsymbol {\tau })$ some function defined on Ω.

We suppose that the elasticity operator ${\mathcal G} : (0,T)\times \varOmega \times S_d \times \mathbb {R} \longrightarrow S_d$ satisfies

$$\displaystyle \begin{aligned} \left\{ \begin{array}{l} \mathrm{(i)} \; {\mathcal G}(\cdot, \cdot, \boldsymbol{\tau}, \lambda) \mbox{ is measurable on } (0,T)\times \varOmega,\ \forall \boldsymbol{\tau} \in S_d, \ \forall \lambda \in \mathbb{R};\\ {} \mathrm{(ii)} \quad \mbox{there exists}\ L_{\mathcal G} > 0\ \mbox{such that}\\ {} \qquad | {\mathcal G}(t,\boldsymbol{x},\boldsymbol{\tau}_1, \lambda_1) - {\mathcal G}(t,\boldsymbol{x},\boldsymbol{\tau}_2, \lambda_2)| \leq L_{\mathcal G}\,( |\boldsymbol{\tau}_1 - \boldsymbol{\tau}_2| + |\lambda_1 - \lambda_2|) \\ {} \qquad \forall \boldsymbol{\tau}_1,\,\boldsymbol{\tau}_2\in S_d,\,\, \forall \lambda_1,\,\lambda_2 \in \mathbb{R},\,\, a.e.\,\, (t,\boldsymbol{x}) \in (0,T)\times \varOmega\,;\\ {} \mathrm{(iii)} \; \mbox{there exists } c_0^{\mathcal G} \in L^2((0,T)\times \varOmega; \mathbb{R}^+),\, c_1^{\mathcal G} \geq 0, \, c_2^{\mathcal G} \geq 0 \ \mbox{ such that } \\ {} \qquad |{\mathcal G}(t, \boldsymbol{x}, \boldsymbol{\tau}, \lambda) | \leq c_0^{\mathcal G}(t,\boldsymbol{x}) + c_1^{\mathcal G}\,|\boldsymbol{\tau}| + c_2^{\mathcal G}\,|\lambda|, \\ {} \qquad \forall \boldsymbol{\tau} \in S_d,\, \forall \lambda \in \mathbb{R}, \, \mbox{ a.e. } (t, \boldsymbol{x}) \in(0,T)\times \varOmega;\\ {} \mathrm{(iv)} \; \mbox{the partial derivatives with respect to the first, third, and fourth }\\ \qquad \mbox{variables of}\ {\mathcal G} \ \mbox{ exist and are bounded}. \end{array} \right. \end{aligned} $$

(20)

We put again ${\mathcal G}(t)(\boldsymbol {\tau }, \lambda ) = {\mathcal G}(t,\cdot ,\boldsymbol {\tau }, \lambda )$ some function defined on Ω for every t ∈ (0, T), τ ∈ S _d, $\lambda \in \mathbb {R}$.

The relaxation tensor ${\mathcal B}\,:\, (0,T) \times \varOmega \times S_d \times \mathbb {R} \longrightarrow S_d$ satisfies

$$\displaystyle \begin{aligned} \left\{ \begin{array}{ll} \mathrm{(i)} \; {\mathcal B}(\cdot, \cdot, \boldsymbol{\tau}, \lambda) \in L^{\infty}((0,T)\times \varOmega; S_d ),\ \forall \boldsymbol{\tau} \in S_d, \ \forall \lambda \in \mathbb{R};\\ {} \mathrm{(ii)} \ \mbox{there exists}\ L_{\mathcal B} > 0\ \mbox{such that}\\ {} \qquad | {\mathcal B}(t,\boldsymbol{x},\boldsymbol{\tau}_1, \lambda_1) - {\mathcal B}(t,\boldsymbol{x},\boldsymbol{\tau}_2, \lambda_2)| \leq L_{\mathcal B}\,( |\boldsymbol{\tau}_1 - \boldsymbol{\tau}_2| + |\lambda_1 - \lambda_2|) \\ {} \qquad \forall \boldsymbol{\tau}_1,\,\boldsymbol{\tau}_2\in S_d,\,\, \forall \lambda_1,\,\lambda_2 \in \mathbb{R},\,\, a.e.\,\, (t,\boldsymbol{x}) \in (0,T)\times \varOmega; \\ {} \mathrm{(iii)} \ \mbox{the partial derivative with respect to the first variable of}\\ \qquad {\mathcal B}\ \mbox{exists and is bunded}. \end{array}\right. \end{aligned} $$

(21)

The body forces and surface tractions satisfy the regularity conditions:

$$\displaystyle \begin{aligned} \boldsymbol{f}_0\in W^{1,2}(0,T;H),\qquad \boldsymbol{f}_F\in W^{1,2}(0,T;L^{2}(\varGamma_F)^d). \end{aligned} $$

(22)

The gap function g  :  (0, T) × Γ _C→R ⁺ verifies

$$\displaystyle \begin{aligned} \left\{ \begin{array}{l} \mathrm{(i)} \; g \in L^\infty((0,T)\times \varGamma_{C};\, {\mathbf{R}}^+);\\ {} \mathrm{(ii)} \ \mbox{the partial derivative with respect to the first variable of}\\ \qquad g\ \mbox{exists and is bounded}. \end{array}\right. \end{aligned} $$

(23)

The thermal expansion tensor $C_e \,:\, (0,T) \times \varOmega \times \mathbb {R} \longrightarrow S_d$ verifies

$$\displaystyle \begin{aligned} \left\{ \begin{array}{ll} \mathrm{(i)} \; C_e(\cdot, \cdot, \vartheta) \mbox{ is measurable on } (0,T)\times \varOmega, \ \forall \vartheta \in \mathbb{R};\\ {} \mathrm{(ii)} \quad \mbox{there exists}\ L_{e} > 0\ \mbox{such that}\\ {} \qquad | {C_e}(t,\boldsymbol{x}, \vartheta_1) - {C_e}(t,\boldsymbol{x}, \vartheta_2)| \leq L_{e}\,|\vartheta_1 - \vartheta_2| \\ {} \qquad \,\, \forall \vartheta_1,\, \vartheta_2 \in \mathbb{R},\,\, a.e.\,\, (t,\boldsymbol{x}) \in (0,T)\times \varOmega; \\ {} \mathrm{(iii)} \; \mbox{there exists } c_0^{C_e} \in L^\infty((0,T)\times \varOmega; \mathbb{R}^+),\ c_1^{C_e} \geq 0 \mbox{ such that } \\ {} \qquad |{C_e}(t, \boldsymbol{x}, \vartheta) | \leq c_0^{C_e}(t,\boldsymbol{x}) + c_1^{C_e}\,|\vartheta|,\\ {} \qquad \forall \vartheta \in \mathbb{R}, \mbox{ for a.e. } (t, \boldsymbol{x}) \in(0,T)\times \varOmega; \\ {} \mathrm{(iv)} \; \mbox{the partial derivatives with respect to the first and third variables}\\ \qquad \mbox{of}\ C_e \ \mbox{ exist and are bounded}. \end{array}\right. \end{aligned} $$

(24)

Here, we use the notation C _e(t, 𝜗) = C _e(t, ⋅, 𝜗) some function defined on Ω, for all t ∈ (0, T) and $\vartheta \in \mathbb {R}$.

The normal compliance function $p_\nu \,:\, (0,T) \times \varGamma _{C} \times \mathbb {R} \longrightarrow \mathbb {R}_+$ satisfies

$$\displaystyle \begin{aligned} \left\{ \begin{array}{l} \mathrm{(i)}\ \mathrm{there\ exists\ } L_\nu>0 \ \mathrm{such\ that}\\ \qquad |p_\nu(t,\boldsymbol{x},r_1)-p_\nu(t,\boldsymbol{x},r_2)| \leq L_\nu |r_1-r_2|,\\ \quad \forall\,r_1,r_2 \in \mathbb{R}, \ \mbox{a.e.}\ (t,\boldsymbol{x}) \in (0,T) \times \varGamma_{C};\\ {} \mathrm{(ii)}\ p_\nu(\cdot,\cdot,r)\ \mathrm{is \ Lebesgue\ measurable\ on\ } (0,T) \times \varGamma_{C},\ \forall\, r\in \mathbb{R}; \\ {} \mathrm{(iii)}\ \mathrm{the\ mapping\ } p_\nu(\cdot,\cdot,r)=0, \ \forall r\le 0;\\ {} \mathrm{(iv)} \; \mbox{the partial derivatives with respect to the first and third variables}\\ \qquad \mbox{of}\ p_\nu \ \mbox{ exist and are bounded}. \end{array} \right. \end{aligned} $$

(25)

The friction bound function $p_\tau \,:\, (0,T) \times \varGamma _{C} \times \mathbb {R} \longrightarrow \mathbb {R}_+$ satisfies

$$\displaystyle \begin{aligned} \left\{ \begin{array}{l} \mathrm{(i)}\ \mathrm{there\ exists\ } L_\tau > 0 \ \mathrm{such\ that}\\ \qquad |p_\tau(t,\boldsymbol{x},r_1)-p_\tau(t,\boldsymbol{x},r_2)| \leq L_\tau |r_1-r_2|,\\ \quad \forall\,r_1,r_2 \in \mathbb{R}, \mbox{ a.e. } (t,\boldsymbol{x}) \in (0,T) \times \varGamma_{C};\\ {} \mathrm{(ii)}\ p_\tau(\cdot,\cdot,r)\ \mathrm{is \ Lebesgue\ measurable\ on\ } (0,T) \times \varGamma_{C},\ \forall\, r\in \mathbb{R}; \\ {} \mathrm{(iii)}\ \mathrm{the\ mapping\ } p_\tau(\cdot,\cdot,r)=0, \ \forall r\le 0 . \end{array} \right. \end{aligned} $$

(26)

The damage source $\phi _d\,: \, \varOmega \times S_d \times S_d \times [0,1] \longrightarrow \mathbb {R}$ verifies

(27)

We assume that the nonlinear function $\mathcal {K}_c : (0,T)\times \varOmega \times \mathbb {R}^d \longrightarrow \mathbb {R}^d$ satisfies

$$\displaystyle \begin{aligned} \left\{ \begin{array}{l} \mathrm{(i)} \; \mathcal{K}_c(\cdot, \cdot, \xi) \mbox{ is measurable on } (0,T)\times \varOmega,\ \forall \xi \in \mathbb{R}^d;\\ {} \mathrm{(ii)} \; \mathcal{K}_c(t,\boldsymbol{x}, \cdot) \mbox{ is continuous on } \mathbb{R}^d, \mbox{ a.e. } (t,\boldsymbol{x})\in (0,T)\times \varOmega;\\ {} \mathrm{(iii)} \; \mbox{there exists } c_0^{\mathcal{K}_c} \in L^2((0,T)\times \varOmega; \mathbb{R}^+),\, c_1^{\mathcal{K}_c} \geq 0, \ \mbox{ such that } \\ \qquad |\mathcal{K}_c(t, \boldsymbol{x}, \xi) | \leq c_0^{\mathcal{K}_c}(t,\boldsymbol{x}) + c_1^{\mathcal{K}_c}\,|\xi|, \\ {} \qquad \forall \xi \in \mathbb{R}^d,\, \mbox{ a.e. } (t, \boldsymbol{x}) \in(0,T)\times \varOmega;\\ {} \mathrm{(iv)} \mbox{ there exists}\ m_{\mathcal{K}_c} > 0\ \mbox{such that}\\ \qquad (\mathcal{K}_c(t, \boldsymbol{x}, \xi_1) - \mathcal{K}_c(t, \boldsymbol{x}, \xi_2) ) \cdot (\xi_1 - \xi_2) \geq m_{\mathcal{K}_c}\, |\xi_1 - \xi_2|{}^2, \\ \qquad \forall \xi_1,\,\xi_2 \in \mathbb{R}^d,\,\, a.e.\,\, (t,\boldsymbol{x}) \in (0,T)\times \varOmega\,;\\ {} \mathrm{(v)} \mbox{ there exists}\ n_{\mathcal{K}_c} > 0\ \mbox{such that} \quad \mathcal{K}_c(t, \boldsymbol{x}, \xi) \cdot \xi \geq n_{\mathcal{K}_c}\, |\xi|{}^2, \\ \qquad \forall \xi \in \mathbb{R}^d,\,\, a.e.\,\, (t,\boldsymbol{x}) \in (0,T)\times \varOmega. \end{array} \right. \end{aligned} $$

(28)

We suppose that the deformation-viscosity heat function $D_{e} : (0,T)\times \varOmega \times S_d \times \mathbb {R} \longrightarrow \mathbb {R}$ satisfies

$$\displaystyle \begin{aligned} \left\{ \begin{array}{l} \mathrm{(i)} \; D_{e}(\cdot, \cdot, \boldsymbol{\tau}, \vartheta) \mbox{ is measurable on } (0,T)\times \varOmega,\ \forall (\boldsymbol{\tau}, \vartheta) \in S_d\times \mathbb{R};\\ {} \mathrm{(ii)} \ \mbox{the function}\ D_{e}(t,\boldsymbol{x},\cdot, \cdot) \ \mbox{is Lypschitz continuous on}\ S_d\times \mathbb{R}, \\ \qquad i.e. \ \exists D_V >0,\, \exists D_T > 0 : \\ {} \qquad \ | D_{e}(t,\boldsymbol{x},\boldsymbol{\tau}_1, \vartheta_1) - D_{e}(t,\boldsymbol{x},\boldsymbol{\tau}_2, \vartheta_2)| \leq D_V\, |\boldsymbol{\tau}_1 - \boldsymbol{\tau}_2| + D_T\,|\vartheta_1 - \vartheta_2|, \\ {} \qquad \quad \forall (\boldsymbol{\tau}_1,\vartheta_1),\, (\boldsymbol{\tau}_2,\vartheta_2) \in S_d\times \mathbb{R},\ \mbox{for a.e.}\,\, (t,\boldsymbol{x}) \in (0,T)\times \varOmega;\\ {} \mathrm{(iii)} \ D_{e}(\cdot, \cdot, 0_{S_d}, 0) \in L^\infty((0,T)\times \varOmega); \\ {} \mathrm{(iv)} \; ( D_{e}(t,\boldsymbol{x},\boldsymbol{\tau}, \vartheta_1) - D_{e}(t,\boldsymbol{x},\boldsymbol{\tau}, \vartheta_2) )\,(\vartheta_1-\vartheta_2) \leq 0, \\ {} \qquad \quad \forall \boldsymbol{\tau} \in S_d,\ \forall \vartheta_1,\,\vartheta_2 \in \mathbb{R},\, \mbox{ a.e. } (t, \boldsymbol{x}) \in(0,T)\times \varOmega. \end{array} \right. \end{aligned} $$

(29)

We notice that these conditions are verified in examples (13)–(15).

The heat sources density verifies

$$\displaystyle \begin{aligned} q \in L^{2}(0,T;L^{2}(\varOmega)). \end{aligned} $$

(30)

We suppose that the nonlinear functions $\varXi ,\,\varphi : (0,T)\times \varGamma _{C} \times \mathbb {R} \longrightarrow \mathbb {R}$ satisfy

$$\displaystyle \begin{aligned} \left\{ \begin{array}{l} \mathrm{(i)} \; \varXi(\cdot, \cdot, r) {\text{ and }} \varphi(\cdot, \cdot, r) \mbox{ are measurable on } (0,T)\times \varGamma_{C},\ \forall r \in \mathbb{R};\\ {} \mathrm{(ii)} \; \varphi(t,\boldsymbol{x},\cdot) \mbox{ is locally Lipschitz on } \mathbb{R} \mbox{ for a.e. } \,\, (t,\boldsymbol{x}) \in (0,T)\times \varGamma_{C};\\ {} \mathrm{(iii)} \; \mbox{there exists } c_0^{\varphi} \in L^2((0,T)\times \varGamma_{C}; \mathbb{R}^+),\, c_1^{\varphi} \geq 0, \ \mbox{ such that } \\ {} \qquad |\varphi^0(t, \boldsymbol{x}, r) | \leq c_0^{\varphi}(t,\boldsymbol{x}) + c_1^{\varphi}\,|r|,\\ {} \qquad \quad \forall r \in \mathbb{R},\, \mbox{ a.e. } (t, \boldsymbol{x}) \in(0,T)\times \varGamma_{C}; \\ {} \mathrm{(iv)} \; (\varXi(t, \boldsymbol{x}, r_1)-\varXi(t, \boldsymbol{x}, r_2))\,(r_1-r_2) \geq 0, \\ {} \qquad \quad \forall r_1,\,r_2 \in \mathbb{R},\, \mbox{ a.e. } (t, \boldsymbol{x}) \in(0,T)\times \varGamma_{C}. \end{array} \right. \end{aligned} $$

(31)

These assumptions are clearly satisfied in example (17).

Finally, we assume that the initial data satisfy the conditions

$$\displaystyle \begin{aligned} \boldsymbol{u}_0 \ \in \ V, \quad \boldsymbol{v}_0 ~ \in ~ V, \quad \theta_0 \in E, \quad \alpha_0 \in \mathcal{K}_{da}. \end{aligned} $$

(32)

Using Green’s formula, we obtain the following weak formulation of the mechanical problem Q, defined by a system of second-order quasi-variational evolution inequality coupled with a first-order evolution equation.

Problem QV : Find a displacement field u : [0, T] → V , a damage field $\alpha : [0,T] \longrightarrow \mathcal {K}_{da}$, and a temperature field θ : [0, T] → E satisfying for a.e. t ∈ (0, T):

$$\displaystyle \begin{aligned} \left\{ \begin{array}{l} \langle \ddot{\boldsymbol{u}}(t)+ A(t)\,\dot{\boldsymbol{u}}(t)+ B(t)(\boldsymbol{u}(t), \alpha(t)) + C(t)\,\theta(t), \, w - \dot{\boldsymbol{u}}(t) \rangle_{V'\times V}, \\ {} + \displaystyle ( \int_0^t\,\mathcal{B}(t-s)\,(\boldsymbol{\varepsilon}(\boldsymbol{u}(s)), \alpha(s) )\,ds, \, \boldsymbol{\varepsilon}(\boldsymbol{w}) - \boldsymbol{\varepsilon}(\dot{\boldsymbol{u}}(t)) )_{\mathcal{H}} \\ {} + j_{\nu}(t,\boldsymbol{u}(t), \boldsymbol{w} - \dot{\boldsymbol{u}}(t) ) + j_{\tau}(t,\boldsymbol{u}(t), \boldsymbol{w}) - j_{\tau}(t,\boldsymbol{u}(t), \dot{\boldsymbol{u}}(t)) \\ {} \qquad \geq \langle \boldsymbol{f}(t),\, \boldsymbol{w} - \dot{\boldsymbol{u}}(t) \rangle_{V'\times V}, \ \forall \boldsymbol{w} \in V. \end{array} \right. \end{aligned} $$

(33)

$$\displaystyle \begin{aligned} \left\{ \begin{array}{l} (\dot{\alpha}(t), \xi- \alpha(t))_{L^2(\varOmega)} + \gamma\,( \nabla\alpha(t),\nabla\xi- \nabla\alpha(t))_{L^2(\varOmega)^d} \\ {} \qquad \geq (\phi_d(\boldsymbol{\sigma}(t),\boldsymbol{\varepsilon}(\boldsymbol{u}(t)),\alpha(t)),\xi- \alpha(t))_{L^2(\varOmega)},\ \forall\,\xi\,\in \mathcal{K}_{da}. \end{array} \right. \end{aligned} $$

(34)

$$\displaystyle \begin{aligned} \left\{ \begin{array}{l} \displaystyle <\dot{\theta}(t), \eta>_{E'\times E} + <K(t)\,\theta(t), \eta>_{E'\times E} + \psi(t,\theta(t);\eta) \\ {} \qquad \geq \, <R(t, \dot{\boldsymbol{u}}(t), \theta(t)), \eta>_{E'\times E} + <Q(t),\eta>_{E'\times E},\ \forall\,\eta\,\in E. \end{array} \right. \end{aligned} $$

(35)

$$\displaystyle \begin{aligned} \boldsymbol{u}(0)=\boldsymbol{u}_0,\quad \dot{\boldsymbol{u}}(0)=\boldsymbol{v}_0,\quad \alpha(0)= \alpha_0,\quad \theta(0)=\theta_0\quad \mbox{in} \quad \varOmega. \end{aligned} $$

(36)

Here, the operators and functions A(t)  :  V →V ′, $B(t)\, : \, V \times \mathcal {K}_{da} \longrightarrow V'$, C(t)  :  E→V ′, $j_{\nu },\, j_{\tau } \, : \, (0,T) \times V^2 \longrightarrow \mathbb {R}^+$, K(t)  :  E→E′, $\psi (t,\cdot ;\cdot )\,:\,E\times E \longrightarrow \mathbb {R}$, R(t, ⋅, ⋅)  :  V × E→E′, f  :  (0, T)→V ′, and Q  :  (0, T)→E′ are defined by, for all v  ∈ V , w  ∈ V , ζ  ∈ E, η  ∈ E, $\xi \in \mathcal {K}_{da}$, for a.e. t ∈ (0, T),

$$\displaystyle \begin{aligned} \begin{array}l \langle A(t)\,\boldsymbol{v},\boldsymbol{w} \rangle_{V'\times V} = (\mathcal{A}(t)(\boldsymbol{\varepsilon} \boldsymbol{v}),\boldsymbol{\varepsilon} \boldsymbol{w})_{\mathcal{H}};\\ {} \langle B(t)(\boldsymbol{v},\xi),\boldsymbol{w}\rangle_{V'\times V} =(\mathcal{G}(t)(\boldsymbol{\varepsilon} \boldsymbol{v}, \xi),\boldsymbol{\varepsilon} \boldsymbol{w})_{\mathcal{H}};\\ {} \langle C(t) \zeta,\boldsymbol{w}\rangle_{V'\times V} = (C_e(t, \zeta(\cdot)),\, \boldsymbol{\varepsilon} \boldsymbol{w})_{\mathcal{H}};\\ {} \displaystyle j_{\nu}(t, \boldsymbol{v}, \boldsymbol{w} ) = \int_{\varGamma_{C}}\,p_{\nu}(t, v_{\nu} - g(t))\,w_{\nu}\,da;\\ {} \displaystyle j_{\tau}(t,\boldsymbol{v}, \boldsymbol{w}) = \int_{\varGamma_{C}}\, p_{\tau}(t, v_{\nu} -g(t))\,|\boldsymbol{w}_{\tau}|\,da;\\ {} \langle {\boldsymbol{f}}(t),\boldsymbol{w} \rangle_{V'\times V} = ({\boldsymbol{f}}_0(t),\boldsymbol{w} )_H \,+ ({\boldsymbol{f}}_F(t),\boldsymbol{w})_{(L^2(\varGamma_F))^d};\\ {} \displaystyle \langle K(t)\,\zeta,\eta\rangle_{E'\times E} = \int_{\varOmega}\, \mathcal{K}_c(t, \nabla\zeta)\cdot \nabla \eta \,dx ;\\ {} \displaystyle \psi(t, \zeta; \eta) = \int_{\varGamma_{C}} \varphi^0(t,x,\zeta(x);\eta(x))\, da(x);\\ {} \displaystyle \langle R(t, \boldsymbol{v}, \zeta),\eta \rangle_{E'\times E} = \int_{\varOmega} \, D_{e}(t,\boldsymbol{\varepsilon}(\boldsymbol{v}), \zeta) \,\eta\,dx;\\ {} \displaystyle \langle Q(t), \eta \rangle_{E'\times E} = \int_\varOmega q(t)\, \eta\,dx. \end{array} \end{aligned}$$

We notice that from (31), then the formula ψ(t, ζ;η) is well defined for all ζ  ∈ E, η  ∈ E, for a.e. t ∈ (0, T).

The inequality (35) is a consequence of the following equation:

$$\displaystyle \begin{aligned} \left\{ \begin{array}{l} \displaystyle <\dot{\theta}(t), \eta>_{E'\times E} + <K(t)\,\theta(t), \eta>_{E'\times E} + \int_{\varGamma_{C}}\, \varXi(t,\theta(t)) \eta \,da \\ {} \qquad = \, <R(t, \dot{\boldsymbol{u}}(t), \theta(t)), \eta>_{E'\times E} + <Q(t),\eta>_{E'\times E},\ \forall\,\eta\,\in E, \end{array} \right. \end{aligned} $$

(37)

where Ξ(t, r) := Ξ(t, ⋅, r) for $(t,r)\in (0,T)\times \mathbb {R}$.

In the case when φ(t, x, ⋅) is differentiable for a.e. (t, x) ∈ (0, T) × Γ _c, we have

$$\displaystyle \begin{aligned} \varXi(t,\boldsymbol{x},r) = \varphi'(t,\boldsymbol{x},r) := [\varphi(t,\boldsymbol{x},\cdot)]'(r) \end{aligned}$$

for $(t,\boldsymbol {x},r)\in (0,T)\times \varGamma _{C} \times \mathbb {R}$.

Then, for all ζ ∈ E and a.e. t ∈ (0, T), the linear functional

$$\displaystyle \begin{aligned} \eta \in E \mapsto \psi(t,\zeta;\eta) =\int_{\varGamma_{C}} \varXi(t,\zeta)\eta da = \int_{\varGamma_{C}} \varphi'(t,x,\zeta(x))\eta(x) da(x) \end{aligned}$$

will be denoted by

$$\displaystyle \begin{aligned} \varPhi(t,\zeta) \in E'.\end{aligned}$$

The inequality (35) or Equation (37) can be written as

$$\displaystyle \begin{aligned} \displaystyle \dot{\theta}(t) + K(t)\,\theta(t) + \varPhi(t,\theta(t)) = R(t, \dot{\boldsymbol{u}}(t), \theta(t)) + Q(t) \quad \mbox{ in }\ E'. \end{aligned}$$

Our main existence and uniqueness result is the following, which we will prove in the next section.

Theorem 1

Assume that (19)–(32) hold, and under the condition that

$$\displaystyle \begin{aligned} L_{\tau} < \frac{m_{\mathcal{A}}}{\sqrt{2}\, T c_0^2},\end{aligned}$$

then there exists an unique solution {u, α, θ} to problem QV  with the regularity:

$$\displaystyle \begin{aligned} \left\{ \begin{aligned} & \boldsymbol{u}\in C^{1}(0,T;H)\cap W^{1,2}(0,T;V) \cap W^{2,2}(0,T;V');\\ & \alpha \in W^{1,2}(0,T;L^2(\varOmega)) \cap L^\infty(0,T;\mathcal{K}_{da});\\ & \theta\in C(0,T;L^2(\varOmega))\cap L^{2}(0,T;E) \cap W^{1,2}(0,T;E'). \end{aligned} \right. \end{aligned} $$

(38)

3 Proof of Theorem 1

The idea is to bring the second-order inequality to a first-order inequality, using monotone operator, convexity, and fixed point arguments, and will be carried out in several steps.

Let us introduce the velocity variable

$$\displaystyle \begin{aligned} \boldsymbol{v} = \dot{\boldsymbol{u}}. \end{aligned}$$

The system in problem QV  is then written as, for a.e. t ∈ (0, T),

$$\displaystyle \begin{aligned} \left\{ \begin{array}l \displaystyle {\boldsymbol{u}}(t) = \boldsymbol{u}_0 + \int_0^t\,{\boldsymbol{v}}(s)\,ds; \\ {} \langle \dot{\boldsymbol{v}}(t)+ A(t)\,{\boldsymbol{v}}(t)+ B(t)(\boldsymbol{u}(t), \alpha(t)) + C(t)\,\theta(t), \, \boldsymbol{w} - {\boldsymbol{v}}(t) \rangle_{V'\times V}, \\ {} + \displaystyle ( \int_0^t\,\mathcal{B}(t-s)\,(\boldsymbol{\varepsilon}(\boldsymbol{u}(s)), \alpha(s) )\,ds, \, \boldsymbol{\varepsilon}(\boldsymbol{w}) - \boldsymbol{\varepsilon}({\boldsymbol{v}}(t)) )_{\mathcal{H}} \\ {} + j_{\nu}(t ,\boldsymbol{u}(t), \boldsymbol{w} - {\boldsymbol{v}}(t) ) + j_{\tau}(t,\boldsymbol{u}(t), \boldsymbol{w}) - j_{\tau}(t,\boldsymbol{u}(t), {\boldsymbol{v}}(t)) \\ {} \qquad \geq \langle \boldsymbol{f}(t),\, \boldsymbol{w} - {\boldsymbol{v}}(t) \rangle_{V'\times V}, \ \forall \boldsymbol{w} \in V; \\ {} (\dot{\alpha}(t), \xi- \alpha(t))_{L^2(\varOmega)} + \gamma\,( \nabla\alpha(t),\nabla\xi- \nabla\alpha(t))_{L^2(\varOmega)^d} \\ {} \qquad \geq (\phi_d(\boldsymbol{\sigma}(t),\boldsymbol{\varepsilon}(\boldsymbol{u}(t)),\alpha(t)),\xi- \alpha(t))_{L^2(\varOmega)},\quad \forall\,\xi\,\in \mathcal{K}_{da}; \\ {} \displaystyle <\dot{\theta}(t), \eta>_{E'\times E} + <K(t)\,\theta(t), \eta>_{E'\times E} +\psi(t,\theta(t);\eta) \\ {} \qquad \geq <R(t, {\boldsymbol{v}}(t), \theta(t)), \eta>_{E'\times E} + <Q(t),\eta>_{E'\times E},\ \forall\,\eta\,\in E;\\ {} {\boldsymbol{v}}(0)=\boldsymbol{v}_0,\quad \alpha(0)= \alpha_0,\quad \theta(0)=\theta_0\quad \mbox{in} \quad \varOmega, \end{array} \right.\end{aligned}$$

with the regularities:

$$\displaystyle \begin{aligned} \left\{ \begin{array}l \boldsymbol{v} \in C(0,T;H)\cap L^{2}(0,T;V) \cap W^{1,2}(0,T;V');\\ {} \alpha \in W^{1,2}(0,T;L^2(\varOmega)) \cap L^\infty(0,T;\cal{K});\\ {} \theta\in C(0,T;L^2(\varOmega))\cap L^{2}(0,T;E) \cap W^{1,2}(0,T;E'). \end{array} \right. \end{aligned}$$

We begin by the following lemma.

Lemma 1

For all η ∈ W ^{1, 2}(0, T;V ′), there exists an unique

$$\displaystyle \begin{aligned} \boldsymbol{v}_\eta \in C(0,T;H)\cap L^{2}(0,T;V) \cap W^{1,2}(0,T;V') \end{aligned}$$

satisfying

$$\displaystyle \begin{aligned} \left\{ \begin{aligned} & \langle \dot{\boldsymbol{v}}_\eta(t) + A(t)\,\boldsymbol{v}_\eta(t),\, \boldsymbol{w} - \boldsymbol{v}_\eta(t) \rangle_{V'\times V} + \langle \eta(t), \boldsymbol{w} - \boldsymbol{v}_\eta(t) \rangle_{V'\times V} \\ & \quad + j_{\tau}(t, \boldsymbol{u}_{\eta}(t), \boldsymbol{w}) - j_{\tau}(t, \boldsymbol{u}_{\eta}(t), {\boldsymbol{v}}_{\eta}(t)) \geq \langle \boldsymbol{f}(t), \boldsymbol{w}-\boldsymbol{v}_\eta(t) \rangle_{V'\times V}, \\ & \qquad \qquad \quad \forall\, \boldsymbol{w} \in V,\quad \mathit{\mbox{a.e.}}\ t \in (0,T); \\ & \boldsymbol{v}_\eta(0)=\boldsymbol{v}_0, \end{aligned} \right. \end{aligned} $$

(39)

where

$$\displaystyle \begin{aligned} {\boldsymbol{u}}_\eta(t) = \boldsymbol{u}_0 + \int_0^t\,{\boldsymbol{v}}_\eta(s)\,ds,\quad \forall t\in [0,T].\end{aligned}$$

Moreover, if $L_{\tau } < \frac {m_{\mathcal {A}}}{\sqrt {2}\, T c_0^2}$ , then ∃c > 0 such that ∀η ₁, η ₂ ∈ W ^{1, 2}(0, T;V ′), ∀t ∈ [0, T]:

$$\displaystyle \begin{aligned} \|{\boldsymbol{v}}_{\eta_2}(t) - {\boldsymbol{v}}_{\eta_1}(t) \|{}_H^2 + \int_0^t\,\| \boldsymbol{v}_{\eta_2}-\boldsymbol{v}_{\eta_1} \|{}_V^2 \leq c\,\int_0^t\,\| \eta_1-\eta_2 \|{}_{V'}^2. \end{aligned} $$

(40)

Proof

Given η ∈ W ^{1, 2}(0, T;V ′) and x ∈ C(0, T;V ), by using a general result on parabolic variational inequality (see e.g. [1]), we obtain the existence of a unique v _{η x} ∈ C(0, T;H) ∩ L ²(0, T;V ) ∩ W ^{1, 2}(0, T;V ′) satisfying

$$\displaystyle \begin{aligned} \left\{ \begin{aligned} & \langle \dot{\boldsymbol{v}}_{\eta\,x}(t) + A(t)\,\boldsymbol{v}_{\eta\,x}(t),\, \boldsymbol{w} - \boldsymbol{v}_{\eta\,x}(t) \rangle_{V'\times V} + \langle \eta(t), \boldsymbol{w} - \boldsymbol{v}_{\eta\,x}(t) \rangle_{V'\times V} \\ & \quad + j_{\tau}(t,x(t), \boldsymbol{w}) - j_{\tau}(t,x(t), {\boldsymbol{v}}_{\eta\,x}(t)) \geq \langle \boldsymbol{f}(t), \boldsymbol{w}-\boldsymbol{v}_{\eta\,x}(t) \rangle_{V'\times V}, \\ & \qquad \qquad \quad \forall\, \boldsymbol{w} \in V,\quad \mbox{a.e.}\ t \in (0,T); \\ & \boldsymbol{v}_{\eta\,x}(0)=\boldsymbol{v}_0. \end{aligned} \right. \end{aligned} $$

(41)

Now, let us fix η ∈ W ^{1, 2}(0, T;V ′) and consider Λ _η  :  C(0, T;V ) → C(0, T;V ) defined by

$$\displaystyle \begin{aligned} \forall x \in C(0,T;V), \quad \varLambda_\eta x \,(t) = \boldsymbol{u}_0 + \int_0^t\, \boldsymbol{v}_{\eta\,x}(s) \, ds. \end{aligned}$$

We check by algebraic manipulation that for all u ₁, u ₂, w ₁, w ₂ ∈ V , a.e. t ∈ (0, T), we have

$$\displaystyle \begin{aligned} j_{\tau}(t,\boldsymbol{u}_1, \boldsymbol{w}_2) - j_{\tau}(t,\boldsymbol{u}_1, \boldsymbol{w}_1) + j_{\tau}(t,\boldsymbol{u}_2, \boldsymbol{w}_1) - j_{\tau}(t,\boldsymbol{u}_2, \boldsymbol{w}_2) \leq c_1\, \| \boldsymbol{u}_2 - \boldsymbol{u}_1 \|{}_V \, \| \boldsymbol{w}_2 - \boldsymbol{w}_1 \|{}_V,\end{aligned}$$

where $c_1 = L_\tau \, c_0^2$ is involving c ₀, which is defined by (18).

Let x ₁, x ₂ ∈ C(0, T;V ) be given. Putting in (41) the data x = x ₁ with $\boldsymbol {w} = \boldsymbol {v}_{\eta \,x_2}$ and x = x ₂ with $\boldsymbol {w} = \boldsymbol {v}_{\eta \,x_1}$, adding then the two inequalities, and integrating over (0, T), we obtain, ∀t ∈ [0, T],

$$\displaystyle \begin{aligned} & \|{\boldsymbol{v}}_{\eta\,x_2}(t) - {\boldsymbol{v}}_{\eta\,x_1}(t) \|{}_H^2 + \int_0^t\,\| \boldsymbol{v}_{\eta\,x_2}(s) -\boldsymbol{v}_{\eta\,x_1}(s) \|{}_V^2 ds \\ & \leq c\,\int_0^t\,\| x_2(s)-x_1(s) \|{}_{V}^2 ds + c\,\int_0^t\, \|{\boldsymbol{v}}_{\eta\,x_2}(s)-{\boldsymbol{v}}_{\eta\,x_1}(s)\|{}_H^2 \,ds. \end{aligned}$$

Using Gronwall’s inequality (see e.g. [2]), we deduce that

$$\displaystyle \begin{aligned} \forall x_1, x_2 \in C(0,T;V),\ \forall t\in [0,T],\quad \| \varLambda_\eta(x_2)(t) - \varLambda_\eta(x_1)(t) \|{}_V^2 \leq c\,\int_0^t\,\| x_2(s)-x_1(s) \|{}_{V}^2 ds.\end{aligned}$$

Thus, by Banach’s fixed point principle, we know that Λ _η has an unique fixed point denoted by x _η. We then verify that

$$\displaystyle \begin{aligned} \boldsymbol{v}_\eta = \boldsymbol{v}_{\eta\,x_\eta} \end{aligned}$$

is the unique solution verifying (39).

Now, let η ₁, η ₂ ∈ W ^{1, 2}(0, T;V ′). Putting in (39) the data η = η ₁ with $\boldsymbol {w} = \boldsymbol {v}_{\eta _2}$ and η = η ₂ with $\boldsymbol {w} = \boldsymbol {v}_{\eta _1}$, adding then the two inequalities and integrating over (0, T), and using the inequality

$$\displaystyle \begin{aligned} |a \, b| \leq \frac{\varepsilon}{4}\,a^2 + \frac{1}{\varepsilon}\,b^2 \end{aligned}$$

for all reals a, b, ε > 0, we obtain for all δ > 0, for all t ∈ [0, T]:

$$\displaystyle \begin{aligned} \begin{array}{l} \displaystyle \frac{1}{2} \, \|{\boldsymbol{v}}_{\eta_2}(t) - {\boldsymbol{v}}_{\eta_1}(t) \|{}_H^2 + m_{\mathcal{A}}\, \int_0^t\,\| \boldsymbol{v}_{\eta_2}(s) -\boldsymbol{v}_{\eta_1}(s) \|{}_V^2 ds \\ {} \displaystyle \leq m_{\mathcal{A}}\,\,\int_0^t\, \|{\boldsymbol{v}}_{\eta_2}(s)-{\boldsymbol{v}}_{\eta_1}(s)\|{}_H^2 \,ds + \frac{c_1^2}{4\delta}\,\int_0^t\, \|{\boldsymbol{u}}_{\eta_2}(s)-{\boldsymbol{u}}_{\eta_1}(s)\|{}_V^2 \,ds\\ {} \displaystyle + \delta\, \int_0^t\,\| \boldsymbol{v}_{\eta_2}(s) -\boldsymbol{v}_{\eta_1}(s) \|{}_V^2 ds + \int_0^t\,\| \boldsymbol{v}_{\eta_2}(s) -\boldsymbol{v}_{\eta_1}(s) \|{}_V\,\| \eta_2(s)-\eta_1(s) \|{}_{V'} ds. \\ {} \displaystyle \leq m_{\mathcal{A}}\,\,\int_0^t\, \|{\boldsymbol{v}}_{\eta_2}(s)-{\boldsymbol{v}}_{\eta_1}(s)\|{}_H^2 \,ds + \frac{c_1^2}{4\delta}\,\int_0^t\, \|{\boldsymbol{u}}_{\eta_2}(s)-{\boldsymbol{u}}_{\eta_1}(s)\|{}_V^2 \,ds\\ {} \displaystyle + 2\delta\, \int_0^t\,\| \boldsymbol{v}_{\eta_2}(s) -\boldsymbol{v}_{\eta_1}(s) \|{}_V^2 ds + \frac{1}{4\delta}\,\int_0^t\,\| \eta_2(s)-\eta_1(s) \|{}_{V'}^2 ds. \end{array} \end{aligned}$$

Now, verifying that

$$\displaystyle \begin{aligned} \int_0^t\, \|{\boldsymbol{u}}_{\eta_2}(s)-{\boldsymbol{u}}_{\eta_1}(s)\|{}_V^2 \,ds \leq T^2\,\int_0^t\, \|{\boldsymbol{v}}_{\eta_2}(s)-{\boldsymbol{v}}_{\eta_1}(s)\|{}_V^2 \,ds, \end{aligned}$$

we have

$$\displaystyle \begin{aligned} \begin{array}{l} \displaystyle \frac{1}{2} \, \|{\boldsymbol{v}}_{\eta_2}(t) - {\boldsymbol{v}}_{\eta_1}(t) \|{}_H^2 + (m_{\mathcal{A}} - 2\delta)\, \int_0^t\,\| \boldsymbol{v}_{\eta_2}(s) -\boldsymbol{v}_{\eta_1}(s) \|{}_V^2 ds \\ {} \leq m_{\mathcal{A}}\,\,\int_0^t\, \|{\boldsymbol{v}}_{\eta_2}(s)-{\boldsymbol{v}}_{\eta_1}(s)\|{}_H^2 \,ds + \frac{c_1^2}{4\delta}\,T^2\,\int_0^t\, \|{\boldsymbol{v}}_{\eta_2}(s)-{\boldsymbol{v}}_{\eta_1}(s)\|{}_V^2 \,ds\\ {} \quad + \frac{1}{4\delta}\,\int_0^t\,\| \eta_2(s)-\eta_1(s) \|{}_{V'}^2 ds. \end{array} \end{aligned}$$

We deduce (40) from Gronwall’s inequality if

$$\displaystyle \begin{aligned} \frac{c_1^2}{4\delta}\,T^2 < m_{\mathcal{A}} - 2\delta, \end{aligned}$$

i.e.

$$\displaystyle \begin{aligned} L_{\tau} < \frac{m_{\mathcal{A}}}{T c_0^2}\, \sqrt{2\varsigma (1-\varsigma)}, \end{aligned}$$

where

$$\displaystyle \begin{aligned} \varsigma = \frac{2\delta}{m_{\mathcal{A}}} \in ]0,1[.\end{aligned}$$

To conclude, we obtain (40) if ∃ς ∈ ]0, 1[ such that $L_{\tau } < \frac {m_{\mathcal {A}}}{T c_0^2}\, \sqrt {2\varsigma (1-\varsigma )}$. This last condition is equivalent to

$$\displaystyle \begin{aligned} L_{\tau} < \frac{m_{\mathcal{A}}}{\sqrt{2} T c_0^2}. \end{aligned}$$

□

Here and below, we denote by c > 0 a generic constant, which value may change from lines to lines.

Lemma 2

For all η ∈ W ^{1, 2}(0, T;V ′), there exists a unique

$$\displaystyle \begin{aligned} \theta_\eta \in C(0,T;L^2(\varOmega))\cap L^{2}(0,T;E) \cap W^{1,2}(0,T;E') \end{aligned}$$

satisfying

$$\displaystyle \begin{aligned} \left\{ \begin{array}{l} \displaystyle <\dot{\theta}_\eta(t), \zeta>_{E'\times E} + <K(t)\,\theta_\eta(t), \zeta>_{E'\times E} + \int_{\varGamma_{C}}\, \varXi(t,\theta_\eta(t))\, \zeta \,da \\ {} \qquad = \, <R(t, {\boldsymbol{v}}_\eta(t), \theta_\eta(t)), \zeta>_{E'\times E} + <Q(t),\zeta>_{E'\times E}, \\ {} \qquad \quad \forall\,\zeta\,\in E,\ \mathit{\mbox{a.e.}} \ t \in (0,T);\\ {} \ \theta_\eta(0)=\theta_0. \end{array} \right. \end{aligned} $$

(42)

Moreover, if $L_{\tau } < \frac {m_{\mathcal {A}}}{\sqrt {2}\, T c_0^2}$ , then ∃c > 0 such that ∀η ₁, η ₂ ∈ W ^{1, 2}(0, T;V ′):

$$\displaystyle \begin{aligned} \| \theta_{\eta_1}(t) - \theta_{\eta_2}(t) \|{}_{L^2(\varOmega)}^2 \leq c\,\int_0^t\,\|{\eta_1} -{\eta_2} \|{}_{V'}^2, \quad \forall t\in [0,T]. \end{aligned} $$

(43)

Proof

Let us fix η ∈ W ^{1, 2}(0, T;V ′). We verify that Q ∈ L ²(0, T;E′).

Let us consider the operator Ψ _η(t)  :  E→E′ defined for a.e. t ∈ (0, T) by

$$\displaystyle \begin{aligned} \left\{ \begin{array}{l} \displaystyle <\varPsi_\eta(t)\,\xi, \zeta>_{E'\times E} := <K(t)\,\xi, \zeta>_{E'\times E} + \int_{\varGamma_{C}}\, \varXi(t,\xi)\, \zeta \,da - <R(t, \boldsymbol{v}_\eta(t), \xi), \zeta>_{E'\times E},\\ {} \quad \forall\,\xi,\,\zeta\,\in E. \end{array} \right. \end{aligned}$$

Then, the problem is to find θ  :  (0, T)→E verifying

$$\displaystyle \begin{aligned} \left\{ \begin{array}{l} \displaystyle \dot{\theta}(t) + \varPsi_\eta(t)\, \theta(t) = Q(t)\ \mbox{in}\ E',\ \mbox{a.e.} \ t \in (0,T);\\ {} \theta(0)=\theta_0. \end{array} \right. \end{aligned}$$

Using the assumptions (28), (29), and (31), Ψ _η(t) is strongly monotone for a.e. t ∈ (0, T). Therefore, the existence and uniqueness result verifying (42) follows from classical result on first-order evolution equation (see e.g. [9], pp. 162–164).

Now, for η ₁, η ₂ ∈ W ^{1, 2}(0, T;V ′), we have, for a.e. t ∈ (0;T),

$$\displaystyle \begin{aligned}\begin{array}{l} \langle \dot{\theta}_{\eta_1}(t)-\dot{\theta}_{\eta_2}(t), {\theta}_{\eta_1}(t) - {\theta}_{\eta_2}(t) \rangle_{E'\times E} + \langle K(t)\,{\theta}_{\eta_1}(t)- K(t)\,{\theta}_{\eta_2}(t),\, {\theta}_{\eta_1}(t)-{\theta}_{\eta_2}(t) \rangle_{E'\times E} \\ {} \leq \langle R(t,\,{\boldsymbol{v}}_{\eta_1}(t), \theta_{\eta_1}(t)) - R(t,\,{\boldsymbol{v}}_{\eta_2}(t), \theta_{\eta_2}(t)),\,{\theta}_{\eta_1}(t)-{\theta}_{\eta_2}(t) \rangle_{E'\times E}. \end{array}\end{aligned}$$

Then, integrating the last property over (0, t), using the strong monotonicity of K(t) and the Lipschitz continuity of R(t, ⋅, ⋅)  :  V × E→E′ independently of t ∈ (0, T), we deduce

$$\displaystyle \begin{aligned} \| \theta_{\eta_1}(t) - \theta_{\eta_2}(t) \|{}_{L^2(\varOmega)}^2 \leq c\,\int_0^t\,\| \boldsymbol{v}_{\eta_1} -\boldsymbol{v}_{\eta_2} \|{}_{V}^2, \quad \forall t\in [0,T]. \end{aligned}$$

The inequality (43) follows then from Lemma 1. □

Lemma 3

For all μ ∈ L ²(0, T;L ²(Ω)), there exists an unique

$$\displaystyle \begin{aligned} \alpha_\mu \in W^{1,2}(0,T;L^2(\varOmega)) \cap L^2(0,T;H^1(\varOmega)) \end{aligned}$$

satisfying

$$\displaystyle \begin{aligned} \left\{ \begin{aligned} & (\dot{\alpha_\mu}(t), \xi- \alpha_\mu(t))_{L^2(\varOmega)} + \gamma\,( \nabla\alpha_\mu(t),\nabla\xi- \nabla\alpha_\mu(t))_{L^2(\varOmega)^d} \\ & \qquad \geq (\mu(t),\xi- \alpha_\mu(t))_{L^2(\varOmega)},\quad \forall\,\xi\,\in \mathcal{K}_{da},\quad \mathit{\mbox{a.e.}} \ t\in (0,T);\\ & \alpha_\mu(t) \in \mathcal{K}_{da},\quad \forall t\in [0,T]; \\ & \alpha_\mu(0) = \alpha_0. \end{aligned} \right. \end{aligned} $$

(44)

Moreover, ∃c > 0 such that ∀μ ₁, μ ₂ ∈ L ²(0, T;L ²(Ω)):

$$\displaystyle \begin{aligned} \| \alpha_{\mu_2}(t) - \alpha_{\mu_1}(t) \|{}_{L^2(\varOmega)}^2 \leq c\,\int_0^t\,\|{\mu_1} -{\mu_2} \|{}_{L^2(\varOmega)}^2, \quad \forall t\in [0,T]. \end{aligned} $$

(45)

Proof

The inequality (44) follows from classical result on parabolic evolution variational inequalities, see e.g. [1].

Now, for any μ ₁, μ ₂ ∈ L ²(0, T;L ²(Ω)), putting in (44) the data μ = μ ₁ with $\xi = \alpha _{\mu _2}$, then μ = μ ₂ with $\xi = \alpha _{\mu _1}$, adding then the two inequalities, and integrating over (0, T), we obtain, ∀t ∈ [0, T],

$$\displaystyle \begin{aligned} &\frac{1}{2} \| \alpha_{\mu_1}(t) - \alpha_{\mu_2}(t) \|{}_{L^2(\varOmega)}^2 + \gamma\,\int_0^t\, \| \nabla\alpha_{\mu_1} - \nabla\alpha_{\mu_2} \|{}_{L^2(\varOmega)^d}^2 \\ &\quad \leq \int_0^t\,\|{\mu_1} -{\mu_2} \|{}_{L^2(\varOmega)}\| \alpha_{\mu_1} - \alpha_{\mu_2} \|{}_{L^2(\varOmega)}. \end{aligned} $$

Thus, the inequality (45) follows from Gronwall’s inequality. □

Consider X := W ^{1, 2}(0, T;V ′) × L ²(0, T;L ²(Ω)), and the operator Λ  :  X → X is defined by, for all (η, μ) ∈ X,

$$\displaystyle \begin{aligned} & \varLambda\,(\eta, \mu) = (\varLambda_1(\eta, \mu),\, \varLambda_2(\eta, \mu)); \\ & \varLambda_1(\eta, \mu)(t) = B(t)(\boldsymbol{u}_\eta(t), \alpha_\mu(t) ) + D(t)(\boldsymbol{u}_\eta,\alpha_\mu) + j_\nu( t, \boldsymbol{u}_\eta(t), \cdot) + C(t)\,\theta_\eta(t);\\ & \varLambda_2(\eta, \mu)(t) = \phi_d(\boldsymbol{\sigma}_{\eta, \mu}(t),\boldsymbol{\varepsilon}(\boldsymbol{u}_\eta (t)),\alpha_\mu(t)), \end{aligned}$$

where

$$\displaystyle \begin{aligned} \langle D(t)(\boldsymbol{u}_\eta,\alpha_\mu),\boldsymbol{w}\rangle_{V'\times V} =( \int_0^t\,\mathcal{B}(t-s)\,(\boldsymbol{\varepsilon}(\boldsymbol{u}_\eta(s)), \alpha_\mu(s))\,ds,\, \boldsymbol{\varepsilon} \boldsymbol{w})_{\mathcal{H}},\quad \forall \boldsymbol{w} \in V;\end{aligned}$$

and

$$\displaystyle \begin{aligned} \boldsymbol{\sigma}_{\eta, \mu}(t) &= \mathcal{A}(t)\boldsymbol{\varepsilon}(\boldsymbol{v}_\eta(t))+ \mathcal{G}(t)(\boldsymbol{\varepsilon}(\boldsymbol{u}_\eta(t)), \alpha_\mu(t)) \\ &+ \int_0^t\,\mathcal{B}(t-s)\,(\boldsymbol{\varepsilon}(\boldsymbol{u}_\eta(s)), \alpha_\mu(s))\,ds + C_e(t, \theta_\eta(t)). \end{aligned} $$

Lemma 4

Under the condition that $L_{\tau } < \frac {m_{\mathcal {A}}}{\sqrt {2}\, T c_0^2}$ , then Λ has a unique fixed point (η ^∗, μ ^∗).

Proof

First, we check that from the definition of the operator C(⋅) and from hypothesis (24), then there exists c > 0, such that for a.e. t ∈ (0, T), for all ξ ₁, ξ ₂ ∈ E, we have

$$\displaystyle \begin{aligned} \| C(t)\,\xi_1 - C(t)\, \xi_2\|{}_{V'} \leq c \, \| \xi_1- \xi_2\|{}_{L^2(\varOmega)}. \end{aligned}$$

Now, let (η ₁, μ ₁) and (η ₂, μ ₂) be given in X. We verify that, for a.e. t ∈ (0, T),

$$\displaystyle \begin{aligned} \begin{array}l \|{\varLambda}(\eta_1, \mu_1)(t) - {\varLambda}(\eta_2, , \mu_2)(t) \|{}_{V'\times L^2(\varOmega)}^2\\ {} \leq c\, \| B(t)(\boldsymbol{u}_{\eta_1}(t), \alpha_{\mu_1}(t) ) - B(t)(\boldsymbol{u}_{\eta_2}(t), \alpha_{\mu_2}(t)) \|{}_{V'}^2 + c\, \| D(t)(\boldsymbol{u}_{\eta_1},\alpha_{\mu_1}) - D(t)(\boldsymbol{u}_{\eta_2},\alpha_{\mu_2}) \|{}_{V'}^2 \\ {} \quad c\, \| j_\nu(t, \boldsymbol{u}_{\eta_1}(t),\cdot) - j_\nu(t, \boldsymbol{u}_{\eta_2}(t),\cdot ) \|{}_{V'}^2 + c\,\| C(t)\,\theta_{\eta_1}(t) - C(t)\,\theta_{\eta_2}(t) \|{}_{V'}^2 \\ {} \quad + \| \phi_d(\boldsymbol{\sigma}_{\eta_1, \mu_1}(t),\boldsymbol{\varepsilon}(\boldsymbol{u}_{\eta_1} (t)),\alpha_{\mu_1}(t)) - \phi_d(\boldsymbol{\sigma}_{\eta_2, \mu_2}(t),\boldsymbol{\varepsilon}(\boldsymbol{u}_{\eta_2} (t)),\alpha_{\mu_2}(t)) \|{}_{L^2(\varOmega)}^2. \end{array}\end{aligned}$$

Thus,

$$\displaystyle \begin{aligned} & \|{\varLambda}(\eta_1, \mu_1)(t) - {\varLambda}(\eta_2, , \mu_2)(t) \|{}_{V'\times L^2(\varOmega)}^2\\ & \leq c\, \| \boldsymbol{u}_{\eta_1}(t) - \boldsymbol{u}_{\eta_2}(t)\|{}_{V}^2 + c\,\| \alpha_{\mu_1}(t)-\alpha_{\mu_2}(t) \|{}_{L^2(\varOmega)}^2 + c\, \| \theta_{\eta_1}(t) - \theta_{\eta_2}(t) \|{}_{L^2(\varOmega)}^2\\ &+ c\, \| \boldsymbol{v}_{\eta_1}(t) - \boldsymbol{v}_{\eta_2}(t)\|{}_H^2. \end{aligned}$$

We deduce from Lemmas 1–3 that if $L_{\tau } < \frac {m_{\mathcal {A}}}{\sqrt {2} T c_0^2}$, then ∃c > 0 satisfying, for all (η ₁, μ ₁), (η ₂, μ ₂) in X and for all t ∈ [0, T],

$$\displaystyle \begin{aligned} \|{\varLambda}(\eta_1, \mu_1)(t) {\kern-1pt}-{\kern-1pt} {\varLambda}(\eta_2, , \mu_2)(t) \|{}_{V'\times L^2(\varOmega)}^2 {\kern-1pt}\leq{\kern-1pt} c\, \int_0^t\,\| {\eta_2} - {\eta_1} \|{}_{V'}^2 {\kern-1pt}+{\kern-1pt} c\, \int_0^t\,\|{\mu_1}{\kern-1pt}-{\kern-1pt}{\mu_2} \|{}_{L^2(\varOmega)}^2.\end{aligned}$$

Then, using again Banach’s fixed point principle, we obtain that Λ has an unique fixed point. □

Proof of Theorem 1

We have now all the ingredients to prove Theorem 1.

We verify then that the functions

$$\displaystyle \begin{aligned} {\boldsymbol{u}} := {\boldsymbol{u}}_{\eta^*},\quad \alpha := \alpha_{\mu^*}, \quad \theta := \theta_{\eta^*}\end{aligned}$$

are solutions to problem QV  with the regularities in (38), the uniqueness follows from the uniqueness in Lemmas 1–3. □

4 Analysis of a Numerical Scheme

In this section, we study a fully discrete numerical approximation scheme of the variational problem QV . For this purpose, let {u, θ} be the unique solution of the problem QV , and introduce the velocity variable

$$\displaystyle \begin{aligned} \boldsymbol{v}(t)=\dot{\boldsymbol{u}}(t),\quad \forall t\in [0,T]. \end{aligned}$$

Then,

$$\displaystyle \begin{aligned} \boldsymbol{u}(t)= \boldsymbol{u}_0 + \int_0^t \boldsymbol{v}(s)\,ds,\quad \forall t\in [0,T]. \end{aligned} $$

(46)

Here, we make the following additional assumptions on the different data, operators, and solution fields:

$$\displaystyle \begin{aligned} \begin{array}l {\mathcal A}(\cdot, \cdot, \boldsymbol{\tau}) \in C( [0,T]\times \varOmega; S_d ),\ \forall \boldsymbol{\tau} \in S_d; \\ {} {\mathcal G}(\cdot, \cdot, \boldsymbol{\tau}, \lambda) \in C( [0,T]\times \varOmega; S_d ),\ \forall (\boldsymbol{\tau}, \lambda) \in S_d \times \mathbb{R}; \\ {} C_e(\cdot, \cdot, \vartheta) \in C( [0,T]\times \varOmega; S_d ), \ \forall \vartheta \in \mathbb{R}; \\ {} \mathcal{B}(\cdot, \cdot, \boldsymbol{\tau}, \lambda) \in C([0,T]\times \varOmega; S_d ),\ \forall (\boldsymbol{\tau}, \lambda) \in S_d \times \mathbb{R};\\ {} \boldsymbol{f}_0 \in C([0,T]\times \varOmega; \mathbb{R}^d );\quad \boldsymbol{f}_F \in C([0,T]\times \varGamma_F; \mathbb{R}^d ); \\ {} \mathcal{K}_c(\cdot, \cdot, \xi) \in C( [0,T]\times \varOmega; \mathbb{R}^d ), \ \forall \xi \in \mathbb{R}^d; \\ {} D_{e}(\cdot, \cdot, \boldsymbol{\tau}, \vartheta) \in C( [0,T]\times \varOmega; \mathbb{R} ), \ \forall (\boldsymbol{\tau}, \vartheta) \in S_d\times \mathbb{R};\\ {} q \in C( [0,T]\times \varOmega; \mathbb{R}^+ ); \\ {} \boldsymbol{v} \in W^{1,1}(0,T;V)\cap C^1([0,T];H), \\ {} \theta \in C([0,T];E)\cap H^{2}(0,T;L^{2}(\varOmega)),\\ {} \alpha \in C(0,T;H^2(\varOmega)) \cap H^{2}(0,T;L^2(\varOmega)), \end{array} \end{aligned} $$

(47)

and for all $r, r_1, r_2 \in \mathbb {R}$, a.e. (t, x) ∈ (0, T) × Γ _C:

$$\displaystyle \begin{aligned} \left\{ \begin{array}{l} \mathrm{(i)} \; \varphi^0(t, \boldsymbol{x}, r; r_1+r_2) \leq \varphi^0(t, \boldsymbol{x}, r; r_1) + \varphi^0(t, \boldsymbol{x}, r; r_2);\\ {} \mathrm{(ii)} \; \varphi^0(t, \boldsymbol{x}, r_2; r_1-r_2) + \varphi^0(t, \boldsymbol{x}, r_1; r_2-r_1) \leq 0;\\ {} \mathrm{(iii)} \; \mbox{there exists } c^{\varphi} \geq 0 \ \mbox{ such that } \\ {} \qquad \varphi^0(t, \boldsymbol{x}, r_1; r) + \varphi^0(t, \boldsymbol{x}, r_2; -r) \leq c^{\varphi}\,|(r_1 - r_2)\,r|. \end{array} \right. \end{aligned} $$

(48)

We remark that the example of φ given in (17) satisfies hypothesis (48).

From Theorem 1, {v, θ, α} verify, for all t ∈ [0, T],

$$\displaystyle \begin{aligned} \left\{ \begin{array}l \langle \dot{\boldsymbol{v}}(t)+ A(t)\,{\boldsymbol{v}}(t)+ B(t)(\boldsymbol{u}(t), \alpha(t)) + C(t)\,\theta(t), \, \boldsymbol{w} - {\boldsymbol{v}}(t) \rangle_{V'\times V}, \\ {} + \displaystyle ( \int_0^t\,\mathcal{B}(t-s)\,(\boldsymbol{\varepsilon}(\boldsymbol{u}(s)), \alpha(s) )\,ds, \, \boldsymbol{\varepsilon}(\boldsymbol{w}) - \boldsymbol{\varepsilon}({\boldsymbol{v}}(t)) )_{\mathcal{H}} \\ {} + j_{\nu}(t, \boldsymbol{u}(t), \boldsymbol{w} - {\boldsymbol{v}}(t) ) + j_{\tau}(t,\boldsymbol{u}(t), \boldsymbol{w}) - j_{\tau}(t,\boldsymbol{u}(t), {\boldsymbol{v}}(t)) \\ {} \qquad \geq \langle \boldsymbol{f}(t),\, \boldsymbol{w} - {\boldsymbol{v}}(t) \rangle_{V'\times V}, \ \forall \boldsymbol{w} \in V. \end{array} \right. \end{aligned} $$

(49)

$$\displaystyle \begin{aligned} \left\{ \begin{array}{l} \displaystyle <\dot{\theta}(t), \eta>_{E'\times E} + <K(t)\,\theta(t), \eta>_{E'\times E} +\psi(t,\theta(t);\eta) \\ {} \qquad \geq <R(t, {\boldsymbol{v}}(t), \theta(t) ), \eta>_{E'\times E} + <Q(t),\eta>_{E'\times E},\ \forall\,\eta\,\in E. \end{array} \right. \end{aligned} $$

(50)

$$\displaystyle \begin{aligned} \left\{ \begin{array}l (\dot{\alpha}(t), \xi- \alpha(t))_{L^2(\varOmega)} + \gamma\,( \nabla\alpha(t),\nabla\xi- \nabla\alpha(t))_{L^2(\varOmega)^d} \\ {} \qquad \geq (\phi_d(\boldsymbol{\sigma}(t),\boldsymbol{\varepsilon}(\boldsymbol{u}(t)),\alpha(t)),\xi- \alpha(t))_{L^2(\varOmega)},\quad \forall\,\xi\,\in \mathcal{K}_{da}. \end{array} \right. \end{aligned} $$

(51)

$$\displaystyle \begin{aligned} {\boldsymbol{v}}(0)=\boldsymbol{v}_0,\quad \alpha(0)= \alpha_0,\quad \theta(0)=\theta_0\quad \mbox{in} \quad \varOmega. \end{aligned} $$

(52)

Now, let V ^h ⊂ V , E ^h ⊂ E, and $\mathcal {K}_{da}^h\subset \mathcal {K}_{da}$ be a family of finite dimensional subspaces, with h > 0 a discretization parameter. We divide the time interval [0, T] into N equal parts: t _n = n k, n = 0, 1, …, N, with the time step k = T∕N.

For a continuous operator or function U ∈ C([0, T];X) with values in a space X, we use the notation U _n = U(t _n) ∈ X.

Then, from (49)–(52), we introduce the following fully discrete scheme.

Problem P ^hk

Find $\boldsymbol {v}^{hk}=\{\boldsymbol {v}^{hk}_n\}_{n=0}^N \subset V^h$, $\theta ^{hk}=\{\theta ^{hk}_n\}_{n=0}^N \subset E^h$ and $\alpha ^{hk}=\{\alpha _n^{hk}\}_{n=0}^N \subset \mathcal {K}_{da}^h$ such that

$$\displaystyle \begin{aligned} \boldsymbol{v}^{hk}_0=\boldsymbol{v}_0^h,\quad \theta^{hk}_0=\theta_0^h, \quad \alpha_0^{hk}=\alpha_0^h {} \end{aligned} $$

(53)

and for n = 1, ⋯ , N,

$$\displaystyle \begin{aligned} \left\{ \begin{array}{l} \Big( \frac{\boldsymbol{v}^{hk}_n-\boldsymbol{v}^{hk}_{n-1}}{k},\,\boldsymbol{w}^h - \boldsymbol{v}^{hk}_n \Big)_H + \langle A_n\,\boldsymbol{v}^{hk}_n , \, \boldsymbol{w}^h - \boldsymbol{v}^{hk}_n \rangle_{ V^\prime\times V}\\ {} +\langle B_n\,\boldsymbol{u}_{n-1}^{hk}, \, \boldsymbol{w}^h - \boldsymbol{v}^{hk}_n \rangle_{ V^\prime\times V} + \langle C_n\,\theta_{n-1}^{hk},\, \boldsymbol{w}^h - \boldsymbol{v}^{hk}_n \rangle_{ V^\prime\times V} \\ {} + (k\,\sum_{m=0}^{n-1} \mathcal{B}(t_n-t_m) \,(\boldsymbol{\varepsilon}(\boldsymbol{u}^{hk}_m), \alpha^{hk}_m) ,\, \boldsymbol{\varepsilon}(\boldsymbol{w}^h) - \boldsymbol{\varepsilon}(\boldsymbol{v}^{hk}_n) )_{\mathcal{H}} \\ {} + j_{\nu}(t_n, \boldsymbol{u}_{n-1}^{hk}, \boldsymbol{w}^h - {\boldsymbol{v}}^{hk}_n) + j_{\tau}(t_n, \boldsymbol{u}_{n-1}^{hk}, \boldsymbol{w}^h) - j_{\tau}(t_n, \boldsymbol{u}_{n-1}^{hk}, {\boldsymbol{v}}^{hk}_n) \\ {} \qquad \geq \langle \boldsymbol{f}_n,\, \boldsymbol{w}^h - \boldsymbol{v}^{hk}_n \rangle_{V^\prime\times V}, \quad \forall\,\boldsymbol{w}^h\in V^h. \end{array} \right. \end{aligned} $$

(54)

$$\displaystyle \begin{aligned} \left\{ \begin{array}{l} \Big(\frac{\theta^{hk}_n-\theta^{hk}_{n-1}}{k},\,\eta^h \Big)_{L^2(\varOmega)} + \langle K_n\,\theta^{hk}_n,\, \eta^h \rangle_{ E^\prime\times E} +\psi(t_n,\theta^{hk}_n;\eta^h) \\ {} \qquad \geq \langle R(t_n, \boldsymbol{v}^{hk}_n, \theta_{n}^{hk}),\, \eta^h \rangle_{ E^\prime\times E} + \langle Q_n, \eta^h \rangle_{ E^\prime\times E}, \quad \forall\,\eta^h\in E^h. \end{array} \right. \end{aligned} $$

(55)

$$\displaystyle \begin{aligned} \left\{ \begin{array}l (\frac{\alpha_n^{hk}-\alpha_{n-1}^{hk}}{k}, \xi^h - \alpha_n^{hk})_{L^2(\varOmega)} + \gamma\,( \nabla \alpha_n^{hk},\nabla( \xi^h - \alpha_n^{hk} ) )_{L^2(\varOmega)^d} \\ {} \qquad \geq (\phi_d(\boldsymbol{\sigma}_{n-1}^{hk},\boldsymbol{\varepsilon}(\boldsymbol{u}_{n-1}^{hk}),\alpha_{n-1}^{hk}),\xi^h - \alpha_{n}^{hk})_{L^2(\varOmega)},\quad \forall\,\xi^h\,\in \mathcal{K}_{da}^h, \end{array} \right. \end{aligned} $$

(56)

where for n = 1, ⋯ , N,

$$\displaystyle \begin{aligned} \boldsymbol{u}_{n}^{hk} = \boldsymbol{u}_{0}^{hk} + k\, \sum_{j=1}^n\, \boldsymbol{v}^{hk}_j;\quad \boldsymbol{u}^{hk}_0 = \boldsymbol{u}_0^h. \end{aligned} $$

(57)

$$\displaystyle \begin{aligned} \left\{ \begin{array}l \boldsymbol{\sigma}_{n}^{hk} = A_n\,\boldsymbol{v}^{hk}_n + B_n\,(\boldsymbol{u}_{n}^{hk}, \alpha_{n}^{hk}) + C_n\,\theta_{n}^{hk} + k\,\sum_{m=0}^{n-1} \mathcal{B}(t_n-t_m)\,(\boldsymbol{\varepsilon}(\boldsymbol{u}^{hk}_m), \alpha^{hk}_m); \\ {} \boldsymbol{\sigma}_{0}^{hk} = \boldsymbol{\sigma}_{0}^{h}. \end{array} \right. \end{aligned} $$

(58)

Here, $\boldsymbol {u}^h_0 \in V^h$, $\boldsymbol {v}^h_0 \in V^h$, $\theta ^{h}_0 \in E^h$, $\alpha ^h_0\in \mathcal {K}_{da}^h$, and $\boldsymbol {\sigma }_{0}^{h} \in \mathcal {H}$ are suitable approximations of the initial values u ₀, v ₀, θ ₀, α ₀, and σ ₀, respectively.

We verify that for n = 1, ⋯ , N, once $\boldsymbol {u}_{n-1}^{hk}, \boldsymbol {v}_{n-1}^{hk}, \theta _{n-1}^{hk}, \alpha _{n-1}^{hk}, and \boldsymbol {\sigma }_{n-1}^{hk}$ are known, then we obtain $\boldsymbol {v}_{n}^{hk}$ by (54), $\theta _{n}^{hk}$ by (55), $\alpha _{n}^{hk}$ by (56), $\boldsymbol {u}_{n}^{hk}$ by (57) (using $\boldsymbol {u}_{n}^{hk} = \boldsymbol {u}_{n-1}^{hk} + k\,\boldsymbol {v}^{hk}_n$), and $\boldsymbol {\sigma }_{n}^{hk}$ by (58).

We now turn to an error analysis of the numerical solution. Here, we use and extend the technique developed in [3], p. 241.

proof

We have to estimate the following numerical solution errors, respectively, for the velocity, temperature, and damage:

$$\displaystyle \begin{aligned} \boldsymbol{v}_n-\boldsymbol{v}^{hk}_n,\quad \theta_n-\theta^{hk}_n, \quad \alpha_n - \alpha^{hk}_n, \quad 1\le n\le N.\end{aligned}$$

First step. Estimate of $( \alpha _n - \alpha ^{hk}_n)_{ 1\le n\le N}$. Let us fix n = 1, ⋯ , N. Using (51) with t = t _n, $\xi = \alpha ^{hk}_n$ and (56) with $\xi ^h = \xi ^{h}_n \in \mathcal {K}_{da}^h$ and then adding the two inequalities, we obtain after some algebraic manipulation, for some constant c > 0,

$$\displaystyle \begin{aligned} \begin{array}l \| \alpha_n - \alpha^{hk}_n \|{}_{L^2(\varOmega)}^2 + k\sum_{j=1}^{n} \| \nabla (\alpha_j - \alpha^{hk}_j) \|{}_{L^2(\varOmega)}^2 \\ {} \quad \leq + c\,\| \boldsymbol{u}_{0} -\boldsymbol{u}_{0}^{h} \|{}_V^2 + c\,\| \boldsymbol{\sigma}_{0} - \boldsymbol{\sigma}_{0}^{h} \|{}_{\mathcal{H}}^2 + c\,\| \alpha_0 - \alpha^{h}_0 \|{}_{L^2(\varOmega)}^2 \\ {} \qquad + c\,k\sum_{j=1}^{n} \,\| \frac{\alpha_j-\alpha_{j-1}}{k} - \dot{\alpha}_j \|{}_{L^2(\varOmega)}^2 + c\,k\sum_{j=1}^{n} \, \| \alpha_j - \alpha^{hk}_j \|{}_{L^2(\varOmega)}^2 \\ {} \qquad + c\,k^2 + c \,k \sum_{j=1}^{n-1} \, \| \boldsymbol{u}_{j} - \boldsymbol{u}_{j}^{hk} \|{}_{V}^2 + c\,\varepsilon \,k \sum_{j=1}^{n-1} \, \| \boldsymbol{\sigma}_{j} - \boldsymbol{\sigma}_{j}^{hk} \|{}_{\mathcal{H}}^2 \\ {} \qquad + c\, A_0^2 + c\, k\, A_1 + c\, k\, A_2 + c\, k\, A_3 + c\, k\, A_4, \end{array} \end{aligned}$$

where ε > 0 is a small parameter which will be chosen later and

$$\displaystyle \begin{aligned} \begin{array}l A_0 := \max_{1\le j\le N} \| \alpha_j - \xi^{h}_j \|{}_{L^2(\varOmega)}; \\ {} \nabla A_1 := \sum_{j=1}^N \| \nabla (\alpha_j - \xi^{h}_j) \|{}_{L^2(\varOmega)}^2; \\ {} A_1 := \sum_{j=1}^N \| \alpha_j - \xi^{h}_j \|{}_{L^2(\varOmega)}^2; \\ {} A_2 := \sum_{j=1}^{N-1} \| (\alpha_{j+1}-\xi_{j+1}^{h} ) - ( \alpha_j-\xi_j^{h} ) \|{}_{L^2(\varOmega)}^2;\\ {} A_3 := \sum_{j=1}^N \| \phi_d(\boldsymbol{\sigma}_{j},\boldsymbol{\varepsilon}(\boldsymbol{u}_{j}),\alpha_{j}) - \frac{\alpha_j-\alpha_{j-1}}{k} + \gamma_j\,\varDelta \alpha_j \|{}_{L^2(\varOmega)} \times \| \alpha_j - \xi^{h}_j \|{}_{L^2(\varOmega)}. \end{array} \end{aligned}$$

From (47), we have

$$\displaystyle \begin{aligned} k\,A_3 \leq c\,A_0 \end{aligned}$$

and

$$\displaystyle \begin{aligned} \Big\| \frac{\alpha_j-\alpha_{j-1}}{k} - \dot{\alpha}_j \Big\|{}_{L^2(\varOmega)} \leq \int_{t_{j-1}}^{t_j}\, \| \ddot{\alpha}(s)\|{}_{L^2(\varOmega)}\,ds,\quad 1\leq j\leq N.\end{aligned}$$

We deduce that

$$\displaystyle \begin{aligned} \sum_{j=1}^{n} \,\| \frac{\alpha_j-\alpha_{j-1}}{k} - \dot{\alpha}_j \|{}_{L^2(\varOmega)}^2 \leq c\,k. \end{aligned}$$

From (46) and (57), we have

$$\displaystyle \begin{aligned} \begin{array}l k\,\sum_{j=1}^{n-1}\, \| \boldsymbol{u}_j - \boldsymbol{u}^{hk}_{j} \|{}_V^2 \\ {} \quad \leq c\,\| \boldsymbol{u}_0 - \boldsymbol{u}^{h}_{0} \|{}_V^2 + c\,k\,I + c\,k\sum_{j=1}^{n-1} \,\Big( k\sum_{i=1}^{j} \,\| \boldsymbol{v}_i-\boldsymbol{v}^{hk}_i \|{}_V^2\Big), \end{array} \end{aligned}$$

where by using (47),

$$\displaystyle \begin{aligned} \displaystyle I := \sum_{j=1}^{N}\, \Big\| \int_0^{t_j}\, \boldsymbol{v} - k\,\sum_{i=1}^{j} \boldsymbol{v}_i \Big\|{}_V^2 \leq c\,k.\end{aligned}$$

From (58), we have for n = 1, ⋯ , N,

$$\displaystyle \begin{aligned} \begin{array}l \| \boldsymbol{\sigma}_{n} - \boldsymbol{\sigma}_{n}^{hk} \|{}_{\mathcal{H}}^2 \\ {} \quad \leq c\,\| \boldsymbol{v}_n-\boldsymbol{v}^{hk}_n \|{}_V^2 + c\,\| \boldsymbol{u}_n-\boldsymbol{u}^{hk}_n \|{}_V^2 + c\,\| \theta_{n} - \theta_{n}^{hk} \|{}_{L^2(\varOmega)}^2 \\ {} \quad + \displaystyle \| \int_0^{t_n}\,\mathcal{B}(t_n-s)\,(\boldsymbol{\varepsilon}(\boldsymbol{u}(s)), \alpha(s))\,ds - k \,\sum_{m=0}^{n-1} \mathcal{B}(t_n-t_m) \,(\boldsymbol{\varepsilon}(\boldsymbol{u}^{hk}_m), \alpha^{hk}_m) \|{}_{\mathcal{H}}^2. \end{array} \end{aligned}$$

Therefore, we arrive to the following error estimate for the damage:

For some constant c > 0 and for n = 1, ⋯ , N,

$$\displaystyle \begin{aligned} \begin{array}l \| \alpha_n - \alpha^{hk}_n \|{}_{L^2(\varOmega)}^2 + k\sum_{j=1}^{n} \| \nabla (\alpha_j - \alpha^{hk}_j) \|{}_{L^2(\varOmega)}^2 \\ {} \quad \leq + c\,\| \boldsymbol{u}_{0} -\boldsymbol{u}_{0}^{h} \|{}_V^2 + c\,\| \boldsymbol{\sigma}_{0} - \boldsymbol{\sigma}_{0}^{h} \|{}_{\mathcal{H}}^2 + c\,\| \alpha_0 - \alpha^{h}_0 \|{}_{L^2(\varOmega)}^2 \\ {} \qquad + c\,k\sum_{j=1}^{n} \, \| \alpha_j - \alpha^{hk}_j \|{}_{L^2(\varOmega)}^2 \\ {} \qquad + c\,k^2 + c\,k\sum_{j=1}^{n-1} \,\Big( k\sum_{i=1}^{j} \,\| \boldsymbol{v}_i-\boldsymbol{v}^{hk}_i \|{}_V^2\Big) \\ {} \qquad + c\,\varepsilon\, k\sum_{j=1}^{n-1} \,\| \boldsymbol{v}_j-\boldsymbol{v}^{hk}_j \|{}_V^2 + c\,\varepsilon \,k \sum_{j=1}^{n-1} \, \| \theta_{j} - \theta_{j}^{hk} \|{}_{L^2(\varOmega)}^2 \\ {} \qquad + c\, A_0 + c\, A_0^2 + c\, k\, \nabla A_1 + c\, k\, A_1 + c\, k\, A_2. \end{array} \end{aligned} $$

(59)

Second step. Estimate of $(\varepsilon _n := \theta _n-\theta ^{hk}_n)_{ 1\le n\le N}$.

Let us fix n = 1, ⋯ , N and denote shortly $\varepsilon _j := \theta _j-\theta ^{hk}_j$, 1 ≤ j ≤ N. We take (50), where t = t _n and η = −η ^h, and add to (55), with η ^h ∈ E ^h, we have

$$\displaystyle \begin{aligned} \begin{array}l \Big( \dot{\theta}_n - \frac{\theta^{hk}_n-\theta^{hk}_{n-1}}{k},\,\eta^h \Big)_{L^2(\varOmega)} + \langle K_n\,\theta_n - K_n\,\theta^{hk}_n,\, \eta^h \rangle_{ E^\prime\times E}\\ {} \quad \leq \psi(t_n, \theta_n; -\eta^h ) + \psi(t_n, \theta_n^{hk}; \eta^h ) + \langle R(t_n,\boldsymbol{v}_n, \theta_n) - R(t_n,\boldsymbol{v}^{hk}_n, \theta^{hk}_{n}),\, \eta^h \rangle_{E^\prime\times E}. \end{array} \end{aligned}$$

Taking $\eta ^h = \eta _n^h - \theta _n + \varepsilon _n$, then we have

$$\displaystyle \begin{aligned} \begin{array}l \Big( \frac{ \varepsilon_n - \varepsilon_{n-1}}{k},\,\varepsilon_n \Big)_{L^2(\varOmega)} + \langle K_n\,\theta_n - K_n\,\theta^{hk}_n,\, \varepsilon_n \rangle_{ E^\prime\times E} \\ {} \qquad \leq \langle K_n\,\theta_n - K_n\,\theta^{hk}_n,\, \theta_n - \eta^h_n \rangle_{ E^\prime\times E} \\ {} \qquad \quad \langle R(t_n,\boldsymbol{v}_n, \theta_n) - R(t_n,\boldsymbol{v}^{hk}_n, \theta^{hk}_{n}),\, \eta^h \rangle_{ E^\prime\times E} \\ {} \qquad \quad + \Big( \dot{\theta}_n - \frac{\theta_n-\theta_{n-1}}{k} +\frac{\varepsilon_n- \varepsilon_{n-1}}{k},\, \theta_n - \eta^h_n \Big)_{L^2(\varOmega)} - \Big( \dot{\theta}_n - \frac{\theta_n-\theta_{n-1}}{k},\, \varepsilon_n \Big)_{L^2(\varOmega)} \\ {} \qquad \quad + \psi(t_n, \theta_n; -\eta^h ) + \psi(t_n, \theta_n^{hk}; \eta^h ). \end{array} \end{aligned}$$

From (28), we have

$$\displaystyle \begin{aligned} | \langle K_n\,\theta_n - K_n\,\theta^{hk}_n,\, \theta_n - \eta^h_n \rangle_{ E^\prime\times E} | \leq c\, \| \theta_n - \theta^{hk}_n\|{}_E \times \| \theta_n - \eta^h_n\|{}_E.\end{aligned}$$

From (29), we have

$$\displaystyle \begin{aligned} \begin{array}{l} | \langle R(t_n,\boldsymbol{v}_n, \theta_n) - R(t_n,\boldsymbol{v}^{hk}_n, \theta^{hk}_{n}), \, \eta^h \rangle_{E^\prime\times E} | \\ {} \quad \leq D_V\, \| \boldsymbol{v}_n - \boldsymbol{v}^{hk}_n \|{}_{V} \times \| \eta^h \|{}_{L^2(\varOmega)} + D_T\, \| \theta_n - \theta^{hk}_n \|{}_{L^2(\varOmega)} \times \| \eta^h \|{}_{L^2(\varOmega)};\\ {} \quad \leq D_V\, \| \boldsymbol{v}_n - \boldsymbol{v}^{hk}_n \|{}_{V} \times \| \eta_n^h - \theta_n \|{}_{L^2(\varOmega)} + D_T\, \| \theta_n - \theta^{hk}_n \|{}_{L^2(\varOmega)} \times \| \eta_n^h - \theta_n \|{}_{L^2(\varOmega)} \\ {} \quad \quad + D_V\, \| \boldsymbol{v}_n - \boldsymbol{v}^{hk}_n \|{}_{V} \times \| \theta_n - \theta^{hk}_n \|{}_{L^2(\varOmega)} + D_T\, \| \theta_n - \theta^{hk}_n \|{}_{L^2(\varOmega)}^2. \end{array} \end{aligned}$$

Then, let us denote

$$\displaystyle \begin{aligned} B_0 := \max_{1\le n\le N}{\|}\theta_n-\eta_n^{h}{\|}_{L^2(\varOmega)}.\end{aligned}$$

We have

$$\displaystyle \begin{aligned} D_V\, \| \boldsymbol{v}_n {\kern-1pt}-{\kern-1pt} \boldsymbol{v}^{hk}_n \|{}_{V} \times \| \eta_n^h {\kern-1pt}-{\kern-1pt} \theta_n \|{}_{L^2(\varOmega)} \leq D_V\, \| \boldsymbol{v}_n {\kern-1pt}-{\kern-1pt} \boldsymbol{v}^{hk}_n \|{}_{V} \, B_0 {\kern-1pt}\leq {\kern-1pt} \frac{1}{2}\,D_V^2\, \| \boldsymbol{v}_n {\kern-1pt}-{\kern-1pt} \boldsymbol{v}^{hk}_n \|{}_{V}^2 + \frac{1}{2}\, B_0^2; \end{aligned}$$

and for 𝜖 ₁ > 0,

$$\displaystyle \begin{aligned} D_T\, \| \theta_n - \theta^{hk}_n \|{}_{L^2(\varOmega)} \times \| \eta_n^h - \theta_n \|{}_{L^2(\varOmega)} \leq \epsilon_1\, \| \theta_n - \theta^{hk}_n \|{}_{L^2(\varOmega)}^2 + \frac{1}{4 \epsilon_1} \, (D_T\, B_0)^2 ;\end{aligned}$$

and for 𝜖 > 0,

$$\displaystyle \begin{aligned} D_V\, \| \boldsymbol{v}_n - \boldsymbol{v}^{hk}_n \|{}_{V} \times \| \theta_n - \theta^{hk}_n \|{}_{L^2(\varOmega)} \leq \frac{D_V^2}{4 \epsilon} \| \boldsymbol{v}_n - \boldsymbol{v}^{hk}_n \|{}_{V}^2 + \epsilon\,\| \theta_n - \theta^{hk}_n \|{}_{L^2(\varOmega)}^2. \end{aligned}$$

To continue, by using (48), we obtain

$$\displaystyle \begin{aligned} \psi(t_n, \theta_n; -\eta^h ) + \psi(t_n, \theta_n^{hk}; \eta^h ) \leq c_0\,c^\varphi\,\| \theta_n - \theta^{hk}_n \|{}_E\, \times \| \eta^h \|{}_E, \end{aligned}$$

and thus

$$\displaystyle \begin{aligned} \psi(t_n, \theta_n; -\eta^h ) + \psi(t_n, \theta_n^{hk}; \eta^h ) \leq c_0\,c^\varphi\, \| \theta_n - \theta^{hk}_n \|{}_E^2 + c_0\,c^\varphi\,\| \theta_n - \theta^{hk}_n \|{}_E\, \times \| \theta_n - \eta^h_n \|{}_E . \end{aligned}$$

Consider the quantity for n = 1, ⋯ , N,

$$\displaystyle \begin{aligned} \varXi_n := \Big( \frac{ \varepsilon_n - \varepsilon_{n-1}}{k},\,\varepsilon_n \Big)_{L^2(\varOmega)} + \langle K_n\,\theta_n - K_n\,\theta^{hk}_n,\, \varepsilon_n \rangle_{ E^\prime\times E}.\end{aligned}$$

We have

$$\displaystyle \begin{aligned} \varXi_n \geq \frac{1}{2k}\,\Big( \| \varepsilon_n \|{}_{L^2(\varOmega)}^2 - \| \varepsilon_{n-1} \|{}_{L^2(\varOmega)}^2 \Big) + m_{\mathcal{K}_c}\, \| \varepsilon_n \|{}_E^2.\end{aligned}$$

Now, we sum Ξ _j from j = 1 to j = n.

From (47), we have

$$\displaystyle \begin{aligned} \sum_{j=1}^{n} \,\| \frac{\theta_j- \theta_{j-1}}{k} - \dot{\theta}_j \|{}_{L^2(\varOmega)}^2 \leq c\,k. \end{aligned}$$

Under the condition that

$$\displaystyle \begin{aligned} D_T + c_0\,c^\varphi < m_{\mathcal{K}_c}, \end{aligned} $$

(60)

we can choose 𝜖 and 𝜖 ₁ such that $\epsilon + \epsilon _1 + D_T + c_0\,c^\varphi < m_{\mathcal {K}_c}$. After some manipulation, we deduce the following error estimate for the temperature.

For some constant c > 0 independent of D _V and for n = 1, ⋯ , N,

$$\displaystyle \begin{aligned} \begin{array}l \| \theta_n-\theta^{hk}_n {\|}_{L^2(\varOmega)}^2+ k\sum_{j=1}^n \| \theta_j-\theta^{hk}_j \|{}_E^2\\ {} \qquad \leq \ c\,\| \theta_0-\theta^{h}_0 \|{}_{L^2(\varOmega)}^2 + c\,B_0^2 + c\,k^2 + c\,k\,B_1 + c\,B_2\,M_\theta \\ {} \qquad + c\,D_V^2\,k\,\sum_{j=1}^n \,\| \boldsymbol{v}_j-\boldsymbol{v}^{hk}_j \|{}_{V}^2. \end{array} \end{aligned} $$

(61)

Here,

$$\displaystyle \begin{aligned} \begin{array}l M_\theta := \max_{1\le n\le N} {\|} \theta_n-\theta^{hk}_n {\|}_{L^2(\varOmega)}, \\ {} B_1 := \sum_{j=1}^N{\|}\theta_j-\eta_j^{h}{\|}_{E}^2,\\ {} B_2 := \sum_{j=1}^N{\|}\theta_j-\eta_j^{h} - ( \theta_{j+1}-\eta_{j+1}^{h}) {\|}_{L^2(\varOmega)}. \end{array} \end{aligned}$$

Third step. Estimate of $( \boldsymbol {v}_n-\boldsymbol {v}^{hk}_n )_{ 1\le n\le N}$. The computation of the estimate for the velocity is similar as in [3], p. 241, which we refer for details. We mention only the main steps.

We obtain, for some constant c > 0 and for n = 1, ⋯ , N,

$$\displaystyle \begin{aligned} \begin{array}l {\|} \boldsymbol{v}_n-\boldsymbol{v}^{hk}_n {\|}_H^2+ k\sum_{j=1}^n \,\| \boldsymbol{v}_j-\boldsymbol{v}^{hk}_j \|{}_V^2 \\ {} \qquad \leq \ c\,{\|} \boldsymbol{v}_0-\boldsymbol{v}^{h}_0 {\|}_H^2 + c\,\| \boldsymbol{u}_0 - \boldsymbol{u}_0^h \|{}_V^2 \\ {} \qquad + c\,C_0 + c\,k^2 + c\,k\,( C_1 + \hat{C}_1 ) + c\,C_2\,M_v \\ {} \qquad + c\,k\sum_{j=1}^{n}\,\mathcal{R}_j^{hk} + c\,k\sum_{j=1}^{n}\,J_{\nu j}^{hk} + c\,k\sum_{j=1}^{n}\,J_{\tau j}^{hk} \\ {} \qquad + \varepsilon \,k\,\sum_{j=0}^{n-1} \,\| \theta_j-\theta^{hk}_j \|{}_{L^2(\varOmega)}^2 + c\,k\sum_{j=1}^{n-1} \,\Big( k\sum_{i=1}^{j} \,\| \boldsymbol{v}_i-\boldsymbol{v}^{hk}_i \|{}_V^2 \Big). \end{array} \end{aligned}$$

Here, we denote by

$$\displaystyle \begin{aligned} \begin{array}l M_v := \max_{1\le n\le N} {\|} \boldsymbol{v}_n-\boldsymbol{v}^{hk}_n {\|}_H; \\ {} C_0 := \max_{1\le n\le N}{\|}\boldsymbol{v}_n-\boldsymbol{w}_n^{h}{\|}_{H};\\ {} C_1 := \sum_{j=1}^N \|\boldsymbol{v}_j-\boldsymbol{w}^h_j\|{}_V^2; \\ {} \widehat{C}_1 := \sum_{j=1}^N \|\boldsymbol{v}_j-\boldsymbol{w}^h_j\|{}_V; \\ {} C_2 := \sum_{j=1}^{N-1}{\|}(\boldsymbol{v}_j-\boldsymbol{w}^h_j) -(\boldsymbol{v}_{j+1}-\boldsymbol{w}^h_{j+1}){\|}_H, \end{array} \end{aligned}$$

and for n = 1, ⋯ , N,

$$\displaystyle \begin{aligned}\begin{array}l \displaystyle \mathcal{R}_n^{hk} = \Big( \int_0^{t_n}\,\mathcal{B}(t_n-s) \,\boldsymbol{\varepsilon}(\boldsymbol{u}(s))\,ds - k\,\sum_{m=0}^{n-1} \mathcal{B}(t_n-t_m) \,\boldsymbol{\varepsilon}(\boldsymbol{u}^{hk}_m) ,\, - \boldsymbol{\varepsilon}(\boldsymbol{e}_n) \Big)_{\mathcal{H}} \\ {} \qquad \quad + \Big( k\,\sum_{m=0}^{n-1} \mathcal{B}(t_n-t_m) \,\boldsymbol{\varepsilon}(\boldsymbol{u}^{hk}_m) ,\, \boldsymbol{\varepsilon}(\boldsymbol{w}^h_n) - \boldsymbol{\varepsilon}(\boldsymbol{v}_n) \Big)_{\mathcal{H}}; \end{array}\end{aligned}$$

and

$$\displaystyle \begin{aligned} J_{\nu n}^{hk} = j_{\nu}(t_n, \boldsymbol{u}_n, \boldsymbol{v}_{n}^{hk} - \boldsymbol{v}_n ) + j_{\nu}(t_n, \boldsymbol{u}_{n-1}^{hk}, \boldsymbol{w}_{n}^{hk} - \boldsymbol{v}_n^{hk} ); \end{aligned}$$

and

$$\displaystyle \begin{aligned} J_{\tau n}^{hk} = j_{\tau}(t_n,\boldsymbol{u}_n, \boldsymbol{v}_{n}^{hk}) - j_{\tau}(t_n,\boldsymbol{u}_n, \boldsymbol{v}_n )+ j_{\tau}(t_n, \boldsymbol{u}_{n-1}^{hk}, \boldsymbol{w}_n^{h} )- j_{\tau}( t_n, \boldsymbol{u}_{n-1}^{hk}, \boldsymbol{v}_n^{hk} ). \end{aligned}$$

We have, for n = 1, ⋯ , N,

$$\displaystyle \begin{aligned} \begin{array}l k\sum_{j=1}^{n}\,\mathcal{R}_j^{hk} \\ {} \quad \leq c\,k^2 + c\,\| \boldsymbol{u}_0 - \boldsymbol{u}_0^h \|{}_V^2 + c\,k\sum_{j=1}^{n-1} \,\Big( k\sum_{i=1}^{j} \,\| \boldsymbol{v}_i-\boldsymbol{v}^{hk}_i \|{}_V^2 \Big) + c\,k\,(C_1 + \widehat{C}_1); \end{array} \end{aligned}$$

and

$$\displaystyle \begin{aligned} \begin{array}l k\sum_{j=1}^{n}\, J_{\nu j}^{hk} \\ {} \quad \leq c\,k^2 + c\,\| \boldsymbol{u}_0 - \boldsymbol{u}^{h}_{0} \|{}_V^2 + c\,k\sum_{j=1}^{n-1} \,\Big( k\sum_{i=1}^{j} \,\| \boldsymbol{v}_i-\boldsymbol{v}^{hk}_i \|{}_V^2\Big) \\ {} \qquad + c\varepsilon\,k\,\sum_{j=1}^{n}\, \| \boldsymbol{v}_j-\boldsymbol{v}^{hk}_j \|{}_V^2 + c\,k\,C_1 + c\,k\,\widehat{C}_1; \end{array} \end{aligned}$$

and

$$\displaystyle \begin{aligned} \begin{array}l k\sum_{j=1}^{n}\, J_{\tau j}^{hk} \\ {} \quad \leq c\,k^2 + c\,\| \boldsymbol{u}_0 - \boldsymbol{u}^{h}_{0} \|{}_V^2 + c\,k\sum_{j=1}^{n-1} \,\Big( k\sum_{i=1}^{j} \,\| \boldsymbol{v}_i-\boldsymbol{v}^{hk}_i \|{}_V^2\Big) \\ {} \qquad + c\varepsilon\,k\,\sum_{j=1}^{n}\, \| \boldsymbol{v}_j-\boldsymbol{v}^{hk}_j \|{}_V^2 + c\,k\,C_1 + c\,k\,\widehat{C}_1. \end{array} \end{aligned}$$

Thus, we obtain the following error estimate for the velocity.

For some constant c > 0 and for n = 1, ⋯ , N,

$$\displaystyle \begin{aligned} \begin{array}l {\|} \boldsymbol{v}_n-\boldsymbol{v}^{hk}_n {\|}_H^2+ k\sum_{j=1}^n \,\| \boldsymbol{v}_j-\boldsymbol{v}^{hk}_j \|{}_V^2 \\ {} \qquad \leq \ c\,{\|} \boldsymbol{v}_0-\boldsymbol{v}^{h}_0 {\|}_H^2 + c\,\| \boldsymbol{u}_0 - \boldsymbol{u}_0^h \|{}_V^2 \\ {} \qquad + c\,C_0 + c\,k^2 + c\,k\,( C_1 + \hat{C}_1 ) + c\,C_2\,M_v \\ {} \qquad + c\,\varepsilon \,k\,\sum_{j=0}^{n-1} \,\| \theta_j-\theta^{hk}_j \|{}_{L^2(\varOmega)}^2 + c\,\varepsilon \,k\,\sum_{j=1}^{n} \,\| \boldsymbol{v}_j-\boldsymbol{v}^{hk}_j \|{}_V^2 \\ {} \qquad + c\,k\sum_{j=1}^{n-1} \,\Big( k\sum_{i=1}^{j} \,\| \boldsymbol{v}_i-\boldsymbol{v}^{hk}_i \|{}_V^2 \Big). \end{array} \end{aligned} $$

(62)

To summarize, adding the three inequalities (59), (61), and (62) and choosing D _V and ε small enough, we obtain, for some constant c > 0 and for n = 1, ⋯ , N,

$$\displaystyle \begin{aligned} \begin{array}l \| \alpha_n - \alpha^{hk}_n \|{}_{L^2(\varOmega)}^2 + k\sum_{j=1}^{n} \| \nabla (\alpha_j - \alpha^{hk}_j) \|{}_{L^2(\varOmega)}^2 + \| \theta_n-\theta^{hk}_n {\|}_{L^2(\varOmega)}^2 \\ {} \ + k\sum_{j=1}^n \| \theta_j-\theta^{hk}_j \|{}_E^2 + {\|} \boldsymbol{v}_n-\boldsymbol{v}^{hk}_n {\|}_H^2+ k\sum_{j=1}^n \,\| \boldsymbol{v}_j-\boldsymbol{v}^{hk}_j \|{}_V^2 \\ {} \quad \leq + c\,\| \boldsymbol{u}_{0} -\boldsymbol{u}_{0}^{h} \|{}_V^2 + c\,\| \boldsymbol{v}_0-\boldsymbol{v}^{h}_0 \|{}_H^2 + c\,\| \boldsymbol{\sigma}_{0} - \boldsymbol{\sigma}_{0}^{h} \|{}_{\mathcal{H}}^2 \\ {} \quad \quad + c\,\| \alpha_0 - \alpha^{h}_0 \|{}_{L^2(\varOmega)}^2 + c\,{\|} \theta_0-\theta^{h}_0 {\|}_{L^2(\varOmega)}^2 \\ {} \qquad + c\,k\sum_{j=1}^{n} \, \| \alpha_j - \alpha^{hk}_j \|{}_{L^2(\varOmega)}^2 \\ {} \qquad + c\,k^2 + c\,k\sum_{j=1}^{n-1} \,\Big( k\sum_{i=1}^{j} \,\| \boldsymbol{v}_i-\boldsymbol{v}^{hk}_i \|{}_V^2\Big) \\ {} \qquad + c\, A_0 + c\, A_0^2 + c\, k\, \nabla A_1 + c\, k\, A_1 + c\, k\, A_2 + + c\,B_0^2 + c\,k\,B_1 + c\,B_2\,M_\theta \\ {} \qquad + c\,C_0 + c\,k\, C_1 + c\,k\,\hat{C}_1 + c\,C_2\,M_v. \end{array} \end{aligned} $$

(63)

To end, let us recall the discrete version of Gronwall’s inequality, see e.g. [2].

Consider a sequence $\{ r_n \}_{0\leq n \leq N} \subset \mathbb {R}^+$ and $a \in \mathbb {R}^+$.

Assume

$$\displaystyle \begin{aligned} r_n \leq a + c\,k\,\sum_{j=0}^{n-1}\,r_j, \quad 1\leq n \leq N.\end{aligned}$$

Then, we have

$$\displaystyle \begin{aligned} r_n \leq (a + c\,k\,r_0)\,(1+c\,k)^{n-1}\leq (a + c\,k\,r_0)\,e^{c\,T}, \quad 1\leq n \leq N.\end{aligned}$$

Now, from Gronwall’s inequality, using estimation (63) and under condition (60), we conclude that for D _V small enough, then there exists some constant c > 0:

$$\displaystyle \begin{aligned} \begin{array}l \displaystyle \max_{1\le n\le N}\, \Big( \| \alpha_n - \alpha^{hk}_n \|{}_{L^2(\varOmega)}^2 + k\sum_{j=1}^{n} \| \nabla (\alpha_j - \alpha^{hk}_j) \|{}_{L^2(\varOmega)}^2 + \| \theta_n-\theta^{hk}_n {\|}_{L^2(\varOmega)}^2 \\ {} \quad + k\sum_{j=1}^n \| \theta_j-\theta^{hk}_j \|{}_E^2 + {\|} \boldsymbol{v}_n-\boldsymbol{v}^{hk}_n {\|}_H^2+ k\sum_{j=1}^n \,\| \boldsymbol{v}_j-\boldsymbol{v}^{hk}_j \|{}_V^2 \Big) \\ {} \quad \leq + c\,\| \boldsymbol{u}_{0} -\boldsymbol{u}_{0}^{h} \|{}_V^2 + c\,\| \boldsymbol{v}_0-\boldsymbol{v}^{h}_0 \|{}_H^2 + c\,\| \boldsymbol{\sigma}_{0} - \boldsymbol{\sigma}_{0}^{h} \|{}_{\mathcal{H}}^2 \\ {} \qquad + c\,\| \alpha_0 - \alpha^{h}_0 \|{}_{L^2(\varOmega)}^2 + c\,{\|} \theta_0-\theta^{h}_0 {\|}_{L^2(\varOmega)}^2 \\ {} \qquad + c\,k^2 + c\, A_0 + c\, A_0^2 + c\, k\, \nabla A_1 + c\, k\, A_1 + c\, k\, A_2 \\ {} \qquad + c\,B_0^2 + c\,k\,B_1 + c\,B_2^2 + c\,C_0 + c\,k\, C_1 + c\,k\,\hat{C}_1 + c\,C_2^2. \end{array} \end{aligned} $$

(64)

As a typical example, let us consider $\varOmega \subset \mathbb {R}^d$, $d\in \mathbb {N}^*$, a polygonal domain. Let ${\mathcal T}^h$ be a regular finite element partition of Ω. Let V ^h ⊂ V , E ^h ⊂ E, and $\mathcal {K}^h_{da}\subset \mathcal {K}_{da}$ be the finite element spaces consisting of piecewise polynomials of degree ≤ m, with m ≥ 1, according to the partition ${\mathcal T}^h$. Denote by $\varPi ^h_V\,:\, H^{m +1}(\varOmega )^d \to V^h$, $\varPi ^h_E\,:\, H^{m +1}(\varOmega )\to E^h$, and $\varPi ^h_K\,:\, H^{m}(\varOmega )\to \mathcal {K}^h_{da}$ the finite element interpolation operators.

Recall (see e.g. [4]) that

$$\displaystyle \begin{aligned} \left\{ \begin{array}l \| \boldsymbol{w} - \varPi_V^h \boldsymbol{w} \|{}_{H^r(\varOmega)^d} \leq c\,h^{m +1-r}\,|\boldsymbol{w}|{}_{H^{m +1}(\varOmega)^d},\quad \forall\, \boldsymbol{w} \in H^{m + 1}(\varOmega)^d; \\ {} \| \eta - \varPi_E^h \eta \|{}_{H^r(\varOmega)} \leq c\,h^{m +1-r}\,|\eta|{}_{H^{m +1}(\varOmega)},\quad \forall\, \eta \in H^{m +1}(\varOmega);\\ {} \| \xi -\varPi_K^h \xi \|{}_{L^{2}(\varOmega)} \leq c\,h^{m}\,|\xi|{}_{H^{m}(\varOmega)},\quad \forall\, \xi \in H^{m}(\varOmega), \end{array} \right. \end{aligned}$$

where r = 0 (for which H ⁰ = L ²) or r = 1.

We assume the following additional data and solution regularities:

$$\displaystyle \begin{aligned} \left\{ \begin{array}l \boldsymbol{u}_0 \in H^{m + 1}(\varOmega)^d ; \quad \alpha_0 \in H^{m}(\varOmega);\\ {} \boldsymbol{v}\in C([0,T];H^{2m +1}(\varOmega)^d),\quad \dot{\boldsymbol{v}} \in L^1(0,T;H^{m}(\varOmega)^d); \\ {} \theta \in C([0,T];H^{m +1}(\varOmega)), \quad \dot{\theta}\in W^{1,2}(0,T;H^{m}(\varOmega)); \\ {} \dot{\alpha}\in W^{1,1}(0,T;H^{m}(\varOmega)). \end{array} \right. \end{aligned} $$

(65)

Then, we choose in (64) the elements

$$\displaystyle \begin{aligned} \boldsymbol{u}_0^{h}=\varPi^h_V\,\boldsymbol{u}_0,\quad \boldsymbol{v}_0^{h}=\varPi^h_V\,\boldsymbol{v}_0,\quad \theta_0^{h}=\varPi^h_E\,\theta_0, \quad \alpha_0^{h}= \varPi^h_K \,\alpha_0,\end{aligned}$$

and

$$\displaystyle \begin{aligned} \boldsymbol{w}_j^{h}=\varPi^h_V\,\boldsymbol{v}_j,\quad \eta_j^{h}=\varPi^h_E\,\theta_j,\quad j=1\cdots N.\end{aligned}$$

From assumption (65), we have

$$\displaystyle \begin{aligned} \begin{array}l \| \boldsymbol{u}_0 - \boldsymbol{u}_0^{h} \|{}_V \leq c\,h^m,\quad \| \boldsymbol{v}_0-\boldsymbol{v}^{h}_0 \|{}_H \leq c\,h^m; \\ {} \| \theta_0-\theta^{hk}_0 \|{}_{L^2(\varOmega)} \leq c\,h^m,\quad \| \alpha_0-\alpha^{h}_0 \|{}_{L^{2}(\varOmega)} \leq c\,h^m;\\ {} A_0 \leq c\,h^{m + 1},\quad B_0 \leq c\,h^{m + 1},\quad C_0 \leq c\,h^{2m + 1};\\ {} k\,A_1 \leq c\,h^{2m},\quad k\,B_1 \leq c\,h^{2m},\quad k\,C_1 \leq c\,h^{2m}, \quad k\,\hat{C}_1 \leq c\,h^{2m}; \\ {} A_2 \leq c\,h^{2m},\quad B_2 \leq c\,h^m,\quad C_2 \leq c\,h^m. \end{array} \end{aligned}$$

Using these estimates in (64), we conclude to the following error estimate result.

Theorem 2

We keep the assumptions of Theorem 1 . Under the additional assumptions (47), (48), and (65), and condition (60), then for D _V small enough, we obtain the error estimate for the corresponding discrete solution $\{ ( \boldsymbol {v}_n^{hk}, \, \theta _n^{hk}, \, \alpha _n^{hk}),\ 1\leq n \leq N \}$:

$$\displaystyle \begin{aligned} \begin{array}l \max_{1\le n\le N}\, {\|}\boldsymbol{v}_n-\boldsymbol{v}_n^{hk}{\|}_H +\Big(k\sum_{n=1}^N \|\boldsymbol{v}_n-\boldsymbol{v}_n^{hk}\|{}_V^2\Big)^{1/2} \\ {} + \max_{1\le n\le N}\, {\|}\theta_n-\theta_n^{hk}{\|}_{L^2(\varOmega)} +\Big(k\sum_{n=1}^N \|\theta_n-\theta_n^{hk}\|{}_E^2\Big)^{1/2} \\ {} + \max_{1\le n\le N}\, \| \alpha_n- \alpha_n^{hk} \|{}_{L^{2}(\varOmega)} \\ {} \quad \le c\,(h^{\frac{m + 1}{2}} + k). \end{array} \end{aligned}$$

In particular, for m = 1, we have

$$\displaystyle \begin{aligned} \begin{array}l \max_{1\le n\le N}\, {\|}\boldsymbol{v}_n-\boldsymbol{v}_n^{hk}{\|}_H +\Big(k\sum_{n=1}^N \|\boldsymbol{v}_n-\boldsymbol{v}_n^{hk}\|{}_V^2\Big)^{1/2} \\ {} + \max_{1\le n\le N}\, {\|}\theta_n-\theta_n^{hk}{\|}_{L^2(\varOmega)} +\Big(k\sum_{n=1}^N \|\theta_n-\theta_n^{hk}\|{}_E^2\Big)^{1/2} \\ {} + \max_{1\le n\le N}\, \| \alpha_n- \alpha_n^{hk} \|{}_{L^{2}(\varOmega)} \\ {} \quad \le c\,(h + k). \end{array} \end{aligned}$$

5 Numerical Computations

In this section, we provide numerical simulations in two-dimensional tests for the variational problem (QV ) by using Matlab computation codes. We refer to the previous numerical scheme and use spaces of continuous piecewise affine functions V ^h ⊂ V , E ^h ⊂ E, and $\mathcal {K}_{da}^{h}\subset \mathcal {K}_{da}$ as families of approximating subspaces.

Here, we consider the following formulas:

$$\displaystyle \begin{aligned} \begin{array}l \mathcal{G}(t)(\boldsymbol{\tau}, \alpha) = \mathcal{G}^0(t) \, \boldsymbol{\tau} - \alpha\,(d_{ij}(t)) \quad \mbox{in} \quad \varOmega; \\ {} {C}_e(t, \theta) := - \theta\, (c_{ij}(t) ) \quad \mbox{in} \quad \varOmega; \\ {} p_\nu(t,\cdot,r) = c_{\nu}(t)\,r_+ \quad \mbox{on} \quad \varGamma_C; \\ {} p_\tau(t,\cdot,r) = \mu_\tau(t)\,c_{\nu}(t)\,r_+ \quad \mbox{on} \quad \varGamma_C; \\ {} \mathcal{K}_c(t,\nabla \theta) = (k_{ij}(t))\,\nabla \theta \quad \mbox{in} \quad \varOmega; \\ {} {D}_e(t, \boldsymbol{v}, \theta ) = -c_{ij}(t)\, \frac{\partial\,v_i}{\partial\,x_j} - \theta\,d_e(t) \quad \mbox{in} \quad \varOmega;\\ {} \phi_d(\sigma,\boldsymbol{\varepsilon}(\boldsymbol{u}),\alpha) = -d_1\,\|\sigma\|{}_{VM} -d_2\,L_d(\alpha) \quad \mbox{in} \quad \varOmega;\\ {} \varphi(t, r) = \frac{1}{2} k_e(t)\,(r -\theta_R(t) )^2 \quad \mbox{on} \quad \varGamma_C. \end{array} \end{aligned}$$

In view of the numerical simulations, we consider a rectangular open set, linear elastic, and linear visco-elastic operators, for a.e. t ∈ (0, T):

$$\displaystyle \begin{aligned} \begin{array}l \varOmega = (0,L_1) \times (0,L_2);\\ {} \varGamma_F = (\{0\}{\times} [0,L_2]) \cup ([0,L_1] {\times} \{L_2\} ) \cup (\{L_1\}\times [0,L_2]); \quad \varGamma_C = [0,L_1] \times \{0\};\\ {} (\mathcal{G}^0(t) \,\boldsymbol{\tau})_{ij}= \frac{E_Y(t)\,r_P(t)}{1-r_P^2(t)}(\tau_{11}+\tau_{22})\,\delta_{ij}+\frac{E_Y(t)}{1+r_P(t)}\tau_{ij}, \quad 1\leq i,\,j\leq 2,\ \boldsymbol{\tau} \in S_2;\\ {} (\mathcal{A}(t) \,\boldsymbol{\tau})_{ij}= \mu(t)\,(\tau_{11}+\tau_{22})\,\delta_{ij}+ \eta(t)\,\tau_{ij}, \quad 1\leq i,\,j\leq 2,\ \boldsymbol{\tau} \in S_2 ;\\ {} ({\mathcal B}(t)\,\boldsymbol{\tau})_{ij}= B_1(t)\,(\tau_{11}+\tau_{22})\,\delta_{ij}+ B_2(t)\,\tau_{ij}, \quad 1\leq i,\,j\leq 2,\ \boldsymbol{\tau} \in S_2. \end{array} \end{aligned}$$

Here, E _Y is the Young’s modulus, r _P is the Poisson’s ratio of the material, δ _ij denotes the Kronecker symbol, and μ and η are viscosity constants.

For computations, we considered the following data (IS unity), for t ∈ (0, T):

Figure 1 represents the initial configuration.

Fig. 1

Initial configuration

In Figures 2, 3, and 4, we compute, respectively, the Von Mise norm, which gives a global measure of the stress, the temperature, and the damage at final time in the body at final time, for θ _R = 0, respectively, for short and long memory visco-elasticity. In Figure 5, we show the evolution of the damage at the particular point S = (L ₁, L ₂) (direction of the surface traction). We observe that the distribution of these parameters is changing for long memory, the deformation is more important, as well as for the damage, temperature, and stress in the neighborhood of the point S.

Fig. 2

Von Mise norm at final time, θ _R = 0

Fig. 3

Temperature field at final time, θ _R = 0

Fig. 4

Damage field at final time, θ _R = 0

Fig. 5

Evolution of damage field at x = (L ₁, L ₂), θ _R = 0

Finally in Figure 6, we show the distribution of the temperature and damage of the body for larger ground temperature. Here, we observe larger deformation, larger damage, and larger temperature in the neighborhood of the contact surface.

Fig. 6

Temperature and damage at final time, $B_1(t)= \frac {0,03}{2+t},\ B_2(t)= 10^{-4}\,e^{-t}$, θ _R = 10