Approximate Solutions to Fractional Boundary Value Problems by Wavelet Decomposition Methods

Abstract

Fractional derivatives, unlike those of natural order, have “memory” and are useful to model systems where the past history is relevant. They are defined by means of integral operators, some of them having singular kernels, and calculations may be difficult. It is for that reason that it is necessary to develop numerical approximation methods to solve most of real problems. In this work we combine the wavelet transform with the fractional derivatives of a particular wavelet basis, by means of a Galerkin scheme, to build an approximate solution to boundary value problems involving Caputo-Fabrizio fractional derivatives. The numerical scheme is simple and stable, and its accuracy can be improved as much as desired. We present some numerical examples to show its performance.

1 Introduction

In the last decades, models described by fractional differential equations have appeared profusely in different areas of science. Several definitions of derivatives of non integer order have been proposed to fit different real phenomena requirements. A great quantity of results concerning solutions to this type of equations involving Riemann-Liouville, Caputo, Caputo-Fabrizio and Atangana-Baleanu fractional derivatives were stated [1,2,3,4,5], and different explicit and numerical solutions were developed [6,7,8,9,10,11,12].

Applications are numerous and in areas as varied as continuum mechanics [13], fluid convection and diffusion [14, 15], thermoelasticity [16], robotics [17], biology and medicine [18,19,20,21], computer viruses [22] or economics [23, 24].

In this work we adapt a methodology developed for fractional ordinary differential equations (FODE) to find approximate solutions to linear fractional partial differential equations (FPDE) involving Caputo or Caputo-Fabrizio fractional derivatives.

Succinctly, the idea of the proposed numerical scheme to solve linear FODE (see [25, 26]) consists of expressing the equation by means of the Fourier transform and decomposing the data and the unknown on a wavelet basis with appropriate properties: well localized in time and frequency domains, smooth, band limited and infinitely oscillating with fast decay. We project the data onto suitable wavelet subspaces and truncate it. Afterwards, through a Galerkin scheme, we calculate the coefficients of the unknown function in the chosen wavelet basis solving a linear system of algebraic equations that involves the fractional derivatives of the basis. Properties of the basis enable us to work on each level separately. Finally, we rebuild the solution from its wavelet coefficient. The proposed method is simple, since only the wavelet coefficients of the data and a matrix derived from the normal equations are needed. The error introduced in the approximation can be controlled improving the computation of the elements of the matrix and considering a more accurate truncated projection of the data. Properties of the basis and the operator guarantee that the resulting approximation scheme is efficient and numerically stable and no additional conditions need to be imposed. Details can be found in [25] and [26].

For the case of linear FPDE, we separate variables to obtain auxiliary FODE that we solve using the proposed scheme. We apply the methodology to solve a fractional diffusion equation with fractional time derivative. We compute the solution to a particular equation for different values of the fractional order of derivation β ∈ (1, 2). When β → 2, as expected, the behaviour of the solution is similar to that of the wave equation, which corresponds to the case β = 2.

This work is organized as follows: in the next section we present the fractional derivate operator; the wavelet basis and the approximation scheme are introduced in Sect. 3. In Sect. 4 a solution to the FPDE is proposed. Some numerical examples are presented in Sect. 5. Finally we state some conclusions.

2 Definitions and Properties

2.1 Caputo and Caputo-Fabrizio Fractional Derivatives

For 0 < α < 1 and f a function in H ¹((a, b)), the Sobolev space of functions defined on (a, b) with f′∈ L ²((a, b)), the Caputo fractional derivative (CFD) introduced in 1967 (see [27]) is defined as

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} {}^{C}_{a}{\mathcal{D}}^{\alpha}_t f(t):=\frac{1}{\Gamma (1-\alpha)}\int_{a}^t \frac{f' (s)}{(t-s)^{\alpha}} ds \end{array} \end{aligned} $$

(1)

where Γ is the standard Gamma function and −∞≤ a < b.

Caputo-Fabrizio fractional derivative (CFFD) introduced in 2015 (see [28]) is defined as

(2)

where M(α) is a normalizing factor verifying M(0) = M(1) = 1.

Both derivatives are integral operators that involve an integral from a to t, i.e. the past “history” of f is taken into account so, contrary to what happens in the natural order derivative case, they have “memory”. It is worth noting that, in the case of Caputo-Fabrizio derivative, the integral operator has a regular kernel while in the Caputo case the kernel is singular.

Some properties of CFD and CFFD resemble those of classical derivatives: CFD and CFFD of order α of a constant function are zero and, for 0 < α < 1,

Note that, when a = −∞, both derivatives can be expressed as convolutions.

For the CFD, if κ is a causal function that coincides with $\frac {1}{t^\alpha }$ for t > 0, we have

(3)

where $\widehat {\kappa }(\omega )=\Gamma (1-\alpha ) (i\omega )^{\alpha -1}$ and the circumflex represents the Fourier transform.

In the case of CFFD,

$$\displaystyle \begin{aligned}^{CF}_{-\infty}{\mathcal{D}}^{\alpha}_t f(t) = \frac{M(\alpha)}{1-\alpha} \; (f'*k) (t)\end{aligned}$$

with the non-singular kernel $k(t)=e^{-\frac {\alpha t}{1-\alpha }}, \, t>0$, from which

$$\displaystyle \begin{aligned} \begin{array}{rcl}{} {}^{CF}_{-\infty}{\mathcal{D}}^{\alpha}_t f(t) = \frac{M(\alpha)}{2\pi (1-\alpha)} \int_{\mathbb{R}} \widehat{f'}(\omega) \,\widehat{k} (\omega)\, e^{i\omega t} d\omega \end{array} \end{aligned} $$

(4)

or

$$\displaystyle \begin{aligned} \begin{array}{rcl}{} {}^{CF}_{-\infty}{\mathcal{D}}^{\alpha}_t f(t)=\frac{M(\alpha)}{1-\alpha} \int_{\mathbb{R}} \widehat{f}(\omega) m(\omega) e^{i\omega t} d\omega \end{array} \end{aligned} $$

(5)

with the not singular kernel $m(\omega )= \frac {1}{2\pi } \,\frac {i\omega } {\frac {\alpha }{1-\alpha }+i\omega }$. Expression (5) in terms of the Fourier transform will be considered in Sects. 3 and 4 to solve FPDE.

2.2 The Wavelet Basis

We briefly introduce the wavelet basis that we will use in the rest of the paper. Details and properties can be found in [29].

We recall that a wavelet is an oscillating function, well localized in time and frequency domains (see [30, 31]). For a special selection of the mother wavelet ψ, the family

is an orthonormal basis of the space $L^{2}( {\mathbb R})$ associated with a hierarchical structure of the space – the multiresolution analysis (MRA) – which is a sequence of nested subspaces V _j, the scale-subspaces, such that:

• 1. V _j ⊂ V _j+1;

• 2. s(t) ∈ V _j if and only if s(2t) ∈ V _j+1;

• 3. if s(t) ∈ V ₀ then s(t + 1) ∈ V ₀;

• 4. $\;\cup _{j \in \mathbb Z} V_j$ is dense in $L^2(\mathbb R)$ and $\cap _ {j \in \mathbb Z} V_j= \{ 0\}$;

• 5. there exists a function ϕ ∈ V ₀, called scaling function, such that the family is an orthonormal basis of V ₀.

The wavelet subspace is the orthogonal complement of V _j in V _j+1 and contains the detailed information needed to go from the approximation with resolution level j to the one corresponding to level j + 1:

Consequently

$$\displaystyle \begin{aligned}L^2(\mathbb R) = \bigoplus_{j\in\mathbb Z} W_j.\end{aligned}$$

Moreover,

The MRA is associated to an efficient method to compute the wavelet coefficients: the Mallat’s algorithm (see [30]).

Looking for solutions to simple FODE as suggests the selection of the mother wavelet. Since the operators (3) and (4) act on Fourier transforms, it is convenient to implement a partition of the frequency domain in quasi-disjoint scale bands,

$$\displaystyle \begin{aligned}{\mathbb R}_{\omega} = \bigcup_{j=-\infty}^{\infty} \; \Omega_{j}\;,\end{aligned}$$

naturally associated with the wavelet subspaces W _j.

In order to achieve these benefits, we choose a Meyer wavelet: a band-limited function ψ, having a smooth Fourier transform $\widehat {\psi }$. In [29] we define the scale function and the wavelet as

with

and

$$\displaystyle \begin{aligned} \widehat{\psi}(\omega) = \sqrt{\phi^2(\omega/2)-\phi^2(\omega)}\; e^{-i \omega/2} \end{aligned}$$

with parameter 0 < β ≤ π∕3.

We recall that $\psi \in \mathcal {S}$, the Schwartz class, and the family $\{ \psi _{jk}, k\in {\mathbb Z} \}$ is an orthonormal basis of $L^2(\mathbb R)$ associated to a MRA, well localized in both, time and frequency domain. Its spectrum, $| \widehat {\psi }(2^{-j} \omega ) \, |$, is supported on the two-sided band

$$\displaystyle \begin{aligned} \Omega_j = \,\left\{\omega: 2^j(\pi-\beta )\le |\omega|\le 2^{j+1}(\pi+\beta)\right\} \end{aligned} $$

(6)

for some 0 < β ≤ π∕3.

In Fig. 1 we show the graphs of ψ and $|\widehat {\psi }|$.

Fig. 1

Mother wavelet for β = π∕4 (above) and $|\widehat {\psi }|$ for ω ≥ 0 (below)

It is important to highlight that the sets Ω_j−1, Ω_j, Ω_j+1 have little overlap (see Fig. 2) and W _j is nearly a basis for the set of functions whose Fourier transform has support in Ω_j. When solving FPDE this property will enable as to work on each level separately.

Fig. 2

The supports Ω_j−1, Ω_j, Ω_j+1 and their overlapping

Details on the basis and its properties can be found in [29]. In [31] approximations of Sobolev, Besov and other functional spaces, using wavelets in the Schwartz class, are developed.

3 Approximate Solutions to a Fractional Initial Value Problem

In this section we resume the technique introduced in [32] to calculate approximate solutions to the following initial value problem:

(7)

where $a \in \mathbb {R}$, −∞≤ a ≤ 0, h is the unknown, r is a known source function verifying r(0) = 0, and $\lambda _0,\lambda _1 \in \mathbb {R}$. Solution to this type of fractional initial value problem (FIVP) will be used to construct approximate solutions to FPDE by separating variables.

We will develop the calculations considering the CFFD. The case of CFD is similar. Details can be found in [25] for the case of CFFD and in [26] for the CFD.

First we will consider a = −∞ in (7). Afterwards we will adapt the procedure to the case a ≠ −∞.

3.1 The Data

Recall that, for any $J\in {\mathbb Z}$, the data function $r\in L^2(\mathbb R)$ can be decomposed as

$$\displaystyle \begin{aligned} \begin{array}{rcl} \begin{array}{rl} r(t) & = \sum_{j\in {\mathbb Z}} (\mathcal{Q}_{j} r)(t) = (\mathcal{P}_{J} r) (t) + \sum_{j \geq J} (\mathcal{Q}_{j} r) (t)= \\\\ & =\sum_{n \in {\mathbb Z}} \left\langle r,\phi_{J n} \right\rangle \phi_{ J n}(t) + \sum_{j \geq J}\; \sum_{k \in \mathbb Z} \left\langle r,\psi_{jk}\right\rangle \psi_{jk}(t) \end{array} \end{array} \end{aligned} $$

where $\mathcal {Q}_{j} r$ and $\mathcal {P}_{j} r$ are the orthogonal projections of r in W _j and V _j, respectively.

We choose $J_{min}, J_{max}\in \mathbb Z$ so that the energy of r is concentrated in levels J _min ≤ j ≤ J _max, $k\in \mathbb {K}_j$:

$$\displaystyle \begin{aligned}r(t)\cong\sum_{j=J_{min}} ^{J_{max}} r_j\cong\sum_{j=J_{min}} ^{J_{max}}\tilde{r}_j(t)\end{aligned}$$

where $r_j=\sum _{k\in {\mathbb {Z}} } c_{jk} \psi _{jk}$ is the projection of r on W _j, $c_{jk}=\left \langle r,\psi _{jk}\right \rangle$ are the wavelet coefficients, and $\tilde {r}_j$ is the truncated projection on W _j: $\tilde {r}_j=\sum _{k\in \mathbb {K}_j} c_{jk} \psi _{jk}$ for $\mathbb {K}_j\subset \mathbb {Z}$, $card({\mathbb {K}_j})=\eta _j<\infty$, satisfying

$$\displaystyle \begin{aligned}\sum_{k\notin \mathbb{K}_j}|\left\langle r,\psi_{jk}\right\rangle|{}^2 < \epsilon ||r_j||{}^2_2\end{aligned}$$

for certain 𝜖 near 0.

3.2 A Solution to the FDE

Let us decompose the solution of (7) in the basis, $h(t)= \sum _{j\in \mathbb {Z}} \sum _{k\in \mathbb {Z}} b_{jk}\psi _{jk}(t)$, and replace it in the equation:

We note that

$$\displaystyle \begin{aligned} \begin{array}{rcl} \begin{array}{rl} {}^{CF}_{-\infty}{\mathcal{D}}^{\alpha}_t h(t)& + \lambda_1 h'(t)+ \lambda_0 h(t)=\\\\ & =\frac{M(\alpha)}{1- \alpha} \int_{ \mathbb{R}} \widehat{h}(\omega) m(\omega) e^{i \omega t} d\omega+\frac{\lambda_1 }{2 \pi} \int_{ \mathbb{R}} i \omega \widehat{h}(\omega) e^{i \omega t} d\omega + \frac{\lambda_0 }{2 \pi} \int_{ \mathbb{R}} \widehat{h}(\omega) e^{i \omega t} d\omega \\\\ & = \int_{ \mathbb{R}} \widehat{h}(\omega) H(\omega) e^{i \omega t} d\omega = r(t), \end{array} \end{array} \end{aligned} $$

where

$$\displaystyle \begin{aligned} \begin{array}{rcl}{} H(\omega) = \dfrac{-\lambda_1(1-\alpha)\omega^2 + i\left(M(\alpha)+\alpha \lambda_1+(1-\alpha)\lambda_0 \right) \omega+\alpha \lambda_0}{2\pi (\alpha+i\omega(1-\alpha))}. \end{array} \end{aligned} $$

(8)

Thus, the images of the basis ψ _jk through the fractional differential operator result in

(9)

From (9), we note that the Fourier transform of u _jk satisfies $\mbox{supp}(\widehat {u}_{jk})\subset \Omega _j$. Then, based on previous observations, we can consider u _jk ∈ W _j and, consequently, we can work on each level J _min ≤ j ≤ J _max separately.

For a fixed j, we restrict ourselves to $\mathbb {K}_j$ to obtain

$$\displaystyle \begin{aligned}^{CF}_{-\infty}{\mathcal{D}}^{\alpha}_t h_j (t)+\lambda_1 h^{\prime}_j(t)+\lambda_0 h_j(t)=\sum_{k\in \mathbb {K}_j} b_{jk}u_{jk}(t)\cong \tilde{r}_j(t). \end{aligned}$$

The coefficients b _jk can be computed from the normal equations

$$\displaystyle \begin{aligned}\sum_{k\in \mathbb {K}_j} b_{jk}\langle u_{jk}, \psi_{jm}\rangle= \sum_{k'\in \mathbb {K}_j} c_{jk'}\langle \psi_{jk'}, \psi_{jm}\rangle\end{aligned}$$

or, in matrix form,

$$\displaystyle \begin{aligned} (\mathcal{M}^j\, {\mathbf{b}}^{j})_{k} = {\mathbf{c}}^j_k,\; k\in \mathbb{K}_j, \end{aligned} $$

(10)

where $\mathcal {M}^j_{km} = \langle u_{jk}, \psi _{jm}\rangle .$

We approximate h _j(t) by $\tilde {h}_j(t)=\sum _{k\in \mathbb {K}_j} b_{jk}\psi _{jk}(t)$, with $({\mathbf {b}}^{j})_{k}=b_{jk}, {k\in \mathbb {K}_j}$ from (10), and $h(t) \cong \sum _{j=J_{min}} ^{J_{max}}\tilde {h}_j(t)$ .

Since r is causal, r(0) = 0, its wavelets coefficients c _jk, associated to t ≤ 0, are almost null and ${\mathbf {b}}^{j}_k$ results nearly null. Thus the proposed solution satisfies h(0) = 0.

We can proceed in a similar way if higher (natural) order derivatives appear in (7).

Further, we can adapt the scheme to the case where initial conditions are not null or a ≠ −∞, particularly, a = 0.

If a = 0, we consider $\overline {h}=h\cdot \chi _{[0,b]}$.

For t < 0 we have $\overline {h}'(t)=0$ and $\overline {h}(t)=0$ and, for t > 0, $\overline {h}'(t)=h'(t)$.

In addition,

and $\overline {h}(0)=0$.

Thus $\overline {h}$ satisfies

When initial conditions are not null (h(0) = h ₀≠0 or r(0) ≠ 0), we perform a “small” perturbation.

In order to solve and the IVP

$$\displaystyle \begin{aligned} \begin{array}{rcl} \left\{ \begin{array}{lcc} L(h)(t)& =&\displaystyle r(t)\\ h(0)& =&\displaystyle h_0 \end{array} \right. \end{array} \end{aligned} $$

with h ₀≠0, we consider $\tilde {r}(t)=r(t)-\lambda _0 h_0$ and, for small ε > 0, $\tilde {r}_{\varepsilon }(t)$ a $C^{\infty }(\mathbb {R})$ function on (0, ε), that is null at the origin and coincides with r(t) for t > ε (see Fig. 3).

Fig. 3

Perturbation for the case h(0) = h ₀≠0

The solution h _ε to $L(h)(t)=\tilde {r}_{\varepsilon }(t)$ will be null at the origin and h = h _ε + h ₀ satisfies the initial condition and

Thus h = h _ε + h ₀ is an approximate solution to the original IVP.

3.3 The Error

We comment on the error introduced in the different steps of the proposed numerical scheme.

First, we project and truncate the data r introducing two sources of error: we consider $r\cong \tilde {r}=\sum _{j=J_{min}} ^{J_{max}} r_j$ , r _j ∈ W _j, satisfying $r-\tilde {r}=e_r$ with ||e _r||₂ < 𝜖∥r∥₂ ≃ 0, and, for each j, we perform a truncation by posing $r_j \cong \tilde {r}_j=\sum _{k\in \mathbb {K}_j} c_{jk} \psi _{jk}(t)$, $\mathbb {K}_j\subset \mathbb {Z}$, $|\mathbb {K}_j|=\eta _j<\infty$. The choice of J _min, J _max and $\mathbb {K}_j$ guarantees that the error introduced at this stage can be neglected. It can also be reduced by choosing a wider range for j and a larger $\mathbb {K}_j$.

Another source of error arises when considering u _jk ∈ W _j. It can be cut down posing the system simultaneously in more (all) levels.

Finally, the linear system (10) is posed and solved. The elements of $\mathcal {M}^j$ are the inner products 〈u _jk, ψ _jm〉. These integrals can be performed in the frequency domain taking advantage of the properties of the wavelets, i.e. on the compact subsets Ω_j:

$$\displaystyle \begin{aligned}\langle u_{jk}, \psi_{jm}\rangle=\frac{1}{2\pi}\int_{\Omega_j} \widehat{u}_{jk}(\omega) \widehat{\psi}_{jm}(\omega) d \omega\end{aligned}$$

and can be computed with good precision.

We observe that, in order to calculate the wavelet coefficients ${\mathbf {b}}^{j}_{k}$, it is not necessary to compute u _jk: we only need the values of 〈u _jk, ψ _jm〉.

Regarding the solution to (10), $\mathcal {M}^j$ can be arbitrarily approximated by band matrices:

Lemma

$\mathcal {M}^j$ is nearly a band matrix.

Proof

From (8), there exist $N\in \mathbb {N}$ such that

$$\displaystyle \begin{aligned} H(\omega) =\frac{1}{2\pi} \, \left( \sum_{n=0}^{N} a_n \, \cos{}( \frac{n \omega}{2^j}) + i \sum_{n=1}^{N} b_n \, \sin{}( \frac{n \omega}{2^j})\right)+ \epsilon(\omega) \end{aligned}$$

where 𝜖(ω) is an error that is small for large N. Then, from (9) ,

$$\displaystyle \begin{aligned} u_{jk}(t) \cong \frac{M(\alpha)}{2 \pi(1-\alpha)} \int_{\Omega_j} \widehat{\psi}_{jk}(\omega) \left( \sum_{n=0}^{N} a_n \, \cos{}( \frac{n \omega}{2^j}) + i \sum_{n=1}^{N} b_n \, \sin{}( \frac{n \omega}{2^j}) \right) e^{i\omega t} d\omega. \end{aligned}$$

We note that

$$\displaystyle \begin{aligned} a_n \cos{}( \frac{n \omega}{2^j}) \widehat{\psi}_{jk}(\omega) = \frac{a_n}{2}( e^{i\frac{n \omega}{2^j}} + e^{-i\frac{n \omega}{2^j}}) \, \widehat{\psi}_{jk}(\omega) = \frac{a_n}{2}( \widehat{\psi}_{j (k-n)}(\omega) + \widehat{\psi}_{j (k+n)}(\omega) ) \end{aligned}$$

and

$$\displaystyle \begin{aligned} b_n \sin{}( \frac{n \omega}{2^j}) \widehat{\psi}_{jk}(\omega) = \frac{b_n}{2i}( e^{i\frac{n \omega}{2^j}} - e^{-i\frac{n \omega}{2^j}}) \, \widehat{\psi}_{jk}(\omega) = \frac{b_n}{2i}( \widehat{\psi}_{j (k-n)}(\omega) - \widehat{\psi}_{j (k+n)}(\omega) ). \end{aligned}$$

Consequently,

$$\displaystyle \begin{aligned}u_{jk}(t) \cong \frac{ M(\alpha)}{1-\alpha}\, \left[ a_0 \psi_{jk}(t) + \sum_{n=1}^{N} \left( \frac{a_n+b_n}{2} \psi_{j(k-n)}(t) + \frac{a_n-b_n}{2} \psi_{j(k+n)}(t)\right)\right]\end{aligned}$$

and for $m\in \mathbb {K}_j$, 0 ≤ m ≤ N, we can approximate the elements of the matrix by

$$\displaystyle \begin{aligned} \mathcal{M}^j_{km}=\left\langle u_{jk}, \psi_{jm}\right\rangle \cong \begin{cases} \frac{ M(\alpha)}{1-\alpha} \frac{a_{k-m}+b_{k-m}}{2}, \; \; \mbox{if } \;\; k-m>0 \\ \frac{ M(\alpha)}{1-\alpha} \frac{a_{k+m}-b_{k+m}}{2}, \; \;\mbox{if } \; \;k-m<0 \end{cases} \end{aligned}$$

$$\displaystyle \begin{aligned} \mathcal{M}^j_{kk}=\left\langle u_{jk}, \psi_{jk }\right\rangle \cong \frac{ M(\alpha)}{1-\alpha} a_{0}. \end{aligned}$$

Since the inner products are zero for m > N, $\mathcal {M}^j$ is nearly a band matrix. ◇

In all the numerical experiments we performed, $\mathcal {M}^j$ was a diagonal dominant matrix, with good condition number, and the linear system was solved efficiently.

4 A Fractional Boundary Value Problem

As we mentioned in the Introduction, we can apply the proposed methodology to find approximate solutions to linear fractional boundary value problems (FBVP). We will explain the method on a specific problem: anomalous diffusion.

A fractional diffusion equation involving fractional temporal derivatives (see [33, 34]) is used to model, for example, dispersion phenomena in heterogeneous media. There are experimental results – like anomalous diffusion in porous, fractal or biological media, in turbulent plasma and in polymers, among others – that show that the mean square displacement of the particles must be considered to be proportional not to the time but to a power of time to fit the empirical data. This power may be less than unity (subdiffusion) or greater than 1 (superdiffusion), and the diffusion model can be expressed by a differential equation of the type

$$\displaystyle \begin{aligned} \begin{array}{rcl}{} {\mathcal{D}}^{\beta}_t u(\mathbf{x},t)-k \nabla^2 u(\mathbf{x},t)=s(\mathbf{x},t), \end{array} \end{aligned} $$

(11)

where β is a fractional order of derivation with respect to time (0 < β < 1 for subdiffusion and β > 1 for superdiffusion).

We will consider Caputo-Fabrizio temporal fractional derivatives in the diffusion equation (11). Computations for the case of CFD are similar.

For the 1D case (i.e. $\mathbf {x} \in \mathbb {R}$) we will solve the following boundary value problem of anomalous diffusion:

(12)

where β = 1 + α, 0 < α < 1 and means (see [28]). The initial data f and g are supposed to be sufficiently smooth, with g(0) = 0. The source s(x, t) is a smooth and causal function (i.e. s(x, t) = 0 for t ≤ 0).

Note that, for h regular enough, we have (see [28, 35, 36])

Integrating by parts we obtain

that is

(13)

Now we replace (13) in (12) and arrive to a time FPDE of order α, 0 < α < 1:

Taking into account the initial conditions we have

or

Let us define

$$\displaystyle \begin{aligned}\tilde{s}(x,t)=-\frac{1-\alpha}{\alpha} s(x,t)-\frac{M(\alpha)}{\alpha}g(x)e^{-\frac{\alpha t}{1-\alpha}} .\end{aligned}$$

The resulting FBVP is

(14)

We will construct an approximate solution to (14) as superposition of smooth functions (in the Schwartz class). As in the standard case (natural order PDE), we propose a solution to (14) by separating variables, and one of the resulting ODE will have fractional order.

If u(x, t) = X(x)T(t) we pose the second order ODE

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} X''-\nu X=0 \end{array} \end{aligned} $$

with boundary condition X(0) = X(L) = 0, and find $\nu = - (\frac {k\pi }{L})^2$, $X_k(x)=\sin {}(\frac {k\pi x}{L}),$ for k ∈ Z.

Now, for $u(x,t)=\sum _{k\ge 1} u_k(t) \sin {}(\frac {k\pi x}{L}),$ and supposing that derivation and summation can be interchanged, we replace this last expression in (14) and obtain

(15)

Note that, if u ∈ C ²(0, 1) × C ¹(0, T), the derivatives u _xx(x, t), u _t(x, t) and are continuous functions in (0, 1) × (0, T).

If $u^{**}_k(t)$ , $u^{\#}_k(t)$ and $u^{*}_k(t)$ are, respectively, the Fourier coefficients of u _xx(x, t), u _t(x, t) and for each t ∈ [0, T], it follows that $u^{**}_k(t)=\frac {-k^2{\pi }^2}{L^2} u_k(t)$, $u^{\#}_k(t)=u_k^{\prime }(t)$ and . From (15) we have that the Fourier coefficients of $\tilde {s}$, $\tilde {s}_k (t)=2\int _0^L \tilde {s}(r,t)\sin {}(\frac {k\pi }{L}r)dr$, must satisfy

Then, the functions u _k are solutions to the following IVP (similar to (7)):

(16)

where $f_k=2\int _0^L f(\mu )\sin {}(\frac {k\pi }{L}\mu )d\mu$ are the Fourier coefficients of f.

Under the assumptions that v(0) = 0 and l causal, there is a unique solution in C ¹[0, T] for

(see [32]) and we can approximate it by a smooth function: a linear combination of wavelets.

Explicit formula for the solution to (16) may also be found in some cases.

Note that, regarding the hypothesis on s, $\tilde {s}_k(0)=2\int _0^L \tilde {s}(\mu ,0)\sin {}(\frac {k\pi }{L}\mu )d\mu$ might not be null because $\tilde {s}(\mu ,0)=-\frac {1-\alpha }{\alpha } s(\mu ,0)-\frac {M(\alpha )}{\alpha }g(\mu )$. In addition, from the initial conditions, we know that u _k(0) = f _k. If f _k ≠ 0, we have to adapt the scheme in order to apply the same methodology, as explained previously.

Finally, $u(x,t)=\sum _{k\ge 1} u_k(t) \sin {}(\frac {k\pi x}{L})$.

5 Numerical Examples

In this section we show the performance of the proposed numerical approximation in some examples. The FPDE is

In Examples 1, 2 and 3 we build approximate solutions following the proposed technique for different initial and boundary conditions.

5.1 Example 1

Let us consider the following FBVP:

where v(t) is a smooth window in [0, 16] and (x, t) ∈ (0, 10) × (0, 16). Following the steps described above, if $u(x,t)=\sum _{k\ge 1} u_k(t) \sin {}(\frac {k\pi x}{L})$, we only need to solve the (16) for k = 1 and arrive to the

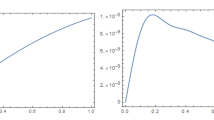
In Table 1 the energy wavelet analysis by levels of the functions $\tilde {s_1}$ and of the solution u ₁ is shown. The significant levels j = −4, −3 contain the 91% of $\tilde {s_1}$. For the reconstruction we consider levels − 1 ≤ j ≤−5. The resulting mean square error is 4.3866 ∗ 10⁻⁶. We plot the exact u ₁ vs. its approximation in Fig. 4 and the solution to the BVP in Fig. 5.

Fig. 4

u ₁(t) vs. u ₁(t) approx.

Fig. 5

u(x, t) approx.

Table 1 Energy distribution of the data function $\tilde {s_1}$ and of the solution u ₁

5.2 Example 2

We consider the same FPDE as in Example 1, but changing the initial condition by $u(x,0)=\sin {}(\frac {\pi }{10}x), \;\forall x\in [0,10]$.

Separating variables we arrive to

$$\displaystyle \begin{aligned} \begin{array}{rcl} \left\{\begin{array}{rl} _0{\mathcal{D}} _t^{1/2}u_1(t)-2u^{\prime}_1(t)-(\frac{\pi}{10})^2u_1(t)& =v(t)\sin{}(3\pi t)=\tilde{s_1}(t), 0<t<16 \\ u_1(0)& =1\\ \end{array} \right. \end{array} \end{aligned} $$

As the initial condition on u ₁ is not null, we perform the perturbation already described.

Table 2 contains the energy wavelet analysis by levels of the functions $\tilde {s_1}$ and of the solution u ₁. The significant levels j = −4, −3 contain the 91% of $\tilde {s_1}$.

Table 2 Energy distribution of the data function $\tilde {s_1}$ and of the solution u ₁

For the reconstruction we consider levels − 1 ≤ j ≤−5. The resulting mean square error is 1.8338 ∗ 10⁻⁴.

In Figs. 6 and 7 we show the approximation for u ₁(t) versus the exact solution and the approximation for u(x, t), respectively.

Fig. 6

u ₁(t) vs. u ₁(t) Approx.

Fig. 7

Approx. u(x, t) sol.

5.3 Example 3

In order to evaluate the performance of the method, we obtain the solutions to (12) for different values of β approaching 2 and compare them with that of the wave equation, which corresponds to β = 2.

Consider

where v(t) is a smooth window in [0, 32] and (x, t) ∈ (0, 10) × (0, 32), with β = 1 + α for different α. When α → 1 the solutions must resemble those of β = 2.

Following the steps described above, if $u(x,t)=\sum _{k\ge 1} u_k(t) \sin {}(\frac {k\pi x}{L})$, we only need to solve (16) for k = 1. We consider β = 1.8, 1.9, 1.95.

See Figs. 8 and 9 where we show, respectively, u ₁(t) and u(x, t) for the different values of β.

Fig. 8

u ₁(t) for different β

Fig. 9

u(x, t) approx. for different β

On the other hand, if β → 1 in (12), the behaviour of the solution u would tend to that of the classical diffusion equation.

6 Conclusions and Future Work

In this work we have adapted a numerical scheme to solve FODE, developed in previous works, to find approximate solutions to a FBVP. Using the proposed method, we built approximate solutions to an advection diffusion equation of order β, 1 < β < 2. When β tends to 2, its behaviour looks like that of the solution to the standard wave equation. We have developed the calculations considering the CFFD but the CFD case is analogous. The same scheme can be proposed to solve different linear FPDE.

We intend to apply this methodology to solve inverse problems involving fractional models. Extensions to some nonlinear equations are also being studied.