Classifying Image Series with a Reoccurring Concept Drift Using a Markov Chain Predictor as a Feedback

Abstract

We consider the problem of classifying images, ordered in a sequence (series), to several classes. A distinguishing feature of this problem is the presence of a slowly varying, reoccurring concept drift which results in the existence of relatively long subsequences of similar images from the same class. It seems useful to incorporate this knowledge into a classifier. To this end, we propose a novel idea of constructing a Markov chain (MC) that predicts a class label for the next image to be recognized. Then, the feedback is used in order to modify slightly a priori probabilities of class memberships. In particular, the a priori probability of the class predicted by the MC is increased at the expense of decreasing the a priori probabilities of other classes.

The idea of applying an MC predictor of classes with the feedback to a priori probabilities is rather general. Thus, it can be applied not only to images but also to vectors of features arising in other applications. Additionally, this idea can be combined with any classifier that is able to take into account a priori probabilities. We provide an analysis when this approach leads to the reduction of the classification errors in comparison to classifying each image separately.

As a vehicle to elucidate the idea we selected a recently proposed classifier (see [23, 25]) that is based on assuming matrix normal distribution (MND) of classes. We use a specific structure of the MND’s covariance matrix that can be estimated directly from images without feature extraction.

The proposed approach was tested on simulated images as well as on an example of the sequence of images from an industrial gas burner’s flames. The aim of the classification is to decide whether natural gas contains a sufficient amount of methane (the combustion process is proper, lower air pollution) or not.

1 Introduction

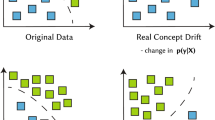
A large number of examples can be pointed out when images should be considered as a series (i.e., a sequence of images that are ordered in time). This is of particular importance when we want to observe and classify selected features over time. We assume that the features of interest can fluctuate over a long time intervals without changing their class membership of subsequent images. At unknown time instants, the observed features can change (abruptly or gradually), leading to the change of their classification for a longer period. Then, the next parts of the series can return to previously visited class memberships. We shall name such sequences image series with a slow reoccurring concept drift. The assumption that we are faced with an image series with a slow reoccurring concept drift is crucial for this paper. The reason is that we can use this fact in order to increase the classification accuracy by predicting a class label of the next image and incorporating this a priori knowledge into a classifier.

The following examples of such image series can be pointed out.

• Quality control of manufacturing processes monitored by cameras. The following two cases can be distinguished:

  • 1. Separate items are produced and classified as proper or improper (conforming to requirements or not). One can expect long sequences of conforming items and shorter sequences of non-conforming ones.

  • 2. Production is running continuously in time (e.g., molding and rolling of copper, other metals or steel alloys). Here also slow changes of the quality can be expected, while the proper classification of a product is crucial for economic efficiency.

• Combustion processes monitored by a camera (see [20, 29] and the bibliography cited therein).

• Automated Guided Vehicles (AGV) are more and more frequently monitored by cameras and/or other sensors. Most of the time they operate in an environment which is well defined and built-in into their algorithms, but sometimes it happens that they meet other AVG’s or other obstacles to be recognized.

For simplicity of the exposition we impose the following constraints on an image series:

• it is not required that class labels of subsequent images strictly form a Markov chain (MC), but if it is possible to indicate the corresponding MC, then the proposed classification algorithm has a stronger theoretical justification,

• images are represented as matrices, i.e., only their grey levels are considered,

• an image series has slow reoccurring concept drift in the sense explained above,

• the probability density functions (p.d.f.’s) of images in each class have covariance structures similar to that of matrix normal distributions (MND’s).

The last assumption will be stated more formally later. We usually do not have enough learning images to estimate the full covariance matrix of large images. An alternative approach, that is based projections is proposed in [26].

The paper is organized as follows:

• in the section that follows we provide a short review of the previous works,

• in Sect. 3, we state the problem more precisely,

• in the next sections, we provide a skeletal algorithm, then its exemplifications and the results of testing are discussed.

• an example of classifying flames of an industrial gas burner is discussed in the section before last.

Notice that we place an emphasis on classifying images forming a time series, but avoiding a tedious (and costly) features extraction step (an image is considered as an entity).

2 Previous Work

We start from papers on the bayesian classifiers that arise in cases when the assumption that class densities have the MND distribution holds. This assumption will be essentially weakened in this paper, but it cannot be completely ignored when one wants to avoid the feature extraction step without having millions of training and testing images.

Then, we briefly discuss classic papers on classifying images when their class labels form a Markov chain. We also indicate the differences in using this information in classic papers and here.

As mentioned in [25], “The role of multivariate normal distributions with the Kronecker product structure of the covariance matrix for deriving classifiers was appreciated in [15], where earlier results are cited. In this paper the motivation for assuming the Kronecker product structure comes from repeated observations of the same object to be classified.”

It was also documented in [22, 23] and [24] that the classifier based on the MND’s assumption is sufficiently efficient for classifying images without features extraction. Furthermore, in [25] it was documented that an extended version of such classifiers is useful for recognizing image sequences, considered as whole entities.

Fig. 1.

A general scheme of classifying an image series.

The second ingredient that is used in the present paper is a Markov chain based predictor of class labels, which is used as feedback between the classifier output and a priori class probabilities for classifying the next image in a sequence. This idea was proposed by the first author (see Fig. 1 for a schematic view of the overall system).

The idea of using the assumption that class labels form a Markov structure has a long history [13] and its usefulness is appreciated up to now (see, e.g., [14, 28]). In these and many other papers, the Markov chain assumption was used in order to improve the classification accuracy of a present pattern using its links to the previous one. Here, we use a Markov chain differently, namely, it serves in the feedback as a predictor of the next class label.

A recurrence in neural networks has reappeared several times. A well-known class is Elman networks (see the original paper [9] and [4] for a learning process of Elman’s networks which is so laborious that it requires parallel computing tools). In Elman’s networks, an input vector is extended by stacking values of all the outputs from the previous iteration.

Hopfield neural networks (HNN) have even a more complicated structure. Their learning is also rather laborious, since after presenting an input vector the HNN internally iterates many times until a stable output is attained. We refer the reader to [18] for the description of the HNN that is dedicated to change detection between two images and to [2] for the HNN designed to classify temporal trajectories.

In the context of Elman’s and Hopfield’s nets, our feedback can be called weak, for the following reasons:

• 1. only limited information (class labels) is transmitted back to the recognizer,

• 2. the transmission is done once per image to be recognized (there are no inner loop iterations),

• 3. feedback information does not influence an input image, but provides only an outer context for its classification, by modifying a priori class probabilities.

The problem of dealing with reoccurring concept drift has been intensively studied in recent years. We refer the reader to [8, 10] and the bibliography cited therein. We adopt the following definition from [8]: “We say that the changes are reoccurring if we know that the concept can appear and disappear many times during processing the stream.” We agree also with the following opinion: “Many methods designed to deal with concept-drift show unsatisfactory results in this case [3].”

Our approach can also be used for data streams, but after a learning phase that is based on long historical sequences of images. We shall not emphasise this aspect here. We refer the reader to [12] for the recent survey paper on learning for data stream analysis.

3 Problem Statement

In this section, we first recall the pattern recognition problem for matrices in the Bayesian setting. Then, we specify additional assumptions concerning a series of images and reoccurring concept drift.

3.1 Classic Bayesian Classification Problem for Random Matrices

A sequence of ordered images $\mathbf {X}_k$, $k=1,\,2,\dots ,K$ is observed one by one. Grey level images are represented by $m\times n$ real-valued¹ matrices.

Each image $\mathbf {X}_k$, $k=1,\,2,\dots ,K$ can be classified to one of $J>1$ classes, labeled as $j=1,\, 2,\ldots ,\, J$. The following assumptions apply to all J classes.

As 1):

Each $\mathbf {X}_k$ is a random matrix, which was drawn according to one of the probability density functions (p.d.f.’s), denoted further by $f_j(\mathbf {X})$, $j=1,\, 2,\ldots ,\, J$, of the $m\times n$ matrix argument $\mathbf {X}$

As 2):

Random matrices $\mathbf {X}_k$, $k=1,\,2,\dots ,K$ are mutually independent (this does not exclude stochastic dependencies between elements of matrix $\mathbf {X}_k$).

As 3):

Each matrix $\mathbf {X}_k$ is associated with class label $j_k\in \mathcal {J}$, $k=1,\,2,\dots ,K$, where $\mathcal {J}{\mathop {=}\limits ^{def}} \{j:\, 1\le j\le J \}$.

Labels $j_k$’s are random variables, but – as opposed to the classic problem statement – they are not required to be mutually independent. When new matrix (image) $\mathbf {X}_0$ has to be classified to one of the classes from $\mathcal {J}$, then the corresponding label $j_0$ is not known. On the other hand, when ordered pairs $(\mathbf {X}_k,\, j_k)$, $k=1,\,2,\dots ,K$ are considered as a learning sequence, then both images $\mathbf {X}_k$’s and the corresponding labels $j_k$’s are assumed to be known exactly, which means that a teacher (an expert) properly classified images $\mathbf {X}_k$’s.

As 4):

We assume that for each class there exists a priori probability $p_j>0$ that $\mathbf {X}$ and $\mathbf {X}_k$’s were drawn from this class. Clearly $\sum _{j=1}^J p_j=1$. Notice that here a priori probabilities are interpreted in the classic way, namely, as the probabilities drawing some of $\mathbf {X}_k$’s from j-th class. In other words, in specifying $p_j$’s we do not take into account the fact that $\mathbf {X}_k$’s form an image series with possible concept drift. Later, we modify this assumption appropriately.

As 5) (optional):

In some parts of the paper we shall additionally assume that class densities $f_j(\mathbf {X})$’s have matrix normal distributions $\mathcal {N}_{n,\, m}(\mathbf {M}_j,\, U_j,\, V_j)$, i.e., with the expectation matrices $\mathbf {M}_j$ and $U_j$ as $n\times n$ inter-rows covariance matrices and $V_j$ as an $m\times m$ covariance matrix between columns, respectively. We refer the reader to [23] and the bibliography cited therein for the definition and basic properties of MND’s.

It is well-known (see, e.g., [7]) that for the 0–1 loss function the Bayes risk of classifying $\mathbf {X}$ is minimized by the following classification rule:

$$\begin{aligned} j^*=\text{ arg }\, \max _{1\le j \le J}\,\, p_j\,f_j(\mathbf {X}), \end{aligned}$$

(1)

since a posteriori probabilities $P(j|\mathbf {X})$ of $\mathbf {X}$ being from class $j\in \mathcal {J}$ are proportional to $p_j\,f_j(\mathbf {X})$, $j\in \mathcal {J}$ for each fixed $\mathbf {X}$.

In [23] particular cases of (1) were derived under assumption As 5).

3.2 Classification of Images in a Series

Consider a discrete-time and discrete states Markov chain (MC) that is represented by $J\times J$ matrix $\mathcal {P}$ with elements $p_{j\,j'}\ge 0$, $j,\,j'\in \mathcal {J}$, where $p_{j\,j'}$ is interpreted as the probability that the chain at state j moves to state $j'$ at the next step. States of the MC are further interpreted as labels attached to $\mathbf {X}$’s. Clearly, $\mathcal {P}$ must be such that $\sum _{j'\in \mathcal {J}} p_{j\,j'}=1$ for each $j\in \mathcal {J}$. Additionally, the MC is equipped with column vector $\bar{q}_{0}\in R^J$ with nonnegative elements that sum up to 1. The elements of this vector are interpreted as the probabilities that the MC starts from one of the states from $\mathcal {J}$. According to the rules governing Markov chains, vectors $\bar{q}_k$ of the probabilities of the states in subsequent steps are given by $\bar{q}_k\,=\, \mathcal {P}\, \bar{q}_{k-1}$, $k=1,\, 2,\, \ldots ,\, K$. At each step k a particular state of the MC is drawn at random according to the probabilities in $\bar{q}_k$.

As 6):

Class labels $j_k$ in series of images $(\mathbf {X}_k,\, j_k)$, $k=1,\, 2,\, \ldots ,\, K$ are generated according to the above described Markov chain scheme.

In order to assure that the MC $\mathcal {P}$ is able to model reoccurring concept drifts, represented by changes of $j_k$’s, we impose the following requirements on $\mathcal {P}$:

As 7):

The MC $\mathcal {P}$ possesses the following properties: all the states are communicating and recurrent, the MC is irreducible and aperiodic.

In the Introduction (see also the section before last) it was mentioned that our motivating example is the combustion process of natural gas, which can have slowly varying contents of methane modelled here as slowly varying, reoccurring concept drift. Similar concept drift changes can be observed in drinking water and the electricity supply networks in which concept drifts appear as changes of parameters of a supplied medium (e.g., the purity of water or the voltage of the current).

The ability of MC to generate long sequences of the same labels is guaranteed by the following assumption.

As 8):

Transition matrix $\mathcal {P}$ of the MC has strongly dominating diagonal elements (by strong dominance we mean the diagonal elements are about 5–10 times larger than other entries of $\mathcal {P}$.

Mimicking decision rule (1) for images in a series, under assumptions A1)-A4) and A6)-A8), it is expedient to consider the following sequence of decision rules:

$$\begin{aligned} j_k^*=\text{ arg }\, \max _{1\le j' \le J}\,\, \left[ p_{j^*_{(k-1)}\,j'}\,f_{j'}(\mathbf {X}_k)\right] ,\quad k=1,\, 2,\, \ldots ,\, K, \end{aligned}$$

(2)

where it is assumed that at step $(k-1)$ it was decided that $j^*_{k-1}$ is the label maximizing the same expression (2), but at the previous step.

Under assumptions As 1) - As 4) and As 6) - As 8), our aim in this paper is the following:

• 1. having learning sequences of images: $(\hat{\mathbf {X}}_k,\, \hat{j}_k)$, $k=1,\, 2,\, \ldots ,\, \hat{K}$

• 2. and assuming proper classifications $\hat{j_k}$ to one of the classes

• 3. to construct an empirical classifier that is based on (2) decision rules.

and to test this rule on simulated and real data.

4 A General Idea of a Classifier with the MC Feedback

Decision rules (2) suggest the following empirical version of decision rules: $\mathbf {X}'_k$ is classified to class $\tilde{j}_k$ at k-th step if

$$\begin{aligned} \tilde{j}_k=\text{ arg }\, \max _{1\le j' \le J}\,\, \left[ \tilde{p}_{\tilde{j}_{(k-1)}\,j'}\,\hat{f}_{j'}(\mathbf {X}'_k)\right] ,\quad k=1,\, 2,\, \ldots ,\, K, \end{aligned}$$

(3)

where $\tilde{j}_{(k-1)}$ is the class indicated at the previous step, while:

• 1. $\hat{f}_{j'}(\mathbf {X}_k)$, $j'\in \mathcal {J}$ are estimators of p.d.f.’s ${f}_{j'}(\mathbf {X}_k)$ that are based on the learning sequence.

• 2. $\tilde{p}_{\tilde{j}_{(k-1)}\,j'}$, $j'\in \mathcal {J}$ plays the role of the a priori class probabilities at k-th step. Possible ways of updating them are discussed below.

As estimators in 1) one can select either

• parametric families with estimated parameters (an example will be given in the next section),

• nonparametric estimators, e.g., from the Parzen-Rosenblat family or apply another nonparametric classifier that allows specifying a priori class probabilities, e.g., the support vector machine (SVM) in which class densities are not explicitly estimated (see an example in the section before last).

The key point of this paper is the way of incorporating the fact that we are dealing with an image series with a reoccurring concept drift into the decision process. As already mentioned (see Fig. 1), the idea of a decision process is to modify a priori class probabilities taking into account the result of classifying the previous image by giving preferences (but not a certainty) to the latter class.

This idea can be formalized in a number of ways. We provide two of them that were tested and reported in this paper.

Skeletal classifier for image series with the MC feedback

Step 0:

Initial learning phase: select estimators $\hat{f}_{j'}(\mathbf {X})$, $j'\in \mathcal {J}$ and calculate them from the learning sequence, estimate the original a priori class probabilities $\tilde{p}^0_{j'}$, $j'\in \mathcal {J}$ as the frequencies of their occurrence in the learning sequence. Then, set

$$\begin{aligned} \tilde{p}_{\tilde{j}_{0}\,j'} = \tilde{p}^0_{j'},\quad \text{ for } \text{ all } j'\in \mathcal {J}\end{aligned}$$

(4)

for the compatibility of the notations in further iterations, where for $k=0$ we select $\tilde{j}_{0}=\text{ arg }\, \max _{1\le j \le J}\,[\tilde{p}^0_{j}]$ as the maximum a priori probability. Estimate transition matrix $\hat{\mathcal {P}}$ of the MC from the labels of the learning sequence. Select $\gamma \in [0,\, 1]$ and $\varDelta _p\in [0,\, 1)$ as parameters of the algorithm (see remarks after the algorithm for explanations). Set $k=1$ and go to Step 1.

Step 1:

Decision: acquire the next image in the series $\mathbf {X}'_k$ and classify it to class

$$\begin{aligned} \tilde{j}_k=\text{ arg }\, \max _{1\le j' \le J}\,\, \left[ \tilde{p}_{\tilde{j}_{(k-1)}\,j'}\,\hat{f}_{j'}(\mathbf {X}'_k)\right] . \end{aligned}$$

(5)

Step 2:

Prediction: run one step ahead of the MC $\hat{\mathcal {P}}$, starting from the initial state: $[0,\,0,\,\ldots ,\, \underbrace{1}_{\tilde{j}_k} ,\,\ldots ,\, 0,\,0]$. Denote by $\check{j}_k$ the label resulting from this operation.

Step 3:

Update the probabilities in (5) as follows:

$$\begin{aligned} \tilde{p}_{\tilde{j}_{k}\,j'} = \check{p}_{\tilde{j}_{k}\,j'}\Big / \sum _{j=1}^J \check{p}_{\tilde{j}_{k}\,j} \text{ for } \text{ all } j'\in \mathcal {J}, \end{aligned}$$

(6)

where $\check{p}_{\tilde{j}_{k}\,j'}$’s are defined as follows: if $j'\ne \check{j}_k$, then for all other $j'\in \mathcal {J}$

$$\begin{aligned} \check{p}_{\tilde{j}_{k}\,j'} = (1-\gamma )\, \tilde{p}^0_{j'} + \gamma \, \tilde{p}_{\tilde{j}_{(k-1)}\,j'} \, , \end{aligned}$$

(7)

otherwise, i.e., for $j'=\check{j}_k$

$$\begin{aligned} \check{p}_{\tilde{j}_{k}\,j'} = (1-\gamma )\, \tilde{p}^0_{j'} + \gamma \, \tilde{p}_{\tilde{j}_{(k-1)}\,j'} + \varDelta _p \, . \end{aligned}$$

(8)

Step 4:

If $\mathbf {X}_k'$ is not the last image in the series (or if $\mathbf {X}_k'$’s form a stream), then set $k:=k+1$ and go to Step 1, otherwise, stop.

The following remarks are in order.

• 1. In (7) and (8) parameter $\gamma \in [0,\, 1]$ influences the mixture of the original a priori information and information gathered during the classification of subsequent images from the series.

• 2. Parameter $\varDelta _p\in [0,\, 1)$ is added only to the probability of the predicted class $\check{j}_k$ in order to increase its influence on the next decision. The necessary normalization is done in (6). In the example presented in the section before last the influence of $\varDelta _p$ on the classification accuracy is investigated.

5 Classifying Series of Images Having Matrix Normal Distributions

In this section, we exemplify and test the skeletal algorithm when As 5) is in force. In more details, for $m\times n$ images (matrices) $\mathbf {X}$ class distributions have the MND’s of the following form (see [17]):

$$\begin{aligned} f_j(\mathbf {X})=\frac{1}{c_j}\,\exp \left[ -\frac{1}{2}\, \text{ tr }[U_j^{-1}(\mathbf {X} - \mathbf {M}_j)\,V_j^{-1}\, (\mathbf {X} - \mathbf {M}_j)^T ] \right] , \; j\in \mathcal {J}, \end{aligned}$$

(9)

where it is assumed that $n\times n$ matrices $U_j$’s and $m\times m$ matrices $V_j$’s are assumed to be nonsingular, while $n\times m$ matrices $\mathbf {M}_j$’s denote the class means. The normalization constants $c_j$’s are defined as follows:

$$\begin{aligned} c_j {\mathop {=}\limits ^{def}} (2\, \pi )^{0.5\,{n\, m}}\, \text{ det }[U_j]^{0.5\,n}\, \text{ det }[V_j]^{0.5\,m}\, , \; j\in \mathcal {J}. \end{aligned}$$

(10)

As one can observe, (9) has a special structure of the covariance matrix, namely, $U_j$’s are the covariance matrices between rows only, while $V_j$’s between columns only, which makes it possible to estimate them from learning sequences of reasonable lengths. This is in contrast to a general case when the full covariance matrix would have $m\,n \times m\,n$ elements, which is formidable for estimation even for small images $m=n=100$. We refer the reader to [16, 27] for the method of estimating $U_j$’s and $V_j$’s from the learning sequence. Further on we denote these estimates by $\hat{U}_j$’s and $\hat{V}_j$’s, respectively. Analogously, we denote by $\hat{\mathbf {M}}_j$’s the estimates of the expectations of $f_j$’s that are obtained as the mean values of the corresponding matrices from the learning sequence, taking into account, however, that the entries of $\mathbf {X}_k$’s are contained either in $[0,\, 255]$ or $[0\, 1]$, depending on the convention.

Matrix Classifier with a Markov Chain Feedback (MCLMCF)

Step 0::

Select $0 <\kappa _{max} \le 100$. Select $\varDelta _p \in (0,1)$.

Step 1::

Initial learning phase: estimate $\hat{\mathbf {M}_j}$, $\hat{U_j}$, $\hat{V_j}$,$\hat{c_j}$ for $j \in \mathcal {J}$ from a learning sequence. Select $c_{min} = min(\hat{c_j})$, estimate the original a priori class probabilities $\tilde{p}_{j}^0$, $j \in \mathcal {J}$ as class occurrence frequencies in a learning sequence. Calculate $\tilde{j}_0 = max(\tilde{p}_{j}^0)$. Set $k=1$. Estimate $\hat{\mathcal {P}}$ based on the learning sequence. If $\hat{\mathcal {P}}$ has an absorbing state then use MCL [23]), otherwise go to step 2.

Step 2::

Verify whether the following conditions hold:

$$\begin{aligned} \frac{\lambda _{max}(\hat{U_j})}{\lambda _{min}(\hat{U_j})}< \kappa _{max}, j\in \mathcal {J} \quad \text {and}\quad \frac{\lambda _{max}(\hat{V_j})}{\lambda _{min}(\hat{V_j})}< \kappa _{max}, j\in \mathcal {J} \end{aligned}$$

(11)

If so, go to step 3a, otherwise, go to step 4.

Step 3a::

Classify new matrix $\mathbf {X}'_k$ to class, according to (12). Go to step 3b.

$$\begin{aligned} \tilde{j}_k = \text{ argmin}_{0<j'\le J} \Big [\frac{1}{2}tr[\hat{U_{j'}}^{-1}(\mathbf {X}'_k-\hat{\mathbf {M}_{j'}}) \hat{V_{j'}}^{-1}(\mathbf {X}'_k-\hat{\mathbf {M}_{j'}})^T]\Big ] \end{aligned}$$

(12)

$$ {} - \text{ log } ({\tilde{p}_{\tilde{j}_{(k-1)}j'}}/{ c_{min}}) $$

Step 3b::

Update estimate of a priori probability $\tilde{p}$, using the following procedure:

(a):

Select class $\check{j}$, according to probabilities in $\tilde{j}_k$ row of transition matrix $\hat{\mathcal {P}}$.

(b):

Set $\tilde{p}_{\tilde{j}_{k}\check{j}}=\tilde{p}_{\tilde{j}_{(k-1)}\check{j}}$.

(c):

For every $j' \ne \check{j}, j'\in \mathcal {J}$ check if $\tilde{p}_{\tilde{j}_{(k-1)}j'}-\frac{\varDelta _p}{J-1}>0$, if so then update $\tilde{p}_{\tilde{j}_{k}j'}$ and $\tilde{p}_{\tilde{j}_{k}\check{j}}$ according to (13), else $\tilde{p}_{\tilde{j}_{k}j'}$ and $\tilde{p}_{\tilde{j}_{k}\check{j}}$ remain unchanged.

$$\begin{aligned} \tilde{p}_{\tilde{j}_{k}j'}=\tilde{p}_{\tilde{j}_{(k-1)}j'}-\frac{\varDelta _p}{J-1} \quad \text {and}\quad \tilde{p}_{\tilde{j}_{k}\check{j}}=\tilde{p}_{\tilde{j}_{k}\check{j}}+\frac{\varDelta _p}{J-1} \end{aligned}$$

(13)

Set $k=k+1$. If $k \le K$ then go to step 3a else stop.

Step 4::

Classify new matrix $\mathbf {X}'_k$ according to the nearest mean rule. Add the current result $(\mathbf {X}'_k,\, \tilde{j}_k)$ to the training set, then update the estimates of $\tilde{p}_{j_0}$, $\hat{\mathbf {M}_j}$, $\hat{U_j}$, $\hat{V_j}$, $\hat{c_j}$ and select $c_{min}$ for $j\in \mathcal {J}$ in the same manner, as described in step 1. Set $k=k+1$. If $k \le K$ then go to step 2, otherwise stop.

6 Experiments on Simulated Data

In this section, we present the results of experiments performed on simulated data for the evaluation of the proposed classifier performance. We generated 486 sequences, each consisting of 300 matrices. Matrices were randomly generated according to one of the three matrix normal distributions, which represents three classes. MNDs parameters are presented in Table 1, where $J_8$ is an $8\times 8$ matrix of ones and $D_8$ is an $8\times 8$ tridiagonal matrix with 2 at the main diagonal and 1 along the bands running above and below the main diagonal. The order of classes in the sequence was modeled by the MC with transition probability matrix $\mathcal {P}$ (see Eq. (14)). In the conducted experiments, the data were divided into a training and testing set in the following manner: the first 100 matrices of a sequence were used as a training set for classifiers, the remaining matrices were used as a test set. Then Gaussian noise with ($\sigma =0.05$) was added to matrices in the test set.

Table 1. Parameters of MND for each class and transition matrix $\mathcal {P}$.

In order to analyze the impact of value of parameter $\varDelta _p$ on the MCLMCF performance, we performed tests for $\varDelta _p$ = [0.01, 0.02, 0.05, 0.1, 0.2, 0.5]. Table 2, which presents the results obtained with the MCL and MCLMCF with different $\varDelta _p$ parameter, reveals that increasing the value of $\varDelta _p$ improves the classification performance of the MCLMCF. We can observe that the proposed classifier outperforms the MCL. We also analyzed the characteristics of sequences in the test set. We divided sequences into two groups: the first group (improved or the same) contains 411 sequences that were classified with higher or same accuracy with the use of MCLMCF with $\varDelta _p=0.5$, the second group (worse) comprises 75 sequences that were better classified with the MCL. Then we measured the lengths of the homogeneous class subsequences (Table 2 - right panel). Our analysis shows that the proposed classifier performs better than MCL on sequences that contain long subsequences of the same class.

Table 2. Left panel – the results of the experiments for different values of $\varDelta _p$. Right panel – the lengths of homogeneous class sub-sequences in the test set.

7 Case Study – Classifying an Image Series of Gas Burner Flames

The proposed approach was also tested on an image series of industrial gas burner flames. The contents of methane in natural gas fluctuate over longer periods of time, leading to proper, admissible or improper combustion that can be compensated by regulating the air rate supply. Thus, the contents of methane in the gas have all the features of the reoccurring concept drift. The mode of the combustion is easy to classify by an operator simply by visual inspection since the flame is either blue, blue and yellow, but still laminar or only yellow with a turbulent flow (see [19] and [20] for images and more details). It is however more difficult to derive an image classifier that works properly in heavy industrial conditions.

In order to test the Skeletal algorithm with the MC predictor, we selected the support vector machine (SVM) as the classifier in Step 1. The learning sequence consisted of 90 images in the series while the testing sequence length was 55. Having such a small testing sequence, we decided to extend it by adding 100 of its repetitions with the noise added (see [1] for the survey of methods of testing classifiers and to [11] for handling possibly missing data). The noise was rather heavy, namely, it was uniformly distributed in $[-0.25,\, 0.25]$ for grey level images represented in $[0,\, 1]$ interval.

Fig. 2.

Left panel – estimated $\mathcal {P}$ matrix of the MC. Right panel – the classification error vs $\varDelta _p$.

Table 3. Left panel – the fraction of the mean occupation time (fMOT) for the labels of the learning system (2nd column) and for the states of MC $\mathcal {P}$ (3rd column) Right panel – basic properties of MC $\mathcal {P}$.

In this study, we apply the estimated transition matrix shown in Fig. 2(left panel). Properties of the MC with matrix $\hat{\mathcal {P}}$ are listed in Table 3(right panel). Alternatively, one can consider the optimization of this matrix so as to attain better classification accuracy. This is however not such an easy task because we have to take into account many constraints (see [21] for a global search algorithm that is able to handle complicated constraints).

The mean occupation time (MOT) of the MC state is the number of discrete times (steps of the MC) that are spent by the MC in a given state. We apply this notion also to the labels of the learning sequence. By the fraction of the MOT (fMOT) we understand MOT’s of the states divided by the length of the observations or the length of the learning sequence, respectively. The comparison of the second and the third columns of Table 3 shows a very good agreement of the fMOT’s, which justifies the usage of our prediction model.

Then the Skeletal algorithm with $\gamma =0.5$ and SVM as the basic classifier was run 100 times for $\varDelta _p$ varying from 0 (i.e., there is no feedback from the MC predictor) to 0.35. As one can observe in Fig. 2 (right panel), for properly selected $\varDelta _p=0.2$ we can reduce the classification error by about 3 % in comparison to the case when the MC feedback is not applied. For long runs of industrial gas burners, the improvements of the decisions by 3 % may lead to essential savings. On the other hand, the same figure indicates the optimum is rather flat and selecting $\varDelta _p$ in the range for 0.1 to 0.25 provides similar improvements.

8 Concluding Remarks

The problem of classifying a series of images with a reoccurring concept drift was considered. The class of algorithms for such problems was proposed and tested both on simulated and industrial images. The idea of introducing feedback from the MC predictor of class labels to a priori class probabilities occurred to be fruitful in both cases, leading to the reduction of the classification error by about 3%, especially when we observe a long series of images from the same class.

Possible applications of the proposed approach include a long image series arising in the medical diagnostics (see, e.g., [5]). One can also combine the idea of the MC predictor with classifiers that are based on deep neural networks, e.g., in the version that was proposed in [6].