Abstract
Communicating systems are nowadays part of everyday life, yet programming and analysing them is difficult. One of the many reasons for this difficulty is their size, hence compositional approaches are a need. We discuss how to ensure relevant communication properties such as deadlock freedom in a compositional way. The idea is that communicating systems can be composed by taking two of their participants and transforming them into coupled forwarders connecting the two systems. It has been shown that, for asynchronous communications, if the participants are “compatible” then composition satisfies relevant communication properties provided that the single systems satisfy them. We show that such a result changes considerably for synchronous communications. We also discuss a different form of composition, where a unique forwarder is used.
Research partly supported by the EU H2020 RISE programme under the Marie Skłodowska-Curie grant agreement No 778233, by the MIUR project PRIN 2017FTXR7S “IT-MaTTerS” (Methods and Tools for Trustworthy Smart Systems) and by the Project PTR - UNICT 2016-19. The first and second authors have also been partially supported by INdAM as members of GNCS (Gruppo Nazionale per il Calcolo Scientifico). The authors thanks the reviewers for their helpful comments and also M. Dezani for her support.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
1 Introduction
The behaviour of systems which communicate via point-to-point message passing can be described in terms of systems of Communicating Finite State Machines (CFSMs) [10], that is systems of finite state automata whose transitions are labelled by sending and receiving actions. Such systems can be then analysed to check whether they enjoy relevant communication properties such as deadlock freedom, lock freedom, etc. (see, e.g., [6, 7, 16, 20, 24]).
Traditionally these systems are viewed as closed, thus one needs full knowledge of the whole system in order to analyse it. In scenarios such as the Internet, the Cloud or serverless computing, such assumption is less and less realistic.
Recently, an approach to the composition of systems of CFSMs has been proposed [3, 4]. The main idea of the approach is to take two systems, select two of their participants (one per system) and transform them into coupled gateways connecting the two systems. More precisely, if a message is sent to one of the gateways, it is forwarded to the other gateway, which sends it to the other system.
Of course, for such a composition to be well-behaved, the two gateways should exhibit behaviours which are essentially dual of each other: when one wants to send a message the other one needs to be willing to receive the same message. Such an intuition has been formalised as a compatibility relation. It has also been shown that compatibility, together with conditions of no mixed states and ?!-determinism on the selected participants, ensures that the composition is well-behaved. For instance, if the components are deadlock-free then the system resulting from the composition is deadlock-free too.
In this paper we first revise such results in a setting of synchronous CFSMs, while [3, 4] focus on the asynchronous FIFO case. Somehow surprisingly, stricter conditions are required to ensure compositionality of deadlock freedom. We then propose a new composition methodology which replaces the two selected participants with a unique gateway. Beyond saving some communications and simplifying the analysis, this second methodology is also more general since the conditions needed for compositionality of deadlock freedom are slightly weaker. We call this second composition semi-direct, to distinguish it also from direct composition as proposed in [5] in a context of multiparty session types [17], which avoids the need for gateways altogether. Notably, two-gateways composition is completely transparent for the participants different from the interface ones, semi-direct composition requires renaming some of their communications, while direct composition may require a non-trivial restructuring of their behaviours.
Structure of the Paper. Section 2 introduces systems of CFSMs and related notions. Composition by gateways and semi-direct composition are discussed in Sect. 3 and Sect. 4, respectively. Conclusions, related and future work are discussed in Sect. 5.
2 Background
Communicating Finite State Machines (CFSMs) [10] are Finite State Automata (FSAs) where transitions are labelled by communications.
Definition 2.1
(FSA). A Finite State Automaton (FSA) is a tuple \(A = \langle {\mathcal {S}, s_0, \mathcal {L}, \rightarrow } \rangle \) where
-
\(\mathcal {S}\) is a finite set of states (ranged over by \(s,q,\ldots \));
-
\(s_0 \in \mathcal {S}\) is the initial state;
-
\(\mathcal {L}\) is a finite set of labels (ranged over by
 );
); -
\(\rightarrow \,\subseteq \, \mathcal {S}{\times } \mathcal {L}{\times } \mathcal {S}\) is a set of transitions.
We use the usual notation \(s_1 \xrightarrow {\lambda } s_2\) for the transition \((s_1,\lambda ,s_2)\in \xrightarrow {}\), and \(s_1 \xrightarrow {} s_2\) when there exists \(\lambda \) such that \(s_1 \xrightarrow {\lambda } s_2\), as well as \(\xrightarrow {}^*\) for the reflexive and transitive closure of \(\xrightarrow {}\). The set of reachable states of A is \(\mathcal {R}({A}) = \{\,s \mid s_0\xrightarrow {}^* s\,\}\).
Let \(s \xrightarrow {\lambda } s' \in A\) emphasise that the transition belongs to (the set of transitions of) an FSA A; likewise, \(q \in A\) stands for “q belongs to the states of A”. A transition \(s \xrightarrow {\lambda } s'\) (resp. \(s' \xrightarrow {\lambda }s\)) is an outgoing (resp. incoming) transition of s. We write \({f}[{x} \mapsto {y}]\) for the update of the function f in a point x of its domain with the value y. Also, \({\text {dom}}({f})\) denotes the domain of the function f.
We now define systems of CFSMs, by adapting the definitions in
[10] to our context. Let \(\mathfrak {P}\) be a set of participants (or roles, ranged over by  ,
,  , etc.) and
, etc.) and  a set of messages (ranged over by
a set of messages (ranged over by  ,
,  , etc.). We take \(\mathfrak {P}\) and
, etc.). We take \(\mathfrak {P}\) and  disjoint.
disjoint.
Definition 2.2
(Communicating system). A communicating finite-state machine (CFSM) is an FSA with labels in the set

of actions. The subject of an output (resp. input) action  (resp.
(resp.  ) is
) is  (resp.
(resp.
 ). A CFSM is
). A CFSM is  -local if all its transitions have subject
-local if all its transitions have subject  .
.
A (communicating) system is a map  assigning an
assigning an  -local CFSM
-local CFSM  to each participant
to each participant  where
where  is finite and any participant occurring in a transition of
is finite and any participant occurring in a transition of  is in
is in  .
.
Note that systems satisfying the above definition are closed: in fact any input or output action does refer to participants belonging to the system itself.
We now define, following [6, 7], the synchronous semantics of systems of CFSMs, which is itself an FSA (differently from the asynchronous case, where the set of states can be infinite).
Definition 2.3
(Synchronous semantics). Let \(\mathsf {S}\) be a communicating system. A synchronous configuration of \(\mathsf {S}\) is a map  assigning a local state
assigning a local state  to each
to each  .
.
The synchronous semantics of \(\,\mathsf {S}\) is the FSA \({\llbracket \mathsf {S}\rrbracket }=\langle {\mathcal {S}, s_0, \mathcal {L}_{\text {int}},\rightarrow } \rangle \) where
-
\(\mathcal {S}\) is the set of synchronous configurations of \(\mathsf {S}\), as defined above;
-
 is the initial configuration where, for each
is the initial configuration where, for each  ,
,  is the initial state of
is the initial state of  ;
; -
 is a set of interaction labels;
is a set of interaction labels; -
 if
if  and
and  .
.
We say that \(s\) enables  (resp.
(resp.  ) when
) when  .
.
As expected, an interaction  occurs when
occurs when  performs an output
performs an output  and
and  the corresponding input
the corresponding input  .
.
As discussed in the Introduction, in this paper we will study preservation of communication properties under composition. As sample property we choose the well-known notion of deadlock freedom. The definition below adapts the one in [13] to a synchronous setting (as done also in [20, 27]).
Definition 2.4
(Deadlock freedom). Let \(\mathsf {S}\) be a communicating system. A configuration \(s\in \mathcal {R}({{\llbracket \mathsf {S}\rrbracket }})\) is a deadlock if
-
\(s\) has no outgoing transitions in \({\llbracket \mathsf {S}\rrbracket }\) and
-
there exists
 such that
such that  has an outgoing transition in
has an outgoing transition in  .
.
System \(\mathsf {S}\) is deadlock-free if for each \(s\in \mathcal {R}({{\llbracket \mathsf {S}\rrbracket }})\), \(s\) is not a deadlock.
3 Composition via Gateways
This section discusses composition of systems of CFSMs via gateways, as introduced in
[3, 4], and studies its properties under the synchronous semantics. The main idea is that two systems of CFSMs, say \(\mathsf {S}_1\) and \(\mathsf {S}_2\), can be composed by transforming one participant in each of them into gateways connected to each other. Let us call  the selected participant in \(\mathsf {S}_1\) and
the selected participant in \(\mathsf {S}_1\) and  the one in \(\mathsf {S}_2\). The gateways for
the one in \(\mathsf {S}_2\). The gateways for  and
and  are connected to each other and act as forwarders: each message sent to the gateway for
are connected to each other and act as forwarders: each message sent to the gateway for  by a participant from the original system \(\mathsf {S}_1\) is now forwarded to the gateway for
by a participant from the original system \(\mathsf {S}_1\) is now forwarded to the gateway for  , that in turn forwards it to the same participant to which
, that in turn forwards it to the same participant to which  sent it in the original system \(\mathsf {S}_2\). The dual will happen to messages that the gateway for
sent it in the original system \(\mathsf {S}_2\). The dual will happen to messages that the gateway for  receives from \(\mathsf {S}_2\). A main advantage of this approach is that no extension of the CFSM model is needed to transform systems of CFSMs, which are normally closed systems, into open systems that can be composed. Another advantage is that the composition is fully transparent to all participants different from
receives from \(\mathsf {S}_2\). A main advantage of this approach is that no extension of the CFSM model is needed to transform systems of CFSMs, which are normally closed systems, into open systems that can be composed. Another advantage is that the composition is fully transparent to all participants different from  and
and  .
.
We will now define composition via gateways on systems of CFSMs, following the intuition above.
Definition 3.1
(Gateway). Given a  -local CFSM \(M\) and a participant
-local CFSM \(M\) and a participant  , the gateway of \(M\) towards
, the gateway of \(M\) towards  is the CFSM
is the CFSM  obtained by replacing:
obtained by replacing:
-
each transition
 with
with  for some fresh state \(q''\);
for some fresh state \(q''\); -
each transition
 with
with  for some fresh state \(q''\).
for some fresh state \(q''\).
We compose systems with disjoint participants through two of them, say  and
and  , by taking all the participants of the original systems but
, by taking all the participants of the original systems but  and
and  , whereas
, whereas  and
and  are replaced by their respective gateways.
are replaced by their respective gateways.
Definition 3.2
(System composition). Let \(\mathsf {S}_1\) and \(\mathsf {S}_2\) be two systems with disjoint domains. The composition of \(\mathsf {S}_1\) and \(\mathsf {S}_2\) via  and
and  is defined as
is defined as

(Note that  .)
.)
We remark again that, by the above approach for composition, we do not actually need to formalise the notion of open system. In fact any closed system can be looked at as open by choosing (according to the current necessities) two suitable participants in the “to-be-connected” systems and transforming them into two forwarders.
We also note that the notion of composition above is structural: a corresponding notion of behavioural composition has been studied in [5] in a context of multiparty session types [17].
Example 3.3
Take the systems \(\mathsf {S}_1\) and \(\mathsf {S}_2\) below

The system consisting of the following CFSMs

is the composition  . \(\diamond \)
. \(\diamond \)
Given a configuration of the composition of systems \(\mathsf {S}_1\) and \(\mathsf {S}_2\) we can retrieve the configurations of the two subsystems by taking only the states of participants in \(\mathsf {S}_i\) (for \(i \in \{1,2\}\)) while avoiding, for the gateways, to take the fresh states introduced by the gateway construction.
Definition 3.4
(Configuration projection). Let \(s\) be a configuration of a composed system  . The projection of \(s\) on \(\mathsf {S}_1\) is the map \(s|_{1}\) defined by
. The projection of \(s\) on \(\mathsf {S}_1\) is the map \(s|_{1}\) defined by

where  . The definition for \(s|_{2}\) is analogous.
. The definition for \(s|_{2}\) is analogous.
Intuitively, in the projection \(s|_{1}\), if  is in a fresh state after receiving from
is in a fresh state after receiving from  , then the other participants in \(\mathsf {S}_1\) are still not aware of the message arrival, hence to have a coherent configuration we take the state of
, then the other participants in \(\mathsf {S}_1\) are still not aware of the message arrival, hence to have a coherent configuration we take the state of  before the receive. If instead
before the receive. If instead  is in a fresh state before sending to
is in a fresh state before sending to  , then the other participants in \(\mathsf {S}_1\) know that the message has been sent, hence to have a coherent configuration we take the state of
, then the other participants in \(\mathsf {S}_1\) know that the message has been sent, hence to have a coherent configuration we take the state of  after the send. (A similar intuition applies to \(s|_{2}\).)
after the send. (A similar intuition applies to \(s|_{2}\).)
Example 3.5
Let us consider the system  of Example 3.3. Take its configuration
of Example 3.3. Take its configuration
 . It is easy to check that \(s\in \mathcal {R}({{\llbracket \mathsf {S}\rrbracket }})\). In fact
. It is easy to check that \(s\in \mathcal {R}({{\llbracket \mathsf {S}\rrbracket }})\). In fact

The projections of \(s\) on, respectively, \(\mathsf {S}_1\) and \(\mathsf {S}_2\) are

Notice that (as we shall prove in Proposition 3.11), from \(s\in \mathcal {R}({{\llbracket \mathsf {S}\rrbracket }})\) it is possible to infer that \(s|_{1} \in \mathcal {R}({{\llbracket \mathsf {S}_1 \rrbracket }})\) and \(s|_{2} \in \mathcal {R}({{\llbracket \mathsf {S}_2 \rrbracket }})\). \(\diamond \)
Being able to build the composition via gateways does not ensure that the result is well-behaved or that its behaviour is related in any way to the behaviour of the original systems. We provide below sufficient conditions for this to happen. We focus in particular on whether deadlock freedom is preserved under composition. Somehow surprisingly, in the synchronous case preservation of deadlock freedom requires stricter conditions than in the asynchronous one.
Informally, two CFSMs \(M_1\) and \(M_2\) are compatible if \(M_1\) is bisimilar to the dual of \(M_2\) provided that the communicating partners are abstracted away. In order to define compatibility, a few simple definitions are handy.
Let  and define the functions
and define the functions
by the following clauses

which extend to CFSMs in the obvious way: given a CFSM \(M= \langle {\mathcal {S},q_0,\mathcal {L}_{\text {act}},\rightarrow } \rangle \), we define \(\mathsf {io}(M) = \langle {\mathcal {S},q_0,\mathcal {L}_{\text {i/o}},\rightarrow '} \rangle \) where  ; and likewise for \(\overline{M}\).
; and likewise for \(\overline{M}\).
Definition 3.6
(Compatibility). Two CFSMs \(M_1\) and \(M_2\) are compatible if \(\mathsf {io}(M_1)\) is bisimilar to \(\overline{\mathsf {io}(M_2)}\). Given two communicating systems \(\mathsf {S}_1\) and \(\mathsf {S}_2\), participants  and
and  are compatible roles if
are compatible roles if  and
and  are compatible CFSMs.
are compatible CFSMs.
We refer to the bisimilarity in Definition 3.6 as compatibility bisimilarity. Note that the compatibility bisimilarity between \(M_1\) and \(M_2\) is a relation between their states. It is easy to check that  and
and  of Example 3.3 are compatible roles.
of Example 3.3 are compatible roles.
Definition 3.7
An
 -local CFSM \(M\) is:
-local CFSM \(M\) is:
-
i)
?-deterministic (resp. !-deterministic) if
 and
and  (resp.
(resp.  and
and  ) implies \(q'=q''\);
) implies \(q'=q''\); -
ii)
?!-deterministic if it is both ?-deterministic and !-deterministic;
-
iii)
mixed-deterministic if
 for all
for all  and
and  .
.
A state \(q \in M\) is a sending (resp. receiving) state if it has outgoing transitions, all of which are labelled with sending (resp. receiving) actions; q is a mixed state if it has outgoing transitions and q is neither sending nor receiving.
Definition 3.8
(  -composability). Two systems \(\mathsf {S}_1\) and \(\mathsf {S}_2\) with disjoint domains are
-composability). Two systems \(\mathsf {S}_1\) and \(\mathsf {S}_2\) with disjoint domains are  -composable if
-composable if  and
and  are two compatible roles whose machines have no mixed states and are ?!-deterministic.
are two compatible roles whose machines have no mixed states and are ?!-deterministic.
Definition 3.9
Let  be a gateway extracted from an
be a gateway extracted from an  -local CFSM. Function
-local CFSM. Function  maps the states of
maps the states of  to the states of
to the states of  as follows:
as follows:

Lemma 3.10
Function  is well-defined.
is well-defined.
Proof
The restriction of  to the states of
to the states of  is the identity. If q is not a state of
is the identity. If q is not a state of  , then it is fresh by definition of
, then it is fresh by definition of  . By definition of
. By definition of  again, there is a unique \(q'\) such that either
again, there is a unique \(q'\) such that either  or
or  . \(\square \)
. \(\square \)
In the system  of Example 3.3 it is easy to check, for example, that
of Example 3.3 it is easy to check, for example, that  and
and  .
.
Function  is close to the definition of configuration projection (but for considering a single state instead of a whole configuration) with a main change. Indeed, when
is close to the definition of configuration projection (but for considering a single state instead of a whole configuration) with a main change. Indeed, when  receives a message from its own system \(\mathsf {S}_1\) going to some fresh state \(q''\), configuration projection maps it to the next state, since the rest of \(\mathsf {S}_1\) is aware of the transition but
receives a message from its own system \(\mathsf {S}_1\) going to some fresh state \(q''\), configuration projection maps it to the next state, since the rest of \(\mathsf {S}_1\) is aware of the transition but  will complete the transition only in the next state. Instead, function
will complete the transition only in the next state. Instead, function  maps \(q''\) to the previous state since \(\mathsf {S}_2\), and
maps \(q''\) to the previous state since \(\mathsf {S}_2\), and  in particular, are not yet aware of the transition. Thus, function
in particular, are not yet aware of the transition. Thus, function  is designed to establish a correspondence with the other system as shown by the next proposition.
is designed to establish a correspondence with the other system as shown by the next proposition.
Proposition 3.11
Let  be the composition of two
be the composition of two  -composable systems \(\mathsf {S}_1\) and \(\mathsf {S}_2\). If \(s\in \mathcal {R}({{\llbracket \mathsf {S}\rrbracket }})\) then exactly one of the following cases hold for
-composable systems \(\mathsf {S}_1\) and \(\mathsf {S}_2\). If \(s\in \mathcal {R}({{\llbracket \mathsf {S}\rrbracket }})\) then exactly one of the following cases hold for  and
and  , the states in \(s\) of the gateway CFSMs:
, the states in \(s\) of the gateway CFSMs:
-
1.
both
 and
and  are not fresh;
are not fresh; -
2.
either
 is fresh,
is fresh,  is not fresh,
is not fresh,  , or, symmetrically,
, or, symmetrically,  is fresh,
is fresh,  is not fresh,
is not fresh,  ;
; -
3.
either
 is fresh,
is fresh,  is not fresh, and there is
is not fresh, and there is  such that
such that  , or, symmetrically,
, or, symmetrically,  is fresh,
is fresh,  is not fresh, and there is
is not fresh, and there is  such that
such that  ;
; -
4.
both
 and
and  are fresh and either
are fresh and either  , and there is
, and there is  such that
such that  , or, symmetrically,
, or, symmetrically,  , and there is
, and there is  such that
such that  .
.
Also, \(s|_{1}\) is reachable in \(\mathsf {S}_1\), \(s|_{2}\) is reachable in \(\mathsf {S}_2\) and  .
.
Proof
The proof is by induction on the number n of transitions performed to reach \(s\). If \(n = 0\) then by construction we are in case 1. The conditions on configurations and on bisimulation hold by construction.
Let us assume that we are in one of the cases above and a further transition is performed. Since composition is symmetric for each possibility we do not detail the symmetric case. Also note that in each of the cases, if the transition does not involve the gateways, then we are still in the same case. The condition on configurations hold since the same step can be taken by the same participants in one of the two systems, and the ones of the other system do not move. The condition on bisimulation holds since the state of the gateways does not change.
If we were in case 1, a transition involving a gateway has necessarily the form  (or a similar one for the gateway for
(or a similar one for the gateway for  ) since an output from a gateway would require a gateway to be in a fresh state. This leads us to case 2. Indeed, the gateway for
) since an output from a gateway would require a gateway to be in a fresh state. This leads us to case 2. Indeed, the gateway for  goes to the fresh state
goes to the fresh state  and is willing to execute the gateway communication
and is willing to execute the gateway communication  , while the state of the gateway for
, while the state of the gateway for  does not change. The condition on configurations hold by induction on \(s|_{2}\) and holds on \(s|_{1}\) since
does not change. The condition on configurations hold by induction on \(s|_{2}\) and holds on \(s|_{1}\) since  and by construction
and by construction  . The condition on bisimulation holds by inductive hypothesis since
. The condition on bisimulation holds by inductive hypothesis since  and the state of the gateway for
and the state of the gateway for  does not change.
does not change.
In case 2 a transition involving the gateway necessarily is the gateway communication  , leading us to case 3. Indeed, the gateway for
, leading us to case 3. Indeed, the gateway for  cannot perform other transitions and thanks to the condition on compatibility and the fact that gateway roles do not have mixed states
cannot perform other transitions and thanks to the condition on compatibility and the fact that gateway roles do not have mixed states  cannot perform any input from its system. Thus, the gateway for
cannot perform any input from its system. Thus, the gateway for  goes to a non-fresh state while the gateway for
goes to a non-fresh state while the gateway for  goes to a fresh state, willing to execute an output
goes to a fresh state, willing to execute an output  towards its system. The condition on configurations holds by inductive hypothesis since projection generates the same configurations as before. The condition on bisimulation holds since the two participants take corresponding steps. The resulting states are in a correspondence thanks to ?!-determinism.
towards its system. The condition on configurations holds by inductive hypothesis since projection generates the same configurations as before. The condition on bisimulation holds since the two participants take corresponding steps. The resulting states are in a correspondence thanks to ?!-determinism.
In case 3 for a transition involving a gateway there are two possibilities, according to whether the gateway taking a transition is in a fresh state or not.
-
The gateway in a fresh state, say
 , takes a transition. By construction it delivers a message
, takes a transition. By construction it delivers a message  to a participant in its system via a transition
to a participant in its system via a transition
 . This leads us to case 1. Indeed,
. This leads us to case 1. Indeed,  goes to a non-fresh state, while
goes to a non-fresh state, while  was in a non-fresh state by hypothesis and does not move. The condition on configurations holds by inductive hypothesis for \(s|_{1}\) and holds for \(s|_{2}\) since
was in a non-fresh state by hypothesis and does not move. The condition on configurations holds by inductive hypothesis for \(s|_{1}\) and holds for \(s|_{2}\) since  can do the same move as in s and the two moves of the gateway for
can do the same move as in s and the two moves of the gateway for  (the gateway transition which was not taken into account yet and the delivery of message
(the gateway transition which was not taken into account yet and the delivery of message  ) correspond to the complementary move of
) correspond to the complementary move of  in \(s|_{2}\). The condition on bisimulation holds by inductive hypothesis since
in \(s|_{2}\). The condition on bisimulation holds by inductive hypothesis since  projects on the same states as before the transition.
projects on the same states as before the transition. -
The gateway in a non-fresh state, say
 , takes a transition. By construction it takes a message from its own system via a transition
, takes a transition. By construction it takes a message from its own system via a transition  . This leads us to case 4. Indeed,
. This leads us to case 4. Indeed,  goes to a fresh state while
goes to a fresh state while  was already in a fresh state. Then
was already in a fresh state. Then  by inductive hypothesis and
by inductive hypothesis and  by construction. The reasoning on conditions of configurations and bisimulation is similar to the one of a message taken by the gateway in case 1.
by construction. The reasoning on conditions of configurations and bisimulation is similar to the one of a message taken by the gateway in case 1.
In case 4, when a transition involving a gateway, say  , is performed, it is necessarily of the form
, is performed, it is necessarily of the form  since the gateway for
since the gateway for  by construction cannot take any other action. This leads to case 2. Indeed,
by construction cannot take any other action. This leads to case 2. Indeed,  remains in a fresh state and willing to execute a transition
remains in a fresh state and willing to execute a transition  while
while  goes to a non-fresh state. The reasoning for the conditions on configurations and bisimulation is similar to the one for case 3 when
goes to a non-fresh state. The reasoning for the conditions on configurations and bisimulation is similar to the one for case 3 when  delivers a message to its system. \(\square \)
delivers a message to its system. \(\square \)
Now, one may think that analogously to what happens in
[3, 4], if two systems are  -composable and deadlock-free then their composition is deadlock-free too. Unfortunately, this is not the case, as shown by the examples below. The first example is based on an example in
[4], that shows that mixed states have to be forbidden and that holds for the synchronous case as well. In the synchronous case, however, we can also exchange some inputs with outputs and obtain the same behaviour without mixed states.
-composable and deadlock-free then their composition is deadlock-free too. Unfortunately, this is not the case, as shown by the examples below. The first example is based on an example in
[4], that shows that mixed states have to be forbidden and that holds for the synchronous case as well. In the synchronous case, however, we can also exchange some inputs with outputs and obtain the same behaviour without mixed states.
Example 3.12
Take the following CFSMs

and consider the composition of the system with participants  and
and  with the one with participants
with the one with participants  and
and  . Clearly, the two systems are
. Clearly, the two systems are  -composable and deadlock-free, yet their composition has a deadlock; in fact, when the gateway for
-composable and deadlock-free, yet their composition has a deadlock; in fact, when the gateway for  receives
receives  , participant
, participant  is waiting only for
is waiting only for  . By considering the second system alone, this is not a deadlock, since
. By considering the second system alone, this is not a deadlock, since  forces
forces  to select the right branch.
to select the right branch.
Note that the situation would be different in an asynchronous setting. Indeed, the second system could deadlock. This is due to the fact that  could send
could send  without synchronising with
without synchronising with  . \(\diamond \)
. \(\diamond \)
Example 3.13
Take the CFSMs below

The same reasoning of Example 3.12 can be applied here, to systems with participants  and
and  . Hence, choices made by different participants are problematic as well. \(\diamond \)
. Hence, choices made by different participants are problematic as well. \(\diamond \)
Example 3.14
Take the CFSMs below

The reasoning is again similar, and shows that the composition of systems  and
and  deadlocks while the two systems in isolation do not. Hence also concurrency diamonds are problematic. \(\diamond \)
deadlocks while the two systems in isolation do not. Hence also concurrency diamonds are problematic. \(\diamond \)
Given the examples above, it is clear that, differently from the asynchronous case, deadlock freedom can be preserved only under very strict conditions on interface participants. Indeed we show below that it can be preserved if interface participants do not contain choices.
Definition 3.15
(Sequential CFSM). A CFSM is sequential if each of its states has at most one outgoing transition.
It is immediate to check that  is sequential if M is so. Moreover, trivially, a sequential M is also ?!-deterministic and with no mixed state (and hence mixed-deterministic).
is sequential if M is so. Moreover, trivially, a sequential M is also ?!-deterministic and with no mixed state (and hence mixed-deterministic).
Theorem 3.16
(Deadlock freedom for sequential interfaces). Let \(\mathsf {S}_1\) and \(\mathsf {S}_2\) be two  -composable and deadlock-free systems, such that
-composable and deadlock-free systems, such that  and
and  are sequential. Then the composed system
are sequential. Then the composed system  is deadlock-free.
is deadlock-free.
Proof
We show that if the composed system  reaches a deadlock configuration s then at least one of \(s|_{1}\) and \(s|_{2}\) is a deadlock. First, we show that if a participant
reaches a deadlock configuration s then at least one of \(s|_{1}\) and \(s|_{2}\) is a deadlock. First, we show that if a participant  (say from \(\mathsf {S}_1\)) is willing to take an action in a configuration \(s\) of the composed system then some participant is willing to take an action in \(s|_{1}\) or in \(s|_{2}\) (and the same for participants in \(\mathsf {S}_2\)). Note that \(s|_{1}\) and \(s|_{2}\) are reachable in, respectively, \(\mathsf {S}_1\) and \(\mathsf {S}_2\) thanks to the condition on configurations in Proposition 3.11.
(say from \(\mathsf {S}_1\)) is willing to take an action in a configuration \(s\) of the composed system then some participant is willing to take an action in \(s|_{1}\) or in \(s|_{2}\) (and the same for participants in \(\mathsf {S}_2\)). Note that \(s|_{1}\) and \(s|_{2}\) are reachable in, respectively, \(\mathsf {S}_1\) and \(\mathsf {S}_2\) thanks to the condition on configurations in Proposition 3.11.
If  then
then  wants to take the same action by definition of \(s|_{1}\).
wants to take the same action by definition of \(s|_{1}\).
If  and it is willing to receive from
and it is willing to receive from  then, by the definition of \(s|_{1}\) and of gateway,
then, by the definition of \(s|_{1}\) and of gateway,  in \(s|_{1}\) is willing to send a message to some participant in \(\mathsf {S}_1\).
in \(s|_{1}\) is willing to send a message to some participant in \(\mathsf {S}_1\).
If  and it is willing to send to
and it is willing to send to  then
then  by the condition on bisimulation of Proposition 3.11. By definition of
by the condition on bisimulation of Proposition 3.11. By definition of  and of gateway,
and of gateway,  is willing to take a message from its own system, hence
is willing to take a message from its own system, hence  is willing to send such a message to its own system thanks to the definition of bisimulation. By definition of configuration projection
is willing to send such a message to its own system thanks to the definition of bisimulation. By definition of configuration projection  is also a state in \(s|_{2}\), hence there is a participant willing to take a transition.
is also a state in \(s|_{2}\), hence there is a participant willing to take a transition.
Now we show that if no transition is enabled in a configuration \(s\) of the composed system then no transition is enabled in \(s|_{1}\) and \(s|_{2}\). We prove the contrapositive, showing that if there is an enabled transition in \(s|_{1}\) or in \(s|_{2}\) then there is a transition enabled in \(s\) as well. There are a few cases to consider.
-
Transition not involving the interface roles: this case follows immediately from the definition of system transition and of configuration projection.
-
Communication towards an interface role: let
 be the sender and
be the sender and  the interface role. The transition is of the form
the interface role. The transition is of the form  . There are two possibilities. If the gateway for
. There are two possibilities. If the gateway for  is not in a fresh state in s then the same transition can trigger in the composed system thanks to the definition of system transition and of configuration projection.
is not in a fresh state in s then the same transition can trigger in the composed system thanks to the definition of system transition and of configuration projection.If it is in a fresh state then thanks to the definition of gateway and of configuration projection it still needs to complete a previous gateway communication. The other gateway,
 , may be in a fresh state or not. If it is not, thanks to the definition of
, may be in a fresh state or not. If it is not, thanks to the definition of  and to the condition on bisimulation of Proposition 3.11 it is willing to accept the gateway communication which can thus trigger as desired. If
and to the condition on bisimulation of Proposition 3.11 it is willing to accept the gateway communication which can thus trigger as desired. If  is in a fresh state then thanks to the definition of configuration projection and of gateway it is willing to deliver a message to \(\mathsf {S}_2\). Since \(\mathsf {S}_2\) is not a deadlock and a participant is willing to take a transition then a transition can trigger in \(\mathsf {S}_2\) too. Thus, we can apply the other cases to find a witness transition in the composed system. Note that the transition in \(\mathsf {S}_2\) cannot be towards an interface role thanks to the condition on bisimulation of Proposition 3.11 and since there are no mixed states, hence this reasoning does not cycle.
is in a fresh state then thanks to the definition of configuration projection and of gateway it is willing to deliver a message to \(\mathsf {S}_2\). Since \(\mathsf {S}_2\) is not a deadlock and a participant is willing to take a transition then a transition can trigger in \(\mathsf {S}_2\) too. Thus, we can apply the other cases to find a witness transition in the composed system. Note that the transition in \(\mathsf {S}_2\) cannot be towards an interface role thanks to the condition on bisimulation of Proposition 3.11 and since there are no mixed states, hence this reasoning does not cycle. -
Communication from an interface role: let
 be the interface role and
be the interface role and  the target participant. Hence, the transition is of the form
the target participant. Hence, the transition is of the form  . Thanks to the definition of gateway and of system projection the gateway for
. Thanks to the definition of gateway and of system projection the gateway for  in s is either willing to deliver a message to some participant in \(\mathsf {S}_2\) or to receive from the gateway for
in s is either willing to deliver a message to some participant in \(\mathsf {S}_2\) or to receive from the gateway for  . In the first case, since the gateway is sequential then the participant is
. In the first case, since the gateway is sequential then the participant is  and the message
and the message  , hence the transition can trigger.
, hence the transition can trigger.If
 is willing to receive from
is willing to receive from  then thanks to the definition of
then thanks to the definition of  and the condition on bisimulation of Proposition 3.11 then the gateway for
and the condition on bisimulation of Proposition 3.11 then the gateway for  is willing to receive a message from its system or has just received it and is willing to send it through the gateway. In the last case the gateway communication can occur.
is willing to receive a message from its system or has just received it and is willing to send it through the gateway. In the last case the gateway communication can occur.If
 is willing to receive a message from some participant in \(\mathsf {S}_1\) since \(\mathsf {S}_1\) is not a deadlock then there is an enabled transition in \(\mathsf {S}_1\) as well. Thus, we can apply the other cases to find a witness transition in the composed system. Note that the transition in \(\mathsf {S}_1\) cannot be from an interface role thanks to the condition on bisimulation of Proposition 3.11 and since there are no mixed states, hence this reasoning does not cycle.
is willing to receive a message from some participant in \(\mathsf {S}_1\) since \(\mathsf {S}_1\) is not a deadlock then there is an enabled transition in \(\mathsf {S}_1\) as well. Thus, we can apply the other cases to find a witness transition in the composed system. Note that the transition in \(\mathsf {S}_1\) cannot be from an interface role thanks to the condition on bisimulation of Proposition 3.11 and since there are no mixed states, hence this reasoning does not cycle.
Thus, if there is a deadlock configuration \(s\) in the composed system then either \(s|_{1}\) or \(s|_{2}\) are deadlocks against the hypothesis. The thesis follows. \(\square \)
We can infer deadlock-freedom of the system  of Example 3.3 by the result above, since \(\mathsf {S}_1\) and \(\mathsf {S}_1\) are
of Example 3.3 by the result above, since \(\mathsf {S}_1\) and \(\mathsf {S}_1\) are  -composable and deadlock-free, and
-composable and deadlock-free, and  and
and  are sequential.
are sequential.
The result above, however, is not fully satisfying since the sequentiality condition is very strict, but, as shown by Examples 3.12, 3.13, and 3.14, any form of choice is problematic.
However, we can complement the result above with an additional one pinpointing where deadlocks can happen when gateways with choices are allowed: deadlocks can only occur in communications from the gateway to its own system.
Equivalently, we can drop the sequentiality condition if the systems are such that, whenever their interface role is willing to send a message, the system is ready to receive it. We formalise this condition by the notion of !live participant.
Definition 3.17
(!live participant). Let \(\mathsf {S}\) be a system and let  . We say that
. We say that  is !live in \(\mathsf {S}\) if, for any \(s\in \mathcal {R}({{\llbracket \mathsf {S}\rrbracket }})\),
is !live in \(\mathsf {S}\) if, for any \(s\in \mathcal {R}({{\llbracket \mathsf {S}\rrbracket }})\),

We remark that !liveness is not a property of the gateway but a property of the system to which it belongs.
It is immediate to check that  is not !live in system \(\mathsf {S}_2\) of Example 3.12, whereas
is not !live in system \(\mathsf {S}_2\) of Example 3.12, whereas  is !live in the following system.
is !live in the following system.

Theorem 3.18
(Deadlock freedom for !live interfaces). Let \(\mathsf {S}_1\) and \(\mathsf {S}_2\) be  -composable and deadlock-free systems. If
-composable and deadlock-free systems. If  and
and  are !live in, respectively, \(\mathsf {S}_1\) and \(\mathsf {S}_2\) then the composed system
are !live in, respectively, \(\mathsf {S}_1\) and \(\mathsf {S}_2\) then the composed system  is deadlock-free.
is deadlock-free.
Proof
The proof has the same structure of the one for Theorem 3.16. The only difference is when showing that if there is an enabled transition in \(s|_{1}\) or in \(s|_{2}\) then there is a transition enabled in \(s\) as well. Just the case of communication from an interface node changes, in particular when the gateway is willing to deliver some message to some participant in its system. There, !liveness can be used instead of sequentiality to show that indeed some transition can happen. Hence, the thesis follows. \(\square \)
4 Semi-direct Composition
One may notice that in the form of composition discussed in the previous section the two gateways simply forward messages, and wonder whether they are strictly needed. Indeed, a form of direct composition, where gateways are completely avoided, has been studied in [5] in a multiparty session type [17] setting. It has also been shown that applying this technique has a non trivial impact on the participants in the connected systems. We discuss here a different form of composition where a unique gateway is used, and we call it semi-direct composition. This has the advantage of saving one gateway and some communications, and also of simplifying some proofs. Moreover, the conditions for deadlock preservation are weaker when non-sequential interfaces are considered (see Theorem 4.10). On the other hand, participants in the composed systems are affected, but just by a renaming.
Definition 4.1
(Semi-direct gateway).
Let \(M_1\) and \(M_2\) be, respectively, an  - and a
- and a  -local CFSM such that
-local CFSM such that
-
\(M_1\) and \(M_2\) are compatible
-
for all
 and
and  the participants occurring in
the participants occurring in  are disjoint from those occurring in
are disjoint from those occurring in 
If  is a fresh role then the semi-direct gateway
is a fresh role then the semi-direct gateway  is the CFSM \(\langle {\mathcal {S}, q_0, \mathcal {L}, \rightarrow } \rangle \) such that
is the CFSM \(\langle {\mathcal {S}, q_0, \mathcal {L}, \rightarrow } \rangle \) such that
-
\(q_0 = (q^0_1,q^0_2)\) with \(q^0_1\) initial state of \(M_1\) and \(q^0_2\) initial state of \(M_2\);
-
\(\mathcal {S}\) includes all pairs \((q_1,q_2)\) and all triples
 such that \(q_1\) is a state of \(M_1\), \(q_2\) of \(M_2\) and
such that \(q_1\) is a state of \(M_1\), \(q_2\) of \(M_2\) and  a message which are reachable from the initial state \((q^0_1,q^0_2)\) via the transitions in \(\rightarrow \);
a message which are reachable from the initial state \((q^0_1,q^0_2)\) via the transitions in \(\rightarrow \); -
\(\rightarrow \) includes, for each \(q_1 \in M_1\) and \(q_2 \in M_2\) related by the compatibility bisimilarity:
-
 where
where 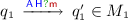 ,
,  ,
, -
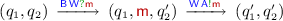 where
where  ,
,  .
.
-
The semi-direct composition of two systems takes all the machines of the participants in each system (with some channel renaming so to turn communications with  or
or  into communications with
into communications with  ) but the interface participants, which are replaced by the semi-direct gateway construction of their CFSMs.
) but the interface participants, which are replaced by the semi-direct gateway construction of their CFSMs.
Definition 4.2
(Semi-direct system composition). Given two systems \(\mathsf {S}_1\) and \(\mathsf {S}_2\) with disjoint domain, two compatible roles  and
and  , and a fresh role
, and a fresh role  , the system
, the system

is the
 -composition of \(\mathsf {S}_1\) and \(\mathsf {S}_2\) with respect to
-composition of \(\mathsf {S}_1\) and \(\mathsf {S}_2\) with respect to  and
and  . In the definition, the notation
. In the definition, the notation  denotes the machine obtained by replacing role
denotes the machine obtained by replacing role  with
with  in all the labels of transitions in \(M\).
in all the labels of transitions in \(M\).
Note that since the gateway construction exploits the compatibility bisimilarity relation then the interface participants need to be compatible for the composition to make sense. This was not the case in the gateway construction in Sect. 3.
In the following simple example we show how the compatibility bisimilarity is exploited in the construction of a semi-direct composition.
Example 4.3
Let us take system \(\mathsf {S}_1\) with participants  and
and  and system \(\mathsf {S}_2\) with participants
and system \(\mathsf {S}_2\) with participants  ,
,  and
and  as defined in Example 3.3. Participants
as defined in Example 3.3. Participants  and
and  are trivially compatible. Then the following system
are trivially compatible. Then the following system

is the semi-direct composition  . \(\diamond \)
. \(\diamond \)
We now study systems obtained by semi-direct composition. As in the previous section, we will focus on preservation of deadlock-freedom.
Configurations of a composed system are projected on the two subsystems by taking only the states of their participants and the respective component of the states of the interfaces.
Definition 4.4
(Projection of configurations). Given a configuration  , the map \(s||_{i}\), for \(i \in \{\,1,2\,\}\), defined as
, the map \(s||_{i}\), for \(i \in \{\,1,2\,\}\), defined as

is the projection of s on \(\mathsf {S}_i\).
As for the composition via gateways we define a notion of state projection to relate the states of the two systems.
Definition 4.5
Let  be a semi-direct gateway. The functions
be a semi-direct gateway. The functions  , where \(i\in \{\,1,2\,\}\), on the states of M are defined as follows
, where \(i\in \{\,1,2\,\}\), on the states of M are defined as follows

We can now discuss the properties of composed systems.
Proposition 4.6
Let \(\mathsf {S}_1\) and \(\mathsf {S}_2\) be two systems with disjoint domains and let  and
and  be two compatible roles. Then for each
be two compatible roles. Then for each  we have that
we have that
-
i)
\(s||_{1}\in \mathcal {R}({{\llbracket \mathsf {S}_1 \rrbracket }})\), \(s||_{2}\in \mathcal {R}({{\llbracket \mathsf {S}_2 \rrbracket }})\) and
 ;
; -
ii)
 iff one of the following holds
iff one of the following holds -
(a)
 and
and  and
and  , for \(i\in \{\,1,2\,\}\);
, for \(i\in \{\,1,2\,\}\); -
(b)
 and
and  and
and  ;
; -
(c)
 and
and  and
and  ;
; -
(d)
 and
and  and
and  ;
; -
(e)
 and
and  and
and  ;
; -
(f)
 and
and  and
and  and \(q=(q_1,q_2)\) and
and \(q=(q_1,q_2)\) and  ;
; -
(g)
 and
and  and
and  and
and  and
and  ;
; -
(h)
 and
and  and
and  and \(q=(q_1,q_2)\) and
and \(q=(q_1,q_2)\) and  ;
; -
(i)
 and
and  and
and  and
and  and
and  ;
;
-
(a)
Proof
The proof of (i) and (ii) is by simultaneous induction on the number of steps from the initial state. In the initial state (i) and (ii) hold by construction.
Let us consider the inductive case. We consider the following possible cases for the last transition.
-
 with
with  (the case
(the case  can be treated similarly). By definition of configuration transition, we have that
can be treated similarly). By definition of configuration transition, we have that  and
and  and
and  for each
for each  . Now, by the induction hypothesis (ii), we have that
. Now, by the induction hypothesis (ii), we have that  and
and 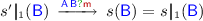 (where the two equalities can be inferred by definition of configuration projection, since
(where the two equalities can be inferred by definition of configuration projection, since  ). Hence we have that
). Hence we have that  . Now, since by the induction hypothesis we have that \(s'||_{1}\in \mathcal {R}({{\llbracket \mathsf {S}_1 \rrbracket }})\), we can infer that \(s||_{1}\in \mathcal {R}({{\llbracket \mathsf {S}_1 \rrbracket }})\). We obtain, instead, \(s||_{2}\in \mathcal {R}({{\llbracket \mathsf {S}_2 \rrbracket }})\) immediately by the induction hypothesis since, from
. Now, since by the induction hypothesis we have that \(s'||_{1}\in \mathcal {R}({{\llbracket \mathsf {S}_1 \rrbracket }})\), we can infer that \(s||_{1}\in \mathcal {R}({{\llbracket \mathsf {S}_1 \rrbracket }})\). We obtain, instead, \(s||_{2}\in \mathcal {R}({{\llbracket \mathsf {S}_2 \rrbracket }})\) immediately by the induction hypothesis since, from  and definition of configuration projection we have that \(s||_{2}= s'||_{2}\). Also
and definition of configuration projection we have that \(s||_{2}= s'||_{2}\). Also  immediately follows from the induction hypothesis since
immediately follows from the induction hypothesis since  implies
implies 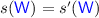 . Regarding (ii), if
. Regarding (ii), if  then the same participant wants to take the same action thanks to (i), as desired. If
then the same participant wants to take the same action thanks to (i), as desired. If  is willing to communicate with some participant in \(\mathsf {S}_1\) then thanks to (i) and definition of semi-direct gateway,
is willing to communicate with some participant in \(\mathsf {S}_1\) then thanks to (i) and definition of semi-direct gateway,  is willing to do the same in \(s||_{1}\). Symmetrically, if
is willing to do the same in \(s||_{1}\). Symmetrically, if  is willing to communicate with some participant in \(\mathsf {S}_2\) then
is willing to communicate with some participant in \(\mathsf {S}_2\) then  is willing to do the same in \(s||_{2}\).
is willing to do the same in \(s||_{2}\). -
 with
with  (the case
(the case  can be treated similarly). By definition of system transition, we have that
can be treated similarly). By definition of system transition, we have that  and
and  and
and  for each
for each  . Moreover, by the induction hypothesis, \(s'||_{1}\in \mathcal {R}({{\llbracket \mathsf {S}_1 \rrbracket }})\), \(s'||_{2}\in \mathcal {R}({{\llbracket \mathsf {S}_2 \rrbracket }})\) and
. Moreover, by the induction hypothesis, \(s'||_{1}\in \mathcal {R}({{\llbracket \mathsf {S}_1 \rrbracket }})\), \(s'||_{2}\in \mathcal {R}({{\llbracket \mathsf {S}_2 \rrbracket }})\) and  . By definition of configuration projection and of semi-direct gateway construction we have that \(s||_{2} = s'||_{2}\), and hence we can immediately infer that \(s||_{2} \in \mathcal {R}({{\llbracket \mathsf {S}_2 \rrbracket }})\).
. By definition of configuration projection and of semi-direct gateway construction we have that \(s||_{2} = s'||_{2}\), and hence we can immediately infer that \(s||_{2} \in \mathcal {R}({{\llbracket \mathsf {S}_2 \rrbracket }})\).Now, by the induction hypothesis (ii), we have that
 and
and and
and  where
where  . Now, by definition of configuration projection, from
. Now, by definition of configuration projection, from  we obtain that
we obtain that  . So, by definition of configuration transition, we have that
. So, by definition of configuration transition, we have that  , and then \(s||_{1}\in \mathcal {R}({{\llbracket \mathsf {S}_1 \rrbracket }})\). For what concerns
, and then \(s||_{1}\in \mathcal {R}({{\llbracket \mathsf {S}_1 \rrbracket }})\). For what concerns  , this is obtained by the induction hypothesis and by definition of
, this is obtained by the induction hypothesis and by definition of  and of semi-direct gateway. Also, (ii) holds, as in the previous case, by (i) and definition of semi-direct gateway and of configuration projection.
and of semi-direct gateway. Also, (ii) holds, as in the previous case, by (i) and definition of semi-direct gateway and of configuration projection. -
 with
with  .
.Similar to the previous case. \(\square \)
We now give a definition of composability for semi-direct composition.
Definition 4.7
(Semi-direct  -composability). Two systems \(\mathsf {S}_1\) and \(\mathsf {S}_2\) with disjoint domains are semi-directly
-composability). Two systems \(\mathsf {S}_1\) and \(\mathsf {S}_2\) with disjoint domains are semi-directly  -composable if
-composable if  and
and  are two compatible roles whose machines are ?!-deterministic and mixed-deterministic.
are two compatible roles whose machines are ?!-deterministic and mixed-deterministic.
Notice that semi-direct  -composability is strictly weaker than
-composability is strictly weaker than  -composability. In fact, whereas both require ?!-determinism, the former enables some mixed states whereas the latter completely forbids them.
-composability. In fact, whereas both require ?!-determinism, the former enables some mixed states whereas the latter completely forbids them.
It is easy to check that the counterexamples for deadlock-freedom preservation of Sect. 3 do hold also in case semi-directed gateways are used on  -composable systems. As before, this forces us to select interface roles which are sequential or which are in systems always willing to receive the messages they send. Before presenting the results we give an auxiliary lemma.
-composable systems. As before, this forces us to select interface roles which are sequential or which are in systems always willing to receive the messages they send. Before presenting the results we give an auxiliary lemma.
Lemma 4.8
Let \(\mathsf {S}_1\) and \(\mathsf {S}_2\) be two semi-directly  -composable systems. Then for each configuration \(s\) of the composed system
-composable systems. Then for each configuration \(s\) of the composed system  we have that:
we have that:
-
if
 then \(q_1,q_2\) are in the compatibility bisimilarity;
then \(q_1,q_2\) are in the compatibility bisimilarity; -
if
 then
then  has a unique transition to and from a state of the form in the item above.
has a unique transition to and from a state of the form in the item above.
Proof
By construction. Uniqueness relies on ?!- and mixed-determinism. \(\square \)
Theorem 4.9
(Deadlock freedom for sequential interfaces). Let \(\mathsf {S}_1\) and \(\mathsf {S}_2\) be two semi-directly  -composable and deadlock-free systems. If
-composable and deadlock-free systems. If  and
and  are sequential, then the composed system
are sequential, then the composed system  is deadlock-free.
is deadlock-free.
Proof
We will show that if  has a deadlock then at least one of \(\mathsf {S}_1\) and \(\mathsf {S}_2\) has a deadlock as well.
has a deadlock then at least one of \(\mathsf {S}_1\) and \(\mathsf {S}_2\) has a deadlock as well.
First, Proposition 4.6(ii) immediately yields that for each configuration \(s\) of  if there is some participant
if there is some participant  such that
such that  has an outgoing transition, then for some participant
has an outgoing transition, then for some participant  either
either  or
or  has an outgoing transition.
has an outgoing transition.
Now we show that if no transition is enabled in a configuration \(s\) of  then no transition is enabled in \(s||_{1}\) and \(s||_{2}\). We prove the contrapositive, showing that if there is an enabled transition in \(s||_{1}\) or in \(s||_{2}\) then there is a transition enabled in \(s\) as well. If the transition does not involve
then no transition is enabled in \(s||_{1}\) and \(s||_{2}\). We prove the contrapositive, showing that if there is an enabled transition in \(s||_{1}\) or in \(s||_{2}\) then there is a transition enabled in \(s\) as well. If the transition does not involve  this follows from Proposition 4.6. Let us now consider a transition involving
this follows from Proposition 4.6. Let us now consider a transition involving  (the case of
(the case of  is symmetric). If the transition is of the form
is symmetric). If the transition is of the form  and the state of
and the state of  in s is a pair, by construction \(s\) can perform a transition
in s is a pair, by construction \(s\) can perform a transition  as desired. If the state of
as desired. If the state of  in s is a triple then thanks to Lemma 4.8 and definition of semi-direct gateway, the previous state was in the compatibility bisimilarity with a state of
in s is a triple then thanks to Lemma 4.8 and definition of semi-direct gateway, the previous state was in the compatibility bisimilarity with a state of  , which has not changed. Hence
, which has not changed. Hence  is willing to take a transition and thanks to deadlock-freedom of \(\mathsf {S}_2\) we can infer that there is a transition enabled in \(s||_{2}\). From this we can deduce that there is a transition enabled in \(s\) too as shown above, but for the case in which the enabled transition is from
is willing to take a transition and thanks to deadlock-freedom of \(\mathsf {S}_2\) we can infer that there is a transition enabled in \(s||_{2}\). From this we can deduce that there is a transition enabled in \(s\) too as shown above, but for the case in which the enabled transition is from  . In this last case thanks to sequentiality the transition towards
. In this last case thanks to sequentiality the transition towards  and the one from
and the one from  are complementary, thus \(\mathsf {S}_2\) is ready to take the message from the gateway, hence the communication can trigger.
are complementary, thus \(\mathsf {S}_2\) is ready to take the message from the gateway, hence the communication can trigger.
A similar reasoning applies in case the transition is of the form  .
.
Thus, if there is a deadlock configuration \(s\) in the composed system then either \(s||_{1}\) or \(s||_{2}\) are deadlocks against the hypothesis. \(\square \)
Notice that \(\mathsf {S}_1\) and \(\mathsf {S}_2\) of Example 4.3 are deadlock-free and  -composable. Besides, both
-composable. Besides, both  and
and  are sequential. Deadlock-freedom of
are sequential. Deadlock-freedom of  can hence be inferred by the above result.
can hence be inferred by the above result.
As done for the composition via gateways, we can extend the above result by dropping the sequentiality condition in presence of !live interfaces.
Theorem 4.10
(Deadlock freedom for !live interfaces). Let \(\mathsf {S}_1\) and \(\mathsf {S}_2\) be two semi-directly  -composable and deadlock-free systems. Moreover, let
-composable and deadlock-free systems. Moreover, let  and
and  be !live, respectively, in \(\mathsf {S}_1\) and \(\mathsf {S}_2\). Then the composed system
be !live, respectively, in \(\mathsf {S}_1\) and \(\mathsf {S}_2\). Then the composed system  is deadlock-free.
is deadlock-free.
Proof
The proof is similar to the one of Theorem 4.9. The only difference is that !liveness is used instead of sequentiality when showing that if there is an enabled transition in \(s||_{1}\) or in \(s||_{2}\) then there is a transition enabled in \(s\) as well.
\(\square \)
5 Related and Future Work
We have considered the synchronous composition of systems of CFSMs following the approach proposed in [3, 4] for asynchronous composition. Quite surprisingly, enforcing that composition preserves deadlock freedom requires very strong conditions on the interface roles, as shown by means of some examples. Indeed, we proved compositionality of deadlock freedom for sequential interface roles only. We hence complemented this result by showing that, if a deadlock occurs, it needs to be when the gateway tries to deliver a message to the other system.
We also discussed semi-direct composition, based on a unique gateway. Beyond sparing some communications, the conditions required to ensure compositionality of deadlock freedom using this second approach are slightly weaker.
While we only discussed deadlock freedom, the same reasonings can be applied to other behavioural properties such as lock freedom [6, 18, 19] and liveness [6, 23].
The above approach to composition has also been discussed in [5], in the setting of systems of processes obtained by projecting well-formed global types [17]. This setting is far less wild than ours, since global types ensure that each send is matched by a receive. Thus, all the counterexamples we showed cannot happen and deadlock freedom is ensured in all typable systems. Thanks to these restrictions they were able to develop a more comprehensive theory, including direct composition, a notion of structural decomposition and notions of behavioural composition and decomposition. Also, they could use as compatibility a relation weaker than bisimilarity. Understanding whether such a theory can be amended to fit in our more general setting is an interesting item for future work.
Compositionality in the setting of global types has been also studied in [22]. There the compositionality mechanism is different since it relies on partial systems, while the approach we use allows one to compose systems which are designed as closed, by transforming some participants into gateways. On the other hand they are able to model ways of interaction more structured than having a single communication channel as in our case. Extending our approach to cope with the composition via multiple interfaces at the same time can be an interesting aim for future work and can contribute to match their expressive power.
A compositional approach for reactive components has been proposed in [12, 25]. Composition is attained by means of a specified protocol regulating the communications between components that are supposed to produce results as soon as they get their inputs. Roughly speaking, this protocol represents the composition interface that rules out, among the communications of components, those not allowed in the composition. In this way, a component may be used in compositions under different protocols if its communications are compliant with (part of) the protocols. A difference with our approach is that the framework in [12, 25], as common in session type approaches, requires the specification of a global type from which to derive local types to type check components in order to compose them.
Among the automata-based models in the literature, I/O automata [21], team automata [26], interface automata [15], and BIP [9] are perhaps the closest to communicating systems. In these models composition strategies based on some notion of compatibility have been proposed. However, these approaches differ from ours on a number of aspects.
First, the result of such a composition is a new automaton, not a system as in our case. Correspondingly, our notion of “interface” is more elaborated than in the other models. Indeed, for us an interface is a pair of automata rather than sets of actions of a single automaton.
Second, such automata have a fixed interface, since they distinguish internal from external actions. Instead, we do not fix an explicit interface: the interface is decided in a relative fashion. This gives a high degree of flexibility; e.g., we could use as interface a CFSM  when composing a system \(\mathsf {S}\) with a system, say \(\mathsf {S}'\), and a different CFSM
when composing a system \(\mathsf {S}\) with a system, say \(\mathsf {S}'\), and a different CFSM  in \(\mathsf {S}\) when composing it with another system \(\mathsf {S}''\).
in \(\mathsf {S}\) when composing it with another system \(\mathsf {S}''\).
As previously pointed out, and related to the previous observations, we could think of our approach as not been based on a notion of “open” systems. We compose closed systems by “opening them up” depending on their relative structures, namely on the fact that they possess compatible components.
Extensive studies about compositionality of interacting systems have been conducted in the context of the BIP model [9]. Composition in BIP happens through operators meant to mediate the behaviour of the connected components. The composition can alter the non-deterministic behaviour by suitable priority models. In [1, 2] it is shown that, under mild hypothesis, priority models do not spoil deadlock freedom. This requires to compromise on expressiveness. Whether our conditions are expressible in some priority model is open and left for future work. BIP features multi-point synchronisations while CFSMs interactions are point-to-point. Very likely CFSMs can be encoded in BIP without priorities and one could use D-Finder [8] to detect deadlock of composed systems. However, our conditions on interfaces allows us to avoid such analysis.
In the present approach, the transformations generating the gateway(s) from the interface roles do not depend on the rest of the systems to be composed. Besides investigating relaxed notions of compatibility (in the style of [5]), it would also be worth considering the possibility of dropping the compatibility requirement altogether and developing methods to generate ad-hoc gateways (i.e., taking into account the other CFSMs of the two systems to be composed) that preserve deadlock freedom and communication properties in general by construction. It would also be worth investigating whether our approach can be extended to cope with types of message passing communications other than point-to-point, such as multicast [14], broadcast or many-to-many [11].
References
Baranov, E., Bliudze, S.: Offer semantics: achieving compositionality, flattening and full expressiveness for the glue operators in BIP. Sci. Comput. Program. 109, 2–35 (2015)
Baranov, E., Bliudze, S.: Expressiveness of component-based frameworks: a study of the expressiveness of BIP. Acta Informatica (2019). https://doi.org/10.1007/s00236-019-00337-7
Barbanera, F., de’Liguoro, U., Hennicker, R.: Global types for open systems. In: Bartoletti, M., Knight, S. (eds.) ICE, Volume 279 of EPTCS, pp. 4–20 (2018)
Barbanera, F., de’Liguoro, U., Hennicker, R.: Connecting open systems of communicating finite state machines. JLAMP 109 (2019)
Barbanera, F., Dezani-Ciancaglini, M., Lanese, I., Tuosto, E.: Composition and decomposition of multiparty sessions. JLAMP (2020). Submitted
Barbanera, F., Lanese, I., Tuosto, E.: Choreography automata. In: Bliudze, S., Bocchi, L. (eds.) COORDINATION 2020. LNCS, vol. 12134, pp. 86–106. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-50029-0_6
Basu, S., Bultan, T., Ouederni, M.: Deciding choreography realizability. In: POPL, pp. 191–202 (2012)
Bensalem, S., Griesmayer, A., Legay, A., Nguyen, T.-H., Sifakis, J., Yan, R.: D-Finder 2: towards efficient correctness of incremental design. In: Bobaru, M., Havelund, K., Holzmann, G.J., Joshi, R. (eds.) NFM 2011. LNCS, vol. 6617, pp. 453–458. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-20398-5_32
Bliudze, S., Sifakis, J.: The algebra of connectors: structuring interaction in BIP. In: International Conference on Embedded Software. ACM, September 2020
Brand, D., Zafiropulo, P.: On communicating finite-state machines. J. ACM 30(2), 323–342 (1983)
Bruni, R., Corradini, A., Gadducci, F., Melgratti, H., Montanari, U., Tuosto, E.: Data-driven choreographies à la Klaim. In: Boreale, M., Corradini, F., Loreti, M., Pugliese, R. (eds.) Models, Languages, and Tools for Concurrent and Distributed Programming. LNCS, vol. 11665, pp. 170–190. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-21485-2_11
Carbone, M., Montesi, F., Vieira, H.T.: Choreographies for reactive programming. CoRR, abs/1801.08107 (2018). http://arxiv.org/abs/1801.08107
Cécé, G., Finkel, A.: Verification of programs with half-duplex communication. I&C 202(2), 166–190 (2005)
Coppo, M., Dezani-Ciancaglini, M., Yoshida, N., Padovani, L.: Global progress for dynamically interleaved multiparty sessions. Mathematical structures in computer science 26(2), 238–302 (2016)
De Alfaro, L., Henzinger, T.: Interface automata. ACM SIGSOFT Softw. Eng. Notes 26(5), 109–120 (2001)
Gouda, M.G., Chang, C.: Proving liveness for networks of communicating finite state machines. ACM Trans. Program. Lang. Syst. 8(1), 154–182 (1986)
Hüttel, H., et al.: Foundations of session types and behavioural contracts. ACM Comput. Surv. 49(1), 3:1–3:36 (2016)
Kobayashi, N.: A partially deadlock-free typed process calculus. ACM TOPLAS 20(2), 436–482 (1998)
Kobayashi, N.: Type-based information flow analysis for the pi-calculus. Acta Informatica 42(4–5), 291–347 (2005)
Lange, J., Tuosto, E., Yoshida, N.: From communicating machines to graphical choreographies. In: POPL, pp. 221–232. ACM (2015)
Lynch, N., Tuttle, M.: Hierarchical correctness proofs for distributed algorithms. In: ACM Symposium Principles of Distributed Computing, pp. 137–151. ACM (1987)
Montesi, F., Yoshida, N.: Compositional choreographies. In: D’Argenio, P.R., Melgratti, H. (eds.) CONCUR 2013. LNCS, vol. 8052, pp. 425–439. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40184-8_30
Padovani, L., Vasconcelos, V.T., Vieira, H.T.: Typing liveness in multiparty communicating systems. In: Kühn, E., Pugliese, R. (eds.) COORDINATION 2014. LNCS, vol. 8459, pp. 147–162. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-43376-8_10
Peng, W., Purushothaman, S.: Analysis of a class of communicating finite state machines. Acta Inf. 29(6/7), 499–522 (1992)
Savanović, Z., Vieira, H., Galletta, L.: A type language for message passing component-based systems. In: ICE, EPTCS (2020). To appear
ter Beek, M.H., Kleijn, J.: Team automata satisfying compositionality. In: Araki, K., Gnesi, S., Mandrioli, D. (eds.) FME 2003. LNCS, vol. 2805, pp. 381–400. Springer, Heidelberg (2003). https://doi.org/10.1007/978-3-540-45236-2_22
Tuosto, E., Guanciale, R.: Semantics of global view of choreographies. JLAMP 95, 17–40 (2018)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 Springer Nature Switzerland AG
About this paper
Cite this paper
Barbanera, F., Lanese, I., Tuosto, E. (2020). Composing Communicating Systems, Synchronously. In: Margaria, T., Steffen, B. (eds) Leveraging Applications of Formal Methods, Verification and Validation: Verification Principles. ISoLA 2020. Lecture Notes in Computer Science(), vol 12476. Springer, Cham. https://doi.org/10.1007/978-3-030-61362-4_3
Download citation
DOI: https://doi.org/10.1007/978-3-030-61362-4_3
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-61361-7
Online ISBN: 978-3-030-61362-4
eBook Packages: Computer ScienceComputer Science (R0)





 );
); is the initial configuration where, for each
is the initial configuration where, for each  ,
,  is the initial state of
is the initial state of  ;
; is a set of interaction labels;
is a set of interaction labels; if
if  and
and  .
. such that
such that  has an outgoing transition in
has an outgoing transition in  .
. with
with  for some fresh state
for some fresh state  with
with  for some fresh state
for some fresh state  and
and  (resp.
(resp.  and
and  ) implies
) implies  for all
for all  and
and  .
. and
and  are not fresh;
are not fresh; is fresh,
is fresh,  is not fresh,
is not fresh,  , or, symmetrically,
, or, symmetrically,  is fresh,
is fresh,  is not fresh,
is not fresh,  ;
; is fresh,
is fresh,  is not fresh, and there is
is not fresh, and there is  such that
such that  , or, symmetrically,
, or, symmetrically,  is fresh,
is fresh,  is not fresh, and there is
is not fresh, and there is  such that
such that  ;
; and
and  are fresh and either
are fresh and either  , and there is
, and there is  such that
such that  , or, symmetrically,
, or, symmetrically,  , and there is
, and there is  such that
such that  .
. , takes a transition. By construction it delivers a message
, takes a transition. By construction it delivers a message  to a participant in its system via a transition
to a participant in its system via a transition
 . This leads us to case
. This leads us to case  goes to a non-fresh state, while
goes to a non-fresh state, while  was in a non-fresh state by hypothesis and does not move. The condition on configurations holds by inductive hypothesis for
was in a non-fresh state by hypothesis and does not move. The condition on configurations holds by inductive hypothesis for  can do the same move as in s and the two moves of the gateway for
can do the same move as in s and the two moves of the gateway for  (the gateway transition which was not taken into account yet and the delivery of message
(the gateway transition which was not taken into account yet and the delivery of message  ) correspond to the complementary move of
) correspond to the complementary move of  in
in  projects on the same states as before the transition.
projects on the same states as before the transition. , takes a transition. By construction it takes a message from its own system via a transition
, takes a transition. By construction it takes a message from its own system via a transition  . This leads us to case
. This leads us to case  goes to a fresh state while
goes to a fresh state while  was already in a fresh state. Then
was already in a fresh state. Then  by inductive hypothesis and
by inductive hypothesis and  by construction. The reasoning on conditions of configurations and bisimulation is similar to the one of a message taken by the gateway in case
by construction. The reasoning on conditions of configurations and bisimulation is similar to the one of a message taken by the gateway in case  be the sender and
be the sender and  the interface role. The transition is of the form
the interface role. The transition is of the form  . There are two possibilities. If the gateway for
. There are two possibilities. If the gateway for  is not in a fresh state in s then the same transition can trigger in the composed system thanks to the definition of system transition and of configuration projection.
is not in a fresh state in s then the same transition can trigger in the composed system thanks to the definition of system transition and of configuration projection. , may be in a fresh state or not. If it is not, thanks to the definition of
, may be in a fresh state or not. If it is not, thanks to the definition of  and to the condition on bisimulation of Proposition
and to the condition on bisimulation of Proposition  is in a fresh state then thanks to the definition of configuration projection and of gateway it is willing to deliver a message to
is in a fresh state then thanks to the definition of configuration projection and of gateway it is willing to deliver a message to  be the interface role and
be the interface role and  the target participant. Hence, the transition is of the form
the target participant. Hence, the transition is of the form  . Thanks to the definition of gateway and of system projection the gateway for
. Thanks to the definition of gateway and of system projection the gateway for  in s is either willing to deliver a message to some participant in
in s is either willing to deliver a message to some participant in  . In the first case, since the gateway is sequential then the participant is
. In the first case, since the gateway is sequential then the participant is  and the message
and the message  , hence the transition can trigger.
, hence the transition can trigger. is willing to receive from
is willing to receive from  then thanks to the definition of
then thanks to the definition of  and the condition on bisimulation of Proposition
and the condition on bisimulation of Proposition  is willing to receive a message from its system or has just received it and is willing to send it through the gateway. In the last case the gateway communication can occur.
is willing to receive a message from its system or has just received it and is willing to send it through the gateway. In the last case the gateway communication can occur. is willing to receive a message from some participant in
is willing to receive a message from some participant in  and
and  the participants occurring in
the participants occurring in  are disjoint from those occurring in
are disjoint from those occurring in 
 such that
such that  a message which are reachable from the initial state
a message which are reachable from the initial state  where
where 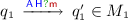 ,
,  ,
,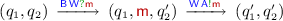 where
where  ,
,  .
. ;
; iff one of the following holds
iff one of the following holds  and
and  and
and  , for
, for  and
and  and
and  ;
; and
and  and
and  ;
; and
and  and
and  ;
; and
and  and
and  ;
; and
and  and
and  and
and  ;
; and
and  and
and  and
and  and
and  ;
; and
and  and
and  and
and  ;
; and
and  and
and  and
and  and
and  ;
; with
with  (the case
(the case  can be treated similarly). By definition of configuration transition, we have that
can be treated similarly). By definition of configuration transition, we have that  and
and  and
and  for each
for each  . Now, by the induction hypothesis (
. Now, by the induction hypothesis ( and
and 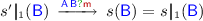 (where the two equalities can be inferred by definition of configuration projection, since
(where the two equalities can be inferred by definition of configuration projection, since  ). Hence we have that
). Hence we have that  . Now, since by the induction hypothesis we have that
. Now, since by the induction hypothesis we have that  and definition of configuration projection we have that
and definition of configuration projection we have that  immediately follows from the induction hypothesis since
immediately follows from the induction hypothesis since  implies
implies 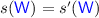 . Regarding (
. Regarding ( then the same participant wants to take the same action thanks to (
then the same participant wants to take the same action thanks to ( is willing to communicate with some participant in
is willing to communicate with some participant in  is willing to do the same in
is willing to do the same in  is willing to communicate with some participant in
is willing to communicate with some participant in  is willing to do the same in
is willing to do the same in  with
with  (the case
(the case  can be treated similarly). By definition of system transition, we have that
can be treated similarly). By definition of system transition, we have that  and
and  and
and  for each
for each  . Moreover, by the induction hypothesis,
. Moreover, by the induction hypothesis,  . By definition of configuration projection and of semi-direct gateway construction we have that
. By definition of configuration projection and of semi-direct gateway construction we have that  and
and and
and  where
where  . Now, by definition of configuration projection, from
. Now, by definition of configuration projection, from  we obtain that
we obtain that  . So, by definition of configuration transition, we have that
. So, by definition of configuration transition, we have that  , and then
, and then  , this is obtained by the induction hypothesis and by definition of
, this is obtained by the induction hypothesis and by definition of  and of semi-direct gateway. Also, (
and of semi-direct gateway. Also, ( with
with  .
. then
then  then
then  has a unique transition to and from a state of the form in the item above.
has a unique transition to and from a state of the form in the item above.