Abstract
In this survey we shall deal with the regularity of characteristic functions \({\mathcal X}_E\) of subsets E of \({\mathbb {R}}^d\) in the framework of Besov spaces. We will describe a number of necessary and sufficient conditions to guarantee membership in a Besov space of given smoothness s and with integrability p. Several examples are discussed in detail.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
- Characteristic functions
- Indicator functions
- Regularity
- Besov spaces
- Snowflake domain
- Twindragon
- Modified Nikodym domains
1 Introduction
Let E be a nontrivial measurable subset of \({\mathbb {R}}^d\) such that 0 < |E| < ∞. By |E| we denote the Lebesgue measure of E and by \({\mathcal X}_E\) the associated characteristic function. For 1 ≤ p ≤∞ and s ≥ 0 we have
and
Neither the Lebesgue spaces \(L_p ({\mathbb {R}}^d)\) nor the first order Sobolev spaces \(W^1_p ({\mathbb {R}}^d)\) nor the Hölder spaces \(C^s({\mathbb {R}}^d)\) allow to distinguish the regularity of those characteristic functions. Intuitively it is clear that these functions have different regularity depending on the quality of the boundary (whatever this means at this moment). To make this clear we have to deal with notions of fractional smoothness s ∈ (0, 1) related to spaces with p < ∞. There are several possibilities. Not only for simplicity we have decided here for Besov spaces \(B^s_{p,q} ({\mathbb {R}}^d)\), see Sect. 2 for a definition. Alternatively we could have chosen Bessel potential spaces \(H^s_p ({\mathbb {R}}^d)\) or even more general Lizorkin–Triebel spaces \(F^s_{p,q} ({\mathbb {R}}^d)\). Parts of the results obtained below carry over from Besov spaces to the spaces \(F^s_{p,q} ({\mathbb {R}}^d)\), but there will be also exceptions, mainly in limiting situations. We will not go into details here.
In this survey we will discuss various notions describing the regularity of the boundary ∂E and to compare this with the regularity of \({\mathcal X}_E\) in Besov spaces. Mostly they will stem from fractal geometry, but not exclusively. For convenience of the reader we have collected some basic facts from fractal geometry in the Appendix at the end of this paper. The paper is written in a way that it is readable also for non-experts in function spaces. The author had spend some time to look for proofs as simple as possible. Only in a few cases we did not include the known but more complicated proofs. This makes the paper essentially self-contained. A certain number of examples is treated in detail.
The motivation of the author to deal with this topic originated from the theory of pointwise multipliers for Besov spaces. Here a function \(f:{\mathbb {R}}^d \to \mathbb {R}\) is called a pointwise multiplier for \(B^s_{p,q} ({\mathbb {R}}^d)\) if f ⋅ g belongs to \(B^s_{p,q} ({\mathbb {R}}^d)\) for all \(g\in B^s_{p,q} ({\mathbb {R}}^d)\). The question, whether the characteristic function of the half space \(E:= {\mathbb {R}}^d_+\) is a pointwise multiplier for Besov and Bessel potential spaces, has attracted a lot of attention since the early sixties. Later Gulisashvili [30, 31], see also Maz’ya and Shaposhnikova [46, 5.5.2], had found necessary and sufficient conditions on a set \(E\subset {\mathbb {R}}^d\) such that \({\mathcal X}_E\) is a pointwise multiplier in specific situations. For a function f to be a pointwise multiplier for \(B^s_{p,q} ({\mathbb {R}}^d)\) it is necessary that f belongs at least locally to \(B^s_{p,q} ({\mathbb {R}}^d)\) itself. Hence, the regularity of the characteristic function \({\mathcal X}_E\) is part of the pointwise multiplier problem for Besov spaces. In my opinion it is interesting enough to be considered as an independent problem.
There will be a continuation of this survey dealing with characteristic functions as pointwise multipliers for Besov spaces.
The paper is organized as follows. Section 2 is devoted to the function spaces under consideration. In Sect. 3 we will discuss the maximal smoothness of characteristic functions related to the case s = 1∕p. Section 4 contains results on less regular characteristic functions, i.e., we consider 0 < s < 1∕p.
1.1 Notation
As usual, \(\mathbb {N}\) denotes the natural numbers, \(\mathbb {N}_0=\mathbb {N}\cup \{0\},\ \mathbb {Z}\) denotes the integers and \(\mathbb {R}\) the real numbers. The letter \(d\in \mathbb {N} \) is always reserved for the underlying dimension in \({\mathbb {R}}^d\). As usual, a domain in \({\mathbb {R}}^d\) is an open, non-trivial and simply connected set. For a subset E of \({\mathbb {R}}^d\) we denote it’s complement by F and the set of inner points of F by  . Furthermore, we put
. Furthermore, we put
Several times we will work with dyadic cubes. Here by a dyadic cube we mean a cube of type
With λQ we denote the cube having the same centre as Q itself, the sides of λQ and Q are parallel and the side-length of λQ is the side-length of Q multiplied with λ > 0. A ball with center in x and radius r will be denoted by B(x, r).
If X and Y are two normed spaces, the symbol X↪Y indicates that the identity operator is continuous. For two sequences (a n)n and (b n)n of nonnegative real numbers we will write \(a_n \lesssim b_n\) if there exists a constant c > 0 such that a n ≤ cb n for all n. We use a n ≍ b n if \(a_n \lesssim b_n\) and \(b_n \lesssim a_n\).
2 Besov Spaces
Nowadays Besov spaces represent a standard version of regularity used in various branches of mathematics. One of their advantages consists in the possibility to describe them in quite different ways. For our purpose the most appropriate one is the characterization by differences.
Definition 1
Let 1 ≤ p, q ≤∞.
-
(i)
Let 0 < s < 1. Then \(B^s_{p,q} ({\mathbb {R}}^d)\) is the collection of all real-valued functions \(f\in L_p ({\mathbb {R}}^d)\) such that
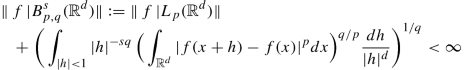
(usual modification if p and/or q are equal to infinity).
-
(ii)
Let 1 ≤ s < 2. Then \(B^s_{p,q} ({\mathbb {R}}^d)\) is the collection of all real-valued functions \(f\in L_p ({\mathbb {R}}^d)\) such that
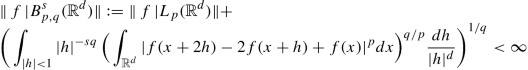
(usual modification if p and/or q are equal to infinity).
Remark 1
-
(i)
Besov spaces can be defined for all \(s\in \mathbb {R}\) and all p, q ∈ (0, ∞] (partly by using simply higher order differences). But for us the above definition will be sufficient.
-
(ii)
Besov spaces are Banach spaces. They can be characterized also in terms of the modulus of smoothness, in a Fourier analytic way, by atoms, molecules and wavelets etc.. Standard references are the monographs by Besov, Il’yin, Nikol’skij [6, 7], Nikol’skij [48], Peetre [51] and Triebel [61, 62, 66].
Normally most important are the parameters p and s. The parameter q may be considered as a fine-index which only comes into play in limiting situations. There will be two cases, namely q = ∞ and q = p, which will be more important for us then the other. In case q = ∞ the norm reads as
if 0 < s < 1 and
if 1 ≤ s < 2. In case q = p we first observe that we can replace ∫|h|<1… by \(\int _{{\mathbb {R}}^d} \ldots \) (since the additional term (∫|h|≥1…)1∕p is dominated by a constant C(s, p, d) (independent of f) times \(\| \, f\, |L_p({\mathbb {R}}^d)\|\)). A change of variables finally results in the following equivalent norms for \(B^s_{p,p}({\mathbb {R}}^d)\):
if 0 < s < 1 and
if 1 ≤ s < 2. If \({\mathbb {R}}^d\) is replaced by a smooth bounded domain Ω these norms are often called Gagliardo norms. Many times we shall employ so-called elementary embeddings. They express the monotonicity of the Besov spaces with respect to s and q. Here we mean the following
where q 0, q 1 are arbitrary in [1, ∞] and 0 < s 1 < s 0.
Remark 2
-
(i)
To restrict the values of h by |h| < 1 is always artificial. If a is an arbitrary positive real number, then the restriction |h| < a leads to an equivalent norm.
-
(ii)
Officially Besov spaces have been introduced by Besov in his Phd thesis published in the papers [3] and [4] in 1959/1961. However, Nikol’skij had already introduced the classes \(B^s_{p,\infty } ({\mathbb {R}}^d)\) in 1951 and Gagliardo had considered \(B^s_{p,p} ({\mathbb {R}}^d)\) in 1956 (in connection with trace problems for \(W^1_p (\Omega )\)).
3 The Limiting Case s = 1∕p
As we shall see below, the smoothness s of a characteristic function \({\mathcal X}_E\) of a measurable set \(E \subset {\mathbb {R}}^d,\ 0 < |E|< \infty \), will be dominated in any case by 1∕p. With this problem we will deal first. Afterwards we will characterize those sets E such that \({\mathcal X}_E\) has maximal regularity.
3.1 Necessary Conditions
Let us start with a very simple example. We choose d = 1 and consider the characteristic function \({\mathcal X}\) of the interval (0, 1). For 1 ≤ p < ∞ and 0 < h < 1 we have
The same argument applies for − 1 < h < 0. Hence
For 1 < p < ∞ this immediately implies \({\mathcal X} \in B^s_{p,\infty }(\mathbb {R})\) if 0 < s ≤ 1∕p and \({\mathcal X} \not \in B^{s}_{p,\infty }(\mathbb {R})\) if 1∕p < s < 1. Since Besov spaces are monotone in s, see (1), we conclude \({\mathcal X} \not \in B^{s}_{p,\infty }(\mathbb {R})\) for all s > 1∕p.
Now we apply the same method to the case of a more general set E. Recall, \(F:= {\mathbb {R}}^d \setminus E\). For \(h \in {\mathbb {R}}^d\) we define
It follows
Hence, we have a first result.
Lemma 1
Let 1 ≤ p < ∞ and 0 < s < 1. Then\({\mathcal X}_E\)belongs to\(B^s_{p,\infty } ({\mathbb {R}}^d)\)if and only if
There is an easy but interesting consequence of Lemma 1. Let 1 < p < ∞. Observe that \({\mathcal X}_E \in B^s_{1,\infty } ({\mathbb {R}}^d)\) implies \({\mathcal X}_E \in B^{s/p}_{p,\infty } ({\mathbb {R}}^d)\) and vice versa.
Figure 1 below shows shifted versions of the supports of characteristic functions of a circle and of a rectangle, respectively. The shaded regions are just E(h) ∪ F(h) in these cases. De facto it is “seen” that |E(h)| + |F(h)|≍|h|, |h| < 1.
As a consequence we obtain a second result.
Lemma 2
Let d ≥ 2. Let 1 ≤ p < ∞ and s > 0. Then the characteristic function\({\mathcal X}_E\)of either a ball or a cuboid, i.e., the cartesian product of d segments, belongs to\(B^s_{p,\infty } ({\mathbb {R}}^d)\)if and only if s ≤ 1∕p.
Proof
Only p = 1 requires an additional comment. Obviously

This explains sufficiency. Necessity follows from Theorem 1 below. □
It will be the main aim of this subsection to show that s = 1∕p is a barrier for the smoothness of characteristic functions \({\mathcal X}_E\) in general. Our point of departure is a generalization of a theorem of Titchmarsh, due to Gulisashvili [30].
Proposition 1
If for some ball \(B,\ B \subset {\mathbb {R}}^d\) , and \(f \in L_1^{\ell oc} ({\mathbb {R}}^d)\) we have
then f ≡const almost everywhere on B.
Now we turn to an application of this Proposition 1. Let \(E \subset {\mathbb {R}}^d,\ 0 < |E|<\infty \). Then the function \(g(x):= |{\mathcal X} (x+h)-{\mathcal X} (x)|,\ x\in {\mathbb {R}}^d\), only takes values in {0, 1}. This implies
for all h and all 1 ≤ p < ∞. Next we need to recall an equivalent characterization of Besov spaces in terms of modulus of smoothness. We put
Let 1 ≤ q < ∞, 1 ≤ p < ∞ and 0 < s < 1. Then there exist positive constants A, B such that
holds for all \(f \in B^s_{p,q}({\mathbb {R}}^d)\), we refer, e.g., to [61, 2.5.12]. A simple monotonicity argument yields that
for any \(f\in B^s_{p,q} ({\mathbb {R}}^d)\). If \(f={\mathcal X}_E\) then the assumption \( {\mathcal X}_E \in B^{1/p}_{p,q} ({\mathbb {R}}^d)\) (1 < p < ∞, 1 ≤ q < ∞) and Proposition 1 yield that \({\mathcal X}_E\) is constant on any ball B. But this is in contradiction with \(E \subset {\mathbb {R}}^d,\ 0 < |E|<\infty \).
Theorem 1
Let 1 ≤ p < ∞ and 1 ≤ q < ∞. Then there exists no subset\(E \subset {\mathbb {R}}^d,\ 0 < |E|<\infty \) , such that\( {\mathcal X}_E \in B^{1/p}_{p,q} ({\mathbb {R}}^d)\).
Proof
The case 1 < p < ∞, 1 ≤ q < ∞ has been treated above. It remains to consider p = 1. Let us assume \({\mathcal X}_E \in B^1_{1,q} ({\mathbb {R}}^d)\). Since the function
can only take values from the set {0, 1, 2}, we obtain
Let 1 ≤ r < ∞. It follows
Since E has finite measure, this implies \({\mathcal X}_E \in B^1_{1,q} ({\mathbb {R}}^d)\) if and only if \({\mathcal X}_E \in B^{1/p}_{p,pq} ({\mathbb {R}}^d)\). For 1 < p < ∞ and q < ∞ we may apply our arguments from above. This yields the claim for p = 1. □
Hence we conclude that the maximal regularity of a characteristic function in the framework of Besov spaces is given by the class \(B^{1/p}_{p,\infty } ({\mathbb {R}}^d)\) for some p. Only in case d = 1 the spaces \(B^{1/p}_{p,\infty } ({\mathbb {R}}^d),\ 1\le p \le \infty \), are comparable. Then we have
The characteristic function \({\mathcal X}\) of the interval (0, 1) not only belongs to \(B^1_{1,\infty } (\mathbb {R})\), it belongs to \(BV(\mathbb {R})\), the space of functions of bounded variation (which represents a strictly smaller class). This will play a role in the next subsection.
3.2 Characteristic Functions with Maximal Regularity
Here we follow Gulisashvili [30]. Therefore we consider functions of bounded variation which are integrable on \({\mathbb {R}}^d\).
Recall, a locally integrable function \(f:~{\mathbb {R}}^d\to \mathbb {R}\) is of bounded variation if its first order partial derivatives (in the distributional sense) are bounded Borel measures. The space \(BV \cap L_1 ({\mathbb {R}}^d)\) will be endowed with the norm
where \(|\frac {\partial f}{\partial x_j}|\) denotes the total variation of the measure. The symbol \(\mathcal {H}^s\) refers to the s-dimensional Hausdorff measure, see the Appendix for details. Then the perimeter of a set E is the quantity
where the limit is taken with respect to all sequences (M j)j of sets with a smooth boundary (or polyhedra) such that
A basic fact in the theory of the BV spaces is the Kronrod–Federer–Fleming–Rishel formula
see, e.g., Fleming, Rishel [26] and Burago, Zalgaller [11]. In particular, it follows
Next we recall the definition of the space \(Lip \, (1,1)({\mathbb {R}}^d)\). A function \(f:~{\mathbb {R}}^d \to \mathbb {R}\) belongs to \(Lip \, (1,1)({\mathbb {R}}^d)\) if \(f \in L_1 ({\mathbb {R}}^d)\) and supt>0 t −1ω 1(f, t) < ∞. The norm is given by
Hardy and Littlewood proved that \(BV \cap L_1 (\mathbb {R})\) coincides with \(Lip\, (1,1)(\mathbb {R})\). The generalization to the case d > 1 has been proved by Gulisashvili [30].
Proposition 2
It holds\(BV \cap L_1 ({\mathbb {R}}^d) = Lip\, (1,1)({\mathbb {R}}^d)\)as sets. There exist positive constants A, B such that
holds for all\(f\in L_1 ({\mathbb {R}}^d)\).
Summarizing we get the following.
Lemma 3
Let\(E\subset {\mathbb {R}}^d\)be a measurable set satisfying 0 < |E| < ∞.
-
(i)
Let per E < ∞. Then\({\mathcal X}_E\)belongs to\(B^{1/p}_{p,\infty } ({\mathbb {R}}^d)\)for all p, 1 ≤ p < ∞.
-
(ii)
Let\({\mathcal X}_E \in B^{1/p_0}_{p_0,\infty } ({\mathbb {R}}^d)\)for some p 0, 1 ≤ p 0 < ∞. Then\(\mathrm {per}\, E < \infty ,\ {\mathcal X}_E \in BV ({\mathbb {R}}^d)\)and\( {\mathcal X}_E \in B^{1/p}_{p,\infty } ({\mathbb {R}}^d)\)for all p, 1 ≤ p < ∞, follows.
Proof
- Step 1. Proof of (i).:
-
Thanks to (5) and per E < ∞ we know that \({\mathcal X}_E \in BV\cap L_1 ({\mathbb {R}}^d)\). Since this space coincides with \(Lip (1,1)({\mathbb {R}}^d)\), see Proposition 2, we conclude
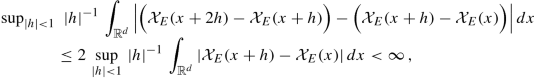
i.e., \({\mathcal X}_E \in B^1_{1,\infty }({\mathbb {R}}^d)\). We put \(\tilde {g}_h(x):= {\mathcal X}_E (x+h)-{\mathcal X}_E (x),\ x\in {\mathbb {R}}^d\). Observe that \(|\tilde {g}(x)| \in \{0,1\}\) for all x. Hence, for all p ∈ (1, ∞) we get
$$\displaystyle \begin{aligned} |h|{}^{-1}\, \| \, \tilde{g}_h\, |L_1 ({\mathbb{R}}^d)\| \asymp |h|{}^{-1}\, \| \, \tilde{g}_h\, |L_p ({\mathbb{R}}^d)\|{}^p \end{aligned} $$(6)with hidden constants independent of h. This yields that \({\mathcal X}_E\) belongs to \(B^{1/p}_{p,\infty }({\mathbb {R}}^d)\) for all these p.
- Step 2. Proof of (ii).:
-
Once again we use (6). Since \({\mathcal X}_E \in L_1 ({\mathbb {R}}^d)\) is guaranteed by |E| < ∞ we conclude that \({\mathcal X}_E \in B^{1/p_0}_{p_0,\infty }({\mathbb {R}}^d)\) implies that \({\mathcal X}_E \in B^{1/p}_{p,\infty }({\mathbb {R}}^d)\) for all p ∈ [1, ∞). We get a bit more. We also obtain that
$$\displaystyle \begin{aligned} \sup_{|h|< 1} \, |h|{}^{-1}\, \int_{{\mathbb{R}}^d} |{\mathcal X}_E (x+h) - {\mathcal X}_E (x)|\, dx <\infty. \end{aligned}$$Now we employ (3) and find
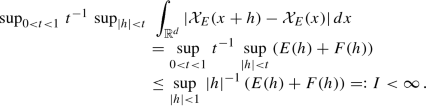
Because of the trivial estimate
$$\displaystyle \begin{aligned} \sup_{t \ge 1} \, t^{-1}\, \sup_{|h|< t}\, \int_{{\mathbb{R}}^d} |{\mathcal X}_E (x+h) - {\mathcal X}_E (x)|\, dx \le I + 2 \, |E| < \infty \end{aligned}$$we conclude \({\mathcal X}_E \in Lip (1,1) \cap L_1({\mathbb {R}}^d)\) and therefore \({\mathcal X}_E \in BV \cap L_1 ({\mathbb {R}}^d)\), see Proposition 2. Finally, formula (5) yields the claim.
□
The second main result in this subsection we get as an immediate consequence.
Theorem 2
Let\(E \subset {\mathbb {R}}^d\)and 0 < |E| < ∞. Then the following assertions are equivalent:
-
(i)
per E < ∞;
-
(ii)
sup|h|<1 |h|−1 (|E(h)| + |F(h)|) < ∞;
-
(iii)
\({\mathcal X}_E \in BV ({\mathbb {R}}^d)\);
-
(iv)
\({\mathcal X}_E \in Lip (1,1) ({\mathbb {R}}^d)\);
-
(v)
\({\mathcal X}_E \in B^{1/p_0}_{p_0,\infty } ({\mathbb {R}}^d)\)for some p 0, 1 ≤ p 0 < ∞.
-
(vi)
\({\mathcal X}_E \in B^{1/p}_{p,\infty } ({\mathbb {R}}^d)\)for all p, 1 ≤ p < ∞.
Proof
Part (i) implies (iii) by using (5). Proposition 2 yields the implication (iii) → (iv). From Lemma 3 we derive (iv) → (v) and (v) → (vi). Lemma 1 shows (vi) → (ii) and at the same time (ii) → (v) (p 0 = 1). Finally, Lemma 3 helps to close the circle since (v) → (i). □
3.3 Examples
Characteristic functions of balls and of rectangles (cuboids) we have already considered. Now we turn to more complicated domains. As usual, a domain is an open connected set in \({\mathbb {R}}^d\). First we apply a well-known fact in the theory of Besov spaces. The classes \(B^s_{p,q} \cap L_\infty ({\mathbb {R}}^d),\ s>0,\ 1\le p,q\le \infty \), are algebras under pointwise multiplication, i.e., there exists a positive constant c such that
holds for all \(f,g \in B^s_{p,q} \cap L_\infty ({\mathbb {R}}^d)\). We refer to Peetre [50] and [52, 4.6]. In addition we shall use that Besov spaces are invariant under rotations, translations and reflections. The combination of these two facts leads to a large number of further examples sharing the same smoothness properties as the characteristic function of a cube. For example, multiplying the characteristic function of a cube with an rotated, shifted and properly enlarged version of it we get that the characteristic function of a triangle has maximal regularity as well. Hence, any domain which allows a finite triangulation, has an associated characteristic function with maximal regularity. All these examples are covered by the classes of characteristic functions which we will consider below. The most important but probably not the most interesting examples are given by characteristic functions of elementary Lipschitz domains. Concerning these domains we shall make use of the following definition, picked up from Burenkov [12, 4.3]. In this definition we shall apply the notation \(x= (x',x_d),\ x'=(x_1, \ldots \, , x_{d-1}) \in \mathbb {R}^{d-1},\ x_d \in \mathbb {R}\).
Definition 2
Let d ≥ 2. An open bounded set E is called elementary Lipschitz domain if there exist a function φ and numbers 0 < D 1 ≤ D 2 < ∞, a 1, …a d, b 1, … , b d−1, L such that
-
(i)
diam (E) ≤ D 2;
-
(ii)
\( E = \{ x \in {\mathbb {R}}^d: ~ a_d < x_d < \varphi (x'), \: x' \in W\}\);
-
(iii)
\(W:= \{{x'} \in \mathbb {R}^{d-1}: \: a_i < x_i < b_i, \: i=1, \ldots \, , d-1\}\);
-
(iv)
a d + D 1 ≤ φ(x′), x′∈ W;
-
(v)
|φ(x′) − φ(y′)|≤ L |x′− y′| , x′, y′∈ W.
For elementary Lipschitz domains it is easy to prove that the associated characteristic function has maximal regularity.
Lemma 4
Let E be an elementary Lipschitz domain. Then\({\mathcal X}_E \in BV \cap B^{1/p}_{p,\infty }({\mathbb {R}}^d)\)for all p ∈ [1, ∞).
Proof
We will apply Theorem 2(ii).
- Step 1. :
-
For positive δ we define
$$\displaystyle \begin{aligned} \partial E^\delta := \{x\in {\mathbb{R}}^d: ~ {\mathrm{dist} \, } (x,\partial E) \le \delta \}\, .\end{aligned} $$(7)Usually ∂E δ is called the δ-neighbourhood of ∂E. Observe, in our particular case we have
$$\displaystyle \begin{aligned} \partial E = \partial W^* \cup \{(x', x_d):~ x' \in \partial W\, , ~ a_d \le x_d \le \varphi (x')\} \cup \{(x', \varphi (x')):~~ x'\in W\} \,, \end{aligned}$$where ∂W ∗ := {(x′, a d) : x′∈ W}. In what follows we concentrate on the last part since the remaining part of the boundary is either regular or can be treated similarly as the last part. Suppose 0 < δ < D 1∕L, where L denotes the Lipschitz constant of φ. Let
$$\displaystyle \begin{aligned} G:= \{(x', \varphi (x')):~~ x'\in W\}. \end{aligned}$$We claim that
$$\displaystyle \begin{aligned} \partial G^\delta \subset \Omega :=\Big\{(x',x_d):~ x' \in W\, , ~~\varphi (x')-(L+1)\delta < x_d < \varphi (x')+ (L+1)\delta \Big\}\, . \end{aligned}$$Let x ∈ G δ and suppose dist (x, G) = ρ ≤ δ. Hence, there is a point y ∈ G such that |x − y| = ρ. Clearly, y = (y′, φ(y′)). This yields
$$\displaystyle \begin{aligned} |x_d-\varphi (x')| \le |x_d -\varphi (y')| + |\varphi (y')-\varphi (x')|\le |x_d -\varphi (y')| + L|x' - y'| \, . \end{aligned} $$(8)Since |x d − φ(y′)|≤dist (x, G) = ρ and |x′− y′|≤ ρ, we find
$$\displaystyle \begin{aligned} |x_d-\varphi (x')|\le (L+1)\delta \end{aligned}$$and therefore x ∈ Ω.
- Step 2. :
-
There is an obvious relation between the δ-neighbourhood of ∂E and E(h) ∪ F(h). We have
$$\displaystyle \begin{aligned} E(h) \cup F(h) \subset \partial E^\delta \, , \quad |h| = \delta\, . \end{aligned} $$(9)Applying the result of Step 1 we find
$$\displaystyle \begin{aligned} |E(h)| + |F(h)| \le |\partial E^\delta| \le |\Omega|= 2 \, (L+1)\, \delta \, |W| \, , \quad \delta = |h|\, . \end{aligned}$$By Theorem 2 the claim follows.
□
As already mentioned above, Besov spaces are invariant under rotations, translations and reflections. This has an immediate consequence.
Corollary 1
Let E be a domain which can be written as the union of the closures of a finite number of pairwise disjoint domains E 1, … , E Nsuch that any of the E j, j = 1, … , N, is the image of an elementary Lipschitz domain under a finite number of rotations, translations and reflections. Then\({\mathcal X}_E \in BV \cap B^{1/p}_{p,\infty }({\mathbb {R}}^d)\)for all p ∈ [1, ∞).
Proof
Lemma 4 yields
for all p ∈ [1, ∞) and all j. Since |∂E j| = 0, j = 1, … , N, see Lemma 5 below, we have
Therefore, Corollary 1 is a consequence of Lemma 4. □
Figure 2 shows a domain with a polygonal boundary of finite length, covered by Corollary 1. Now we turn to examples in \(\mathbb {R}^3\). In Fig. 3, we have a
polyhedral cone and in Fig. 4 we see an Icosahedron. Both are elementary Lipschitz domains. But Lipschitz regularity of the boundary is not necessary for maximal regularity of the associated characteristic function. Here are a few examples. First we take the domain \(A \subset \mathbb {R}^2\) with boundary ∂A given by the Astroid. The determining functional equation of this curve is given by
Afterwards we consider the rotation of this curve around the y-axis resulting in the domain \(A_{\mathrm {rot}} \subset \mathbb {R}^3\).
Figure 5 shows a vertical cut through A rot, which gives us the domain A itself. Obviously the boundary ∂A has Hölder regularity α = 2∕3, see (10), and is therefore not Lipschitz (in four isolated points). Concerning the δ-neigbourhood it is easy to show that there exists a positive constant c such that
Hence, Theorem 2 yields \({\mathcal X}_A \in BV \cap B^{1/p}_{p,\infty }(\mathbb {R}^2)\) for all p ∈ [1, ∞). Figure 6 shows the set A rot itself. Obviously the boundary ∂A rot is not Lipschitz in north and south pole and on the equator. However, we can argue as in case of A itself, i.e., there exists a positive constant C such that
Hence, Theorem 2 yields \({\mathcal X}_{A_{\mathrm {rot}}} \in BV \cap B^{1/p}_{p,\infty }(\mathbb {R}^3)\) for all p ∈ [1, ∞).
The next example is even simpler, see Fig. 7. Let ε ∈ (0, 1). We define
The domain E ε has a boundary with Hölder regularity α = ε. So the Hölder regularity can be arbitrarily small. However, the same argument as above can be applied. For any ε there exists a positive constant c ε such that
Hence, Theorem 2 yields that the characteristic function of the domain E ε belongs to \( BV \cap B^{1/p}_{p,\infty }({\mathbb {R}}^d)\) for all p ∈ [1, ∞).
Now we turn to d = 3 again. There is a famous example of a polyhedral domain in \(\mathbb {R}^3\) which is not a Lipschitz domain, see Fig. 8. A convenient reference is given by Dobrowolski [20], see page 103.
The red dot indicates one of the critical points of the boundary when one tries to describe the neigbourhood as an elementary Lipschitz domain.
But in our situation it is simpler. We may apply Corollary 1. By the obvious splitting of the domain into the two subdomains, each of them given by one cuboid, it is immediate that the associated characteristic function has maximal regularity, see Lemma 2. This is the reason why we avoided the notion of a Lipschitz domain in Corollary 1. The class of domains used in this corollary covers the class of the Lipschitz domains, but is more general.
4 Less Regular Characteristic Functions
Now we turn to characteristic functions of sets with a more wild boundary. First we will investigate some necessary conditions.
4.1 Necessary Conditions
Let us start with some basics.
Lemma 5
Let E be a bounded domain. If\({\mathcal X}_E \in B^s_{p,q} ({\mathbb {R}}^d)\)for some s > 0, 1 ≤ p < ∞ and 1 ≤ q ≤∞, then |∂E| = 0 follows.
Proof
We employ the Withney-type decomposition of E into dyadic cubes, cf. Stein [58, VI.1] for details. By dyadic cubes we mean cubes of the type
\(j \in \mathbb {Z},\ k \in {{\mathbb {Z}}^d}\). Hence
where Q = Q j,k for some nonnegative integer j and \(k \in {{{\mathbb {Z}}^d}}\), \(\mathcal {F}\) denotes a subset of the set of all dyadic cubes and the cubes Q are pairwise disjoint. To each point x ∈ ∂E we can associate a sequence of points (x j)j ⊂ E approaching x. Each of the points x j belongs to one of the dyadic cubes \(Q \in \mathcal {F}\) and these cubes have the property
Consequently, for any ε > 0 and each x ∈ ∂E there exist x j ∈ E and a cube \(Q(x^j) \in \mathcal {F}, \: x \in Q(x^j)\) such that diam Q(x j) < ε. Since Besov spaces are monotonically ordered with respect to s and q, see (1), we may concentrate on the classes \(B^s_{p,p}({\mathbb {R}}^d)\) for some small positive s < 1. It follows
where C does not depend on ε. This proves the claim. □
Now we will continue with a more serious result due to Jaffard and Meyer [35]. To establish further necessary conditions we need to have additional information on the set E, in particular we need to know how thick the sets E and F ∖ ∂E are in a neighbourhood of the boundary. We define
Let A be a subset of \({\mathbb {R}}^d\). By dimP(A) we denote the packing dimension, cf. the Appendix.
Theorem 3 ([35, Thm. 2.2])
Let E be a nontrivial subset of\({\mathbb {R}}^d\) . Suppose\({\mathcal X}_E\)belongs to\(B^s_{p,p}({\mathbb {R}}^d)\)for some s > 0 and 1 ≤ p < ∞. Then dimP(∂E +) ≤ d − sp.
Remark 3
-
(i)
Jaffard and Meyer [35] worked with a slightly modified definition for the set ∂E +. They replaced |A ε| , |B ε|≥ με 2d by the more restrictive conditions |A ε|≥ με d and |B ε|≥ με d. But this change has no relevance for the proof. Since we shall not apply Theorem 3 below we skip the proof.
-
(ii)
It seems that the method of proof does not apply to the Besov spaces with p ≠ q (but it extends to Lizorkin–Triebel spaces).
Of course, of interest are those domains E satisfying ∂E = ∂E +. We discuss some examples.
-
(a)
John domains. We say that a bounded domain E is a John domain provided there is a constant C ≥ 1 and a distinguished point x 0 ∈ E, so that each point x ∈ E can be joint to x 0 (inside E) by a rectifiable curve γ : [0, ℓ] → E, γ(0) = x, γ(ℓ) = x 0, parameterized by arc-length (ℓ may depend on x), and such that the distance to the boundary satisfies
$$\displaystyle \begin{aligned} {\mathrm{dist} \, }(\gamma(t),\partial E) > C^{-1} \, t \, . \end{aligned}$$We refer to Martio, Sarvas [43] or Hajlasz, Koskela [32]. Relatives of John domains are investigated by Besov, we refer to Definition 6 below and [5], [7]. A direct consequence of the definition of John domains is the observation that for all x ∈ ∂E there exists a μ > 0 such that for all ε ∈ (0, 1) there exists a ball A ε satisfying A ε ⊂ B(x, ε) ∩ E and |A ε|≥ με n.
Now, select a cube Q such that E ⊂ Q and dist (∂E, ∂Q) > 1. For a given set A we denote by
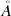 the set of all inner points of A. Define G := F ∩ Q. If E and
the set of all inner points of A. Define G := F ∩ Q. If E and 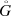 are John domains then we conclude that ∂E = ∂E
+.
are John domains then we conclude that ∂E = ∂E
+. -
(b)
(ε, δ) domains. Let 0 < ε < ∞ and 0 < δ ≤∞. Then a domain E is called an (ε, δ) domain whenever x, y ∈ E and |x − y| < δ, there is a rectifiable arc γ ⊂ E joining x to y and satisfying
$$\displaystyle \begin{aligned} \ell (\gamma) \le \frac{1}{\varepsilon} \, |x-y| \end{aligned}$$(ℓ(γ) denotes the length of the arc γ) and
$$\displaystyle \begin{aligned} {\mathrm{dist} \, } (z,\partial E) \ge \varepsilon \frac{|x-z|\, |y-z|}{|x-y|}\qquad \mbox{for all}\quad z \in \gamma\, .\end{aligned} $$It is known that for an (ε, δ) domain it holds |∂E| = 0. One of the key properties of (ε, δ) domains is the following. Denote by W 1 the collection of all dyadic cubes which form the Whitney decomposition of E. By W 2 we denote the collection of all dyadic cubes which form the Whitney decomposition of
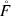 . Then, for each cube Q ∈ W
2 with sidelength ℓ(Q) ≤ εδ∕(16d) there exists a cube Q
∗∈ W
1 such that $$\displaystyle \begin{aligned} 1 \le \frac{\ell (Q^*)}{\ell (Q)}\le 4\qquad \mbox{and}\qquad {\mathrm{dist} \, } (Q,Q^*) \le C \, \ell (Q)\end{aligned} $$
. Then, for each cube Q ∈ W
2 with sidelength ℓ(Q) ≤ εδ∕(16d) there exists a cube Q
∗∈ W
1 such that $$\displaystyle \begin{aligned} 1 \le \frac{\ell (Q^*)}{\ell (Q)}\le 4\qquad \mbox{and}\qquad {\mathrm{dist} \, } (Q,Q^*) \le C \, \ell (Q)\end{aligned} $$where C = C(d) but independent of Q and E. For all these properties we refer to Jones [36]. Hence, for E being an (ε, δ) domain we have ∂E = ∂E +.
-
(c)
Regular domains. A domain E is called regular if it satisfies the measure density condition: there exists a constant c > 0 such that for all x ∈ E and all r ∈ (0, 1]
$$\displaystyle \begin{aligned} |B(x,r) \cap E| \ge c\, r^d\, .\end{aligned} $$If E and
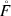 are regular then ∂E = ∂E
+ follows.
are regular then ∂E = ∂E
+ follows. -
(d)
Extension and embedding domains. We say that a bounded domain \(\Omega \subset {\mathbb {R}}^d\) is a \(B^s_{p,p}\)-extension domain if every function \(u \in B^s_{p,p}(\Omega )\) can be extended to a function \(\tilde {u} \in B^s_{p,p}({\mathbb {R}}^d)\), the mapping \(u \mapsto \tilde {u}\) is continuous and there exists a constant C = C(d, p, s, Ω) such that
$$\displaystyle \begin{aligned} \| \, \tilde{u}\, |B^{s}_{p,p} ({\mathbb{R}}^d)\| \le C\, \| \, {u}\, |B^{s}_{p,p} (\Omega)\|\, . \end{aligned}$$Here we use the following definition for \(B^{s}_{p,p} (\Omega ),\ 0< s < 1,\ 1\le p \le \infty \). A function u ∈ L p( Ω) belongs to \(B^{s}_{p,p} (\Omega )\) if
$$\displaystyle \begin{aligned} \begin{array}{rcl}{} \|\, f \, |B^s_{p,p} (\Omega)\|{}^* := \|\, f\, |L_p (\Omega)\| + \Bigg( \int_{\Omega}\, \int_{\Omega} \frac{|f(x)-f(y)|{}^p}{|x-y|{}^{sp + d}} dx \, dy \Bigg)^{1/p} <\infty\, . \qquad \end{array} \end{aligned} $$(12)Often these spaces are denoted by \(W^s_p (\Omega )\) and called Sobolev spaces of fractional order s on Ω. In a remarkable paper Zhou [68] proved the following. Let d ≥ 2 and Ω a domain in \({\mathbb {R}}^d\). Then the following assertions are equivalent:
-
Ω is a regular domain;
-
Ω is a \(B^s_{p,p}\)-extension domain for all s ∈ (0, 1) and all p ∈ [1, ∞);
-
Ω is a \(B^s_{p,p}\)-extension domain for some s ∈ (0, 1) and some p ∈ [1, ∞).
In addition Zhou was able to prove that a similar characterization takes place when the existence of a continuous extension operator is replaced by the validity and continuity of the standard Sobolev embeddings into Lebsgue spaces/Hölder spaces. We refer to [68] for more details.
-
4.2 Sufficient Conditions: Approximation by Piecewise Constant Functions
Now we turn to sufficient conditions. There are several ways to attack this problem. All methods are related to specific characterizations of Besov spaces. The first one is given by the characterization in terms of best approximation by piecewise constant functions.
Let us turn to Lemma 1 again. There we have already a sharp result. However, to make it more easy to deal with, we may use a further easy observation already employed in the proof of Lemma 4. Recall, the δ-neighbourhood ∂E δ of ∂E has been defined in (7). We have
see (9). As a consequence, if |h|−s |∂E |h|| stays bounded in a neighborhood of 0 the function \({\mathcal X}_E\) belongs to \(B^{s/p}_{p,\infty } ({\mathbb {R}}^d)\). For later reference we fix this. Concerning the definition of upper Minkowski content and upper Minkowski dimension (box counting dimension) we refer to the Appendix below.
Lemma 6
Let\(E \subset {\mathbb {R}}^d\)such that 0 < |E| < ∞. Let 1 ≤ p < ∞, 0 < s ≤ 1 and 0 < a ≤ 1.
-
(i)
If
$$\displaystyle \begin{aligned} \sup_{0 < \delta< a} \, \delta^{-s} \, |\partial E^{\delta}|< \infty\, ,\end{aligned} $$then\({\mathcal X}_E \in B^{s/p}_{p,\infty } ({\mathbb {R}}^d)\).
-
(ii)
If the d − s-dimensional upper Minkowski content of ∂E, denoted by\({\mathcal M}^{*(d-s)}(\partial E)\) , is finite, then\({\mathcal X}_E \in B^{s/p}_{p,\infty } ({\mathbb {R}}^d)\).
-
(iii)
If the upper Minkowski dimension\(\overline {\dim }_M \partial E = t\) , then\({\mathcal X}_E \in B^{s'}_{p,\infty } ({\mathbb {R}}^d)\)for all\(s'< \frac {d-t}{p}\).
Proof
Part (i) follows directly from Lemma 1. In view of the definition of the Minkowski content part (ii) is just a reformulation of (i). Finally (iii) is a consequence of (21). □
Remark 4
We recall a result from Falconer [22, Prop. 9.6]. Let \(\mathcal {S}\) be an m-tuple of contractions on a closed subset D of \({\mathbb {R}}^d\) such that
where r i ∈ (0, 1) for all i = 1, … , m. Then the invariant set K satisfies dimH K ≤ s and dimM K ≤ s, where s is the unique number for which
Let E be a bounded domain with boundary ∂E = K. Hence, Lemma 6 yields \({\mathcal X}_E \in B^{s'}_{p,\infty } ({\mathbb {R}}^d)\) for all \(s'< \frac {d-s}{p}\) and all p ∈ [1, ∞).
But we can do a little bit better. For \(f\in L_p ({\mathbb {R}}^d)\) we define
The number E j(f)p expresses the minimal error in approximating f with first order splines (piecewise constant functions) with respect to the dyadic cubes \(Q_{j,k},\ k \in {{\mathbb {Z}}^d}\). By assumption any approximant has the form
Here the α j,k are appropriate real numbers and \({\mathcal X}_{j,k}\) denotes the characteristic function of the dyadic cube Q j,k. There is a well-known characterization of Besov spaces in terms of these numbers E j(f)p. Let 1 ≤ p < ∞, 1 ≤ q ≤∞ and 0 < s < 1∕p. Then \(f \in B^s_{p,q} ({\mathbb {R}}^d)\) if and only if \(f \in L_p ({\mathbb {R}}^d)\) and
cf., e.g., Oswald [49]. Let E be a bounded domain in \({\mathbb {R}}^d\). Choosing the approximant g in (13) such that α j,k = 1 as long as Q j,k ⊂ E and α j,k = 0 otherwise, then it follows
For a subset E of \({\mathbb {R}}^d\) and δ > 0 we put
i.e., we concentrate on that part of the neigbourhood of the boundary which is part of E.
Theorem 4
Let E be a bounded domain in\({\mathbb {R}}^d\) . Let 1 ≤ p < ∞, 1 ≤ q ≤∞ and 0 < s < 1∕p. Suppose
Then \({\mathcal X}_E \in B^{s}_{p,q}({\mathbb {R}}^d)\) holds.
Proof
The condition |E| < ∞ implies \({\mathcal X}_E \in L_p\). Let q < ∞. As a consequence of (15) and obvious monotonicity arguments we have
Since
the claim follows from (14). In case q = ∞ the needed modifications are obvious. □
Remark 5
As mentioned above, in case q = ∞ our sufficient condition is close to the property that \({\mathcal M}^{*(d-sp)} (\partial E) < \infty \). The usefulness of the (upper) Minkowski content in connection with the regularity of characteristic functions has been pointed out at several places, e.g. Strichartz [59] (but traced there to Madych), Jaffard and Meyer [35, Prop.2.1], Runst, S. [52, 2.3.1] and Sickel [57].
There is a further improvement possible. In our context it is quite easy to find the best approximation of \({\mathcal X}_E\). For \(j \in \mathbb {N}_0\) and \(k \in {{\mathbb {Z}}^d}\) we define
It follows
If we change the definition of the α j,k for one cube Q j,k, then it is easy to see that the error increases. This explains the last identity. Now we obtain an analog of Lemma 1.
Lemma 7
Let E be a bounded nontrivial domain in\({\mathbb {R}}^d\) . Let 1 ≤ p < ∞, 1 ≤ q ≤∞ and 0 < s < 1∕p. Then\({\mathcal X}_E\)belongs to\(B^s_{p,q} ({\mathbb {R}}^d)\)if and only if
(standard modification for q = ∞).
Both, Lemmas 1 and 7 seem to have the disadvantage that they are not of great help with respect to the understanding of concrete examples.
4.3 Examples: I
First we continue our study of elementary domains.
Definition 3
Let d ≥ 2. We define an elementary domain with Hölder continuous boundary of order α ∈ (0, 1] by replacing (v) in Definition 2 by
Lemma 8
Let d ≥ 2. Let α ∈ (0, 1). Let E be an elementary domain with Hölder continuous boundary of order α. Then\({\mathcal X}_E \in B^{\alpha /p}_{p,\infty }({\mathbb {R}}^d)\)for all p ∈ [1, ∞).
Proof
The proof is almost the same as in case of Lemma 4. We indicate the needed modifications only. By applying the same notation as there we have to change the estimate (8). This yields in case ρ ≤ δ < 1
Hence ∂G δ ⊂ Ω, where
The remaining part of the boundary is regular, i.e., for the sets E(h) and F(h) we conclude
with a constant C > 0 independent on δ. Now the claim follows from Lemma 1. □
4.4 On the Dimension of Graphs of Functions and Consequences
There is a certain number of contributions in the literature where the problem of the Hausdorff or Minkowski dimension of a graph of a function is studied, we refer, e.g., to Carvalho and Caetano [16], Deliu and Jawerth [19], Falconer [22, Cor. 11.2], Hunt [33], Kamont and Wolnik [38], Kaplan et al. [39] and Triebel [63, Thm. 16.2].
In view of Lemma 6 any bound of the Minkowski dimension of the graph results in an estimate for the smoothness of the characteristic function of the associated domain. The most prominent example is the family of Weierstrass functions. Here we will have a short look onto the simplified version
For more general Weierstrass functions we refer to Kaplan et al. [39] and Hunt [33]. Since f λ represents a lacunary Fourier series, the regularity in periodic Besov spaces \( B^s_{\infty ,\infty } (\mathbb {T})\) is well understood. For the case λ = 2 one may consult [53, Chapt. 3], for the general case λ ≠ 2 one has to apply in addition some arguments from Triebel [60, 2.2.1], replacing the dyadic resolution of unity by more general resolutions of unity (depending on λ). It follows \(f_\lambda \in B^\beta _{\infty ,\infty } (\mathbb {T})\) and this is just the periodic subspace of \(C^\beta (\mathbb {R})= B^\beta _{\infty ,\infty }(\mathbb {R})\), see also [53, Chapt. 3], since 0 < β < 1. Define \(a_\lambda := \min _{t\in \mathbb {R}} f_\lambda (t)\) and
The Fig. 9 shows the graph of the function f 2 on [0, 2π], i.e., below of the graph we see Ω2.
Then
follows. We refer also to Falconer [22, Ex. 11.3].
Let us mention that Triebel [63, proof of Thm. 16.2], [65] has constructed another example of a Hölder continuous function of order α ∈ (0, 1) such that the characteristic function \({\mathcal X}_\Omega \) of the associated domain Ω satisfies
and
We make a short summary. Hölder continuity of the boundary of order α ∈ (0, 1] is a sufficient condition for regularity of order α∕p but by no means necessary. Triebel’s example shows that for the class C α itself the result is unimprovable. However, also our examples from Figs. 5, 6, and 7 show, that Hölder regularity and Lipschitz regularity are not well adapted to our problem of determining the smoothness of \({\mathcal X}_E\).
There is one more general class of domains we would like to investigate.
4.5 Domains with a Boundary Being an h-Set
We follow Bricchi [8, 9], but see also [63,64,65] and [54].
Definition 4
Let h : (0, 1] → (0, ∞) be a positive non-decreasing function such that there exists a positive constant c with
Let Γ be a non-empty compact set in \({\mathbb {R}}^d\). Then Γ is called an h-set if there exists a finite Radon measure μ in \({\mathbb {R}}^d\) satisfying
Observe that for any such function h there exists at least one such set Γ (for an explicit construction we refer to [8]). We recall a few more properties of h-sets. Again our references are [8, 9].
Lemma 9
Let Γ be an h-set. Then the following assertions are true.
-
(i)
All h-measures related to Γ are equivalent to the generalized Hausdorff measure \(\mathcal {H}^h\) restricted to Γ (see the Appendix below for a definition).
-
(ii)
The related Radon measure μ is a doubling measure, i.e., there exists a constant c > 0 such that
$$\displaystyle \begin{aligned} \mu (B(y,2r))\le c\, \mu (B(y,r))\qquad \mathit{\mbox{for all}}\quad y\in \Gamma\quad \mathit{\mbox{and all}}\quad 0 < r < 1\, .\end{aligned} $$ -
(iii)
For any t ∈ (0, 1] and any y ∈ Γ one has
$$\displaystyle \begin{aligned} \dim_{H} \Gamma \cap B(y,t) = \liminf_{r \to 0} \, \frac{\log h(r)}{\log r}\qquad \mathit{\mbox{and}}\qquad \dim_{P} \Gamma \cap B(y,t) = \limsup_{r \to 0} \, \frac{\log h(r)}{\log r} \end{aligned}$$
There is a list of examples in [9]. All these functions are defined on a small intervall (0, a), 0 < a < 1, and then suitably prolonged on the whole (0, 1].
-
h 1(r) = r δ 0 ≤ δ ≤ d;
-
\(h_2 (r) = r^\delta \, |\log r|{ }^b \) , \(0 < \delta < d,\ b \in \mathbb {R}\);
-
\(h_3 (r) = |\log r|{ }^b\) , b < 0;
-
\(h_4 (r) = r^d\, |\log r|{ }^b \) , b > 0;
-
\(h_5 (r) = r^\delta \, \exp ( b\, |\log r|{ }^\kappa )\) , \(0 < \delta < d,\ b \in \mathbb {R}\), 0 < κ < 1;
-
h 6(r) = r δS(r), where S is a slowly varying function.
Here a slowly varying function \(S:~(0,1] \to \mathbb {R}\) is a positive measurable function such that limr→0S(λr)∕S(r) = 1 for all λ ∈ (0, 1].
The most important special case is the first one. The compact sets Γ related to h 1 are called δ-sets (in most of the cases the letter d is used instead of δ, but d has already a different meaning). δ-sets are discussed at various places, sometimes they are also called regular or Ahlfors regular sets, see, e.g., Bechtel and Egert [2], Frazer [27], Jonsson and Wallin [37], Schneider and Vybíral [54] or Triebel [63, 65, 66].
The main step to understand domains E with ∂E being an h-set is made with the following lemma, see Bricchi [8].
Lemma 10
Let E be a bounded domain in\({\mathbb {R}}^d\)with boundary ∂E being an h-set. Then there exists a constant c > 0 such that
Proof
The proof is based on the fact that the finite Radon measure controls the thickness of ∂E r for r sufficiently small.
The starting point is the Whitney decomposition of E, see [58]. More exactly, let \(\mathcal {F}\) denote the collection of all dyadic cubes representing the Whitney decomposition of E , i.e.,
all the cubes Q j,ℓ(j) are pairwise disjoint and
We shall need an estimate of the numbers M j. Let
By \({\mathcal F}_j\) we denote the collection of all \(\ell \in {{\mathbb {Z}}^d}\) such that the dyadic cube \(Q_{j,\ell } \in {\mathcal F}\) is contained in E j. Then, if \(k \in {\mathcal F}_j\), the cube \(3 \sqrt {d}\, Q_{j,k}\) intersects Γ. Furthermore, there exists a point y k ∈ Γ such that the cube P k, side-length \(\sqrt {d}2^{-j}\), sides parallel to the axes and with center in y k, is contained in \(3 \sqrt {d}\, Q_{j,k}\). Let us denote the centre of Q j,k by x k. Then, by definition, x k is the centre of \(3 \sqrt {d}\, Q_{j,k}\) as well and |x k − x ℓ|≥ 2−j, k ≠ ℓ. Hence, every y ∈ Γ is contained in at most C = C(d) (independent of j) cubes \(3 \sqrt {d}\, Q_{j,k}\) with \(k \in {\mathcal F}_j\). Let μ be the associated finite Radon measure on Γ. By assumption on μ it follows
Here \(|{\mathcal F}_j| \) denotes the cardinality of \({\mathcal F}_j\). Hence
This inequality is the key step in the proof. The inequality (20) can be turned immediately into an estimate of the Lebesgue measure of the sets \(\partial E_+^r\). For a moment we put \(r:= \sqrt {d} 2^{-j-1},\ j\in \mathbb {N}\). Then
and therefore
where c is a positive constant independent of j. In the last step we used the monotonicity of h and the doubling property, see Lemma 9. □
In view of Theorem 4 the Lemma 10 implies the following.
Corollary 2
Let E be a bounded domain in \({\mathbb {R}}^d\) with boundary ∂E being an h-set.
-
(i)
Let 1 ≤ p < ∞ and 0 < s < 1∕p. Then the characteristic function\({\mathcal X}_E\)belongs to\(B^s_{p,\infty } ({\mathbb {R}}^d)\)if
$$\displaystyle \begin{aligned} \sup_{0 < r < 1}\, \frac{r^{d-sp}}{h(r)}<\infty\, . \end{aligned}$$ -
(ii)
Let 1 ≤ p, q < ∞ and 0 < s < 1∕p. Then the characteristic function\({\mathcal X}_E\)belongs to\(B^s_{p,q} ({\mathbb {R}}^d)\)if
$$\displaystyle \begin{aligned} \int_0^1 r^{(\frac dp -s -\frac 1q)q} \, h(r)^{-\frac qp}\, dr < \infty\, . \end{aligned}$$
As an immediate consequence we get the following.
Corollary 3
Let E be a bounded domain in\({\mathbb {R}}^d\)with boundary ∂E being an δ-set for some d − 1 < δ < d. Let 1 ≤ p < ∞. Then we have\({\mathcal X}_E \in B^{\frac {d-\delta }{p}}_{p,\infty } ({\mathbb {R}}^d)\)for all p ∈ [1, ∞).
Remark 6
-
(i)
Corollary 3 originates from Triebel [65, Thm. 3, Rem. 9] and Schneider, Vybíral [54]. The proofs in [65] and [54] are partly different. They are based on the characterization of Besov spaces by atoms.
-
(ii)
Also Triebel [65] and Schneider, Vybíral [54] have dealt with h-sets. However, for more general sets than δ-sets the sufficient condition
$$\displaystyle \begin{aligned} I_{s,p,q}:= \sup_{j\in \mathbb{N}_0} \Bigg(\sum_{k=0}^\infty 2^{ksq} \Big( \frac{h(2^{-j})}{h(2^{-j-k})} \, 2^{-kd}\Big)^{q/p}\bigg)^{1/q} <\infty \end{aligned}$$for \({\mathcal X}_E\), to belong to \(B^s_{p,q} ({\mathbb {R}}^d)\), given in the quoted papers, is in general stronger than that one from Corollary 2. It is not difficult to see that
$$\displaystyle \begin{aligned} \Big(\int_0^1 r^{(\frac dp -s -\frac 1q)q} \, h(r)^{-\frac qp}\, dr\Big)^{1/q} \le c_h\, I_{s,p,q} \end{aligned}$$always holds with some constant c h, depending on h. As an example for the non-equivalence of these quantities may serve \(h_2(r):= r^\delta \, |\log r|{ }^b,~0 < r < 1\). Let E denote a bounded domain with boundary being an h-set with respect to h 2. In case d − 1 < δ < d and b > 0 Corollary 2 yields \({\mathcal X}_E \in B^{\frac {d-\delta }{p}}_{p,q}({\mathbb {R}}^d)\) if b > p∕q. But \(I_{s,p,q} = \infty ,\ s = \frac {d-\delta }{p}\) for all q < ∞. However, let us mention that Triebel, Schneider and Vybíral showed that I s,p,q < ∞ implies \({\mathcal X}_E \in B^{\frac {d-\delta }{p}}_{p,q,selfs}({\mathbb {R}}^d)\), a smaller space than the corresponding Besov space. The classes \(B^{s}_{p,q,selfs}({\mathbb {R}}^d)\) are of some relevance in connection with pointwise multipliers of Besov spaces.
Particular examples of δ-sets are self-similar sets, see the Appendix.
Corollary 4
Let K be a bounded domain in\({\mathbb {R}}^d\)with boundary ∂K being a self-similar set satisfying the assumptions in Proposition5with s = δ, see the Appendix. Let 1 ≤ p < ∞. Then we have\({\mathcal X}_K \in B^{\frac {d-\delta }{p}}_{p,\infty } ({\mathbb {R}}^d)\)for all p ∈ [1, ∞).
Now we turn to the next concrete example.
4.6 The Twindragon
The twindragon is a space filling curve with a fractal boundary, see Fig. 10. More information, also about relatives (heighway dragon, Levy dragon) of this curve, may be found in Wikipedia, see https://en.wikipedia.org/wiki/Dragon-curve.
Let \(T \subset \mathbb {R}^2\) denote the set which is filled by this curve. It is known that ∂T is a self-similar set, which satisfies the assumptions of Proposition 5 in the Appendix below. It holds that dimH ∂T =dimM ∂T = δ, where δ is the unique solution of
given by
see Mandelbrot [42, p. 78]. Most important for us is the existence of a finite Radon measure on ∂T, which turns ∂T into a δ-set. Here we may take the Hausdorff measure \(\mathcal {H}^\delta \) restricted to ∂T. Hence, as a consequence of Corollary 3 we conclude
Let us mention that we do not know whether this number δ is optimal. In particular, we do not know whether Theorem 3 is applicable. If that would be the case, we could conclude that this number δ is best possible.
There are further interesting properties of \({\mathcal X}_T\), in particular of interest in the theory of wavelets. It can be used as a scaling function, we refer to Gröchenig, Madych [29] and Wojtaszczyk [67, 5.3]. It is not difficult to see that the associated wavelets have the same regularity as \({\mathcal X}_T\) has.
4.7 Some Sufficient Conditions: Quasiballs
An essential step forward has been done by Faraco and Rogers [25]. These authors worked with quasiballs.
A homeomorphism \(f:~{\mathbb {R}}^d\to {\mathbb {R}}^d\) is called K-quasiconformal if there is a constant K < ∞ such that for all \(x\in {\mathbb {R}}^d\)
A K-quasiball is the image of the unit ball under a K-quasiconformal mapping. For d = 2 also the name quasicircle is commonly used.
Theorem 5 ([25, Thm. 1.3])
Let 1 ≤ p < ∞, 0 < s < 1 and let\(E \subset {\mathbb {R}}^d\)be a K-quasiball. Then
where\(\delta ^*:= \inf \{\delta :~ E \subset \partial E^\delta \}\).
The proof is not short enough to be included into this survey. The more interesting part in Theorem 5 is the estimate of \(\|\, {\mathcal X}_E\, |B^s_{p,p} ({\mathbb {R}}^d)\|\) from below, because this part is missing in Theorem 4. In general there is some gap between the sufficient conditions in Theorem 4 and the necessary condition in Theorem 3. However, in case of certain domains with a fractal boundary they almost touch. For later use we formulate a simple consequence, already known to [25].
Corollary 5
Let 1 ≤ p < ∞, 0 < s < 1 and let\(E \subset {\mathbb {R}}^d\)be a K-quasiball. If we assume\({\mathcal X}_E \in B^s_{p,p} ({\mathbb {R}}^d)\) , then
follows.
Proof
The mapping δ↦|∂E δ| is monotone in δ. Hence
where k 0 has to be chosen in dependence of δ ∗. This yields the claim. □
Remark 7
A reformulation of Corollary 5 (just by definition) reads as follows. Under the given restrictions we obtain \({\mathcal M}^{*d-s} (\partial E)=0\).
The most beautiful example we discuss next.
4.8 The Snowflake Domain
The standard construction of the von Koch curve is as follows, see Fig. 11. We start with an equilateral triangle. Then we subdivide each side into three equal parts and remove the middle one. This middle part is replaced by an equilateral triangle again.
Sidelength is now 1∕3 of the original one. This procedure is iterated. After a few further iterations one obtains Fig. 12 which might be seen as a reasonable approximation of the von Koch curve. The domain Ω with the von Koch curve as its boundary is called the snowflake domain.
We collect a few facts about its properties.
-
(i)
Ω is a (ε, ∞) domain, see [36];
-
(ii)
Ω is a John domain, see [10];
-
(iii)
Ω is a quasiball, see [47, 1.2];
-
(iv)
Ω is a selfsimilar set, which fulfils the conditions in Proposition 5 in the
-
(v)
∂ Ω+ = ∂ Ω, see (i);
-
(vi)
\(\dim _H \partial \Omega = \dim _M \partial \Omega = {\log 4}/{\log 3}\), see, e.g., Falconer [22, Ex.9.5]);
-
(vii)
∂ Ω is a δ-set with \(\delta = {\log 4}/{\log 3}\), see Proposition 5 in the Appendix.
-
(viii)
\(0 < \mathcal {H}^{\log 4/ \log 3} (\partial \Omega ) \le {\mathcal M}_*^{\log 4/ \log 3} (\partial \Omega ) \le {\mathcal M}^{*\log 4/ \log 3} (\partial \Omega ) \),
As a combination of Theorem 5, Corollary 5 and property (viii) we obtain now the following.
Corollary 6 ([25, Cor. 1.4])
Let 1 ≤ p < ∞. The characteristic function\({\mathcal X}_\Omega \)of the snowflake domain belongs to\(B^s_{p,p}(\mathbb {R}^2)\)if and only if\(s < \frac 1p \, \Big (2 -\frac {\log 4}{\log 3}\Big )\).
This result has a counterpart for q = ∞.
Theorem 6
Let 1 ≤ p < ∞. The characteristic function\({\mathcal X}_\Omega \)of the snowflake domain Ω belongs to\(B^{s}_{p,\infty } (\mathbb {R}^2)\)if and only if\(s \le \big (2-\log 4/\log 3\big )/p\).
Proof
Sufficiency follows from Proposition 5, see the Appendix, and Corollary 3. If we assume that \({\mathcal X}_\Omega \in B^{t}_{p,\infty } (\mathbb {R}^2)\) for some \(t > \frac {2-s}{p}\) then by the elementary embeddings of the Besov spaces in (1) it follows \({\mathcal X}_\Omega \in B^{(2-s)/p}_{p,p} (\mathbb {R}^2)\). But this contradicts Corollary 6. □
The author conjectures that, for fixed p ∈ [1, ∞), the smallest Besov space containing \({\mathcal X}_\Omega \) is given by \( B^{s}_{p,\infty } (\mathbb {R}^2)\) with \( s:= \frac {2-\log 4/\log 3}{p}\).
4.9 The Rotating Snowflake
The Fig. 13 below is obtained by first shifting an approximation of the snowflake domain Ω in the (x, y)-plane to the right such that it will be located to the right of x = 1. Afterwards this shifted domain is rotated around the y-axes. In the limit the outcome in \(\mathbb {R}^3\) is denoted by Ωrot. What we have in mind is a spiked car tyre.
Lemma 11
Let 1 ≤ p < ∞. The characteristic function\({\mathcal X}_{\Omega _{\mathrm {rot}}}\)of the rotating snowflake domain belongs to\(B^s_{p,\infty }(\mathbb {R}^3)\)if\(s \le \frac 1p \, \Big (2 -\frac {\log 4}{\log 3}\Big )\).
Proof
Lemma 10 yields
Hence, because of
we get the same inequality for \(|\Omega _{\mathrm {rot}}^r|\). Lemma 6(i) can be used to complete the argument. □
4.10 Some Sufficient Conditions: The Aikawa Dimension
This time we shall work with a sufficient condition related to the Aikawa dimension of the boundary of a domain. In [1] Aikawa introduced the following definition of a fractal dimension (for simplicity we concentrate on the situation in \({\mathbb {R}}^d\) and the Lebesgue measure).
Definition 5
Let A be a subset of \({\mathbb {R}}^d\) and let G(A) be the set of those t > 0 for which there exists a constant c t such that
Then the Aikawa dimension of A is defined to be \(\dim _{\mathcal {A}\mathcal {I}} A = \inf G(A)\).
Our point of departure is Lemma 1. Let p = 1, 0 < s < 1 and |h| < a < 1. First, observe that
and similarly for F(h) = F a(h). Furthermore
This is almost all what is needed to prove the following supplement to Lemma 1.
Theorem 7
Let 1 ≤ p < ∞ and 0 < s < 1. Let E be a bounded domain.
-
(i)
If
$$\displaystyle \begin{aligned} \sup_{x\in \partial E} \int_{B(x,1)} \, {\mathrm{dist} \, } (y,\partial E)^{-s}\, dy < \infty \, , \end{aligned}$$then\({\mathcal X}_E\)belongs to\(B^{s/p}_{p,\infty } ({\mathbb {R}}^d)\).
-
(ii)
If\(\dim _{\mathcal {A}\mathcal {I}} \partial E = t\) , then\({\mathcal X}_E\)belongs to\(B^{s'}_{p,\infty } ({\mathbb {R}}^d)\)for all\(s'< \frac {d-t}{p}\).
Proof
The sets E a and F a can be covered by finitely many balls B(x k, 1), x k ∈ ∂E, since E is bounded. Hence
is finite if
for all k. This proves (i). On the other hand part (ii) is an obvious consequence of (i). □
Remark 8
-
(i)
For deciding about membership of \({\mathcal X}_E\) in a Besov space we do not need the full power of the Aikawa dimension since we only work with balls of radius 1. This will be different when we switch to the question whether \({\mathcal X}_E\) is a pointwise multiplier for a Besov space. For more details we refer to Frazier and Jawerth [28], Bechtel and Egert [2] and [56, 57].
-
(ii)
It is interesting to notice that on \({\mathbb {R}}^d\) the probably more popular Assouad dimension dimA and the Aikawa dimension coincide. We refer to Lehrbäck and Tuominen [41] and Fraser [27] for more details.
-
(iii)
On \({\mathbb {R}}^d\) we have the following chain of inequalities
$$\displaystyle \begin{aligned} \dim_H \partial E \le \underline{\dim}_M \partial E \le \overline{\dim}_M \partial E \le \dim_A \partial E = \dim_{\mathcal{A}\mathcal{I}} \partial E\, . \end{aligned}$$Let E be a bounded domain with the boundary being a δ-set for some d − 1 < δ < d. Then dimA ∂E =dimM ∂E =dimH ∂E = δ. We refer to Frazer [27], see also [2].
Mainly Besov [5], but see also [7, 2.8], has worked with domains satisfying a flexible horn condition.
Definition 6
The domain Ω satisfies a flexible horn condition if there exist δ 0 > 0 and T > 0 such that for any x ∈ Ω there exist an arc
with the following properties.
-
(i)
For all i ∈{1, … , d} the functions γ i(t, x) are absolutely continuous with respect to t and |γ i(u, x)|≤ 1 for almost all u ∈ [0, T].
-
(ii)
γ(0, x) = 0 and x +⋃0≤t≤T(γ(t, x) + tδ 0[−1, 1]d) ⊂ Ω .
This is quite close to the definition of a John domain.
Lemma 12
Let 1 ≤ p < ∞.
-
(i)
Let\(\Omega \subset {\mathbb {R}}^d\)be a bounded domain which satisfies a flexible horn condition with parameters δ 0and T. Then there exists a positive number s ≤ 1 such that\({\mathcal X}_\Omega \)belongs to\( B^{s/p}_{p,\infty }({\mathbb {R}}^d)\).
-
(ii)
Let\(\Omega \subset {\mathbb {R}}^d\)be a John domain. Then there exists a positive number s ≤ 1 such that\({\mathcal X}_\Omega \in B^{s/p}_{p,\infty } ({\mathbb {R}}^d)\).
Proof
In both cases it is known that the Aikawa dimension of the boundary ∂ Ω is positive. In case (i) this is proved in Besov [5]. For John domains we refer to Hajlasz and Koskela [32]. □
4.11 The Distance Zeta Function of a Set
Let A be a bounded subset of \({\mathbb {R}}^d\). In the recent book [40] Lapidus, Radunović and Žubrinić studied the function
where A δ denotes the δ-neigbourhood of A. The chosen fixed δ > 0 is of no importance in their context. They call ζ A the distance zeta function of A. For us of interest are Lemmas 2.1.3 and 2.1.6 in [40]. They read as follows.
Proposition 3
Let A be an arbitrary subset of \({\mathbb {R}}^d\) and let δ be an arbitrary positive number.
-
(i)
If\(\sigma > d- \overline {\dim }_M A\) , then\(\int _{A^\delta } \, {\mathrm {dist} \, } (x,A)^{-\sigma }\, dx = + \infty \).
-
(ii)
If\(-\infty < \sigma < d- \overline {\dim }_M A\) , then\(\int _{A^\delta } \, {\mathrm {dist} \, } (x,A)^{-\sigma }\, dx < \infty \).
Consequently, if \(0 < s < d- \overline {\dim }_M \partial E \), then in view of Theorem 7(i) we obtain \({\mathcal X}_\Omega \in B^{s/p}_{p,\infty } ({\mathbb {R}}^d)\) for all p ∈ [1, ∞), which is just a different proof of Lemma 6(iii). Part (i) of Proposition 3 illustrates that on this way we can not improve our conclusion.
4.12 Some Further Examples
When looking at the two examples of the twindragon and the snowflake domain one could conjecture that the following formula holds:
In what follows we shall investigate a two-parameter family E α,γ of domains in the plane, see Fig. 14, with a quite different behaviour. These domains are related to the shark-domain on the cover of the monograph of Maz’ya [45] (and on the cover of its Russian edition). In a certain sense the domains under consideration are also limit cases of the classical Nikodym domains, cf. [45, 1.1.4].
Let γ ≥ α > 1. Then we define
Further we put

and
What we have in mind are two combs where the teeth come closer and closer together. Just by looking at the neigbourhood of the line {(β, y) : 1∕2 < y < 1} it is clear that E α,γ is neither an (ε, δ)-domain nor an John domain nor a domain satisfying a flexible horn condition in the sense of Besov. They do not belong to the regular domains as well.
Proposition 4
Let 1 ≤ p < ∞ and γ ≥ α > 1. Then the sets E α,γhave the following properties.
-
(i)
dimM(∂E α,γ) = 1 + 1∕α.
-
(ii)
dimH(∂E α,γ) =dimP(∂E α,γ) = 1.
-
(iii)
\(\chi _{E_{\alpha , \gamma }} \in B^s_{p,\infty } (\mathbb {R}^2) \: \)if and only if s p ≤ (1 − 1∕γ).
-
(iv)
Let 1 ≤ q < ∞. Then\(\chi _{E_{\alpha , \gamma }} \in B^s_{p,q} (\mathbb {R}^2) \: \)if and only if s p < (1 − 1∕γ).
The rather technical proofs can be found in [56]. Let γ > α. Obviously we have
Clearly, in case of these domains neither the Hausdorff dimension nor the Minkowski dimension characterize the smoothness s of the characteristic function. Furthermore, from our knowledge on this family E α,γ we can derive the following conclusions.
-
Let s ∈ (0, 1), p ∈ [1, ∞) and q ∈ [1, ∞] be fixed. Then there exists a set \(E\subset \mathbb {R}^2,\ 0 < |E|< \infty \), such that \({\mathcal X}_E \not \in B^s_{p,q}(\mathbb {R}^2)\).
-
Let s ∈ (0, 1) be fixed. Then for any s′∈ (s, 1) there exists a set \(E\subset \mathbb {R}^2,\ 0 < |E|< \infty \), such that the Minkowski dimension of ∂E equals 2 − s and
$$\displaystyle \begin{aligned} {\mathcal X}_E \in B^{s'/p}_{p,q}(\mathbb{R}^2) \qquad \mbox{for all}\quad p \in [1,\infty)\quad \mbox{and}\quad q \in [1,\infty]. \end{aligned}$$Hence, our sufficient conditions given in Lemma 6 and Theorem 4 are not sharp in general.
-
Let p ∈ [1, ∞) and q ∈ [1, ∞] be fixed. Then for any s ∈ (0, 1] there exists a set \(E\subset \mathbb {R}^2,\ 0 < |E|< \infty \), such that the Hausdorff and the packing dimension of ∂E equals 1 and
$$\displaystyle \begin{aligned} {\mathcal X}_E \not\in B^{s/p}_{p,q}(\mathbb{R}^2) \, . \end{aligned}$$
Summarizing one observes that in general the Hausdorff dimension and the packing dimension of ∂E are too small to characterize the smoothness of \({\mathcal X}_E\). On the other hand the Minkowski dimension of ∂E is oversized for a characterization of the smoothness of \({\mathcal X}_E\) in many cases.
4.13 The Mandelbrot Set
We finish this subsection with one well-known extreme example, the famous Mandelbrot set, see Fig. 15. This set, denoted by D, satisfies dimH D = 2 and dimH ∂D = 2, see Shishikura [55]. Obviously this implies dimM ∂D = 2. Hence, in view of Lemma 6, we do not expect any positive smoothness of \({\mathcal X}_D\).
References with respect to the Mandelbrot set are, e.g., [42] and [22, 14.2].
Concerning the smoothness of \({\mathcal X}_D\) there is at least a chance that it belongs to some Besov spaces \(B^{0,b}_{p,\infty } (\mathbb {R}^2)\) of logarithmic smoothness b > 0, characterized by the norm
Recently, those function spaces have showed up in various publications, see, e.g., [13,14,15, 17, 18].
4.14 A Final Comment
The three methods, to obtain sufficient conditions for the regularity of \({\mathcal X}_E\), discussed in this section, seem to be more adapted to situations where
exists and does not depend on y ∈ ∂E, compare with Lemma 9(iii). If this quantity depends on y as in case of the domains E α,γ, then we need more sophisticated criteria.
References
Aikawa, H.: Quasiadditivity of Riesz capacity. Math. Scand. 69, 15–30 (1991)
Bechtel, S., Egert, M.: Interpolation theory for Sobolev functions with partially vanishing trace on irregular open sets. J. Fourier Anal. Appl. 25, 2733–2781 (2019)
Besov, O.V.: On a family of function spaces. Embedding theorems and extensions. Dokl. Acad. Nauk SSSR 126, 1163–1165 (1959)
Besov, O.V.: On a family of function spaces in connection with embeddings and extensions. Trudy Mat. Inst. Steklov 60, 42–81 (1961)
Besov, O.V.: Extension by zero of functions of several variables. Math. Notes 64(3), 359–365 (1998)
Besov, O.V., Il’in, V.P., Nikol’skij, S.M.: Integral representations of functions and imbedding theorems, vol. I+II. V.H. Winston, Washington D.C. (1978/1979)
Besov, O.V., Il’in, V.P., Nikol’skij, S.M.: Integralnye predstavleniya funktsii i teoremy vlozheniya (in Russian), 2nd edn. Fizmatlit “Nauka”, Moscow (1996)
Bricchi, M.: Existence and properties of h-sets. Georgian Math. J. 9(1), 13–32 (2002)
Bricchi, M.: Tailored Besov spaces and h-sets. Math. Nachr. 263–264, 36–52 (2004)
Bukley, S., Koskela, P.: Sobolev-Poincaré implies John. Math. Res. Lett. 2, 577–593 (1995)
Burago, Yu.D., Zalgaller, V.A.: Geometric Inequalities. Springer, Berlin (1988)
Burenkov, V.I.: Sobolev spaces on domains. Teubner-Texte zur Mathematik, vol. 137. Teubner, Stuttgart and Leipzig (1998)
Caetano, A.M., Gogatishvili, A., Opic, B.: Sharp embeddings of Besov spaces involving only logarithmic smoothness. J. Approx. Theory 152(2), 188–214 (2008)
Caetano, A.M., Gogatishvili, A., Opic, B.: Embeddings and the growth envelope of Besov spaces involving only slowly varying smoothness. J. Approx. Theory 163(10), 1373–1399 (2011)
Caetano, A.M., Gogatishvili, A., Opic, B.: Erratum to “Embeddings and the growth envelope of Besov spaces involving only slowly varying smoothness”. J. Approx. Theory 164(4), 516–516 (2012)
Carvalho, A., Caetano, A.: On the Hausdorff dimension of continuous functions belonging to Hölder and Besov spaces on fractal d-sets. J. Fourier Anal. Appl. 18, 386–409 (2012)
Cobos, F., Domínguez, O.: On the relationship between two kinds of Besov spaces with smoothness near zero and some other applications of limiting interpolation. J. Fourier Anal. Appl. 22(5), 1174–1191 (2016)
Cobos, F., Domínguez, O., Triebel, H.: Characterizations of logarithmic Besov spaces in terms of differences, Fourier-analytical decompositions, wavelets and semi-groups. J. Funct. Anal. 270(12), 4386–4425 (2016)
Deliu, A., Jawert, B.: Geometrical dimension versus smoothness. Constr. Appr. 8, 211–222 (1992)
Dobrowolski, M.: Angewandte Funktionalanalysis. Springer, Berlin (2010)
Falconer, K.: Geometry of Fractal Sets. Cambridge University Press, Cambridge (1985)
Falconer, K.: Fractal Geometry. Mathematical Foundations and Applications. Wiley, Chichester (1990)
Falconer, K.: Sub-self-similar sets. Trans. AMS 347(8), 3121–3129 (1995)
Falconer, K.: Techniques in Fractal Geometry. Wiley, Chichester (1997)
Faraco, D., Rogers, K.: The Sobolev norm of characteristic functions with applications to the Calderón inverse problem. Quaterly J. Math. 64, 133–147 (2012)
Fleming, W.H., Rishel, R.: An integral formula for the total gradient variation. Arch. Math. 11, 218–222 (1960)
Fraser, J.M.: Assouad type dimensions and homogeneity of fractals. Trans. AMS 366(12), 6687–6733 (2014)
Frazier, M., Jawerth, B.: A discrete transform and decomposition of distribution spaces. J. Funct. Anal. 93, 34–170 (1990)
Gröchenig, K., Madych, W.R.: Multiresolution analysis, Haar bases and self-similar tilings of \(\mathbb {R}\). IEEE Trans. Inf. Theory 38, 556–568 (1992)
Gulisashvili, A.B.: On multipliers in Besov spaces. Sapiski nautch. Sem. LOMI 135, 36–50 (1984)
Gulisashvili, A.B.: Multipliers in Besov spaces and traces of functions on subsets of the Euclidean n-space DAN SSSR 281, 777–781 (1985)
Hajlasz, P., Koskela, P.: Isoperimetric inequalities and imbedding theorems in irregular domains. J. Lond. Math. Soc. 58(2), 425–450 (1998)
Hunt, B.R.: The Hausdorff dimension of graphs of Weierstrass functions. Proc. AMS 126(3), 791–800 (1998)
Hutchinson, J.E.: Fractals and self-similarity. Ind. Univ. Math. J. 30, 713–747 (1981)
Jaffard, S., Meyer, Y.: Wavelet methods for pointwise regularity and local oscillations of functions. Memoirs AMS, vol. 587. American Mathematical Society, Providence (1996)
Jones, P.: Quasiconformal mappings and extendiability of functions in Sobolev spaces. Acta Math. 147, 71–88 (1981)
Jonsson, A., Wallin, H.: Function Spaces on Subsets of \(\mathbb {R}\). Mathematical Reports, vol. 2. Harwood Academic Publishers, London (1984)
Kamont, A., Wolnik, B.: Wavelet expansions and fractal dimensions. Constr. Approx. 15, 97–108 (1999)
Kaplan, J.L., Mallet-Paret, J., Yorke, J.A.: The Lyapunov dimension of a nowhere differentiable attracting torus. Ergod. Theory Dyn. Syst. 4, 261–281 (1984)
Lapidus, L.M., Radunović, G., Žubrinić, D.: Fractal Zeta Functions and Fractal Drums. Springer, Berlin (2017)
Lehrbäck, J., Tuominen, H.: A note on the dimensions of Assouad and Aikawa. J. Math. Soc. Jpn. 65(2), 343–356 (2013)
Mandelbrot, B.B.: Die Fraktale Geometrie der Natur. Birkhäuser, Basel (1987)
Martio, O., Sarvas, J.: Injectivity theorems in plane and space. Ann. Acad. Sci. Fenn. Ser. AI Math. 4, 383–401 (1978/1979)
Mattila, P.: Geometry of sets and measures in Euclidean spaces. Cambridge University Press, Cambridge (1995)
Maz’ya, V.G.: Sobolev Spaces, Springer, Berlin (1985)
Maz’ya, V.G., Shaposhnikova, T.O.: Theory of Sobolev Multipliers: With Applications to Differential and Integral Operators. Springer, Berlin (2009)
Meyer, D.: Snowballs are quasiballs. Trans. AMS 362(3), 1247–1300 (2010)
Nikol’skij, S.M.: Approximation of Functions of Several Variables and Imbedding Theorems. Springer, Berlin (1975)
Oswald, P.: Multilevel Finite Element Approximation: Theory and Applications. Teubner, Stuttgart (1995)
Peetre, J.: Interpolation of Lipschitz operators and metric spaces. Mathematica (Cluj) 12, 1–20 (1970)
Peetre, J.: New Thoughts on Besov Spaces. Duke University Press, Durham (1976)
Runst, T., Sickel, W.: Sobolev Spaces of Fractional Order, Nemytskij Operators, and Nonlinear Partial Differential Equations. Walter de Gruyter, Berlin (1996)
Schmeisser, H.J., Triebel, H.: Topics in Fourier Analysis and Function Spaces. Geest & Portig/Wiley Leipzig/Chichester (1987)
Schneider, C., Vybíral, J.: Non-smooth atomic decompositions, traces on Lipschitz domains, and pointwise multipliers in function spaces. J. Funct. Anal. 264, 1197–1237 (2013)
Shishikura, M.: The Hausdorff dimension of the boundary of the Mandelbrot set and Julia sets. Ann. Math. 147(2), 225–267 (1998)
Sickel, W.: On pointwise multipliers for \(F^s_{p,q} ( \operatorname {\mathrm {Re}}^n)\). The case σ p,q < s < n∕p. Ann. Mat. Pura Appl. 176(4), 209–250 (1999)
Sickel, W.: Pointwise multipliers of Lizorkin-Triebel spaces. The Maz’ya anniversary collection, Vol. 2 (Rostock, 1998). Operator Theory: Advances and Applications, vol. 110, pp. 295–321. Birkhäuser, Basel (1999)
Stein, E.M.: Singular Integrals and Differentiability Properties of Functions. Princeton University Press, Princeton (1970)
Strichartz, R.S.: Wavelets and self-affine tilings. Constr. Approx. 9, 327–346 (1993)
Triebel, H.: Fourier analysis and function spaces. Teubner-Texte zur Mathematik, vol. 7, Teubner, Leipzig (1977)
Triebel, H.: Theory of Function Spaces. Birkhäuser, Basel (1983)
Triebel, H.: Theory of Function Spaces II. Birkhäuser, Basel (1992)
Triebel, H.: Fractals and Spectra. Birkhäuser, Basel (1998)
Triebel, H.: The Structure of Functions. Birkhäuser, Basel (2001)
Triebel, H.: Non-smooth atoms and pointwise multipliers in function spaces. Ann. Mat. Pura Appl. 182, 457–486 (2003)
Triebel, H.: Theory of Function Spaces III. Birkhäuser, Basel (2006)
Wojtaszczyk, P.: A mathematical Introduction to Wavelets. London Mathematical Society Student Texts, vol. 37. Cambridge University Press, Cambridge (1997)
Zhou, Y.: Fractional Sobolev extension and imbedding. Trans. Am. Math. Soc. 367(2), 959–979 (2015)
Acknowledgements
I would like to thank my friends and colleagues Cornelia Schneider, Joachim Jüngel and Marc Hovemann for helping me with the various figures in this manuscript. In addition the author has to thank Jan Vybíral for several hints related to the proof of Lemma 10 and Martina Zähle for several helpful remarks to the literature.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendix
Appendix
We recall some basic notions from fractal geometry. Our main sources are the monographs of Falconer [21, 22] and Mattila [44].
1.1 Fractal Dimensions
Here we recall Hausdorff, Minkowski and packing dimension as well as the Minkowski content.
1.2 Hausdorff Dimension
Let A be a subset of \({\mathbb {R}}^d\). A countable (or finite) collection of sets U i with diameter diam U i is called a δ-cover of A if
for all i. Let s be a nonnegative real number. For any δ > 0 we put
We shall write
This limit exists in [0, ∞] for any subset of \({\mathbb {R}}^d\). \(\mathcal {H}^s (A)\) is called the s-dimensional Hausdorff measure of A. If \(s=d \in \mathbb {N}\) we have
where |A| and |B(0, 1)| refer to the d-dimensional Lebesgue measure of these sets.
Definition 7
The Hausdorff dimension of a set \(A \subset {\mathbb {R}}^d\) is given by
We also need a generalization due to Bricchi [8, 9]. Let h : (0, 1] → (0, ∞) be a positive non-decreasing function such that there exists a positive constant c with
Then, for a set \(A \subset {\mathbb {R}}^d\), we put h(A) := h(diam A) if A ≠ ∅ and h(∅) := 0. The set function
is called the Hausdorff measure corresponding to h.
1.3 Minkowski Dimensions
Let A be a non-empty bounded subset of \({\mathbb {R}}^d\). For 0 < ε < ∞, let
N(A, ε) is sometimes called covering number.
Definition 8
The upper and lower Minkowski dimension of a set \(E \subset {\mathbb {R}}^d\) are defined by
and
In case \(\overline {\dim }_M A = \underline {\dim }_M A\) we call this number the Minkowski dimension of A.
It follows
see Mattila [44, pp. 78]. Let us mention that the Minkowski dimension is sometimes also called box counting dimension.
1.4 Minkowski Content
Recall, for a given set \(A\subset {\mathbb {R}}^d\) the family of δ-neighbourhoods A δ, δ > 0, are defined as
Definition 9
The s-dimensional upper Minkowski content of A is defined by
and the s-dimensional lower Minkowski content of A by
The Minkowski content and the Minkowski dimension are related as follows
A useful relation between Minkowski content and Hausdorff measure is given by
see, e.g., Mattila [44, pp. 79].
1.5 Packing Dimension
We define upper and lower packing dimension as follows
where A is an arbitrary subset of \({\mathbb {R}}^d\). If both numbers coincide, they are called packing dimension of A.
1.6 Self-Similar and Sub-self-similar Sets
A mapping \(S:{\mathbb {R}}^d \to {\mathbb {R}}^d\) is called a similarity with ratio r if
If 0 < r < 1 we say that S is contracting. Suppose \(\mathcal {S}:= (S_1, \ldots \, S_N),\ N \ge 2\), is a finite sequence of similarities with contraction ratios r 1, … , r N ∈ (0, 1). Then there exists a unique non-empty compact set K such that
This set K will be called self-similar. A non-empty compact set \(K\subset {\mathbb {R}}^d\) is called sub-self-similar for \(\mathcal {S}\) if
see [23]. Furthermore, \(\mathcal {S}\) satisfies the open set condition if there exists a bounded non-empty open set O such that
We shall need the following two results, see Hutchinson [34] and Falconer [22, Thm. 9.3].
Proposition 5 ([22, Thm. 9.3])
If\(\mathcal {S}\)satisfies the open set condition, then the invariant set K is self-similar and\(0 < \mathcal {H}^s (K)< \infty \) , whence s =dimH K, where s is the unique number for which
Moreover, there are positive and finite numbers a and b such that
In addition dimH K =dimM K.
There is a partial generalization to sub-self-similar sets which covers boundaries of self-similar sets as well, see [23].
Proposition 6 ([24, Cor. 3.4], [23, Thm. 3.5])
Let\(\mathcal {S}\)satisfy the open set condition and let the non-empty compact set K be sub-self-similar for\(\mathcal {S}\) . Define s as the unique solution of (23). Then\(0 < \mathcal {H}^s (K)\)and s =dimH K =dimM K.
Rights and permissions
Copyright information
© 2021 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this paper
Cite this paper
Sickel, W. (2021). On the Regularity of Characteristic Functions. In: Cicognani, M., Del Santo, D., Parmeggiani, A., Reissig, M. (eds) Anomalies in Partial Differential Equations. Springer INdAM Series, vol 43. Springer, Cham. https://doi.org/10.1007/978-3-030-61346-4_18
Download citation
DOI: https://doi.org/10.1007/978-3-030-61346-4_18
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-61345-7
Online ISBN: 978-3-030-61346-4
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)




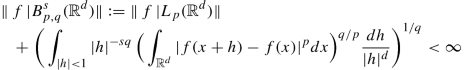
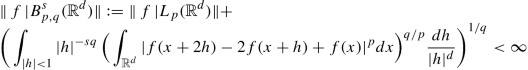

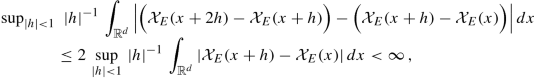
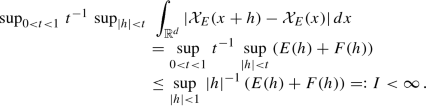







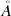 the set of all inner points of A. Define G := F ∩ Q. If E and
the set of all inner points of A. Define G := F ∩ Q. If E and 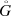 are John domains then we conclude that ∂E = ∂E
+.
are John domains then we conclude that ∂E = ∂E
+.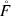 . Then, for each cube Q ∈ W
2 with sidelength ℓ(Q) ≤ εδ∕(16d) there exists a cube Q
∗∈ W
1 such that
. Then, for each cube Q ∈ W
2 with sidelength ℓ(Q) ≤ εδ∕(16d) there exists a cube Q
∗∈ W
1 such that 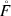 are regular then ∂E = ∂E
+ follows.
are regular then ∂E = ∂E
+ follows.





