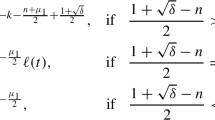Blow-Up Results for Semi-Linear Structurally Damped σ-Evolution Equations

Abstract

We would like to prove a blow-up result for Sobolev solutions to the Cauchy problem for semi-linear structurally damped σ-evolution equations, where σ ≥ 1 and δ ∈ [0, σ) are assumed to be any fractional numbers. To deal with the fractional Laplacian (− Δ)^σ and (− Δ)^δ as well-known non-local operators, a modified test function method is applied to prove a blow-up result in the subcritical case and in the critical case as well.

1 Introduction

The main goal of this paper is to discuss the critical exponent to the following Cauchy problem for semi-linear structurally damped σ-evolution models:

$$\displaystyle \begin{aligned} \begin{cases} u_{tt}+ (-\Delta)^\sigma u+ (-\Delta)^{\delta} u_t=|u|{}^p, \\ u(0,x)= u_0(x),\quad u_t(0,x)=u_1(x), \end{cases} \end{aligned} $$

(1)

with some σ ≥ 1, δ ∈ [0, σ) and a given real number p > 1. Here, critical exponent p _crit = p _crit(n) means that for some range of admissible p > p _crit there exists a global (in time) Sobolev solution for small initial data from a suitable function space. Moreover, one can find suitable small data such that there exists no global (in time) Sobolev solution if 1 < p ≤ p _crit. In other words, we have, in general, only local (in time) Sobolev solutions under this assumption for the exponent p.

For the local existence of Sobolev solutions to (1), we address the interested readers to Proposition 9.1 in the paper [2]. The proof of blow-up results in the present paper is based on a contradiction argument by using the test function method. The test function method is not influenced by higher regularity of the data. For this reason, we restrict ourselves to the critical exponent to (1) in the case, where the data are supposed to belong to the energy space. In this paper, we use the following notations.

• For given nonnegative f and g we write $f\lesssim g$ if there exists a constant C > 0 such that f ≤ Cg. We write f ≈ g if $g\lesssim f\lesssim g$.

• We denote $\widehat {v}=\widehat {v}(\xi ):= \mathfrak {F}_{x\rightarrow \xi }\big (v(x)\big )$ as the Fourier transform with respect to the spatial variables of a function v = v(x).

• As usual, H ^a with a ≥ 0 stands for Bessel potential spaces based on L ².

• We denote by [b] the integer part of $b \in \mathbb {R}$. We put $\big < x\big >:= \sqrt {1+|x|{ }^2}$.

• Moreover, we introduce the following two parameters:

  $$\displaystyle \begin{aligned}\mathtt{k}^-:= \min\{\sigma;2\delta\}\quad \text{ and }\quad \mathtt{k}^+:= \max\{\sigma;2\delta\} \quad \text{ if }\delta \in [0,\sigma). \end{aligned}$$

In order to state our main result, we recall the global (in time) existence result of small data energy solutions to (1) in the following theorem.

Theorem 1 (Global Existence)

Let m ∈ [1, 2) and n > m ₀ k ⁻with$\frac {1}{m_0}=\frac {1}{m}- \frac {1}{2}$ . We assume the conditions

$$\displaystyle \begin{aligned} &\frac{2}{m} \le p < \infty &\qquad \mathit{\text{ if }}&\, n \le 2\mathtt{k}^+, \\ &\frac{2}{m} \le p \le \frac{n}{n- 2\mathtt{k}^+} &\qquad \mathit{\text{ if }}&\, n \in \Big(2\mathtt{k}^+, \frac{4\mathtt{k}^+}{2-m}\Big]. \end{aligned} $$

Moreover, we suppose the following condition:

$$\displaystyle \begin{aligned} p> 1+\frac{m(\mathtt{k}^+ +\sigma)}{n- m\mathtt{k}^-}. {} \end{aligned} $$

(2)

Then, there exists a constant ε ₀ > 0 such that for any small data

$$\displaystyle \begin{aligned} (u_0,u_1) \in \big(L^m \cap H^{\mathtt{k}^+}\big) \times \big(L^m \cap L^2\big) \end{aligned}$$

satisfying the assumption $\|u_0\|{ }_{L^m \cap H^{\mathtt {k}^+}}+ \|u_1\|{ }_{L^m \cap L^2} \le \varepsilon _0,$ we have a uniquely determined global (in time) small data energy solution

$$\displaystyle \begin{aligned} u \in \mathcal{C}\left([0,\infty),H^{\mathtt{k}^+}\right)\cap \mathcal{C}^1\left([0,\infty),L^2\right) \end{aligned}$$

to (1). Moreover, the following estimates hold:

$$\displaystyle \begin{aligned} \|u(t,\cdot)\|{}_{L^2}& \lesssim (1+t)^{-\frac{n}{2(\mathtt{k}^+ -\delta)}(\frac{1}{m}-\frac{1}{2})+ \frac{\mathtt{k}^-}{2(\mathtt{k}^+ -\delta)}} \big(\|u_0\|{}_{L^m \cap H^{\mathtt{k}^+}}+ \|u_1\|{}_{L^m \cap L^2}\big), \\ \big\||D|{}^{\mathtt{k}^+} u(t,\cdot)\big\|{}_{L^2}& \lesssim (1+t)^{-\frac{n}{2(\mathtt{k}^+ -\delta)}(\frac{1}{m}-\frac{1}{2})- \frac{\mathtt{k}^+- \mathtt{k}^-}{2(\mathtt{k}^+ -\delta)}} \big(\|u_0\|{}_{L^m \cap H^{\mathtt{k}^+}}+ \|u_1\|{}_{L^m \cap L^2}\big), \\ \|u_t(t,\cdot)\|{}_{L^2}& \lesssim (1+t)^{-\frac{n}{2(\mathtt{k}^+ -\delta)}(\frac{1}{m}-\frac{1}{2})- \frac{\sigma- \mathtt{k}^-}{\mathtt{k}^+ -\delta}} \big(\|u_0\|{}_{L^m \cap H^{\mathtt{k}^+}}+ \|u_1\|{}_{L^m \cap L^2}\big). \end{aligned} $$

We are going to prove the following main result.

Theorem 2 (Blow-Up)

Let σ ≥ 1, δ ∈ [0, σ) and n > k ⁻ . We assume that we choose the initial data u ₀ = 0 and u ₁ ∈ L ¹satisfying the following relation:

$$\displaystyle \begin{aligned} \int_{\mathbb{R}^n} u_1(x)dx > \epsilon_0, \end{aligned} $$

(3)

where 𝜖 ₀ is a suitable nonnegative constant. Moreover, we suppose the condition

$$\displaystyle \begin{aligned} p \in \Big(1, 1+ \frac{2\sigma}{n- \mathtt{k}^-}\Big]. \end{aligned} $$

(4)

Then, there is no global (in time) Sobolev solution$u \in \mathcal {C}\big ([0,\infty ),L^2\big )$to (1).

Remark 1

We want to underline that the lifespan T _ε of Sobolev solutions to given data (0, εu ₁) for any small positive constant ε in the subcritical case of Theorem 2 can be estimated as follows:

$$\displaystyle \begin{aligned} T_\varepsilon \le C\varepsilon^{-\frac{(2\sigma- \mathtt{k}^-)(p-1)}{2\sigma- (n- \mathtt{k}^-)(p-1)}} \quad \text{ with } C>0. \end{aligned} $$

(5)

Nevertheless, catching the sharp lower bound of the lifespan T _ε to verify whether the obtained upper bound in (5) is optimal or not still remains open so far.

Remark 2

If we choose m = 1 in Theorem 1, then from Theorem 2 it is clear that the critical exponent p _crit = p _crit(n) is given by

$$\displaystyle \begin{aligned} p_{crit}(n)= 1+\frac{2\sigma}{n-2\delta} \quad \text{ if }\delta \in \Big[0,\frac{\sigma}{2}\Big] \text{ and }4\delta <n \leq 4\sigma. \end{aligned}$$

However, in the case $\delta \in (\frac {\sigma }{2},\sigma )$ there appears a gap between the exponents given by $1+\frac {2\delta +\sigma }{n-\sigma }$ from Theorem 1 and $1+\frac {2\sigma }{n-\sigma }$ from Theorem 2 for 2σ < n ≤ 8δ. Related to such a gap in the latter case, quite recently, the authors in [3] have succeeded to indicate the global (in time) existence of small data energy solutions to (1), with σ > 1, in low space dimensions for any $p>1+\frac {2\sigma }{n-\sigma }$ by using suitable $L^{r_1}- L^{r_2}$ decay estimates, with 1 ≤ r ₁ ≤ r ₂ ≤∞, for solutions to the corresponding linear equation, after application of the stationary phase method. For this reason, at least in low space dimensions, we can claim that the critical exponent p _crit = p _crit(n) in the case $\delta \in (\frac {\sigma }{2},\sigma )$ with σ > 1 is

$$\displaystyle \begin{aligned} p_{crit}(n)= 1+\frac{2\sigma}{n-\sigma}. \end{aligned}$$

2 Preliminaries

In this section, we collect some preliminary knowledge needed in our proofs.

Definition 1 ([8, 10])

Let s ∈ (0, 1). Let X be a suitable set of functions defined on $\mathbb {R}^n$. Then, the fractional Laplacian (− Δ)^s in $\mathbb {R}^n$ is a non-local operator given by

$$\displaystyle \begin{aligned} (-\Delta)^s: \,\,v \in X \to (-\Delta)^s v(x):= C_{n,s}\,\, p.v.\int_{\mathbb{R}^n}\frac{v(x)- v(y)}{|x-y|{}^{n+2s}}dy \end{aligned}$$

as long as the right-hand side exists, where p.v. stands for Cauchy’s principal value, $C_{n,s}:= \frac {4^s \Gamma (\frac {n}{2}+s)}{\pi ^{\frac {n}{2}}\Gamma (-s)}$ is a normalization constant and Γ denotes the Gamma function.

Lemma 1

Let q > 0. Then, the following estimate holds for any multi-index α satisfying |α|≥ 1:

$$\displaystyle \begin{aligned} \big|\partial_x^\alpha \big< x\big>^{-q}\big| \lesssim \big< x\big>^{-q-|\alpha|}. \end{aligned}$$

Proof

First, we recall the following formula of derivatives of composed functions for |α|≥ 1:

$$\displaystyle \begin{aligned} \partial_x^\alpha h\big(f(x)\big)= \sum_{k=1}^{|\alpha|}h^{(k)} \big(f(x)\big)\left(\sum_{\substack{\gamma_1+\cdots+\gamma_k \le \alpha\\ |\gamma_1|+\cdots+|\gamma_k|= |\alpha|,\, |\gamma_i|\ge 1}}\big(\partial_x^{\gamma_1} f(x)\big) \cdots \big(\partial_x^{\gamma_k} f(x)\big)\right), \end{aligned}$$

where h = h(z) and $h^{(k)}(z)=\frac {d^k h(z)}{dz^k}$. Applying this formula with $h(z)= z^{-\frac {q}{2}}$ and f(x) = 1 + |x|² we obtain

$$\displaystyle \begin{aligned} \big|\partial_x^\alpha \big< x\big>^{-q}\big|&\le \sum_{k=1}^{|\alpha|} (1+|x|{}^2)^{-\frac{q}{2}-k} \\ &\quad \times \left(\sum_{\substack{\gamma_1+\cdots+\gamma_k \le \alpha\\ |\gamma_1|+\cdots+|\gamma_k|= |\alpha|,\, |\gamma_i|\ge 1}}\big|\partial_x^{\gamma_1} (1+|x|{}^2)\big| \cdots \big|\partial_x^{\gamma_k} (1+|x|{}^2)\big|\right) \end{aligned} $$

$$\displaystyle \begin{aligned} &\le C_1\sum_{k=1}^{|\alpha|} (1+|x|{}^2)^{-\frac{q}{2}-k} \\ &\quad \times \begin{cases} 1 & \text{ if } 0 \le |x| \le 1, \\ \left(\displaystyle\sum_{\substack{\gamma_1+\cdots+\gamma_k \le \alpha\\ |\gamma_1|+\cdots+|\gamma_k|= |\alpha|,\, |\gamma_i|\ge 1}}|x|{}^{2-|\gamma_1|} \cdots |x|{}^{2-|\gamma_k|}\right) & \text{ if } |x| \ge 1, \end{cases} \\ &\le C_2\sum_{k=1}^{|\alpha|} (1+|x|{}^2)^{-\frac{q}{2}-k} \begin{cases} 1 &\quad \text{ if }\quad 0 \le |x| \le 1, \\ |x|{}^{2k-|\alpha|} &\quad \text{ if }\quad |x| \ge 1, \end{cases} \\ &\le \begin{cases} C_2|\alpha|\big<x\big>^{-q-2}&\quad \text{ if }\quad 0 \le |x| \le 1, \\ C_2|\alpha|\big< x\big>^{-q}|x|{}^{-|\alpha|}&\quad \text{ if }\quad |x| \ge 1, \end{cases} \end{aligned} $$

where C ₁ and C ₂ are some suitable constants. This completes the proof. □

Lemma 2

Let$m \in \mathbb {Z}$ , s ∈ (0, 1) and γ := m + s. If$v \in H^{2\gamma }(\mathbb {R}^n)$ , then it holds

$$\displaystyle \begin{aligned} (-\Delta)^{\gamma}v(x)= (-\Delta)^{m}\big((-\Delta)^{s}v(x)\big)= (-\Delta)^{s}\big((-\Delta)^{m}v(x)\big). \end{aligned}$$

One can find the proof of Lemma 2 in Remark 3.2 in [1].

Lemma 3

Let$m \in \mathbb {Z}$ , s ∈ (0, 1) and γ := m + s. Let q > 0. Then, the following estimates hold for all$x \in \mathbb {R}^n$:

$$\displaystyle \begin{aligned} \big|(-\Delta)^\gamma \big< x\big>^{-q}\big| \lesssim \begin{cases} \big< x\big>^{-q-2\gamma} &\quad \mathit{\text{ if }}\quad 0< q+2m< n, \\ \big< x\big>^{-n-2s}\log(e+|x|) &\quad \mathit{\text{ if }}\quad q+2m= n, \\ \big< x\big>^{-n-2s} &\quad \mathit{\text{ if }}\quad q+2m> n. \end{cases} {} \end{aligned} $$

(6)

Proof

We follow ideas from the proof of Lemma 1 in [7] devoting to the case m = 0 and $s=\frac {1}{2}$, that is, the case $\gamma = \frac {1}{2}$ is generalized to any fractional number γ > 0. To do this, for any s ∈ (0, 1) we shall divide the proof into two cases: m = 0 and m ≥ 1.

Let us consider the first case m = 0. Denoting by ψ = ψ(x) := <x>^−q we write (− Δ)^s<x>^−q = (− Δ)^s(ψ)(x). According to Definition 1 of fractional Laplacian as a singular integral operator, we have

$$\displaystyle \begin{aligned}(-\Delta)^s (\psi)(x):= C_{n,\delta}\,\, p.v.\int_{\mathbb{R}^n}\frac{\psi(x)- \psi(y)}{|x-y|{}^{n+ 2s}}dy. \end{aligned}$$

A standard change of variables leads to

$$\displaystyle \begin{aligned} (-\Delta)^s (\psi)(x)&= -\frac{C_{n,s}}{2}\,\, p.v.\int_{\mathbb{R}^n}\frac{\psi(x+y)+ \psi(x-y)- 2\psi(x)}{|y|{}^{n+ 2s}}dy \end{aligned} $$

$$\displaystyle \begin{aligned} &= -\frac{C_{n,s}}{2}\lim_{\varepsilon \to 0+}\int_{\varepsilon\le |y|\le 1}\frac{\psi(x+y)+ \psi(x-y)- 2\psi(x)}{|y|{}^{n+ 2s}}dy \\ &\quad - \frac{C_{n,s}}{2}\int_{|y|\ge 1}\frac{\psi(x+y)+ \psi(x-y)- 2\psi(x)}{|y|{}^{n+ 2s}}dy. \end{aligned} $$

To deal with the first integral, after using a second order Taylor expansion for ψ we arrive at

$$\displaystyle \begin{aligned} \frac{|\psi(x+y)+ \psi(x-y)- 2\psi(x)|}{|y|{}^{n+2s}} \lesssim \frac{\|\partial_x^2 \psi\|{}_{L^\infty}}{|y|{}^{n+ 2s- 2}}. \end{aligned}$$

Thanks to the above estimate and s ∈ (0, 1), we may remove the principal value of the integral at the origin to conclude

$$\displaystyle \begin{aligned} (-\Delta)^s (\psi)(x)= -\frac{C_{n,s}}{2} \int_{\mathbb{R}^n}\frac{\psi(x+y)+ \psi(x-y)- 2\psi(x)}{|y|{}^{n+ 2s}}dy. \end{aligned}$$

To prove the desired estimates, we shall divide our considerations into two cases. In the first subcase {x : |x|≤ 1}, we can proceed as follows:

$$\displaystyle \begin{aligned} \big|(-\Delta)^s (\psi)(x)\big|&\lesssim \int_{|y|\le 1}\frac{|\psi(x+y)+ \psi(x-y)- 2\psi(x)|}{|y|{}^{n+ 2s}}dy \\ &\quad + \int_{|y|\ge 1}\frac{|\psi(x+y)+ \psi(x-y)- 2\psi(x)|}{|y|{}^{n+ 2s}}dy \\ &\lesssim \|\partial_x^2 \psi\|{}_{L^\infty} \int_{|y|\le 1}\frac{1}{|y|{}^{n+ 2s- 2}}dy+ \|\psi\|{}_{L^\infty} \int_{|y|\ge 1}\frac{1}{|y|{}^{n+ 2s}}dy. \end{aligned} $$

Due to the boundedness of the above two integrals, it follows immediately

$$\displaystyle \begin{aligned} \big|(-\Delta)^s (\psi)(x)\big| \lesssim 1 \quad \text{ for } |x|\le 1. {} \end{aligned} $$

(7)

In order to deal with the second subcase {x : |x|≥ 1}, we can re-write

$$\displaystyle \begin{aligned} (-\Delta)^s (\psi)(x)&= -\frac{C_{n,s}}{2}\int_{|y|\ge 2|x|} \frac{\psi(x+y)+ \psi(x-y)- 2\psi(x)}{|y|{}^{n+ 2s}}dy \\ &\quad - \frac{C_{n,s}}{2}\int_{\frac{1}{2}|x|\le |y|\le 2|x|} \frac{\psi(x+y)+ \psi(x-y)- 2\psi(x)}{|y|{}^{n+ 2s}}dy \\ &\quad - \frac{C_{n,s}}{2}\int_{|y|\le \frac{1}{2}|x|} \frac{\psi(x+y)+ \psi(x-y)- 2\psi(x)}{|y|{}^{n+ 2s}}dy. {} \end{aligned} $$

(8)

For the first integral, we notice that the relations |x + y|≥|y|−|x|≥|x| and |x − y|≥|y|−|x|≥|x| hold for |y|≥ 2|x|. Since ψ is a decreasing function, we obtain the following estimate:

$$\displaystyle \begin{aligned} &\Big|\int_{|y|\ge 2|x|} \frac{\psi(x+y)+ \psi(x-y)- 2\psi(x)}{|y|{}^{n+ 2s}}dy\Big| \\ &\qquad \le 4|\psi(x)| \int_{|y|\ge 2|x|} \frac{1}{|y|{}^{n+ 2s}}dy \lesssim \big< x\big>^{-q} \int_{|y|\ge 2|x|} \frac{1}{|y|{}^{1+ 2s}}d|y| \\ &\qquad \lesssim \big< x\big>^{-q} |x|{}^{-2s}\lesssim \big< x\big>^{-q-2s} \qquad \big(\text{due to } |x| \approx \big< x\big> \text{ for } |x|\ge 1\big). {} \end{aligned} $$

(9)

It is clear that |y|≈|x| in the second integral domain. Moreover, it follows

$$\displaystyle \begin{aligned} \Big\{y: \frac{1}{2}|x|\le |y|\le 2|x|\Big\} &\subset \big\{y: |x+y|\le 3|x|\big\}, {} \end{aligned} $$

(10)

$$\displaystyle \begin{aligned} \Big\{y: \frac{1}{2}|x|\le |y|\le 2|x|\Big\} &\subset \big\{y: |x-y|\le 3|x|\big\}. {} \end{aligned} $$

(11)

For this reason, we arrive at

(12)

where we used the relation

$$\displaystyle \begin{aligned} \int_{|x+y|\le 3|x|} \psi(x+y)dy= \int_{|x-y|\le 3|x|} \psi(x-y)dy.\end{aligned}$$

By the change of variables r = |x + y|, we apply the inequality $1+r^2 \ge \frac {(1+r)^2}{2}$ to get

$$\displaystyle \begin{aligned} \int_{|x+y|\le 3|x|} \psi(x+y)dy&\lesssim \int_{r \le 3|x|} (1+r^2)^{-\frac{q}{2}}\,r^{n-1}dr \lesssim \int_{r \le 3|x|} (1+r)^{n-q-1}dr \\ &\lesssim \begin{cases} (1+3|x|)^{n-q} &\quad \text{ if }\quad 0< q< n, \\ \log(e+3|x|) &\quad \text{ if }\quad q= n, \\ 1 &\quad \text{ if }\quad q> n. \end{cases} {} \end{aligned} $$

(13)

By |x|≈<x> for |x|≥ 1, combining (12) and (13) leads to

$$\displaystyle \begin{aligned} &\Big|\int_{\frac{1}{2}|x|\le |y|\le 2|x|} \frac{\psi(x+y)+ \psi(x-y)- 2\psi(x)}{|y|{}^{n+ 2s}}dy\Big| \\ &\qquad \lesssim \begin{cases} \big< x\big>^{-q-2s} & \text{ if }\quad 0< q< n, \\ \big< x\big>^{-n-2s}\log(e+3|x|) & \text{ if }\quad q= n, \\ \big< x\big>^{-n-2s}& \text{ if }\quad q> n. \end{cases} {} \end{aligned} $$

(14)

For the third integral in (8), using again the second order Taylor expansion for ψ we obtain

$$\displaystyle \begin{aligned} &\Big|\int_{|y|\le \frac{1}{2}|x|} \frac{\psi(x+y)+ \psi(x-y)- 2\psi(x)}{|y|{}^{n+ 2s}}dy\Big| \\ &\qquad \le \int_{|y|\le \frac{1}{2}|x|} \frac{|\psi(x+y)+ \psi(x-y)- 2\psi(x)|}{|y|{}^{n+ 2s}}dy \\ &\qquad \lesssim \int_{|y|\le \frac{1}{2}|x|} \max_{\theta \in [0,1]}\big|\partial_x^2 \psi(x\pm \theta y)\big|\frac{1}{|y|{}^{n+ 2s- 2}}dy \end{aligned} $$

$$\displaystyle \begin{aligned} &\qquad \lesssim \int_{|y|\le \frac{1}{2}|x|} \max_{\theta \in [0,1]}\big< x\pm \theta y\big>^{-q-2}\frac{1}{|y|{}^{n+ 2s- 2}}dy \\ &\qquad \lesssim \big< x\big>^{-q-2}\int_{|y|\le \frac{1}{2}|x|} |y|{}^{1-2s}d|y| \lesssim \big< x\big>^{-q-2s}. {} \end{aligned} $$

(15)

Here we used the relation $|x\pm \theta y| \ge |x|- \theta |y|\ge |x|- \frac {1}{2}|x|= \frac {1}{2}|x|$. From (8), (9), (14), and (15) we arrive at the following estimates for |x|≥ 1:

$$\displaystyle \begin{aligned} \big|(-\Delta)^s (\psi)(x)\big| \lesssim \begin{cases} \big< x\big>^{-q-2s} &\quad \text{ if }\quad 0< q< n, \\ \big< x\big>^{-n-2s}\log(e+3|x|) &\quad \text{ if }\quad q= n, \\ \big< x\big>^{-n-2s}&\quad \text{ if }\quad q> n. \end{cases} {} \end{aligned} $$

(16)

Finally, combining (7) and (16) we may conclude all desired estimates for m = 0.

Next let us turn to the second case m ≥ 1. First, a straight-forward calculation gives the following relation:

$$\displaystyle \begin{aligned} -\Delta \big< x\big>^{-r}= r\Big((n-r-2)\big< x\big>^{-r-2} + (r+2)\big< x\big>^{-r-4}\Big) \quad \text{ for any } r>0. {} \end{aligned} $$

(17)

By induction argument, carrying out m steps of (17) we obtain the following formula for any m ≥ 1:

$$\displaystyle \begin{aligned} (-\Delta)^m \big< x\big>^{-q}&= (-1)^m \prod_{j=0}^{m-1}(q+2j)\Big(\prod_{j=1}^{m}(-n+q+2j)\big< x\big>^{-q-2m} \\ &\quad - C^1_m \prod_{j=2}^{m}(-n+q+2j)(q+2m)\big< x\big>^{-q-2m-2} \\ &\quad + C^2_m \prod_{j=3}^{m}(-n+q+2j)(q+2m)(q+2m+2)\big< x\big>^{-q-2m-4} \\ &\quad +\cdots+ (-1)^m \prod_{j=0}^{m-1}(q+2m+2j)\big< x\big>^{-q-4m}\Big). {} \end{aligned} $$

(18)

Then, thanks to Lemma 2, we derive

$$\displaystyle \begin{aligned} (-\Delta)^\gamma \big< x\big>^{-q}&= (-\Delta)^s \big((-\Delta)^m \big< x\big>^{-q}\big) \\ &= (-1)^m \prod_{j=0}^{m-1}(q+2j)\Big(\prod_{j=1}^{m}(-n+q+2j)\, (-\Delta)^s \big< x\big>^{-q-2m} \\ &\quad - C^1_m \prod_{j=2}^{m}(-n+q+2j)(q+2m)\, (-\Delta)^s \big< x\big>^{-q-2m-2} \\ &\quad + C^2_m \prod_{j=3}^{m}(-n+q+2j)(q+2m)(q+2m+2)\, (-\Delta)^s \big< x\big>^{-q-2m-4} \\ &\quad +\cdots+ (-1)^m \prod_{j=0}^{m-1}(q+2m+2j)\, (-\Delta)^s \big< x\big>^{-q-4m}\Big). {} \end{aligned} $$

(19)

For this reason, in order to conclude the desired estimates, we only indicate the following estimates for k = 0, ⋯ , m:

$$\displaystyle \begin{aligned} \big|(-\Delta)^s \big< x\big>^{-q-2(m+k)}\big| \lesssim \begin{cases} \big< x\big>^{-q-2\gamma} &\text{ if } 0< q+2m< n, \\ \big< x\big>^{-n-2s}\log(e+|x|) &\text{ if } q+2m= n, \\ \big< x\big>^{-n-2s} &\text{ if } q+2m> n. \end{cases} {} \end{aligned} $$

(20)

Indeed, substituting q by q + 2(m + k) with k = 0, ⋯ , m and γ = s into (6) leads to

$$\displaystyle \begin{aligned} \big|(-\Delta)^s \big< x\big>^{-q-2(m+k)}\big| \lesssim \begin{cases} \big< x\big>^{-q-2\gamma} &\text{ if } 0< q+2(m+k)< n, \\ \big< x\big>^{-n-2s}\log(e+|x|) &\text{ if } q+2(m+k)= n, \\ \big< x\big>^{-n-2s} &\text{ if } q+2(m+k)> n. \end{cases}\end{aligned} $$

From these estimates, it follows immediately (20) to conclude (6) for any m ≥ 1. Summarizing, the proof of Lemma 3 is completed. □

Lemma 4

Let s ∈ (0, 1). Let ψ be a smooth function satisfying$\partial _x^2 \psi \in L^\infty$ . For any R > 0, let ψ _Rbe a function defined by

$$\displaystyle \begin{aligned} \psi_R(x):= \psi\big(R^{-1} x\big) \end{aligned}$$

for all$x \in \mathbb {R}^n$ . Then, (− Δ)^s(ψ _R) satisfies the following scaling properties for all$x \in \mathbb {R}^n$:

$$\displaystyle \begin{aligned}(-\Delta)^s (\psi_R)(x)= R^{-2s}\big((-\Delta)^s \psi \big)\big(R^{-1} x\big). \end{aligned}$$

Proof

Thanks to the assumption $\partial _x^2 \psi \in L^\infty$, following the proof of Lemma 3 we may remove the principal value of the integral at the origin to conclude

$$\displaystyle \begin{aligned} &(-\Delta)^s (\psi_R)(x) = -\frac{C_{n,s}}{2} \int_{\mathbb{R}^n}\frac{\psi_R(x+y)+ \psi_R(x-y)- 2\psi_R(x)}{|y|{}^{n+ 2s}}dy \\ &\quad = -\frac{C_{n,s}}{2 R^{2s}} \int_{\mathbb{R}^n}\frac{\psi\big(R^{-1} x+ R^{-1} y\big)+ \psi\big(R^{-1} x- R^{-1} y\big)- 2\psi\big(R^{-1} x\big)}{|R^{-1} y|{}^{n+ 2s}}d(R^{-1} y) \\ &\quad = R^{-2s}\big((-\Delta)^s \psi\big)\big(R^{-1} x\big). \end{aligned} $$

This completes the proof. □

Lemma 5 (One Mapping Property in the Scale of Fractional Spaces $\{H^s\}_{s \in \mathbb {R}}$)

Let $\gamma ,\,s \in \mathbb {R}$ . Then, the fractional Laplacian

$$\displaystyle \begin{aligned} (-\Delta)^\gamma:\,\, f \to (-\Delta)^\gamma f=\big((-\Delta)^\gamma f\big)(x):= \mathfrak{F}^{-1}\big(|\xi|{}^{2\gamma}\widehat{f}(\xi)\big)(x) \end{aligned}$$

maps isomorphically the space H ^sonto H ^s−2γ.

This result can be found in Section 2.3.8 in [12].

Lemma 6

Let f = f(x) ∈ H ^sand g = g(x) ∈ H ^−swith$s \in \mathbb {R}$ . Then, the following estimate holds:

$$\displaystyle \begin{aligned} \Big|\int_{\mathbb{R}^n}f(x)\,g(x)dx\Big| \le \|f\|{}_{H^s}\,\|g\|{}_{H^{-s}}. \end{aligned}$$

The proof of Lemma 6 can be found in Theorem 16 in [6].

Lemma 7

Let$s \in \mathbb {R}$ . Let v ₁ = v ₁(x) ∈ H ^sand v ₂ = v ₂(x) ∈ H ^−s . Then, the following relation holds:

$$\displaystyle \begin{aligned} \int_{\mathbb{R}^n}v_1(x)\,v_2(x)dx= \int_{\mathbb{R}^n}\widehat{v}_1(\xi)\,\widehat{v}_2(\xi)d\xi. \end{aligned}$$

Proof

We present the proof from Theorem 16 in [6] to make the paper self-contained. Since the space $\mathcal {S}$ is dense in H ^s and H ^−s, there exist sequences {v _1,k}_k and {v _2,k}_k with $v_{1,k}=v_{1,k}(x) \in \mathcal {S}$ and $v_{2,k}=v_{2,k}(x) \in \mathcal {S}$ such that

$$\displaystyle \begin{aligned}\|v_{1,k}-v_1\|{}_{H^s} \to 0 \quad \text{ and }\quad \|v_{2,k}-v_2\|{}_{H^{-s}} \to 0 \quad \text{ for } k \to \infty. \end{aligned}$$

On the one hand, for k →∞ we have the relations

$$\displaystyle \begin{aligned} \widehat{V}_{1,k}(\xi):= (1+|\xi|{}^2)^{\frac{s}{2}}\,\widehat{v}_{1,k}(\xi) &\to \widehat{V}_1(\xi):= (1+|\xi|{}^2)^{\frac{s}{2}}\,\widehat{v}_1(\xi) \quad \text{ in }L^2, \\ \widehat{V}_{2,k}(\xi):= (1+|\xi|{}^2)^{-\frac{s}{2}}\,\widehat{v}_{2,k}(\xi) &\to \widehat{V}_2(\xi):= (1+|\xi|{}^2)^{-\frac{s}{2}}\,\widehat{v}_2(\xi) \quad \text{ in }L^2. \end{aligned} $$

On the other hand, by Parseval–Plancherel formula we arrive at

$$\displaystyle \begin{aligned} \int_{\mathbb{R}^n}v_{1,k}(x)\,v_{2,k}(x)\,dx &= \big(v_{1,k},\,v_{2,k}\big)_{L^2}= \big(\widehat{v}_{1,k},\,\widehat{v}_{2,k}\big)_{L^2}=\int_{\mathbb{R}^n}\widehat{v}_{1,k}(\xi)\,\widehat{v}_{2,k}(\xi)\,d\xi \\ &= \int_{\mathbb{R}^n}(1+|\xi|{}^2)^{\frac{s}{2}}\,\widehat{v}_{1,k}(\xi)\,(1+|\xi|{}^2)^{-\frac{s}{2}}\,\widehat{v}_{2,k}(\xi)\,d\xi \\ &= \int_{\mathbb{R}^n}\widehat{V}_{1,k}(\xi)\,\widehat{V}_{2,k}(\xi)\,d\xi, {} \end{aligned} $$

(21)

where $(\cdot ,\cdot )_{L^2}$ stands for the scalar product in L ². Moreover, applying Lemma 6 we may estimate

$$\displaystyle \begin{aligned} &\Big|\int_{\mathbb{R}^n}\big(v_{1,k}(x)\,v_{2,k}(x)- v_1(x)\,v_2(x)\big)\,dx\Big| \\ &\qquad \le \Big|\int_{\mathbb{R}^n}\big(v_{1,k}(x)- v_1(x)\big)\,v_{2,k}(x)dx\Big|+ \Big|\int_{\mathbb{R}^n}v_1(x)\,\big(v_{2,k}(x)- v_2(x)\big)\,dx\Big| \\ &\qquad \le \|v_{1,k}- v_1\|{}_{H^s}\,\|v_{2,k}\|{}_{H^{-s}}+ \|v_1\|{}_{H^s}\,\|v_{2,k}- v_2\|{}_{H^{-s}} \to 0 \quad \text{ as }k \to \infty. \end{aligned} $$

This is equivalent to

$$\displaystyle \begin{aligned} \int_{\mathbb{R}^n}v_{1,k}(x)\,v_{2,k}(x)\,dx \to \int_{\mathbb{R}^n}v_1(x)\,v_2(x)\,dx \quad \text{ as }k \to \infty. {} \end{aligned} $$

(22)

In the same way we also derive

$$\displaystyle \begin{aligned} \int_{\mathbb{R}^n}\widehat{V}_{1,k}(\xi)\,\widehat{V}_{2,k}(\xi)\,d\xi \to \int_{\mathbb{R}^n}\widehat{V}_1(\xi)\,\widehat{V}_2(\xi) \,d\xi\quad \text{ as }k \to \infty. {} \end{aligned} $$

(23)

Summarizing from (21) to (23) we may conclude

$$\displaystyle \begin{aligned} \int_{\mathbb{R}^n}v_1(x)\,v_2(x)\,dx= \int_{\mathbb{R}^n}\widehat{V}_1(\xi)\,\widehat{V}_2(\xi)\,d\xi= \int_{\mathbb{R}^n}\widehat{v}_1(\xi)\,\widehat{v}_2(\xi)\,d\xi. \end{aligned}$$

Therefore, the proof of Lemma 7 is completed. □

3 Proof of Theorem 2

We divide the proof of Theorem 2 into several cases.

3.1 The Case that Both Parameters σ and δ Are Integers

Proof

The proof of this case can be found in the paper [2]. □

3.2 The Case that the Parameter σ Is Integer and the Parameter δ Is Fractional from (0, 1)

Proof

The first case is devoted to the subcritical case $p<1+ \frac {2\sigma }{n- \mathtt {k}^-}$. First, we introduce the function φ = φ(|x|) := <x>^−n−2δ and the function η = η(t) having the following properties:

$$\displaystyle \begin{aligned} &1.\quad \eta \in \mathcal{C}_0^\infty([0,\infty)) \text{ and } \eta(t)=\begin{cases} 1 &\quad \text{ for }0 \le t \le \frac{1}{2}, \\ \text{decreasing } &\quad \text{ for }\frac{1}{2} \le t \le 1, \\ 0 &\quad \text{ for }t \ge 1, \end{cases} \\ &2.\quad \eta^{-\frac{p'}{p}}(t)\big(|\eta'(t)|{}^{p'}+|\eta''(t)|{}^{p'}\big) \le C \quad \text{ for any } t \in \Big[\frac{1}{2},1\Big], {} \end{aligned} $$

(24)

where p′ is the conjugate of p > 1. Let R be a large parameter in [0, ∞). We define the following test function:

$$\displaystyle \begin{aligned} \phi_R(t,x):= \eta_R(t) \varphi_R(x), \end{aligned} $$

where η _R(t) := η(R ^−α t) and φ _R(x) := φ(R ⁻¹ x) with a fixed parameter α := 2σ −k ⁻. We define the functionals

$$\displaystyle \begin{aligned} I_R:= \int_0^{\infty}\int_{\mathbb{R}^n}|u(t,x)|{}^p \phi_R(t,x)\,dxdt= \int_0^{R^{\alpha}}\int_{\mathbb{R}^n}|u(t,x)|{}^p \phi_R(t,x)\,dxdt \end{aligned} $$

and

$$\displaystyle \begin{aligned} I_{R,t}:= \int_{\frac{R^\alpha}{2}}^{R^{\alpha}}\int_{\mathbb{R}^n}|u(t,x)|{}^p \phi_R(t,x)\,dxdt.\end{aligned} $$

Let us assume that u = u(t, x) is a global (in time) Sobolev solution from $\mathcal {C}\big ([0,\infty ),L^2\big )$ to (1). After multiplying the Eq. (1) by φ _R = φ _R(t, x), we carry out partial integration to derive

$$\displaystyle \begin{aligned} 0\le I_R &= -\int_{\mathbb{R}^n} u_1(x)\varphi_R(x)\,dx + \int_{\frac{R^\alpha}{2}}^{R^{\alpha}}\int_{\mathbb{R}^n}u(t,x) \partial_t^2 \eta_R(t) \varphi_R(x)\,dxdt \\ &\quad + \int_0^{\infty}\int_{\mathbb{R}^n} \eta_R(t) \varphi_R(x)\, (-\Delta)^{\sigma} u(t,x)\,dxdt \\ &\quad - \int_{\frac{R^\alpha}{2}}^{R^\alpha}\int_{\mathbb{R}^n} \partial_t \eta_R(t) \varphi_R(x)\,(-\Delta)^{\delta} u(t,x)\,dxdt \end{aligned} $$

$$\displaystyle \begin{aligned} &=: -\int_{\mathbb{R}^n} u_1(x)\varphi_R(x)\,dx+ J_1+ J_2- J_3. {} \end{aligned} $$

(25)

Applying Hölder’s inequality with $\frac {1}{p}+\frac {1}{p'}=1$ we may estimate as follows:

$$\displaystyle \begin{aligned} |J_1| &\le \int_{\frac{R^\alpha}{2}}^{R^{\alpha}}\int_{\mathbb{R}^n} |u(t,x)|\, \big|\partial_t^2 \eta_R(t)\big| \varphi_R(x) \, dxdt \\ &\lesssim \Big(\int_{\frac{R^\alpha}{2}}^{R^{\alpha}}\int_{\mathbb{R}^n} \Big|u(t,x)\phi^{\frac{1}{p}}_R(t,x)\Big|{}^p \,dxdt\Big)^{\frac{1}{p}} \\ &\qquad \qquad \times \Big(\int_{\frac{R^\alpha}{2}}^{R^{\alpha}}\int_{\mathbb{R}^n} \Big|\phi^{-\frac{1}{p}}_R(t,x) \partial_t^2 \eta_R(t) \varphi_R(x)\Big|{}^{p'}\, dxdt\Big)^{\frac{1}{p'}} \\ &\lesssim I_{R,t}^{\frac{1}{p}}\, \Big(\int_{\frac{R^\alpha}{2}}^{R^{\alpha}}\int_{\mathbb{R}^n} \eta_R^{-\frac{p'}{p}}(t) \big|\partial_t^2 \eta_R(t)\big|{}^{p'} \varphi_R(x)\, dxdt\Big)^{\frac{1}{p'}}. \end{aligned} $$

By the change of variables $\tilde {t}:= R^{-\alpha }t$ and $\tilde {x}:= R^{-1}x$, a straight-forward calculation gives

$$\displaystyle \begin{aligned} |J_1| \lesssim I_{R,t}^{\frac{1}{p}}\, R^{-2\alpha+ \frac{n+\alpha}{p'}}\Big(\int_{\mathbb{R}^n} \big< \tilde{x}\big>^{-n-2\delta}\, d\tilde{x}\Big)^{\frac{1}{p'}}. {} \end{aligned} $$

(26)

Here we used $\partial _t^2 \eta _R(t)= R^{-2\alpha }\eta ''(\tilde {t})$ and the assumption (24). Now let us turn to estimate J ₂ and J ₃. First, by using φ _R ∈ H ^2σ and $u \in \mathcal {C}\big ([0,\infty ),L^2\big )$ we apply Lemma 7 to conclude the following relations:

$$\displaystyle \begin{aligned} \int_{\mathbb{R}^n} \varphi_R(x)\, (-\Delta)^{\sigma} u(t,x)\,dx &= \int_{\mathbb{R}^n}|\xi|{}^{2\sigma}\widehat{\varphi}_R(\xi)\,\widehat{u}(t,\xi)\,d\xi \\ &= \int_{\mathbb{R}^n} u(t,x)\, (-\Delta)^{\sigma}\varphi_R(x)\,dx, \\ \int_{\mathbb{R}^n} \varphi_R(x)\,(-\Delta)^{\delta} u(t,x)\,dx &= \int_{\mathbb{R}^n}|\xi|{}^{2\delta}\widehat{\varphi}_R(\xi)\,\widehat{u}(t,\xi)\,d\xi \\ &= \int_{\mathbb{R}^n} u(t,x)\,(-\Delta)^{\delta}\varphi_R(x)\,dx. \end{aligned} $$

Hence, we obtain

$$\displaystyle \begin{aligned} J_2 &= \int_0^{\infty}\int_{\mathbb{R}^n} \eta_R(t) \varphi_R(x)\, (-\Delta)^{\sigma} u(t,x)\,dxdt \\ &= \int_0^{\infty}\int_{\mathbb{R}^n} \eta_R(t) u(t,x)\, (-\Delta)^{\sigma}\varphi_R(x) \,dxdt, \end{aligned} $$

$$\displaystyle \begin{aligned} J_3 &= \int_{\frac{R^\alpha}{2}}^{R^\alpha}\int_{\mathbb{R}^n} \partial_t \eta_R(t) \varphi_R(x)\,(-\Delta)^{\delta} u(t,x)\,dxdt \\ &= \int_{\frac{R^\alpha}{2}}^{R^\alpha}\int_{\mathbb{R}^n} \partial_t \eta_R(t) u(t,x)\,(-\Delta)^{\delta}\varphi_R(x)\, dxdt. \end{aligned} $$

Applying Hölder’s inequality again as we estimated J ₁ leads to

$$\displaystyle \begin{aligned} |J_2| &\le I_R^{\frac{1}{p}}\, \Big(\int_0^{R^{\alpha}}\int_{\mathbb{R}^n} \eta_R(t) \varphi^{-\frac{p'}{p}}_R(x)\, \big|(-\Delta)^{\sigma}\varphi_R(x)\big|{}^{p'} \, dxdt\Big)^{\frac{1}{p'}}, \\ |J_3| &\le I_{R,t}^{\frac{1}{p}}\, \Big(\int_{\frac{R^\alpha}{2}}^{R^{\alpha}}\int_{\mathbb{R}^n} \eta^{-\frac{p'}{p}}_R(t) \big|\partial_t \eta_R(t)\big|{}^{p'} \varphi^{\frac{-p'}{p}}_R(x)\, \big|(-\Delta)^{\delta}\varphi_R(x)\big|{}^{p'} \, dxdt\Big)^{\frac{1}{p'}}. \end{aligned} $$

In order to control the above two integrals, the key tools rely on results from Lemmas 1, 3 and 4. Namely, at first carrying out the change of variables $\tilde {t}:= R^{-\alpha }t$ and $\tilde {x}:= R^{-1}x$ we arrive at

$$\displaystyle \begin{aligned} |J_2| &\lesssim I_R^{\frac{1}{p}}\, R^{-2\sigma+ \frac{n+\alpha}{p'}}\Big(\int_0^{1}\int_{\mathbb{R}^n} \eta(\tilde{t}) \varphi^{-\frac{p'}{p}}(\tilde{x})\, \big|(-\Delta)^{\sigma}(\varphi)(\tilde{x})\big|{}^{p'}\, d\tilde{x}d\tilde{t}\Big)^{\frac{1}{p'}} \\ &\lesssim I_R^{\frac{1}{p}}\, R^{-2\sigma+ \frac{n+\alpha}{p'}}\Big(\int_{\mathbb{R}^n} \varphi^{-\frac{p'}{p}}(\tilde{x})\, \big|(-\Delta)^{\sigma}(\varphi)(\tilde{x})\big|{}^{p'}\, d\tilde{x}\Big)^{\frac{1}{p'}}, \end{aligned} $$

where we note (σ is an integer) that $(-\Delta )^{\sigma }\varphi _R(x)= R^{-2\sigma }(-\Delta )^{\sigma }\varphi (\tilde {x}).$ Using Lemma 1 implies the following estimate:

$$\displaystyle \begin{aligned} |J_2|\lesssim I_R^{\frac{1}{p}}\, R^{-2\sigma+ \frac{n+\alpha}{p'}}\Big(\int_{\mathbb{R}^n} \big< \tilde{x}\big>^{-n-2\delta-2\sigma p'}\, d\tilde{x}\Big)^{\frac{1}{p'}}. {} \end{aligned} $$

(27)

Next carrying out again the change of variables $\tilde {t}:= R^{-\alpha }t$ and $\tilde {x}:= R^{-1}x$ and employing Lemma 4 we can proceed J ₃ as follows:

$$\displaystyle \begin{aligned} |J_3| &\lesssim I_{R,t}^{\frac{1}{p}}\, R^{-2\delta-\alpha+ \frac{n+\alpha}{p'}} \\ &\qquad \times \Big(\int_{\frac{1}{2}}^{1}\int_{\mathbb{R}^n} \eta^{-\frac{p'}{p}}(\tilde{t}) \big|\eta'(\tilde{t})\big|{}^{p'} \varphi^{-\frac{p'}{p}}(\tilde{x})\, \big|(-\Delta)^{\delta}(\varphi)(\tilde{x})\big|{}^{p'}\, d\tilde{x}d\tilde{t}\Big)^{\frac{1}{p'}} \\ &\lesssim I_{R,t}^{\frac{1}{p}}\, R^{-2\delta-\alpha+ \frac{n+\alpha}{p'}}\Big(\int_{\mathbb{R}^n} \varphi^{-\frac{p'}{p}}(\tilde{x})\, \big|(-\Delta)^{\delta}(\varphi)(\tilde{x})\big|{}^{p'}\, d\tilde{x}\Big)^{\frac{1}{p'}}. \end{aligned} $$

Here we used $\partial _t \eta _R(t)= R^{-\alpha }\eta '(\tilde {t})$ and the assumption (24). To deal with the last integral, we apply Lemma 3 with q = n + 2δ and γ = δ, that is, m = 0 and s = δ to get

$$\displaystyle \begin{aligned} |J_3| \lesssim I_{R,t}^{\frac{1}{p}} R^{-2\delta-\alpha+ \frac{n+\alpha}{p'}}\Big(\int_{\mathbb{R}^n} \big< \tilde{x}\big>^{-n-2\delta}\, d\tilde{x}\Big)^{\frac{1}{p'}}. {} \end{aligned} $$

(28)

Because of the assumption (3), there exists a sufficiently large constant R ₀ > 0 such that it holds

$$\displaystyle \begin{aligned} \int_{\mathbb{R}^n} u_1(x) \varphi_R(x)\, dx >0 {} \end{aligned} $$

(29)

for all R > R ₀. Combining the estimates from (25) to (29) we may arrive at

$$\displaystyle \begin{aligned} 0< \int_{\mathbb{R}^n} u_1(x) \varphi_R(x)\, dx &\lesssim I_{R,t}^{\frac{1}{p}} \big(R^{-2\alpha+ \frac{n+\alpha}{p'}}+ R^{-\alpha- 2\delta+ \frac{n+\alpha}{p'}}\big) \\ &\quad + I_R^{\frac{1}{p}}\, R^{-2\sigma+ \frac{n+\alpha}{p'}}- I_R \lesssim I_R^{\frac{1}{p}}\, R^{-2\sigma+ \frac{n+\alpha}{p'}}- I_R {} \end{aligned} $$

(30)

for all R > R ₀. Moreover, applying the inequality

$$\displaystyle \begin{aligned} A\,y^\gamma- y \le A^{\frac{1}{1-\gamma}} \quad \text{ for any } A>0,\, y \ge 0 \text{ and } 0< \gamma< 1 \end{aligned}$$

leads to

$$\displaystyle \begin{aligned} 0< \int_{\mathbb{R}^n} u_1(x)\varphi_R(x)dx \lesssim R^{-2\sigma p'+ n+\alpha} {} \end{aligned} $$

(31)

for all R > R ₀. It is clear that the assumption (4) is equivalent to − 2σp′ + n + α ≤ 0. For this reason, in the subcritical case, that is, − 2σp′ + n + α < 0 letting R →∞ in (31) we obtain

$$\displaystyle \begin{aligned} \int_{\mathbb{R}^n} u_1(x)\,dx= 0. \end{aligned}$$

This is a contradiction to the assumption (3).

Let us turn to the critical case $p=1+ \frac {2\sigma }{n- \mathtt {k}^-}$. It follows immediately $-2\sigma + \frac {n+\alpha }{p'}=0$. Then, repeating some arguments as we did in the subcritical case we may conclude the following estimate:

$$\displaystyle \begin{aligned} 0< C_0:= \int_{\mathbb{R}^n} u_1(x) \varphi_R(x)\, dx \le C_1 I_R^{\frac{1}{p}}- I_R, \end{aligned}$$

where $C_1:= \Big (\displaystyle \int _{\mathbb {R}^n} \big < \tilde {x}\big >^{-n-2\delta }\, d\tilde {x}\Big )^{\frac {1}{p'}},$ that is,

$$\displaystyle \begin{aligned} C_0+ I_R \le C_1 I_R^{\frac{1}{p}}. {} \end{aligned} $$

(32)

From (32) it is obvious that $I_R \le C_1 I_R^{\frac {1}{p}}$ and $C_0 \le C_1 I_R^{\frac {1}{p}}$. Hence, we obtain

$$\displaystyle \begin{aligned} I_R \le C_1^{p'} {} \end{aligned} $$

(33)

and

$$\displaystyle \begin{aligned} I_R \ge \frac{C_0^p}{C_1^p}, {} \end{aligned} $$

(34)

respectively. By substituting (34) into the left-hand side of (32) and calculating straightforwardly, we get

$$\displaystyle \begin{aligned} I_R \ge \frac{C_0^{p^2}}{C_1^{p+p^2}}. \end{aligned}$$

For any integer j ≥ 1, an iteration argument leads to

$$\displaystyle \begin{aligned} I_R \ge \frac{C_0^{p^j}}{C_1^{p+p^2+\cdots+p^j}}= \frac{C_0^{p^j}}{C_1^{\frac{p^{j+1}-p}{p-1}}}= C_1^{\frac{p}{p-1}}\Big(\frac{C_0}{C_1^{\frac{p}{p-1}}}\Big)^{p^j}. {} \end{aligned} $$

(35)

Now we choose the constant

$$\displaystyle \begin{aligned} \epsilon_0= \int_{\mathbb{R}^n} \big< \tilde{x}\big>^{-n-2\delta}\, d\tilde{x} \end{aligned}$$

in the assumption (3). Then, there exists a sufficiently large constant R ₁ > 0 so that

$$\displaystyle \begin{aligned} \int_{\mathbb{R}^n} u_1(x) \varphi_R(x)\, dx > \epsilon_0 \end{aligned}$$

for all R > R ₁. This is equivalent to

$$\displaystyle \begin{aligned} C_0> C_1^{p'}= C_1^{\frac{p}{p-1}}, \quad \text{that is, }\quad \frac{C_0}{C_1^{\frac{p}{p-1}}}> 1. \end{aligned}$$

Therefore, letting j →∞ in (35) we derive I _R →∞, which is a contradiction to (33). Summarizing, the proof is completed. □

Let us now consider the case of subcritical exponent to explain the estimate for lifespan T _ε of solutions in Remark 1. We assume that u = u(t, x) is a local (in time) Sobolev solution to (1) in $[0,T)\times \mathbb {R}^n$. In order to prove the lifespan estimate, we replace the initial data (0, u ₁) by (0, εu ₁) with a small constant ε > 0, where u ₁ ∈ L ¹ satisfies the assumption (3). Hence, there exists a sufficiently large constant R ₂ > 0 so that we have

$$\displaystyle \begin{aligned} \int_{\mathbb{R}^n} u_1(x)\varphi_R(x)\,dx \ge c >0 \end{aligned}$$

for any R > R ₂. Repeating the steps in the above proofs we arrive at the following estimate:

$$\displaystyle \begin{aligned} \varepsilon \le C\, R^{-2\sigma p'+ n+ \alpha} \le C\, T^{-\frac{2\sigma p'- n- \alpha}{\alpha}} \end{aligned}$$

with $R= T^{\frac {1}{\alpha }}$. Finally, letting $T\to T^-_\varepsilon$ we may conclude (5).

Remark 3

We want to underline that in the special case σ = 1 and $\delta = \frac {1}{2}$ the authors in [4] have investigated the critical exponent $p_{crit}=p_{crit}(n)= 1+ \frac {2}{n- 1}$. If we plug σ = 1 and $\delta = \frac {1}{2}$ into the statements of Theorem 2, then the obtained results for the critical exponent p _crit coincide.

3.3 The Case that the Parameter σ Is Integer and the Parameter δ Is Fractional from (1, σ)

Proof

We follow ideas from the proof of Sect. 3.2. At first, we denote s _δ := δ − [δ]. Let us introduce test functions η = η(t) as in Sect. 3.2 and $\varphi =\varphi (x):=\big < x\big >^{-n-2s_\delta }$. We can repeat exactly, the estimates for J ₁ and J ₂ as we did in the proof of Sect. 3.2 to conclude

$$\displaystyle \begin{aligned} |J_1| &\lesssim I_{R,t}^{\frac{1}{p}}\, R^{-2\alpha+ \frac{n+\alpha}{p'}}, {} \end{aligned} $$

(36)

$$\displaystyle \begin{aligned} |J_2| &\lesssim I_R^{\frac{1}{p}}\, R^{-2\sigma+ \frac{n+\alpha}{p'}}. {} \end{aligned} $$

(37)

Let us turn to estimate J ₃, where δ is any fractional number in (1, σ). In the first step, applying Lemma 7 and Hölder’s inequality leads to

$$\displaystyle \begin{aligned}|J_3|\le I_{R,t}^{\frac{1}{p}}\, \Big(\int_{\frac{R^\alpha}{2}}^{R^{\alpha}}\int_{\mathbb{R}^n} \eta^{-\frac{p'}{p}}_R(t) \big|\partial_t \eta_R(t)\big|{}^{p'} \varphi^{-\frac{p'}{p}}_R(x)\, \big|(-\Delta)^{\delta}\varphi_R(x)\big|{}^{p'} \, dxdt\Big)^{\frac{1}{p'}}. \end{aligned}$$

Now we can re-write δ = m _δ + s _δ, where m _δ := [δ] ≥ 1 is integer and s _δ is a fractional number in (0, 1). Employing Lemma 2 we derive

$$\displaystyle \begin{aligned} (-\Delta)^{\delta}\varphi_R(x)= (-\Delta)^{s_\delta} \big((-\Delta)^{m_\delta}\varphi_R(x)\big). \end{aligned}$$

By the change of variables $\tilde {x}:= R^{-1}x$ we also notice that

$$\displaystyle \begin{aligned} (-\Delta)^{m_\delta}\varphi_R(x)= R^{-2m_\delta}(-\Delta)^{m_\delta}(\varphi)(\tilde{x}) \end{aligned}$$

since m _δ is an integer. Using the formula (18) we re-write

$$\displaystyle \begin{aligned} (-\Delta)^{m_\delta}\varphi_R(x)&= (-1)^{m_\delta} R^{-2m_\delta} \prod_{j=0}^{m_\delta-1}(q+2j)\Big(\prod_{j=1}^{m_\delta}(-n+q+2j)\big< \tilde{x}\big>^{-q-2m_\delta} \\ &\quad - C^1_{m_\delta} \prod_{j=2}^{m_\delta}(-n+q+2j)(q+2m_\delta)\big< \tilde{x}\big>^{-q-2m_\delta-2} \\ &\quad + C^2_{m_\delta} \prod_{j=3}^{m_\delta}(-n+q+2j)(q+2m_\delta)(q+2m_\delta+2)\big< \tilde{x}\big>^{-q-2m_\delta-4} \\ &\quad +\cdots+ (-1)^{m_\delta} \prod_{j=0}^{m_\delta-1}(q+2m_\delta+2j)\big< \tilde{x}\big>^{-q-4m_\delta}\Big), \end{aligned} $$

where q := n + 2s _δ. For simplicity, we introduce the following functions:

$$\displaystyle \begin{aligned} \varphi_k(x):= \big< x\big>^{-q-2m_\delta-2k}\quad \text{ and }\quad \varphi_{k,R}(x):= \varphi_k(R^{-1}x)=\big< \tilde{x}\big>^{-q-2m_\delta-2k} \end{aligned}$$

with k = 0, ⋯ , m _δ. As a result, by Lemma 4 we arrive at

$$\displaystyle \begin{aligned} (-\Delta)^{\delta}\varphi_R(x)&= (-1)^{m_\delta} R^{-2m_\delta} \prod_{j=0}^{m_\delta-1}(q+2j)\Big(\prod_{j=1}^{m_\delta}(-n+q+2j)\, (-\Delta)^{s_\delta}(\varphi_{0,R})(x) \\ &\quad - C^1_{m_\delta} \prod_{j=2}^{m_\delta}(-n+q+2j)(q+2m_\delta)\, (-\Delta)^{s_\delta}(\varphi_{1,R})(x) \\ &\quad + C^2_{m_\delta} \prod_{j=3}^{m_\delta}(-n+q+2j)(q+2m_\delta)(q+2m_\delta+2)\, (-\Delta)^{s_\delta}(\varphi_{2,R})(x) \\ &\quad +\cdots+ (-1)^{m_\delta} \prod_{j=0}^{m_\delta-1}(q+2m_\delta+2j)\, (-\Delta)^{s_\delta}(\varphi_{m_\delta,R})(x)\Big) \\ &= (-1)^{m_\delta} R^{-2m_\delta-2s_\delta} \prod_{j=0}^{m_\delta-1}(q+2j)\Big(\prod_{j=1}^{m_\delta}(-n+q+2j)\, (-\Delta)^{s_\delta}(\varphi_0)(\tilde{x}) \\ &\quad - C^1_{m_\delta} \prod_{j=2}^{m_\delta}(-n+q+2j)(q+2m_\delta)\, (-\Delta)^{s_\delta}(\varphi_1)(\tilde{x}) \\ &\quad + C^2_{m_\delta} \prod_{j=3}^{m_\delta}(-n+q+2j)(q+2m_\delta)(q+2m_\delta+2)\, (-\Delta)^{s_\delta}(\varphi_2)(\tilde{x}) \\ &\quad +\cdots+ (-1)^{m_\delta} \prod_{j=0}^{m_\delta-1}(q+2m_\delta+2j)\, (-\Delta)^{s_\delta}(\varphi_{m_\delta})(\tilde{x})\Big) \\ &= R^{-2\delta} (-\Delta)^{\delta}(\varphi)(\tilde{x}). \end{aligned} $$

For this reason, performing the change of variables $\tilde {t}:= R^{-\alpha }t$ we obtain

$$\displaystyle \begin{aligned} |J_3| &\lesssim I_{R,t}^{\frac{1}{p}}\, R^{-2\delta-\alpha+ \frac{n+\alpha}{p'}} \\ &\qquad \times \Big(\int_{\frac{1}{2}}^{1}\int_{\mathbb{R}^n} \eta^{-\frac{p'}{p}}(\tilde{t}) \big|\eta'(\tilde{t})\big|{}^{p'} \varphi^{-\frac{p'}{p}}(\tilde{x})\, \big|(-\Delta)^{\delta}(\varphi)(\tilde{x})\big|{}^{p'}\, d\tilde{x}d\tilde{t}\Big)^{\frac{1}{p'}} \\ &\lesssim I_{R,t}^{\frac{1}{p}}\, R^{-2\delta-\alpha+ \frac{n+\alpha}{p'}}\Big(\int_{\mathbb{R}^n} \varphi^{-\frac{p'}{p}}(\tilde{x})\, \big|(-\Delta)^{\delta}(\varphi)(\tilde{x})\big|{}^{p'}\, d\tilde{x}\Big)^{\frac{1}{p'}}. \end{aligned} $$

Here we used $\partial _t \eta _R(t)= R^{-\alpha }\eta '(\tilde {t})$ and the assumption (24). After applying Lemma 3 with q = n + 2s _δ and γ = δ, i.e. m = m _δ and s = s _δ, we may conclude

$$\displaystyle \begin{aligned} |J_3|\lesssim I_{R,t}^{\frac{1}{p}}\, R^{-2\delta-\alpha+ \frac{n+\alpha}{p'}}\Big(\int_{\mathbb{R}^n} \big< \tilde{x}\big>^{-n-2s_\delta}\, d\tilde{x}\Big)^{\frac{1}{p'}}\lesssim I_{R,t}^{\frac{1}{p}}\, R^{-2\delta-\alpha+ \frac{n+\alpha}{p'}}. {} \end{aligned} $$

(38)

Finally, combining (36)–(38) and repeating arguments as in Sect. 3.2 we may complete the proof of Theorem 2. □

3.4 The Case that the Parameter σ Is Fractional from (1, ∞) and the Parameter δ Is Integer

Proof

We follow ideas from the proofs of Sects. 3.2 and 3.3. At first, we denote s _σ := σ − [σ]. Let us introduce test functions η = η(t) as in Sect. 3.2 and $\varphi =\varphi (x):=\big < x\big >^{-n-2s_\sigma }$. Then, repeating the proof of Sects. 3.2 and 3.3 we may conclude what we wanted to prove. □

3.5 The Case that the Parameter σ Is Fractional from (1, ∞) and the Parameter δ Is Fractional from (0, 1)

Proof

We follow ideas from the proofs of Sects. 3.2 and 3.4. At first, we denote s _σ := σ − [σ]. Next, we put $s^*:= \min \{s_\sigma ,\,\delta \}$. It is obvious that s ^∗ is fractional from (0, 1). Let us introduce test functions η = η(t) as in Sect. 3.2 and $\varphi =\varphi (x):=\big < x\big >^{-n-2s^*}$. Then, repeating the proof of Sects. 3.2 and 3.4 we may conclude what we wanted to prove. □

3.6 The Case that the Parameter σ Is Fractional from (1, ∞) and the Parameter δ Is Fractional from (1, σ)

Proof

We follow ideas from the proofs of Sects. 3.2 and 3.5. At first, we denote s _σ := σ − [σ] and s _δ := δ − [δ]. Next, we put $s^*:= \min \{s_\sigma ,\,s_\delta \}$. It is obvious that s ^∗ is fractional from (0, 1). Let us introduce test functions η = η(t) as in Sect. 3.2 and $\varphi =\varphi (x):=\big < x\big >^{-n-2s^*}$. Then, repeating the proof of Sects. 3.2 and 3.5 we may conclude what we wanted to prove. □

4 Critical Exponent Versus Critical Nonlinearity

In Remark 2 we explained that for some models (1) we determined the critical exponent p _crit = p _crit(n) in the scale of power nonlinearities {|u|^p}_p>1. But is this observation sharp? In the paper [5] the authors discussed this issue for the classical damped wave model with power nonlinearity. Here we want to extend this idea to some models of type (1). For this reason, we discuss the following model:

$$\displaystyle \begin{aligned} \begin{cases} u_{tt}+ (-\Delta)^\sigma u+ (-\Delta)^{\delta} u_t=|u|{}^{p_{crit}(n)}\mu(|u|), \\ u(0,x)= u_0(x),\quad u_t(0,x)=u_1(x), \end{cases} \end{aligned} $$

(39)

where σ ≥ 1, $\delta \in [0,\frac {\sigma }{2}]$ and $p_{crit}(n)= 1+\frac {2\sigma }{n- 2\delta }$ with n ≥ 1. Here the function μ = μ(|u|) is a suitable modulus of continuity.

4.1 Main Results

First we state a global (in time) existence result of small data Sobolev solutions to (39).

Theorem 3 (Global Existence)

Let σ ≥ 1, $\delta \in [0,\frac {\sigma }{2}]$and m ∈ [1, 2). Let 0 < θ ≤ σ. We assume the conditions

$$\displaystyle \begin{aligned} \begin{cases} 2m_0\delta< n< 2\theta &\quad \mathit{\text{ if }}\quad \delta \in [0,\frac{\sigma}{2}), \\ m\sigma< n< 2\theta &\quad \mathit{\text{ if }}\quad \delta= \frac{\sigma}{2}. \end{cases} {} \end{aligned} $$

(40)

Moreover, we suppose the following assumptions of modulus of continuity:

$$\displaystyle \begin{aligned} s\mu'(s) \lesssim \mu(s) {} \end{aligned} $$

(41)

and

$$\displaystyle \begin{aligned} \int^{C_0}_0 \frac{\mu(s)}{s}\,ds < \infty {} \end{aligned} $$

(42)

with a sufficiently small constant C ₀ > 0. Then, there exists a constant ε ₀ > 0 such that for any small data

$$\displaystyle \begin{aligned} (u_0,u_1) \in \big(L^m \cap H^\theta \big) \times \big(L^m \cap L^2\big) \end{aligned}$$

satisfying the assumption $\|u_0\|{ }_{L^m \cap H^\theta }+ \|u_1\|{ }_{L^m \cap L^2} \le \varepsilon _0,$ we have a uniquely determined global (in time) small data Sobolev solution

$$\displaystyle \begin{aligned} u \in \mathcal{C}\big([0,\infty),H^\theta\big) \end{aligned}$$

to (39). The following estimates hold:

$$\displaystyle \begin{aligned} \|u(t,\cdot)\|{}_{L^2}&\lesssim (1+t)^{-\frac{n}{2(\sigma -\delta)}(\frac{1}{m}-\frac{1}{2})+ \frac{\delta}{\sigma -\delta}} \big(\|u_0\|{}_{L^m \cap H^\theta}+ \|u_1\|{}_{L^m \cap L^2}\big), \\ \big\||D|{}^\theta u(t,\cdot)\big\|{}_{L^2}&\lesssim (1+t)^{-\frac{n}{2(\sigma -\delta)}(\frac{1}{m}-\frac{1}{2})- \frac{\theta- 2\delta}{2(\sigma -\delta)}} \big(\|u_0\|{}_{L^m \cap H^\theta}+ \|u_1\|{}_{L^m \cap L^2}\big). \end{aligned} $$

Now we state a blow-up result to (39).

Theorem 4 (Blow-Up)

Let σ ≥ 1 and$\delta \in [0,\frac {\sigma }{2}]$be integer numbers. We assume that we choose the initial data u ₀ = 0 and u ₁ ∈ L ¹satisfying the following relation:

$$\displaystyle \begin{aligned} \int_{\mathbb{R}^n} u_1(x)\,dx >0. \end{aligned} $$

(43)

Moreover, we suppose the following assumption of modulus of continuity:

$$\displaystyle \begin{aligned} s^k\mu^{(k)}(s)= o\big(\mu(s)\big) \quad \mathit{\text{ as }}s \to +0 \mathit{\text{ with }}k=1,2, {} \end{aligned} $$

(44)

and

$$\displaystyle \begin{aligned} \int^{C_0}_0 \frac{\mu(s)}{s}\,ds= \infty, {} \end{aligned} $$

(45)

where C ₀ > 0 is a sufficiently small constant. Then, there is no global (in time) Sobolev solution to (39).

In the following we restrict ourselves to prove the blow-up result.

4.2 Proof of Theorem 4

The ideas of the following proof are based on the recent paper [5] of the second author and his collaborators in which the authors focused on their considerations to (39) with σ = 1 and δ = 0. For simplicity, we use the abbreviations $p_c:= p_{crit}(n)= 1+\frac {2\sigma }{n- 2\delta }$ to (39) in the following proof.

Proof of Theorem 4

First, we introduce a test function φ = φ(τ) having the following properties:

$$\displaystyle \begin{aligned} \varphi \in \mathcal{C}_0^\infty([0,\infty)) \text{ and } \varphi (\tau)=\begin{cases} 1 &\quad \text{ for }0 \le \tau \le \frac{1}{2}, \\ \text{decreasing } &\quad \text{ for }\frac{1}{2} \le \tau \le 1, \\ 0 &\quad \text{ for } \tau \ge 1. \end{cases} \end{aligned}$$

Moreover, we also introduce the function φ ^∗ = φ ^∗(τ) satisfying

$$\displaystyle \begin{aligned} \varphi^*(\tau)= \begin{cases} 0 &\quad \text{ for } 0 \le \tau< \frac{1}{2}, \\ \varphi(\tau) &\quad \text{ for } \frac{1}{2} \le \tau< \infty. \end{cases} \end{aligned}$$

Let R be a large parameter in [0, ∞). We define the following two functions:

$$\displaystyle \begin{aligned} \phi_R(t,x)= \Big(\varphi\Big(\frac{|x|{}^{2(\sigma-\delta)}+ t}{R}\Big)\Big)^{n+2(\sigma-\delta)} \end{aligned}$$

and

$$\displaystyle \begin{aligned} \phi^*_R(t,x)= \Big(\varphi^*\Big(\frac{|x|{}^{2(\sigma-\delta)}+ t}{R}\Big)\Big)^{n+2(\sigma-\delta)}. \end{aligned}$$

Then it is clear that

$$\displaystyle \begin{aligned} &\text{supp} \,\phi_R \subset Q_R:= \big\{(t,x) \,\,:\,\, (t,|x|) \in [0,R] \times \big[0,R^{1/(2(\sigma-\delta))}\big] \big\}, \\ &\text{supp} \,\phi^*_R \subset Q^*_R:= Q_R \,\setminus \,\big\{(t,x) \,\,:\,\, (t,|x|) \in [0,R/2] \times \big[0,(R/2)^{1/(2(\sigma-\delta))}\big] \big\}. \end{aligned} $$

Now we define the functional

$$\displaystyle \begin{aligned} I_R:= &\int_0^{\infty}\int_{\mathbb{R}^n}|u(t,x)|{}^{p_c}\mu\big(|u(t,x)|\big) \phi_R(t,x)\,dxdt \\ = &\int_{Q_R}|u(t,x)|{}^{p_c}\mu\big(|u(t,x)|\big) \phi_R(t,x)\,d(x,t). \end{aligned} $$

Let us assume that u = u(t, x) is a global (in time) Sobolev solution to (39). After multiplying the Eq. (39) by φ _R = φ _R(t, x), we carry out partial integration to derive

$$\displaystyle \begin{aligned} 0\le I_R &= -\int_{\mathbb{R}^n} u_1(x)\phi_R(0,x)\,dx \\ &\,\,\,+ \int_{Q_R}u(t,x) \big(\partial_t^2 \phi_R(t,x)+ (-\Delta)^{\sigma} \phi_R(t,x)- (-\Delta)^{\delta}\partial_t \phi_R(t,x) \big)\,d(x,t) \\ &=: -\int_{\mathbb{R}^n} u_1(x)\phi_R(0,x)\,dx + J_R. \end{aligned} $$

Because of the assumption (43), there exists a sufficiently large constant R ₀ > 0 such that for all R > R ₀ it holds

$$\displaystyle \begin{aligned} \int_{\mathbb{R}^n} u_1(x)\phi_R(0,x)\,dx >0. \end{aligned}$$

Consequently, we obtain

$$\displaystyle \begin{aligned} 0\le I_R < J_R \quad \text{ for all } R > R_0. {} \end{aligned} $$

(46)

In order to estimate J _R, firstly we have

$$\displaystyle \begin{aligned} |\partial_t \phi_R(t,x)| &\lesssim \Big|\frac{1}{R}\Big(\varphi\Big(\frac{|x|{}^{2(\sigma-\delta)}+ t}{R}\Big)\Big)^{n+2(\sigma-\delta)-1} \varphi'\Big(\frac{|x|{}^{2(\sigma-\delta)}+ t}{R}\Big)\Big| \\ &\lesssim \frac{1}{R}\Big(\varphi^*\Big(\frac{|x|{}^{2(\sigma-\delta)}+ t}{R}\Big)\Big)^{n+2(\sigma-\delta)-1}. {} \end{aligned} $$

(47)

Further calculations lead to

$$\displaystyle \begin{aligned} |\partial_t^2 \phi_R(t,x)| &\lesssim \Big|\frac{1}{R^2}\Big(\varphi\Big(\frac{|x|{}^{2(\sigma-\delta)}+ t}{R}\Big)\Big)^{n+2(\sigma-\delta)-2} \Big(\varphi'\Big(\frac{|x|{}^{2(\sigma-\delta)}+ t}{R}\Big)\Big)^2\Big| \\ &\qquad + \Big|\frac{1}{R^2}\Big(\varphi\Big(\frac{|x|{}^{2(\sigma-\delta)}+ t}{R}\Big)\Big)^{n+2(\sigma-\delta)-1} \varphi''\Big(\frac{|x|{}^{2(\sigma-\delta)}+ t}{R}\Big)\Big| \\ &\lesssim \frac{1}{R^2}\Big(\varphi^*\Big(\frac{|x|{}^{2(\sigma-\delta)}+ t}{R}\Big)\Big)^{n+2(\sigma-\delta)-2} {}. \end{aligned} $$

(48)

To control (− Δ)^σ φ _R(t, x), we shall apply Lemma 8 as a main tool. Indeed, we divide our consideration into three sub-steps as follows:

Step 1::

Applying Lemma 8 with $h(z)= \frac {z^{\sigma -\delta }+t}{R}$ and z = f(x) = |x|² we derive the following estimate for |α|≥ 1:

$$\displaystyle \begin{aligned} &\Big|\partial_x^\alpha \Big(\frac{|x|{}^{2(\sigma-\delta)}+t}{R}\Big)\Big| \\ &\qquad \le \sum_{k=1}^{|\alpha|} \frac{|x|{}^{2(\sigma-\delta)-2k}}{R}\left(\sum_{\substack{|\gamma_1|+\cdots+|\gamma_k|= |\alpha| \\ |\gamma_i|\ge 1}}\big|\partial_x^{\gamma_1} \big(|x|{}^2\big)\big| \cdots \big|\partial_x^{\gamma_k} \big(|x|{}^2\big)\big|\right) \\ &\qquad \le \sum_{k=1}^{|\alpha|} \frac{|x|{}^{2(\sigma-\delta)-2k}}{R}\left(\sum_{\substack{|\gamma_1|+\cdots+|\gamma_k|= |\alpha| \\ 1\le |\gamma_i|\le 2}}\big|\partial_x^{\gamma_1} \big(|x|{}^2\big)\big| \cdots \big|\partial_x^{\gamma_k} \big(|x|{}^2\big)\big|\right) \\ &\qquad \lesssim \sum_{k=1}^{|\alpha|} \frac{|x|{}^{2(\sigma-\delta)-2k}}{R} \left(\displaystyle\sum_{\substack{|\gamma_1|+\cdots+|\gamma_k|= |\alpha| \\ 1\le |\gamma_i|\le 2}}|x|{}^{2-|\gamma_1|} \cdots |x|{}^{2-|\gamma_k|}\right) \\ &\qquad \lesssim \sum_{k=1}^{|\alpha|} \frac{|x|{}^{2(\sigma-\delta)-2k}}{R} |x|{}^{2k-|\alpha|} \lesssim \frac{|x|{}^{2(\sigma-\delta)-|\alpha|}}{R}. \end{aligned} $$

This estimate holds for |α|≤ 2(σ − δ). But we may conclude that it holds for all |α|≥ 1, too and small |x|. More precisely, the singularity appearing in the case |α| > 2(σ − δ) does not really bring any difficulty in the further treatment.

Step 2::

Applying Lemma 8 with h(z) = φ(z) and $z=f(x)= \frac {|x|{ }^{2(\sigma -\delta )}+ t}{R}$ we get for all |α|≥ 1 the following estimate:

$$\displaystyle \begin{aligned} &\Big|\partial_x^\alpha \varphi\Big(\frac{|x|{}^{2(\sigma-\delta)}+ t}{R}\Big)\Big| \\ &\quad \le \sum_{k=1}^{|\alpha|}\Big|\varphi^{(k)} \Big(\frac{|x|{}^{2(\sigma-\delta)}+ t}{R}\Big) \Big| \\ &\qquad \times \left(\sum_{\substack{|\gamma_1|+\cdots+|\gamma_k|= |\alpha| \\ 1 \leq |\gamma_i|\leq 2(\sigma-\delta)}} \Big|\partial_x^{\gamma_1}\Big(\frac{|x|{}^{2(\sigma-\delta)}+t}{R}\Big)\Big| \cdots \Big|\partial_x^{\gamma_k}\Big(\frac{|x|{}^{2(\sigma-\delta)}+t}{R}\Big)\Big| \right) \end{aligned} $$

$$\displaystyle \begin{aligned} &\quad \le \sum_{k=1}^{|\alpha|}\Big|\varphi^{(k)} \Big(\frac{|x|{}^{2(\sigma-\delta)}+ t}{R}\Big)\Big| \\ &\qquad \times \left(\sum_{\substack{|\gamma_1|+\cdots+|\gamma_k|= |\alpha| \\ 1 \leq |\gamma_i|\leq 2(\sigma-\delta)}} \frac{|x|{}^{2(\sigma-\delta)- |\gamma_1|}}{R} \cdots \frac{|x|{}^{2(\sigma-\delta)- |\gamma_k|}}{R} \right) \\ &\quad \lesssim \sum_{k=1}^{|\alpha|} \Big(\frac{|x|{}^{2(\sigma-\delta)}}{R}\Big)^k |x|{}^{-|\alpha|} \lesssim \frac{|x|{}^{2(\sigma-\delta)- |\alpha|}}{R}\quad \big(\text{since }\,\, |x|{}^{2(\sigma-\delta)} \le R \text{ in } Q^*_R\big). \end{aligned} $$

Step 3::

Applying Lemma 8 with h(z) = z ^n+2(σ−δ) and $z=f(x)= \varphi \big (\frac {|x|{ }^{2(\sigma -\delta )}+ t}{R}\big )$ we obtain

$$\displaystyle \begin{aligned} &\big|(-\Delta)^{\sigma} \phi_R(t,x)\big| \lesssim \sum_{|\alpha|=2\sigma}\big|\partial_x^\alpha \phi_R(t,x)\big| \\ &\quad \lesssim \sum_{k=1}^{2\sigma} \Big(\varphi\Big(\frac{|x|{}^{2(\sigma-\delta)}+ t}{R}\Big)\Big)^{n+2(\sigma-\delta)- k} \\ &\qquad \times \left(\sum_{\substack{|\gamma_1|+\cdots+|\gamma_k|= 2\sigma \\ |\gamma_i|\ge 1}} \Big|\partial_x^{\gamma_1} \varphi\Big(\frac{|x|{}^{2(\sigma-\delta)}+ t}{R}\Big)\Big|\, \cdots \, \Big|\partial_x^{\gamma_k} \varphi\Big(\frac{|x|{}^{2(\sigma-\delta)}+ t}{R} \Big)\Big| \right) \\ &\quad \lesssim \sum_{k=1}^{2\sigma} \Big(\varphi^*\Big(\frac{|x|{}^{2(\sigma-\delta)}+ t}{R}\Big)\Big)^{n+2(\sigma-\delta)- k} \\ &\qquad \times \sum_{\substack{|\gamma_1|+\cdots+|\gamma_k|= 2\sigma \\ |\gamma_i|\ge 1}} \frac{|x|{}^{2(\sigma-\delta)- |\gamma_1|}}{R} \cdots \frac{|x|{}^{2(\sigma-\delta)- |\gamma_k|}}{R} \end{aligned} $$

(49)

$$\displaystyle \begin{aligned} &\quad \lesssim \sum_{k=1}^{2\sigma} \Big(\varphi^*\Big(\frac{|x|{}^{2(\sigma-\delta)}+ t}{R}\Big)\Big)^{n+2(\sigma-\delta)- k}\,\, \frac{|x|{}^{2k(\sigma-\delta)- 2\sigma}}{R^k} \\ &\quad \lesssim \frac{1}{R^{\frac{\sigma}{\sigma-\delta}}} \Big(\varphi^*\Big(\frac{|x|{}^{2(\sigma-\delta)}+ t}{R}\Big)\Big)^{n- 2\delta}\quad \big(\text{since }\,\, |x|{}^{2(\sigma-\delta)} \approx R \text{ in } Q^*_R\big). {} \end{aligned} $$

(50)

It is clear that if δ = 0, then |(− Δ)^δ ∂ _t φ _R(t, x)| was estimated in (47). For the case $\delta \in (0,\frac {\sigma }{2}]$, we can proceed in an analogous way as we controlled |(− Δ)^σ φ _R(t, x)| to derive

$$\displaystyle \begin{aligned} \big|(-\Delta)^{\delta}\partial_t \phi_R(t,x)\big| \lesssim \frac{1}{R^{\frac{\sigma}{\sigma-\delta}}} \Big(\varphi^*\Big(\frac{|x|{}^{2(\sigma-\delta)}+ t}{R}\Big)\Big)^{n+2(\sigma-2\delta)-1}. {} \end{aligned} $$

(51)

From (47) to (51), we arrive at the following estimate:

$$\displaystyle \begin{aligned} &\big|\partial_t^2 \phi_R(t,x)+ (-\Delta)^{\sigma} \phi_R(t,x)- (-\Delta)^{\delta}\partial_t \phi_R(t,x)\big| \\ &\qquad \lesssim \frac{1}{R^{\frac{\sigma}{\sigma-\delta}}} \Big(\varphi^*\Big(\frac{|x|{}^{2(\sigma-\delta)}+ t}{R}\Big)\Big)^{n-2\delta}= \frac{1}{R^{\frac{\sigma}{\sigma-\delta}}}\big(\phi^*_R(t,x)\big)^{\frac{n-2\delta}{n+2(\sigma-\delta)}}. \end{aligned} $$

Hence, we may conclude

$$\displaystyle \begin{aligned} J_R= |J_R| \lesssim \frac{1}{R^{\frac{\sigma}{\sigma-\delta}}} \int_{Q_R}|u(t,x)|\, \big(\phi^*_R(t,x)\big)^{\frac{n-2\delta}{n+2(\sigma-\delta)}}\,d(x,t). {} \end{aligned} $$

(52)

Now we focus our attention to estimate the above integral. To do this, we introduce the function $\Psi (s)= s^{p_c}\mu (s)$. Then, we derive

$$\displaystyle \begin{aligned} &\Psi\Big( |u(t,x)|\, \big(\phi^*_R(t,x)\big)^{\frac{n-2\delta}{n+2(\sigma-\delta)}}\Big) \\ &\qquad = |u(t,x)|{}^{p_c}\, \big(\phi^*_R(t,x)\big)^{\frac{p_c(n-2\delta)}{n+2(\sigma-\delta)}} \mu\Big( |u(t,x)|\, \big(\phi^*_R(t,x)\big)^{\frac{n-2\delta}{n+2(\sigma-\delta)}}\Big) \\ &\qquad \le |u(t,x)|{}^{p_c}\, \phi^*_R(t,x) \mu\big( |u(t,x)|\big)= \Psi\big( |u(t,x)|\big)\, \phi^*_R(t,x). {} \end{aligned} $$

(53)

Here we used the increasing property of the function μ = μ(s) and the relation

$$\displaystyle \begin{aligned}0\le \big(\phi^*_R(t,x)\big)^{\frac{n-2\delta}{n+2(\sigma-\delta)}} \le 1. \end{aligned}$$

Due to the assumption (44), we may verify that Ψ is a convex function on a small interval (0, c ₀] by the following relation:

$$\displaystyle \begin{aligned} \Psi''(s)= s^{p_c-2}\Big(p_c (p_c-1)\mu(s)+2p_c\, s\mu'(s)+ s^2 \mu''(s)\Big) \ge 0. \end{aligned}$$

Moreover, we can choose a convex continuation of Ψ outside this interval to guarantee that Ψ is convex on [0, ∞). Applying Proposition 1 with h(s) =  Ψ(s), $f(t,x)= |u(t,x)|\big (\phi ^*_R(t,x)\big )^{\frac {n-2\delta }{n+2(\sigma -\delta )}}$ and γ ≡ 1 gives the following estimate:

$$\displaystyle \begin{aligned} &\Psi\Big(\frac{\int_{Q^*_R} |u(t,x)|\big(\phi^*_R(t,x)\big)^{\frac{n-2\delta}{n+2(\sigma-\delta)}}\,d(x,t)}{\int_{Q^*_R} 1\,d(x,t)}\Big) \\ &\qquad \le \frac{\int_{Q^*_R} \Psi\Big( |u(t,x)|\big(\phi^*_R(t,x)\big)^{\frac{n-2\delta}{n+2(\sigma-\delta)}}\Big)\,d(x,t)}{\int_{Q^*_R} 1\,d(x,t)}. \end{aligned} $$

We may compute

$$\displaystyle \begin{aligned} \int_{Q^*_R} 1\,d(x,t)\approx R^{1+ \frac{n}{2(\sigma-\delta)}}. \end{aligned}$$

Hence, we get

$$\displaystyle \begin{aligned} &\Psi\Big(\frac{\int_{Q^*_R} |u(t,x)|\big(\phi^*_R(t,x)\big)^{\frac{n-2\delta}{n+2(\sigma-\delta)}}\,d(x,t)}{R^{1+ \frac{n}{2(\sigma-\delta)}}}\Big) \\ &\qquad \le \frac{\int_{Q^*_R} \Psi\Big( |u(t,x)|\big(\phi^*_R(t,x)\big)^{\frac{n-2\delta}{n+2(\sigma-\delta)}}\Big)\,d(x,t)}{R^{1+ \frac{n}{2(\sigma-\delta)}}} \\ &\qquad \le \frac{\int_{Q_R} \Psi\Big( |u(t,x)|\big(\phi^*_R(t,x)\big)^{\frac{n-2\delta}{n+2(\sigma-\delta)}}\Big)\,d(x,t)}{R^{1+ \frac{n}{2(\sigma-\delta)}}}. {} \end{aligned} $$

(54)

Combining the estimates (53) and (54) we may arrive at

$$\displaystyle \begin{aligned} &\Psi\Big(\frac{\int_{Q^*_R} |u(t,x)|\big(\phi^*_R(t,x)\big)^{\frac{n-2\delta}{n+2(\sigma-\delta)}}\,d(x,t)}{R^{1+ \frac{n}{2(\sigma-\delta)}}}\Big) \\ &\qquad \le \frac{\int_{Q_R} \Psi\big( |u(t,x)|\big)\, \phi^*_R(t,x)\,d(x,t)}{R^{1+ \frac{n}{2(\sigma-\delta)}}}. {} \end{aligned} $$

(55)

Since μ = μ(s) is a strictly increasing function, it immediately follows that Ψ =  Ψ(s) is also a strictly increasing function on [0, ∞). For this reason, from (55) we deduce

$$\displaystyle \begin{aligned} &\int_{Q_R} |u(t,x)|\big(\phi^*_R(t,x)\big)^{\frac{n-2\delta}{n+2(\sigma-\delta)}}\,d(x,t) \\ &\qquad = \int_{Q^*_R} |u(t,x)|\big(\phi^*_R(t,x)\big)^{\frac{n-2\delta}{n+2(\sigma-\delta)}}\,d(x,t) \\ &\qquad \le R^{1+ \frac{n}{2(\sigma-\delta)}}\,\Psi^{-1}\Big(\frac{\int_{Q_R} \Psi\big( |u(t,x)|\big)\, \phi^*_R(t,x)\,d(x,t)}{R^{1+ \frac{n}{2(\sigma-\delta)}}}\Big). {} \end{aligned} $$

(56)

From (46), (52) and (56) we may conclude

$$\displaystyle \begin{aligned} I_R \lesssim R^{\frac{n-2\delta}{2(\sigma-\delta)}}\,\Psi^{-1}\Big(\frac{\int_{Q_R} \Psi\big( |u(t,x)|\big)\, \phi^*_R(t,x)\,d(x,t)}{R^{1+ \frac{n}{2(\sigma-\delta)}}}\Big) {} \end{aligned} $$

(57)

for all R > R ₀. Next we introduce the following two functions:

$$\displaystyle \begin{aligned} g(r)= \int_{Q_R} \Psi\big( |u(t,x)|\big)\, \phi^*_r(t,x)\,d(x,t) \quad \text{ with } r\in (0,\infty) \end{aligned}$$

and

$$\displaystyle \begin{aligned} G(R)= \int_0^R g(r)r^{-1}\,dr. \end{aligned}$$

Then, we re-write

$$\displaystyle \begin{aligned} G(R) &= \int_0^R \Big(\int_{Q_R} \Psi\big( |u(t,x)|\big)\, \phi^*_r(t,x)\,d(x,t)\Big) r^{-1}\,dr \\ &= \int_{Q_R} \Psi\big( |u(t,x)|\big)\Big(\int_0^R \Big(\varphi^*\Big(\frac{|x|{}^{2(\sigma-\delta)}+ t}{r}\Big)\Big)^{n+2(\sigma-\delta)} r^{-1}\,dr\Big)\,d(x,t). \end{aligned} $$

Carrying out change of variables $\tilde {r}= \frac {|x|{ }^{2(\sigma -\delta )}+ t}{r}$ we derive

(58)

Moreover, it holds the following relation:

$$\displaystyle \begin{aligned} G'(R)R= g(R)= \int_{Q_R} \Psi\big( |u(t,x)|\big)\, \phi_R^*(t,x)\,d(x,t). {} \end{aligned} $$

(59)

From (57) to (59) we get

$$\displaystyle \begin{aligned} \frac{G(R)}{\log(1+e)} \le I_R \le C_1 R^{\frac{n-2\delta}{2(\sigma-\delta)}}\,\Psi^{-1}\Big(\frac{G'(R)}{R^{\frac{n}{2(\sigma-\delta)}}}\Big) \end{aligned}$$

for all R > R ₀ and with a suitable positive constant C ₁. This implies

$$\displaystyle \begin{aligned} \Psi\Big(\frac{G(R)}{C_2 R^{\frac{n-2\delta}{2(\sigma-\delta)}}}\Big) \le \frac{G'(R)}{R^{\frac{n}{2(\sigma-\delta)}}} \end{aligned}$$

for all R > R ₀ and $C_2:= C_1\log (1+e)> 0$. By the definition of the function Ψ, the above inequality is equivalent to

$$\displaystyle \begin{aligned} \Big(\frac{G(R)}{C_2 R^{\frac{n-2\delta}{2(\sigma-\delta)}}}\Big)^{p_c}\mu\Big(\frac{G(R)}{C_2 R^{\frac{n}{2(\sigma-\delta)}}}\Big) \le \frac{G'(R)}{R^{\frac{n}{2(\sigma-\delta)}}} \end{aligned}$$

for all R > R ₀. Therefore, we have

$$\displaystyle \begin{aligned} \frac{1}{C_3 R}\mu\Big(\frac{G(R)}{C_2 R^{\frac{n-2\delta}{2(\sigma-\delta)}}}\Big) \le \frac{G'(R)}{\big(G(R)\big)^{p_c}} \end{aligned}$$

for all R > R ₀ and $C_3:= C_2^{p_c}> 0$. Because G = G(R) is an increasing function, for all R > R ₀ it holds the following inequality:

$$\displaystyle \begin{aligned} \frac{1}{C_3 R}\, \mu\Big(\frac{G(R_0)}{C_2 R^{\frac{n-2\delta}{2(\sigma-\delta)}}}\Big) \le \frac{G'(R)}{\big(G(R)\big)^{p_c}}. \end{aligned}$$

After denoting $\tilde {s}:= R$ and integrating two sides over [R ₀, R] we arrive at

$$\displaystyle \begin{aligned} \frac{1}{C_3} \int_{R_0}^R \frac{1}{\tilde{s}}\, \mu\Big(\frac{1}{C_4 \tilde{s}^{\frac{n-2\delta}{2(\sigma-\delta)}}}\Big)\,d\tilde{s} &\le \int_{R_0}^R\frac{G'(\tilde{s})}{\big(G(\tilde{s})\big)^{p_c}}\,d\tilde{s} \\ &= \frac{n-2\delta}{2\sigma} \Big(\frac{1}{\big(G(R_0)\big)^{\frac{2\sigma}{n-2\delta}}}- \frac{1}{\big(G(R)\big)^{\frac{2\sigma}{n-2\delta}}}\Big) \\ &\le \frac{n-2\delta}{2\sigma \big(G(R_0)\big)^{\frac{2\sigma}{n-2\delta}}}, \end{aligned} $$

where $C_4:= \frac {C_2}{G(R_0)}> 0$. Letting R →∞ leads to

$$\displaystyle \begin{aligned} \frac{1}{C_3} \int_{R_0}^\infty \frac{1}{\tilde{s}}\, \mu\Big(\frac{1}{C_4 \tilde{s}^{\frac{n-2\delta}{2(\sigma-\delta)}}}\Big)\,d\tilde{s} \le \frac{n-2\delta}{2\sigma \big(G(R_0)\big)^{\frac{2\sigma}{n-2\delta}}}. \end{aligned}$$

Finally, using change of variables $s= C_4 \tilde {s}^{\frac {n-2\delta }{2(\sigma -\delta )}}$ we may conclude

$$\displaystyle \begin{aligned} C\int_{C_0}^\infty \frac{\mu\big(\frac{1}{s}\big)}{s}\,ds \le \frac{n-2\delta}{2\sigma \big(G(R_0)\big)^{\frac{2\sigma}{n-2\delta}}}, \end{aligned}$$

where $C:= \frac {2\sigma }{C_3(n-2\delta )}> 0$ and $C_0:= C_4 R_0^{\frac {n-2\delta }{2(\sigma -\delta )}}> 0$ is a sufficiently large constant. This is a contradiction to the assumption (45). Summarizing, the proof of Theorem 4 is completed.

□

Remark 4

From the condition (42) in Theorem 3 and the condition (45) in Theorem 4, we recognize that determining the critical exponent $p_{crit}= 1+ \frac {2\sigma }{n- 2\delta }$ in the scale of power nonlinearities {|u|^p}_p>1 is really sharp to (39) in the case $\delta \in [0,\frac {\sigma }{2}]$, i.e. for “parabolic like models”. However, up to now this observation remains an open problem for “σ-evolution like models” in the remaining case $\delta \in (\frac {\sigma }{2},\sigma ]$, the so-called “hyperbolic like models” or “wave like models” in the case σ = 1.

Appendix

Proposition 1 (A Generalized Jensen’s Inequality)

Let γ = γ(x) be a defined and nonnegative function almost everywhere on Ω, provided that γ is positive in a set of positive measure. Then, for each convex function h on$\mathbb {R}$the following inequality holds:

$$\displaystyle \begin{aligned} h\left(\frac{\displaystyle\int_\Omega f(x)\gamma(x)\,dx}{\displaystyle\int_\Omega \gamma(x)\,dx}\right) \le \frac{\displaystyle\int_\Omega h\big(f(x)\big)\gamma(x)\,dx}{\displaystyle\int_\Omega \gamma(x)\,dx}, \end{aligned}$$

where f is any nonnegative function satisfying all the above integrals are meaningful.

The proof of this result can be found in [5, 9].

Lemma 8 (Useful Lemma)

The following formula of derivative of composed function holds for any multi-index α:

$$\displaystyle \begin{aligned} \partial_\xi^\alpha h\big(f(\xi)\big)= \sum_{k=1}^{|\alpha|}h^{(k)} \big(f(\xi)\big)\left(\sum_{\substack{\gamma_1+\cdots+\gamma_k \le \alpha\\ |\gamma_1|+\cdots+|\gamma_k|= |\alpha|,\, |\gamma_i|\ge 1}}\big(\partial_\xi^{\gamma_1} f(\xi)\big) \cdots \big(\partial_\xi^{\gamma_k} f(\xi)\big)\right), \end{aligned}$$

where h = h(z) and$h^{(k)}(z)=\frac {d^k h(z)}{d\,z^k}$.

The result can be found in [11] at page 202.