1 Introduction

Graphs have emerged as a powerful model for representing different types of data, such as social networks and collaboration networks. In these graphs, discovering communities that naturally exist as groups of fine-connected users is one the most important tasks for network data analytics and has tremendous real applications. Nevertheless, most of the previous studies  [1, 4, 5, 10, 24, 29] have focused on finding communities from a graph without considering attributes. As such, the returned communities may miss out important attributes describing a variety of features of real applications. Recently, community search in graphs having attributes called attributed graphs has begun to attract attention  [6, 7, 11, 15, 20, 28]. These works endeavour to find communities that are both structure and attribute cohesive. Besides, there are also a few works  [18] that aim to find communities which are attribute diversified among them. However, a study for community search that takes serious consideration of structure cohesiveness but attribute diversification within a community is still at preliminary stage.

In this paper we focus on introducing our recent works for attribute diversified community search, including three attribute diversified community models in which the attribute diversification takes different roles for presenting an objective, a query requirement, and a constraint.

Maximizing Attribute Diversification. Discovering a community with members as diversified as possible has numerous applications. One example is building a team for group brainstorming to address a cognitive bottleneck of idea generation. Group brainstorming shall engage diversified individuals to collaborate by communicating and sharing ideas in groups, where diversified individuals can substantially broaden the knowledge base available for idea generation and the social engagements among the individuals allow the creative effort to be aggregated. Other examples are: gathering socially connected experts of different marketing fields to brainstorm a marketing session of different new products, selecting a panel of concerted engineers with different technological expertise for reviewing and testing different products to show the collective information pool of the panel, etc. For these applications, since they target community members for innovations and there are evidences that maximizing diversity leads to creativity  [22], the desired community would be preferred to maximise the attribute diversity of its members  [9].

Attribute Diversification with Specific Requirement. For some applications, the diversification requirements could be specific. Let us consider a real event happened in 2019. A small town in Australia was devastated by the severe bushfire, which results in at least 11 damaged properties and 33 people injured. The town needs community spirit to rebuild. This naturally arises the needs of several activities with diverse demands. A group needs to be formed urgently to react on the disaster, with at least 3 members having expertise in building temporary accommodations, 5 doctors, 4 psychologists, 2 members having the expertise in community support, etc. Each member may contribute to as many skills as possible in this kind of group. Due to damaged properties, a construction team also needs to be built for rebuilding these properties, with members having different skills, such as at least 2 architects, 11 members handling masonry, 5 members dealing with welding, etc. Due to the intensive labouring, each member may contribute at most 2 skills in this kind of construction teams since multi-tasking may lead to multi-failing. Due to the disaster, people may suffer a lot mentally. To help relief psychological pressure from these people, it would be great to organize an improvised music show to soothe them, which needs to discover musicians to form a band. The found musicians may be able to play multiple instruments. However, since they perform as a band, each of them shall focus on a single instrument. From these examples, it is clear that, apart from social cohesiveness and spatial closeness requirements, an effective community model for impromptu activities with diverse demands should allow people to express specific diversification requirements including: 1) collective capabilities of the group w.r.t. a particular skill, e.g., at least 3 members have expertise in building temporary accommodation; and 2) capacity of each member on maximum contribution the member can make, e.g., at most 2 skills in a construction team. This motivates us to study how to find an attribute diversified geo-social group with specific diversification requirements  [8].

Attribute Diversification as Constraint. Some applications would like to find a community that exhibits certain level of attribute diversification but has members with social relationships as cohesive as possible. For instance, assume that we need to find a group of organisers for organising a conference. To make the organisation smooth, the organisers are expected to communicate and collaborate with each other extensively. The more that organisers identify with each other, the more likely they are to believe that they hold similar goals for successfully organising the conference. On the other hand, to make the conference accept various ideas, we also expect that the organisers would jointly share a variety of domains. Similar applications include promoting a product through commonly associated experts of difference domains, team formations for maximising productivity, etc. Motivated by these applications, we introduce a novel community model that considers attribute diversification as a constraint while maximising the structure cohesiveness as the primary searching objective.

Road Map. The rest of this paper is organized as follows. In Sect. 2, we introduce and discuss basics for attributed graphs. In Sects. 3, 4, and 5 we discuss our recent attribute diversification community search works. We discuss the related works and conclude this paper in Sects. 6 and 7.

2 Preliminaries

In this section, we first formally introduce the commonly used community cohesiveness metrics and attributes diversification metrics.

An attributed graph is denoted as \(G=(V,E,A)\), where V(G), E(G), A denote the set of vertices in G, the set of edges in G, and the set of attributes in terms of keywords respectively. Each vertex \(v\in V(G)\) is attached with a set of attributes \(A(v) \subseteq A\). Given \(v\in V(G)\), deg(v, G) denotes the degree of v in G and N(v, G) denotes the neighbours of v in G. A triangle in G is a cycle of length 3. A triangle induced on vertices \(u,v,w\in V(G)\) is denoted as \(\triangle _{uvw}\) and when these vertices are not specified we omit the subscript. Given a subgraph \(H\subseteq G\), Tri(H) denotes the set of triangles in H.

2.1 Social Cohesiveness Metrics

Coreness. Coreness is defined according to the degree of every vertex.

Definition 1

k -core subgraph. Given a subgraph \(H\subseteq G\), an integer k, H is called k-core subgraph if for every \(v\in V(H)\), \(deg(v,H)\ge k\) and such maximum k is called the coreness of H.

Intuitively, a k-core is a subgraph in which vertex has at least k neighbours. A k-core with a large value k indicates strong internal connections over vertices. A k-core is maximal if it cannot be extended.

Trussness. Trussness is defined based on the number of triangles each edge is involved in a graph. In general, given a subgraph \(H\subseteq G\), we use \(\bigtriangleup _{uvw}\) to denote a triangle, a cycle with length of 3, consisting of vertices \(u,v,w\in V(H)\).

Support. The support of an edge \(e(u,v)\in E(H)\), denoted by sup(e, H), is the number of triangles containing e, i.e., \(sup(e,H)=|\{\bigtriangleup _{uvw}:w\in N(v,H)\cap N(u,H)\}|\), where N(v, H) and N(u, H) are the neighbours of u, v in H correspondingly.

Minimum Subgraph Trussness. The trussness for a subgraph H is defined as an integer k that is 2 plus the minimum possible support for edges in E(H). That is, the minimum subgraph trussness defines that for every edge \(e\in E(H)\), the number of triangles in which e participates shall be no less than k - 2.

Definition 2

c -truss constraint. A subgraph H satisfies c-truss constraint if the trussness of H is c, and c is connected.

Intuitively, if H satisfies c-truss constraint, the vertices of an edge in H have at least c-2 common neighbours in H, every vertex in H has no less than c-1 neighbours and at least c-1 edges have to be deleted in order to make H disconnected. The communication cost of H is at most \(\lfloor \frac{2|V(H)|-2}{c} \rfloor \). A H with a large value c indicates strong internal social relationships over vertices.

2.2 Attribute Diversification Metrics

Diversity for Two Vertices. Given a pair of vertices, \(u,v\in V(G)\) with attributes A(u) and A(v), a diversity function is defined as \(div((u,v)) = 1- \frac{|A(u)\cap A(c)|}{|A(u)\cup A(v)|}\).

Average Based Diversity. Given H, the attribute diversification of H is measured by \(avgDiv(H) = \frac{\sum _{(u,v)\in H}div((u,v))}{|V(H)|}\).

We will introduce detailed attribute diversification metrics when introducing the specific models.

Fig. 1.
figure 1

Graph with edge diversity

Full size image

3 Discovering a Community Maximizing Attribute Diversity

In this section, we introduce an attribute diversified community search work  [9] that aims to find a community maximizing the attribute diversity. We first introduce the community model and search problem, then discuss the search framework and optimizations, respectively.

3.1 Problem Definition

Attribute Diversified Community. We propose the attribute diversified community model, using k-core and average based diversification metric.

Definition 3

Attribute diversified community. Given a subgraph \(H\subseteq G\), an integer k, H is defined as an attribute diversified community if H satisfies the following constraints simultaneously:

  • Connectivity: H is connected;

  • Structure Cohesiveness: H is a k-core subgraph;

  • Maximizing Average Diversity: for avgDiv(H), H is \(argmax_{H^{\prime }}\) \(\{avgDiv(H^{\prime }) | H^{\prime }\subseteq G\}\);

Accordingly, given G and an integer k, the research problem we focus on in this paper is as follows.

Research Problem. Find the subgraph \(H\subseteq G\) that maximises avgDiv(H).

Example 1

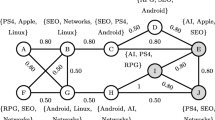
To briefly show the results of the above problem, we discuss the example shown in Fig. 1. For the attribute diversified community search problem with \(k=2\), the result is the \(\{B, C, F, G, H, I, J, L, M\}\) induced subgraph with diversity of 1.44.

3.2 Search Framework

For ease of understanding, we first show the basic enumeration used in the branch and bound algorithm.

figure a

Algorithm 1 shows the basic enumeration that derives the optimum result. Initially the input of the algorithm is G. By recursively calling itself, Algorithm 1 tries all possible subgraphs of G if the subgraphs may contain the optimum result and checks if there is a feasible solution in the current recursion. If there is a feasible solution h in the recursion and the feasible solution is greater than the current optimum one \(H^{*}\), \(H^{*}\) is updated to h.

Search Space Reduction. Algorithm 1 also applies space reduction optimisations based on the observations as follows.

Observation 1

The optimum result can only be contained in a connected k-core of G if it exists when the enumeration starts.

Observation 2

During the recursion with an input H, the optimum result can only be contained in a connected k-core of H.

With the observations, when a recursion starts, Algorithm 1 first reduces the input to the maximal k-core, which would transform the input into a set of maximal connected k-cores. Algorithm 1 only tries combinations in each connected k-core. As such, the search space can be reduced significantly.

3.3 Optimisations

Upper Bound Based Pruning. The idea is that we estimate the upper bound of the average edge diversity of the current search branch. If the upper bound is smaller than the diversity of the optimum result found so far, we terminate the search branch.

Next, we will propose three upper bounds.

Upper Bound Based on Core Property. We firstly show an upper bound for a connected k-core based on core property. The upper bound for h is defined as follows.

$$\begin{aligned} ubcore(h)= \frac{\sum _{(u,v)\in E(h)} div((u,v))}{k+1} \end{aligned}$$
(1)

The upper bound based on core property would only be tight when h contains an optimum result with size close to \(k+1\). However, it has limited pruning effectiveness when h contains large-size results. Next we study tight bounds for arbitrary h.

Maximum Average Diversity in a Core. Given a connected k-core h, this bound is defined as follows.

$$\begin{aligned} ubavg(h)= max\{avgDiv(h')|h'\subseteq h\} \end{aligned}$$
(2)

Lemma 1

ubavg(h) is an upper bound for h.

Approximate Maximum Average Diversity in a Core. The computational cost of ubavg(h) is high. It would take \(O(|V(h)|^{3})\) if using the algorithm in  [13]. However, there is a simple but effective approximate algorithm  [3] that can achieve \(\frac{1}{2}\)-approximation with complexity O(|E(h)|). As such we can use the approximation algorithm to get an at least \(\frac{1}{2}\) ubavg(h) value first and then multiple it by 2 to derive a slightly loose bound, denoted as apxubavg(h). In implementation, ubcore(h) and apxubavg(h) are prioritised as they are cheap.

Search Order. For each connected k-cores that cannot be pruned, we sort them in non-increasing order according to their upper bounds. By doing this, we can heuristically find communities with large average diversity as early as possible. This would make the upper bound based pruning more effective.

4 Discovering Attribute Diversified Geo-Social Group with Specific Requirement

In this section, we tackle the problem of finding an attribute diversified geo-social group with the given specific diversification requirements  [8]. We first introduce the query, model and search problem. Then the novel search framework is discussed. After that, the optimizations for speeding up the search are introduced.

Fig. 2.
figure 2

Running example

Full size image

4.1 Problem Formulation

Data. We consider an undirected graph data \(G=(V,E)\) with network structure, spatial attribute and textual attributes. For each vertex \(v\in V(G)\), v has a piece of location information expressed as latitude and longitude denoted as (v.x, v.y), and has a set of keyword attributes denoted as v.A.

Since our proposed group model would satisfy minimum keyword, capacity and social constraints while optimizing spatial closeness, we name the proposed model as \(\textsf {MKCSSG}\). Our proposed geo-social model is introduced as follows.

We formally define the query for searching MKCSSG.

Query for . The query Q for MKCSSG consists of a social parameter c (an integer), a set of keywords \(\varphi \), keyword parameters P (a set of integers), r (an integer), and a location \(\lambda \) (latitude and longitude).

Minimum Keyword and Capacity Constraints. Given a set of query keywords \(\varphi \) \(=\) \(\{k_{1},\ldots , k_{|\varphi |} \}\), \(P=\{\rho _{1},\ldots , \rho _{|\varphi |} \}\), r, and S, MKCC is defined below.

Definition 4

Minimum keyword and capacity constraints, . S satisfies MKCC if there is a \(v.A^{\prime }\subseteq \varphi \cap v.A\) for every \(v\in \) V(S) such that:

  • Capacity constraint: \(|v.A^{\prime }|\le r\),

  • Minimum keyword constraint (MKC): \(\forall \) \(k_{i}\in \varphi \), \(|V(S_{k_{i}})|\) \(\ge \rho _{i}\), where \(V(S_{k_{i}})\) is the set of vertices such that for each \(v\in V(S_{k_{i}})\), \(v.A^{\prime }\) contains \(k_{i}\in \varphi \).

Searching Objective. Now, we formalize the spatial closeness for MKCSSG and the research problem.

Spatial Closeness. Given a query location \(\lambda \), we consider a distance function to measure the closeness between \(\lambda \) and an MKCSSG S as:

Definition 5

Spatial closeness. \(dist(\lambda ,S) = max\{\Vert \lambda -v\Vert |v\in V(S)\}\),

where \(\Vert \lambda -v \Vert \) denotes Euclidean distance between v and \(\lambda \).

Definition 6

(P, c, r, d)-truss. Given \(Q=\{\lambda ,P,\varphi ,c, r\}\) and a distance threshold d, a subgraph \(S\subseteq G\) is a (P, c, r, d)-truss, if it satisfies all the conditions: 1) S satisfies MKCC, 2) S satisfies c-truss constraint, 3) \(dist(\lambda ,S)\) \(\le \) d.

Research Problem.  search. Given \(Q=\{\lambda \), P \(\varphi ,\) c,  \(r\}\) and G, return (P, c, r, d)-truss \(S^{*}\) so that there is no \((P,c, r, d')\)-truss \(S'\) with \(d'\le d\).

Example 2

An example dataset is shown in Fig. 2, where Fig. 2(a) shows locations for vertices of graph data in Fig. 2(b). Let the query be: Q \(=\) {\(\lambda ,\) \(P=\{2,2,2\}\), \(\varphi =\{k_{1}, k_{2}, k_{3}\}\), \(c=4\), \(r=1\)}. \(\{d,e,f,g,h,i\}\) induced subgraph \(S^{*}\) is the optimum result for Q for this dataset. \(S^{*}\) satisfies social constraint, i.e., every edge in \(E(S^{*})\) involves no less than 2 triangles. \(S^{*}\) satisfies MKCC. That is, it firstly satisfies capacity constraint, i.e., every vertex contributes to at most one keyword in \(\varphi \), where \(d.A'=\{k_{1}\}\), \(e.A'=\{k_{2}\}\), \(f.A'=\{k_{3}\}\), \(g.A^{'}=\{k_{1}\}\), \(h.A'=\{k_{2}\}\), \(i.A'=\{k_{3}\}\). Then it satisfies MKC, i.e., with the \(A'\) for each vertex (those underlined), the keyword vertex frequency for every query keyword is no less than 2. Last but not least, among all groups satisfying the constraints, \(S^{*}\) is the closest one to \(\lambda \) and the most distant vertex (to \(\lambda \)) in \(S^{*}\) is f.

4.2 Search Framework

We firstly introduce some definitions.

Definition 7

d radius bounded graph. Given a query location \(\lambda \), a subgraph H and a distance threshold d, d radius bounded graph, denoted as \(H_{\le d}\), is the subgraph of H induced by vertices of H with distance to \(\lambda \) no greater than d.

We would like to highlight an instance of d radius bounded graph, \(d^{*}\) radius bounded graph, \(H_{\le d^{*}}\). \(H_{\le d^{*}}\) has the property below. There is no \(H_{\le d'}\) such that \(H_{\le d'}\) contains MKCSSG and \(d'\) < \(d^{*}\).

Optimum Search Space. We refer \(H_{\le d^{*}}\) as optimum search space since it is just large enough to contain MKCSSG for the query.

The Framework. MKCSSG search framework consists of two stages: expanding stage and reducing stage. During the expanding stage, it intends to quickly identify \(H_{\le d}\) that is just sufficiently large to contain the optimum search space \(H_{\le d^{*}}\) by exploring \(H_{\le d}\) that progressively gets larger, in which it determines the existence of a subgraph satisfying all constraints. For the reducing stage, to get the optimum result, it attempts to progressively remove the vertex that is the most distant to \(\lambda \) in \(S^{*}\). The last survived (\(\rho \), c)-truss during the vertices removing process is the optimum result.

4.3 Optimizations for Expanding Stage

Expanding Strategy. We first define an expanding invariant as follows.

Definition 8

\(\varDelta \) size invariant. Let \(\{d_{1}, d_{2}, \ldots , d_{i}\}\) be the series of radius for defining d radius graphs, for any two consecutive d, \(d'\), we define \(\varDelta \) invariant as \(\varDelta \) \(=\) \(\frac{|E(H_{\le d'})|}{|E(H_{\le d})|}\), in which \(\varDelta > 1\) must hold.

The Strategy. The strategy applied for the expanding stage is to maintain \(\varDelta \) size invariant over any two consecutively evaluated \(H_{\le d}\), \(H_{\le d'}\). Applying \(\varDelta \) invariant for expanding stage guarantees two nice properties below. Now, let us show the tight bound that is guaranteed by applying the proposed expanding strategy.

Initial Expanding Range. Intuitively, if the initial search range is close to \(d^{*}\), the total amount of subgraphs that has to be evaluated to approaching \(H_{\le d^{*}}\) is less. This motivates us to study a lower bound of d radius subgraph.

Definition 9

\(H_{\le \underline{d}}\). A subgraph \(H_{\le \underline{d}}\) of H is a lower bound d radius subgraph of \(H_{\le d^{*}}\) if it satisfies conditions: 1) \(H_{\le \underline{d}}\) is connected, 2) \(H_{\le \underline{d}}\) satisfies minimum keyword constraint and 3) there is no \(H'\subseteq H_{\le \underline{d}}\) such that \(H'\) satisfies the first two constraints and \(dist(\lambda ,H^{\prime })\) < \(dist(\lambda ,\) \(H_{\le \underline{d}})\).

Checking (\(\varvec{\rho }\), \(\textit{\textbf{c}}\))-truss in \(\textit{\textbf{d}}\) Radius Subgraph. To simplify the discussion, for any two consecutive \(H_{\le d}\) and \(H_{\le d'}\) with \(\frac{|H_{\le d'}|}{|H_{\le d}|} = \varDelta \), let us introduce a new notation \(H_{d'\setminus d}\) to denote the subgraph of \(H_{\le d'}\) induced by vertices appearing in edges of \(E(H_{\le d'})\) \(\setminus \) \(E(H_{\le d})\).

We propose two techniques to speed up (\(\rho \), c)-truss checking below.

. Given \(H_{\le d}\), we only apply \((\rho , c)\)-truss checking on any subgraph potentially containing \((\rho , c)\)-truss, defined as \(\rho \) potential subgraph below.

\(\rho \) potential subgraph \(P_{\le d}\). A subgraph \(P_{\le d}\) \(\subseteq \) \(H_{\le d}\) is defined as \(\rho \) potential subgraph if it is connected, satisfies minimum keyword constraint and is maximal within \(H_{\le d}\).

The Strategy. Since a \((\rho , c)\)-truss should reside in \(P_{\le d}\), we propose lazy \((\rho , c)\)-truss checking strategy that applies \((\rho , c)\)-truss constraint checking on every \(P_{\le d}\) in \(H_{\le d}\) only instead of the entire \(H_{\le d}\).

Union with Existing Truss. To avoid graph traversing for checking minimum keyword constraint and connectivity after updating trussness, we propose a solution below. Firstly, we maintain every maximal connected c truss subgraph in every \(P_{\le d}\), each of which is attached with keyword vertex frequency. Secondly, after \(P_{\le d}\) is expanded to \(P_{\le d'}\), we update the maintained c-truss subgraphs if applicable. Although this approach cannot update trussness for existing truss subgraphs precisely, it is sufficient and efficient to check the existence of \((\rho , c)\)-truss in \(P_{\le d'}\). As such, minimum keyword constraint and connectivity checking for truss subgraphs can be performed simultaneously and incrementally.

4.4 Optimizations for Reducing Stage

We will maintain a minimum spanning forest for S (the result of the expanding stage) augmented with aggregated keyword vertex frequency. Notice that initially, every spanning tree in the forest satisfies minimum keyword constraint. After an edge is deleted from S, one of the two cases below may happen.

Case 1: the deleted edge is not in the forest. The remaining subgraphs are still connected and each connected subgraph still satisfies minimum keyword constraint.

Case 2: the deleted edge is in the forest. In this case, one of the tree in the minimum spanning forest is cut into two trees, which may lead to one of the following subcases.

Subcase 1: cannot link the cut trees. We cannot find a replacement edge from the remaining S to link the two trees, which means the subgraph referred by the two trees becomes two disjoint subgraphs. We update keyword vertex frequency for each of the cut tree. After the update, we safely prune the cut tree from the maintained spanning forest if it does not satisfy minimum keyword constraint since they cannot contribute to MKCSSG.

Subcase 2: can link the cut trees. If we can find a replacement edge, the subgraph referred by two cut trees is still connected. We link the two trees with the replacement edge. Keyword vertex frequency remains the same.

To efficiently maintain the above index, we borrow the idea from [14]. Given S, every edge in E(S) is associated with a level progressively increased as edges are deleted, which is equivalent to progressively partitioning S hierarchically. Edges with high level refer to a more restricted part of S. In contrast, edges with low level refer to a more general part of S (super graphs of the high level subgraphs). As such when deleting an edge with a certain level, we do not need to consider any edge with lower level as a replacement edge, which elegantly reduces the search space for finding a replacement edge.

4.5 Optimizations for Keyword Constraint Checking

We will show that MKCC checking for a set of vertices S, query keywords \(\varphi \) \(=\) \(\{k_{1},\ldots , k_{|\varphi |} \}\), \(P=\{\rho _{1},\ldots , \rho _{|\varphi |} \}\) and r can be reduced to an instance of the min cut problem.

The Instance of Maximum Flow Problem. We construct the flow network N based on \(\varphi \), P, r and S. N consists of different types of nodes below. For each keyword in \(\varphi \), we create a keyword node. For each vertex in S, we create a vertex node. Additionally, we create a source node s and a sink node t. The edges and capacities for N are as follows. For each vertex node n, we create an edge from s to n with capacity of r. For each keyword node \(n'\) representing \(k_{i}\), we create an edge from \(n'\) to t with capacity of \(\rho _{i}\). In addition, there is an edge between a vertex node n and a keyword node \(n'\) (from n to \(n'\)) if the keyword attributes of n representing vertex contain the query keyword represented by \(n'\), and the capacity between n and \(n'\) is set to \(\infty \).

Lemma 2

S satisfies MKCC if there exists a min cut for N whose T part contains the node t only.

We adopt preflow–push (push-relabel) algorithm to solve the min cut problem. As such, the time complexity of MKCC checking for MKCSSG search is shown below.

checking complexity for the expanding stage. This part can be bounded by \(\mathcal {O}\) \(((1+\varDelta ^{3} + \frac{1}{\varDelta ^{3}-1})\) \(\times \) \(|V(H_{\le d^{*}})|^{3})\), assuming \(|\varphi |\ll |V(H_{\le d^{*}})|\). As discussed previously, by letting \(\varDelta =2\), the time complexity becomes the minimum, \(\mathcal {O}\) \((|V(H_{\le d^{*}})|^{3})\).

checking complexity for the reducing stage. This part can be bounded by \(\mathcal {O}\) \((|V(H_{\le d^{*}})|^{3})\) as well, by taking advantage of the preflow-push algorithm.

5 Discovering a Community with Attribute Diversification Constraint

In this section we introduce an attribute diversified community search work that focuses on finding a community maximizing the structure cohesiveness while maintaining the attribute diversity to a certain level. The community model is discussed firstly. Then the solution vision is introduced.

5.1 Problem Formulation

We formally define the subgraph diversity below.

Definition 10

Subgraph diversity. Given a subgraph \(H\subseteq G\), we define its subgraph diversity as:

$$ \tau (H) = min\{div(u,v)|\forall u,v \in V(H), u\ne v\} $$

Definition 11

\((k,\tau )\) -core. Given a subgraph \(H\subseteq G\), a pairwise vertex diversity threshold \(\tau \), H is a \((k,\tau )\)-core if H satisfies the following constraints simultaneously: 1) H is connected, 2) \(\forall v\in V(H)\), \(deg(v)\ge k\), 3) \(\tau (H)\ge \tau \).

Research Problem. Most cohesive diversified community search. Given an attributed graph G, a user given attribute diversity threshold \(\tau \), find a \((k,\tau )\)-core \(H\subseteq G\) such that there is no \((k',\tau )\)-core \(H'\) with \(k'\) greater than k.

5.2 Solution Vision

We introduce a definition and an observation as follows.

Definition 12

Diversity Subgraph. Given a subgraph diversity threshold \(\tau \), let D denote a new graph named as diversity graph with \(V(D) = V(G)\) and \(E(D) = \{(u, v)\) | \(div(u, v) \ge \tau \) and \(u, v \in V(G)\}\).

Observation 3

Given a \((k,\tau )\)-core H, the V(H) induced subgraph of D is a complete subgraph (i.e., a clique).

We are ready to discuss the vision of our proposed algorithms.

\(\underline{{Baseline}}\). The baseline algorithm enumerates all maximal cliques of D using the state-of-the-art clique enumeration algorithm. When a maximal clique C is generated, it runs core decomposition for G(C). If the largest core number of G(C) is greater than the largest k of the \((k,\tau )\)-core found so far, then G(C) contains the best \((k,\tau )\)-core found so far. After evaluating all the maximal cliques in D, the optimum result is found. The correctness of the baseline algorithm is clear since the vertices in a most cohesive \((k,\tau )\)-core must be resident at one of the maximal cliques in D.

Core Based Heuristic. To speed up the baseline, we consider a core based heuristic: vertices in a large core will be considered prior to the vertices in a small core. Using this heuristic, we may terminate the search quite early, i.e., let k be the largest k for \((k,\tau )\)-core found so far, if the core number of the current explored vertex is smaller than k, then we can terminate the search.

Advanced Heuristic. The core based heuristic just considers prioritising vertices that are structurally promising. Since the definition of the \((k,\tau )\)-core considers both the structure and the attribute properties, a heuristic that prioritises vertices that are promising from both structure cohesive and attribute diversified perspectives would be better. We propose a novel index denoted as KD-Index to help us identify the vertices that are promising from both the structure cohesive and the attribute diversified perspectives. To make the index general for different \(\tau \), we pre-compute promising vertices for different diversity thresholds. When a query \(\tau \) is given, we evaluate the precomputed index that is just smaller than \(\tau \) for speeding up the search.

Better Local Enumeration Order. The advanced heuristic provides an overall search order. However, when evaluating each promising subgraph, the local search order can be further optimised for speeding up the search. We propose to use the degeneracy order when evaluating vertices in a promising subgraph, which can nicely bound the search depth of the promising subgraph to the degeneracy of the subgraph. The degeneracy of the subgraph is much smaller than the total number of vertices contained in the subgraph.

6 Related Work

Community Search in Attributed Graph. In  [18], Li et al. propose a skyline community model for searching communities in attributed graph. Zhang et al. propose (k, r)-core community model that considers k-core and pairwise vertex similarity  [28]. Fang et al. propose a community model that is sensitive to query attributes. In  [16], an attributed community model is proposed by using k-truss for capturing social cohesiveness and the resultant community shall contain attributes similar with query attributes. In  [12, 23], community models considering spatial closeness are studied. The works above would find communities with users having similar attributes while our work find communities with users having diversified attributes. In [6], a parameter-free contextual community model is studied. Community models considering influence are studied in  [2, 17, 19]. In  [2, 19], the authors use max-min objective function, which aims to find influential communities where scores are defined on vertices.

Community Detection in Attributed Graph. Works including [21] consider graph structure with LDA model to detect attributed communities. Unified distance  [30] is also considered for detecting attributed communities. In  [30], attributed communities are detected by using proposed structural/attribute clustering methods, in which structural distance is unified by attribute weighted edges. Xu et al.   [26] propose a Bayesian based model. In  [15], Huang et al. propose a community model considering attributes based on an entropy-based model. Recently, Wu et al. propose an attributed community model  [25] based on an attributed refined fitness model. Yang et al.  [27] propose a model using probabilistic generative model.

7 Conclusion and Open Problems

In this paper, we introduce our recent works on attribute diversified community search. Based on the detailed real application scenarios, different attribute diversified community models are introduced where the attribute diversification takes the roles of objective, query requirement and constraint. For each of the community model, the search framework as well as major optimizations for speeding up the search are discussed in great detail.

Although we have made a fair effort for discovering attribute diversified communities, however the study is still at preliminary stage. We conclude by introducing an open problem for attribute diversified community search.

How to effectively model and efficiently search top-r attribute diversified community considering both inter and intra attribute diversifications?