Keywords

1 Introduction

New drug research and development is still a time-consuming, high-risky and tremendously costly process [1,2,3,4]. Although the investment in new drug research and development has been increasing, the number of new drugs approved by the US Food and Drug Administration (FDA) has remained limited in the past few decades [5,6,–7]. Therefore, more and more biomedical researchers and pharmaceutical companies are paying attention to the repositioning for existing drugs, which aims to infer the new therapeutic uses for these drugs [8,9,10,11]. For example, Thalidomide, and Minoxidil, were repositioned as a treatment to insomnia and the androgenic alopecia, respectively [12,13,14,15]. In other words, drug repositioning is actually to infer and discover potential drug-disease associations [16].

Recently, some computational methods have been presented to identify associations of drugs with diseases, such as deep walk embedding [17, 18], rotation forest [19,20,21,22], network analysis [23,24,25], text mining [26, 27] and machine learning [28,29,30,31], etc. Martínez et al. proposed a new approach named DrugNet, which performs disease-drug and drug-disease prioritization by constructing a heterogeneous network of interconnected proteins, drugs and diseases [32]. Wang et al. developed a triple-layer heterogeneous network model called TL-HGBI to infer drug-disease potential associations [33]. The network integrates association data and similarity about targets, drugs and diseases. Luo et al. utilized Bi-Random walk algorithm and comprehensive similarity measures (MBiRW) to infer new indications for existing drugs [34]. In fact, predicting associations of drug with disease can be transformed into a recommendation system problem [35,36,37,38]. Luo et al. developed a drug repositioning recommendation system (DRRS) to identify new indications for a given drug [39]. In this work, we develop a novel computational model WGMFDDA, which utilizes graph regularized matrix factorization to infer the potential associations between drugs and diseases. The experiment results indicate that the performance of WGMFDDA is better than other compared methods.

2 Methods and Materials

2.1 Method Overview

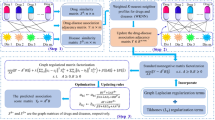
To predict potential associations of drugs with diseases, the model of WGMFDDA consists of three steps (See Fig. 1): (1) we measure the similarity for drugs and diseases based on the collected dataset; (2) According to the weighted \( {\text{K}} \)-nearest neighbor profiles of drugs and diseases, the drug-disease association adjacency matrix is re-established; (3) the graph Laplacian regularization and Tikhonov (\( {\text{L}}_{2} \)) terms are incorporated into the standard Non-negative matrix factorization (NMF) framework to calculate the drug-disease association scores.

Fig. 1.
figure 1

Overview of the WGMFDDA framework.

Full size image

2.2 Dataset

In this study, we obtain the dataset (Fdataset) from Gottlieb et al. [40]. This dataset is used as the gold standard datasets for identifying drug-disease associations, which includes 1933 known associations between 313 diseases and 593 drugs [41, 42]. In order to more conveniently describe the drug-disease associations information, the drug-disease association adjacency matrix \( Y^{n \times m} \) is constructed, where \( n \) and \( m \) are the number of drugs and diseases, respectively. The element \( Y\left( {i,j} \right) = 1 \) if drug \( r_{i} \) associated with disease \( d_{j} \), otherwise \( Y\left( {i,j} \right) = 0 \). The similarities for drugs and diseases are obtained from the Chemical Development Kit (CDK) [43] based on SMILES [44] and MimMiner [45] based on the OMIM [41] database, respectively. In ten-fold cross-validation experiments, all known associations are random divided into ten equal sized subsets, in which the training data set occupies 9/10, and the remaining partition is utilized as the test set.

2.3 Reformulate the Drug-Disease Association Adjacency Matrix

Let \( R = \left\{ {r_{1} ,r_{2} , \cdots ,r_{n} } \right\} \) and \( D = \left\{ {d_{1} ,d_{2} , \cdots ,d_{m} } \right\} \) are the set of \( n \) drugs and \( m \) diseases. \( Y\left( {r_{i} } \right) = \left( {Y_{i1} ,Y_{i2} , \cdots ,Y_{im} } \right) \) and \( Y\left( {d_{j} } \right) = \left( {Y_{1j} ,Y_{2j} , \cdots ,Y_{nj} } \right) \) are the \( i{\text{th}} \) row vector and \( j{\text{th}} \) column vector of matrix \( Y \), respectively. \( Y\left( {r_{i} } \right) \) and \( Y\left( {d_{j} } \right) \) denote the interaction profiles of drugs and diseases, respectively. Since many drug-disease pairs with unknown associations (i.e. the value of these elements in \( Y \) is zero) may be potential true associations, this will affect prediction performance. In order to assign associated likelihood scores to drug-disease pairs with unknown associations, weighted \( K \)-nearest neighbor (WKNN) is implemented to calculate new interaction profiles of drugs and diseases [38, 46].

For each drug \( r_{p} \) (or disease \( d_{q} \)), the novel interaction profile can be calculated as follows:

$$ Y_{r} \left( {r_{p} } \right) = \frac{1}{{\mathop \sum \nolimits_{1 \le i \le K} S^{R} \left( {r_{i,} r_{p} } \right)}}\sum\nolimits_{i = 1}^{k} {a^{i - 1} *S^{R} \left( {r_{i,} r_{p} } \right)Y\left( {r_{i} } \right)} $$
(1)

or

$$ Y_{d} \left( {d_{q} } \right) = \frac{1}{{\mathop \sum \nolimits_{1 \le j \le K} S^{D} \left( {d_{j,} d_{q} } \right)}}\sum\nolimits_{j = 1}^{k} {a^{j - 1} *S^{D} \left( {d_{j,} d_{q} } \right)Y\left( {d_{j} } \right)} $$
(2)

\( a \in \left[ {0,\,1} \right] \) denotes a decay term. \( S^{R} \) and \( S^{D} \) are the similarity matrices for drugs and diseases, respectively.

Subsequently, we define the updated association adjacency matrix \( Y \) as follows:

$$ Y = { \hbox{max} }\left( {Y,\,Y_{rd} } \right) $$
(3)

where

$$ Y_{rd} = \left( {Y_{r} + Y_{d} } \right)/2 $$
(4)

2.4 WGMFDDA

The standard Nonnegative matrix factorization (NMF) aims to find two low-rank Nonnegative matrices whose product as more as possible to approximation to the original matrix [36, 47,48,49]. \( Y \cong A^{T} B\left( {k \le { \hbox{min} }\left( {n,m} \right)} \right) \), \( A \in R^{k \times n} \) and \( B \in R^{k \times m} \). To avoid overfitting, the graph Laplacian regularization and Tikhonov (\( L_{2} \)) terms are introduced into the standard NMF model. The objective function of WGMFDDA can be constructed as follows:

$$ \begin{aligned} \mathop {\hbox{min} }\limits_{A, B} \left\| {Y - A^{T} B} \right\|_{F}^{2} + \lambda \left( {\sum\nolimits_{i \le j}^{n} {\left\| {a_{i} - a_{j} } \right\|^{2} S_{ij}^{R*} + \sum\nolimits_{i \le j}^{m} {\left\| {b_{i} - b_{j} } \right\|^{2} S_{ij}^{D*} } } } \right) \hfill \\ + \beta \left( {\left\| A \right\|_{F}^{2} + \left\| B \right\|_{F}^{2} } \right) s.t. A \ge 0, B \ge 0 \hfill \\ \end{aligned} $$
(5)

where \( \left\| \cdot \right\|_{F} \) denotes the Frobenius norm. \( \lambda \) and \( \beta \) are the regularization parameters. \( a_{j} \) and \( b_{j} \) are \( j{\text{th}} \) column of matrices \( A \) and \( B \), respectively. \( S^{R*} \) and \( S^{D*} \) denote the sparse similarity matrices for drugs and diseases, respectively.

According to the spectral graph theory, the \( p \)-nearest neighbor graph can preserve the intrinsic geometrical structure of the original data [46]. Therefore, \( p \)-nearest neighbors is utilized to construct the graphs \( S^{R*} \) and \( S^{D*} \). The details are as follows:

$$ W_{ij}^{R} = \left\{ \begin{aligned} \begin{array}{*{20}c} 1 & {i \in N_{p} \left( {r_{j} } \right)\& j \in N_{p} \left( {r_{i} } \right)} \\ \end{array} \hfill \\ \begin{array}{*{20}c} 0 & {i \notin N_{p} \left( {r_{j} } \right)\& j \notin N_{p} \left( {r_{i} } \right)} \\ \end{array} \hfill \\ \begin{array}{*{20}c} {0.5} & {otherwise} \\ \end{array} \hfill \\ \end{aligned} \right. $$
(6)

where \( N_{p} \left( {r_{i} } \right) \) and \( N_{p} \left( {r_{j} } \right) \) denote the sets of \( p \)-nearest neighbors of \( r_{i} \) and \( r_{j} \) respectively. Then, we define the sparse matrix \( S^{R*} \) of drug as follows:

$$ \forall i, j\quad S_{ij}^{R*} = S_{ij}^{R} W_{ij}^{R} $$
(7)

Similarly, the sparse matrix \( S^{D*} \) of disease can be expressed as follows:

$$ \forall i, j \quad S_{ij}^{D*} = S_{ij}^{D} W_{ij}^{D} $$
(8)

The Eq. (5) can be written as:

$$ \begin{aligned} \mathop {\hbox{min} }\limits_{A, B} \left\| {Y - A^{T} B} \right\|_{F}^{2} + \lambda Tr\left( {AL_{r} A^{T} } \right) + \lambda Tr\left( {BL_{d} B^{T} } \right) \hfill \\ + \beta \left( {\left\| A \right\|_{F}^{2} + \left\| B \right\|_{F}^{2} } \right)\quad \quad s.t. A \ge 0, B \ge 0 \hfill \\ \end{aligned} $$
(9)

Here, \( L_{r} = D_{r} - S^{R*} \) and \( L_{d} = D_{d} - S^{D*} \) are the graph Laplacian matrices for \( S^{R*} \) and \( S^{D*} \), respectively. \( D_{r} \left( {i,i} \right) = \sum\nolimits_{p} {S_{ip}^{R*} } \) and \( D_{d} \left( {j,j} \right) = \sum\limits_{q} {S_{jq}^{D*} } \) are diagonal matrices, \( Tr\left( \cdot \right) \) denotes the trace of matrix.

In order to optimize the objective function in Eq. (9), the corresponding Lagrange function \( {\mathcal{H}}_{f} \) is defined as:

$$ \begin{aligned} {\mathcal{H}}_{f} = Tr\left( {YY^{T} } \right) - 2Tr\left( {YB^{T} A} \right) + Tr\left( {A^{T} BB^{T} A} \right) + \lambda Tr\left( {AL_{r} A^{T} } \right) + \lambda Tr\left( {BL_{d} B^{T} } \right) \hfill \\ \quad \quad \quad \quad \quad \quad + \beta Tr\left( {AA^{T} } \right) + \beta Tr\left( {BB^{T} } \right) + Tr\left( {\varPhi A^{T} } \right) + Tr\left( {\varPsi B^{T} } \right) \hfill \\ \end{aligned} $$
(10)

In which, \( \varPhi = \left\{ {\phi_{ki} } \right\} \) and \( \varPsi = \left\{ {\psi_{kj} } \right\} \) are Lagrange multipliers that constrain \( a_{ki} \ge 0 \) and \( b_{kj} \ge 0 \), respectively. We calculate \( \frac{{\partial {\mathcal{H}}_{f} }}{\partial A} \) and \( \frac{{\partial {\mathcal{H}}_{f} }}{\partial B} \) as follows:

$$ \frac{{\partial {\mathcal{H}}_{f} }}{\partial A} = - 2BY^{T} + 2BB^{T} A + 2\lambda AL_{r} + 2\beta A + \varPhi $$
(11)
$$ \frac{{\partial H_{f} }}{\partial B} = - 2AY + 2AA^{T} B + 2\lambda BL_{d} + 2\beta B + \varPsi $$
(12)

After using Karush–Kuhn–Tucker (KKT) conditions \( \phi_{ki} a_{ki} = 0 \) and \( \psi_{kj} b_{kj} = 0 \), the updating rules can be obtained as follows:

$$ a_{ki} \leftarrow a_{ki} \frac{{BY^{T} + \lambda AS^{R*} }}{{\beta A + \lambda AD_{r} + BB^{T} A}} $$
(13)
$$ b_{kj} \leftarrow b_{kj} \frac{{AY + \lambda BS^{D*} }}{{\beta B + \lambda BD_{d} + AA^{T} B}} $$
(14)

The predicted drug-disease association matrix is obtained by \( Y^{*} = A^{T} B \). Generally, the larger the element value in predicted matrix \( Y^{*} \), the more likely the drug is related to the corresponding disease.

3 Experimental Results

In this study, the model of WGMFDDA has six parameters that determine by grid search. The ROC curve and AUC value are widely used to evaluate the predictor [50,51,52,53,54]. WGMFDDA produces best AUC values when \( P = 5 \), \( K = 5 \), \( a = 0.5 \), \( k = 160 \), \( \lambda = 1 \) and \( \beta = 0.02 \). We implement ten-fold cross-validation (CV) experiments on the Fdataset and compare it with the previous methods: DrugNet [32], HGBI [33], MBiRW [34] and DDRS [39]. To implement 10-CV experiment, all known drug-disease associations in Fdataset are random divided into ten equal sized subsets. the training data set occupies 9/10, while the remaining partition is utilized as the test set. As shown in Fig. 2 and Table 1, WGMFDDA achieves the AUC value of 0.939, while DrugNet, HGBI, MBiRW and DDRS are 0.778, 0.829, 0.917and 0.930, respectively. This result shows that compared with DDRS, MBiRW, HGBI and DrugNet, WGMFDDA obtains the best performance.

Fig. 2.
figure 2

The ROC curves of WGMFDDA on Fdataset under ten-fold cross-validation.

Full size image
Table 1. The average AUC values of WGMFDDA and other compared methods on Fdataset.
Full size table

4 Conclusions

The purpose of drug repositioning is to discover new indications for existing drugs. Compared to traditional drug development, drug repositioning can reduce risk, save time and costs. In this work, we present a new prediction approach, WGMFDDA, based on weighted graph regularized matrix factorization. The proposed method casts the problem of inferring the associations between drugs and diseases into a matrix factorization problem in recommendation system. The main contribution of our method is that a preprocessing step is performed before matrix factorization to reformulate the drug-disease association adjacency matrix. In ten-fold cross-validation, experiment results indicate that our proposed model outperforms other compared methods.