1 Introduction

The Independent Set problem, which asks for a maximum sized set of pairwise non-adjacent vertices in a graph, is one of the most well-studied problems in algorithmic graph theory. It was among the first 21 problems that were proven to be NP-hard by Karp  [22], and is also known to be hopelessly difficult to approximate in polynomial time: Håstad  [21] proved that under standard assumptions from classical complexity theory the problem admits no \((n^{1-\varepsilon })\)-approximation, for any \(\varepsilon >0\) (by n we always denote the number of vertices in the input graph). This was later strengthened by Khot and Ponnuswami  [23], who were able to exclude any algorithm with approximation ratio \(n/(\log n)^{3/4 + \varepsilon }\), for any \(\varepsilon > 0\). Let us point out that the currently best polynomial-time approximation algorithm for Independent Set achieves the approximation ratio \(\mathcal {O}(n \frac{(\log \log n)^2}{(\log n)^3})\)  [17].

There are many possible ways of approaching such a difficult problem, in order to obtain some positive results. One could give up on generality, and ask for the complexity of the problem on restricted instances. For example, while the Independent Set problem remains NP-hard in subcubic graphs  [18], a straightforward greedy algorithm gives a 3-approximation.

H-Free Graphs. A large family of restricted instances, for which the Independent Set problem has been well-studied, comes from forbidding certain induced subgraphs. For a (possibly infinite) family \(\mathcal {H}\) of graphs, a graph G is \(\mathcal {H}\)-free if it does not contain any graph of \(\mathcal {H}\) as an induced subgraph. If \(\mathcal {H}\) consists of just one graph, say \(\mathcal {H}= \{H\}\), then we say that G is H-free. The investigation of the complexity of Independent Set in H-free graphs dates back to Alekseev, who proved the following.

Theorem 1

(Alekseev  [2]). Let \(s \ge 3\) be a constant. The Independent Set problem is NP-hard in graphs that do not contain any of the following induced subgraphs: (1) a cycle on at most s vertices, (2) the star \(K_{1,4}\), and (3) any tree with two vertices of degree at least 3 at distance at most s.

We can restate Theorem 1 as follows: the Independent Set problem is NP-hard in H-free graphs, unless H is a subgraph of a subdivided claw (i.e., three paths which meet at one of their endpoints). The reduction also implies that for each such H the problem is APX-hard and cannot be solved in subexponential time, unless the Exponential Time Hypothesis (ETH) fails. On the other hand, polynomial-time algorithms are known only for very few cases. First let us consider the case when \(H=P_t\), i.e., we forbid a path on t vertices. Note that the case of \(t=3\) is trivial, as every \(P_3\)-free graph is a disjoint union of cliques. Already in 1981 Corneil et al.  [10] showed that Independent Set is tractable for \(P_4\)-free graphs. For many years there was no improvement, until the breakthrough algorithm of Lokshtanov et al.  [25] for \(P_5\)-free graphs. Their approach was recently extended to \(P_6\)-free graphs by Grzesik et al.  [19]. We still do not know whether the problem is polynomial-time solvable in \(P_7\)-free graphs, and we do not know it to be NP-hard in \(P_t\)-free graphs, for any constant t.

Even less is known for the case if H is a subdivided claw. The problem can be solved in polynomial time in claw-free (i.e., \(K_{1,3}\)-free) graphs, see Sbihi  [32] and Minty  [31]. This was later extended to H-free graphs, where H is a claw with one edge once subdivided (see Alekseev  [1] for the unweighted version and Lozin and Milanič  [27] for the weighted one).

When it comes to approximations, Halldórsson  [20] gave an elegant local search algorithm that finds a \((\frac{d-1}{2}+\delta )\)-approximation of the maximum independent set in \(K_{1,d}\)-free graphs for any constant \(\delta >0\) in polynomial time. Very recently, Chudnovsky et al.  [9] designed a QPTAS (quasi-polynomial-time approximation scheme) that works for every H, which is a subgraph of a subdivided claw (in particular, a path). Recall that on all other graphs H the problem is APX-hard.

Parameterized Complexity. Another approach that one could take is to look at the problem from the parameterized perspective: we no longer insist on finding the maximum independent set, but want to verify whether some independent set of size at least k exists. To be more precise, we are interested in knowing how the complexity of the problem depends on k. The best type of behavior we are hoping for is fixed-parameter tractability (FPT), i.e., the existence of an algorithm with running time \(f(k) \cdot n^{\mathcal {O}(1)}\), for some function f (note that since the problem is NP-hard, we expect f to be super-polynomial).

It is known  [11] that on general graphs the Independent Set problem is W[1]-hard parameterized by k, which is a strong indication that it does not admit an FPT algorithm. Furthermore, it is even unlikely to admit any non-trivial fixed-parameter approximation (FPA): a \(\gamma \)-FPA algorithm for the Independent Set problem is an algorithm that takes as input a graph G and an integer k, and in time \(f(k) \cdot n^{\mathcal {O}(1)}\) either correctly concludes that G has no independent set of size at least k, or outputs an independent set of size at least \(k/\gamma \) (note that \(\gamma \) does not have to be a constant). It was shown in  [5] that on general graphs no o(k)-FPA exists for Independent Set, unless the randomized Gap-ETH fails.

Parameterized Complexity in H-Free Graphs. As we pointed out, none of the discussed approaches, i.e., considering H-free graphs or considering parameterized algorithms, seems to make the Independent Set problem more tractable. However, some positive results can be obtained by combining these two settings, i.e., considering the parameterized complexity of Independent Set in H-free graphs. For example, the Ramsey theorem implies that any graph with \(\varOmega (4^{p})\) vertices contains a clique or an independent set of size \(\varOmega (p)\). Since the proof actually tells us how to construct a clique or an independent set in polynomial time  [16], we immediately obtain a very simple FPT algorithm for \(K_p\)-free graphs. Dabrowski  [12] provided some positive and negative results for the complexity of the Independent Set problem in H-free graphs, for various H. The systematic study of the problem was initiated by Bonnet et al.  [3] and continued by Bonnet et al.  [4]. Among other results, Bonnet et al.  [3] obtained the following analog of Theorem 1.

Theorem 2

(Bonnet et al.  [3]). Let \(s \ge 3\) be a constant. The Independent Set problem is W[1]-hard in graphs that do not contain any of the following induced subgraphs: (1) a cycle on at least 4 and at most s vertices, (2) the star \(K_{1,4}\), and (3) any tree with two vertices of degree at least 3 at distance at most s.

Note that, unlike in Theorem 1, we are not able to show hardness for \(C_3\)-free graphs: as already mentioned, the Ramsey theorem implies that Independent Set is FPT in \(C_3\)-free graphs. Thus, graphs H for which there is hope for FPT algorithms in H-free graphs are essentially obtained from paths and subdivided claws (or their subgraphs) by replacing each vertex with a clique.

Let us point out that, even though it is not stated there explicitly, the reduction of Bonnet et al.  [3] also excludes any algorithm solving the problem in time \(f(k) \cdot n^{o(\sqrt{k})}\), unless the ETH fails.

Our Results. We study the approximation of the Independent Set problem in H-free graphs, mostly focusing on approximation hardness. Our first two results are related to Halldórsson’s  [20] polynomial-time \((\frac{d-1}{2}+\delta )\)-approximation algorithm for \(K_{1,d}\)-free graphs. We extend this result to \(K_{a,b}\)-free graphs, for any constants a, b. Moreover, we show that the approximation ratio of the algorithm of Halldórsson  [20] is optimal, up to logarithmic factors.

Theorem 3

Given a \(K_{a,b}\)-free graph G, an \(\mathcal {O}\bigl ((a+b)^{1/a} \cdot \alpha (G)^{1-1/a}\bigr )\)-approximation can be computed in \(n^{\mathcal {O}(a)}\) time.

Theorem 4

There is a function \(\gamma =\varTheta (d/\log d)\) such that the Independent Set problem does not admit a polynomial time \(\gamma \)-approximation algorithm in \(K_{1,d}\)-free graphs, unless ZPP = NP.

The proofs of Theorems 3 and 4 can be find in the full version of the paper  [15]. Note that the factor \(\gamma \) determining the approximation gap in Theorem 4 is expressed as an asymptotic function of d, i.e., for growing d. In our case however, it is an interesting question how small the degree d can be so that we obtain an inapproximability result. We prove Theorem 4 by a reduction from the Label Cover problem, and a corresponding inapproximability result by Laekhanukit  [24]. By calculating the bounds given in [24] (which heavily depend on the constant of Chernoff bounds) it can be shown that an inapproximability gap exists for \(d\ge 31\) in Theorem 4.

Then in Sect. 3 we study the existence of fixed-parameter approximation algorithms for the Independent Set problem in H-free graphs. We show the following strengthening of Theorem 2, which also gives (almost) tight runtime lower bounds assuming the ETH or the randomized Gap-ETH (for more information about complexity assumptions used in Theorem 5 see Sect. 2).

Theorem 5

Let \(s \ge 4\) be a constant, and let \(\mathcal {G}\) be the class of graphs that do not contain any of the following induced subgraphs: (1) a cycle on at least 5 and at most s vertices, (2) the star \(K_{1,5}\), and (3) (i) the star \(K_{1,4}\) or (ii) a cycle on 4 vertices and any tree with two vertices of degree at least 3 at distance at most s. The Independent Set problem on \(\mathcal {G}\) does not admit the following:

  1. (a)

    an exact algorithm with runtime \(f(k) \cdot n^{o(k/\log k)}\), for any computable function f, under the ETH,

  2. (b)

    a \(\gamma \)-approximation algorithm with runtime \(f(k) \cdot n^{\mathcal {O}(1)}\) for some constant \(\gamma >0\) and any computable function f, under the deterministic Gap-ETH,

  3. (c)

    a \(\gamma \)-approximation algorithm with runtime \(f(k) \cdot n^{o(k)}\) for some constant \(\gamma >0\) and any computable function f, under the randomized Gap-ETH.

Finally, in Sect. 4 we study a slightly different setting, where the graph H is not considered to be fixed. As mentioned before, Independent Set is known to be polynomial-time solvable in \(P_t\)-free graphs for \(t \le 6\). The algorithms for increasing values of t get significantly more complicated and their complexity increases. Thus it is natural to ask whether this is an inherent property of the problem and can be formalized by a runtime lower bound when parameterized by t.

We give an affirmative answer to this question, even if the forbidden family is not a family of paths: note that the independent set number \(\alpha (P_t)\) of a path on t vertices is \(\lceil t/2\rceil \).

Proposition 1

Let d be an integer and let \(\mathcal {H}_d\) be a family of graphs, such that \(\alpha (H) > d\) for every \(H \in \mathcal {H}_d\). The Independent Set problem in \(\mathcal {H}_d\)-free graphs is W[1]-hard parameterized by d and cannot be solved in \(n^{o(d)}\) time, unless the ETH fails.

The proof of Proposition 1 can be found in the full version of the paper. We also study the special case when \(H=K_{1,d}\) and consider the inapproximability of the problem parameterized by both \(\alpha (K_{1,d})=d\) and k. Unfortunately, for the parameterized version we do not obtain a clear-cut statement as in Theorem 4, since in the following theorem d cannot be chosen independently of k in order to obtain an inapproximability gap.

Proposition 2

Let \(\varepsilon >0\) be any constant and \(\xi (k)=2^{(\log k)^{1/2+\varepsilon }}\). The Independent Set problem in \(K_{1,d}\)-free graphs has no \(d/\xi (k)\)-approximation algorithm with runtime \(f(d,k) \cdot n^{\mathcal {O}(1)}\) for any computable function f, unless the deterministic Gap-ETH fails.

Note that this in particular shows that if we allow d to grow as a polynomial \(k^\varepsilon \) for any constant \(\frac{1}{2}> \varepsilon >0\), then no \(k^{\delta }\)-approximation is possible for any \(\delta <\varepsilon \) (since \(\xi (k)=k^{o(1)}\)). This indicates that the \((\frac{d-1}{2}+\delta )\)-approximation for \(K_{1,d}\)-free graphs  [20] is likely to be best possible (up to sub-polynomial factors), even when parameterizing by k and d.

2 Preliminaries

All our hardness results for Independent Set are obtained by reductions from some variant of the Maximum Colored Subgraph Isomorphism ( ) problem. This optimization problem has been widely studied in the literature, both to obtain polynomial-time and parameterized inapproximability results, but also in its decision version to obtain parameterized runtime lower bounds. We note that by applying standard transformations, contains the well-known problems Label Cover  [24] and Binary CSP  [26]: for Binary CSP the graph J is a complete graph, while for Label Cover J is usually bipartite.

figure c

Given an instance \(\varGamma =(G,V_1,\ldots ,V_\ell ,J)\) of , we refer to the number of vertices of G as the size of \(\varGamma \). Any assignment \(\phi : V(J) \rightarrow V(G)\), such that for every i it holds that \(\phi (i) \in V_i\), is called a solution of \(\varGamma \). The value of a solution \(\phi \) is \({{\,\mathrm{val}\,}}(\phi ) := S(\phi )/|E(J)|\), i.e., the fraction of satisfied edges. The value of the instance \(\varGamma \), denoted by \({{\,\mathrm{val}\,}}(\varGamma )\), is the maximum value of any solution of \(\varGamma \).

When considering the decision version of , i.e., determining whether \({{\,\mathrm{val}\,}}(\varGamma )=1\) or \({{\,\mathrm{val}\,}}(\varGamma )<1\), a result by Marx  [29] gives a runtime lower bound for parameter \(\ell \) under the Exponential Time Hypothesis (ETH). That is, no \(f(\ell ) \cdot n^{o(\ell /\log \ell )}\) time algorithm can solve for any computable function f, assuming there is no deterministic \(2^{o(n)}\) time algorithm to solve the 3-SAT problem. For the optimization version, an \(\alpha \)-approximation is a solution \(\phi \) with \({{\,\mathrm{val}\,}}(\phi )\ge 1/\alpha \). When J is a complete graph, a result by Dinur and Manurangsi  [13, 14] states that there is no \(\ell /\xi (\ell )\)-approximation algorithm (where \(\xi (\ell )=2^{(\log \ell )^{1/2+\varepsilon }}\) for any constant \(\varepsilon >0\)) with runtime \(f(\ell ) \cdot n^{O(1)}\) for any computable function f, unless the deterministic Gap-ETH fails (see Theorem 9). This hypothesis assumes that there exists some constant \(\delta >0\) such that no deterministic \(2^{o(n)}\) time algorithm for 3-SAT can decide whether all or at most a \((1-\delta )\)-fraction of the clauses can be satisfied. A recent result by Manurangsi  [28] uses an even stronger assumption, which also rules out randomized algorithms, and in turn obtains a better runtime lower bound at the expense of a worse approximation lower bound: he shows that, when J is a complete graph, there is no \(\gamma \)-approximation algorithm for with runtime \(f(\ell ) \cdot n^{o(\ell )}\) for any computable function f and any constant \(\gamma \), under the randomized Gap-ETH. This assumes that there exists some constant \(\delta >0\) such that no randomized \(2^{o(n)}\) time algorithm for 3-SAT can decide whether all or at most a \((1-\delta )\)-fraction of the clauses can be satisfied. (Note that the runtime lower bound under the stronger randomized Gap-ETH does not have the \(\log (\ell )\) factor in the polynomial degree as the runtime lower bound under ETH does.)

For our results we will often need the special case of when the graph J has bounded degree. We define this problem in the following.

figure i

The bounded degree case has been considered before, and we harness some of the known hardness results for in our proofs. First, let us point out that the lower bound for exact algorithms holds even for the case when \(t=3\), as shown by Marx and Pilipczuk  [30]. We also use a polynomial-time approximation lower bound given by Laekhanukit  [24], where t can be set to any constant and the approximation gap depends on t. The complexity assumption of this algorithm is that NP-hard problems do not have polynomial time Las Vegas algorithms, i.e., NP \(\ne \) ZPP. For parameterized approximations, we use a result by Lokshtanov et al.  [26], who obtain a constant approximation gap for the case when \(t=3\) (see Theorem 6). It seems that this result for parameterized algorithms is not easily generalizable to arbitrary constants t so that the approximation gap would depend only on t, as in the result for polynomial-time algorithms provided by Laekhanukit  [24]: neither the techniques found in  [24] nor those of  [26] seem to be usable to obtain an approximation gap that depends only on t but not the parameter \(\ell \). However, we develop a weaker parameterized inapproximability result for the case when \(t\ge \xi (\ell )=\ell ^{o(1)}\) (see Theorem 7 in Sect. 4), and use it to prove Proposition 2.

3 Parameterized Approximation for Fixed H

In this section we prove Theorem 5. Let us define an auxiliary family of classes of graphs: for integers \(4 \le a \le b\) and \(c \ge 3\), let \(\mathcal {C}([a,b],c)\) denote the class of graphs that are \(K_{1,c}\)-free and \(C_p\)-free for any \(p \in [a,b]\). Let \(\mathcal{T}(b)\) be the class of trees with two vertices of degree at least 3 at distance at most b. Let \(\mathcal {C}^*([a,b],c) \subseteq \mathcal {C}([a,b],c)\) be the set of those \(G \in \mathcal {C}([a,b],c)\), which are are also \(\mathcal{T}(\lceil \frac{b - 1}{2}\rceil )\)-free. Actually, we will prove a stronger statement that Theorem 5 holds for \(G \in \mathcal {C}^*([4,z],5) \cup \mathcal {C}([5,z],4)\) for a constant \(z \ge 5\).

The proof consists of two steps: first we will prove it for graphs in \(\mathcal {C}^*([4,z],5)\), and then for graphs in \( \mathcal {C}([5,z],4)\). In both proofs we will reduce from the problem. Here, we sketch the proof for the class \(\mathcal {C}^*([4,z],5)\). The rest of the proof can be found in the full version  [15]. Let \(\varGamma = (G,V_1,\dots ,V_\ell ,H)\) be an instance of . For \(ij \in E(H)\), by \(E_{ij}=E_{ji}\) we denote the set of edges between \(V_i\) and \(V_j\). Note that we may assume that H has no isolated vertices, each \(V_i\) is an independent set, and \(E_{ij}\ne \emptyset \) if and only if \(ij \in E(H)\).

Lokshtanov et al.  [26] gave the following hardness result (the first statement actually follows from Marx  [29] and Marx and Pilipczuk  [30]). We note that Lokshtanov et al.  [26] conditioned their result on the Parameterized Inapproximability Hypothesis (PIH) and W[1] \(\ne \) FPT. Here we use stronger assumptions, i.e., the deterministic and randomized Gap-ETH, which are more standard in the area of parameterized approximation. The reduction in  [26] yields the following theorem, when starting from [13, 14] and [28], respectively (see also [7, Corollary 7.9]).

Theorem 6

(Lokshtanov et al.  [26]). Consider an arbitrary instance \(\varGamma = (G,V_1,\dots ,V_\ell ,H)\) of with size n.

  1. 1.

    Assuming the ETH, for any computable function f, there is no \(f(\ell )\cdot n^{o(\ell /\log \ell )}\) time algorithm that solves \(\varGamma \).

  2. 2.

    Assuming the deterministic Gap-ETH there exists a constant \(\gamma > 0\), such that for any computable function f, there is no \(f(\ell )\cdot n^{\mathcal {O}(1)}\) time algorithm that can distinguish between the two cases: (YES-case) \({{\,\mathrm{val}\,}}(\varGamma ) = 1\), and (NO-case) \({{\,\mathrm{val}\,}}(\varGamma ) < 1 - \gamma \).

  3. 3.

    Assuming the randomized Gap-ETH there exists a constant \(\gamma > 0\), such that for any computable function f, there is no \(f(\ell )\cdot n^{o(\ell )}\) time algorithm that can distinguish between the two cases: (YES-case) \({{\,\mathrm{val}\,}}(\varGamma ) = 1\), and (NO-case) \({{\,\mathrm{val}\,}}(\varGamma ) < 1 - \gamma \).

Let \(\varGamma = (G,V_1,\dots ,V_\ell ,H)\) be an instance of . We aim to build an instance \((G',k)\) of Independent Set, such that the graph \(G' \in \mathcal {C}^*([4,z],5)\).

For each \(ij \in E(H)\), we introduce a clique \(C_{ij}\) of size \(|E_{ij}|\), whose every vertex represents a different edge from \(E_{ij}\). The cliques constructed at this step will be called primary cliques, note that their number is |E(H)|. Choosing a vertex v from \(C_{ij}\) to an independent set of \(G'\) will correspond to mapping i and j to the appropriate endvertices of the edge from \(E_{ij}\), corresponding to v.

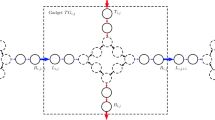
Now we need to ensure that the choices in primary cliques corresponding to edges of G are consistent. Consider \(i \in V(H)\) and suppose it has three neighbors \(j_1,j_2,j_3\) (the cases if i has fewer neighbors are dealt with analogously). We will connect the cliques \(C_{ij_1},C_{ij_2},C_{ij_3}\) using a gadget called a vertex-cycle, whose construction we describe below. For each \(a \in \{1,2,3\}\), we introduce s copies of \(C_{ij_a}\) and denote them by \(D^1_{ij_a},D^2_{ij_a},\ldots ,D^s_{ij_a}\), respectively. Let us call these copies secondary cliques. The vertices of secondary cliques represent the edges from \(E_{ij_a}\) analogously as the ones of \(C_{ij_a}\). We call primary and secondary cliques as base cliques. We connect the base cliques corresponding to the vertex \(i \in V(H)\) into vertex-cycle \(\mathcal{C}_i\). Imagine that secondary cliques, along with primary cliques \(C_{ij_1},C_{ij_2},C_{ij_3}\), are arranged in a cycle-like fashion, as follows: \(C_{ij_1},D_{ij_1}^1,D_{ij_1}^2,\ldots ,D_{ij_1}^s,C_{ij_2},D_{ij_2}^1,D_{ij_2}^2,\ldots ,D_{ij_2}^s,C_{ij_3},D_{ij_3}^1,D_{ij_3}^2,\ldots ,D_{ij_3}^s,C_{ij_1}.\) This cyclic ordering of cliques constitutes the vertex-cycle, let us point out that we treat this cycle as a directed one. As we describe below we put some edges between two base cliques \(D_1\) and \(D_2\) only if they belong to some vertex-cycle \(\mathcal{C}_i\). See Fig. 1 for an example of how we connect base cliques.

Fig. 1.
figure 1

A part of the construction of \(G'\) for \(s = 2\). Cliques \(C_{ab}\) representing edge sets \(E_{ab} \subseteq E(G)\) are connected through secondary cliques \(D^p_{ab}\).

Full size image

Now, we describe how we connect the consecutive cliques in \(\mathcal{C}_i\). Recall that each vertex v of each clique represents exactly one edge uw of G, whose exactly one vertex, say u, is in \(V_i\). We extend the notion of representing and say that v represents u, and denote it by \(r_{i}(v)=u\).

Let us fix an arbitrary ordering \(\prec _i\) on \(V_i\). Now, consider two consecutive cliques of the vertex-cycle. Let v be a vertex of the first clique and \(v'\) be a vertex from the second clique, and let u and \(u'\) be the vertices of \(V_i\) represented by v and \(v'\), respectively. The edge \(vv'\) exists in \(G'\) if and only if \(u \prec _i u'\). See Fig. 2 how we connect two consecutive base cliques in a vertex-cycle. This finishes the construction of \(\mathcal{C}_i\). We introduce a vertex-cycle \(\mathcal{C}_i\) for every vertex i of H, note that each primary clique \(C_{ij}\) is in exactly two vertex-cycles: \(\mathcal{C}_i\) and \(\mathcal{C}_j\). The number of all base cliques is

$$\begin{aligned} k:=\underbrace{|E(H)|}_{\begin{array}{c} \text {primary}\\ \text {cliques} \end{array}} + \underbrace{\sum \nolimits _{i \in V(H)} \deg _H(i) \cdot s }_{\text {secondary cliques}} = |E(H)| \cdot \Bigl (1 + \frac{s}{2}\Bigr ) \le \frac{3\ell }{2} \cdot \Bigl (1 + \frac{s}{2}\Bigr ) = \mathcal {O}(\ell ). \end{aligned}$$

This concludes the construction of \((G',k)\). Since \(V(G')\) is partitioned into k base cliques, k is an upper bound on the size of any independent set in \(G'\), and a solution of size k contains exactly one vertex from each base clique.

We claim that the graph \(G'\) is in the class \(\mathcal {C}^*([4,z],5)\). Moreover, if \({{\,\mathrm{val}\,}}(\varGamma ) = 1\), then the graph \(G'\) has an independent set of size k and if the graph \(G'\) has an independent set of size at least \((1 - \gamma ')\cdot k\) for \(\gamma ' = \frac{\gamma }{6 + 3s}\), then \(\text {val}(\varGamma ) \ge 1 - \gamma \).

Fig. 2.
figure 2

Edges between two consecutive cliques \(D_1\) and \(D_2\) in a vertex-cycle \(\mathcal{C}_i\), where \(V_i = \{v_1,\dots ,v_5\}\). We show only edges incident to \(u \in V(D_1)\) such that \(r_i(u) \in \{v_2,v_4\}\).

Full size image

4 Parameterized Approximation with H as a Parameter

Now let us consider the Independent Set problem in \(K_{1,d}\)-free graphs, parameterized by both k and d. In this case we are able to give parameterized approximation lower bounds based on the following sparsification of . Recall that \(\xi (\ell )=2^{(\log \ell )^{1/2+\varepsilon }}=\ell ^{o(1)}\) for any constant \(\frac{1}{2}> \varepsilon >0\), i.e., the term grows slower than any polynomial (but faster than any polylogarithm).

Theorem 7

Consider an instance \(\varGamma = (G,V_1,\dots ,V_\ell ,J)\) of with size n and \(t>\xi (\ell )\). Assuming the deterministic Gap-ETH, for any computable function f, there is no \(f(\ell )\cdot n^{O(1)}\) time algorithm that can distinguish between the two cases: (YES-case) \({{\,\mathrm{val}\,}}(\varGamma ) = 1\), and (NO-case) \({{\,\mathrm{val}\,}}(\varGamma ) \le \xi (\ell )/t\).

Proposition 2 follows from Theorem 7 by easy reduction (see the full version  [15]). To prove Theorem 7 we need two facts. The first is the Erdős-Gallai theorem on degree sequences, which are sequences of non-negative integers \(d_1,\ldots ,d_n\), for each of which there exists a simple graph on n vertices such that vertex \(i\in [n]\) has degree \(d_i\). We use the following constructive formulation due to Choudum  [8].

Theorem 8

(Erdős-Gallai theorem  [8]). A sequence of non-negative integers \(d_1 \ge \dots \ge d_n\) is a degree sequence of a simple graph on n vertices if \(d_1 + \dots + d_n\) is even and for every \(1 \le k \le n\) the following inequality holds: \( \sum _{i = 1}^k d_i \le k(k-1) + \sum _{i = k+1}^n \min (d_i, k).\) Moreover, given such a degree sequence, a corresponding graph can be constructed in polynomial time.

We also need a parameterized approximation lower bound for , as given by Dinur and Manurangsi  [13].

Theorem 9

(Dinur and Manurangsi  [13]). Consider an instance \(\varGamma = (G,V_1,\dots ,V_\ell ,J)\) of with size n and J a complete graph. Assuming the deterministic Gap-ETH, there is no \(f(\ell )\cdot n^{O(1)}\) time algorithm for any computable function f, that can distinguish between the following two cases: (YES-case) \({{\,\mathrm{val}\,}}(\varGamma ) = 1\), and (NO-case) \({{\,\mathrm{val}\,}}(\varGamma ) \le \xi (\ell )/{\ell }\).

Proof of Theorem 7. Let \(t < \ell \) and let \(\varGamma = (G,V_1,\dots ,V_\ell ,J)\) be an instance of where J is a complete graph. To find an instance of , we want to construct a graph \(J'\) on \(\ell \) vertices with maximum degree t, for which we use the Erdős-Gallai theorem. By Theorem 8 it is easy to verify that a t-regular graph on \(\ell \) vertices exists if \(t\ell \) is even. However, if \(t\ell \) is odd, there is a graph with \(\ell - 1\) vertices of degree t and one vertex of degree \(t-1\). Moreover, the proof of Theorem 8 by Choudum  [8] is constructive, and gives a polynomial time algorithm. Hence we can compute a graph \(J'\) with maximum degree t and \(|E(J')|\ge (t\ell -1)/2\). Since J is a complete graph, \(J'\) is a subgraph of J.

We create a graph \(G'\) by removing edges from G according to \(J'\): we remove all edges between sets \(V_i\) and \(V_j\) of G if and only if \(ij \not \in E(J')\), and call the resulting graph \(G'\). Thus, we get new instance \(\varGamma ' = (G',V_1,\dots ,V_\ell ,J')\) of .

It is easy to see that if \(\text {val}(\varGamma ) = 1\), then \(\text {val}(\varGamma ') = 1\) as well: we just use the optimal solution for \(\varGamma \). Now suppose that \(\text {val}(\varGamma ) \le \nu \), which means that each solution \(\phi \) satisfies at most a \(\nu \)-fraction of edges of J. Let \(\phi \) be an arbitrary solution of \(\varGamma '\), which is also a solution for \(\varGamma \) because \(V(G) = V(G')\) and \(V(J) = V(J')\). By our assumption we know that it satisfies at most \(\nu \cdot E(J)\) edges of J. Thus, the solution \(\phi \) satisfies at most \(\nu \cdot E(J)\) edges of \(J'\) as well. Hence we obtain

$$\begin{aligned} {{\,\mathrm{val}\,}}(\varGamma ') \le \frac{\nu \cdot E(J)}{E(J')} = \nu \cdot \frac{\ell (\ell - 1)}{t\ell - 1} \le \nu \cdot \frac{\ell }{t - 1/\ell }. \end{aligned}$$

Now, by Theorem 9 we know that under the deterministic Gap-ETH, no \(f(\ell ) \cdot n^{O(1)}\) time algorithm can distinguish between \({{\,\mathrm{val}\,}}(\varGamma )=1\) and \({{\,\mathrm{val}\,}}(\varGamma )\le {\xi (\ell )}/{\ell }\) given \(\varGamma \). By the above calculations, for \(\varGamma '\) we obtain that no such algorithm can distinguish between \({{\,\mathrm{val}\,}}(\varGamma ')=1\) and \({{\,\mathrm{val}\,}}(\varGamma ')\le \frac{\xi (\ell )}{t-1/\ell }\) by setting \(\nu ={\xi (\ell )}/{\ell }\). Recall that \(\xi (\ell )=2^{(\log \ell )^{1/2+\varepsilon }}\) where \(\varepsilon \) can be set to any positive constant in Theorem 9. Given any constant \(\varepsilon '>0\), we choose \(\varepsilon \) such that \(2^{(\log \ell )^{1/2+\varepsilon }}/2^{(\log \ell )^{1/2+\varepsilon '}}\le (t-1/\ell )/t\). It can be verified that such a constant \(\varepsilon >0\) always exists, assuming w.l.o.g. that \(\ell \) is larger than some sufficiently large constant. This implies that \({{\,\mathrm{val}\,}}(\varGamma ')\le \frac{\xi (\ell )}{t-1/\ell }\le 2^{(\log \ell )^{1/2+\varepsilon '}}/t\). Note that \({{\,\mathrm{val}\,}}(\varGamma ')<1\) if \(t>2^{(\log \ell )^{1/2+\varepsilon '}}\), and so we obtain Theorem 7 (for \(\xi (\ell ):=2^{(\log \ell )^{1/2+\varepsilon '}}\)).    \(\square \)

5 Conclusion and Open Problems

Our parameterized inapproximability results of Theorem 5 suggest that the Independent Set problem is hard to approximate to within some constant, whenever it is W[1]-hard to solve on H-free graphs, according to Theorem 2. In most cases it is unclear though whether any approximation can be computed (either in polynomial time or by exploiting the parameter k), which beats the strong lower bounds for polynomial-time algorithms for general graphs. The only known exceptions to this are the \(K_{1,d}\)-free case, where a polynomial-time \((\frac{d-1}{2}+\delta )\)-approximation algorithm was shown by Halldórsson  [20], and the \(K_{a,b}\)-free case, for which we showed a polynomial-time \(\mathcal {O}\bigl ((a+b)^{1/a} \cdot \alpha (G)^{1-1/a}\bigr )\)-approximation algorithm in Theorem 3. For \(K_{1,d}\)-free graphs, we were also able to show an almost asymptotically tight lower bound for polynomial-time algorithms in Theorem 4. For parameterized algorithms, our lower bound of Proposition 2 for \(K_{1,d}\)-free graphs does not give a tight bound, but seems to suggest that parameterizing by k does not help to obtain an improvement. For \(P_t\)-free graphs, for which the Independent Set problem is conjectured to be polynomial-time solvable, we showed in Proposition 1 that the complexity of any such algorithm must grow with the length t of the excluded path.

Settling the question whether H-free graphs admit better approximations to Independent Set than general graphs, remains a challenging open problem, both for polynomial-time algorithms and algorithms exploiting the parameter k.

Let us point out one more, concrete open question. Recall from Theorem 2 Bonnet et al.  [3] were able to show W[1]-hardness for graphs which simultaneously exclude \(K_{1,4}\) and all induced cycles of length in [4, z], for any constant \(z \ge 5\). On the other hand, we presented two separate reductions, one for \((K_{1,5},C_4,\ldots ,C_z)\)-free graphs, and another one for \((K_{1,4},C_5,\ldots ,C_z)\)-free graphs. It would be nice to provide a uniform reduction, i.e., prove hardness for parameterized approximation in \((K_{1,4},C_4,\ldots ,C_z)\)-free graphs.