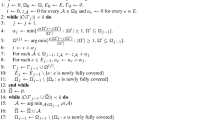A Primal-Dual Randomized Algorithm for the Online Weighted Set Multi-cover Problem

Abstract

Given a ground set $\mathcal {U}$ of n elements and a family of m subsets $\mathcal {S} = \{S_i : S_i\subseteq \mathcal {U}\}$. Each subset $S\in \mathcal {S}$ has a positive cost c(S) and every element $e\in \mathcal {U}$ is associated with an integer coverage requirement $r_e>0$, which means that e has to be covered at least $r_e$ times. The weighted set multi-cover problem asks for the minimum cost subcollection which covers all of the elements such that each element e is covered at least $r_e$ times.

In this paper, we study the online version of the weighted set multi-cover problem. We give a randomized algorithm with competitive ratio $8(1+\ln m)\ln n$ for this problem based on the primal-dual method, which improve previous competitive ratio $12\log m\log n$ for the online set multi-cover problem that is the special version where each cost c(S) is 1 for every subset S.

1 Introduction

The weighted set multi-cover problem is the generalization of the set cover problem, which is defined as follows. Given a ground set $\mathcal {U}=\{1,\ldots , n\}$ of n elements and a family of m subsets $\mathcal {S} = \{S_i: 1\le i \le m \}$, where $S_i\subseteq \mathcal {U}$ for all i. Each subset $S\in \mathcal {S}$ has a positive cost c(S) and every element $e\in \mathcal {U}$ is associated with an integer coverage requirement $r_e>0$, which means that e has to be covered at least $r_e$ times. The goal is to find a minimum cost subcollection that covers all of the elements such that each element e is covered at least specified times $r_e$. When all $r_e=1$, the set multi-cover problem becomes the set cover problem. Let $R=\max \limits _{e\in \mathcal {U}} r_e$. We assume that $R= O(n)$.

Similarly, the online weighted set multi-cover problem is the generalization of the online set cover problem, which is described as follows. An adversary gives elements and their coverage requirement to the algorithm from $\mathcal {U}$ one-by-one. When a new element e and its coverage requirement $r_e$ are given, the algorithm has to cover it at least $r_e$ times by choosing some sets of $\mathcal {S}$ containing it. We assume that the elements of $\mathcal {U}$ and the coverage requirement of elements and the members of $\mathcal {S}$ are known in advance to the algorithm, however, the set of elements given by the adversary is not known in advance to the algorithm. The objective is to minimize the total cost of the sets chosen by the algorithm.

The performance of an online algorithm is measured by the competitive ratio, which is defined as follows. Given an instance I of a minimization optimization problem M. Let OPT(I) denote the optimum cost of off-line algorithms for instance I. If for each instance I of M, an online algorithm OA outputs a solution with cost at most $c\cdot OPT(I)+\alpha$, where $\alpha$ is a constant independent of the input sequence, then the competitive ratio of OA is c. If for each instance I of M, a randomized online algorithm ROA outputs a solution with expected cost at most $c\cdot OPT(I)+\alpha$, where $\alpha$ is independent of the input sequence, then the competitive ratio of ROA is c.

The set cover problem has wide application and is a well-known problem in algorithms and complexity. In [11], Karp shows that the set cover problem is NP-compete. Johnson [10] and Lovasz [13] give the greedy approximation algorithm for the unweighted set cover problem. Chvatal [7] proposes the greedy approximation algorithm for the weighted set cover problem. These greedy algorithms are of approximation ratio $H_n$, where $H_n = 1+1/2+\ldots +1/n$. Lund and Yannakakis show that the approximation ratio $O(\log n)$ for the set cover problem is essentially tight [14]. Later, Feige proves that it is impossible to have an approximation algorithm for the set cover problem with approximation ratio better than $O(\log n)$ [8]. Rajagopalan and Vazirani propose primal-dual RNC approximation algorithms for the set mullti-cover and covering integer programs problems [15]. Noga Alon et al. study the online set cover problem. Based on the techniques from computational learning theory, Noga Alon et al. propose a deterministic algorithm for this problem with competitive ratio $O(\log m\log n)$ [1]. The set cover problem is related to the budgeted maximum coverage problem, which is a flexible model for many applications [16,17,18,19,20].

In the areas of exact and approximation algorithms, the primal-dual method is one of powerful design methods. To our best of knowledge, the first time that the primal-dual method is used to the design of online algorithms is in Young’ work about weighted paging [21], where he design an k-competitive online algorithm. In recent several years, Buchbinder and Naor have shown that the primal-dual method can be widely used to the design and analysis of online algorithms for many problems such as ski-rental, ad-auctions, routing and network optimization problems and so on [2,3,4,5,6].

In [12], Kuhnle et al. introduce the online set multi-cover problem and design randomized algorithms with $12\log m\log n$-competitive ratio. In this paper, we study the online weighted set multi-cover problem. We present an $8(1+\ln m)\ln n$ competitive randomized algorithm for this problem based on the primal-dual method. Specially, when each cost c(S) is 1 for every subset S, the online weighted set multi-cover problem become the online set multi-cover problem. Thus, our algorithm improve Kuhnle et al.’s competitive ratio for the online set multi-cover problem.

2 A Fractional Primal-Dual Algorithm For the Online Weighted Set Multi-cover Problem

In this section, we design a fractional algorithm for the online weighted set multi-cover problem via the primal-dual method. A fractional algorithm allows an element e is fractionally covered its $f_S$ part by a set S such that $\sum \limits _{e\in S}f_S=1$.

First, the weighted set multi-cover problem can be formulated as a 0–1 integer program as follows.

Its Linear Programs relaxation is as follows.

Its Dual Programs is as follows

In the following, we design the online fractional algorithm for the weighted set multi-cover problem via the primal-dual design method developed in recent years [2,3,4,5,6] (see Algorithm 2.1).

Theorem 1

The fractional online algorithm for the weighted set multi-cover problem is of competitive ratio $2(1+\ln m)$.

Proof

Let P denote the value of the objective function of the primal solution and D denote the value of the objective function of the dual solution. Initially, let $P=0$ and $D=0$. In the following, we prove three claims:

• (1) The primal solution produced by the fractional algorithm is feasible.

• (2) Every dual constraint in the dual program is violated by a factor of at most $(1+\ln m)$.

• (3) $P\le 2D$.

By three claims and weak duality of linear programs, the theorem follows immediately.

First, we prove the claim (1) as follows. Consider a primal constraint $\sum \limits _{S:e\in S}x_S\ge r_e$. In each While iteration (From line 5 to line 8 in the fractional algorithm), when this new primal constraint $\sum \limits _{S:e\in S}x_S\ge r_e$ becomes be satisfied, the variable $x_S$ stop increasing its value and its value is not greater than 1. Upon $x_S$ become 1, the fractional algorithm begin to increase $z_S$ and $y_e$ at the same ratio. After that, the increases of $z_S$ and $y_e$ cannot result in infeasibility.

Second, we prove the claim (2) as follows. Consider any dual constraint $\sum \limits _{e\in S}y_e-z_S\le c(S)$. Since its corresponding variable $x_S$ is not greater than 1, we get that:

$x_S=\frac{1}{m}\cdot$exp$(\frac{1}{c(S)}[(\sum \limits _{e\in S}y_e)-z_S- c(S) ])\le 1$.

So exp$(\frac{1}{c(S)}[(\sum \limits _{e\in S}y_e)-z_S- c(S) ])\le m.$

Then, $(\sum \limits _{e\in S}y_e)-z_S-c(S)\le c(S)\ln m$.

Thus, we get that: $(\sum \limits _{e\in S}y_e)-z_S\le c(S)(1+\ln m)$.

Third, we prove claim (3) as follows. The contribution to the primal cost consists of two parts. Let $C_1$ denote the contribution part which is from (6) of the fractional algorithm, where variables $x_S$ are increased from $0\rightarrow \frac{1}{m}$. Let $C_2$ denote the other contribution part which is from (7) of the fractional algorithm, where variables $x_S$ are increased from $\frac{1}{m}$ up to at most 1 by the exponential function.

Bounding $C_1$: Let $\tilde{x}_S=\min (x_S, \frac{1}{m})$. We bound the term $\sum \limits _{S\in \mathcal {S}}c(S) \tilde{x}_S$. To do this, we need the following several facts.

First, from the fractional algorithm, we get that if $x_S>0$, and therefore $\tilde{x}_S>0$, then:

$$\begin{aligned} \sum \limits _{e\in S}y_e-z_S\ge c(S). \end{aligned}$$

(1)

We call (1) as the primal complementary slackness condition.

At the time t, let $B'(S)=\{S|x_S=1, e\in S\}$. Then $|B'(S)|\le r_e$ since otherwise the constraint at time t has been already satisfied and the fractional algorithm stops increasing the variable $y_e$. Thus, $(m-1)|B'(S)|\le (m-1)r_e$. So $\frac{m-|B'(S)|}{m}\le r_e-|B'(S)|$. Since $\tilde{x}_S\le \frac{1}{m}$, $\sum \limits _{S\in \mathcal {S}\backslash B'(S)}\tilde{x}_S\le \frac{m-B'(S)}{m}$. Hence

$$\begin{aligned} \sum \limits _{S\in \mathcal {S}\backslash B'(S)}\tilde{x}_S\le r_e-|B'(S)| \end{aligned}$$

(2)

Also, it follows from the algorithm that if $z_S>0$, then:

$$\begin{aligned} x_S\ge 1. \end{aligned}$$

(3)

We call (2) as the dual complementary slackness and (3) as the second dual complementary slackness condition.

Using the primal and dual complementary slackness conditions, we show the following conclusions:

$$\sum \limits _{S\in \mathcal {S}}c(S)\tilde{x}_S$$

$$\begin{aligned} \le \sum \limits _{S\in \mathcal {S}}(\sum \limits _{e\in S}y_e-z_S)\tilde{x}_S \end{aligned}$$

(4)

$$\begin{aligned} =\sum \limits _{S\in \mathcal {S}}(\sum \limits _{e\in S}y_e\tilde{x}_S)-\sum _{S\in \mathcal {S}}z_S\tilde{x}_S \end{aligned}$$

(5)

$$\begin{aligned} =\sum \limits _{e}(\sum \limits _{S:e\in S}\tilde{x}_S)y_e)-\sum _{S\in \mathcal {S}}z_S\tilde{x}_S \end{aligned}$$

(6)

$$\begin{aligned} \le \sum \limits _{e}r_ey_e-\sum _{S\in \mathcal {S}}z_S \end{aligned}$$

(7)

Where inequality (4) follows from inequality (1) and equality (6) follows by changing the order of summation. As for the reason why inequality (7) holds, we consider some time t. At the time t when e with coverage requirement $r_e$ arrive. From the fractional algorithm, we know that $z_S$ is increased at the same ratio as $y_e$ only when $x_S=1$. Thus, $\frac{dy_e}{dt}=\frac{dz_S}{dt}$ only when $S\in B'(S)$. Hence, the increasing ratio of the left-hand side of (7) at the time t is $(\sum \limits _{S\in \mathcal {S}\backslash B'(S)}\tilde{x}_S)\frac{dy_e}{dt}$. But, at the time t, the increasing ratio of the right-hand side of (7) is $( r_e-|B'(S)|) \frac{dy_e}{dt}$. By inequality (2), we get $(\sum \limits _{S\in \mathcal {S}\backslash B'(S)}\tilde{x}_S)\frac{dy_e}{dt} \le ( r_e-|B'(S)|) \frac{dy_e}{dt}$. So inequality (7) holds

Thus, $C_1$ is at most D.

Bounding $C_2:$ At some time t, we show that the increase $\varDelta C_2$ is most $\varDelta D$ in the same round.

$$\begin{aligned} \varDelta {C_2}=\sum \limits _{S\in \mathcal {S},\frac{1}{m}\le x_S<1}c(S)\cdot \varDelta x_S \end{aligned}$$

(8)

From the line 7 of the fractional algorithm, we get that $\frac{dx_S}{dy_e}=\frac{1}{c(S)}\cdot x_S$. So, $\varDelta x_S=\frac{1}{c(S)}\cdot x_S\cdot \varDelta y_e$. Thus, we get that:

$$\begin{aligned} \varDelta {C_2}=(\sum \limits _{S\in \mathcal {S},\frac{1}{m}\le x_S<1}x_S)\cdot \varDelta y_e \end{aligned}$$

(9)

At the time t, the new primal constraints are not yet satisfied, so we get that: $\sum \limits _{S\in \mathcal {S},\frac{1}{m}\le x_S<1}x_S+\sum \limits _{x_S=1}1<r_e$. Thus, $\sum \limits _{S\in \mathcal {S},\frac{1}{m}\le x_S<1}x_S <r_e-\sum \limits _{x_S=1}1$. Hence,

$$\begin{aligned} \varDelta {C_2}\le (r_e-\sum \limits _{x_S=1}1)\cdot \varDelta y_e \end{aligned}$$

(10)

From the line 8 of the fractional algorithm, $\varDelta y_e=\varDelta z_S$ when $x_S=1$ in the same sound at the time t. So,

$$\begin{aligned} \varDelta {C_2}\le r_e\cdot \varDelta y_e-\sum \limits _{x_S=1}\varDelta z_S=\varDelta D \end{aligned}$$

(11)

Thus, $C_2\le D$.

Hence, we get that $P=C_1+C_2\le 2D$. So, claim (3) holds. Furthermore, the theorem holds.    $\square$

3 Randomized Algorithm for the Online Weighted Set Multi-cover Problem

In this section, we design a randomized algorithm for the online weighted set multi-cover problem with competitive ratio $8(1+\ln m)\ln n$.

Theorem 2

The randomized algorithm is of competitive ratio $8(1+\ln m)\ln n$.

Proof

First, we show that the randomized algorithm produces a feasible solution with high probability $1-O(\frac{1}{n^2})>\frac{1}{2}$.

Consider any an element e, assume that it appears at time t. let $A_i$ denote the event that e isn’t covered in the i-th round from 5-th to 7-th line in the randomized algorithm. Let $\mathcal {S}_{t_i}$ denote the unchosen sets of $\mathcal {S}$ and $\mathcal {C}_{t_i}$ denote the chosen sets at the beginning of in the i-th round. $c(e,t_i)$ denote the number of e has been covered at the beginning of in the i-th round.

Then, we compute the probability that $A_i$ occurs. Consider any $j ( 1\le j \le 4\ln n)$, let $D_j$ denote the event that e is not covered due to j, which means that for all unchosen sets $S\in \mathcal {S}_{t_i}$ and $e\in S$, none of the value of V(S, j) is less than $x_S$. Thus, $Pr(A_i=1)=\bigcap \limits _{1\le j\le 4\ln n}Pr(D_j=1)$

The probability $Pr(V(S,i)\le x_S)$ is $x_S$. So $Pr(D_j=1)=\prod \limits _{S\in \mathcal {S}_{t_i}|e\in S}(1-x_S)$. Since $1-x\le exp(-x)$, we get that: $Pr(D_j=1)\le exp (-\sum \limits _{S\in \mathcal {S}_{t_i}|e\in S}x_S)$. Since all $x_S$ consist of a fractional solution after the fractional algorithm, we get that $\sum \limits _{S\in \mathcal {S}:e\in S}x_S\ge r_e$. Thus, $\sum \limits _{S\in \mathcal {S}_{t_i}|e\in S}x_S+\sum \limits _{S\in \mathcal {C}_{t_i}|e\in S}x_S\ge r_e$. So $\sum \limits _{S\in \mathcal {S}_{t_i}|e\in S}x_S\ge r_e-\sum \limits _{S\in \mathcal {C}_{t_i}|e\in S}x_S=r_e-c(e,t_i)$. Hence, $Pr(D_j=1)\le exp (-\sum \limits _{S\in \mathcal {S}_{t_i}|e\in S}x_S)\le exp(-n_i)$, where $n_i=r_e-c(e,t_i)$. So, $Pr(D_j=1)\le exp(-1)$. Hence, $Pr(A_i=1)\le (exp(-1))^{4\ln n}=exp(-4\ln n)=\frac{1}{n^4}$.

So, the probability that e is not covered $r_e$ times is $Pr(A_1=1\vee \ldots \vee A_{u_e}=1)\le \sum _{i=1}^{u_e}Pr(A_i=1)\le \sum _{i=1}^{u_e} \frac{1}{n^4}=\frac{n_e}{n^4}\le \frac{r_e}{n^4}\le \frac{R}{n^4}\le \frac{O(n)}{n^4}=O(\frac{1}{n^3})$.

By the union bound that the probability of union events is at most the sum of the probability of each event, the probability that there is an element e which is not covered $r_e$ times is at most $n\times O(\frac{1}{n^3})=O(\frac{1}{n^2})$ since there are at most n elements.

Hence, the randomized algorithm produces a feasible solution with high probability $1-O(\frac{1}{n^2})>\frac{1}{2}$.

Second, we show that the expected cost of the solution of randomized algorithms is $O(\log n)$ times the fractional solution.

Let $B_i$ denote the event that $V(S,i)\le x_S$. Then, $Pr(B_i=1)=x_S$. The probability that the set S is chosen to the solution is at most the probability that there exists an $i, 1\le i\le 4\ln n$, such that $V(S,i)\le x_S$.

Thus, the probability that S is chosen to the solution is at most the probability of $\bigcup _{i=1}^{4\ln n}B_i$. By the union bound this probability is at most the sum of the probabilities of the different events, which is $4x_S\ln n$. Therefore, using the linearity of expectation, the expected cost of the solution is at most $4\ln n$ times the cost of the fractional solution.

By Theorem 1, the cost of the fractional solution is $2(1+\ln m)$ times the optimal solution. So the competitive ratio of the randomized algorithm is $8(1+\ln m)\ln n$.    $\square$

4 Conclusion

In this paper, we have studied the online version of the weighted set multi-cover problem. We have proposed a $8(1+\ln m)\ln n$-competitive randomized algorithm for this problem based on the primal-dual method. An interesting open problem is to design deterministic algorithms for the online weighted set multi-cover problem.