1 Introduction

Most clustering algorithms are based on some kind of assumptions about the distribution or form of the data. K-Means [9], for example, is based on the assumption of Gaussian distributed clusters, with the variance in all directions being basically the same. EM [2], on the other hand, does not necessarily assume a uni-directional variance but is capable of finding lopsided, stretched Gaussian-distributed clusters. The assumption behind it though is a Gaussian distribution. To overcome these restrictions, purely distance-based clustering techniques like SingleLink [12] and DBSCAN [3], which no longer make assumptions about the distribution of data, have been created. These techniques, however, often need at least one parameter to help them to estimate how dense the expected clusters should be. Since the density of the data set might vary, this may cause that clusters with different densities can be cut out very poorly. DBSCAN is well known to have problems with varying densities [11]. SingleLink, on the other hand, suffers from the “SingleLink-Effect”, where clusters are combined, if they have a “bridge” of data points connecting them. All these difficulties are caused by the strict focus on the given parameters, which does not always give the leeway needed.

The technique that we would like to present here, RandomLink, avoids such problems by using randomised effects to determine the clusters. It does not need parameter(s) or model assumptions to find the clusters. Its only premise is that the closer data points are, the more likely they belong into the same cluster. It starts with a fully connected data set (all data points are connected) and deletes all connections between data points. The order of deletion is remembered and inverted to connect data points until a certain number of clusters is found. This number of clusters would be a parameter which we want to avoid. Therefore, we also present a simple strategy to get rid of it. Connections are deleted depending on their length. A long connection is more likely to be deleted. Thus, every pair of data points can stay connected, but distant ones are less likely to. Direct connections between them are highly unlikely to consist for a long time, but they can nevertheless be connected via other data points. If the density between them is high, then there might be a path of data points linking them. If there is a path between them, then they are part of the same cluster, as clusters are defined as “connected components”, i.e. all data points that are connected via paths.

Fig. 1.
figure 1

The principle behind RandomLink.

Full size image

See Fig. 1 for this. The direct connection between data points A and B is highly unlikely to exist for a long time, as it is rather long. Compared to it, the line between B and C has a relatively high chance to remain for longer. This would link two clusters, which clearly do not belong together, and split one cluster into two, which do. RandomLink removes – with a certain probability – longer links first, which means that while it does remove the link between A and B, it will eventually also remove the link between B and C. Since the links between clusters are – as a tendency – longer than many links inside a cluster, the connection between clusters will eventually be cut. Inside the cluster though, many links will consist for a long time and thus a path (like the one shown in the Fig. 1) between A and B may remain and link them indirectly. There is, of course, the chance that this specific path is also interrupted, but as there is a high number of possible paths between A and B, at least one will - most likely - remain.

Thus, not only the distance between data points is relevant for RandomLink, but also the placement and relative distances of the other data points are very important to decide if data points are considered part of the same cluster. While the direct connection will be – very often – erased, indirect paths will remain inside the cluster, that link different parts of the cluster with each other. One possible clustering result then might look like Fig. 1b. The direct connection between A and B is gone, but an indirect path remains. RandomLink potentially takes all connections between data points into account in every step. One might state that RandomLink considers the whole data set, not only the local environment.

The similarity to SingleLink is clear. SingleLink connects the closest data points, while RandomLink is only likely to connect them or might link them via other close data points. It has a broader approach because the length gives the probability of a link remaining, not the absolute 0/1-decision of SingleLink. With this RandomLink can e.g. alleviate the SingleLink-effect (or chain effect), from which SingleLink suffers and cluster a data set more naturally. The SingleLink-effect is caused by a sort of bridge between clusters, which will keep them connected, no matter how long the bridge. With RandomLink the connections of the bridge will be thinned out while clustering until it eventually is no longer connecting. The specifics, of course, depend on the length, density, etc of the bridge, but RandomLink can overcome, or at least lessen, the difficulty of the SingleLink-effect. RandomLink is as a whole not purely dependent on local density, as e.g. DBSCAN is, but evaluates on a broader spectrum, as stated before. This leads to a reduced dependency on the rigidity of fixed parameters compared to DBSCAN or SingleLink have. We will talk in more detail about this in Sect. 4, on how we intend to use random effects to our advantage.

1.1 Related Work

RandomLink computes the distances between all data points and determines an order by deleting them depending on their length combined with random numbers. After this order is fixed, it starts connecting the data points until the clusters are found. The closest related methods are clearly hierarchical clustering approaches like SingleLink. The differences in these methods are how they decide on the order of connecting the data points to clusters. SingleLink connects data points/clusters depending on the closest data points in the clusters, AverageLink [13] connects the clusters depending on the average distance between data points, CompleteLink [1] on the maximal distance between data points and Ward’s Criterion [16] on the change in variance in the clusters. These methods all decide on the order of connecting data points deterministic while RandomLink uses random effects and connects the likely closest clusters. As a distance between clusters, we use the SingleLink approach of the minimal distance between data points in clusters. It could be easily adapted to other definitions of distance, as e.g. AverageLink uses.

One could consider Graph-clustering methods like Highly Connected Subgraphs (HCS) [5] or Chameleon [7] as related, as we plot various Graph-like Figures, but these are used to explain RandomLink. Graph-clustering methods are focused on clustering graphs, while RandomLink clusters numerical data. One can create a Graph out of numerical data and employ these methods, but other clustering approaches are more closely related. HCS divides graphs along a minimum cut [6] multiple times before it starts re-connecting them. Chameleon [7] creates a sparse kNN graph, partitions it into many sub-graphs and merges them using a minimum cut criterion.

Both these methods have parameters which are hard to tune. RandomLink needs no parameters at all. In the straightforward implementation, we would leave the number of clusters to be found to the user, but we created an approach for estimating the optimal stopping point in creating the final clusters (details in Sect. 2.2). This stopping criterion could be construed as an ensemble-approach (also called consensus clustering, see [8] for an introduction). Ensemble methods are a relatively new approach to data mining. They try to combine multiple clustering results into one and this single result should be better than any of the input clusterings. RandomLink uses k-Means to find the best stopping point, but it does not combine clustering results, so it is not exactly an ensemble-approach.

Spectral Clustering-approaches start with a similarity/distance matrix on which they eventually employ k-Means. RandomLink computes the distances and uses k-Means to decide the stopping point. There are some similarities and we take them as interesting comparison methods, in particular, the fundamental algorithm of Ng, Jordan and Weiss [10], which has become one of the classical clustering approaches by now. These standard methods should be used as comparison methods as they provide a baseline of what one can expect as a clustering result. Another standard approach is DBSCAN, one of the best-known examples of distance-based clustering methods, which we will discuss in more detail later.

1.2 Contributions

In this paper we propose the clustering algorithm RandomLink, which is extensively tested on various real world datasets. It performs especially well on data sets where other clustering approaches have difficulties to reach even a minimal level of clustering quality. Thus, it can be used as an approach for difficult data sets, where not much is known. The advantages of RandomLink are the following:

  • RandomLink tends to find decent clusterings even when well-established algorithms fail.

  • RandomLink is completely parameter-free and needs no input from the user. It does not need the number of clusters and stops completely automatic.

  • RandomLink has no assumption about the shape of distribution of clusters. They can be of arbitrary shape and distributions.

  • The source code of RandomLink is publicly available for everyone to corroborate our results.

2 The Algorithm

As stated, RandomLink determines the order of connecting clusters by first deleting them using their length as probability for being deleted. Thus, we start by computing the distances between all data points and store them in a distance matrix S. We can imagine the data as a fully connected data set, i.e. each pair of data points has an edge, i.e. link, e in between them with the length of this link defined by the Euclidean distance of the data points. The algorithm now deletes one link after another, with the length of an link determining the probability of that happening.

2.1 Deleting Links

All links are lined up and the total length of all links \(sum_S\) is computed. See Fig. 2 for a simple example. A random number in the interval \([0,sum_S]\) is drawn, here it is 3.1415, and the corresponding link \(e_2\) is removed. It is simply the link into which’ interval the number falls. Link \(e_2\) is then removed from the concatenated links and the total length is now 18, i.e. \(sum_S-l(e_2)\) with l(e) being the length of link e. A new number is now drawn from the interval \([0,sum_S-l(e_2)]\) and the same step is repeated.

Fig. 2.
figure 2

How we determine the order of connecting clusters.

Full size image

The probability of a specific link \(e_x\) being removed is thus

$$\begin{aligned} p(e_x)=\frac{l(e_x)}{\sum _{e} l(e)} \end{aligned}$$
(1)

It is linearly dependent on the length of the e, i.e. longer links are more likely of being removed. This approach is commonly referred to as Roulette Wheel Selection [4].

RandomLink starts by creating a distance matrix \(S_{n\times n}\) computed from a data set \(D_{d\times n}\) using a distance function. We use the Euclidean distance, but any other distance or similarity measure could be used as well. Using Manhattan distance or Cosine and Gaussian similarity lead only to tiny differences. The results reported in Sect. 3 are almost uninfluenced by the used distance/similarity function. The values in S give the probability (if scaled as in Eq. (1)) for every link connecting two data points to be deleted. We calculate the sum of S and store it as \(sum_{S}\). As explained earlier, we choose a random value r in the range \([0,sum_{S}]\). There is a link corresponding to r and this link is deleted from the data set and its value in S set to 0. Its index is stored in a stack and identifies the deleted link. This procedure is then continued until all links are deleted.

figure a
Fig. 3.
figure 3

Different amount of links and the connected components. The algorithm deletes more and more connections, until eventually all data points are singletons. The order of the connections is determined by the deletion of links and the clusters found by inserting the links in reverse order.

Full size image

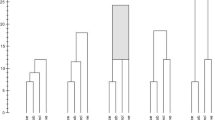
The algorithm starts with a fully connected data set from which the links are deleted until every data point is a singleton. Thus, the order of the links between the data points is determined and the algorithm can start connecting them, i.e. the clusters will be created. The algorithm adds the first link as determined in the order of the links, reducing the number of connected components from n to \(n-1\). After a few links are added, we will have a situation like in Fig. 3d. Many clusters exist and the correct clusters are still separated. Adding a few more links will lead to Fig. 3c, where the clusters start to make sense. In the beginning, most added links will be small until, eventually, longer links are added. Connections between the clusters become more and more likely. This is the situation depicted in Fig. 3b. The number of connected components decreases with those longer links being added and interconnecting clusters. The algorithm terminates as soon as the number of connected components |cc| becomes one. All data points are connected and the clustering no longer changes.

Somewhere between the two extremes of \(|cc|=n\) and \(|cc|=1\) is the point where we want to stop. If we were to look for exactly k clusters, we could simply stop as soon as we found k connected components, but we want to have a completely parameter-free clustering approach which determines the number of clusters automatically. It is possible to apply RandomLink with k as a parameter, but knowing the correct number of clusters is seldom trivial and we can not expect that the user always knows exactly for what he/she is looking for. We found a heuristic that helps us find the optimal stopping point.

We make here use of a union-find data structure which is also known as disjoint-set for an online connected components analysis and benefit from quasi constant time per operation [14]. Every time clusters are merged the number of connected components decreases by one and the root nodes for every data point in the disjoint-set data structure are used as cluster labels.

2.2 Stopping Criterion

In-between \(|cc|=n\) and \(|cc|=1\) is the point where we want to stop. If \(|cc|=n\) then every point is its own cluster. Adding links leads to the data points creating clusters. Adding even more links leads to the clusters becoming connected until eventually \(|cc|=1\). The typical progress of this can be seen in Fig. 4. The measure for clustering quality used there is Normalised Mutual Information (NMI) [15] which is widely used to evaluate clustering results. NMI scales between 1.0 (perfect clustering) and 0.0 (purely random cluster assignments). We see in Fig. 4 that there is a peak between the fully connected data set and fully isolated data points. The NMI is maximal there, i.e. it is the best result that can be reached with our approach and we find it the following way:

Fig. 4.
figure 4

Average NMI when deleting links for our running example.

Full size image

Whenever the number of connected components |cc| changes, a score is computed by our stopping criterion (Algorithm 2). This score changes for different values of |cc|. When the score has become maximal, \(max_{score}\), the ideal state of the clustering has been reached and the connected components cc at that time will be returned as the clustering result. The score itself is computed by comparing our current clustering result with the result of k-Means by executing k-Means on the data D and using the number of connected components |cc| as the number of clusters k. Thus, we compare the clusterings of RandomLink and k-Means with NMI and remember the comparison value. Finding the stopping point this way ensures that we need no further parameters (the k for k-Means is given by RandomLink) and although it is purely heuristic, it is easy to understand.

figure b

Thus, we know when the algorithm should stop. It would be beneficial for RandomLink to know k, as we will see in Sect. 3.2, but this way we remove the last parameter at the cost of a relatively small loss in clustering quality. Hence, one can use RandomLink and set a number of clusters as e.g. SingleLink does it, or use it automatically in combination with this stopping criterion.

3 Experiments

3.1 Real World Data

We tested RandomLink with various real world data sets from the UCI Machine Learning Repository to evaluate its performance. The most important comparison method is clearly SingleLink, as it is closest to our approach. We also included AverageLink [13], CompleteLink [1] and Ward’s method [16] as further representatives of hierarchical clustering methods. We also included the standard clustering methods, i.e. EM [2], as they give a realistic value of what can be expected from clustering for a data set. K-Means [9] is a standard approach and also employed to evaluate the optimal stopping point and therefore a necessary comparison method. DBSCAN [3] is one of the most prominent distance-based clustering methods which we will talk about more later on. We mentioned the similarities to Spectral Clustering-methods and have thus also included STSC [17] as a popular method and FUSE [18] as a more recent one. With Spectral Clustering we refer to the essential algorithm by Ng et al. [10], which was foundational for this type of clustering methods. Furthermore, the aforementioned Chameleon [7] is chosen to represent graph clustering methods.

Table 1. Experimental results. All non-deterministic results have been repeated 100 times and the average is given. The correct value for k is always given for the comparing algorithms. Results given in NMI and best result bold marked.
Full size table

The results are shown in Table 1. “RandomLink max” value stands for the best result which could have been reached with our approach, while “RandomLink” denotes the actual result we reach in combination with the stopping criterion. On the data sets, RandomLink always yields a good NMI value while the other algorithms partially completely fail and are sometimes clearly outperformed by RandomLink. RandomLink is the best choice on all of the 8 data sets and loses only once by a tiny deficit. The data sets have a wide range of dimensionality and number of clusters, which shows that RandomLink is not restricted in these regards. We want to especially emphasise the improvement over SingleLink. Including these random effects into it, massively improved the clustering results. The stopping criterion works most of the time as intended and returns a result close to the optimum. Furthermore, the clustering results are mostly stable. The small deviations in clustering quality show that the algorithm behaves predictably in a certain range.

Parameters. We tried to be as fair as possible to the comparison methods. The algorithms were given correct k if needed and using Euclidean distance. For DBSCAN we performed a grid search on the parameter range \(\epsilon = [0.01--10.0]\) in 0.5 increments and \(minPts = {2,5,8,11,14}\) and report the best found NMI value. For Chameleon, the kNN graph was constructed with \(k=10\) and the default value of \(\alpha = 2.0\) was used for the cluster merging, besides that, the authors stated that Chameleon is not very sensitive to the parametrization [7]. The similarity matrix for spectral clustering was created by using the Euclidean distance of the 10-nearest neighbours reassuring a connected graph. For Self Tuning Spectral Clustering (STSC) [17] the default parameters were used. For SingleLink, FUSE, k-Means etc. the correct k is always given, as stated. RandomLink was executed 100 times for every data set listed in Table 1 and the mean NMI is reported as well as the standard deviation. We use NMI to evaluate clustering quality, as it is widely used and often considered the standard when evaluating clustering results.

Table 2. We compare the clustering result of the stopping criterion to knowing k in regard to clustering quality (NMI) and runtime. Best result in bold.
Full size table

Sourcecode. Under the following links, one can find code and data sets:

https://github.com/53RT/RandomLink

https://dm.cs.univie.ac.at/research/downloads/

We do so as we feel that it is important that our claims can be validated and fellow researchers can build upon our results if they feel so inclined.

3.2 Adding the Number of Clusters as a Parameter

We pride ourselves on RandomLink being completely parameter-free, i.e. no density-parameter or number of clusters is needed. The question is whether this has deteriorated the clustering quality, and if so, by how much? Thus, we ran RandomLink to find exactly \(|cc|=k\) clusters and compared it to the results of our stopping criterion. In Table 2 is the effect of supplying k described.

Two relevant effects can be observed here: 1) The runtime does clearly decrease if k is supplied as a parameter. Computing the stopping criterion is no longer necessary and one can stop the algorithm as soon as the correct number of clusters is reached, which means one has to perform less operations with the disjoint-set data structure used in the link insertion phase. 2) The difference in NMI is small. This means that our method either stops at the correct number of clusters or, if it stops at a different point, finds a stopping point that is comparable in regard to clustering quality. There is a tendency for the results to be better with given k, but this is not exactly surprising as the additional information makes things easier. Knowing when to stop, reduces the risk of generating poor clustering results.

A user has, therefore, the possibility to either let the algorithm find the number of clusters automatically or ask for a specific number of clusters, which entails a speed-up of a factor of roughly 2–3. Automatic setting of k is a major advantage in an unsupervised setting, as most of the time the data set is not very well understood and any decision a user has to make might be false. RandomLink takes this responsibility from the user, though, at the cost of runtime, but in similar clustering quality.

3.3 Runtime

We omit extensive experiments on runtime, as we are more interested if this approach is valid in principle, but we do calculate the estimations. For the algorithm RandomLink itself, we first need to compute the distances between all data points. This takes \(\mathcal {O}(n^2)\) operations to do. Alternatively, we can also start with an adjacency matrix, and perform RandomLink on it, but this is not a massive overall improvement, as we still need to determine the order of links. There are \(n^2\) many links. Selecting a specific one, as described in Sect. 2.1, entails a binary search, i.e. a runtime of \(\mathcal {O}(\log _{2}(n^2))\). This link is now removed. Finding the next link entails again a binary search, but this time on \(n^2-1\) many elements, thus the runtime for it is \(\mathcal {O}(\log _{2}(n^2-1))\). Summing up over all binary searches from \(n^2\) to 1 link(s) is \(\sum _{i=0}^{n^2} \log _{2}(i)\). Using Stirling’s approximation this can be estimated as

$$\begin{aligned} \mathcal {O}(n^2 \cdot \log _{2}(n)) \end{aligned}$$
(2)

With this, the order of the links is determined and we start to create the clusters. The stopping criterion consists of executing k-Means, whenever the number of connected components changes. K-Means has an estimation of \(\mathcal {O}(n)\) and has to be computed at most n times. Thus, it adds to the total actual runtime but does not add anything in regards to the \(\mathcal {O}\)-calculation.

The second phase of RandomLink - inserting the links in the reversed top-down order - can be solved efficiently using a disjoint-set data structure [14]. First the make set method initialises the data structure with creating a node for every item with the parent node pointing at itself. This takes \(\mathcal {O}(n)\) time. The parent node is used for a recursive traversal to determine if two data objects are connected which is true if they have the same root. If path compression and union by size or rank is used in the data structure the complexity reduces to \(\mathcal {O}(\alpha (n))\) for the find and union operations which is optimal and quasi constant. As we have \(\approx n^2\) links to insert in a fully connected setting there will be at most \(\mathcal {O}(n^2 \cdot \alpha (n))\) operations which is never reached in reality as the connected components reaches one with a fraction of inserted links. The number of connected components can be retrieved as a byproduct as it always decreases by one if clusters are united and the cluster labels can be easily extracted from the root node of every item.

Since \(\alpha (n)\) is essentially constant, creating the clusters is \(\mathcal {O}(n^2)\) and the dominating part of the estimation is computing the order of the links, i.e. \(\mathcal {O}(n^2 \cdot \log _{2}(n))\). Equation (2) gives therefore the total of the runtime-estimation.

4 Using Random Effects

Every pair of data points entertains the possibility in RandomLink to not be connected with each other. This drastically lessens linkage-effects, which necessarily happens for SingleLink for data sets like the one depicted in Fig. 5. The SingleLink-effect, often referred to as chaining-effect or chain-effect, describes the tendency of SingleLink to create long chains of clusters, i.e. linking clusters through small bridges of data points which do not belong together. The example, shown in Fig. 5 is a prime, if somewhat extreme, example of this happening. The two clusters do have a bridge in between them and this bridge needs to be broken for them to be correctly clustered. SingleLink is not capable of this. Even if the bridge were far longer SingleLink would still connect the two clusters. RandomLink, on the other hand, will break this bridge and the further away the two clusters are, the faster this will happen.

Somewhat similar is the situation for DBSCAN. We see in Fig. 6 two Gaussian clusters with different density. DBSCAN is well known to have problems with this type of setting, where density varies. We see the difference in NMI and how much more capable RandomLink is in clustering this data set.

Distance-based techniques are most of the times deterministic and, therefore, forced to “obey” their parameters. Since these parameters are necessarily based on local density (that is either the closest neighbour (e.g. SingleLink) or the number of neighbours in a certain environment (e.g. DBSCAN)), the local density determines if data points are put into the same cluster. The difficulty now lies therein that only taking local density into account might lead to troubling clustering results. This is obvious for SingleLink with data sets like the one shown in Fig. 5, where the local density in the bridge between clusters is relatively high and SingleLink will, therefore, connect the clusters. This drawback is also present in DBSCAN, as it is not fit to handle clusters with different densities (see Fig. 6). Such a situation will lead to sub-par clustering results. RandomLink, on the other hand, can handle such situations due to its more “holistic” approach as it takes the whole data set into account. It splits the clusters in Fig. 5 apart, without falling into the same trap as SingleLink. It can also handle a situation like in Fig. 6, where DBSCAN (as well as SingleLink) would fare very badly. The idea for the future is to combine random effects with DBSCAN and SingleLink to overcome these difficulties these algorithms have with such data sets. The approach of RandomLink that employs randomised effects, helps overcome the restrictions of “fixed” parameters.

This is what we did with SingleLink: In the classical form, SingleLink first computes all distances and then continues linking the closest clusters until either k connected components are created, with k as a given parameter, or a stopping criterion tells it to. RandomLink, on the other hand, computes all distances, deletes them and then continues linking the likely closest clusters until the stopping criterion tells it to stop. The similarities are obvious. One can consider RandomLink as an extension of SingleLink with the help of random effects, and a stopping criterion. SingleLink is essentially the expected result of RandomLink, but the random effects present in RandomLink help to overcome the chaining-effect and to break the bridge between clusters.

Figure 6 also suggests that the same approach is also possible for other deterministic distance-based methods like DBSCAN, i.e. that we can to combine DBSCAN with randomized effects to lessen the dependency on fixed parameters. The goal is to establish the inclusion of randomised effects into distance-based clustering algorithms as a general principle, which helps with overcoming certain restrictions, that these algorithms suffer as a consequence of their rigidity.

Fig. 5.
figure 5

SingleLink-Effect for two Gaussian cluster with a bridge in between. RandomLink separates the Link, while SingleLink cannot.

Full size image
Fig. 6.
figure 6

Gaussians with different density. RandomLink can separate them better than the carefully parametrized DBSCAN.

Full size image

5 Outlook and Conclusion

RandomLink in combination with the stopping criterion is a completely parameter-free clustering approach that can handle a wide range of data sets. It assumes no specific distribution for a cluster, thus, can handle clusters of arbitrary shape. One might think that the use of k-Means to estimate the optimal stopping point, limits it to Gaussian clusters, but k-Means has no influence on how the clusters are constructed. The shape of the clusters found is determined solely by the order in which the links are added to the data set. Instead of k-Means, we also tried Spectral Clustering, which can handle non-convex clusters, and the results barely differ. Since it does increase runtime, we stuck with k-Means.

RandomLink does not have some of the drawbacks of other distance-based clustering approaches, as we have shown in comparisons with SingleLink and DBSCAN, the main representatives of this group. It can handle bridges between clusters and clusters with varying density. We outlined our idea about including randomised effects into other distance-based clustering algorithms, as we have done here with RandomLink for SingleLink. The idea to use random effects for clustering might not be the most obvious one, but we are convinced that we established here the usefulness of such an approach, especially when comparing the clustering results of SingleLink and RandomLink in Table 1. RandomLink can be taken as an extension of SingleLink with random effects (and a stopping criterion) and we are certain that this can also be done with other algorithms. Our main concern in this work has been to establish that the combination of clustering with random effects can prove useful, especially for overcoming the restrictions that these algorithms have. We are optimistic that this has been implied heavily by RandomLink for SingleLink and we are looking forward to combining this approach with other methods like DBSCAN.