Keywords

1 Introduction

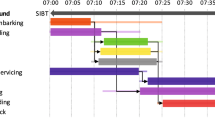
Effective planning and scheduling is crucial in many areas of airport operations, where decisions are interconnected with each other and the potential for flight delays due to knock-on effects is rather high. Careful planning for the day of operations is essential. With many factors out of the control of any airport decision maker—weather conditions, aircraft technical faults, delays, late passengers on boarding, etc.—, plans that are in some form robust should be sought. This is particularly true for aircraft turnaround and airport ground services. When an aircraft lands, it proceeds to a parking stand. Here, it undergoes a sequence of operations to get ready for the following take-off. A mix of operations may be needed: passenger disembarking/boarding, baggage unloading/loading, refueling, cabin cleaning, catering, toilet and potable water servicing, and aircraft push-back. Precedence relations do apply—e.g. refueling often cannot start before passengers have disembarked due to safety regulations. Figure 1 shows an example of a single aircraft turnaround. Conjunctive arcs represent the precedence relations. There exist specific time windows through which each activity should be performed. Each time window shortens/stretches out depending on what happens to other related operations. The turnaround should ideally start as soon as an aircraft arrives at its stand, ideally at the time for which it was scheduled to arrive there—or start of in-block time (SIBT)—and should be completed by the time it was scheduled to be pushed-back into the taxiway on its way to the runway—also called its start of off-block time (SOBT).

Fig. 1.
figure 1

An example of aircraft turnaround operations and precedence relationships between them within a timeline

Full size image

Turnaround operations are often handled by different service providers (SPs). A great deal of coordination is required to make sure they do not delay any aircraft, and for delays not to propagate to other aircraft. Cross-turnaround delay propagation may happen if teams from SPs are scheduled back-to-back between subsequent aircraft: team A finishing late on aircraft turnaround X will surely start late on turnaround Y if it was immediately assigned to it. Team A will also be occupying the stand for longer, with turnaround Z of the aircraft next assigned to the same stand likely to start late, and operations of team B (possibly of a different SP), that was assigned to Z also impacted. Propagation of delays across the airport parking lot—apron for short—is a certainty.

Organizations in aviation have long been aware of such issues and have devised an approach named Airport Collaborative Decision Making (A-CDM) ( [5]), which is currently in place in just a minority of airports in Europe—albeit some of the biggest ones in terms of passenger numbers per year. According to A-CDM, most of the actors involved in aircraft operations must share certain pieces of information with one another to keep tighter levels of coordination. A central piece of information is the Target Off-Blocks Time (TOBT), which is calculated on the day of operations and used as a reference for all other ground service operations. A-CDM focuses on the coordination of aircraft movements, seen, probably correctly, as the center-piece of airport operations. But coordination of the movements of ground service staff and related equipment across busy aprons is equally critical, as it contributes to delays, but also because certain pieces of costly equipment are shared by multiple turnaround teams working for separate SPs. While A-CDM is an appealing concept, to work as expected, a certain degree of information sharing among the airport and the various SPs need to be in place, which happens typically only if enforced. Busier hub airports represent the typical example where the enabling conditions are met. In non-A-CDM airports, though, coordination is also needed, but without data sharing mechanisms it is virtually impossible to achieve. The remainder of this paper proposes a feasible and robust way to support this more general scenario.

2 Related Literature

The Operations Research (OR) community has, in the past three decades, worked on the modeling and solution of problems related to coordinating the movements, usage, and sharing of turnaround teams and equipment, but only partially.

The body of work by Norin and colleagues [18, 19] shares quite a few elements with our study. As we, and others do (e.g., [1] and [21]), the problem is modeled as a form of Vehicle Routing Problem with Time Windows (VRPTW)  [22]. Similarly to us, they work in an A-CDM setting, albeit with a different objective function: they minimize the weighted sum of flight delays and traveling distance. Due to the computational complexity of the underlying problem, they also focus on finding reasonable solutions in short times adopting a form of Greedy Randomized Adaptive Search Procedure (GRASP). They also make use of simulation to test the robustness of their heuristic plans under a range of uncertain conditions. Differently from us, the authors focus on one turnaround operation only: de-icing, with one type of vehicle/related staff to operate them. Stockholm Arlanda provides for their data set and motivating example.

In another closely related study [12], the authors did not see an option to adopt a fully centralized solution process, as the ground service providers are effectively separate legal entities making independent decisions. They also did not see the point of adopting a complex negotiation mechanism between different service providers, essentially ruling out in their assumptions any form of information sharing. This is a very relevant paper based on the same problem as ours, but examined through a substantially different perspective.

Padron et al.  [21] probably represents the closest work to our study. They also consider scheduling all the ground handling vehicles at an airport, and they combine CP with heuristic search techniques such as Large Neighborhood Search (LNS) and Variable Neighborhood Descent (VND). Unlike us, their turnarounds have a fixed sequence of tasks. In a subsequent paper [20], as we do here, they integrate simulation at the bottom-end of their methodology to investigate the robustness of the generated heuristic solutions.

Among the remaining studies, less related to ours, [7] represents a more recent example of VRPTW formulation, but focuses on individual workers and their synchronization with vehicles, and has no view on collaborative mechanisms. Works such as [1, 10], and [23] provide different heuristic approaches to solve the vehicle routing problems implied by aircraft turnaround operations at airports. Finally, many older studies had approached apron resource allocation problems from a multi-agent distributed planning perspective. Among these, [11, 14, 16] and [13] modeled their problems—as we also do in one of our steps—after the Resource-Constrained Project Scheduling Problem (RCPSP)  [2], while [6] modeled the problem as a form of job shop scheduling.

3 Planning Process and Related Models

There are two levels to the turnaround planning problem studied in this paper—long-term and short-term (Fig. 2). All decisions are of tactical nature, as they take place ahead of the day of operation. Real-time management of apron operations and related resources is out of scope for the present paper.

Fig. 2.
figure 2

Proposed turnaround planning process

Full size image

In the longer term, flight schedules for the next few months are known to both the airport operator (AO) and the SPs. The AO needs this information to coordinate the scheduling of all the turnaround operations for each of the days in the planning horizon, aiming at minimum delays. The main decision maker in the longer-term is the AO, wanting to fix time windows for all operations whilst keeping overall resource requirements for the airport reasonably contained. After these decisions are made centrally, each SP can start thinking about their own resource requirements for each day of operation, and run their own staff rostering processes.

In the shorter term, approximately a week before the day of operations, the updated flight schedule is shared with all SPs and the same tactical reasoning can be rerun, with time windows revisited by the AO and rosters updated by the SPs.

In the even shorter term, closer to the start of the day of operations, time windows remain fixed and turnaround teams are known to SPs with a high degree of certainty. Then, each SP makes sure they can optimally route their staff through all turnaround tasks, by keeping some slack time to compensate for unforeseeable delays. At this stage, the objectives and constraints can differ by SP, but all SPs still have to stick to the time windows set by the AO.

Although our approach would ultimately help to plan for all kinds of resources in apron operations, we focus on planning for ‘teams’ of handling agents of each SP, i.e. we focus on human resources. Each of the turnaround operations is normally executed by small teams of employees, of size known to each SP, and planning for the sequence of turnarounds to be visited and serviced by each team during the day of operation is of utmost importance. In the following, we assume that all needed equipment is either carried over by the teams as they move from one turnaround to the next, or sourced across the apron area as they move through their jobs for the day, and as such is not modeled directly.

From an OR perspective, two classes of problems are involved in the description given above: project scheduling provides a convenient framework to the AO’s problem of fixing time windows and keeping resource requirements under control, while vehicle routing comes to the rescue of SPs for optimal routing of their turnaround teams.

We consider (Subsect. 3.1) both versions of project scheduling problems (PSPs), with and without constraints in the number of resources (e.g., teams for unloading/loading baggage, cleaning, catering service, refueling, etc.), the latter class of problems taking the name of resource-constrained project scheduling problems (RCPSP). The first objective we seek is to minimize the overall tardiness for the airport. After achieving a minimal-delay ideal schedule, the total resource requirement for the airport is minimized by enforcing any optimal solution found at this stage to maintain at least the same level of tardiness coming from the PSP.

Moving to optimal routing of teams for each SP (Subsect. 3.2), the frameworks of reference are two: multi-traveling salesmen problem with time windows (mTSPTW)  [4] and vehicle routing problem with time windows (VRPTW). The choice depends on whether the vehicles that are operated by teams are capacitated or not. Most resources/teams use a vehicle with limited capacity in order to service an aircraft, such as catering trucks, where the catering team is responsible for loading a certain number of galley trolleys into the aircraft. Other resources are uncapacitated and have no limitations on the number of aircraft that can be serviced before returning to the depot (e.g., push-back vehicles). Unlike the typical objective of both mTSPTW and VRPTW, which is minimizing the traveling distance, we first maximize the slack between tasks, in order to give enough time to absorb any small disruptions. This is meant to enforce a certain degree of robustness to the plan. After that, we try and maximize the workload balance among teams of the same SP, as much as possible, to foster fairness of the plan. Finally, we maximize the total slack time, when the minimum slack time cannot be improved further, with the effect of increasing all slack times between tasks except the minimum among all.

Details of our models are provided in the next two sub-sections. Many powerful global constraints from the Constraint Programming (CP) community are available for PSP/RCPSP and mTSPTW/VRPTW, hence our CP formulations. By employing such global constraints and taking advantage of the strength of different solvers, one would expect better computational performance with respect to, say, Mixed-Integer Programming (MIP) formulations and solvers. All models were developed in MiniZinc  [17], a solver-independent modeling framework that allows the model to be run on many different solvers. This feature was crucial to enable our solution approach (Sect. 4).

3.1 Project Scheduling Models

For a given day of operations, we set the start time \(start_i\in [0,t_{max}]\) of all tasks \(i\in I=\{1\dots \phi \}\) that cover all aircraft turnarounds expected at the given airport (\(t_{max}\) is the length of the day of operation). We do so in two steps. In the first (PSP, Eqs. (1a) and (2)–(6)), we aim at minimum costs resulting from tardy turnarounds, assuming unlimited resources. In the second (RCPSP, Eqs. (1b), (2)–(6), (7b) and (8b)), we aim for minimal resource needs whilst maintaining tardiness performance established in the first step.

Each task has an expected processing time \(duration_i\). Based on the known flight timetables, both the Scheduled Time of Arrival (STA) and Scheduled Time of Departure (STD) of each aircraft are known. As a result of this and of the precedence relations among all tasks (Fig. 1), earliest start times \({sta}_{i}\) and earliest end times \({std}_{i}\) of all tasks are also known in advance. The set of all tasks \(j\in I\) which can only start after a given task \(i\in I\) is completed is denoted as \(S_i\). This set will be empty for push-back tasks, which represent the natural conclusion of the related turnarounds. In between any two tasks, a fixed setup time \({setup}_i\) will ensure resources can effectively be gathered and moved from one location to another across the apron. This parameter can be estimated as a function of the maximum distance among all stands.

Each task represents a specific activity \(A=\{1\dots \alpha \}\), e.g. baggage loading. By \(AT_a\) we denote the set of all tasks of type \(a \in A\). Sets SO and SI represent, respectively, activities that are only allowed to start a certain time before STD, or after STA (mostly due to process specifications).

Certain pairs of tasks cannot be performed simultaneously, e.g. potable water and toilet servicing of the same turnaround. \(P=\{1\dots N \}\) is the set of such forbidden pairings, and \(D_p\) is the set of (two) tasks for each \(p \in P\).

Each task requires, uninterruptedly from start to end, a given amount \(rr_{i_k}\) of a given type of resource \(k \in K=\{1\dots \kappa \}\). Resource types effectively represent teams of handling agents providing services of different nature. Resource capacity per resource type \(rc_k\) also needs to be decided.

In the joint CP formulation of the PSP/RCPSP steps that follows, we also denote (Objective \(Z_{1}\), see (1a)) the cost of tardy turnarounds per unit of time as costtardy, while parameter \(sobt_a\)—see constraint (4)—states that certain activities need to be completed within given bounds from the planned departure time. Finally, we employ two global constraints: global constraint (6) ensures non permitted task pairs are scheduled separately, while global constraint (8b) ensures resource levels are not exceeded at any time.

CP Formulation

$$\begin{aligned} \begin{array}{r} Z_1^{*} = \min Z_1 = \min \sum \limits _{\begin{array}{c} i\in I \\ \text { where } \\ S_i=\{\} \end{array}} costtardy\times max\{0, start_i + duration_i - std_{i}\} \qquad \qquad \quad \\ \end{array} \end{aligned}$$
(1a)
$$\begin{aligned} \begin{array}{r} Z_2^{*} = \min Z_2 = \min \sum \limits _{ k \in K } rc_k \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \quad \qquad \qquad \quad \\ \end{array} \end{aligned}$$
(1b)

subject to

$$\begin{aligned} start_i \ge sta_{i}&\forall i \in I \end{aligned}$$
(2)
$$\begin{aligned} start_j \ge start_i + duration_i&\forall i \in I, \forall j \in S_i \end{aligned}$$
(3)
$$\begin{aligned} start_i + duration_i \ge std_{i} - sobt_a&\forall a \in SO, \, \forall i \in AT_a \end{aligned}$$
(4)
$$\begin{aligned} start_i = sta_{i}&\forall a \in SI, \, \forall i \in AT_a \end{aligned}$$
(5)
$$\begin{aligned} disjunctive( [ start_i |i \in D_p ],[ duration_i |i \in D_p])&\forall p \in P \end{aligned}$$
(6)
$$\begin{aligned} Z_1 = Z_1^{*} \end{aligned}$$
(7b)
$$\begin{aligned}&cumulative ( [ start_i \mid i \in I], [duration_i + setup_i \mid i \in I], [ rr_{k,i} \mid i \in I], rc_k) \nonumber \\&\qquad \qquad \qquad \qquad \qquad \forall k \in K \, \text { where } rc_k < \sum \limits _{i \in I}rr_{k,i}\qquad \qquad \qquad \qquad \,\,\, \end{aligned}$$
(8b)

3.2 Routing Models

After solving the above project scheduling problems, both the AO and all SPs know all time windows in which tasks should be executed on the given day of operation, as well as the number of teams of all types that are likely required to do the job. Each SP then takes this information to optimally schedule for their own teams to cover all turnaround tasks they are contracted to service. In the following we will see how this single-SP decision can be supported.

As in Subsect. 3.1, we provide a joint formulation following a lexicographic approach, with three objectives/sub-problems in this case. The sequence of three is then repeatedly solved as many times as the resource types managed by the given SP. For some resource types (teams), the vehicles used, e.g. re-fueling trucks, have finite capacity, hence they may need to be replenished before visiting the next turnaround. For these resource types, capacity constraints (20)–(22) will need to be included in the three models. The sub-problems take then the form of a VRPTW, irrespective of the objective/step in the sequence. For other resource types (teams), e.g. push-back trucks, capacity is not an issue, constraints (20)–(22) are excluded, and the sub-problems take the form of an mTSPTW.

The objective of utmost importance, and the one to pursue first (Eqs. (9) and (12)–(23)), is to maximize the minimum slack time between any two tasks, in an attempt to absorb short delays and prevent minor knock-on effects. The second step in the sequence (Eqs. (10), (12)–(23) and (24b)) looks at maximizing the workload balance among teams, to enforce some form of fairness in the plan, something which would be required in highly-unionized settings. Workload equity and its calculation is a subject of interest in the literature [15] on routing problems. The general suggestion points at minimizing the maximum distance in order to achieve a balanced workload while still ensuring the minimization of traveling distances. However, we are not as concerned with traveling times in between tasks as we are with the much higher processing times for each task. The last step (Eqs. (11), (12)–(23), (24b) and (24c)) then seeks to maximize the total slack time in the plan, in a way to increase its robustness.

On the given day of operation, we focus on a given working shift \(S=[ startshift , endshift ]\) for which a staff roster of the given SP is available. Within that, we know the number of teams \( t\in T_{SP,k}=\{1\dots t_{SP,k}\}\) of resource type k, who need to cover, overall, a known number of tasks \(i\in I_{SP,k}=\{1\dots \phi _{SP,k}\}\subset I\), by moving across a given number of parking stands \(h\in H =\{1\dots \eta \}\), where tasks are performed. The SP wants to set, for each task i:

  • the start time of the task, or \(stime_i\in S\);

  • the team \(rt_i\in T_{SP,k}\) assigned to i;

  • the task \(s_i\) immediately following i;

  • whether replenishment is needed prior to moving to \(s_i\).

For each available team, a specific route needs to be set up for the given shift (hence the letters ‘rt’ in \(rt_i\)), where the first task is a dummy task the label of which is a function of the label/index of the team in question, while all other tasks are ‘genuine’ tasks from set \(I_{SP,k}\). Task labels then, whether genuine or dummy, take on value in set \(N = I_{SP,k} \cup \{\phi _{SP,k}+1, \ldots , \phi _{SP,k}+ t_{SP,k}\}\). As a result, any task that is not the first task in each route is a task \(s_i\in I_{SP,k}\). Constraint (14) ensures all the dummy nodes represent the start of individual routes. Constraint (15) makes sure both i and \(s_i\) belong to the same route.

CP Formulation

$$\begin{aligned} z_1^{*} ={}&\max z_1 = \max \min \limits _{ i\in I_{SP,k}}slack_i \qquad \qquad \qquad \qquad \quad \end{aligned}$$
(9)
$$\begin{aligned} z_2^{*} ={}&\max z_2 = \max (\min \limits _{t \in T_{SP,k}} workload_t - \max \limits _{t \in T_{SP,k}} workload_t)\qquad \qquad \qquad \qquad \quad \end{aligned}$$
(10)
$$\begin{aligned} z_3^{*} ={}&\max z_3 = \max \sum \limits _{ i\in I_{SP,k}}slack_i \qquad \qquad \qquad \qquad \quad \end{aligned}$$
(11)

subject to

$$\begin{aligned} {circuit\,([ s_i \mid \, i \in N ])}&\end{aligned}$$
(12)
$$\begin{aligned} { alldifferent \,([ s_i \mid \, i \in N ])}&\end{aligned}$$
(13)
$$\begin{aligned} rt_{\phi +t} = t&\forall t \in T_{SP,k} \end{aligned}$$
(14)
$$\begin{aligned} rt_{s_i} = rt_i&\forall i \in I_{SP,k} \end{aligned}$$
(15)
$$\begin{aligned} stime_i = start_i&\forall i \in I_{SP,k} \end{aligned}$$
(16)
$$\begin{aligned} busy_i = {\left\{ \begin{array}{ll} stime_i + duration_i + \\ traveltime_{h_i,h_j} + x_i\times replenish, &{} \forall i \in I_{SP,k} \\ endshift, &{} otherwise \end{array}\right. }&\mid s_i \in I_{SP,k} \end{aligned}$$
(17)
$$\begin{aligned} stime_{s_i} \ge busy_i&\forall i \in I_{SP,k} \end{aligned}$$
(18)
$$\begin{aligned} slack_i = stime_{s_i} - busy_i&\forall i \in I_{SP,k} \end{aligned}$$
(19)
$$\begin{aligned} q_{i} = cap&\forall i \in N\setminus I_{SP,k} \end{aligned}$$
(20)
$$\begin{aligned} q_{s_i} = q_i - demand_{s_i}&\forall i \in N\setminus I_{SP,k} \end{aligned}$$
(21)
$$\begin{aligned} q_{s_i} = {\left\{ \begin{array}{ll} cap - demand_{s_i}, &{} if \, x_i=1 \\ q_i - demand_{s_i}, &{} otherwise \end{array}\right. }&\forall i \in I_{SP,k} \end{aligned}$$
(22)
$$\begin{aligned} workload_t = \sum \limits _{\begin{array}{c} i \in I_{SP,k} \\ \text {where } rt_i=t \end{array}} duration_i&\forall t \in T_{SP,k} \end{aligned}$$
(23)
$$\begin{aligned} {}&z_1 = z_1^{*}&\qquad \qquad \qquad \qquad \end{aligned}$$
(24b)
$$\begin{aligned}&z_2 \ge z_2^{*}&\qquad \qquad \qquad \qquad \end{aligned}$$
(24c)

Tasks should start at a time \(stime_i\) that is no earlier than the \(start_i\) that was assigned at the PSP/RCPSP stage. Later starts could be advisable/needed, e.g. because of resource limitations. Hence, although potentially contributing to causes of delays, at this routing stage decisions on task start times could be reconsidered, in principle at least. In our approach we simplify this aspect by fixing \(start_i\) exactly as in constraint (16), as this is more akin to maximizing the form of slack in the system that we have in two out of three objectives.

Tasks should also not start until their immediate predecessor has been completed, as in constraints (18) and (17). Any time available in between tasks i and \(s_i\) is defined as slack—see constraint (19). The replenishment decision is enacted through binary decision variable \(x_i\), which takes on value 1 if replenishment needs to happen between task i and task \(s_i\), 0 otherwise. Each replenishment takes replenish time. Moving between two consecutive tasks requires \(traveltime_{h_i,h_j}\), with \(h_i,h_j\in H\), \(h_i\ne h_j\). Task duration is again denoted as \(duration_i\). The sum of the duration of all tasks assigned to a given team contribute to defining the total workload \(workload_t\) for the team, as in constraint (23).

For capacity constrained turnaround services, initial capacity \(q_i\) for the team and related vehicle is set to cap—constraint (20); capacity then depletes as required by the demand from each subsequent task \(s_i\) but is topped-up any time a replenishment decision is made—see constraints (21) and (22).

Global constraint (12) builds a single overall sequence for all tasks of all routes, with dummy tasks signposting the start of each team’s own route. Global constraint (13) is redundant and added to help propagation.

4 Solution Approach

From the above discussion, we know that our overall approach develops as in Fig. 2, with perspectives from both the AO and all the SPs supported by the models presented, respectively, in Subsects. 3.1 and 3.2.

Table 1. Solution steps
Full size table

Table 1 shows further details around solvers and search strategies we used, as well as additional parameters around any time limits adopted as stopping criterion, or whether we made use of a warm-start. Numbers in the first column to the left correspond to component steps of Steps 1 and 2 from Fig. 2. Variable names in the table refer to the formulations from Sect. 3.

figure a

All models were implemented in MiniZinc, which enabled us to test the performance of different solvers for each model, and ultimately select the most suitable for use in each case. In the case of steps 1.1 and 1.2, Chuffed  [3] clearly outperformed all other available solvers and we were able to prove optimality for all instances. The first sub-problem of Step 2 though, that is the maximization of minimum slack time, proved slightly different, and had to be broken down into two further component steps. We first used CP with a specialized search strategy (step 2.1.1) which allowed us to reach the maximum as quickly as possible with Gecode  [8]. However, it took very long for CP to prove optimality in almost all cases. Thus, by taking advantage of the warm-start possibility, we used the same model and the solution provided by Gecode as a warm start for a MIP solver (Gurobi  [9]) (2.1.2), thanks to which we managed to prove optimality for all instances in a very short time.

Choosing the right search strategy also proved decisive in terms of solving times wherever we adopted a CP approach. In steps 1.1 and 1.2, we chose the \(start_i\) variables to lead the search. The variable selection strategy smallest means a variable is chosen with the smallest value in its domain, and the assignment of the value to that variable is done using \(indomain\_min\), meaning that it will get assigned the minimum value in its domain. On the other hand, for the mTSPTW/VRPTW component, we noticed the model was unable to solve quickly without specifying any search strategies. We then noticed that the two forms of the problem claim for different choices of search strategy. We observed that first_fail, where the variable with the smallest domain is chosen, outperforms other strategies for all mTSPTWs, while smallest performed better for all VRPTWs. On the variable assignment for mTSPTW, indomain_max ruled out the rest, meaning the assignment was made with the maximum value in its domain. For VRPTW, on the other hand, indomain_min performed better.

The very last step of our approach involves adopting a Large Neighborhood Search (LNS) schema (Algorithm 1) to further improve the solutions obtained from each of the routing sub-problems composing step 2.2. In our implementation of LNS, we take the solution from maximizing \(z_3\) as a starting point, then ‘destroy’ two routes, chosen at random from the given solution, and finally use again the same model from step 2.3 to ‘repair’ it. If the new solution is better than the incumbent, we update the record of the best solution, and repeat the process for up to 200 iterations.

5 Experiments

In this study we used real data coming from Europe’s 6th busiest commercial airport, Barcelona - El Prat (BCN). Our data relate to one given day of operation and include seven resource types, with each type handled by a different SP, and ten different turnaround activity types, for a total of 914 tasks to be scheduled at the PSP/RCPSP stage. At the mTSPTW/VRPTW stage, we considered the two shifts per day as currently adopted at the given airport, irrespective of resource type/SP. There are approximately 50 turnarounds in each shift, amounting to approximately the same number of tasks to be assigned per resource type and shift. In some cases from out data set, two teams are required to perform a task—e.g., baggage loading/unloading for wide-body aircraft. In these cases, the tasks are duplicated to ensure two teams, not one, perform the same task.

We ran all models on a personal laptop (1.6 GHz Intel Core i5) running mac-OS High Sierra. The overall integration was achieved in Python 3.7 using MiniZinc Python (MiniZinc version 2.3.2), which allowed us to solve the models in an incremental way, whilst providing a platform for easy integration of our LNS implementation. Computation times are not of primary concern when dealing with our problem, as clear from Fig. 2, hence the average 45 min taken to run the whole solution approach end to end does not represent a problem, to start with. In reality though, the AO will only run the PSP/RCPSP stage, which will take only approximately 7 min. Each SP will instead run the mTSPTW/VRPTW separately, on its own, for two shifts, which will take up to around 6 min for each SP, LNS step included. The RCPSP is proven to be optimal for minimizing tardiness, as well as for minimizing total resources/teams per SP. Moreover, in the second stage, we prove optimality for the maximum minimum slack time for the given tardiness and resource levels. Work balance is between 0 and 66 min, and 15 min on average, within the allowed time limit. Ensuring optimal workload balance proved too challenging, hence we limited the time available for this stage.

The most time-consuming part of the whole approach was to find the optimal solution for total slack time for each VRPTW. This is due to the workload balance objective and constraints. When we relaxed this and maximized it for \(z_1\) and \(z_3\), we could get an optimal solution using Gurobi for almost all resource types and shifts, with only a few instances not proven in 5 hours of solving time. We compared the results of the objective bounds with our lexicographic approach (excluding workload balance objective and constraint). The average gap was 0.68% for 14 instances of a mix of mTSPTW and VRPTW (each for one shift). The maximum gap was 2.72%. The average solution time for our approach was 1.78 min, while it required 60 min for Gurobi to prove optimality, if reached.

Padron and Guimarans  [20] tackled an extremely similar ground-handling problem on the exact same data set. Compared to them, our approach was able to reduce the number of resources used per resource type when tested in the same instance for BCN. This was largely because in the RCPSP stage we give flexibility to the ordering of tasks for an individual turnaround, rather than using a preset plan for each turnaround as they do.

To test our optimization results under the uncertainty that normally permeates real airport settings, we developed, validated and used a discrete event simulator. Uncertain factors in our problem include: aircraft arrival time, task duration, traveling time between stands, and replenishment time. A bounded exponential probability distribution was used for the traveling time, and triangular distributions for the rest.

In addition to the real case from BCN, we generated several instances with different mix of aircraft and frequencies of arrivals and departures. Instances are presented as ta\([\theta ]\)_t[tmax], where \(\theta \) is the number of turnarounds and tmax is the planning horizon in minutes. We study these scenarios, together with the one from Barcelona Airport, by setting different levels of variability (normal and high variability). We use this experimental setting to evaluate our approach using two different objectives: maximizing slack time and minimizing traveling time, as in typical VRPTWs. Ten independent replications were produced for each scenario. Table 2 provides a summary of relevant indicators. \(\varSigma \) is the total delay time, N is the number of delays, \(N_\%\) is the percentage of delays and \(\varSigma _{>15}\) shows the sum of delays that are in excess of 15 min. Superscripts s and t refer to the two approaches: maximizing slack and minimizing traveling distance, respectively. Computation time, including solving the RCPSP plus the average solving time (in seconds) of all VRPs and excluding simulation for a deterministic bound, are indicated by \(\tau ^s\) and \(\tau ^t\) for the respective approaches. Times for the simulated instances with _normal and _high variability are not provided in the table since the deterministic instances’ computation times (_det) are the main indicators of the solution approach and simulation is not part of the solution but only used as a tool for evaluation.

Table 2. Simulation Key Performance Indicators (KPIs) for slack time maximization and travel time minimization approaches
Full size table

In the deterministic case, the KPIs are the same since there are enough teams to perform the given tasks on time, no matter what the objective is. In the normal and high variability cases, except one, we observe that our approach maximizing slack outperforms the typical minimization of traveling time. In the real case of BCN, we only have partial information provided by a ground handling company, and the instance does not correspond to the whole operation at the airport—i.e., it only includes the flights corresponding to the airlines currently having a contract with the ground handler. This implies a lower arrival frequency in the instance, causing long idle times between the majority of tasks. In these cases, our approach is not significantly better than simply minimizing traveling time, as long as variability remains low. However, as aircraft arrival frequency and variability increase, we observe a significant difference between the two objectives. Figure 3 shows how our approach is able to outperform travel time minimization, reducing the total delay across all turnarounds. This figure also shows that our approach provides more predictable delays, with a more contained spread across simulations for all instances.

Fig. 3.
figure 3

Total delay per instance among 10 simulation replications

Full size image

Table 2 also includes other important key performance indicators (KPIs), such as percentage of delayed turnarounds and total minutes of delay exceeding the on time threshold of 15 min. The latter is a big concern for SPs, since failing to meet this target carries penalties and potential further delays due to air traffic management. Our approach clearly reduces the total delay over 15 min, for up to 70% over the day of operation, except for one instance under high variability. Considering each minute of delay incurs a cost, deploying our approach in real-life scenarios could potentially result in significant cost savings.

6 Conclusion

In this work, we proposed a novel two-step solution approach to the airport ground service scheduling and team planning problem. With respect to earlier approaches, the RCPSP step allows service providers to operate their busy schedules with potentially fewer human resources. Our focus on maximizing minimum slack in the second step ensures they can do so efficiently. Our simulation proves the robustness of our approach. Still, tighter links between simulation and the optimization components could help, in the future, to enhance the performance of our LNS-based approach, e.g., by generating cuts from the simulation results for the benefit of the heuristic search component or using simulation within the CP search strategy.