A Resource Constraint Approach for One Global Constraint MINLP

Abstract

Many industrial optimization problems are sparse and can be formulated as block-separable mixed-integer nonlinear programming (MINLP) problems, where low-dimensional sub-problems are linked by a (linear) knapsack-like coupling constraint. This paper investigates exploiting this structure using decomposition and a resource constraint formulation of the problem. The idea is that one outer approximation master problem handles sub-problems that can be solved in parallel. The steps of the algorithm are illustrated with numerical examples which shows that convergence to the optimal solution requires a few steps of solving sub-problems in lower dimension.

1 Introduction

Mixed Integer Nonlinear Programming (MINLP) is a paradigm to optimize systems with both discrete variables and nonlinear constraints. Many real-world problems are large-scale, coming from areas like machine learning, computer vision, supply chain and manufacturing problems, etc. A large collection of real-world MINLP problems can be found in MINLPLib [13].

In general, the problems are hard to solve. Many approaches have been implemented over the last decades. Most of the nonconvex MINLP deterministic solvers apply one global branch-and-bound (BB) search tree [3, 4], and compute a lower bound by a polyhedral relaxation, like ANTIGONE [8], BARON [11], Couenne [1], Lindo API [7] and SCIP [12]. The challenge for these methods is to handle a rapidly growing global search tree, which fills up the computer memory. An alternative to BB is successive approximation. Such methods solve an optimization problem without handling a single global search tree. The Outer-Approximation (OA) method [5, 6, 9, 15] and the Extended Cutting Plane method [14] solve convex MINLPs by successive linearization of nonlinear constraints. One of the challenges we are dealing with is how to handle this for nonconvex MINLP problems.

In this paper, we focus on practical potentially high dimension problems, which in fact consist of sub-problems that are linked by one coupling constraint. This opens the opportunity to reformulate the problem as a resource constraint bi-objective problem similar to the multi-objective view used in [2] for integer programming problems. We investigate the potential of this approach combining it with Decomposition-based Inner- and Outer-Refinement (DIOR), see [10].

To investigate the question, we first write the general problem formulation with one global constraint and show that this can be approached by a resource constrained formulation in Sect. 2. Section 3 presents a possible algorithm to solve such problems aiming at a guaranteed accuracy. The procedure is illustrated stepwise in Sect. 4. Section 5 summarizes our findings.

2 Problem Formulation and Resource Constraint Formulation

We consider block-separable (or quasi-separable) MINLP problems where the set of decision variables $x \in \mathbb {R}^n$ is partitioned into |K| blocks

$$\begin{aligned} \min \, c^Tx {{\,\mathrm{\quad s.t. \quad }\,}}a^Tx\le b,\,\, x_k\in X_k,\,\, k\in K \end{aligned}$$

(1)

with

$$\begin{aligned} X_k:=\{ y \in [\underline{x}_k, \overline{x}_k] \subset \mathbb {R}^{n_{k}}| y_j\in \mathbb {Z}, j\in J_k, g_{ki}(y)\le 0,\ i\in I_k\}. \end{aligned}$$

(2)

The dimension of the variables $x_k\in \mathbb {R}^{n_k}$ in block k is $n_k$ such that $n=\sum \limits _{k \in K}n_k$. The vectors $\underline{x}, \overline{x} \in \mathbb {R}^{n}$ denote lower and upper bounds on the variables. The linear constraint $a^Tx\le b$ is called the resource constraint and is the only global link between the sub-problems. We assume that the part $a_k$ corresponding to block k has $a_k\ne 0$, otherwise the corresponding block can be solved independently. The constraints defining feasible set $X_k$ are called local. Set $X_k$ is defined by linear and nonlinear local constraint functions, $g_{ki}: \mathbb {R}^{n_k}\rightarrow \mathbb {R}$, which are assumed to be bounded on the set $[\underline{x}_k, \overline{x}_k]$. The linear objective function is defined by $c^Tx:=\sum \limits _{k\in K}c_k^Tx_k$, $c_k\in \mathbb {R}^{n_k}$. Furthermore, we define set $X:= \prod \limits _{k\in K} X_k$.

The Multi-objective approach of [2] is based on focusing on the lower dimensional space of the global constraints of the sub-problems rather than on the full $n-$dimensional space. We will outline how they relate to the so-called Bi-Objective Programming (BOP) sub-problems based on a resource-constrained reformulation of the MINLP.

2.1 Resource-Constrained Reformulation

If the MINLP (1) has a huge number of variables, it can be difficult to solve it in reasonable time. In particular, if the MINLP is defined by discretization of some infinitely dimensional variables, like in stochastic programming or in differential equations. For such problems, a resource-constrained perspective can be promising.

The idea is to view the original problem (1) in n–dimensional space from two objectives; the objective function and the global resource constraint. Define the $2\times n_k$ matrix $C_k$ by

$$\begin{aligned} C_{k}= \left[ \begin{array}{l} c_k^T \\ a_{k}^T \end{array}\right] \end{aligned}$$

(3)

and consider the transformed feasible set:

$$\begin{aligned} V_k:= \{ v_k:=C_{k}x_k\, : \, x_k\in X_k\}\subset \mathbb {R}^{2}. \end{aligned}$$

(4)

The resource-constrained formulation of (1) is

$$\begin{aligned} \begin{aligned} \min \sum _{k\in K} v_{k0} {{\,\mathrm{\quad s.t. \quad }\,}}&\sum _{k\in K} v_{k1} \le b, \\&v_k\in V_k,\,\,k\in K. \end{aligned} \end{aligned}$$

(5)

The approach to be developed uses the following property.

Proposition 1

Problem (5) is equivalent to the two-level program

$$\begin{aligned} \begin{aligned} \min&\sum _{k\in K} v_{k0}^*\\ {{\,\mathrm{\quad s.t. \quad }\,}}&\sum _{k\in K} v_{k1} \le b, \end{aligned} \end{aligned}$$

(6)

of finding the appropriate values of $v_{k1}$ where $v_{k0}^*$ is the optimal value of sub-problem RCP$_k$ given by

$$\begin{aligned} v_{k0}^*:=\min c_k^Tx_k {{\,\mathrm{\quad s.t. \quad }\,}}x_k \in X_k, \, C_{k1}x_k \le v_{k1}. \end{aligned}$$

(7)

Proof

From the definition it follows that the optimum of (6) coincides with

$$ \min c^Tx {{\,\mathrm{\quad s.t. \quad }\,}}x\in X,\quad a^Tx\le b. $$

   $\square$

This illustrates the idea, that by looking for the right assignment $v_{k1}$ of the resource, we can solve the lower dimensional sub-problems in order to obtain the complete solution. This provokes considering the problem as a potentially continuous knapsack problem. Approaching the problem as such would lead having to solve the sub-problems many times to fill a grid of state values with a value function and using interpolation. Instead, we investigate the idea of considering the problem as a bi-objective one, where we minimize both, $v_{k0}$ and $v_{k1}$.

2.2 Bi-objective Approach

A bi-objective consideration of (5) changes the focus from the complete image set $V_k$ to the relevant set of Pareto optimal points. Consider the sub-problem BOP$_k$ of block k as

$$\begin{aligned} \min C_k\,x_k {{\,\mathrm{\quad s.t. \quad }\,}}x_k \in X_k. \end{aligned}$$

(8)

The Pareto front of BOP$_k$ (8) is defined by a set of vectors, $v_k=C_kx_k$ with $x_k\in X_k$ with the property that there does not exist another feasible solution $w=C_ky_k$ with $y_k\in X_k$, which dominates $v_k$, i.e., for which $w_{i}\le v_{ki}$ for $i =0, 1$, and $w_{i}< v_{ki}$ for $i=0$ or $i=1$. We will call an element of the Pareto front a nondominated point (NDP). In other words, a NDP is a feasible objective vector for which none of its components can be improved without making at least one of its other components worse. A feasible solution $x_k \in X_k$ is called efficient (or Pareto optimal) if its image $v_k = C_k x_k$ is a NDP, i.e. it is nondominated. Let us denote the Pareto front of NDPs of (8) as

$$ V_k^*:=\{v\in V_k : v\, \hbox { is a NDP of (8)}\}. $$

Proposition 2

The solution of problem (5) is attained at $v^*\in V^*$.

$$\begin{aligned} \begin{aligned} \min \sum _{k\in K} v_{k0} {{\,\mathrm{\quad s.t. \quad }\,}}&\sum _{k\in K} v_{k1} \le b,\\&v_k\in V_k^*,\,\,k\in K. \end{aligned} \end{aligned}$$

(9)

Proof

Assume there exist parts of $\hat{v}^*_k\notin V^*$ of an optimal solution $v^*$, i.e the parts are dominated. This implies $\exists w_k\in V^*_k$ which dominates $v^*_k$, i.e. $w_{ki}\le v^*_{ki}$ for $i= 0,1$. Consider $\hat{v}$ the corresponding solution where in $v^*$ the parts $v_k^*$ are replaced by $w_k$. Then $\hat{v}$ is feasible for RCP given $\sum _{k\in K} \hat{v}_{k1} \le \sum _{k\in K} v_{k1}^* \le b$ and its objective value is at least as good, $\sum _{k\in K} \hat{v}_{k0} \le \sum _{k\in K} v_{k0}^*$, which means that the optimum is attained at NDP point $\hat{v}\in V^*$.    $\square$

In bi-objective optimization, a NDP can be computed by optimizing a weighted sum of the objectives

$$\begin{aligned} \min d^T C_kx_k {{\,\mathrm{\quad s.t. \quad }\,}}x_k \in X_k. \end{aligned}$$

(10)

For a positive weight vector $d\in \mathbb {R}^2$, an optimal solution of (10) is an efficient solution of (8), i.e., its image is nondominated. Such a solution and its image are called a supported efficient solution and a supported NDP, respectively. Thus, an efficient solution $x_k$ is supported if there exists a positive vector d for which $x_k$ is an optimal solution of (10), otherwise $x_k$ is called unsupported.

Example 1

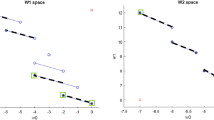
To illustrate the concepts, we use a simple numerical example which can be used as well to follow the steps of the algorithms to be introduced. Consider $n=4$, $K=\{1,2\}$, $c=(-1, -2, -1, -1)$, $a=(2,1,2,1)$, $b=10$, $\underline{x} =(0,0,2,1)$ and $\overline{x}=(5,1.5,5,3)$. Integer variables are $J_1=\{1\},J_2=\{3\}$ and the local constraints are given by $g_{11}(x_1,x_2)=3x_2-x_1^3+6x_1^2-8x_1-3$ and $g_{21}(x_3,x_4)=x_4\,-\,\frac{5}{x_3}\,-\,5$. The optimal solution is $x=(1, 1.5, 2, 2.5)$ with objective value $-8.5$. The corresponding points in the resource space are $v_1=(-4, 3.5)$ and $v_2=(-4.5, 6.5)$.

Figure 1 sketches the resource spaces $V_1$ and $V_2$ with the corresponding Pareto front. In blue, now the dominated part of $V_k$ not covered by the Pareto front $V^*_k$ is visible. The number of supported Pareto points is limited.

The example suggests that we should look for an optimal resource $v_k$ in a two-dimensional space, which seems more attractive than solving an n-dimensional problem. Meanwhile, sub-problems should be solved as few times as possible.

Fig. 1.

Resource constraint spaces $V_1$ and $V_2$ in blue with extreme points as circles. The Pareto front is in black. Supported NDPs are marked with a green square. The red squares represent the Ideal $\underline{v}_k$ (left under) and the Nadir point $\overline{v}_k$ (right-up).

3 Algorithmic Approach

The optimization of problem (1) according to Proposition 1 reduces to finding $v_k^ *$ in the search space which according to Proposition 2 can be found in the box $\mathcal {W}_k=[\underline{v}_k, \overline{v}_k]$. First of all, if the global constraint is not binding, dual variable $\mu =0$ and the sub-problems can be solved individually. However, usually $\mu >0$ gives us a lead of where to look for $v_k^*$. Notice that if $v_k^*$ is a supported NDP, it can be found by optimizing sub-problem

$$\begin{aligned} y_k(\beta )\in {{\,\mathrm{argmin}\,}}\{c_k^Tx+\beta a_k^Tx, \ x\in X_k\}, \end{aligned}$$

(11)

for $\beta =\mu$. In that case, $v^*_k = C_k^Ty_k$. However, we do not know the dual value $\mu$ beforehand and moreover, $v^*_k$ can be a nonsupported NDP. Notice that the resulting solution $y_k$ is an efficient point and $C_ky_k$ is a supported NDP for $\beta \ge 0$.

To look for the optimum, we first create an outer approximation (OA) $\mathcal {W}_k$ of $V^*$ by adding cuts using an LP master problem to estimate the dual value and iteratively solving 11. Second, we will use the refinement of $\mathcal {W}_k$ in a MIP OA, which may also generate nonsupported NDPs.

3.1 LP Outer Approximation

Initially, we compute the Ideal and Nadir point $\underline{v}_k$ and $\overline{v}_k$ for each block k. This is done by solving (11) with $\beta =\varepsilon , \beta =\frac{1}{\varepsilon }$ respectively. Let $r_1=C_ky_k(\varepsilon )$ and $r_2=C_ky_k(\frac{1}{\varepsilon })$, then $\underline{v}_k=(r_{1,0},r_{2,1})^T$ and $\overline{v}_k=(r_{2,0},r_{1,1})^T$. These vectors bound the search space for each block and initiate a set $P_k$ of outer cuts. We use set $R_k=\{(r,\beta )\}$ of supported NDPs with a corresponding weight $\beta$, to define local cut sets

$$P_k=\{v\in [\underline{v}_k, \overline{v}_k] (1,\beta )v\ge (1,\beta )r, \forall (r,\beta )\in R_k\}.$$

An initial cut is generated using the orthogonal vector of the plane between $r_1$ and $r_2$, i.e. find $y_k(\beta _{k0})$ in (11) with

$$\begin{aligned} \beta _{k0}=\frac{\overline{v}_{k0}-\underline{v}_{k0}}{\overline{v}_{k1}-\underline{v}_{k1}}. \end{aligned}$$

(12)

Notice that if $r_1$ is also a solution of the problem, then apparently there does not exist a (supported) NDP v at the left side of the line through $r_1$ and $r_2$, i.e. $(1,\beta )v<(1,\beta )r_1$. The hyperplane is the lower left part of the convex hull of the Pareto front. Basically, we can stop the search for supported NDPs for the corresponding block.

An LP outer approximation of (5) is given by

$$\begin{aligned} \begin{aligned} w={{\,\mathrm{argmin}\,}}\sum _{k\in K} v_{k0} {{\,\mathrm{\quad s.t. \quad }\,}}&\sum _{k\in K} v_{k1} \le b,\\&v_k\in P_k,\,\,k\in K. \end{aligned} \end{aligned}$$

(13)

It generates a relaxed solution w and an estimate $\beta$ of the optimal dual $\mu$. Then $\beta$ is used to generate more support points by solving problem (11). Notice that for several values of $\beta$ the same support point $C_ky_k(\beta )$ may be generated. However, each value leads to another cut in $P_k$. Moreover, the solution w of (13) will be used later for refinement of the outer approximation. A sketch of the algorithm is given in Algorithm 1.

3.2 MIP Outer Approximation

An outer approximation $\mathcal {W}_k$ of the Pareto front $V_k^*$ is given by the observation that the cone $\{v\in \mathbb {R}^2, v\ge \underline{v}\}$ contains the Pareto front. Basically, we refine this set as a union of cones based on all found NDPs. We keep a list $\mathcal {P}_k = \{p_{k0}, p_{k1}, \ldots ,p_{k|\mathcal {P}_k|}\}$ of NDPs of what we will define as the extended Pareto front ordered according to the objective value $p_{k00}<p_{k10}<\ldots <p_{k|\mathcal {P}_k|0}$. Initially, the list $\mathcal {P}_k$ has the supported NDPs we found in $R_k$. However, we will generate more potentially not supported NDPs in a second phase. Using list $\mathcal {P}_k$, the front $V^*_k$ is (outer) approximated by $\mathcal {W}_k=\cup W_{ki}$ with

$$ W_{ki}= \{v\in \mathbb {R}^2| v_0\ge p_{k(i-1)0}, v_1 \ge p_{ki1}\}. $$

We solve a MIP master problem (starting with the last solution found by the LP-OA) to generate a solution w, for which potentially not for all blocks k we have $w_k\in V^*_k$. Based on the found points, we generate new NDPs $v_k$ to refine set $\mathcal {W}_k$, up to convergence takes place. Moreover, we check whether $v_k$ is supported NDP, or generate a new supported NDP in order to add a cut to $P_k$.

The master MIP problem is given by

$$\begin{aligned} \begin{aligned} w={{\,\mathrm{argmin}\,}}\sum _{k\in K} v_{k0} {{\,\mathrm{\quad s.t. \quad }\,}}&\sum _{k\in K} v_{k1} \le b,\\&v_k\in P_k\cap \mathcal {W}_k,\,\,k\in K, \end{aligned} \end{aligned}$$

(14)

which can be implemented as

$$\begin{aligned} \begin{aligned} w={{\,\mathrm{argmin}\,}}\sum _{k\in K} v_{k0}\\ {{\,\mathrm{\quad s.t. \quad }\,}}&\sum _{k\in K} v_{k1} \le b,\\&v_k\in P_k,\,\,k\in K,\\&v_{k0}\ge \underline{v}_{k0}+\sum _{i=1}^{| \mathcal {P}_k|} (p_{k(i-1)0}-\underline{v}_0)\delta _{ki},\,\,k\in K,\\&v_{k1}\ge \underline{v}_{k1}+\sum _{i=1}^{| \mathcal {P}_k|}(p_{i0}-v_{k1})\delta _{ki},\,\,k\in K\\&\sum _{i=1}^{| \mathcal {P}_k|} \delta _{ki}=1,\,\,k\in K,\\&\delta _{ki} \in \{0,1\}, \,\,i=1,\ldots , | \mathcal {P}_k|, k\in K. \end{aligned} \end{aligned}$$

(15)

Basically, if the solution w of (14) corresponds to NDPs, i.e. $w_k\in V^*_k$ for all blocks k, we are ready and solved the problem according to Proposition 2. If $w_k\notin V^*_k$, we refine $\mathcal {W}_k$ such that $w_k$ is excluded in the next iteration. In order to obtain refinement points p, we introduce the extended Pareto front, which also covers the gaps. Define the extended search area as

$$\begin{aligned} \overline{V}_k =[\underline{v}_k, \overline{v}_k]\setminus \{w\in \mathbb {R}^2| \exists v\in V^*_k, w<v\}. \end{aligned}$$

(16)

Then the extended Pareto front is given by

$$\begin{aligned} \overline{V}_k^* =\{v\in \mathbb {R}^2| v \text { is NDP of } \min v {{\,\mathrm{\quad s.t. \quad }\,}}v\in \overline{V}_k\}. \end{aligned}$$

(17)

To eliminate $w_k$ in the refinement, we perform line-search $v=w_k+\lambda (1,\beta )^T, \lambda \ge 0$ in the direction $(1,\beta )^T$, with

$$\begin{aligned} \beta = \frac{\overline{v}_1-w_1}{\overline{v}_0-w_0}. \end{aligned}$$

(18)

A possible MINLP sub-problem line search is the following:

$$\begin{aligned} \begin{aligned} \lambda _k={{\,\mathrm{argmin}\,}}\lambda \\ {{\,\mathrm{\quad s.t. \quad }\,}}Cx\le w_k + \lambda (1,\beta )^T,\\ \lambda \ge 0, x\in X_k \end{aligned} \end{aligned}$$

(19)

and taking $v_k=w_k+\lambda _k(1,\beta )^T$ as NDP of the (extended) Pareto front. Notice that if $\lambda _k=0$, apparently $w_k\in V^*_k$.

Moreover, we try to generate an additional cut by having a supported NDP. The complete idea of the algorithm is sketched in Algorithm 2. Let $z_k=w_{k0}$, if $w_k\in \mathcal {P}_k$ and $z_k=v_{k0}$ else. Then $\sum z_k$ provides an upper bound on the optimal function value. In this way, an implementation can trace the convergence towards the optimum. Based on the concept that in each iteration the MIP-OA iterate w is cut out due to the refinement in $v_k$, it can be proven that the algorithm converges to an optimal resource allocation $v^*$.

4 Numerical Illustration

In this section, we use several instances to illustrate the steps of the presented algorithms. All instances use an accuracy $\varepsilon =0.001$ and we focus on the number of times OA-MIP (14) is solved and sub-problem (11) and line-search sub-problem (19). First we go stepwise through example problem. Second, we focus on a concave optimization problem known as ex_2_1_1 of the MINLPlib [13]. At last, we go through the convex and relatively easy version of ex_2_1_1 in order to illustrate the difference in behaviour.

4.1 Behaviour for the Example Problem

Fig. 2.

Generated cuts (green) and refinement (mangenta) define the outer approximation after one iteration for both search areas. (Color figure online)

Fig. 3.

Outer approximation of the Pareto front given by generated cuts (green) and refinement (mangenta) after convergence of the algorithm to the optimal resource allocation. (Color figure online)

First of all, we build OA $W_k$ of the Pareto front following Algorithm 1. Ideal and Nadir point for each block, $W_1=\left[ \left( \begin{array}{r} -8\\ 0 \end{array}\right) ,\left( \begin{array}{r} 0\\ 11.5 \end{array}\right) \right]$ and $W_2=\left[ \left( \begin{array}{r} -6\\ 5 \end{array}\right) ,\left( \begin{array}{r} -3\\ 11 \end{array}\right) \right]$ are found by minimizing cost and resource. Based on these extreme values, we run sub-problem (11) for step 8 in Algorithm 1 using direction vectors $\beta _{1,0}=0.6957$ and $\beta _{2,0}=0.5$ according to (12). For this specific example, we reach the optimal solution corresponding to $(v_{1,0}, v_{1,1}, v_{2,0}, v_{2,1})= (-4, 3.5, -4.5, 6.5)^T$ which still has to be proven to be optimal.

One can observe the first corresponding cuts in Fig. 2. We run the LP OA which generates a dual value of $\beta _{k1}=0.6957$, which corresponds to the angle of the first cut in the $V_1$ space. This means that sub-problem (11) does not have to be run for the first block, as it will generate the same cut. For the second block, it finds the same support point $v_{2}= (-4.5, 6.5)^T$, but adds a cut with a different angle to $P_2$, as can be observed in the figure.

Algorithm 2 first stores the found extreme points and optimal sub-problem solutions in point sets $\mathcal {P}_k$. The used matlab script provides an LP-OA solution of $w=(-4.0138, 3.5198, -4.4862, 6.4802)$, which is similar to the optimal solution with rounding errors. Solving the line search (19) provides a small step into the feasible area of $\lambda _1=0.014$ and $\lambda _2=0.0015$ in the direction of the Nadir point.

Due to the errors, both blocks do not consider $v_k=w_k$ and add a cut according to step 12 in the algorithm. Interesting enough is that the MIP OA in the space as drawn in Fig. 2 reaches an infeasible point w, i.e. $w_k\in \mathcal {W}_k$, but $w_k\notin V_k$ further away from the optimum. This provides the incentive for the second block to find $v_1$ in the extended Pareto set as sketched in Fig. 3. This helps to reach the optimum with an exact accuracy.

For this instance, the MIP OA was solved twice and in the end contains 6 binary variables. Both blocks solve two sub-problems to reach the Ideal and 2 times the line search problem (19). The first block solves sub-problem (11) 3 times and the second block once more to generate an additional cut. In general, in each iteration at most two sub-problems are solved for each block. The idea is that this can be done in parallel. Notice that the refinement causes the MIP OA to have in each iteration at most |K| additional binary variables.

4.2 Behaviour for ex_2_1_1

Fig. 4.

At the left, the Pareto front of all sub-problems combined. The minimum resource point $r_2=(0,0)^T$ is common for all sub-problems and the minimum cost solution is given by a blue circle. The only cut (line between $r_1$ and $r_2$) is sketched in green. At the right, OA for $V_1$ after one iteration. The line search between $w_1$ and Nadir point providing $v_1$ and first refinement of the OA (mangenta) are sketched. (Color figure online)

This instance can be characterised as a worst-case type of knapsack problem, where the usual heuristic to select the items with the best benefit-weight ratio first provides the wrong solution. As we will observe, a similar behaviour can be found using the OA relaxations. All variables are continuous and we are implicitly minimizing a concave quadratic function. In our description $n=10$, $c=(0, 1, 0, 1, 0,1,0,1, 0,1)$, $a=(20, 0, 12, 0, 11, 0, 7, 0, 4, 0)$, $b=40$, $K=\{1,2,3,4,5\}$ and divides vector x into 5 equal blocks $x_k=(x_{2k-1},x_{2k}), k\in K$. The local constraints are given by $g_{k}(y,z)=q_ky-50y^2-z$, where $q=(42, 44, 45, 47, 47.5)$. The bounds on the variables are given by $[\underline{x}_{k1}, \overline{x}_{k1}] =[0,1]$ and $[\underline{x}_{k2}, \overline{x}_{k2}] =[q_k-50,0], k\in K$.

Fig. 5.

Final refinement to reach the accuracy of $\varepsilon =0.001$ of the approximation w of the optimal solution; $w_1$ given by a black star. In each iteration a new refinement point $v_1$ is generated, indicated by a black triangle.

The optimal solution is $x=(1, -8, 1, -6, 0, 0, 1, -3, 0, 0)$ with objective value $-17$. However, the LP OA relaxation provides a first underestimate of the objective of $-18.9$, where all subproblems take point $r_1$ apart from the first one, where $w_1=(-2.4,6)$. The solution and its consequence for the first iteration is sketched in Fig. 4. One can also observe the resulting line-search to find the first solution $v_1$ to come to the first refinement. The bad approximation of the first solution corresponds to a result of a greedy knapsack algorithm. For this instance, an iterative refinement is necessary that generates the points $v_k$ up to convergence is reached.

Another typical characteristic is the concave shape of the Pareto front. This implies that the first cut is in fact the green line between $r_1$ and $r_2$. This is detected in step 6 of Algorithm 1 and implies that there are no more supported NDPs than $r_1$ and $r_2$, so that one does not have run sub-problem (11) anymore. However, the algorithm requires to solve for more and more sub-problems the line search problem (19) in each MIP OA iteration.

In total, the algorithm requires 9 steps of the MIP OA algorithm to reach the accuracy. In the end, the problem contains 26 binary variables $\delta$ over all subproblems. The intensity is best depicted by the refinement of $\mathcal {W}_1$ in Fig. 5. The algorithm requires 3 times solving sub-problem (11) to generate $r_1$, $r_2$ and to find the cut for each block. In total it solved the line search (19) 21 times.

4.3 Behaviour for a Convex Variant of ex_2_1_1

Fig. 6.

At the left, the Pareto front of all sub-problems combined. The minimum resource point $r_2=(0,0)^T$ is common for all sub-problems and the minimum cost solution is given by a blue circle. The first cut is illustrated by a green line. At the right, OA for $V_1$ after one iteration. Actually, it stays the same during future iterations, as $w_1$ coincides numerically with a found NDP. (Color figure online)

Convex problems are usually considered easy to solve. The idea of having a so-called zero duality gap is captured by solving the problem already by the LP OA using the dual value to generate cuts. We use the data of the former instance, but are now implicitly minimizing a convex quadratic function. Again $n=10$, $c=(0, 1, 0, 1, 0,1,0,1, 0,1)$, $a=(20, 0, 12, 0, 11, 0, 7, 0, 4, 0)$, but now taking $b=15$ in order to have a binding global constraint. The local constraints are given by $g_{k}(y,z)=-q_ky+50y^2-z$, where $q=(42, 44, 45, 47, 47.5)$. The bounds on the variables are given by $[\underline{x}_{k1}, \overline{x}_{k1}] =[0,1]$ and $[\underline{x}_{k2}, \overline{x}_{k2}] =[0,-\frac{q_k^2}{200}], k\in K$.

The optimal objective function value is $-45.62$. The Pareto fronts do not exhibit gaps, but are smooth quadratic curves. This means that solving the weighted problem with different values of $\beta$ provides different optima. In Fig. 6, all Pareto fronts are depicted together with the first generated cut. However, the LP OA relaxation of Algorithm 1 provides a first relatively sharp underestimate of the objective of $-45.7$. This illustrates the idea of decomposition for convex problems where a good value for the dual provides the optimum for the primal problem.

The big difference with the concave case is that now in each iteration in principle new cuts can be generated. Considering the first block $V_1$, this does not really happen, as the optimum $w_1$ coincides with a point $v_1$ on the Pareto front found by the line search. Figure 6 illustrates at the right the MIP OA based on the points in set $\mathcal {P}_1$ on the Pareto front. Further refinement does not improve the bound, as the optimum has already been approximated in the first iteration.

5 Conclusions

Mixed Integer Nonlinear Programming (MINLP) is a strong concept for formulating practical optimization problems. Solvers based on the branch and bound concept, usually suffer from the number of variables n of the problem. For instances having one global inequality, we investigated the potential of using decomposition requiring sub-problems of a smaller size $n_k, k\in K$ to be solved using a MIP master problem exploiting the concept of resource constraint programming and a Pareto front.

The result of our investigation is a decomposition algorithm aiming at convergence up to a guaranteed accuracy. In each iteration, a MIP master problem is solved and at most 2|K| sub-problems, that can be solved in parallel. The process is illustrated with graphical examples which are solved up to an accuracy of $\varepsilon =0.001$ after a few iterations.

At the moment, we are working on designing algorithms for instances with more than one global constraint, resulting in a Pareto set in higher dimension. The approach presented here can be extended and proven to converge. However, to obtain an algorithm with reasonable practical performance requires rethinking the cut generation in a resource space of higher dimension. We will report on this topic in future papers.