The Confidence Constraint: A Step Towards Stochastic CP Solvers

Abstract

We introduce the Confidence constraint, a chance constraint that ensures, with probability $\gamma$, that a set of variables are no smaller than random variables for which the probability distribution is given. This constraint is useful in stochastic optimization to ensure that a solution is robust to external random events. It allows to control the trade-off between optimizing the objective function and ensuring the satisfiability of the solution under random parameters. We present a filtering algorithm for this constraint with explanations. We apply the constraint to a case study, an industrial scheduling problem where tasks have random processing times due to possible breakdowns during their execution. We evaluate our solutions with simulations and show that this new constraint allows robust solutions in decent computation time.

1 Introduction

Decisions in an organization are taken at different levels: strategic, tactical, operational, and execution. In some situations, it is important that decisions taken at the operation level take into account what could happen at the execution level. For instance, one can schedule tasks while taking into account that breakdowns might occur during the execution and that the schedule might not be followed as expected. Stochastic optimization allows taking decisions at one level while coping with random events at the next level. One way to achieve this goal is by using chance constraints in the optimization model to guarantee that the solution holds beyond a given threshold probability.

We introduce a new chance constraint called Confidence that forces variables to take sufficiently large values so that random variables, following a known distribution, are unlikely to be greater. Let $X_1, \ldots , X_n$ be decision variables, let $D_1, \ldots , D_n$ be statistical distributions, and let $\gamma$ be the confidence threshold (a constant parameter). Each distribution $D_i$ must have a well-defined cumulative distribution function $\text{ cdf}_i$. The Confidence constraint is defined as follows.

$$\begin{aligned} \textsc {Confidence}([X_1, \ldots , X_n], [\text{ cdf}_1, \ldots , \text{ cdf}_2], \gamma ) \iff&\prod _{i=1}^n \text{ cdf}_i(X_i) \ge \gamma \end{aligned}$$

(1)

In other words, let $Y_i$ be an independent random variable following a distribution $D_i$. The chance that at least one random variable $Y_i$ takes a value greater than $X_i$ must be less than $\gamma$.

Such a constraint is particularly useful in stochastic scheduling where tasks can execute for a longer time than expected. In order to let sufficient time for the tasks to execute in a schedule, one can assign processing times to the tasks that are sufficiently long $\gamma$ percent of the time. We will show that such an approach has many advantages and is particularly well suited for constraint programming.

The rest of the paper is divided as follows. Section 2 presents background information about stochastic optimization. Section 3 introduces the Confidence constraint and its filtering algorithm. Section 4 presents a case study, an industrial scheduling problem that led to (and financed) this research. Section 5 presents our simulator that will be used in our experiments in Sect. 6. We present and analyze the results in Sect. 6.3. We conclude in Sect. 7.

2 Background

Stochastic problems are optimization problems for which part of the input is given with random variables. One aims at a solution of good quality over all possible values that these random variables can take. Usually, one wants to optimize the expected objective value and/or to ensure feasibility occurs with a given probability.

Stochastic linear programs are linear programs $\min \{c^T x \mid Ax \le b, x \ge 0\}$ for which some parameters in c, A, or b are replaced by random variables. These linear problems are particularly well studied  [10]. They can, for instance, encode scheduling problems where processing times are subject to random delays  [4].

There are several approaches to stochastic optimization. One important approach is called scenario-based optimization. It consists, in one way or another, in achieving deterministic optimization on sample data called scenarios. A scenario is a possible outcome of stochastic events. The number of possible scenarios grows exponentially with the number of stochastic variables. Chance constraints  [20] can achieve scenario-based optimization by constraining the solution to satisfy a scenario with a given probability. The concept emerged in stochastic linear programming, but is not intrinsically linear and can be applied to any constraint satisfaction problem. The formulae described in  [20] inspired the ones stated in Sect. 3. However, as the they sum probabilities over possible scenarios, some formulae might take too much time to compute for problems with hundreds of stochastic variables.

In constraint programming, Walsh  [18] proposes an extension of a constraint satisfaction problem by modeling decision problems with uncertainty. In this extension, stochastic variables based on probabilistic distributions coexist with common constraint programming decision variables. The solver computes a policy, i.e. a solution for each possible outcome of the stochastic variables. While this suits the needs for many problems, for problems with hundreds of random variables, one cannot state (not to mention computing) a complete policy.

The modeling language MiniZinc  [12, 17] is also adapted to stochastic optimization  [13] keeping the modeling process independent from the solving technique. It requires to encode a sample of scenarios in a vector. As the number of random variables grows, the cardinality of the sample scenarios set become insignificant compared to the number of possibilities and the quality of the solutions decays.

Stochastic problems is one way to obtain solutions robust to change. However, there exist other robust optimization approaches that do not rely on probabilities. For instance, super solutions are solutions that adapt themselves in case of a change  [9]. Such solutions are, however, hard to compute and are often restricted to small instances. The FlexC constraint  [6, 7] can model cumulative scheduling problems where tasks have two processing times: a normal processing time and a delayed one. The constraint ensures that if any subset of k tasks is delayed, the cumulative resource is not overloaded. However, the constraint does not support delays of variable duration.

The outreach of chance constraints goes far beyond scheduling problems. Rossi et al.  [14] present an algorithm designed to compute an optimal policy for inventory levels. Based on current demand, chance constraints are used in such a way that one can predict more accurate future demand. While we do not aim at solving the same problem, this is the closest chance constraint algorithm we could find in constraint programming to what we propose.

3 The Confidence Constraint

3.1 Description

The Confidence constraint defined in (1) has for scope a vector of integer variables $[X_1, \ldots , X_n]$ and has for parameters a vector of random distributions $[D_1, \ldots , D_n]$. A collection of independent random variables $Y_1, \ldots , Y_n$ following these distributions i.e. the random variable $Y_i$ follows the distribution $D_i$. Each distribution $D_i$ is fully described by its cumulative distribution function $\text{ cdf}_i(v) = P[Y_i \le v]$ that computes the probability that the random variable $Y_i$ takes a value smaller than or equal to a value v. We also consider its inverse function called the quantile function $Q_{i}({p}) = \min \{v \mid P[Y_i \le v] \ge p\}$ that computes the smallest value v for which variable $Y_i$ takes a value no greater than v with probability p. The distributions can be common distributions (e.g. Poisson, Uniform, ...) or can be custom much like the one shown in Sect. 4. The distributions can be different for every variable. Finally, the constraint takes a parameter $\gamma$ that is a confidence threshold, a probability between 0 and 1. Note that even if this constraint handles probabilities, it constrains integer variables and is therefore compatible with solvers that only handle this type of variable. Moreover, if the solver does not handle floating point parameters, it is possible to express $\gamma$ in percents and to give it an integer value.

The constraint is satisfied when, with probability at least $\gamma$, all random variables $Y_i$ take a value smaller than or equal to their corresponding threshold $X_i$. Since the random variables $Y_i$ are independent, the constraint is satisfied when

$$\begin{aligned} P[\bigwedge _{i=1}^n Y_i \le X_i]&\ge \gamma . \end{aligned}$$

(2)

Since the random variables are independent, we obtain

$$\begin{aligned} \prod _{i=1}^n P[Y_i \le X_i]&\ge \gamma . \end{aligned}$$

(3)

For numerical stability reasons, we use this form

$$\begin{aligned} \sum _{i=1}^n \ln (P[Y_i \le X_i])&\ge \ln (\gamma ). \end{aligned}$$

(4)

The Confidence constraint is useful in problems where unknown events might arise. In a scheduling problem, it is common to have tasks that take longer to execute than expected. One usually plans more time than necessary for these tasks in a schedule. Let $X_i$ be the processing time of task i and $D_i$ be a distribution on the observed processing times in the past. The Confidence constraint allows planning sufficient times for the execution of the tasks in say, $\gamma = 95\%$ of the time. This confidence threshold allows making schedules that can be executed without modification 95% of the time without over estimating the duration of the tasks.

In a production problem where we want to produce sufficient goods to satisfy an unknown demand, we let $X_i$ be the amount of good i that is produced and $Y_i$ be the amount that needs to be produced to fulfill the demand. We want $X_i \ge Y_i$ which is equivalent to $-X_i \le -Y_i$. The Confidence constraint can restrict the quantities $-X_i$ to be smaller than the random variable $-Y_i$ with probability $\gamma$.

3.2 Filtering Algorithm

Algorithm 1 is the filtering algorithm directly derived from applying interval arithmetic on inequality (4). Line 1 computes $\alpha$, the log of the highest probability that can be reached on the left-hand side of the inequality. It is computed from the random variables’ cumulative distribution functions. If this probably is too low, line 2 triggers a failure. Otherwise, the lower bound of each variable domain is tested for consistency. The test on line 3 is equivalent to testing $\sum _{j \ne i} \ln (P[Y_j \le \max (\mathop {\mathrm {dom}}\nolimits (X_j))]) + \ln (P[Y_i \le \min (\mathop {\mathrm {dom}}\nolimits (X_i))]) < \ln (\gamma )$. If the test is positive, then $\min (\mathop {\mathrm {dom}}\nolimits (X_i))$ does not have a support and should be filtered out from the domain. In order to evaluate what is the smallest value in $\mathop {\mathrm {dom}}\nolimits (X_i)$ with a support, we use the quantile function on line 4. We search for the smallest value $v \in \mathop {\mathrm {dom}}\nolimits (X_i)$ such that $\beta + \ln (P[Y_i \le v]) \ge \ln (\gamma )$ which is equivalent to $P[Y_i \le v] \ge \gamma e^{-\beta }$. This is directly provided by the quantile function $Q_i(\gamma e^{-\beta })$.

The algorithm accepts any distribution for which the functions $\text{ cdf}_i$ and $Q_i$ can be computed. Such functions for common distributions are already implemented in libraries like Boost  [15]. This includes Pareto, Gaussian, Poisson, Laplace, Uniform, etc. It is also possible to create custom distributions.

From the arithmetic of intervals, the algorithm enforces bounds consistency on the Confidence constraint, but also domain consistency. Indeed, the algorithm tests on line 3 the assignment $[\max (\mathop {\mathrm {dom}}\nolimits (X_1)), \ldots , \max (\mathop {\mathrm {dom}}\nolimits (X_{i-1})), \min (\mathop {\mathrm {dom}}\nolimits (X_i)), \max (\mathop {\mathrm {dom}}\nolimits (X_{i+1})), \ldots , \max (\mathop {\mathrm {dom}}\nolimits (X_n))]$. If this assignment satisfies the Confidence constraint, so does $[\max (\mathop {\mathrm {dom}}\nolimits (X_1)), \ldots , \max (\mathop {\mathrm {dom}}\nolimits (X_{i-1})), v, \max (\mathop {\mathrm {dom}}\nolimits (X_{i+1})), \ldots , \max (\mathop {\mathrm {dom}}\nolimits (X_n))]$ for any value $v \in \mathop {\mathrm {dom}}\nolimits (X_i)$. Hence, all values in $\mathop {\mathrm {dom}}\nolimits (X_i)$ are domain consistent. Otherwise, the value $\min (\mathop {\mathrm {dom}}\nolimits (X_i))$ is filtered out from the domain of $X_i$ and the quantile function guarantees that the new lower bound on the domain satisfies the constraint.

The running time complexity is dominated by the number of calls to the cumulative distribution functions and the quantile functions. In the worst case, the algorithm performs 3n calls to the cumulative distribution functions and at most n calls to the quantile functions. This leads to a running time complexity of O(n).

4 Case Study

4.1 The Deterministic Version

We have an industrial partner in the textile industry whose needs motivate the theoretical contribution and whose data allow to empirically evaluate this contribution on an industrial problem.

The textile manufacturer has to schedule a set of tasks $\mathcal {I}$ on looms $L$. The tasks represent textile pieces to weave or setups to prepare a loom for the next textile. A piece of textile i has a style $z_{i}$ which is a number that encodes the width of the textile, the type of thread, the weaving pattern, etc. A task i is pre-assigned to loom $l_{i} \in L$ in order to simplify the problem. In order to process the task, this loom needs to be set up with configuration $c_{i}$. Each task $i \in \mathcal {I}$ has a due date $d_i$ and a priority $r_i$. The higher the priority, the more urgent the task is. In the deterministic version of the problem, every piece of textile i has a predefined weaving duration $p_i$.

Looms are disjunctive resources  [3] that can only weave one piece of textile at the time or being subject to one set up at the time. A loom $l \in L$ becomes available at time $a_{l}$. Prior to this time point, the loom completes tasks that were started and that cannot be changed. A loom l is initially in configuration $c^\mathrm{init}_{l}$ and upon a major setup operation of duration $p^\mathrm{major}_{l}$, its new configuration becomes $c^\mathrm{final}_{l}$. There is only one possible major setup per loom. A loom l can only execute a task i if it is assigned to that loom ($l_{i} = l$). It executes the task before its major setup if $c_{i} = c^\mathrm{init}_{l}$ or after if $c_{i} = c^\mathrm{final}_{l}$. A major setup is performed by a worker from the set $W$. Hence, at most $|W|$ major setups can be performed simultaneously.

A minor setup takes place between two consecutive weaving tasks on a loom, but does not change the configuration of the loom. There are up to 3 types of employees $p \in P$ interacting with a loom during a minor setup. The order is always as follows: weavers, beam tiers, and mechanics. Therefore, a minor setup is decomposed into an ordered sequence of 3 tasks, one associated for each profession. The minor setup duration is sequence-dependent in the sense that the duration $t_{i,j,p}$ for the profession p is a function of the task i before the setup and the task j after. Employees are cumulative resources. Since there are $q_{p}$ employees of profession $p \in P$, up to $q_{p}$ minor setup tasks associated to profession p can be simultaneously executed across the looms.

In the deterministic version of the problem, the unknowns are the starting time $S_{i}$ of each task $i \in \mathcal {I}$, the starting time $S^\mathrm{minor}_{i,p}$ of the minor setup succeeding a task $i \in \mathcal {I}$ for each profession $p \in P$, and the starting time $S^\mathrm{major}_{l}$ of the major setup of loom $l \in L$. The objective function is the weighted tardiness where the weights are the task priorities. We use this metric since the tight deadlines make it unreasonable to search for a schedule without tardiness.

Fig. 1.

Model equations directly taken from our previous paper [1]

The constraint model is similar to the one of a resource-constrained project scheduling problem (RCPSP)  [2]. In a RCPSP, there are tasks to schedule and cumulative resources. Our problem differs from the RCPSP in the sense that minor setups have sequence-dependent processing times.

Figure 1 presents the constraint model of the deterministic problem as published in  [1]. The variable $F_{l}$ encodes the first task on loom l. The order of the tasks is encoded in an array of variables N such that for any piece of textile i, $N_i$ is the next piece of textile to weave. The dummy task $\sigma _l$ acts as a sentinel to encode the last task to execute on loom l. The task following the last task on a loom is the first task on the next loom (see constraints (11) and (12)). The vector N forms a circuit visiting all the tasks hence Constraint (13). We model the disjunctive resources using less than or equal to constraints. Two Cumulative constraints model the different setup types (minor and major).

4.2 The Stochastic Version

The solver acts as a black box and returns a solution that satisfies the constraints. The resulting schedule is valid, yet this solution does not consider the probabilities of different stochastic events. Since a loom weaves many threads, each job has a high chance of having multiple breakdowns. Each task is subject to two types of breakdowns with different probabilities and repair time. A warp thread has a high chance of breaking, but is quick to repair and the repair process is often automated. However, a weft thread rarely breaks, but when it does, an employee gets involved. Since both types of breakdowns are observable on a day-to-day basis, we must be able to consider them in a single distribution. In our case, the breakdowns follow Poisson distributions. We suppose the independence of both types of breakdowns (warp thread and weft thread). Since the sum of two independent random Poisson variables is a random Poisson variable  [8], we can sum the $\lambda$-parameters of both breakdown distributions. Therefore, the duration of the breakdowns in our problem is a random variable that follows the sum of two Poisson distributions, which is equivalent to a single Poisson distribution. Depending on the task $i \in \mathcal {I}$ and the loom $l \in L$, the weft thread has an average number of breakdowns $\beta ^\mathrm{weft}_{i,l}$ between 0 to 10 times and when it breaks, it takes 10 min to repair. The warp thread has an average number of breakdowns $\beta ^\mathrm{warp}_{i,l}$ between 0 and 40 times and it takes 2 or 4 min to repair. The average numbers of breakdowns $\beta ^\mathrm{weft}_{i,l}$ and $\beta ^\mathrm{warp}_{i,l}$ are proportional to the duration of task i on loom l. The $\lambda$-parameter of the Poisson distribution for the delay caused by the breakdowns is therefore $10 \cdot \beta ^\mathrm{weft}_{i,l} + 2 \cdot \beta ^\mathrm{warp}_{i,l}$ or $10 \cdot \beta ^\mathrm{weft}_{i,l} + 4 \cdot \beta ^\mathrm{warp}_{i,l}$. Our case study is about solving the stochastic version of this problem when weaving tasks might take longer to execute than expected.

A Solution with Fixed Processing Times: One way to solve the problem could be to artificially increase the duration of the weaving tasks by a given percentage. This prevents the unplanned events from starving the resource pool available for setups which causes ripple effects. The drawback of this technique happens when we overestimate the duration and the number of delays. The delays must be chosen in a smart and intuitive manner. Giving the solver a choice of where to take risks can lead to a better solution. This is where our constraint comes in.

A Solution with Flexible Processing Times: As a second solution, we rather modify the constraint model with an additional variable $P_i$ to represent the duration of a weaving task, including breakdowns, and a variable $B_i$ that includes only the breakdowns. The task duration $P_i$ cannot be shorter than the deterministic version of the problem, but could be longer if we plan time for breakdowns. We therefore insert this constraint.

$$\begin{aligned} P_i = p_i + B_i \end{aligned}$$

(17)

We impose a Confidence constraint on the duration of the breakdowns to ensure that we plan for sufficiently long breakdowns with probability $\gamma$.

$$\begin{aligned} \textsc {Confidence}([B_i \mid i \in \mathcal {I}], [cdf_i \mid i \in \mathcal {I}], \gamma ) \end{aligned}$$

(18)

The Confidence constraint can guarantee that a breakdown does not alter the subsequent tasks with probability $\gamma$. That is, if the breakdown is shorter than what is computed by the solver, all tasks can still start at the expected time. If the breakdown is longer than what was planned, it might cause a ripple effect and delay the execution of the future tasks, but this only happens with probability $1 - \gamma$. Therefore, a valid solution to our problem is a solution that causes no disturbances, $\gamma$ % of the time. The rest of the new model with variable processing time is similar to  [11]. The constraints 6 and 8 are modified by replacing $p_i$ with $P_i$.

5 Simulation

The simulation model is used to evaluate the quality of the solutions. This implies measuring robustness by emulating scenarios and how well the solutions cope with stochastic events such as breakdowns. The simulator produces an in-depth three-dimensional depiction of the work environment. It considers the number of employees, their positions, the time each employee takes to move between looms, the number of looms, etc. By using a simulator, we can compare different solutions without trying them in practice. Since the company might be reluctant to directly apply the results to their schedules, this also acts as a way to alleviate doubts. The simulator was designed to test scenarios and to answer questions that are much beyond the scope of this paper and even beyond scheduling in general. It can be used to see the effect of strategic decisions on textile production and the effect of modifying the number of resources on the performance of the plant.

For our purpose, the simulation model receives as input the same data as our optimization model (configuration of the looms, availability of the resources, duration of the tasks) and the output of the optimization (the starting time of the tasks). One point that is worth mentioning is that the optimization model uses, for each weaving task, a distinct distribution for the duration of the breakdowns. However, the simulator averages out these distributions per loom and uses the same distribution for all weaving tasks on a given loom.

6 Experiments

6.1 Methodology

Three different methods were compared. First, in the Deterministic model, we ignore the stochastic events. The Deterministic model consists of using the model from Fig. 1 without any change. In the Fixed model, we artificially increase the tasks’ processing times by the sum of the average breakdown duration multiplied by the average number of breakdowns. This corresponds to the first solution presented in Sect. 4.2. Finally, the Confidence method is the model that uses our chance constraint with $\gamma \in \{$0.01, 0.05, 0.1, 0.2, 0.3, $\ldots$, 0.8, 0.9, 0.95, 0.99$\}$. The processing time of a task becomes a variable equal to the sum of the deterministic processing time (a constant) and the duration of breakdowns (another variable). These breakdown duration variables are subject to the Confidence constraint using the Poisson distributions. This corresponds to the second solution presented in Sect. 4.2.

The CP model was written in the MiniZinc 2.4.2 language  [12]. We use the solver Chuffed  [5] with the free search parameter  [16]. The simulation is modeled using the academic version of SIMIO  [19]. We ran the experiments on a computer with the configuration: Ubuntu 19.10, 64 GB ram, Processor Intel(R) Core(TM) i7-6700K CPU @ 4.00 GHz, 4 Cores, 8 Logical Processors. All optimization processes were given a timeout of 30 min and 10 h.

To compare the quality of the schedules provided by the different methods, we use the mean simulated weighted tardiness. Let $E_i^s$ be the ending time of task i in simulation s. The mean simulated weighted tardiness $\bar{T}$ is calculated as follows:

$$\begin{aligned} \bar{T} = \frac{1}{n} \sum _{s=1}^n \sum _{i \in \mathcal {I}} r_i \max (0, E_i^s - d_i) \end{aligned}$$

(19)

The inner sum computes the weighted tardiness of a simulation s while the outer sum averages over n simulations. We use $n=100$ simulations. A simulation is a randomly generated scenario based on probabilities, i.e. that the duration of the breakdowns are randomly drawn according to the Poisson distributions we established.

During the simulation of a schedule, tasks can be delayed by breakdowns that were not planned by the solver. The task on a loom can only start after its predecessor, on the same loom, is completed. An idle technician always start working on a setup when the loom gets ready. If s/he has the choice between setting up two looms, the priority is given to the setup that was planned earlier in the original schedule. A loom that completes a task earlier than expected must wait before starting the next task as we suppose that the material for this next task is not necessarily ready before its planned start time. Indeed, when a task is planned, it instructs people on the floor to prepare the material in order for the task to start on time. This preparation is not part of the optimization since it adds too much complexity to the decision process. The resources in charge of preparing the material are voluntary omitted from the problem definition. However, if, during the execution of the plan, we inform at the last minute that a task can start earlier, we cannot assume that the preparation will be ready. In other words, the tasks are subject to precedence constraints with tasks that are external to the problem.

6.2 Instances

To compare the methods, we had access to four datasets. In these datasets, there are 5 workers for minor setups, 1 for major setups, and a total of 81 looms available. The scheduling horizon is 14,400 min which is roughly two weeks of work time. Table 1 shows the characteristics of each instance, including the number of pieces of textiles to weave. It also reports the resource usage rate $r = \frac{1}{H|L|} \sum _i p_i$ where H is the scheduling horizon, |L| is the number of looms and $p_i$ is the processing time (without breakdowns) of task i. We also report the usage rate when processing times are augmented with the expected breakdown duration. These breakdowns approximately add $4\%$ to the resource usage in the last three datasets.

Dataset 1 consists of a reduced dataset where pieces of textiles with a due date of 0 (these tasks are already late) and some others with due dates larger than the horizon are removed. This leads to an easier dataset to solve for which optimal solutions are obtained within 30 minutes of computation time with every method.

Datasets 2, 3, and 4 are not modified, but cannot be optimally solved even after 10 hours. These datasets are more realistic with respect to what is usually observed in the industry where one has to work with suboptimal solutions. Those are directly extracted from our industrial partner’s database.

In every instance, there is $|W| = 1$ mechanic available for major setups, 2 mechanics, 5 weavers, and 3 beam tiers available at all time for minor setups.

Table 1. Dataset descriptions

6.3 Results

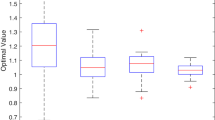
In Figs. 2, 4, 6, and 8, we present the results of our models with different methods on the x-axis. The Confidence method was tested with different confidence thresholds $\gamma$. The y-axis is the weighted tardiness. There are two colors of dots and lines. Red presents the prediction value. The prediction is essentially the objective value of the solution returned by the solver, i.e. the weighted tardiness if the plan executes as expected by the Confidence constraint. Blue shows the mean simulated weighted tardiness of the 100 runs with its 95% confidence interval.

Figure 2 shows the results for the reduced dataset solvable to optimality. Notice that the red curve is non-decreasing, since an optimal schedule that satisfies the Confidence constraint with threshold $\gamma$ is a feasible, but potentially suboptimal, schedule for a smaller threshold. For this instance, which is rather trivial to solve since few tasks were competing for the resources, the best strategy was to plan no extra time for the breakouts. In case of a breakout, the next tasks are simply postponed until the delayed task is completed. At this time, the resource is always available to perform the setup to execute the next task and no further delay is caused. This strategy is achieved by the Deterministic method and the Confidence constraint with $\gamma = 0.01$. However, the Confidence predicted value is closer to reality. At the opposite, for $\gamma = 0.99$, the weighted tardiness is at its highest since the duration of nearly all tasks is set to the longest possible duration. Notice how the Fixed method offers a performance similar to the Confidence method with $\gamma = 0.5$.

Fig. 2.

Dataset with 448 textile pieces to weave (Color figure online)

Fig. 3.

Dataset with 602 textile pieces to weave. 30 min timeout. (Color figure online)

Fig. 4.

Dataset with 602 textile pieces to weave. 10 h timeout. (Color figure online)

Fig. 5.

Dataset with 480 textile pieces to weave. 30 min timeout. (Color figure online)

Fig. 6.

Dataset with 480 textile pieces to weave. 10 h timeout. (Color figure online)

Fig. 7.

Dataset with 525 textile pieces to weave. 30 min timeout. (Color figure online)

Fig. 8.

Dataset with 525 textile pieces to weave. 10 h timeout. (Color figure online)

For the datasets 2, 3, and 4, we clearly see on Figs. 3, 4, 5, 6, 7 and 8 that the solver does not produce optimal solutions even within 10 h. Indeed, the red curve is non-monotonic. Moreover, results of the dataset 2 with $\gamma 95\%$ are not reported as no solution was obtained within 10 h. This happens with even lower confidence thresholds when using a timeout of 30 min. However, notice that the simulation follows the predictions of the model for the higher values of $\gamma$. The gap between the objective value obtained by the solver (red) and the simulation (blue) decreases by increasing $\gamma$. In every case, the best solution, as evaluated by the simulator (blue), comes from the Confidence method. In Dataset 4, the best solution is obtained at $\gamma = 20\%$. The Confidence model trades objective value for robustness. The Confidence model outperforms the Fixed model in both objective value and robustness. We can also notice that choosing a bad $\gamma$ value can make or break the quality of a solution. The solutions for $\gamma = 1\%$ and $\gamma = 95\%$ are worse than the Deterministic model solution.

With the confidence intervals, we notice that the mean is usually quite precise with 100 runs of the simulation model. The lengthy events are rarer, therefore, increasing the number of simulations decreases the variability. Yet, using a higher value of $\gamma$ also reduces the variability. With Confidence the prediction expects more tardiness, but the guarantee of not causing ripple effects makes it so the mean simulated weighted tardiness is better.

The Deterministic method has no stochastic optimization involved and completely ignores potential breakdowns. We would have thought that during the simulation, this method would most likely lag behind the planned schedule and finally execute a non-optimize schedule. However, it seems that in a context where resources are not scarce (dataset 1), repairing the plan as it executes is not a bad way to proceed. This pattern gradually vanishes with bigger instances.

On the harder datasets (datasets 2, 3, and 4), the objective value adopts a wavy form. Our main hypothesis is that varying $\gamma$ does not only affect the objective value, it also affects the difficulty to solve the problem. So decreasing $\gamma$ would normally decrease the objective value, but in some situations, the search heuristic gets trapped and the solver returns a worse solution once the timeout is reached. This is especially apparent with a timeout of 30 min.

The harder datasets (2, 3, and 4) have tighter schedules. A ripple effect from a breakdown can produce increasingly more lateness. We assume that the usefulness of the Confidence scales with the risk of the ripple effect. In Figs. 4, 6, and 8, the curves are respectively centered around $\gamma = 50\%, 5\%, 20\%$. The red curve seems to show that $\gamma = 100\%$ cannot be achieved. This can be explained by the difficulty of satisfying the higher percent of a Poisson $\text{ cdf }$ function and the tendency of probability products to tend towards 0.

When we compare the different solutions graphs with the Table 1, we can notice the following. The more resource usage there is, the harder it is to solve the problem with a higher $\gamma$ value. The instances also get harder as the number of tasks increases. While we don’t include computation times, we noticed that in the dataset 1, the computation times were similar (less than a second of difference) to the deterministic model until $99\%$ where it spiked. The computation times for the other datasets where inconclusive since no optimal solution was found.

The Fixed method often overestimates the breakdown times needed to create robustness and produces schedules where tasks are planned to be executed late. The Fixed method is more rigid compared to Confidence because it cannot allow to choose where the risk should be taken in order to minimize the weighted tardiness. More often than not, the Fixed approach gives results similar to the Confidence method with $\gamma =0.5$, but slightly worse. In a context where resources are abundant, it would be interesting to compute the processing times by using a value shorted than the average breakdown time.

The Confidence method shows that the weighted tardiness computed by the solver is a good indicator of the weighted tardiness obtained in the simulation. It would be interesting to push further the evaluation with instances, not necessarily industrial, for which we can control the scarcity of the resources. A search heuristic adapted to stochastic optimization could also help with this type of problem and reduce the computation times.

7 Conclusion

We presented the Confidence constraint, a new global chance constraint that provides robust solutions in stochastic contexts. We presented a linear time filtering algorithm with explanations. We compared the Confidence constraint to a Deterministic and Fixed approach and determined that the new global chance constraint offers good prediction about the weighted tardiness obtained in the simulation. It is planned that our industrial partner sets the $\gamma$-parameter according to how much risk they are willing to take and readjusts it every week. The deterministic method is implemented and being deployed by our industrial partner, while the stochastic optimization is still under evaluation. More stochastic events need to be taken into account such as the arrival of new orders.