First Steps Towards a Runtime Analysis When Starting with a Good Solution

Abstract

The mathematical runtime analysis of evolutionary algorithms traditionally regards the time an algorithm needs to find a solution of a certain quality when initialized with a random population. In practical applications it may be possible to guess solutions that are better than random ones. We start a mathematical runtime analysis for such situations. We observe that different algorithms profit to a very different degree from a better initialization. We also show that the optimal parameterization of the algorithm can depend strongly on the quality of the initial solutions. To overcome this difficulty, self-adjusting and randomized heavy-tailed parameter choices can be profitable. Finally, we observe a larger gap between the performance of the best evolutionary algorithm we found and the corresponding black-box complexity. This could suggest that evolutionary algorithms better exploiting good initial solutions are still to be found. These first findings stem from analyzing the performance of the $(1+1)$ evolutionary algorithm and the static, self-adjusting, and heavy-tailed $(1 + (\lambda ,\lambda ))$ GA on the OneMax benchmark, but we are optimistic that the question how to profit from good initial solutions is interesting beyond these first examples.

1 Introduction

The mathematical runtime analysis (see, e.g,.  [4, 15, 20, 28]) has contributed to our understanding of evolutionary algorithms (EAs) via rigorous analyses how long an EA takes to optimize a particular problem. The overwhelming majority of these results considers a random or worst-case initialization of the algorithm. In this work, we argue that it also makes sense to analyze the runtime of algorithms starting already with good solutions. This is justified because such situations arise in practice and because, as we observe in this work, different algorithms show a different runtime behavior when started with such good solutions. In particular, we observe that the $(1 + (\lambda ,\lambda ))$ genetic algorithm (${(1 + (\lambda , \lambda ))}$ GA) profits from good initial solutions by much more than, e.g., the $(1 + 1)$ EA. From a broader perspective, this work suggests that the recently proposed fine-grained runtime notions like fixed budget analysis  [22] and fixed target analysis  [6], which consider optimization up to a certain solution quality, should be extended to also take into account different initial solution qualities.

1.1 Starting with Good Solutions

As just said, the vast majority of the runtime analyses assume a random initialization of the algorithm or they prove performance guarantees that hold for all initializations (worst-case view). This is justified for two reasons. (i) When optimizing a novel problem for which little problem-specific understanding is available, starting with random initial solutions is a recommended approach. This avoids that a wrong understanding of the problem leads to an unfavorable initialization. Also, with independent runs of the algorithm automatically reasonably diverse initializations are employed. (ii) For many optimizations processes analyzed with mathematical means it turned out that there is not much advantage of starting with a good solution. For this reason, such results are not stated explicitly, but can often be derived from the proofs. For example, when optimizing the simple OneMax benchmark via the equally simple $(1 + 1)$ EA, then results like  [10, 11, 16, 26] show a very limited advantage from a good initialization. When starting with a solution having already 99% of the maximal fitness, the expected runtime has the same $en \ln (n) \pm O(n)$ order of magnitude. Hence the gain from starting with the good solution is bounded by an O(n) lower order term. Even when starting with a solution of fitness $n - \sqrt{n}$, that is, with fitness distance $\sqrt{n}$ to the optimum of fitness n, then only a runtime reduction by asymptotically a factor of a half results. Clearly, a factor-two runtime improvement is interesting in practice, but the assumption that an initial solution can be found that differs from the optimum in only $\sqrt{n}$ of the n bit positions, is very optimistic.

Besides this justification for random initializations, we see a number of situations in which better-than-random solutions are available (and this is the motivation of this work). The obvious one is that a problem is to be solved for which some, at least intuitive, understanding is available. This is a realistic assumption in scenarios where similar problems are to be solved over a longer time period or where problems are solved by combining a human understanding of the problem with randomized heuristics. A second situation in which we expect to start with a good solution is reoptimization. Reoptimization  [30, 34] means that we had already solved a problem, then a mild change of the problem data arises (due to a change in the environment, a customer being unhappy with a particular aspect of the solution, etc.), and we react to this change not by optimizing the new problem from scratch, but by initializing the EA with solutions that were good in the original problem. While there is a decent amount of runtime analysis literature on how EAs cope with dynamic optimization problems, see  [27], almost all of them regard the situation that a dynamic change of the instance happens frequently and the question is how well the EA adjusts to these changes. The only mathematical runtime analysis of a true reoptimization problem we are aware of is  [9]. The focus there, however, is to modify an existing algorithm so that it better copes with the situation that the algorithm is started with a solution that is structurally close to the optimum, but has a low fitness obscuring to the algorithm that the current solution is already structurally good.

We note that using a known good solution to initialize a randomized search heuristic is again a heuristic approach. It is intuitive that an iterative optimization heuristic can profit from such an initialization, but there is no guarantee and, clearly, there are also situations where using such initializations is detrimental. As one example, assume that we obtain good initial solutions from running a simple hill-climber. Then these initial solutions could be local optima which are very hard to leave. An evolutionary algorithm initialized with random solutions might find it easier to generate a sufficient diversity that allows to reach the basin of attraction of the optimum. So obviously some care is necessary when initializing a search heuristic with good solutions. Several practical applications of evolutionary algorithms have shown advantages of initializations with good solutions, e.g.,  [24] on the open shop scheduling problem.

While there are no explicit mathematical runtime analyses for EAs starting with a good solution, it is clear that many of the classic results in their proofs reveal much information also on runtimes starting from a good solution. This is immediately clear for the fitness level method  [32], but also for drift arguments like  [12, 19, 23, 25] when as potential function the fitness or a similar function is used, and for many other results. By not making these results explicit, however, it is hard to see the full picture and to draw the right conclusions.

1.2 The ${(1 + (\lambda , \lambda ))}$ GA Starting with Good Solutions

In this work, we make explicit how the ${(1 + (\lambda , \lambda ))}$ GA optimizes OneMax when starting from a solution with fitness distance D from the optimum. We observe that the ${(1 + (\lambda , \lambda ))}$ GA profits in a much stronger way from such a good initialization than other known algorithms. For example, when starting in fitness distance $D = \sqrt{n}$, the expected time to find the optimum is only $\tilde{O}(n^{3/4})$ when using optimal parameters. We recall that this algorithm has a runtime of roughly $n \sqrt{\log n}$ when starting with a random solution  [7, 8]. We recall further that the $(1 + 1)$ EA has an expected runtime of $(1 \pm o(1)) \frac{1}{2} e n \ln (n)$ when starting in fitness distance $\sqrt{n}$ and an expected runtime of $(1 \pm o(1)) e n \ln n$ when starting with a random solution. So clearly, the ${(1 + (\lambda , \lambda ))}$ GA profit to a much higher degree from a good initialization than the $(1 + 1)$ EA. We made this precise for the $(1 + 1)$ EA, but it is clear from other works such as  [3, 13, 21, 33] that similar statements hold as well for many other $(\mu +\lambda )$ EA s optimizing OneMax, at least for some ranges of the parameters.

The runtime stated above for the ${(1 + (\lambda , \lambda ))}$ GA assumes that the algorithm is used with the optimal parameter setting, more precisely, with the optimal setting for starting with a solution of fitness-distance D. Besides that we usually do not expect the algorithm user to guess the optimal parameter values, it is also not very realistic to assume that the user has a clear picture on how far the initial solution is from the optimum. For that reason, we also regard two parameter-less variants of the ${(1 + (\lambda , \lambda ))}$ GA (where parameterless means that parameters with a crucial influence on the performance are replaced by hyperparameters for which the influence is less critical or for which we can give reasonable general rules of thumb).

Already in  [8], a self-adjusting choice based on the one-fifth success rule of the parameters of the ${(1 + (\lambda , \lambda ))}$ GA was proposed. This was shown to give a linear runtime on OneMax in  [7]. We note that this is, essentially, a parameterless algorithm since the target success rate (the “one-fifth”) and the update factor had only a small influence on the result provided that they were chosen not too large (where the algorithm badly fails). See  [7, Sect. 6.4] for more details. For this algorithm, we show that it optimizes OneMax in time $O(\sqrt{nD})$ when starting in distance D. Again, this is a parameterless approach (when taking the previous recommendations on how to set the hyperparameters).

A second parameterless approach for the ${(1 + (\lambda , \lambda ))}$ GA was recently analyzed in  [1], namely to choose the parameter $\lambda$ randomly from a power-law distribution. Such a heavy-tailed parameter choice was shown to give a performance only slightly below the one obtainable from the best instance-specific values for the $(1 + 1)$ EA optimizing jump functions  [14]. Surprisingly, the ${(1 + (\lambda , \lambda ))}$ GA with heavy-tailed parameter choice could not only overcome the need to specify parameter values, it even outperformed any static parameter choice and had the same O(n) runtime that the self-adjusting ${(1 + (\lambda , \lambda ))}$ GA had  [1]. When starting with a solution in fitness distance D, this algorithm with any power-law exponent equal to or slightly above two gives a performance which is only by a small factor slower than $O(\sqrt{nD})$.

1.3 Experimental Results

We support our theoretical findings with an experimental validation, which shows that both the self-adjusting and the heavy-tailed version of the ${(1 + (\lambda , \lambda ))}$ GA indeed show the desired asymptotic behavior and this with only moderate implicit constants. In particular, the one-fifth self-adjusting version can be seen as a very confident winner in all cases, and the heavy-tailed versions with different power-law exponents follow it with the accordingly distributed runtimes. Interestingly enough, the logarithmically-capped self-adjusting version, which has been shown to be beneficial for certain problems other than OneMax   [5] and just a tiny bit worse than the basic one-fifth version on OneMax, starts losing ground to the heavy-tailed versions at distances just slightly smaller than $\sqrt{n}$.

1.4 Black-Box Complexity and Lower Bounds

The results above show that some algorithms can profit considerably from good initial solutions (but many do not). This raises the question of how far we can go in this direction, or formulated inversely, what lower bounds on this runtime problem we can provide. We shall not go much into detail on this question, but note here that one can define a black-box complexity notion for this problem. Informally speaking, the input to this problem is an objective function from a given class of functions and a search point in Hamming distance D from the optimum. The unrestricted black-box complexity is the smallest expected number of fitness evaluations that an otherwise unrestricted black-box algorithm performs to find the optimum (of a worst-case input).

If the class of functions consists of all OneMax-type functions, that is, OneMax and all functions with an isomorphic fitness landscape, then the classic argument via randomized search trees and Yao’s minimax principle from  [17]¹ shows that the black-box complexity is at least $\varOmega (\frac{D \log (n/D)}{\log n})$. A matching upper bound follows from evaluating random search points until all evaluation results leave only one solution (out of the originally $\left( {\begin{array}{c}n\\ D\end{array}}\right)$ ones) fitting to the evaluations results (this is the classic random guessing strategy of  [18]). For small D, this black-box complexity of order $\varTheta (\frac{D \log (n/D)}{\log n})$ is considerably lower than our upper bounds. Also, this shows a much larger gap between black-box complexity and EA performance than in the case of random initialization, where the black-box complexity is $\varTheta (\frac{n}{\log n})$ and simple EAs have an $O(n \log n)$ performance.

1.5 Synopsis and Structure of the Paper

Overall, our results show that the question of how EAs work when started with a good initial solution is far from trivial. Some algorithms profit more from this than others, the question of how to set the parameters might be influenced by the starting level D and this may make parameterless approaches more important, and the larger gap to the black-box complexity could suggest that there is room for further improvements.

The rest of the paper is organized as follows. In Sect. 2 we formally define the considered algorithms and the problem and collect some useful analysis tools. In Sect. 3 we prove the upper bounds on the runtime of the algorithms and deliver general recommendations on how to use each algorithm. In Sect. 4 we check how our recommendations work in experiments.

2 Preliminaries

2.1 The ${(1 + (\lambda , \lambda ))}$ GA and Its Modifiactions

We consider the ${(1 + (\lambda , \lambda ))}$ GA, which is a genetic algorithm for the optimization of n-dimensional pseudo-Boolean functions, first proposed in  [8]. This algorithm has three parameters, which are the mutation rate p, the crossover bias c, and the population size $\lambda$.

The ${(1 + (\lambda , \lambda ))}$ GA stores the current individual x, which is initialized with a random bit string. Each iteration of the algorithm consists of a mutation phase and a crossover phase. In the mutation phase we first choose a number $\ell$ from the binomial distribution with parameters n and p. Then we create $\lambda$ offsprings by flipping $\ell$ random bits in x, independently for each offspring. An offspring with the best fitness is chosen as the mutation winner $x'$ (all ties are broken uniformly at random). Note that $x'$ can and often will have a worse fitness than x.

In the crossover phase we create $\lambda$ offspring by applying a biased crossover to x and $x'$ (independently for each offspring). This biased crossover takes each bit from x with probability $(1 - c)$ and from $x'$ with probability c. A crossover offspring with best fitness is selected as the crossover winner y (all ties are broken uniformly at random). If y is not worse than x, it replaces the current individual. The pseudocode of the ${(1 + (\lambda , \lambda ))}$ GA is shown in Algorithm 1.

Based on intuitive considerations and rigorous runtime analyses, a standard parameter settings was proposed in which the mutation rate and crossover bias are defined via the population size, namely, $p = \frac{\lambda }{n}$ and $c = \frac{1}{\lambda }$.

It was shown in  [8] that with a suitable static parameter value for $\lambda$, this algorithm can solve the OneMax function in $O(n\sqrt{\log (n)})$ fitness evaluations (this bound was minimally reduced and complemented with a matching lower bound in  [7]). The authors of  [8] noticed that with the fitness-dependent parameter $\lambda = \sqrt{\frac{n}{d}}$ the algorithm solves OneMax in only $\varTheta (n)$ iterations.

The fitness-depending parameter setting was not satisfying, since it is too problem-specific and most probably does not work on practical problems. For this reason, also a self-adjusting parameter choice for $\lambda$ was proposed in  [8] and analyzed rigorously in  [7]. It uses a simple one-fifth rule, multiplying the parameter $\lambda$ by some constant $A > 1$ at the end of the iteration when $f(y) \le f(x)$, and dividing $\lambda$ by $A^4$ otherwise (the forth power ensures the desired property that the parameter does not change in the long run when in average one fifth of the iterations are successful). This simple rule was shown to keep the parameter $\lambda$ close to the optimal fitness-dependent value during the whole optimization process, leading to a $\varTheta (n)$ runtime on OneMax. However, this method of parameter control was not efficient on the MAX-3SAT problem, which has a lower fitness-distance correlation than OneMax   [5]. Therefore, capping the maximal value of $\lambda$ at $2\ln (n + 1)$ was needed to obtain a good performance on this problem.

Inspired by  [14], the recent paper  [1] proposed use a heavy-tailed random $\lambda$, which gave a birth to the fast ${(1 + (\lambda , \lambda ))}$ GA. In this algorithm the parameter $\lambda$ is chosen from the power-law distribution with exponent $\beta$ and with upper limit u. Here for all $i \in {\mathbb {N}}$ we have

$$\begin{aligned} \Pr [\lambda = i] = {\left\{ \begin{array}{ll} C_{\beta , u}i^{-\beta }, \text { if } i \in [1..u], \\ 0, \text { otherwise,} \end{array}\right. } \end{aligned}$$

where $C_{\beta , u} = (\sum _{j = 1}^u j^{-\beta })^{-1}$ is the normalization coefficient. It was proven that the fast ${(1 + (\lambda , \lambda ))}$ GA finds the optimum of OneMax in $\varTheta (n)$ fitness evaluations if $\beta \in (2, 3)$ and u is large enough. Also it was empirically shown that this algorithm without further capping of $\lambda$ is quite efficient on MAX-3SAT.

When talking about the runtime of the ${(1 + (\lambda , \lambda ))}$ GA, we denote the number of iterations until the optimum is found by $T_I$ and the number of fitness evaluations until the optimum is found by $T_F$. We denote the distance of the current individual to the optimum by d.

2.2 Problem Statement

The main object of this paper is the runtime of the algorithms discussed in Sect. 2.1 when they start in distance D from the optimum, where D should be smaller than the distance of a random solution. For this purpose we consider the classic OneMax function, which is defined on the space of bit strings of length n by

$$\begin{aligned} \textsc {OneMax} (x) = \textsc {OM} (x) = \sum _{i = 1}^n x_i. \end{aligned}$$

2.3 Probability for Progress

To prove our upper bounds on the runtimes we use the following estimate for the probability that the ${(1 + (\lambda , \lambda ))}$ GA finds a better solution in one iteration.

Lemma 1

The probability that $\textsc {OM} (y) > \textsc {OM} (x)$ is $\varOmega (\min \{1, \frac{d\lambda ^2}{n}\})$.

To prove this lemma we use the following auxiliary result from  [1], a slight adaptation of  [29, Lemma 8].

Lemma 2

(Lemma 2.2 in  [1]). For all $p \in [0, 1]$ and all $\lambda > 0$ we have

$$ 1 - (1 - p)^\lambda \ge \frac{\lambda p}{1 + \lambda p}. $$

Proof

(of Lemma 1). By Lemma 7 in  [8] the probability to have a true progress in one iteration is $\varOmega (1 - (\frac{n - d}{n})^\frac{\lambda ^2}{2})$. By Lemma 2 this is at least $\varOmega (\min \{1, \frac{d\lambda ^2}{n}\})$.

3 Runtime Analysis

In this section we conduct a rigorous runtime analysis for the different variants of the ${(1 + (\lambda , \lambda ))}$ GA and prove upper bounds on their runtime when they start in distance D from the optimum. We start with the standard algorithm with static parameters.

Theorem 3

The expected runtime of the ${(1 + (\lambda , \lambda ))}$ GA with static parameter $\lambda$ (and mutation rate $p = \frac{\lambda }{n}$ and crossover bias $c = \frac{1}{\lambda }$ as recommended in  [8]) on OneMax with initialization in distance D from the optimum is

$$ E[T_F] = O\left( \frac{n}{\lambda } \ln \left( \frac{n}{\lambda ^2}\right) + D\lambda \right) $$

fitness evaluations. This is minimized by $\lambda = \sqrt{\frac{n\ln (D)}{D}}$, which gives a runtime guarantee of $E[T_F] = O(\sqrt{nD\ln (D)}\,)$.

We omit the proof for reasons of space². We move on to the ${(1 + (\lambda , \lambda ))}$ GA with optimal fitness-dependent parameters.

Theorem 4

The expected runtime of the ${(1 + (\lambda , \lambda ))}$ GA with fitness-dependent $\lambda = \lambda (d) = \sqrt{\frac{n}{d}}$ on OneMax with initialization in distance D from the optimum is $E[T_F] = O(\sqrt{nD}).$

We omit the proof for reasons of space and since it trivially follows from Lemma 1.

The one-fifth rule was shown to be to keep the value of $\lambda$ close to its optimal fitness-dependent value, when starting in the random bit string. The algorithm is initialized with $\lambda =2$, which is close-to-optimal when starting in a random bit string. In the following theorem we show that even when we start in a smaller distance D, the one-fifth rule is capable to quickly increase $\lambda$ to its optimal value and keep it there.

Theorem 5

The expected runtime of the ${(1 + (\lambda , \lambda ))}$ GA with self-adjusting $\lambda$ (according to the one-fifth rule) on OneMax with initialization in distance D from the optimum is $E[T_F] = O(\sqrt{nD}).$

We only sketch the proof for reasons of space. We first show that there is some distance $d \le D$ at which the algorithm reaches the optimal fitness-dependent value of $\lambda$ for the first time. This happens in a relatively short time after the start of the algorithm. In a similar manner as in  [7] we show that from that moment on the value of $\lambda$ always stays close to the optimal fitness-dependent one, yielding asymptotically the same runtime.

For the fast ${(1 + (\lambda , \lambda ))}$ GA with different parameters of the power-law distribution, we show the following runtimes.

Theorem 6

The expected runtime of the fast ${(1 + (\lambda , \lambda ))}$ GA on OneMax with initialization in distance D from the optimum is as shown in Table 1. The runtimes for $\beta > 2$ hold also for all $u \ge \sqrt{n}$.

We omit the proof for reasons of space, but sketch the main arguments. We deliver the upper bounds for the fast ${(1 + (\lambda , \lambda ))}$ GA in two steps. First we find an upper bound on the expected number of iterations $E[T_I]$ of the algorithm in the same way as in Theorem 3.1 in  [1]. Then we use Lemma 3.5 in the same paper to find the expected cost of one iteration, which is $2E[\lambda ]$. Finally, by the Wald’s equation  [31] we compute the expected number of iterations $E[T_F] = 2E[\lambda ]E[T_I]$.

Table 1. Runtime of the heavy-tailed ${(1 + (\lambda , \lambda ))}$ GA for different ranges of $\beta$ and for two variants of choosing u. The best possible fitness dependent choice of $u = \sqrt{\frac{n}{d}}$ is given rather for reasons of comparison. The best fitness-independent choice is $u = \sqrt{n}$, but larger values of u are not harmful when $\beta > 2$ (for $\beta =2$, the $\log n$ is actually a $\log u$, so the influence of u is small). Our recommendation when D is not known is to use $\beta = 2$ and $u = \sqrt{n}$.

From Table 1 we see that choosing $\beta = 2$ and $u = \sqrt{n}$ is the most universal option. The empirical results in  [14] let us assume that different values of $\beta$, but close to two might also be effective in practice. The results of our experiments provided in the Sect. 4 confirm this and show that using $\beta < 2$ with $u = \sqrt{n}$ can be beneficial when starting from a small distance.

4 Experiments

To highlight that the theoretically proven behavior of the algorithms is not strongly affected by the constants hidden in the asymptotic notation, we conducted experiments with the following settings:

• fast ${(1 + (\lambda , \lambda ))}$ GA with $\beta \in \{2.1, 2.3, 2.5, 2.7, 2.9\}$ and the upper limit $u=n/2$;

• self-adjusting ${(1 + (\lambda , \lambda ))}$ GA, both in its original uncapped form and with $\lambda$ capped from above by $2 \log (n+1)$ as proposed in  [5];

• the mutation-only algorithms $(1+1)$ EA and RLS.

In all our experiments, the runtimes are averaged over 100 runs, unless said otherwise.

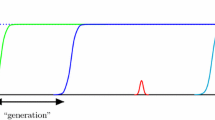
In Fig. 1 we show the mean running times of these algorithms when they start in Hamming distance roughly $\sqrt{n}$ from the optimum. For this experiment, to avoid possible strange effects from particular numbers, we used a different initialization for all algorithms, namely that in the initial individual every bit was set to 0 with probability $\frac{1}{\sqrt{n}}$ and it was set to 1 otherwise. As the figure shows, all algorithms with a heavy-tailed choice of $\lambda$ outperformed the mutation-based algorithms, which struggled from the coupon-collector effect.

Fig. 1.

Mean runtimes and their standard deviation of different algorithms on OneMax with initial Hamming distance D from the optimum equal to $\sqrt{n}$ in expectation. By $\lambda \in [1..u]$ we denote the self-adjusting parameter choice via the one-fifth rule in the interval [1..u]. The indicated confidence interval for each value X is $[E[X] - \sigma (X), E[x] + \sigma (X)]$, where $\sigma (X)$ is the standard deviation of X. The runtime is normalized by $\sqrt{nD}$, so that the plot of the self-adjusting ${(1 + (\lambda , \lambda ))}$ GA is a horizontal line.

Fig. 2.

Mean runtimes and their standard deviation of different algorithms on OneMax with initial Hamming distance D from the optimum equal to $\log (n+1)$ in expectation.

We can also see that the logarithmically capped self-adjusting version, although initially looking well, starts to lose ground when the problem size grows. For $n=2^{22}$ it has roughly the same running time as the ${(1 + (\lambda , \lambda ))}$ GA with $\beta \le 2.3$. To see whether this effect is stronger when the algorithm starts closer to the optimum, we also conducted the series of experiments when the initial distance to the optimum being only logarithmic. The results are presented in Fig. 2. The logarithmically capped version loses already to $\beta =2.5$ this time, indicating that the fast ${(1 + (\lambda , \lambda ))}$ GA is faster close to the optimum than that.

In order to understand better how different choices for $\beta$ behave in practice when the starting point also varies, we conducted additional experiments with problem size $n=2^{22}$, but with expected initial distances D equal to $2^i$ for $i \in [0..21]$. We also normalize all the expected running times by $\sqrt{nD}$, but this time we vary D. The results are presented in Fig. 3, where the results are averaged over 10 runs for distances between $2^9$ and $2^{20}$ due to the lack of computational budget. At distances smaller than $2^{12}$ the smaller $\beta > 2$ perform noticeably better, as specified in Table 1, however for larger distances the constant factors start to influence the picture: for instance, $\beta = 2.1$ is outperformed by $\beta = 2.3$ at distances greater than $2^{13}$.

We also included in this figure a few algorithms with $\beta < 2$, namely $\beta \in \{1.5,1.7,1.9\}$, which have a distribution upper bound of $\sqrt{n}$, for which running times are averaged over 100 runs. From Fig. 3 we can see that the running time of these algorithms increases with decreasing $\beta$ just as in Table 1 for comparatively large distances ($2^{12}$ and up), however for smaller distances their order is reversed, which shows that constant factors still play a significant role.

Fig. 3.

Mean runtimes and their standard deviation of different algorithms on OneMax with problem size $n=2^{22}$ and with initial Hamming distances of the form $D = 2^i$ for $0 \le i \le 21$. The starred versions of the fast ${(1 + (\lambda , \lambda ))}$ GA have a distribution upper bound of $\sqrt{n}$.

5 Conclusion

In this paper we proposed a new notion of the fixed-start runtime analysis, which in some sense complements the fixed-target notion. Among the first results in this direction we observed that different algorithms profit differently from having an access to a solution close to the optimum.

The performance of all observed algorithms, however, is far from the theoretical lower bound. Hence, we are still either to find the EAs which can benefit from good initial solutions or to prove a stronger lower bounds for unary and binary algorithms.