A Parallel Algorithm for Constructing Two Edge-Disjoint Hamiltonian Cycles in Crossed Cubes

Abstract

The n-dimensional crossed cube CQ_n, a variation of the hypercube Q_n, has the same number of vertices and the same number of edges as Q_n, but it has only about half of the diameter of Q_n. In the interconnection network, some efficient communication algorithms can be designed based on edge-disjoint Hamiltonian cycles. In addition, two edge-disjoint Hamiltonian cycles also provide the edge-fault tolerant Hamiltonicity for the interconnection network. Hung [Discrete Applied Mathematics 181, 109–122, 2015] designed a recursive algorithm to construct two edge-disjoint Hamiltonian cycles on CQ_n in O(n2ⁿ) time. In this paper, we provide an O(n) time algorithm for each vertex in CQ_n to determine which two edges were used in Hamiltonian cycles 1 and 2, respectively. With the information of each vertex, we can construct two edge-disjoint Hamiltonian cycles in CQ_n with n ≥ 4.

1 Introduction

The design of an interconnection network is an important issue for the multicomputer system. The hypercube [17, 18] is one of the most popular interconnection networks because of its attractive properties, including regularity, node symmetric, link symmetric, small diameter, strong connectivity, recursive construction, partition capability, and small link complexity. The architecture of an interconnected network is usually modeled by a graph with vertices representing processing units and edges representing communication links. We will use graph and network interchangeably in this paper.

The n-dimensional crossed cube CQ_n, proposed first by Efe [4, 5], is a variant of an n-dimensional hypercube. One advantage of CQ_n is that the diameter is only about one half of the diameter of an n-dimensional hypercube. Hung et al. [11] showed that CQ_n contains a fault-free Hamiltonian cycle, even if there are up to 2n – 5 edge faults. Wang studied the embedding of the Hamiltonian cycle in CQ_n [19]. For more properties of CQ_n, the reader can refer to [4,5,6, 12].

A Hamiltonian cycle is a graph cycle through a graph that visits each node exactly once. The ring structure is important for the multicomputer system, and its benefits can be found in [13]. Two Hamiltonian cycles in the graph are said to be edge-disjoint if they do not share any common edges. Edge-disjoint Hamilton cycles can provide advantages for algorithms using ring structures, and their application can be found in [16]. Further, edge-disjoint Hamiltonian cycles also provide the edge-fault tolerant hamiltonicity for the interconnection network. That is, when one edge in the Hamiltonian cycle fails, the other edge-disjoint Hamiltonian cycle can be adopted to replace it for transmission.

Previous related works are described below. Barth and Raspaud [3] showed that the butterfly networks contain two edge-disjoint Hamiltonian cycles. Bae et al. [1] studied edge-disjoint Hamiltonian cycles in k-ary n-cubes and hypercubes. Then, Barden et al. [2] constructed the maximum number of edge-disjoint spanning trees in a hypercube. Petrovic and Thomassen [15] characterized the number of edge-disjoint Hamiltonian cycles in hypertournaments. Hung presented how to construct two edge-disjoint Hamiltonian cycles in locally twisted cubes [7], augmented cubes [8], twisted cubes [10], transposition networks, and hypercube-like networks [9], respectively. In [9], Hung designed a recursive algorithm to construct two edge-disjoint Hamiltonian cycles in CQ_n. In this paper, we provide a parallel algorithm to construct two edge-disjoint Hamiltonian cycles in CQ_n with n ≥ 4. Each vertex of CQ_n can simultaneously run this algorithm to know which two edges were used in Hamiltonian cycles 1 and 2, respectively. The recursive algorithm [9] can be adopted by one vertex to constructs two Hamiltonian cycles and this vertex must transfer this message to all other vertices. However, according to our algorithm, each vertex can calculate to get the message, which is more helpful for implementation.

The rest of the paper is organized as follows: In Sect. 2, the structure of crossed cubes is introduced and some notations are given. Section 3 presented two edge-disjoint Hamiltonian cycles in CQ₄. Based on this result, we further show a parallel algorithm to construct two edge-disjoint Hamiltonian cycles in CQ_n with n ≥ 4. Finally, Sect. 4 is the concluding remarks of this paper.

2 Preliminaries

Interconnection networks are usually modeled as undirected simple graphs G = (V, E), where the vertex set V (=V(G)) and the edge set E (=E(G)) represent the set of processing units and the set of communication links between nodes, respectively. The neighborhood of a vertex v in a graph G, denoted by N(v), is the set of vertices adjacent to v in G. A cycle C_k of length k in G, denoted by v₀ − v₁ − v₂ − … − v_k−2 − v_k-1 − v₀, is a sequence (v₀, v₁, v₂, …, v_k−1, v₀) of nodes such that (v_k−1, v₀) ∈ E and (v_i, v_i+1) ∈ E for 0 ≤ i ≤ k − 2.

Now, we introduce crossed cubes. A vertex of the n-dimensional crossed cube CQ_n is represented by a binary string of length n. A binary string b of length n is denoted by b_n−1b_n−2 ······ b₁b₀, where b_n−1 is the most significant bit. Suppose that G is a labeled graph whose vertices are associated with distinct binary strings, and let G^x be the graph obtained from G by prefixing the binary string on every node with x. Two binary strings x = x₁x₀ and y = y₁y₀ are pair-related, denoted x–y, if and only if (x, ∈ y{(00, 00), (10, 10), (01, 11), (11, 01)}. In [5], Efe introduced the notion of pair-related to obtain that the diameter of CQ_n is only about one half of the diameter of Q_n.

Definition 1

(Efe [5].) The n-dimensional crossed cube CQ_n is the labeled graph with the following recursive fashion:

1) CQ₁ is the complete graph on two vertices with labels 0 and 1.

2) For n ≥2, CQ_n is composed of two subcubes CQ ⁰_n−1 and CQ ¹_n−1 such that two vertices x = 0x_n−2······x₁x₀ ∈ V(CQ ⁰_n−1 ) and y = 1y_n−2······y₁y₀ ∈ V(CQ ¹_n−1 ) are joined by an edge if and only if

• (i) x_n−2= y_n−2 if n is even, and

• (ii) x_2i+1x_2i–y_2i+1y_2i for 0 ≤ i < $\left\lfloor {(n - 1)/2} \right\rfloor$,

where x and y are called the (n − 1)-neighbors to each other, and denote as N_n−1(x) = y or N_n−1(y) = x.

For conciseness, an edge (x, N_j(x)) is denoted as e_j(x), and an e_j-edge is an edge (x, N_j(x)) in G. Obviously, there are 8 e₃-edges, 8 e₂-edges, 8 e₁-edges and 8 e₀-edges in CQ₄. For example, Fig. 1 shows a 4-dimensional crossed cube CQ₄. A CQ₄ is composed of two subcubes CQ ⁰₃ (the left half in Fig. 1) and CQ ¹₃ (the right half in Fig. 1). According to Definition 1 and the notion of pair-related, there exists an e₃-edge connecting vertices 0000 and 1000, and so on. In this paper, sometimes the labels of vertices are changed to their decimal.

Fig. 1.

A 4-dimensional crossed cube CQ₄.

3 Main Results

3.1 Two Edge-Disjoint Hamiltonian Cycles in CQ₄

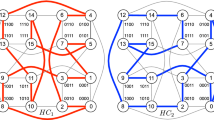
Hung [9] provided two edge-disjoint Hamiltonian cycles in CQ₄. The first cycle C₁₆ is equal to 0100–0000–1000–1001–1111–1101–0111–0101–0011–0001−1011–1010–0010–0110–1110–1100–0100, and there are 6 e₃-edges, 4 e₂-edges, 4 e₁-edges and 2 e₀-edges in it. Since the cycle adopts a different number of edges in each dimension, the parallel construction algorithm that will be presented in the next section becomes more complicated. Fortunately, we found another set of two edge-disjoint Hamiltonian cycles in CQ₄, and each cycle has the same number of edges in each dimension. We described this result in Proposition 2, and its validness can check by Fig. 2.

Fig. 2.

(a) The first Hamiltonian cycle HC₁ in CQ₄, and (b) the second Hamiltonian cycle HC₂ in CQ₄, where the thick lines indicate the cycle.

Proposition 2.

Let HC₁ = 0000–0010–0110–0100–1100–1101–1011–1010–1110–1111–0101–0111–0001–0011–1001–1000–0000, and HC₂ = 0000–0001–1011–1001–1111–1101–0111–0110–1110–1100–1000–1010–0010–0011–0101–0100–0000. HC₁ and HC₂ form two edge-disjoint Hamiltonian cycles in CQ₄.

3.2 Constructing Two Edge-Disjoint Hamiltonian Cycles in CQ₄

Based on the previous results, we now design an algorithm called Algorithm 2HCBase to construct two edge-disjoint Hamiltonian cycles in CQ₄. Each vertex (processing unit) in CQ₄ calls this algorithm and inputs its label to get which two edges are used in Hamiltonian cycles 1 and 2, respectively.

Algorithm 2HCBase Input: b₃b₂b₁b₀ in B //B : the label of this vertex Output: H₁ and H₂ //H_i : edge set of the i-th Hamiltonian cycle step 1. if b₃ = 0 then H₁ ← {e₁} else H₁ ← {e₀}; step 2. if b₃ = 0 then step 3.      if b₂ = 0 then step 4.         if b₁ xor b₀ = 0 then H₁ ← H₁∪{e₃} else H₁ ← H₁∪{e₂}; step 5.      else step 6.         if b₁ = 0 then H₁ ← H₁∪{e₃} else H₁ ← H₁∪{e₂}; step 7.      end if step 8. else step 9.      if b₂ = 0 then step 10.         if b₁ = 0 then H₁ ← H₁∪{e₃} else H₁ ← H₁∪{e₂}; step 11.      else step 12.         if b₁ xor b₀ = 0 then H₁ ← H₁∪{e₃} else H₁ ← H₁∪{e₂}; step 13.      end if step 14. end if step 15. H₂ ← {e₃, e₂, e₁, e₀} \ H₁;

In Algorithm 2HCBase, each vertex determines which two edges are used in the first Hamiltonian cycles H₁. In step 1, either e₀-edge or e₁-edge will be selected into H₁. Then, it will add e₂-edge or e₃-edge into H₁ according to steps 2 to 14. Finally, the remaining two edges will be adopted in the second Hamiltonian cycle. Since there is no loop in Algorithm 2HCBase, we have the following lemma.

Lemma 3.

The time complexity of Algorithm 2HCBase is O(1).

Lemma 4.

By inputting the label of each vertex into Algorithm 2HCBase, we can obtain 2 cycles, which form two edge-disjoint Hamiltonian cycles in CQ₄.

Proof.

According to step 1 in the algorithm, each vertex selects either e₀-edge or e₁-edge into H₁ by b₀. Then, we provide the decision tree shown in Fig. 3 to illustrate steps 2 through 14 in the algorithm. The two edges selected for each vertex can be checked by Fig. 2. □

Fig. 3.

A decision tree to illustrate steps 2 through 14 in the Algorithm 2HCBase, where v_i represents the vertex i in CQ₄.

3.3 Constructing Two Edge-Disjoint Hamiltonian Cycles in CQ_n for n ≥ 5

We all know that CQ_n+1 is composed of CQ ⁰_n and CQ ¹_n . As described in the previous subsection, there exist two edge-disjoint Hamiltonian cycles in CQ₄. The construction method of Hamiltonian cycle in CQ_n+1 is as follows. First, we have the Hamiltonian cycle HC_A in CQ ⁰_n and the Hamiltonian cycle HC_B in CQ ¹_n . Second, remove an edge in HC_A (respectively, HC_B) to get the Hamiltonian path HP_A (respectively, HP_B). Third, connect one end vertex of HP_A and one end vertex of HP_B with an e_n-edge. Finally, connect the other end vertex of HP_A and the other end vertex of HP_B to obtain a Hamiltonian cycle in CQ_n+1. Figure 4 illustrates the construction of two such edge-disjoint Hamiltonian cycles in CQ_n+1. Base on this method, we design Algorithm 2HC as shown below.

Fig. 4.

The construction of two edge-disjoint Hamiltonian cycles in CQ_n+1 while n ≥ 4, where thin red lines (respectively, thick blue lines) indicate the first (respectively, the second) Hamiltonian cycle.

Algorithm 2HC Input: B(= b_n−1b_n−2······b₁b₀) and n //B : the label of this vertex, n : the dimension Output: HC₁ and HC₂ //HC_i : edge set of the i-th Hamiltonian cycle step 1. By calling Algorithm 2HCBase, HC₁ ← H₁ and HC₂ ← H₂; step 2. if b₂ = 0 and b₁ = 0 and b₀ = 0 then step 3.        flag ← 1 step 4.        for i = 3 to n – 3 do step 5.          if b_i = 1 then step 6.             HC₁ ← HC₁ \ {e₃}∪{e_i+1}; flag ← 0; break for; step 7.          end if step 8.        end for step 9.        if flag = 1 then HC₁ ← HC₁ \ {e₃}∪{e_n-1}; step 10. end if //end if at step 2 step 11. if b₂ = 0 and b₁ = 1 and b₀ = 0 then step 12.        flag ← 1 step 13.        for i = 3 to n – 3 do step 14.             if b_i = 1 then step 15.             HC₂ ← HC₂ \ {e₂}∪{e_i+1}; flag ← 0; break for; step 16.             end if step 17.        end for step 18.        if flag = 1 then HC₂ ← HC₂ \ {e₂}∪{e_n-1}; step 19. end if //end if at step 11

In Algorithm 2HC, each vertex will call Algorithm 2HCBase to obtain HC₁ and HC₂, where HC_i is the edge set of the i-th Hamiltonian cycle. In steps 2 to 10, if this vertex is one end vertex of the Hamiltonian path, it will modify its HC₁. For example, in CQ₆, vertex 000000 obtains HC₁ = {e₁, e₃} by call Algorithm 2HCBase. Since vertex 000000 is one end vertex of the Hamiltonian path, HC₁ = {e₁, e₃} \ {e₃}  ∪ {e₅}. By the same way, in steps 11 to 19, if this vertex is one end vertex of Hamiltonian path, it will modify its HC₂. For example, in CQ₆, vertex 000010 obtains HC₂ = {e₁, e₂} by call Algorithm 2HCBase. Since vertex 000010 is one end vertex of the Hamiltonian path, HC₂ = {e₁, e₂} \ {e₂} ∪ {e₅}. According to Lemma 3 and steps 4, 13 in Algorithm 2HC, we have the following lemma.

Lemma 5.

The time complexity of Algorithm 2HC is O(n).

Theorem 6.

By inputting the label of each vertex into Algorithm 2HC, we can obtain 2 cycles, which form two edge-disjoint Hamiltonian cycles in CQ_n with n ≥ 4 in O(n2ⁿ) time. In particular, it can be parallelized on CQ_n to run in O(n) time.

Proof.

Each vertex of CQ_n can simultaneously run Algorithm 2HC to know which two edges were used in Hamiltonian cycles 1 and 2, respectively. By lemma 5, it can be parallelized on CQ_n to run in O(n) time.

Without loss of generality, we consider vertex 0 to be the starting vertex in CQ_n. By Algorithm 2HC, vertex 0 obtains two edges used in the Hamiltonian cycle. With the dimension of the edge, we can obtain the next vertex of the Hamiltonian cycle. In the same way, the vertex sequence of the Hamiltonian cycle can be get. Since there are 2ⁿ vertices in CQ_n, two edge-disjoint Hamiltonian cycles in CQ_n can be obtained in O(n2ⁿ) time. □

For the convenience of checking the correctness of all results, we provide an interactive verification at the website [14]. It shows the usefulness and efficiency of our algorithms in practical settings.

4 Concluding Remarks

In this paper, we first present two edge-disjoint Hamiltonian cycles in CQ₄, and each cycle has the same number of edges in each dimension. Then, we provide an O(n) time algorithm for each vertex in CQ_n to determine which two edges were used in Hamiltonian cycles 1 and 2, respectively. It is interesting to see if there are three edge-disjoint Hamiltonian cycles in CQ_n for n ≥ 6. So far it is still an open problem.