Abstract
Over the last few years, there has been a surge of new cryptographic results, including laconic oblivious transfer [13, 16], (anonymous/ hierarchical) identity-based encryption [9], trapdoor functions [19, 20], chosen-ciphertext security transformations [32, 33], designated-verifier zero-knowledge proofs [30, 34, 37], due to a beautiful framework recently introduced in the works of Cho et al. [13], and Döttling and Garg [14]. The primitive of one-way function with encryption (OWFE) [19, 20] and its relatives (chameleon encryption, one-time signatures with encryption, hinting PRGs, trapdoor hash encryption, batch encryption) [9, 14, 16, 17, 33] have been a centerpiece in all these results.
While there exist multiple realizations of OWFE (and its relatives) from a variety of assumptions such as CDH, Factoring, and LWE, all such constructions fall under the same general “missing block” framework [13, 14]. Although this framework has been instrumental in opening up a new pathway towards various cryptographic functionalities via the abstraction of OWFE (and its relatives), it has been accompanied by undesirable inefficiencies that might inhibit a much wider adoption in many practical scenarios. Motivated by the surging importance of the OWFE abstraction (and its relatives), a natural question to ask is whether the existing approaches can be diversified to not only obtain more constructions from different assumptions, but also in developing newer frameworks. We believe answering this question will eventually lead to important and previously unexplored performance trade-offs in the overarching applications of this novel cryptographic paradigm.
In this work, we propose a new accumulation-style framework for building a new class of OWFE as well as hinting PRG constructions with a special focus on achieving shorter ciphertext size and shorter public parameter size (respectively). Such performance improvements parlay into shorter parameters in their corresponding applications. Briefly, we explore the following performance trade-offs—(1) for OWFE, our constructions outperform in terms of ciphertext size as well as encryption time, but this comes at the cost of larger evaluation and setup times, (2) for hinting PRGs, our constructions provide a rather dramatic trade-off between evaluation time versus parameter size, with our construction leading to significantly shorter public parameter size. The trade-off enabled by our hinting PRG construction also leads to interesting implications in the CPA-to-CCA transformation provided in [33]. We also provide concrete performance measurements for our constructions and compare them with existing approaches. We believe highlighting such trade-offs will lead to a wider adoption of these abstractions in a practical sense.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
A major goal in cryptography is to study cryptographic primitives that could be used for securely implementing useful functionalities as well as lead to interesting applications. Significant effort in cryptographic research is geared towards diversifying existing frameworks and constructions for realizing such primitives to improve efficiency as well as obtain more constructions from a wider set of well-studied assumptions. Over the last few years there has been a surge of new constructions [1, 2, 9, 14,15,16,17, 19,20,21,22, 24,25,26, 30, 32,33,34, 37] due to a beautiful framework recently introduced in the works of Cho et al. [13], and Döttling and Garg [14]. This new wave of cryptographic results, including laconic oblivious transfer [13, 16], (anonymous/hierarchical) identity-based encryption [9], trapdoor functions [19, 20], chosen-ciphertext security transformations [32, 33], designated-verifier zero-knowledge proofs [30, 34, 37], registration-based encryption [21, 22] has been propelled by the primitive of one-way function with encryption (OWFE) [19, 20] and its relatives (chameleon encryption, one-time signatures with encryption, hinting PRGs, trapdoor hash encryption, batch encryption) [9, 14, 16, 17, 33] .
A one-way function with encryption scheme extends the notion of one-way functions to allow a special form of encryption. During setup one samples public parameters \(\mathsf {pp}\) that fixes an underlying one-way function \(f = f_{\mathsf {pp}}\). In an OWFE scheme, the encryption procedure is abstracted out into two components—algorithms \(E_1, E_2\) which work as follows. Both \(E_1\) and \(E_2\) share the same random coins \(\rho \), and take as inputs a value y (that lies in the image space of f), an index-bit pair (i, b), and parameters \(\mathsf {pp}\). Algorithm \(E_1\) is used to compute the “ciphertext” \(\mathsf {ct}\), whereas \(E_2\) computes the encrypted KEM key k. The decryption algorithm D on input a ciphertext \(\mathsf {ct}\), pre-image string x, and parameters \(\mathsf {pp}\), outputs a decrypted KEM key \(k'\). For correctness it is important that if the string x is such that \(y = f_{\mathsf {pp}}(x)\) and \(x_i = b\), then the KEM keys should match, i.e., \(k' = k\). While for security, other than the unpredictability of the OWF f, it is required that the ciphertext does not leak the KEM key trivially. That is, given an input x, parameters \(\mathsf {pp}\), and a ciphertext \(\mathsf {ct}\), the associated KEM key k must be indistinguishable from random as long as the encryption is performed for some value \(y = f_{\mathsf {pp}}(x)\) and any index-bit pair of the form \((i, 1 - x_i)\).
Intuitively, an OWFE scheme is simply a one-way function f equipped with matching encryption-decryption procedures such that encryption allows to encrypt messages with respect to an OWF output string y and a pre-image bit (i, b), while decryption requires a pre-image x such that \(f(x) = y\) and \(x_i = b\).
The “Missing Block” Framework. While there exist multiple realizations of OWFE (and its relatives) from a variety of assumptions such as CDH, Factoring, and LWE, all such constructions fall under the same general “missing block” framework [13, 14]. To illustrate the aforementioned framework we sketch a DDH-based variant of the OWFE construction provided by Garg and Hajiabadi [20]. The public parameters consists of 2n randomly sampled group generators \(\left\{ g_{i, b}\right\} _{(i, b) \in [n] \times \{0,1\}}\), where n is the input length of the OWF. The function output is computed by performing subset-product on the public parameters, where the subset selection is done as per the input bits. Concretely, on an input \(x \in \{0, 1\}^{n}\), the output is \(f(x) = \prod _i g_{i, x_i}\). The ciphertext structurally looks like the public parameters, that is it also consists of 2n group elements \(\left\{ c_{i, b}\right\} _{i, b}\). Here to encrypt to pre-image bit \((i^{*}, b^{*})\) under randomness \(\rho \), the encryption algorithm \(E_1\) simply sets \(c_{i, b} = g_{i, b}^\rho \) for all \((i, b) \ne (i^{*}, 1 - b^{*})\), with the \((i^{*}, 1 - b^{*})^{th}\) term not being set (i.e., \(c_{i^{*}, 1 - b^{*}} =\ \perp \)). Pictorially, this can be represented as follows (where \(i^{*}= 2\) and \(b^{*}= 0\)):

The KEM key is simply computed by the encryptor as \(y^\rho \), where y is the output of the OWF. The decryptor on the other hand does not know the randomness \(\rho \), thus given the ciphertext \(\mathsf {ct}\) and a valid pre-image x, it computes the subset-product on \(\mathsf {ct}\) (followed by applying the hardcore predicate), where the subset selection is done as per x. That is, decryptor computes the key as \(\prod _i c_{i, x_i}\).
This notion of not setting up the \((i^{*}, 1 - b^{*})^{th}\) term in the ciphertext is what we refer to as adding a “missing block”. The intuition behind this is that the ciphertext should only be decryptable using pre-images x such that \(x_{i^{*}} = b^{*}\), thus the ciphertext component corresponding to the pre-image bit \((i^{*}, 1 - b^{*})\) can be omitted. Here the omission of the \((i^{*}, 1 - b^{*})^{th}\) block is very crucial in proving the security of encryption.
Limitations of the Framework. Although the “missing block” framework has been instrumental in opening up a new pathway towards various cryptographic functionalities via the abstraction of OWFE (and its relatives), it has been accompanied with undesirable inefficiencies that have led to large system parameters in most of the applications. In particular, the OWFE described above in this framework leads to large “ciphertexts” where the size grows linearly with the input length n of the OWF. Now this inefficiency gets amplified differently in each of its applications. For instance, large OWFE ciphertexts lead to large public parameters of a trapdoor function (/deterministic encryption) [19, 20], since the public parameters as per those transformations consist of a polynomial number of OWFE ciphertexts which themselves grow linearly with n. Similar situations arise when we look at a related primitive called Hinting PRG (introduced by Koppula and Waters [33]), where the existing constructions via the “missing block” framework leads to much worse public parameters, and the performance overhead gets significantly amplified if we look at its application to chosen-ciphertext security transformations [33].Footnote 1
Motivated by the surging importance of the abstraction of one-way function with encryption and its relatives, a natural question to ask is whether the existing approaches can be diversified to not only obtain more constructions from different assumptions, but also in developing newer frameworks. We believe answering this question will eventually lead to important and previously unexplored performance trade-offs in the overarching applications of this novel cryptographic paradigm.
1.1 Our Approach
In this work, we develop a new framework for building a new class of one-way function with encryption (as well as hinting PRG) constructions with a special focus on achieving shorter ciphertext size (and shorter public parameter size, respectively), which will parlay into shorter parameters in their corresponding applications.Footnote 2
Concretely, we explore the following performance trade-offs. For OWFE, our constructions based on this new framework outperform the existing ones in terms of ciphertext size as well as encryption time, but this comes at the cost of larger evaluation and setup times. In terms of applications of OWFE to deterministic encryption, this trade-off translates to a scheme with much smaller public parameters and setup time, but larger encryption/decryption times. For hinting PRGs, our constructions provide a rather dramatic trade-off between evaluation time versus parameter size compared to prior schemes, with our construction leading to significantly shorter public parameter size. In terms of applications of hinting PRG to chosen-ciphertext security transformations, the trade-off between public parameter size and evaluation time in the hinting PRG constructions carries forward to a trade-off between encryption key/ciphertext sizes and encryption/decryption times in the resultant CCA-secure construction. Next, we describe the main ideas behind our constructions, and later we give some concrete performance metrics.
OWF with Encryption from \(\varPhi \)-Hiding Assumption. We begin by sketching our \(\varPhi \)-Hiding based construction and security proof. Recall that the the \(\varPhi \)-Hiding assumption states that given an RSA modulus N and a prime e, no polynomial time adversary can distinguish whether e divides \(\phi (N)\) or not. Our construction is summarized as follows:
-
The public parameters \(\mathsf {pp}\) of our OWFE scheme consist of an RSA modulus N, n pairs of \(\lambda \)-bit primes \(\left\{ e_{i,b}\right\} _{(i, b) \in [n] \times \{0,1\}}\), and a generator \(g \in \mathbb {Z}_N^*\). (Here n is the input length.)
-
For any input \(x \in \{0,1\}^n\), the one-way function \(f_{\mathsf {pp}}(x)\) is computed as \(g^{H(x) \cdot \prod _i e_{i, x_i}} (\text {mod }N)\), where H is a pairwise independent hash function sampled during setup.
-
The encryption algorithm \(E_1\) on input a pre-image bit \((i^{*}, b^{*})\) and randomness \(\rho \), outputs ciphertext as \(\mathsf {ct}= g^{\rho \cdot e_{i^{*}, b^{*}}} (\text {mod }N)\).Footnote 3 The corresponding KEM key is set as \(k = y^\rho (\text {mod }N)\), where y is the output of the OWF.
-
Lastly, the decryption procedure given a ciphertext \(\mathsf {ct}\) and a pre-image x such that \(f_{\mathsf {pp}}(x) = y\) and \(x_{i^{*}} = b^{*}\), computes the key as \(k' = \mathsf {ct}^{\prod _{i \ne i^{*}} e_{i, x_i}} (\text {mod }N)\). Next, we briefly sketch the main arguments behind the security of this construction.
For security, we will need to show (1) that the function is one way, (2) that encryption security holds and (3) that an additional smoothness property holds. We will sketch the arguments for the first two here. The final smoothness property is only needed for some applications. This involves a more nuanced number theory to prove which we defer to the main body.
The one-wayness argument proceeds as follows—suppose an adversary finds a collision \(x \ne x'\), i.e. \(f_{\mathsf {pp}}(x) = f_{\mathsf {pp}}(x')\), then a reduction algorithm can sample the \(\lambda \)-bit primes in such a way that, as long as n is larger than \(\log N + \lambda \), it can break RSA assumption for one of the primes sampled as part of the public parameters.
For proving security of encryption we need to slightly modify the construction wherein we need to apply an extractor on the KEM key to prove it looks indistinguishable from random, that is \(k = \mathsf {Ext}(\mathfrak {s}, y^\rho )\) where \(\mathsf {Ext}\) is a strong seeded extractor and seed \(\mathfrak {s}\) is sampled during setup. Recall that security of encryption requires that for any index-bit pair \((i^{*}, b^{*})\) and input x such that \(x_{i^{*}} \ne b^{*}\), given a ciphertext \(\mathsf {ct}= E_1(\mathsf {pp}, (i^{*}, b^{*}); \rho )\) the associated KEM key \(k = E_2(\mathsf {pp}, f_{\mathsf {pp}}(x), (i^{*}, b^{*}); \rho )\) must be indistinguishable from random.
The idea behind proving the same for the above construction is the following—a ciphertext looks like \(\mathsf {ct}= g^{\rho \cdot e_{i^{*}, b^{*}}}\) whereas the key is computed as \(k = \mathsf {Ext}(\mathfrak {s}, g^{\rho \cdot \prod _{i} e_{i, x_i}})\). Since \(b^{*}\ne x_{i^{*}}\), thus the key can be re-written as \(k = \mathsf {Ext}(\mathfrak {s}, (\mathsf {ct}^{\prod _{i} e_{i, x_i}})^{e_{i^{*}, b^{*}}^{-1}})\). Now under the \(\varPhi \)-hiding assumption, we can argue that an adversary can not distinguish between the cases where \(e_{i^{*}, b^{*}}\) is co-prime with respect to \(\phi (N)\), and when \(e_{i^{*}, b^{*}}\) divides \(\phi (N)\). Note that in the latter case, there are \(e_{i^{*}, b^{*}}\) many distinct \(e_{i^{*}, b^{*}}^{th}\) roots of \(\mathsf {ct}^{\prod _{i} e_{i, x_i}}\). Thus, by strong extractor guarantee we can conclude that key k looks uniformly random to the adversary as the underlying source has large (\(\lambda \) bits of) min-entropy.
Comparing with DDH-Based Constructions. Comparing the asymptotic efficiency of our \(\varPhi \)-Hiding based OWFE construction with the existing DDH-based constructions, we observe the following: (1) the size of the public parameters grows linearly with the input length n in both constructions, (2) both OWF evaluation and decryption operations require O(n) group operations and O(n) exponentiations (with \(\lambda \)-bit exponents) respectively, (3) for the \(\varPhi \)-hiding based construction, both \(E_1\) and \(E_2\) algorithms perform single exponentiation, and outputs a ciphertext and key containing just one group element; whereas for DDH-based construction, the \(E_1\) algorithm performs O(n) exponentiations and outputs a ciphertext containing O(n) group elements.
We implemented the above construction and observed that, at 128-bit security level, our \(\varPhi \)-hiding based construction has \(\sim \)80x shorter ciphertext size over the existing DDH-based construction [20]. Also, the \(E_1\) algorithm of our \(\varPhi \)-hiding based construction is \(\sim \)14x faster than the DDH baseline. A detailed efficiency comparison for other security levels is discussed in Sect. 6.1.
Hinting PRGs from \(\varPhi \)-Hiding Assumption. We also provide a hinting PRG [33] construction based on \(\varPhi \)-hiding that leads to similar performance trade-offs. Let us briefly recall the notion of hinting PRGs. It consists of two algorithms—\(\mathsf {Setup}\) and \(\mathsf {Eval}\), where the setup algorithm generates the public parameters \(\mathsf {pp}\), and the PRG evaluation algorithm takes as input the parameters \(\mathsf {pp}\), a seed \(s \in \{0, 1\}^{n}\) and a block index \(i \in \left\{ 0, 1, \ldots , n\right\} \). The Hinting PRG security requirement is that for a randomly choosen seed \(s \in \{0, 1\}^{n}\), the following two distributions over \(\left\{ r_{i, b}\right\} _{(i, b) \in [n] \times \{0,1\}}\) are indistinguishable: in the first distribution, \(r_{i, s_i} = \mathsf {Eval}(\mathsf {pp}, s, i)\) and \(r_{i, 1 - s_i}\) is sampled uniformly at random for every i; whereas in the second distribution, all \(r_{i, b}\) terms are sampled uniformly at random.
Our hinting PRG construction is based on our OWFE construction, where the setup algorithm is identical, that is the public parameters \(\mathsf {pp}\) consist of an RSA modulus N, n pairs of \(\lambda \)-bit primes \(\left\{ e_{i,b}\right\} _{(i, b) \in [n] \times \{0,1\}}\), a generator \(g \in \mathbb {Z}_N^*\), and a pairwise independent hash H. And, the evaluation algorithm also bears strong resemblance with the one-way function f described previously. Concretely, the \({i^{*}}^{th}\) block of the PRG output, i.e. \(\mathsf {Eval}(\mathsf {pp}, s, i^{*})\), is computed as \(g^{H(s) \cdot \prod _{i \ne i^{*}} e_{i, s_i}} (\text {mod }N)\). Proving security of this construction follows in a similar line to our OWFE construction. More details on this are provided later in full version of the paper.
Comparing with DDH-Based Constructions. Comparing the asymptotic efficiency of our \(\varPhi \)-Hiding based hinting PRG construction with the existing DDH-based constructions, we observe the following: (1) the public parameters consists of 2n (\(\lambda \)-bit) prime exponents along with the RSA modulus, extractor seed, group generator, and a hash key; whereas in the DDH-based constructions, it contains \(O(n^2)\) group elements, (2) for evaluating a single hinting PRG block, the evaluator needs to perform O(n) exponentiations in our new construction; whereas in the DDH case it performs O(n) group operations. Additionally, using an elegant Dynamic Programming style algorithm, we can reduce the number of exponentiation operations needed per block to grow only logarithmically in n. The intuition behind such an improvement is that we show how to re-use various intermediate exponentiations obtained during a single hinting PRG block evaluation for accelerating the PRG evaluation for other blocks.
We implemented the above construction and observed that, at 128-bit security level, our \(\varPhi \)-hiding based construction has \(\sim \)80x shorter ciphertext size over the existing DDH-based construction [20]. Also, the \(E_1\) algorithm of our \(\varPhi \)-hiding based construction is \(\sim \)14x faster than the DDH baseline. A detailed efficiency comparison for other security levels is discussed in full version of the paper.
Limitations of \(\varPhi \)-Hiding Based Constructions. A quick glance shows that these new constructions lead to much shorter ciphertext size (in the case of OWFE) and public parameters (in the case of hinting PRGs), therefore they will lead to better parameters in their corresponding applications such as deterministic encryption [19] and chosen-ciphertext security transformations [33]. However, looking more closely we observe that our \(\varPhi \)-hiding based construction has an undesirable consequence which is the hinting PRG seed length (or equivalently input length for OWF) n is much larger for our \(\varPhi \)-hiding based scheme when compared with its DDH counterpart. This is due to the fact because of number field sieve attacks, the recommended RSA modulus length (and thereby the input/seed length n) increases super linearly with target security level for the \(\varPhi \)-based construction. While the recommended field size (and thereby the input/seed length n) will increase only linearly for the elliptic curve DDH-based constructions.
Fortunately, the notion of accumulators has been well studied in prime order group setting [3, 10, 12, 36] as well, thus this gives us a different type of number theoretic accumulator. Pivoting to such accumulators, we show how to achieve performance improvements similar to that in the \(\varPhi \)-hiding setting while keeping the input/seed length n close to that in their existing counterparts. Next, we provide our OWFE construction which uses bilinear maps in the prime order group setting.
OWF with Encryption from DBDHI. Let us start by recalling the Decisional Bilinear Diffie-Hellman Inversion (DBDHI) assumption [7]. The strength of the assumption is characterized by a parameter \(\ell \), and it states that given a sequence of group elements as follows—\((g, g^\alpha , g^{\alpha ^2}, \ldots , g^{\alpha ^\ell })\), where g is a random group generator and \(\alpha \) is a randomly chosen non-zero exponent, no PPT adversary should be able to distinguish \(e(g, g)^{1/\alpha }\) from a random element in the target group. Below we describe our OWFE construction in which we directly include the sequence of elements as described above as part of the public parameters.
Concretely, the public parameters \(\mathsf {pp}\) consist of \(n + 1\) group elements \((g, g^{\alpha }, \ldots , g^{\alpha ^n})\) for a random exponent \(\alpha \) and group generator g, and a pairwise independent hash H. (Here n is the input length.) Given an input \(x \in \{0,1\}^n\), the one-way function \(f_{\mathsf {pp}}(x)\) is computed in two stages. First, the evaluator symbolically evaluates (i.e. simplifies) the polynomial \(p(z) = H(x) \cdot \prod _i (z + 2i + x_i)\). Let \(p(z) = \sum _{j = 0}^n c_j z^j\) be the evaluated polynomial. Next, the evaluator sets the output of the OWF as \(\prod _j (g^{\alpha ^j})^{c_j}\). The encryption algorithm \(E_1\) on input a pre-image bit \((i^{*}, b^{*})\) and randomness \(\rho \), outputs ciphertext as \(\mathsf {ct}= (g^{\alpha + 2 i^{*}+ b^{*}})^\rho \).Footnote 4 The corresponding KEM key is set as \(k = e(g^\rho , y)\), where y is the output of the OWF. Lastly, the decryption procedure given a ciphertext \(\mathsf {ct}\) and a pre-image x such that \(f_{\mathsf {pp}}(x) = y\) and \(x_{i^{*}} = b^{*}\), also takes a two step approach where first it symbolically evaluates the polynomial \(p'(z) = H(x) \cdot \prod _{i \ne i^{*}} (z + 2i + x_i)\). Let \(p'(z) = \sum _{j = 0}^{n - 1} c_j' z^j\) be the evaluated polynomial. Lastly, the decryptor computes the key as \(k' = e(\mathsf {ct}, \prod _j (g^{\alpha ^j})^{c_j'})\).
The proof of one-wayness is similar to that in the case of \(\varPhi \)-hiding where if an adversary finds a collision \(x \ne x'\), i.e. \(f_{\mathsf {pp}}(x) = f_{\mathsf {pp}}(x')\), then a reduction algorithm can set the public parameters appropriately such that, as long as n is large enough, it can be used to not only distinguish the DBDHI challenge but also directly compute the DBDHI challenge. The proof of encryption security is also quite similar, where the main idea can be described as follows: the ciphertext looks like \(\mathsf {ct}= (g^{\alpha + 2 i^{*}+ b^{*}})^\rho \) whereas the key is computed as \(k = e(g^\rho , \prod _j (g^{\alpha ^j})^{c_j})\). Whenever \(b^{*}\ne x_{i^{*}}\), then the key can be re-written such that it is of the form \(k = e(g, g)^{c'/\beta } \cdot e(g, \prod _j (g^{\beta ^j})^{c_j'})\) for some constants \(c', c'_1, \ldots , c'_{n - 1}\), and where \(\beta \) linearly depends on \(\alpha \). By careful analysis, we can reduce this to the DBDHI assumption. Lastly, the proof of smoothness for this construction is significantly simpler than that of its \(\varPhi \)-hiding based counterpart. This is primarily because in this case, we can directly prove that the function \(H(x) \cdot \prod _i (\alpha + 2i + x_i) (\text {mod }p)\), where p is the order of the group is an (almost) 2-universal hash function, therefore by applying LHL, we can argue smoothness of the OWF. More details are provided later in Sect. 5.
We implemented the above construction and observed that, at 128-bit security level, our DBDHI-based construction has \(\sim \)340x shorter ciphertext size over the existing DDH-based construction [20] and \(\sim \)4x over our \(\varPhi \)-hiding based construction. Also, the \(E_1\) algorithm of our DBDHI-based construction is \(\sim \)300x faster than the DDH baseline and \(\sim \)22x faster than our \(\varPhi \)-hiding construction. Note that even though \(\varPhi \)-hiding and DBDHI-based constructions have nearly identical asymptotic complexity, DBDHI-based construction still performs better as the recommended group size for the elliptic curve groups is smaller than that for RSA.
Hinting PRGs from DDHI and OWFE Without Bilinear Maps. Again to emphasize the general applicability of our accumulation-style framework, we provide a hinting PRG construction based on the DDHI assumption as well. The translation from OWFE to hinting PRG is done analogous to that for \(\varPhi \)-hiding based constructions, except in our hinting PRG construction we do not require the bilinear map functionality. Briefly, this is because (unlike OWFE schemes) hinting PRGs do not provide any decryption-like functionality, and for evaluating the hinting PRG, standard group operations are sufficient. Our construction is described in detail later in full version of the paper. We also point out that in full version of the paper we provide an OWFE construction in the prime order group setting without using bilinear maps, but the caveat is that it does not lead to better performance when compared with existing DDH-based constructions.
We implemented the above schemes and observed that, at 128-bit security level, the setup algorithm of our \(\varPhi \)-hiding and DDHI-based HPRGs are \(\sim \)1.35x and \(\sim \)200x respectively faster than the DDH baseline [33]. Our constructions also have \(\sim \)105x and \(\sim \)2100x shorter public parameters respectively than DDH baseline. However, our schemes have less efficient \(\mathsf {Eval}\) algorithm, and thereby offer a noticeable trade-off between efficiency of \(\mathsf {Setup}\) and \(\mathsf {Enc}\) algorithm when used in chosen-ciphertext security transformation of [33]. More details are provided later in full version of the paper.
Recent Work in Trapdoor Functions. One of the applications of our result is in constructing trapdoor functions (TDFs) with smaller parameter sizes. Building on the work of [20], Garg, Gay, and Hajiabadi [19] show how OWF with encryption gives trapdoor functions with image size linear in the input size. However, their construction requires a quadratic number of group elements. Plugging in either our bilinear map or \(\phi \)-hiding constructions will reduce the public parameter size to O(n) group elements. (Since our OWFE schemes also satisfy the smoothness criteria, thus the resulting TDF also leads to a construction of deterministic encryption.)
In a concurrent work, Garg, Hajiabadi, and Ostrovsky [23] using different techniques give new constructions for “trapdoor hash functions” [16] with small public key size. Among other applications, this also gives an injective trapdoor function whose public key contains O(n) group elements. They prove security from the q-power DDH assumption and use other ideas to also reduce the evaluation time. From bilinear maps, however, the work of Boyen and Waters [8] provides TDF constructions secure under the Decisional Bilinear Diffie-Hellman (DBDH) assumption in which the public keys also have only O(n) group elements. Later, [16] presented a TDF construction with \(O(\sqrt{n})\) group elements in the public key using SXDH assumption on bilinear maps.
One interpretation is that the primitive of OWF with encryption can perhaps serve a broader range of applications, but to squeeze out better performance for a particular, more narrow set of applications a more specialized abstraction such as trapdoor hash functions might be more useful. This mirrors our experience with hinting PRGs, where our direct constructions had efficiency benefits. Finally, we emphasize that part of our contribution is to provide concrete experimental performance measurements of our constructions.
Roadmap. We recall the notions of Hinting PRG and OWFE in Sect. 2. We then present number-theoretic techniques introduced in this work in Sect. 3. We then present our OWFE constructions based on \(\varPhi \)-hiding, DBDHI assumptions in Sects. 4 and 5. Finally, we implement our schemes and analyze their performance in Sect. 6. In full version of the paper, we present our OWFE from DDHI assumption, our HPRG constructions based on \(\varPhi \)-hiding and DDHI assumptions, and also describe how to construct Hinting PRG generically from OWFE.
2 Preliminaries
Notations. Let PPT denote probabilistic polynomial-time. We denote the set of all positive integers up to n as \([n] := \left\{ 1, \ldots , n\right\} \). Throughout this paper, unless specified, all polynomials we consider are positive polynomials. For any finite set S, \(x\leftarrow S\) denotes a uniformly random element x from the set S. Similarly, for any distribution \(\mathcal {D}\), \(x \leftarrow \mathcal {D}\) denotes an element x drawn from distribution \(\mathcal {D}\). The distribution \(\mathcal {D}^n\) is used to represent a distribution over vectors of n components, where each component is drawn independently from the distribution \(\mathcal {D}\). We call any distribution on n-length bit strings with minimum entropy k as a (k, n) source.
2.1 One Way Function with Encryption
Here we recall the definition of recyclable one-way function with encryption from [19, 20]. We adapt the definition to a setting where the KEM key is an \(\ell \)-bit string instead of just a single bit. A recyclable \((k, n, \ell )\)-OWFE scheme consists of the PPT algorithms \(K, f, E_1, E_2\) and D with the following syntax.
-
\(K(1^\lambda ) \rightarrow \mathsf {pp}\): Takes the security parameter \(1^\lambda \) and outputs public parameters \(\mathsf {pp}\).
-
\(f(\mathsf {pp}, x) \rightarrow y\): Takes a public parameter \(\mathsf {pp}\) and a preimage \(x \in \{0,1\}^n\), and deterministically outputs y.
-
\(E_1(\mathsf {pp},(i, b); \rho ) \rightarrow \mathsf {ct}\): Takes public parameters \(\mathsf {pp}\), an index \(i \in [n]\), a bit \(b \in \{0,1\}\) and randomness \(\rho \), and outputs a ciphertext \(\mathsf {ct}\).
-
\(E_2(\mathsf {pp}, y, (i, b); \rho ) \rightarrow k\): Takes a public parameter \(\mathsf {pp}\), a value y, an index \(i \in [n]\), a bit \(b \in \{0,1\}\) and randomness \(\rho \in \{0,1\}^r\), and outputs a key \(k \in \{0,1\}^\ell \). Notice that unlike \(E_1\), which does not take y as input, the algorithm \(E_2\) does take y as input.
-
\(D(\mathsf {pp}, \mathsf {ct}, x) \rightarrow k\): Takes a public parameter \(\mathsf {pp}\), a ciphertext \(\mathsf {ct}\), a preimage \(x \in \{0,1\}^n\), and deterministically outputs a key \(k \in \{0,1\}^\ell \).
We require the following properties.
-
Correctness. For security parameter \(\lambda \), for any choice of \(\mathsf {pp}\in K(1^\lambda )\), any index \(i \in [n]\), any preimage \(x \in \{0,1\}^n\) and any randomness value \(\rho \), the following holds: letting \(y := f(\mathsf {pp}, x)\), and \(\mathsf {ct}:= E_1(\mathsf {pp},(i, x_i); \rho )\), we have \(E_2(\mathsf {pp}, y,(i, x_i); \rho ) = D(\mathsf {pp}, \mathsf {ct}, x)\).
Definition 1
((k, n)-One-wayness.). For any PPT adversary \(\mathcal {A}\), there exists a negligible function \(\text {negl}(\cdot )\) such that for all \(\lambda \in \mathbb {N}\), we have
Here, the adversary is constrained to output only a (k, n)-source.
Definition 2
(Security for encryption.). For any PPT adversary \(\mathcal {A}\), there exists a negligible function \(\text {negl}(\cdot )\) such that for all \(\lambda \in \mathbb {N}\), we have
Definition 3
((k, n)-Smoothness.). We say that \((K, f, E_1, E_2, D)\) is (k, n)-smooth if for any PPT adversary \(\mathcal {A}\), there exists a negligible function \(\text {negl}(\cdot )\), such that for all \(\lambda \in \mathbb {N}\), we have
where the distributions \(S_0\) and \(S_1\) output by the adversary \(\mathcal {A}\) are constrained to be (k, n)-sources.
2.2 Hinting PRG
Next, we review the definition of Hinting PRG proposed in [33]. Let \(n(\cdot )\) and \(\ell (\cdot )\) be some polynomials. An \((n,\ell )\)-hinting PRG scheme consists of two PPT algorithms \(\mathsf {Setup}\), \(\mathsf {Eval}\) with the following syntax.
-
\(\mathsf {Setup}(1^\lambda ) \rightarrow (\mathsf {pp}, n)\): The setup algorithm takes as input the security parameter \(\lambda \), and length parameter \(\ell \), and outputs public parameters \(\mathsf {pp}\) and input length \(n = n(\lambda )\).
-
\(\mathsf {Eval}(\mathsf {pp}, s \in \{0,1\}^n, i \in [n] \cup \{0\}) \rightarrow y \in \{0,1\}^\ell \): The evaluation algorithm takes as input the public parameters \(\mathsf {pp}\), an n-bit string s, an index \(i \in [n] \cup \{0\}\) and outputs an \(\ell \) bit string y.
Definition 4
An \((n, \ell )\)-hinting PRG scheme \((\mathsf {Setup}, \mathsf {Eval})\) is said to be secure if for any PPT adversary \(\mathcal {A}\), there exists a negligible function \(\text {negl}(\cdot )\) such that for all \(\lambda \in \mathbb {N}\), the following holds:
3 Hashing and Randomness Extraction Under \(\varPhi \)-Hiding
In this section, we will prove two useful lemmas about universal hashing and randomness extraction under the \(\varPhi \)-hiding assumption. Here we consider special groups defined w.r.t. an RSA modulus N. These lemmas will be crucial in proving the security of our \(\varPhi \)-hiding based constructions later in Sect. 4.
3.1 A New Hashing Lemma
Consider an RSA modulus \(N = p q\) for \(\kappa /2\)-bit primes p, q, and let \(g \in \mathbb {Z}_N^{*}\) be a random element in the multiplicative group \(\mathbb {Z}_N^{*}\). Consider the following family of hash functions which hash an n-bit string x (\(x \in \mathcal {X}= \{0,1\}^n\)) to an element in \(\mathbb {Z}_N\):
Here x is intepreted as an integer for arithmetic operations, and \(x_i\) denotes the \(i^{th}\) bit of x when intepreted as a binary string. Whenever it is clear from context, we will drop the hash key as an explicit input to the function and write either H(x) or \(H_K(x)\) instead of H(K, x) for some hash key \(K = (a, b, \left\{ e_{i, c}\right\} _{i, c})\). Also, throughout we assume that n is sufficiently large, i.e. \(n > \kappa + 2 \lambda \).
Consider any integer T, and let \(T = \prod _{i=1}^t r_i^{k_i}\) be its prime factorization i.e., \(k_i \ge 1\) and \(r_i\)’s are the distinct prime factors arranged in an increasing order. For any integer \(y \in \mathbb {Z}_T\), we define its chinese remainder theorem (CRT) representation to be the vector \((y^{(1)}, y^{(2)}, \cdots , y^{(t)})\), where for each \(i \in [t]\), \(y^{(i)} = y~ \text {mod }r_i^{k_i}\). Note that each integer \(y \in \mathbb {Z}_T\) has distinct CRT representation.
Looking ahead to our HPRG and OWFE constructions based on \(\varPhi \)-hiding assumption, we use the hash function described above. For security, we require that (for a randomly chosen key K and input \(x \leftarrow \mathcal {X}\)) the output distribution of the hash function H(K, x) to be indistinguishable from a distribution with large enough min-entropy while looking independent of the input x. A natural idea would be to use a variant of Leftover Hash Lemma (LHL) to prove such a statement, but since \(e_{i,c}\)’s are randomly sampled primes (and not random exponents), thus the distribution of the exponent \((ax + b) \prod _{i} e_{i, x_i} ~\text {mod }\varPhi (N)\) is not well understood. Due to this, we could not rely only on LHL to prove pseudorandomness of the desired distribution, but instead, show that hash function satisfies the following weaker property which is sufficient for our applications. The technical difficulty here lies in proving that the hash function satisfies this weaker property and utilizing this to prove the security of our HPRG and OWFE constructions.
Theorem 1
Let \(p_i\) denote the \(i^{th}\) prime, i.e. \(p_1 = 2, p_2 = 3, \ldots \), and \(\widetilde{e_i} = \lceil \log _{p_i} N \rceil \). And, let \(f_i\) denote \(p_i^{\widetilde{e_i}}\) for all i.
Assuming the \(\varPhi \)-hiding assumption holds, for every PPT adversary \(\mathcal {A}\), non-negligible function \(\epsilon (\cdot )\), polynomial \(v(\cdot )\), for all \(\lambda , \kappa \in \mathbb {N}\), satisfying \(\kappa \ge 5 \lambda \) and \(\epsilon = \epsilon (\lambda ) > 1/v(\lambda )\), the following holds:

where the experiment  is described in Fig. 1.
is described in Fig. 1.
Proof
Let the prime factorization of \(\phi (N)\) be \(\phi (N) = \prod _i r_i^{k_i}\) for \(i = 1\) to \(\ell _N\), where \(k_i \ge 1\), \(\ell _N\) denotes number of distinct prime factors of \(\phi (N)\), and \(r_i\)’s are the distinct prime factors arranged in an increasing order. The proof is divided into two parts. First, we argue that \((ax + b) \prod _{i} e_{i, x_i} \text { mod } r_j^{k_j}\) is statistically close to random over \(\mathbb {Z}_{r_j^{k_j}}\) for all prime factors of \(\phi (N)\) greater than \(p_{j_\epsilon }\). In the second part of the proof, we show using \(\varPhi \)-hiding that the hash function H could be made lossy on all prime factors of \(\phi (N)\) less than or equal to \(p_{j_\epsilon }\). Thus, the theorem follows. For proving the first part, we employ a tight Leftover Hash Lemma proof. And for the second part, we rely on \(\varPhi \)-hiding to introduce lossiness.
Notation. Here and throughout, for any n-bit string x, we use \(\varvec{\mathrm {e}}_x\) to denote the following product \(\prod _{i \in [n]} e_{i, x_i}\).
Part 1. The statistical argument. Here we show that if we look at the congruent CRT representation of the exponent \((ax + b) \cdot \varvec{\mathrm {e}}_x\) corresponding to prime factors greater \(p_{j_\epsilon }\), then (for a randomly chosen hash key K and input x) they are at most \(\epsilon /3\)-statistically far from an integer that is chosen at random with the constraint that its congruent CRT representation corresponding to prime factors less than or equal to \(p_{j_\epsilon }\) is same as for \((ax + b) \cdot \varvec{\mathrm {e}}_x\). Concretely, we show that following:
Lemma 1
Let \(p_i\) denote the \(i^{th}\) prime, i.e. \(p_1 = 2, p_2 = 3, \ldots \), and \(\widetilde{e_i} = \lceil \log _{p_i} N \rceil \).
For every (possibly unbounded) adversary \(\mathcal {A}\), non-negligible function \(\epsilon (\cdot )\), polynomial \(v(\cdot )\), for all \(\lambda , \kappa \in \mathbb {N}\), satisfying \(\kappa \ge 5 \lambda \) and \(\epsilon = \epsilon (\lambda ) > 1/v(\lambda )\), the following holds:

where the experiment  is described in Fig. 2.
is described in Fig. 2.
Security Game for Lemma 1
Proof
Due to space constraints, we postpone the proof to full version of the paper.
Part 2. The computational argument. Here we show that, using \(\varPhi \)-hiding, the generator g instead of sampling uniformly at random could be sampled as \(g^{\prod _{i = 1}^{j_\epsilon } f_i}\), where \(j_\epsilon \) is the smallest index such that \(p_{j_\epsilon } > (2\sqrt{2} \log N/\epsilon )3\). This removes information about the input x completely. Concretely, we show that following:
Lemma 2
Let \(p_i\) denote the \(i^{th}\) prime, i.e. \(p_1 = 2, p_2 = 3, \ldots \), and \(\widetilde{e_i} = \lceil \log _{p_i} N \rceil \) and let \(f_i\) denote \(p_i^{\widetilde{e_i}}\) for all i. Assuming the \(\varPhi \)-hiding assumption holds, for every PPT adversary \(\mathcal {A}\), non-negligible function \(\epsilon (\cdot )\), polynomial \(v(\cdot )\), for all \(\lambda , \kappa \in \mathbb {N}\), satisfying \(\kappa \ge 5 \lambda \) and \(\epsilon = \epsilon (\lambda ) > 1/v(\lambda )\), there exists a negligible function \(\text {negl}(\cdot )\) such that the following holds,

where the experiment  is described in Fig. 3.
is described in Fig. 3.
Security Game for Lemma 2
Proof
Due to space constraints, we postpone the proof to full version of the paper.
Lastly, by combining Lemmas 1 and 2, we obtain the proof of Theorem 1.
Strengthening the Hash Lemma. In this section, we briefly provide a slight strengthening of the Theorem 1 where we argue that the indistinguishability holds even if the input \(x \in \mathcal {X}\), instead of being sampled uniformly at random, is sampled from any arbitrary distribution with certain min-entropy. Formally, we prove the following.
Theorem 2
Let \(p_i\) denote the \(i^{th}\) prime, i.e. \(p_1 = 2, p_2 = 3, \ldots \), and \(\widetilde{e_i} = \lceil \log _{p_i} N \rceil \). And, let \(f_i\) denote \(p_i^{\widetilde{e_i}}\) for all i.
Assuming the \(\varPhi \)-hiding assumption holds, for every PPT adversary \(\mathcal {A}\), non-negligible function \(\epsilon (\cdot )\), polynomial \(v(\cdot )\), for all \(\lambda , \kappa \in \mathbb {N}\), satisfying \(\kappa \ge 5 \lambda \) and \(\epsilon = \epsilon (\lambda ) > 1/v(\lambda )\), and every (m, n)-source \(\mathcal {S}\) over \(\mathcal {X}\) such that \(n - m = O(\log \lambda )\), the following holds,

where the experiment  is described in Fig. 4.
is described in Fig. 4.
Security experiment for Smooth Hashing Lemma (Theorem 2)
Proof
Due to space constraints, we postpone the proof to full version of the paper.
3.2 \(\varPhi \)-Hiding Based Extractor Lemma
In this section, we prove a useful lemma that will aid in proving the security of our \(\varPhi \)-hiding based constructions later. This has appeared (and implicitly used) in most existing \(\varPhi \)-hiding based works. Here we abstract it out for ease of exposition.
Let \(\mathsf {Ext}: \mathbb {Z}_N\times \mathbb {S} \rightarrow \mathcal {Y}\) be a \((\lambda - 1, \epsilon )\) strong extractor, where \(\epsilon \) is negligible in the parameter \(\lambda \). Informally, the lemmas states that, for every \(\lambda \)-bit prime e, applying extractor on an \(e^{th}\) root of a generator \(g \in \mathbb {Z}_N^{*}\) is indistinguishable from random. Formally, we claim the following:
Lemma 3
Assuming the \(\varPhi \)-hiding assumption holds, then for every admissible stateful PPT adversary \(\mathcal {A}\), there exists a negligible function \(\text {negl}(\cdot )\) such that for all \(\lambda , \kappa \in \mathbb {N}\), such that \(\kappa \ge 5 \lambda \), the following hold,
where \(\mathcal {A}\) is an admissible adversary as long as \(e \not \mid F\).
Proof
Due to space constraints, we postpone the proof to full version of the paper.
4 One-Way Function with Encryption from \(\varPhi \)-Hiding Assumption
In this section, we construct \((k,n,\ell )\)-recyclable One-Way Function with Encryption (OWFE) from Phi-Hiding assumption. The construction assumes \(k \ge 7\lambda \) and \(n - k \le \alpha \log n\) for any fixed constant \(\alpha \). For any parameters \(\lambda , \ell \), let \(\mathsf {Ext}_{\lambda , \ell } : \{0,1\}^\lambda \times \mathcal {S}\rightarrow \{0,1\}^\ell \) be a \((\lambda - 1, \epsilon _\mathsf {Ext})\) strong seeded extractor, where \(\epsilon _\mathsf {Ext}\) is negligible in \(\lambda \).Footnote 5 Let \(p_i\) denote the \(i^{th}\) (smallest) prime, i.e. \(p_1 = 2, p_2 = 3, \ldots \), and \(\widetilde{e_i} = \lceil \log _{p_i} N \rceil \) for all i. And, let \(f_i\) denote \(p_i^{\widetilde{e_i}}\) for all i. The construction proceeds as follows.
-
\(K(1^\lambda )\): On input security parameter \(\lambda \) and length \(\ell \), set RSA modulus length \(\kappa = 5\lambda \), and sample RSA modulus \(N \leftarrow \mathsf {RSA}(\kappa )\). Next, sample a generator \(g \leftarrow \mathbb {Z}_N^*\), 2n (\(\lambda \)-bit) primes \(e_{i,b} \leftarrow \textsc {PRIMES}(\lambda )\) for \((i,b) \in [n] \times \{0,1\}\) and elements \(d_0, d_1 \leftarrow \mathbb {Z}_N\). Then, sample a seed \(\mathfrak {s}\leftarrow \mathcal {S}\) of extractor \(\mathsf {Ext}_{\lambda ,\ell }\) and output public parameters \(\mathsf {pp}= (N, \mathfrak {s}, g, \{e_{i,b}\}_{i,b}, d_0, d_1)\).
-
\(f(\mathsf {pp}, x)\): Let \(\mathsf {pp}= (N, \mathfrak {s}, g, \{e_{i,b}\}_{i,b}, d_0, d_1)\). Output \(y = g^{f_1\cdot f_2\cdot (d_0 x + d_1)}\) \({\prod _i e_{i,x_i}}\; \text {mod }N\).
-
\(E_1(\mathsf {pp}, (i,b); \rho )\): Parse \(\mathsf {pp}\) as \(\mathsf {pp}= (N, \mathfrak {s}, g, \{e_{i,b}\}_{i,b}, d_0, d_1)\). Output ciphertext \(\mathsf {ct}= (g^{\rho \cdot e_{i,b}}\; \text {mod }N, i, b)\).
-
\(E_2(\mathsf {pp}, (y,i,b); \rho )\): Let \(\mathsf {pp}\) be \(\mathsf {pp}= (N, \mathfrak {s}, g, \{e_{i,b}\}_{i,b}, d_0, d_1)\). Compute \(h = y^\rho \;\text {mod }N\) and output \(z = \mathsf {Ext}(h, \mathfrak {s})\).
-
\(D(\mathsf {pp}, \mathsf {ct}, x)\): Let \(\mathsf {pp}= (N, \mathfrak {s}, g, \{e_{i,b}\}_{i,b}, d_0, d_1)\). Parse \(\mathsf {ct}\) as (t, i, b). If \(b = x_i\), compute \(h = t^{f_1\cdot f_2\cdot (d_0x+d_1)\prod _{j \ne i}e_{j, x_j}}\; \text {mod }N\) and output \(\mathsf {Ext}(h, \mathfrak {s})\). Otherwise, output \(\perp \).
Correctness. For any public parameters \(\mathsf {pp}= (N, \mathfrak {s}, g, \{e_{i,b}\}_{i,b}, d_0, d_1)\), any string \(x \in \{0,1\}^n\), any index \(i \in [n]\), any randomness \(\rho \), we have \(D(\mathsf {pp}, E_1(\mathsf {pp}, (i, x_i);\) \(\rho ), x) = g^{\rho f_1\cdot f_2\cdot (d_0x+d_1)\prod _{j}e_{j, x_j}} = f(\mathsf {pp}, x)^\rho = E_2(\mathsf {pp}, (f(\mathsf {pp}, x), i, x_i);\rho )\).
4.1 Security
We now prove the one-wayness, encryption security and smoothness properties of the above scheme.
One-Wayness. We now prove that the above construction satisifes (k, n)-one-wayness property when \(k \ge 7\lambda \) and \(n - k \le \alpha \log n\) for any fixed constant \(\alpha \).
Theorem 3
Assuming the \(\varPhi \)-hiding assumption holds, the above construction satisfies \((k,n,\ell )\)-one-wayness property as per Definition 1.
Proof
We first prove that no PPT adversary can win the following game with non-negligible advantage assuming the \(\varPhi \)-hiding assumption. We then prove how a PPT adversary breaking one-wayness property of the above scheme can be used to break the following game.
-
Game G: The challenger chooses RSA modulus \(\kappa = 5\lambda \), samples \(N \leftarrow \mathsf {RSA}(\kappa )\), prime \(e \leftarrow \textsc {PRIMES}(\lambda )\) and a value \(z \leftarrow \mathbb {Z}_N^*\). The challenger sends (N, e, z) to the adversary, which then outputs w. The adversary wins if \(w^e = z\;\text {mod }N\).
We now argue that no PPT adversary can win the above game with non-negligible probability.
Lemma 4
Assuming the \(\varPhi \)-hiding assumption holds, for every PPT adversary \(\mathcal {A}\), there exists a negligible function \(\text {negl}(\cdot )\) such that for every \(\lambda \in \mathbb {N}\), the probability that \(\mathcal {A}\) wins in Game G is at most \(\text {negl}(\lambda )\).
Proof
We prove the lemma using the following intermediate Game H.
-
Game H: The challenger chooses RSA modulus \(\kappa = 5\lambda \), samples prime \(e \leftarrow \textsc {PRIMES}(\lambda )\) and \(N \leftarrow \mathsf {RSA}(\kappa )\) s.t. \(e | \phi (N)\). It then samples an element \(z \leftarrow \mathbb {Z}_N^*\). The challenger sends (N, e, z) to the adversary, which then outputs w. The adversary wins if \(w^e = z\;\text {mod }N\).
Let the advantage of any adversary \(\mathcal {A}\) in Game G be \(\mathsf {Adv}_G^\mathcal {A}\) and in Game H be \(\mathsf {Adv}_H^\mathcal {A}\).
Claim 1
For every adversary \(\mathcal {A}\), there exists a negligible function \(\text {negl}(\cdot )\) such that for every \(\lambda \in \mathbb {N}\), \(\mathsf {Adv}_H^\mathcal {A}\le \text {negl}(\lambda )\).
Proof
As \(e | \phi (N)\), only a negligible fraction of \(z \in \mathbb {Z}_N^*\) have a w s.t. \(w^e = z\;\text {mod }N\). Therefore, no PPT adversary can find a w s.t. \(w^e = z\;\text {mod }N\) with non-negligible probability.
Claim 2
Assuming the \(\varPhi \)-hiding assumption holds, for every PPT adversary \(\mathcal {A}\), there exists a negligible function \(\text {negl}(\cdot )\) such that for every \(\lambda \in \mathbb {N}\), \(|\mathsf {Adv}_G^\mathcal {A}- \mathsf {Adv}_H^\mathcal {A}| \le \text {negl}(\lambda )\).
Proof
Suppose there exists a PPT adversary \(\mathcal {A}\) such that \(|\mathsf {Adv}_G^\mathcal {A}- \mathsf {Adv}_H^\mathcal {A}|\) is non-negligible. We construct a reduction algorithm that breaks \(\varPhi \)-hiding assumption. \(\mathcal {B}\) samples \(e \leftarrow \textsc {PRIMES}(\lambda )\) and plays \(\varPhi \)-hiding game for e. The challenger sends RSA modulus N to \(\mathcal {B}\), which samples \(z \leftarrow \mathbb {Z}_N^*\) and sends (N, e, z) to \(\mathcal {A}\). If \(\mathcal {A}\) outputs w s.t. \(w^e = z\;\text {mod }N\), then \(\mathcal {B}\) guesses that \(\phi (N)\) is uniformly sampled from \(\mathsf {RSA}(\kappa )\). Otherwise, it guesses that \(e | \phi (N)\).
By the above 2 claims and triangle inequality, no PPT adversary can win Game G with non-negligible advantage.
Lemma 5
Assuming the \(\varPhi \)-hiding assumption holds, for every PPT adversary \(\mathcal {A}\), there exists a negligible function \(\text {negl}(\cdot )\) such that for every \(\lambda \in \mathbb {N}\), the advantage of \(\mathcal {A}\) in (k, n)-one-wayness game is at most \(\text {negl}(\lambda )\).
Proof
Suppose there exist a PPT adversary \(\mathcal {A}\) that breaks (k, n)-one-wayness property of the encryption scheme with non-negligible probability \(\epsilon \). We construct a reduction algorithm \(\mathcal {B}\) that wins against Game G challenger \(\mathcal {C}\).
The adversary first sends a (k, n) source S to \(\mathcal {B}\). The challenger \(\mathcal {C}\) then sends (N, e, z) to \(\mathcal {B}\). The reduction algorithm samples a bit string \(x \leftarrow S\), an index \(j \leftarrow [n]\), extractor seed \(\mathfrak {s}\leftarrow \mathcal {S}\), exponents \(d_0, d_1 \leftarrow \mathbb {Z}_p\) primes \(e_{i,b'} \leftarrow \textsc {PRIMES}(\lambda )\) for \((i,b') \ne (j,1-x_j)\). It then sets generator \(g = z\) and prime \(e_{j,1-x_j} = e\). \(\mathcal {B}\) then sends public parameters \(\mathsf {pp}= (N, \mathfrak {s}, g, \{e_{i,b'}\}_{i,b'}, d_0, d_1)\) and challenge \(y = z^{\prod _i e_{i,x_i}}\;\text {mod }N\) to the adversary. The adversary outputs \(x'\). If \(f(\mathsf {pp}, x') \ne f(\mathsf {pp}, x)\) or \(x_j = x'_j\), then \(\mathcal {B}\) aborts. Otherwise, we have \(h^e = z^F\;\text {mod }N\), where \(F = f_1\cdot f_2\cdot (d_0 x + d_1)\prod _i e_{i,x_i}\) and \(h = z^{f_1\cdot f_2\cdot (d_0x'+d_1)\prod _{i \ne j}e_{i,x'_i}}\;\text {mod }N\). As e is a randomly sampled \(\lambda \)-bit prime, \(e \not \mid F\) with overwhelming probability. \(\mathcal {B}\) computes \(z^{1/e}\;\text {mod }N\) using Shamir’s trick [39]. Concretely, \(\mathcal {B}\) first computes integers a, b s.t. \(a\cdot e + b\cdot F = 1\) and outputs \(w = h^b\cdot z^a\;\text {mod }N\).
We now analyze the advantage of \(\mathcal {B}\) in Game G. By our assumption, \(f(\mathsf {pp}, x') = f(\mathsf {pp}, x)\) with non-negligible probability \(\epsilon \). We prove that \(x' \ne x\) with non-negligible probability. As \(k \ge \kappa +2\lambda \), we know that for any \(\mathsf {pp}\), \(\Pr _{x \leftarrow S}[\exists t \in \{0,1\}^n\text { s.t. } x \ne t \wedge f(\mathsf {pp}, x) = f(\mathsf {pp}, t)] \ge 1-\text {negl}(\lambda )\). Therefore, \(\Pr [x' \ne x \wedge f(\mathsf {pp}, x) = f(\mathsf {pp}, x')] \ge \epsilon /2-\text {negl}(\lambda )\) and \(\Pr [x'_j \ne x_j \wedge f(\mathsf {pp}, x) = f(\mathsf {pp}, x')] \ge \epsilon /{2n}-\text {negl}(\lambda )\) as j is sampled uniformly from [n]. Note that if \(\mathcal {B}\) does not abort, it outputs w s.t. \(w^e = z\;\text {mod }N\) with overwhelming probability. Therefore, \(\mathcal {B}\) breaks Game G security with non-negligible probability \(\epsilon /{2n}-\text {negl}(\lambda )\).
Security of Encryption. We now prove that the above construction satisifes encryption security property.
Theorem 4
Assuming the \(\varPhi \)-hiding assumption holds, the above construction satisfies encryption security property as per Definition 2.
Proof
We prove the above theorem via a sequence of following hybrids.
-
Hybrid \(H_0\): This is same as original OWFE security of encryption game when the challenger chooses \(\beta = 0\).
-
1.
The adversary sends bit string \(x \leftarrow \{0,1\}^n\) and index \(j \in [n]\) to the challenger.
-
2.
The challenger sets modulus length \(\kappa = 5\lambda \) and samples \(N \leftarrow \mathsf {RSA}(\kappa )\), generator \(g \leftarrow \mathbb {Z}_N^*\), extractor seed \(\mathfrak {s}\leftarrow \mathcal {S}\) and primes \(e_{i,b} \leftarrow \textsc {PRIMES}(\lambda )\) for \((i,b) \in [n] \times \{0,1\}\).
-
3.
The challenger samples \(\rho \leftarrow \mathbb {Z}_N\), computes \(\mathsf {ct}= g^{\rho \cdot e_{j,1-x_j}},\)
\(z = \mathsf {Ext}(g^{\rho f_1\cdot f_2\cdot (d_0 x + d_1)\cdot \prod _i e_{i,x_i}}\; \text {mod }N, \mathfrak {s})\).
-
4.
The challenger sends \(\mathsf {pp}= (N, \mathfrak {s}, g, \{e_{i,b}\}_{i,b}), \mathsf {ct}, z\) to the adversary \(\mathcal {A}\), which outputs a bit \(\alpha \).
-
1.
-
Hybrid \(H_1\): This hybrid is similar to previous hybrid except for the following changes.
-
3.
The challenger samples
 , computes
, computes
 ,
, .
.
-
3.
-
Hybrid \(H_2\): This hybrid is same as previous game except that the challenger samples z uniformly at random.
-
3.
The challenger samples \(\tilde{g} \leftarrow \mathbb {Z}_N^*\), computes
 .
.
-
3.
-
Hybrid \(H_3\): This is same as original OWFE security of encryption game when the challenger chooses \(\beta = 1\).
-
3.
The challenger samples
 , computes
, computes 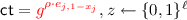 .
.
-
3.
For any PPT adversary \(\mathcal {A}\), let the probability that \(\mathcal {A}\) outputs 1 in Hybrid \(H_s\) be \(p_s^\mathcal {A}\). We prove that Hybrids \(H_0\) and \(H_3\) are computationally indstinguishable via the sequence of following lemmas.
Lemma 6
For any adversary \(\mathcal {A}\), there exists a negligible function \(\text {negl}(\cdot )\) such that for every security parameter \(\lambda \in \mathbb {N}\), we have \(|p_0^\mathcal {A}- p_1^\mathcal {A}| \le \text {negl}(\lambda )\).
Proof
We first observe that for any N, prime \(e \not \mid \phi (N)\) and generator \(g \in \mathbb {Z}_N^*\), the distribution of \(g^{\rho \cdot e}\;\text {mod }N\) for a randomly sampled \(\rho \leftarrow \mathbb {Z}_{\phi (N)}\) is identical to the distribution \(\tilde{g} \leftarrow \mathbb {Z}_N^*\). This follows from the fact that g and \(g^e\) are generators of \(\mathbb {Z}_N^*\). For a randomly sampled \(\lambda \) bit prime e, we know that \(e \not \mid \phi (N)\) with overwhelming probability. Similarly, for a randomly sampled \(\rho \leftarrow \mathbb {Z}_N\), we know that \(\rho \in \mathbb {Z}_{\phi (N)}\) with overwhelming probability. As a result, \(\{\tilde{g} : \tilde{g} \leftarrow \mathbb {Z}_N^*\}\) is statistically indistinguishable from \(\{g^{\rho \cdot e}: g \leftarrow \mathbb {Z}_N^*, \rho \leftarrow \mathbb {Z}_{N}, e \leftarrow \textsc {PRIMES}(\lambda )\}\). By a similar argument, for any F, the distribution \(\{(g^{\rho \cdot e}\;\text {mod }N, g^{\rho \cdot F}\;\text {mod }N): g \leftarrow \mathbb {Z}_N^*, \rho \leftarrow \mathbb {Z}_N, e \leftarrow \textsc {PRIMES}(\lambda )\}\) is statistically indistinguishable from the distribution \(\{(\tilde{g}, \tilde{g}^{F\cdot e^{-1}}\;\text {mod }N) : \tilde{g} \leftarrow \mathbb {Z}_N^*, e \leftarrow \textsc {PRIMES}(\lambda )\}\). Therefore, for every adversary \(\mathcal {A}\), \(|p_0^\mathcal {A}- p_1^\mathcal {A}| \le \text {negl}(\lambda )\).
Lemma 7
Assuming the \(\varPhi \)-hiding assumption holds, for any PPT adversary \(\mathcal {A}\), there exists a negligible function \(\text {negl}(\cdot )\) such that for every security parameter \(\lambda \in \mathbb {N}\), we have \(|p_1^\mathcal {A}- p_2^\mathcal {A}| \le \text {negl}(\lambda )\).
Proof
The above lemma follows from \(\phi \)-based Extractor lemma (Lemma 3). Suppose there exists a PPT adversary \(\mathcal {A}\) such that \(|p_1^\mathcal {A}- p_2^\mathcal {A}|\) is non-negligible. We construct a reduction algorithm \(\mathcal {B}\) that violates \(\phi \)-based extractor lemma.
The extractor lemma challenger first samples \(N \leftarrow \mathsf {RSA}(\kappa )\), \(\mathfrak {s}\leftarrow \mathcal {S}\), \(e \leftarrow \textsc {PRIMES}(\lambda )\), \(\tilde{g} \leftarrow \mathbb {Z}_N^*\) and sends \((N, \mathfrak {s}, e, \tilde{g})\) to reduction algorithm \(\mathcal {B}\). The adversary \(\mathcal {A}\) then sends a string \(x \in \{0,1\}^n\) and index \(j \in [n]\) to \(\mathcal {B}\). \(\mathcal {B}\) samples generator g, values \(d_0, d_1 \leftarrow \mathbb {Z}_N\), and primes \(e_{i,b} \leftarrow \textsc {PRIMES}(\lambda )\) for \((i,b) \ne (j, 1-x_j)\). \(\mathcal {B}\) then sets \(e_{j, 1-x_j} = e\) and computes \(F = f_1\cdot f_2\cdot (d_0 x + d_1)\prod _i e_{i,x_i}\). If e|F, the reduction algorithm aborts and guesses randomly. As e is a \(\lambda \)-bit prime, this happens with negligible probability. If \(e \not \mid F\), then \(\mathcal {B}\) sends F to the challenger, which samples a bit \(\gamma \leftarrow \{0,1\}\). If \(\gamma = 0\), \(\mathcal {C}\) computes \(\tilde{z} \leftarrow \mathsf {Ext}(\tilde{g}^{F/e}, \mathfrak {s})\). If \(\gamma = 1\), \(\mathcal {C}\) samples \(\tilde{z} \leftarrow \{0,1\}^\ell \). The challenger sends \(\tilde{z}\) to \(\mathcal {B}\). The reduction algorithm sets \(\mathsf {ct}= \tilde{g}, z = \tilde{z}\) and sends \(\mathsf {pp}= (N, \mathfrak {s}, g, \{e_{i,b}\}_{i,b}, d_0, d_1), \mathsf {ct}, z\) to \(\mathcal {A}\). The adversary outputs a bit \(\alpha \). \(\mathcal {B}\) outputs \(\alpha \) as its guess in extractor lemma game.
Note that if \(\gamma = 0\), then the distribution of \(\mathsf {pp}, \mathsf {ct}, z\) sent by \(\mathcal {B}\) is statistically indistinguishable from that of Hybrid \(H_1\) challenger. If \(\gamma = 1\), then the distribution of \(\mathsf {pp}, \mathsf {ct}, z\) sent by \(\mathcal {B}\) is statistically indistinguishable from that of \(H_2\) challenger. Consequently if \(\mathcal {B}\) does not abort, the advantage \(|\Pr [\alpha = 1 | \gamma - 0] - \Pr [\alpha =1 | \gamma =1]| \ge |p_1^\mathcal {A}- p_2^\mathcal {A}| - \text {negl}(\lambda )\) is non-negligible. As \(\mathcal {B}\) aborts with only negligible probability, it wins the extractor lemma game with non-negligible probability.
Lemma 8
For any PPT adversary \(\mathcal {A}\), there exists a negligible function \(\text {negl}(\cdot )\) such that for every security parameter \(\lambda \in \mathbb {N}\), we have \(|p_2^\mathcal {A}- p_3^\mathcal {A}| \le \text {negl}(\lambda )\).
Proof
The distribution \(\{\tilde{g} : \tilde{g} \leftarrow \mathbb {Z}_N^*\}\) is statistically indistinguishable from \(\{g^{\rho \cdot e}: g \leftarrow \mathbb {Z}_N^*, \rho \leftarrow \mathbb {Z}_{N}, e \leftarrow \textsc {PRIMES}(\lambda )\}\) as mentioned in proof of Claim 6.
By the above lemmas and triangle theorem, no PPT adversary can distinguish between Hybrids \(H_0\) and \(H_3\) with non-negligible probability assuming the \(\varPhi \)-hiding assumption.
Smoothness. We now prove that the above construction satisifes (k, n)-smoothness property when \(k \ge 7\lambda \) and \(n - k \le \alpha \log n\) for any fixed constant \(\alpha \).
Theorem 5
Assuming the \(\varPhi \)-hiding assumption holds, the above construction satisfies (k, n)-smoothness security property as per Definition 3.
Proof
First, we introduce a useful notation. For any constant \(\epsilon > 0\), let \(j_\epsilon \) be the smallest index such that \(p_{j_\epsilon } > (2^{n-k+2} \log N/\epsilon )^3\). Note that \((2^{n-k+2} \log N/\epsilon )^3\) is polynomial in \(\lambda \) for the given setting of parameters. The proof of security follows via a sequence of hybrids. Below we first describe the sequence of hybrids and later argue indistinguishability to complete the proof. At a very high level, the proof structure is somewhat similar to that used in [40], where for proving security one first assumes (for the sake of contradiction) that the adversary wins with some non-negligible probability \(\delta \) and then depending upon \(\delta \), one could describe a sequence of hybrids such that no PPT adversary can win with probability more than \(2\delta /3\). This acts as a contradiction, thereby completing the proof.
For any PPT adversary \(\mathcal {A}\), let \(p_s^\mathcal {A}\) be the probability that \(\mathcal {A}\) outputs 1 in Hybrid \(H_s\). For the sake of contradiction, we assume that \(\mathcal {A}\) breaks (k, n)-smoothness property with non-negligible advantage \(\delta (\lambda )\) i.e., there exists a polynomial \(v(\cdot )\) s.t. \(|p_0^\mathcal {A}- p_2^\mathcal {A}| = \delta (\lambda ) > \frac{1}{v(\lambda )}\) for infinitely often \(\lambda \in \mathbb {N}\). Let \(\epsilon = \frac{1}{2v(\lambda )}\). We provide a non-uniform reduction where the description of hybrids and the reduction algorithm depends on \(\epsilon \).
-
Hybrid \(H_0\): This is same as the original smoothness security game, except that the challenger always chooses source \(S_0\).
-
1.
The adversary first sends two (k, n) sources \(S_0, S_1\) to the challenger. The challenger sets modulus length \(\kappa = 5\lambda \) and samples \(N \leftarrow \mathsf {RSA}(\kappa )\), extractor seed \(\mathfrak {s}\leftarrow \mathcal {S}\), elements \(d_0, d_1 \leftarrow \mathbb {Z}_N\) and primes \(e_{i,b} \leftarrow \textsc {PRIMES}(\lambda )\) for \((i,b) \in [n] \times \{0,1\}\).
-
2.
The challenger then samples a generator \(g \leftarrow \mathbb {Z}_N^*\) and sets public parameters \(\mathsf {pp}= (N, \mathfrak {s}, g, \{e_{i,b}\}_{i,b}, d_0, d_1)\).
-
3.
The challenger samples \(x \leftarrow S_0\) and sends \(\mathsf {pp}, y = g^{f_1\cdot f_2\cdot (d_0 x + d_1)\prod _{i=1}^n e_{i,x_i}}\;\text {mod }N\) to the adversary.
-
4.
The adversary outputs a bit \(b'\).
-
1.
-
Hybrid \(H_1\): In this hybrid, the challenger does not sample x and picks the challenge y from a uniform distribution.
-
2.
The challenger then samples a generator
 ,
,
 and sets public parameters \(\mathsf {pp}= (N, \mathfrak {s}, g, \{e_{i,b}\}_{i,b}, d_0, d_1)\).
and sets public parameters \(\mathsf {pp}= (N, \mathfrak {s}, g, \{e_{i,b}\}_{i,b}, d_0, d_1)\). -
3.
The challenger samples
 and sends
and sends  to the adversary.
to the adversary.
-
2.
-
Hybrid \(H_2\): This is same as the original smoothness security game, except that the challenger always chooses source \(S_1\).
-
2.
The challenger then samples a generator
 and sets public parameters \(\mathsf {pp}= (N, \mathfrak {s}, g, \{e_{i,b}\}_{i,b}, d_0, d_1)\).
and sets public parameters \(\mathsf {pp}= (N, \mathfrak {s}, g, \{e_{i,b}\}_{i,b}, d_0, d_1)\). -
3.
The challenger samples
 and sends
and sends  to the adversary.
to the adversary.
-
2.
Lemma 9
Assuming the \(\varPhi \)-hiding assumption holds, for any PPT adversary \(\mathcal {A}\), there exists a negligible function \(\text {negl}(\cdot )\) such that for all \(\lambda \in \mathbb {N}\) satisfying \(\delta (\lambda ) \ge 2\epsilon = 1/v(\lambda )\), we have \(|p_0^\mathcal {A}- p_1^\mathcal {A}| \le \epsilon /2 + \text {negl}(\lambda )\).
Proof
Suppose there exists a PPT adversary \(\mathcal {A}\) that has a non-negligible advantage \(\delta (\lambda )\) in smoothness game, and can distinguish between Hybrids \(H_0\) and \(H_1\) with probability \(\epsilon /2 + \gamma \) for some non-negligible value \(\gamma \). We construct a reduction algorithm \(\mathcal {B}\) that breaks our strengthened hashing lemma (Theorem 2) and thereby breaking \(\varPhi \)-hiding assumption.
The adversary \(\mathcal {A}\) sends two (k, n)-sources \(S_0, S_1\) to the reduction algoritm \(\mathcal {B}\). \(\mathcal {B}\) plays hashing lemma game for source \(S_0\) with the challenger \(\mathcal {C}\). The hashing lemma challenger \(\mathcal {C}\) sends \((N, g, a,b, \{e_{i,b}\}_{i,b}, y)\) to the reduction algorithm \(\mathcal {B}\). The reduction algorithm samples a seed \(\mathfrak {s}\leftarrow S\), sets \(d_0 = a, d_1 = b\) and sends public parameters \(\mathsf {pp}= (N, \mathfrak {s}, g, \{e_{i,b}\}_{i,b}, d_0,d_1)\), challenge y to the adverary \(\mathcal {A}\). The adversary outputs a bit \(b'\). \(\mathcal {B}\) outputs \(b'\) as its guess in hashing lemma game.
Let us analyze advantage of \(\mathcal {B}\) in hashing lemma game. If the challenger samples \(g \leftarrow \mathbb {Z}_N^*, x \leftarrow S_0, y = g^{f_1\cdot f_2\cdot (ax+b)\prod _{i=1}^n e_{i,x_i}}\;\text {mod }N\), then \(\mathcal {B}\) emulates Hybrid \(H_0\) challenger to \(\mathcal {A}\). If the challenger samples \(\tilde{g} \leftarrow \mathbb {Z}_N^*, z \leftarrow \mathbb {Z}_N^*\) and sets \(g = \tilde{g}^{\prod _{i=3}^{j_\epsilon } f_i}\), \(y = z^{\prod _{i=1}^{j_\epsilon } f_i}\), then \(\mathcal {B}\) emulates Hybrid \(H_1\) challenger to \(\mathcal {A}\). Therefore, \(\mathcal {B}\) breaks hashing lemma game with advantage \(|p_1^\mathcal {A}- p_2^\mathcal {A}| \ge \epsilon /2 + \gamma \).
Lemma 10
Assuming the \(\varPhi \)-hiding assumption holds, for any PPT adversary \(\mathcal {A}\), there exists a negligible function \(\text {negl}(\cdot )\) such that for all \(\lambda \in \mathbb {N}\) satisfying \(\delta (\lambda ) \ge 2\epsilon = 1/v(\lambda )\), we have \(|p_1^\mathcal {A}- p_2^\mathcal {A}| \le \epsilon /2 + \text {negl}(\lambda )\).
Proof
This proof is similar to the proof of Lemma 9.
By the above 2 lemmas and triangle inequality, \(\mathcal {A}\) can distinguish between Hybrids \(H_0\) and \(H_2\) with probability at most \(\epsilon + \text {negl}(\lambda ) < 2\delta /3\). This contradicts the assumption that \(\mathcal {A}\) has an advantage of \(\delta \).Footnote 6 Therefore, no PPT adversary can break (k, n)-smoothness property of the above construction with non-negligible probability.
5 One-Way Function with Encryption from q-DBDHI Assumption
We now construct \((k,n,\ell )\)-OWFE from any n-DBDHI hard group generator \(\mathsf {GGen}\). Suppose \(\mathsf {GGen}(1^\lambda )\) generates a group of size \(\theta (2^{m})\), the below construction requires \(k \ge m + 2\lambda \) and \(n \le k + m - 2\lambda \). For the sake of simplicity, we construct a OWFE scheme where the encryption algorithm outputs elements in a group. The construction can be extended to output \(\ell \)-length bit strings by using PRGs and randomness extractors. We present a variant of this construction with longer ciphertext from n-DDHI assumption (without pairings) in the full version of the paper.
-
\(K(1^\lambda )\): Sample a group \(\mathcal {G}= ({\mathbb {G}}_1, {\mathbb {G}}_T, e, p) \leftarrow \mathsf {GGen}(1^\lambda )\). Sample a generator \(g \leftarrow {\mathbb {G}}_1\) and random values \(\alpha , d_0, d_1 \leftarrow \mathbb {Z}_p\). Output the public parameters \((\mathcal {G}, g, g^\alpha , g^{\alpha ^2}, \cdots , g^{\alpha ^{n}}, d_0, d_1)\).
-
\(f(\mathsf {pp}, x)\): Parse public parameters \(\mathsf {pp}\) as \(\mathsf {pp}= (\mathcal {G}, g, g^\alpha , g^{\alpha ^2}, \cdots , g^{\alpha ^{n}}, d_0, d_1)\). Let the polynomial \((d_0 x + d_1)\cdot \prod _{j=1}^n (\alpha + 2j + x_j) = \sum _{i=0}^n c_i \alpha ^i\), where \(c_i\) is a function of \(d_0, d_1, x\). Output \(\prod _{i=0}^n \Big (g^{\alpha ^i}\Big )^{c_i}\).
-
\(E_1(\mathsf {pp}, (i,b); h)\): Compute and output \((h^{(\alpha +2i+b)}, i)\).
-
\(E_2(\mathsf {pp}, (y,i,b); h)\): Compute and output e(h, y).
-
\(D(\mathsf {pp}, \mathsf {ct}, x)\): Let \(\mathsf {ct}= (\mathsf {ct}', i)\). Consider the polynomial \((d_0 x + d_1)\cdot \prod _{j\ne i} (\alpha + 2j + x_j) = \sum _{j=0}^{n-1} c_j \alpha ^j\), where \(c_j\) is a function of \(d_0, d_1, x\). Compute and output \(e\Big (\mathsf {ct}', \prod _{j=0}^{n-1} \Big (g^{\alpha ^j}\Big )^{c_j}\Big )\).
Correctness. For any set of public parameters \(\mathsf {pp}= (\mathcal {G}, g, g^\alpha , g^{\alpha ^2}, \cdots , g^{\alpha ^{n}}, d_0, d_1)\), string \(x \in \{0,1\}^n\), index \(j \in [n]\) and randomness h, we have \(\mathsf {ct}= E_1(\mathsf {pp}, (j,x_j); h) = (h^{(\alpha + 2j +x_j)}, j)\) and \(D(\mathsf {pp}, \mathsf {ct}, x) = e(g,h)^{(d_0 x + d_1) \prod _{i} (\alpha + 2i + x_i)} = e(h,f(\mathsf {pp}, x)) = E_2(\mathsf {pp}, (f(\mathsf {pp}, x), j, x_j); h)\).
5.1 Security
We now prove that the above construction satisfies one-wayness, encryption security, and smoothness properties.
One-Wayness. We now prove that the above construction satisfies (k, n)-one-wayness property for any \(k \ge m + 2\lambda \) and \(n \le k + m - 2\lambda \).
Lemma 11
Assuming n-DBDHI assumption holds, the above construction satisfies (k, n)-one-wayness property for any (k, n) s.t. \(k \ge m + 2\lambda \) and \(n \le k + m - 2\lambda \) as per Definition 1.
Proof
Suppose there exists a PPT adversary \(\mathcal {A}\) that breaks one-wayness property of the above construction with non-negligible probability. We construct a reduction algorithm \(\mathcal {B}\) that wins n-DBDHI game with non-negligible probability.
The adversary \(\mathcal {A}\) first sends a (k, n)-source S to the reduction algorithm \(\mathcal {B}\). The challenger then sends \((\mathcal {G}, h, h^\alpha , h^{\alpha ^2}, \cdots , h^{\alpha ^{n}}, T)\) to the reduction algorithm \(\mathcal {B}\). The reduction algorithm samples a string \(x \leftarrow S\), \(d_0, d_1 \leftarrow \mathbb {Z}_p\), computes public parameters \(\mathsf {pp}= (\mathcal {G}, h, h^\alpha , h^{\alpha ^2}, \cdots h^{\alpha ^n}, d_0, d_1)\) and sends \(\mathsf {pp}, y = f(\mathsf {pp}, x)\) to the adversary \(\mathcal {A}\). The adversary outputs a string \(x'\). If \(x' = x\) or \(f(\mathsf {pp},x) \ne f(\mathsf {pp}, x')\), the reduction algorithm aborts and outputs a random bit. Otherwise, \(\mathcal {B}\) computes \(\alpha \) s.t. \((d_0 x + d_1)\cdot \prod _{i=1}^n (\alpha +2i+x_i) = (d_0 x' + d_1)\cdot \prod _{i=1}^n (\alpha +2i+x'_i) ~\text {mod }p\). The reduction algorithm then checks if \(T = e(g,g)^{1/\alpha }\). If \(T = e(g,g)^{1/\alpha }\), it outpus 1. Otherwise, it outputs 0.
We now analyze the advantage of \(\mathcal {B}\) in n-DBDHI game. By our assumption, \(f(\mathsf {pp}, x') = f(\mathsf {pp}, x)\) with non-negligible probability \(\epsilon \). We prove that the reduction algorithm does not abort with non-negligible probability. As \(k \ge m+2\lambda \), we know that for any \(\mathsf {pp}\), \(\Pr _{x \leftarrow S}[\exists t \in \{0,1\}^n\text { s.t. } x \ne t \wedge f(\mathsf {pp}, x) = f(\mathsf {pp}, t)] \ge 1-\text {negl}(\lambda )\). Therefore, \(\Pr [x' \ne x \wedge f(\mathsf {pp}, x) = f(\mathsf {pp}, x')] \ge \epsilon /2-\text {negl}(\lambda )\). Note that if \(\mathcal {B}\) does not abort, it breaks the n-DBDHI game with advantage 1/2. Therefore, the overall advantage of \(\mathcal {B}\) in breaking n-DBDHI game is \(\epsilon /4 - \text {negl}(\lambda )\).
Security of Encryption. We now prove that the above construction satisfies encryption security property.
Lemma 12
Assuming n-DBDHI assumption holds, the above construction satisfies encryption security property as per Definition 2.
Proof
Suppose there exists a PPT adversary \(\mathcal {A}\) that breaks encryption security of the above construction with non-negligible probability. We construct a reduction algorithm \(\mathcal {B}\) that wins n-DBDHI game with non-negligible probability.
The challenger \(\mathcal {C}\) first samples a group structure \(\mathcal {G}= ({\mathbb {G}}_1, {\mathbb {G}}_T, e, p) \leftarrow \mathsf {GGen}(1^\lambda )\), a generator \(h \leftarrow {\mathbb {G}}_1\), a value \(\beta \leftarrow \mathbb {Z}_p^*\) and a bit \(\gamma \leftarrow \{0,1\}\). If \(\gamma = 0\), it sets \(T = e(h,h)^{1/\beta }\). Otherwise, it samples \(T \leftarrow {\mathbb {G}}_T\). The challenger then sends \((\mathcal {G}, h, h^\beta , h^{\beta ^2}, \cdots , h^{\beta ^{n}}, T)\) to the reduction algorithm \(\mathcal {B}\). The adversary sends a string \(x \in \{0,1\}^n\) and an index j to \(\mathcal {B}\). \(\mathcal {B}\) samples \(d_0, d_1 \leftarrow \mathbb {Z}_p\) and implicitly sets \(\alpha = \beta - 2j - 1 + x_j\). It then computes public parameters \(\mathsf {pp}= (\mathcal {G}, h, h^\alpha , h^{\alpha ^2}, \cdots , h^{\alpha ^n}, d_0, d_1)\), samples \(\rho \leftarrow \mathbb {Z}_p\) and implicitly uses \(h^{\rho /(\alpha +2j+1-x_j)}\) as randomness for encryption. It computes \(\mathsf {ct}^* = (h^\rho , j)\). Consider the polynomial
where \(c, \{c_i\}_i\) are dependent only on \(\rho , x, d_0, d_1\). The reduction algorithm computes \(k^* = T^c\cdot e\Big (h,\prod _{i=0}^{n-1}\Big (h^{\beta ^i}\Big )^{c_i}\Big )\) and sends \(\mathsf {pp}, \mathsf {ct}^*, k^*\) to the adversary. The adversary outputs a bit \(\gamma '\). \(\mathcal {B}\) outputs \(\gamma '\) as its guess in n-DBDHI game.
We now analyze the advantage of \(\mathcal {B}\) in n-DBDHI game. As \(\beta \) is sampled uniformly, \(\alpha \) is also uniformly distributed. As \(\beta \ne 0\;\text {mod }p\) and \(\rho \) is uniformly distributed, \(h^{\rho /\beta }\) is also uniformly distributed in \({\mathbb {G}}_1\). If \(\gamma = 0\), then \((\mathsf {pp}, \mathsf {ct}^*, k^*)\) is same as \(\Big (\mathsf {pp}, E_1(\mathsf {pp}, (j, 1-x_j);\rho '), E_2(\mathsf {pp}, (f(\mathsf {pp},x),j,1-x_j); \rho ')\Big )\). If \(\gamma = 1\), then \(k^*\) is uniformly random. As \(\mathcal {A}\) distinguishes these 2 distributions with non-negligible probability, \(|\Pr [\gamma ' = 1|\gamma = 0] - \Pr [\gamma ' = 1|\gamma = 1]|\) is non-negligible. Therefore, \(\mathcal {B}\) breaks n-DBDHI assumption.
Smoothness. We now prove that the above construction satisfies (k, n)-smoothness property for any \(k \ge m + 2\lambda \) and \(n \le k + m - 2\lambda \).
Lemma 13
The above construction satisfies (k, n)-smoothness property for any \(k \ge m + 2\lambda \) and \(n \le k + m - 2\lambda \) as per Definition 3.
Proof
We prove the theorem via a sequence of following hybrids.
-
Hybrid \(H_0\): This is same as the original smoothness security game.
-
1.
The adversary sends two (k, n)-sources \(S_0\) and \(S_1\) to the challenger. The challenger samples a group \(\mathcal {G}= ({\mathbb {G}}_1, {\mathbb {G}}_T, e, p) \leftarrow \mathsf {Setup}(1^\lambda )\), a generator \(g \leftarrow {\mathbb {G}}_1\) and exponents \(d_0, d_1 \leftarrow \mathbb {Z}_p\).
-
2.
It then samples exponent \(\alpha \leftarrow \mathbb {Z}_p^*\) and computes \(\mathsf {pp}= (\mathcal {G}, g, g^\alpha , \cdots , g^{\alpha ^{n}}, d_0, d_1)\).
-
3.
The challenger samples a bit \(b \leftarrow \{0,1\}\), a string \(x \leftarrow S_b\) and sends \(\mathsf {pp}, y = g^{(d_0 x + d_1)\cdot \prod _{j=1}^n (\alpha + 2j + x_j)}\) to the adversary.
-
4.
The adversary outputs a bit \(b'\).
-
1.
-
Hybrid \(H_1\): In this hybrid, the challenger samples \(\alpha \) in public parameters from \([1, p-2n-2]\) instead of \(\mathbb {Z}_p^*\)
-
2.
It then samples exponent
 and computes
and computes\(\mathsf {pp}= (\mathcal {G}, g, g^\alpha , \cdots ,\) \(g^{\alpha ^{n}}, d_0, d_1)\).
-
2.
-
Hybrid \(H_2\): In this hybrid, the challenger samples the challenge y uniformly at random.
-
3.
The challenger samples
 and sends \(\mathsf {pp}, y\) to the adversary.
and sends \(\mathsf {pp}, y\) to the adversary.
-
3.
For any adversary \(\mathcal {A}\), let the probability that \(b' = b\) in Hybrid \(H_s\) be \(p_s^\mathcal {A}\). We know that, \(p_2^\mathcal {A}= 1/2\) as y is independent of b. We prove that for every PPT adversary \(\mathcal {A}\), \(|p_0^\mathcal {A}- p_2^\mathcal {A}|\) is negligible.
Claim 3
For every adversary \(\mathcal {A}\), there exists a negligible function \(\text {negl}(\cdot )\) such that for every \(\lambda \in \mathbb {N}\), \(|p_0^\mathcal {A}- p_1^\mathcal {A}| \le \text {negl}(\lambda )\).
Proof
The distribution of challenger’s output is same in Hybrids \(H_0\) and \(H_1\), except when \(\alpha \in [p - 1, p-2n-1]\). This event happens with probability \((2n+1)/p\). Assuming p is super-polynomial in \(\lambda \), the event \(\alpha \in [p - 1, p-2n-1]\) happens with negligible probability.
Claim 4
For every adversary \(\mathcal {A}\), there exists a negligible function \(\text {negl}(\cdot )\) such that for every \(\lambda \in \mathbb {N}\), \(|p_1^\mathcal {A}- p_2^\mathcal {A}| \le \text {negl}(\lambda )\).
Proof
As the minimum entropy of the distribution \(\{x : b \leftarrow \{0,1\}, x \leftarrow S_b\}\) is \(k \ge \log p + 2\lambda \) and as \(\alpha \) is sampled from \([1, p-2n-2]\), \((d_0 x + d_1)\cdot \prod _{j=1}^n (\alpha + 2j + x_j)\) for \(x \leftarrow S_b\) is indistinguishable from uniform distribution on \(\mathbb {Z}_p\). We present more details in the full version of the paper.
By the above claims and triangle inequality, the advantage of any adversary in the original smoothness game \(H_0\) is negligible.
6 Performance Evaluation
In this section, we discuss how our HPRG and OWFE constructions based on \(\varPhi \)-Hiding and D(B)DHI assumptions compare with the constructions based on DDH provided in [20, 33]. In the full version of the paper, we present our performance evaluation for Hinting PRG constructions.
6.1 OWF with Encryption: Comparing with [20]
We now discuss the efficiency of our OWFE constructions and compare it with existing constructions. First, we provide an asymptotic comparison and then give a more concrete performance evaluation.
An Asymptotic Comparison. In the [20] construction, the public parameters consist of O(n) group elements, where n is at least \(\log p + 2\lambda \), and p is the group size. The function evaluation and decryption algorithm performs O(n) group operations. The \(E_1\) algorithm performs O(n) exponentiations and outputs a ciphertext containing O(n) group elements. The \(E_2\) algorithm performs one exponentiation and outputs a key containing one group element.
Comparing that to our \(\varPhi \)-Hiding based OWFE construction described in Sect. 4, the public parameters consist of 2n (\(\lambda \)-bit) prime exponents along with the RSA modulus N, extractor seed, group generator, and a hash key. The function evaluation and decryption algorithm performs O(n) exponentiations with \(\lambda \)-bit exponents, where n is at least \(\log N + 2\lambda \). Both \(E_1\) and \(E_2\) algorithms perform single exponentiation and output a ciphertext and key containing just one group element, respectively.
In our DDHI based construction described in the full version of the paper, the setup phase performs O(n) exponentiations and outputs public parameters containing n group elements, where n is at least \(\log p + 2\lambda \), and p is the group size. The function evaluation and decryption algorithms evaluate a degree-n polynomial symbolically and later on performs n exponentiation operations and n group operations. The \(E_1\) algorithm performs O(n) exponentiations and outputs a ciphertext containing O(n) group elements. The \(E_2\) algorithm performs one exponentiation and outputs a key containing 1 group element. We also provide a more efficient OWFE construction Sect. 5 by relying on bilinear maps and prove it secure under DBDHI. It is similar to the DDHI based OWFE, except that \(E_1\) algorithm only performs O(1) exponentiations, \(E_2\) and decryption algorithms additionally perform a pairing operation, and ciphertext contains only one group element.
Concrete Performance Evaluation. The evaluations were performed on a 2015 Macbook Pro with Dual Core 2.7 GHz Intel Core i5 CPU and 8 GB DDR3 RAM. We evaluated the performance of DDH and DDHI based constructions using MCL Library [29] (written in C++) on NIST standardized elliptic curves P-192, P-224, P-256, P-384 and P-521 providing 96, 112, 128, 192 and 260-bit security respectively. We evaluated our \(\varPhi \)-Hiding based construction using Flint Libary [28] written in C++ on 1024, 2048, 3072, 7680 and 15360 bit RSA modulus providing 80, 112, 128, 192 and 256-bit security respectively.Footnote 7 We evaluated the performance of DBDHI based OWFE using MCL Library [29] on BN-254, BN-381, BN-462 pairing-friendly elliptic curves [5] (providing 100, 128, 140-bit security after the recent tower number field sieve attacks [18, 31, 35]).
It turns out that the baseline DDH based OWFE offers the shortest setup, evaluation, and decryption times. Whereas the \(\varPhi \)-hiding based OWFE outperforms in terms of \(E_1\) time and ciphertext size. And, due to smaller group size (and thereby smaller n), DBDHI based OWFE leads to shortest \(E_1\) time and ciphertext size. Lastly, for the shortest \(E_2\) time and key size, both the DDH and DDHI based constructions are equally useful. The concrete performance numbers are provided in Table 1.
Note that even though both DDHI and DBDHI based OWFE schemes have the same one-way function, DDHI based scheme has faster evaluation time. In fact, the DDHI based construction is more efficient than DBDHI construction in all aspects other than \(E_1\) time and ciphertext size. This is because the recommended group size of pairing-based elliptic curves grows super linearly in the security parameter due to the number field sieve attacks. And, the function evaluation and decryption procedures of \(\varPhi \)-hiding based scheme performs O(n) exponentiations, when compared to O(n) group operations performed by other schemes. As a result, \(\varPhi \)-hiding based scheme has the slowest function evaluation and decryption procedures.
Deterministic Encryption from OWFE. A very interesting application of OWFE is of deterministic encryption as shown by [19]. In the deterministic encryption scheme of [19], the setup phase invokes the OWFE setup phase once and \(E_1\) algorithm \(O(\ell )\) times, where \(\ell \) is proportional to the length of message being encrypted. The encryption key includes OWFE public parameters and \(O(\ell )\) OWFE ciphertexts. The encryption algorithm invokes OWFE f algorithm once and OWFE D algorithm \(O(\ell )\) times. The decryption algorithm invokes OWFE \(E_2\) algorithm \(O(\ell )\) times. Consequently, our DBDHI based OWFE leads to a deterministic encryption scheme with much smaller public parameters and setup time. Concretely, at 128-bit security, the setup phase and public parameters of our DBDHI based deterministic encryption scheme for 128-bit messages is more than 200x faster and 240x shorter respectively than the baseline DDH based deterministic encryption described in [19].
Notes
- 1.
Roughly speaking, a hinting PRG is same as a regular PRG, except that it has a stronger pseudorandomness property in the sense that the adversary must not break pseudorandomness even when given a hint about the preimage of the challenge string.
- 2.
- 3.
Technically, the ciphertext should also include the index \(i^{*}\) but we drop it for ease of exposition.
- 4.
Technically, the ciphertext should also include the index \(i^{*}\) but we drop it for ease of exposition.
- 5.
Note that such an extractor exists for \(\ell = c \cdot \lambda \) for some constant \(c < 1\). The construction can be extended for any \(\ell \ge \lambda \) with the help of PRGs.
- 6.
Note that the contradiction does not happen when \(\delta \) is negligible. If \(\delta \) is negligible, then \(j_\epsilon \) is superpolynomial and the reduction algorithm takes superpolynomial time to execute.
- 7.
Note that we proved the security of our schemes in an asymptotic sense. However, for experiments, we use NIST recommended RSA modulus for the sake of simplicity. The RSA modulus derived from applying a concrete analysis is slightly higher. However as we mention in proof of Sect. 3.1 (full version of the paper), the analysis could be improved further by using a tighter bound for \(\varPi (r^i)\), which is \(O(1/r^i)\).
References
Alamati, N., Montgomery, H., Patranabis, S.: Symmetric primitives with structured secrets. In: Boldyreva, A., Micciancio, D. (eds.) CRYPTO 2019. LNCS, vol. 11692, pp. 650–679. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-26948-7_23
Alamati, N., Montgomery, H., Patranabis, S., Roy, A.: Minicrypt primitives with algebraic structure and applications. In: Ishai, Y., Rijmen, V. (eds.) EUROCRYPT 2019. LNCS, vol. 11477, pp. 55–82. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-17656-3_3
Au, M.H., Tsang, P.P., Susilo, W., Mu, Y.: Dynamic universal accumulators for DDH groups and their application to attribute-based anonymous credential systems. In: Fischlin, M. (ed.) CT-RSA 2009. LNCS, vol. 5473, pp. 295–308. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-00862-7_20
Barić, N., Pfitzmann, B.: Collision-free accumulators and fail-stop signature schemes without trees. In: Fumy, W. (ed.) EUROCRYPT 1997. LNCS, vol. 1233, pp. 480–494. Springer, Heidelberg (1997). https://doi.org/10.1007/3-540-69053-0_33
Barreto, P.S.L.M., Naehrig, M.: Pairing-friendly elliptic curves of prime order. In: Preneel, B., Tavares, S. (eds.) SAC 2005. LNCS, vol. 3897, pp. 319–331. Springer, Heidelberg (2006). https://doi.org/10.1007/11693383_22
Benaloh, J., de Mare, M.: One-way accumulators: a decentralized alternative to digital signatures. In: Helleseth, T. (ed.) EUROCRYPT 1993. LNCS, vol. 765, pp. 274–285. Springer, Heidelberg (1994). https://doi.org/10.1007/3-540-48285-7_24
Boneh, D., Boyen, X.: Efficient selective-id secure identity-based encryption without random oracles. In: Cachin, C., Camenisch, J.L. (eds.) EUROCRYPT 2004. LNCS, vol. 3027, pp. 223–238. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-24676-3_14
Boyen, X., Waters, B.: Shrinking the keys of discrete-log-type lossy trapdoor functions. In: Zhou, J., Yung, M. (eds.) ACNS 2010. LNCS, vol. 6123, pp. 35–52. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-13708-2_3
Brakerski, Z., Lombardi, A., Segev, G., Vaikuntanathan, V.: Anonymous IBE, leakage resilience and circular security from new assumptions. Cryptology ePrint Archive, Report 2017/967 (2017). http://eprint.iacr.org/2017/967
Camenisch, J., Kohlweiss, M., Soriente, C.: An accumulator based on bilinear maps and efficient revocation for anonymous credentials. In: Jarecki, S., Tsudik, G. (eds.) PKC 2009. LNCS, vol. 5443, pp. 481–500. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-00468-1_27
Camenisch, J., Lysyanskaya, A.: Dynamic accumulators and application to efficient revocation of anonymous credentials. In: Yung, M. (ed.) CRYPTO 2002. LNCS, vol. 2442, pp. 61–76. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-45708-9_5
Catalano, D., Fiore, D.: Vector commitments and their applications. In: Kurosawa, K., Hanaoka, G. (eds.) PKC 2013. LNCS, vol. 7778, pp. 55–72. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-36362-7_5
Cho, C., Döttling, N., Garg, S., Gupta, D., Miao, P., Polychroniadou, A.: Laconic oblivious transfer and its applications. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017. LNCS, vol. 10402, pp. 33–65. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63715-0_2
Döttling, N., Garg, S.: Identity-based encryption from the Diffie-Hellman assumption. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017. LNCS, vol. 10401, pp. 537–569. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63688-7_18
Döttling, N., Garg, S., Hajiabadi, M., Masny, D.: New constructions of identity-based and key-dependent message secure encryption schemes. In: Abdalla, M., Dahab, R. (eds.) PKC 2018. LNCS, vol. 10769, pp. 3–31. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-76578-5_1
Döttling, N., Garg, S., Ishai, Y., Malavolta, G., Mour, T., Ostrovsky, R.: Trapdoor hash functions and their applications. In: Boldyreva, A., Micciancio, D. (eds.) CRYPTO 2019. LNCS, vol. 11694, pp. 3–32. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-26954-8_1
Döttling, N., Garg, S.: From selective IBE to full IBE and selective HIBE. In: Kalai, Y., Reyzin, L. (eds.) TCC 2017. LNCS, vol. 10677, pp. 372–408. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70500-2_13
Fotiadis, G., Konstantinou, E.: TNFS resistant families of pairing-friendly elliptic curves. IACR Cryptology ePrint Archive (2018). https://eprint.iacr.org/2018/1017
Garg, S., Gay, R., Hajiabadi, M.: New techniques for efficient trapdoor functions and applications. In: Ishai, Y., Rijmen, V. (eds.) EUROCRYPT 2019. LNCS, vol. 11478, pp. 33–63. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-17659-4_2
Garg, S., Hajiabadi, M.: Trapdoor functions from the computational Diffie-Hellman assumption. In: Shacham, H., Boldyreva, A. (eds.) CRYPTO 2018. LNCS, vol. 10992, pp. 362–391. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-96881-0_13
Garg, S., Hajiabadi, M., Mahmoody, M., Rahimi, A.: Registration-based encryption: removing private-key generator from IBE. In: Beimel, A., Dziembowski, S. (eds.) TCC 2018. LNCS, vol. 11239, pp. 689–718. Springer, Cham (2018). https://doi.org/10.1007/978-3-030-03807-6_25
Garg, S., Hajiabadi, M., Mahmoody, M., Rahimi, A., Sekar, S.: Registration-based encryption from standard assumptions. In: Lin, D., Sako, K. (eds.) PKC 2019. LNCS, vol. 11443, pp. 63–93. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-17259-6_3
Garg, S., Hajiabadi, M., Ostrovsky, R.: Efficient range-trapdoor functions and applications: Rate-1 OT and more. Cryptology ePrint Archive, Report 2019/990 (2019). https://eprint.iacr.org/2019/990
Garg, S., Ostrovsky, R., Srinivasan, A.: Adaptive garbled RAM from laconic oblivious transfer. In: Shacham, H., Boldyreva, A. (eds.) CRYPTO 2018. LNCS, vol. 10993, pp. 515–544. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-96878-0_18
Garg, S., Srinivasan, A.: Garbled protocols and two-round MPC from bilinear maps. In: FOCS 2017 (2017)
Garg, S., Srinivasan, A.: Adaptively secure garbling with near optimal online complexity. In: Nielsen, J.B., Rijmen, V. (eds.) EUROCRYPT 2018. LNCS, vol. 10821, pp. 535–565. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-78375-8_18
Gentry, C., Ramzan, Z.: RSA accumulator based broadcast encryption. In: Zhang, K., Zheng, Y. (eds.) ISC 2004. LNCS, vol. 3225, pp. 73–86. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-30144-8_7
Hart, W.B.: Fast library for number theory: an introduction. In: Fukuda, K., Hoeven, J., Joswig, M., Takayama, N. (eds.) ICMS 2010. LNCS, vol. 6327, pp. 88–91. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-15582-6_18, http://flintlib.org
Herumi: A portable and fast pairing-based cryptography library (2019). https://github.com/herumi/mcl
Katsumata, S., Nishimaki, R., Yamada, S., Yamakawa, T.: Designated verifier/prover and preprocessing NIZKs from Diffie-Hellman assumptions. In: Ishai, Y., Rijmen, V. (eds.) EUROCRYPT 2019. LNCS, vol. 11477, pp. 622–651. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-17656-3_22
Kim, T., Barbulescu, R.: Extended tower number field sieve: a new complexity for the medium prime case. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016. LNCS, vol. 9814, pp. 543–571. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53018-4_20
Kitagawa, F., Matsuda, T., Tanaka, K.: CCA security and trapdoor functions via key-dependent-message security. In: Boldyreva, A., Micciancio, D. (eds.) CRYPTO 2019. LNCS, vol. 11694, pp. 33–64. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-26954-8_2
Koppula, V., Waters, B.: Realizing chosen ciphertext security generically in attribute-based encryption and predicate encryption. In: Boldyreva, A., Micciancio, D. (eds.) CRYPTO 2019. LNCS, vol. 11693, pp. 671–700. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-26951-7_23
Lombardi, A., Quach, W., Rothblum, R.D., Wichs, D., Wu, D.J.: New constructions of reusable designated-verifier NIZKs. In: Boldyreva, A., Micciancio, D. (eds.) CRYPTO 2019. LNCS, vol. 11694, pp. 670–700. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-26954-8_22
Menezes, A., Sarkar, P., Singh, S.: Challenges with assessing the impact of NFS advances on the security of pairing-based cryptography. In: Phan, R.C.-W., Yung, M. (eds.) Mycrypt 2016. LNCS, vol. 10311, pp. 83–108. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-61273-7_5
Nguyen, L.: Accumulators from bilinear pairings and applications. In: Menezes, A. (ed.) CT-RSA 2005. LNCS, vol. 3376, pp. 275–292. Springer, Heidelberg (2005). https://doi.org/10.1007/978-3-540-30574-3_19
Quach, W., Rothblum, R.D., Wichs, D.: Reusable designated-verifier NIZKs for all NP from CDH. In: Ishai, Y., Rijmen, V. (eds.) EUROCRYPT 2019. LNCS, vol. 11477, pp. 593–621. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-17656-3_21
Sander, T., Ta-Shma, A., Yung, M.: Blind, auditable membership proofs. In: Frankel, Y. (ed.) FC 2000. LNCS, vol. 1962, pp. 53–71. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-45472-1_5
Shamir, A.: On the generation of cryptographically strong pseudorandom sequences. ACM Trans. Comput. Syst. 1(1), 38–44 (1983)
Zhandry, M.: The magic of ELFs. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016. LNCS, vol. 9814, pp. 479–508. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53018-4_18
Acknowledgements
We thank anonymous reviewers for useful feedback. The work is done in part while the first author was at UT Austin (supported by IBM PhD Fellowship), and at the Simons Institute for the Theory of Computing (supported by Simons-Berkeley research fellowship). The second author is supported by Packard Fellowship, NSF CNS-1908611, CNS-1414082, DARPA SafeWare and Packard Foundation Fellowship. The third author is supported by NSF CNS-1908611, CNS-1414082, DARPA SafeWare and Packard Foundation Fellowship.
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 International Association for Cryptologic Research
About this paper
Cite this paper
Goyal, R., Vusirikala, S., Waters, B. (2020). New Constructions of Hinting PRGs, OWFs with Encryption, and More. In: Micciancio, D., Ristenpart, T. (eds) Advances in Cryptology – CRYPTO 2020. CRYPTO 2020. Lecture Notes in Computer Science(), vol 12170. Springer, Cham. https://doi.org/10.1007/978-3-030-56784-2_18
Download citation
DOI: https://doi.org/10.1007/978-3-030-56784-2_18
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-56783-5
Online ISBN: 978-3-030-56784-2
eBook Packages: Computer ScienceComputer Science (R0)









 , computes
, computes
 ,
, .
. .
. , computes
, computes  .
. ,
,
 and sets public parameters
and sets public parameters  and sends
and sends  to the adversary.
to the adversary. and sets public parameters
and sets public parameters  and sends
and sends  to the adversary.
to the adversary. and computes
and computes and sends
and sends 