Eco-evolutionary Spatial Dynamics of Nonlinear Social Dilemmas

Abstract

Spatial dynamics can promote the evolution of cooperation. While dispersal processes have been studied in simple evolutionary games, real-world social dilemmas are much more complicated. When the investment is low, for example, every additional unit of investment may substantially raise the public goods. However, the effect vanishes as the number of investments increases. Such nonlinear public goods are the norm in a variety of social as well as biological systems. Therefore, we investigate the effect of the nonlinearity on the evolution of cooperation. We show how the nonlinearity in payoffs, resulting in synergy or discounting of public goods, can alter the return on the cooperative investments compared to the linear game. The alteration affects the resulting spatial patterns, not just quantitatively, but in some cases, drastically changing the outcomes. Notably, in cases where a linear game would lead to extinction, synergy can support the coexistence of cooperators and defectors. The eco-evolutionary trajectory can thus be qualitatively different in cases on nonlinear social dilemmas.

1 Introduction

The most significant impact of evolutionary game theory has been in the field of social evolution. When an individual’s action results in a conflict between the individual and the group benefit, a social dilemma arises. Social dilemmas can be captured by the two-player prisoners dilemma game [6] and its multiplayer version, the public goods game [8, 17, 24]. The domain of public goods games ranges from behavioural economists, cognitive scientists, psychologists, to biologists given the ubiquity of multiplayer interactions in nature. Situations impossible in two-player games can occur in multiplayer games, which can lead to drastically different evolutionary outcomes [7, 14, 35, 39, 44, 52].

In public goods games, while cooperation raises the group benefit, cooperators themselves get less benefit than defectors. The group benefit typically increases linearly with the number of cooperators in the group. However, in the context of helping behaviour, reference [10] discusses a case where each additional cooperator in the group provides more benefit than the previous (superadditivity of benefit). The approach has been further generalised using a particular nonlinear function where the additional cooperators can provide not only more (synergy) but also less (discounting) benefit than the previous cooperator [20]. The study [5] presents an excellent review of the use and importance of nonlinear public goods game.

The nonlinear public goods game as proposed in [20] has been extended in [13] to include population dynamics. In ecological public goods games, the total density of cooperators and defectors changes, effectively changing the interaction group size. Changes in group size have been shown to result in a stable coexistence of cooperators and defectors [19, 30, 38]. A spatial version of ecological public goods games, where multiple populations of cooperators and defectors are present on a lattice and connected by diffusion, can promote cooperation [53]. The spread of cooperation, in such a case, is possible by a variety of pattern-forming processes.

They use of spatially extended system in different forms such as grouping, explicit space and deme structures, and other ways of limiting interactions have been studied for long [18, 33, 40, 45, 47, 55]. In particular, in [29], the authors provide conditions for strategy selection in nonlinear games about population structure coefficients. The study cited above by [53] while incorporating ecological dynamics focusses solely on linear public goods games.

Previously we have combined a linear social dilemma with density-dependent diffusion coefficients [12, 37]. Including a dynamic diffusion coefficient comes closer to analysing real movements seen across species from bacteria to humans [16, 23, 27, 28, 32, 34, 43]. Incorporating aspects of ecological games as in [19], spatial dynamics per [53] and nonlinear social dilemmas from [13] we develop our previous approach in this study to nonlinear social dilemmas.

We begin by introducing nonlinearity in the payoff function of the social dilemma, including population dynamics. Then we include simple diffusion dynamics and analyse the resulting spatial patterns. For the parameter set comprising of the diffusion coefficients and the multiplication factor, we can observe the extinction, heterogenous or homogenous non-extinction patterns. Under certain simplifying assumptions, we can also characterise the stability of the fixed point and discuss the dynamics of the Hopf-bifurcation transition and the phase boundary between heterogenous- and homogenous-patterned phases. Overall, our results suggest that the spatial patterns while remaining in the same regions relative to each other in the parameter space, synergy and discounting effects shift the boundaries including the phase boundary between extinction and surviving phases. For synergy, the extinction region shrinks as the effective benefit increases resulting in an increased possibility of cooperator persistence. For discounting, however, the extinction region expands. Crucially, the change in the extinction region is not symmetric for synergy and discounting. The above asymmetry is due to the asymmetries in the nonlinear function that we employ for calculating the benefit. The development will help contrast the results with the work of [53] and relates our work to realistic public goods scenarios where the contributions often have a nonlinear impact [9].

2 Model and Results

2.1 Nonlinear Public Goods Game

Complexity of evolutionary games increases as we move from two-player games to multiplayer games [14]. A similar trend ensues as we move from linear public goods games to nonlinear payoff structures [5]. One of the ways of moving from linear to nonlinear multiplayer games is given in [20]. To introduce this method in our notational form, we will first derive the payoffs in a linear setting.

In the classical version of the public goods game (PGG), the cooperators invest c to the common pool while the defectors contribute nothing. The value of the pool increases by a certain multiplication factor r, $1<r<N$, where N is the group size. The amplified returns are equally distributed to all the N players in the game. For such a setting, the payoffs for cooperators and defectors are given by

$$\begin{aligned} P_D(m)= & {} \frac{r c m}{N},\nonumber \\ P_C(m)= & {} \frac{r c m}{N} - c, \end{aligned}$$

(1)

where m is the number of cooperators in the group. The nonlinearity in the payoffs can be introduced by the parameter $\varOmega$ as in [20],

$$\begin{aligned} P_D(m)= & {} \frac{r c}{N} (1 + \varOmega + \varOmega ^2 + \ldots + \varOmega ^{m-1}) = \frac{r c}{N} \frac{1-\varOmega ^m}{1-\varOmega }, \nonumber \\ P_C(m)= & {} P_D(m) - c = \frac{r c}{N} \varOmega (1 + \varOmega + \ldots + \varOmega ^{m-2}) + \frac{r c}{N} - c. \end{aligned}$$

(2)

If $\varOmega >1$ every additional cooperator contributes more than the previous, thus providing a synergistic effect. If $\varOmega <1$ then every additional cooperator contributes less than the previous, thus saturating the benefits and providing a discounting effect. The linear version of the PGG can be recovered by setting $\varOmega = 1$.

As in [19] besides the evolutionary dynamics (change in the frequency of cooperators over time), we are also interested in the ecological dynamics (change in the population density over time). This system analysed in [19, 21] is briefly re-introduced in our notation for later extension. We characterise the densities of cooperators and defectors in the population as u and v. Thus $0\le u+v \le 1$ and the empty space is given by $w = 1-u-v$. Low population density means that it is hard to encounter other individuals and accordingly hard to interact with them. Hence, the group size N, the maximum group size, in this case, is not always reachable. Instead, S individuals form an interacting group. With fixed N the interacting group size S is bounded, $S \le N$, and the probability p(S; N) of interacting with $S-1$ individuals is depending on the total population density $u+v=1-w$. When we consider the focal individual, the probability p(S; N) of interacting with $S-1$ individuals among a maximum group of size $N-1$ individuals (excluding the focal individual),

$$\begin{aligned} p(S;N) = {{N-1}\atopwithdelims (){S-1}} (1-w)^{S-1} w^{N-S}. \end{aligned}$$

(3)

Then, the average payoffs for defectors and cooperators, $f_D$ and $f_C$, are given as

$$\begin{aligned} f_D&= \sum _{S=2}^{N} p(S;N) \overline{P_D}(S),\nonumber \\ f_C&= \sum _{S=2}^{N} p(S;N) \overline{P_C}(S), \end{aligned}$$

(4)

where $\overline{P_D}(S)$ and $\overline{P_C}(S)$ are the expected payoffs for defectors and cooperators at a given S. The sum for the group sizes S starts at two as for a social dilemma there need to be at least two interacting individuals.

To derive the expected payoffs, we first need to assess the probability of having a certain number of cooperators m in a group of size $S-1$ which is given by $p_c(m;S)$,

$$\begin{aligned} p_c(m;S) = {{S-1}\atopwithdelims (){m}} \left( \frac{u}{1-w}\right) ^m \left( \frac{v}{1-w}\right) ^{S-1-m}. \end{aligned}$$

(5)

Thus, the payoffs in Eq. (2) are weighted with the probability of there being m cooperators, giving us the expected payoffs,

$$\begin{aligned} \overline{P_D} (S)= & {} \sum _{m=0}^{S-1} p_c(m;S)P_D(m), \nonumber \\ \overline{P_C} (S)= & {} \sum _{m=0}^{S-1} p_c(m;S)P_C(m+1). \end{aligned}$$

(6)

The average payoffs $f_D$ and $f_C$ are thus given by

$$\begin{aligned} f_D&= \displaystyle \frac{r}{N}\frac{1}{1\!-\!w\!-\!u(1\!-\!\varOmega )} \left[ \frac{(u (\varOmega -1)+1)^{N}\!-\!1}{\varOmega -1} - \frac{u (1-w^N)}{1-w}\right] , \nonumber \\ f_C&= f_D - 1 - (r-1) w^{N-1} + \displaystyle \frac{r}{N} \frac{(1-u (1-\varOmega ))^{N}-w^N}{1-w-u (1-\varOmega )}, \end{aligned}$$

(7)

where the investment cost has been set to $c=1$ without loss of generality. Again, the linear version of the PGG can be recovered by setting $\varOmega = 1$,

$$\begin{aligned} f_D= & {} \frac{ru}{1-w} \left[ 1 - \frac{(1-w^N)}{N(1-w)}\right] , \nonumber \\ f_C= & {} f_D - 1 - (r-1) w^{N-1} + \frac{r}{N} \frac{1-w^N}{1-w}. \end{aligned}$$

(8)

2.2 Spatial Nonlinear Public Goods Games

For tracing the population dynamics, we are interested in the change in the densities of cooperators and defectors over time. Both cooperators and defectors are assumed to have a baseline birth rate of b and death rate of d. Growth is possible only when there is empty space available, i.e. $w>0$. We track the densities of cooperators and defectors by an extension of the replicator dynamics [19, 22, 48],

$$\begin{aligned} \dot{u}&= u [w (f_C+b) -d], \nonumber \\ \dot{v}&= v [w (f_D+b) -d]. \end{aligned}$$

(9)

To include spatial dynamics in the above system, we assume that a population of cooperators and defectors resides in a given patch. Game interactions only occur within patches, and the individuals can move adjacent patches. The patches live in a two-dimensional space connected in the form of a regular lattice. Taking a continuum limit, we obtain the differential equations with constant diffusion coefficients for cooperators $D_c$ and defectors $D_d$,

$$\begin{aligned} \dot{u}&= D_c \nabla ^2 u + u [w (f_C+b) -d], \nonumber \\ \dot{v}&= D_d \nabla ^2 v + v [w (f_D+b) -d]. \end{aligned}$$

(10)

At the boundaries, there is no in- and out-flux. As in classical activator-inhibitor systems, the different ratio of the diffusion coefficients $D=D_d/D_c$ can generate various patterns from coexistence, extinction as well as chaos [53].

Nonlinearity in PGG is implemented by $\varOmega \ne 1$. Previous work shows that the introduction of $\varOmega$ is enriching the dynamics [13, 20]. Synergy ($\varOmega >1$) enhances cooperation while discounting ($\varOmega <1$) suppresses it. Accordingly, synergy and discounting with a multiplication factor r can map into the linear game with the higher or lower multiplication factor $r'$, respectively: $r'>r$ for synergy and $r'<r$ for discounting. We call $r'$ as the effective multiplication factor. As shown in Fig. 1, for synergy effect ($\varOmega =1.1$), we can find a chaotic coexistence of cooperators and defectors. The same parameter for a linear case ($\varOmega = 1.0$) resulted in total extinction of the population [53]. In the linear case, chaotic patterns were observed for r values larger than that of extinction patterns. Thus, our observation implies the mechanism of how synergy works by effectively increasing r value.

The change in the resulting patterns due to synergy or discounting is not limited to extinction or chaos but is a general feature of the nonlinearity in payoffs. To illustrate this change, we show how a stable pattern under linear PGG ($\varOmega = 1$) can change the shape under discounting or synergy in Fig. 2. Such changes in the final structure happen all over the parameter space. To confirm this tendency, we examine the spatial patterns for various parameters and find five phases, same as in the linear PGG case [53] but now with shifted phase boundaries (see Fig. 3). The effective multiplication factor $r'$ increases with an increasing $\varOmega$, and thus the location of the Hopf bifurcation also shifts. As a result of shifting $r_{\mathrm {Hopf}}$, extinction region is reduced in the parameter space with synergy effect. We thus focus our attention on the Hopf-bifurcation point $r_{\mathrm {Hopf}}$.

Fig. 1

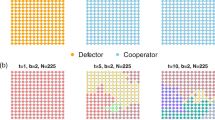
Pattern formation on the two-dimensional square lattice. We observe the chaotic pattern for $\varOmega =1.1$ (synergy effect) where extinction comes out with $\varOmega =1$  [53]. Mint green and Fuchsia pink colours represent the cooperator and defector densities, respectively. For a full explanation of the colour scheme, we refer to the appendix. Black indicates no individual on the site, whereas blue appears when the ratio of cooperators and defectors is the same. For a system of size L, initially, a disc with radius L/10 at the centre is occupied by cooperator and defector with densities 0.1. We use multiplication factor $r=2.2$ and diffusion coefficient ratio $D=2$. Throughout the paper, for simulations, we used the system size $L=283$, $dt=0.1$ and $dx=1.4$ with the Crank–Nicolson algorithm

Fig. 2

Synergy and discounting effects on pattern formation. We get the different patterns under discounting and synergy effects distinct from the linear PGG game at a given the same parameter set. While diffusion-induced instability is observed in the linear PGG, the discounting effect makes diffusion-induced coexistence pattern implying that the discounting effect makes the Hopf-bifurcation point shift to the larger value. Under the synergy effect, on the contrary, we obtain the opposite trend observing the homogenous coexistence pattern. In the linear PGG, the homogenous patterns are observed in higher multiplication factor r, implying the shift of $r_{\mathrm {Hopf}}$ to the smaller value under the synergy effect

Fig. 3

Spatial patterns and corresponding phase diagram for $\varOmega =1.1$. There are five phases (framed using different colours), extinction (black), chaos (blue), diffusion-induced coexistence (red), diffusion-induced instability (green) and homogeneous coexistence (orange). The Hopf-bifurcation point $r_{\mathrm {Hopf}}\simeq 2.2208$ and the boundary between diffusion-induced instability and homogeneous coexistence are analytically calculated, while the other boundaries are from the simulation results. All boundaries and $r_{\mathrm {Hopf}}$ shift to the left, indicating that the multiplication factor r with the synergy maps into the higher multiplication factor $r'$ in the linear game

Fig. 4

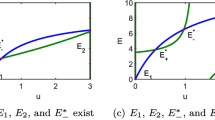
Hopf-bifurcation points in $\varOmega$ and shift of the phase boundary. a The Hopf-bifurcation point $r_{\mathrm {Hopf}}$ for various $\varOmega$ (solid line with points). Synergy ($\varOmega >1$) decreases $r_{\mathrm {Hopf}}$ while discounting ($\varOmega <1$) increases $r_{\mathrm {Hopf}}$. By decreasing $r_{\mathrm {Hopf}}$, the surviving region is extended in the parameter space. The solid line without points is a tangential line at $\varOmega =1$. b The phase boundaries between diffusion-induced instability and homogeneous coexistence phases are also examined for various $\varOmega$. Since $r_{\mathrm {Hopf}}$ increases with a decreasing $\varOmega$, the boundaries also move to the right

2.2.1 Hopf Bifuraction in Nonlinear PGG

We find the Hopf-bifurcation point $r_{\mathrm {Hopf}}$ for various $\varOmega$ values using Eq. (7). The effective multiplication factor $r'$ increases as $\varOmega$ increases, and thus $r_{\mathrm {Hopf}}$ is monotonically decreasing with $\varOmega$ as in Fig. 4a. The tangential line at $\varOmega =1$ is drawn for comparing the effects of synergy and discounting. If we focus on the differences between the tangent and $r_{\mathrm {Hopf}}$ line, synergy changes $r_{\mathrm {Hopf}}$ more dramatically than discounting. Synergy and discounting effects originate from $1+(1\pm \Delta \varOmega )+(1\pm \Delta \varOmega )^2+\cdots +(1\pm \Delta \varOmega )^{m-1}$ in Eq. (2), where $\Delta \varOmega >0$ and plus and minus signs for synergy and discounting, respectively. Straightforwardly, the difference between 1 and $(1+\Delta \varOmega )^k$ is larger than that of $(1-\Delta \varOmega )^k$ for $k>2$. Hence, the nonlinear PGG itself gives different $\Delta r_{\mathrm {Hopf}}$ for the same $\Delta \varOmega$.

2.2.2 Criterion for Diffusion-Induced Instability

Since $\varOmega$ changes $r'$ value, the phase boundary also moves. By using the linear stability analysis, we find phase boundaries between diffusion-induced instability and homogeneous coexistence phases in r-D space shown in Fig. 4b. To do that, we introduce new notations, and two reaction–diffusion equations in Eq. (10) can be written as

$$\begin{aligned} \partial _t\mathbf{u} = \mathbf{D} \nabla ^2\mathbf{u} +\mathbf{R} (\mathbf{u} ), \end{aligned}$$

(11)

with density vector $\mathbf{u} =(u, v)^T$ and matrix $\mathbf{D} =\left( \begin{array}{ll}D_c&{}0 \\ 0&{}D_d \end{array}\right)$. Elements of the vector $\mathbf{R} (\mathbf{u} )=\left( \begin{array}{ll}g(u, v) \\ h(u,v) \end{array}\right)$ indicate reaction terms for each density which is the second terms in Eq. (10). Without diffusion, the differential equations have homogeneous solution $\mathbf{u} _0=(u_0, v_0)^T$ where $g(u_0, v_0)=h(u_0, v_0)=0$. We assume that the solution is a fixed point, and examine its stability under diffusion.

If we consider small perturbation $\tilde{\mathbf{u }}$ from the homogeneous solution, $\mathbf{u} \cong \mathbf{u} _0+\tilde{\mathbf{u }}$, we get the relation,

$$\begin{aligned} \partial _t\tilde{\mathbf{u }} = \mathbf{D} \nabla ^2\tilde{\mathbf{u }}+\mathbf{J} \tilde{\mathbf{u }}, \end{aligned}$$

(12)

where $\mathbf {J}=(\partial \mathbf {R}/\partial \mathbf {u})_{\mathbf {u_0}} \equiv \left. \left( \begin{array}{ll}g_u&{}g_v \\ h_u&{} h_v \end{array}\right) \right| _{\mathbf {u_0}}$. Subscripts of the g and h mean partial derivative of that variable, e.g. $g_u$ means $\partial g/\partial u$. Decomposing $\tilde{\mathbf {u}}=\sum _k \mathbf {a}_k e^{ik\mathbf {r}}$ based on propagation wave number k gives us relation $\dot{\mathbf {a}_k}=\mathbf {B}\mathbf {a}_k$ where $\mathbf {B}\equiv \mathbf {J}-k^2\mathbf {D}$. Therefore, the stability of the homogeneous solution can be examined by the matrix $\mathbf{B}$. Note that $\mathrm {Tr}(\mathbf{B} )<0$ is guaranteed because $\mathrm {Tr}(\mathbf{J} )<0$. Hence, if the determinant of $\mathbf{B}$ is smaller than zero $[\det (\mathbf{B} )<0]$, it means one of the eigenvalues of the matrix $\mathbf{B}$ is positive. The homogeneous solution becomes unstable and Turing patterns appear.

The condition for $\det (\mathbf{B} )<0$ is given by

$$\begin{aligned} \left( \frac{g_u}{D_c}+\frac{h_v}{D_d}\right) ^2>\frac{4\det (\mathbf{J} )}{D_cD_d}. \end{aligned}$$

(13)

It can be rewritten as following form:

$$\begin{aligned} \frac{D_d}{D_c} > \frac{g_uh_v-2g_vh_u+2\sqrt{-g_vh_u\det (\mathbf{J} )}}{g_u^2}. \end{aligned}$$

(14)

With our model parameters this inequality is equivalent to

$$\begin{aligned} D > \left. \frac{v}{u} \frac{1}{C_u^2} \left[ C_u D_v - 2C_v D_u \left( 1-\sqrt{C_v D_u E} \right) \right] \right| _{u=u^*, v=v^*}, \end{aligned}$$

(15)

where $u^*$ and $v^*$ are values at the fixed point. The symbols indicate

$$\begin{aligned} \left( \begin{array}{ll}C_u&{}C_v \\ D_u&{} D_v \end{array}\right)= & {} \left( \begin{array}{ll}d-w^2\partial _u f_C &{}d-w^2\partial _v f_C \\ d-w^2\partial _u f_D&{} d-w^2\partial _v f_D \end{array}\right) ,\\\nonumber \\\nonumber E= & {} C_v \partial _u f_D - C_u \partial _v f_D + d \partial _u f_C - d\partial _v f_C, \end{aligned}$$

(16)

with $\partial _x y = \frac{\partial y}{\partial x}$. If the above criterion is satisfied, the stable fixed point predicted without diffusion becomes unstable with diffusion (Fig. 5).

Fig. 5

Schematic figure for expected shift of phase boundaries. According to the change of $r_{\mathrm {Hopf}}$, over all phase boundaries may shift together at the same direction. As we have seen in Fig. 4b, the phase boundaries with $r_{\mathrm {Hopf}}$ move to the right with discounting effect and move to the left with synergy effect, respectively. Accordingly, the surviving region in the parameter space expands with synergy effect while it shrinks with discounting effect

3 Discussion

Linear public goods game is a useful approximation of the real nonlinearities in social dilemmas from microbes to macro-life [15, 36, 49] with applications such as in antibiotic resistance [25] as well as cancer [1]. However, taking nonlinearities into account might show different resulting outcomes from naive expectations [13]. Especially, nonlinearities in interactions have a profound effect in ecology when it comes to fecundity and avoiding predation [56, 57]. In this manuscript, we have extended the analysis of spatial public goods games beyond the traditional linear public goods games.

The benefits, in our case, accumulate in a nonlinear fashion in the number of cooperators in the group. Each cooperator can provide a larger benefit than the last one as the number of cooperators increases (resulting in a synergy), or each cooperator provides a smaller benefit than the previous one (thus leading to discounting) [20]. Such an extension to public goods game was proposed very early on by [10]. Termed as superadditivity in benefits, extending from this particular model framework, we can visualise nonlinearities in costs as well, a concept not yet dealt with. Again, such economies of scale [9] can be justified in both bacterial and human interactions as proxies for quorum sensing (or quenching) or accruing of wealth (or austerity) [3, 4, 40].

We show that including such nonlinearities in the benefit function affects the effective rate of return from the public goods game, irrespective of the types of diffusion dynamics. With spatial dynamics, synergy increases the effective rate of return on the investment and expands the region in the parameter space where survival of the population is possible. This itself may make cooperation a favourable strategy. Besides the trivial observation that synergy helps cooperators, we show that as we move symmetrically away from the linear case towards more synergy or discounting, the change in the eventual dynamics is not symmetric. It would be interesting to check if the asymmetry holds for different designs of benefit functions.

We used the particular functional form of the benefit function, including nonlinearities in payoffs [20]. However, there are various ways of including nonlinearities in the benefit function [4, 7, 40]. The model considered in [40] extends the results of [20] to games between relatives. Furthermore, [40] has described the relationships between different nonlinear social dilemma models with a variety of benefit functions. Also these nonlinear social dilemmas have been analysed in a structured population [29, 40, 41]. However, previous studies have focused on the approach presented in [46], which provide a criterion for strategy selection rather than explicitly positioning the populations on a grid and including diffusion. When studying games in structured populations, often a network structure is considered [2, 42]. The role of network connectivity is determined to be critical for the eventual evolutionary outcome [41, 50, 51] and some structures can result in hindering the evolution of cooperation as well [26]. In contrast, our approach focuses more on the ecological framework but not in network structures. We take into account not only the changes in frequencies of cooperators and defectors but also the population dynamics, which is usually missed in a network approach. While both approaches make evolutionary games ecologically explicit, the models are thoroughly different in their setup and implementation.

Fig. 6

The exact colour scheme developed for colouring the patterns. Each patch in a pattern is coloured using this palette by choosing the corresponding f and $\rho$ values. For brightness we used Eq. (17) with $a=15$

The importance of including ecology in evolutionary games has been known for long, but the complexity that it generates has prevented it from garnering widespread attention [11]. Seasonal variations in the rate of return radically change the selection pressures on cooperation and defection. Changes in the ecology may not feedback directly to the frequencies of cooperators and defectors but on to a variable in benefit–cost functions. If the variable affects the frequency of cooperators and defectors (or even the group size) in a nonlinear fashion, then the results are not trivial [13, 38]. Thus, even a simple connection between evolutionary and ecological dynamics may already generate rich dynamics [31, 54], and the feedback between the two is often already convoluted. Similar to [12, 37], it is possible to include feedback between the population dynamics and diffusion here, but together with a nonlinear social dilemma, we envision that the formal analysis and the computational implementation will be a considerable challenge.

Appendix

1.1 Colour Coding

Similar to the colour coding used in [37] we use mint green (colour code: #A7FF70) and Fuchsia pink (colour code: #FF8AF3) colours for denoting the cooperator and defector densities, respectively, for each type. The colour spectrum and saturation is determined by the ratio of cooperators to defectors which results in the Maya blue colour for equal densities of cooperators and defectors. For convenience, we use HSB colour space which is a cylindrical coordinate system $(r, \theta , h)=$ (saturation, hue, brightness). The radius of circle r indicates saturation or the colour whereas $\theta$ helps us transform the RGB space to HSB. The total density of the population $\rho =u+v$ is represented by the brightness h of the colour. For better visualisation, we formulate the brightness h as

$$\begin{aligned} \frac{\log {a\rho +1}}{\log {a+1}}, \end{aligned}$$

(17)

where a control parameter a $(>-1$ and $\ne 0)$ (see Fig. 6). The complete colour scheme so developed passes the standard tests for colour blindness.