Network Invariants and Their Use in Performability Analysis

Abstract

Network-type systems with binary components have important structural parameters known in literature as Signature, Internal Distribution, D-spectra and BIM-spectra. The knowledge of these parameters allows obtaining the probabilistic description of network behaviour in the process of their component failures, and probabilistic description of such network parameters as resilience, component importance, system failure probability as a function of component failure probability q, and the approximation to reliability if q tends to 0. When the network has many components, the exact calculation of Signatures or D-spectra becomes a very complicated issue. We suggest using efficient Monte Carlo procedures. All relevant calculations are illustrated by examples of networks, including flow in random networks and network structural comparison in the process of network gradual destruction process.

Prof. Gertsbakh has sadly passed away prior to the publication of this manuscript.

10.1 Introduction

Reliability and availability [1] are two important probabilistic attributes of performability of any network or system with binary states. This chapter lays down discussion of important structural parameters known as Signature, Internal Distribution, D-spectra and BIM-spectra. Before we do that some definitions are provided to make the discussion meaningful.

10.1.1 Networks, Node and Edge Failures. Success Criteria

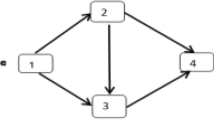
We meet networks every day and everywhere in our life. For the formal study of network properties, we must operate with abstract models of networks. In further, our principal network model will be a triple $N = \left( {V,E,T} \right)$, where V is the vertex or node set, E is the edge or link set and T is a set of special nodes called terminals, $T \in V$. In simple words, a network is a collection of circles (nodes) and links (edges), i.e. line segments connecting the nodes. Terminals are special nodes that do not fail and they are represented as bold circles, like in Fig. 10.1.

Fig. 10.1

Network with six nodes and nine edges. Nodes 1 and 6 are Terminals

Our exposition will be centred around network behaviour when its elements (nodes and/or links) fail. We will deal with so-called binary elements that can be in two states up and down denoted by 1 and 0, respectively. When speaking about links, link i failure means that this link is erased, i.e. it does not exist.

The state of link $i,i = 1, \ldots ,n$ is denoted by binary variable $x_{i}$. If $x_{i} = 1$, link i is up; if $x_{i} = 0$, link i is down. $x_{i}$ is often called link indicator variable. In some models, the elements subjected to failure are network nodes (vertices). If the indicator variable of node j is $y_{j} = 0$, i.e. node j is down, it means that all links incident to node j are erased, but the node itself remains intact. By an agreement, the terminals do not fail.

By network state, we mean the set of all its elements (nodes and edges) that are in up state. We will distinguish network UP (operating) and DOWN (non-operating) states according to a certain criterion.

Below we give several examples of different UP and DOWN criteria. All examples relate to the network are shown in Fig. 10.1. This network has two terminals: 1 and 6.

Terminal Connectivity Criterion. Nodes Unreliable, Edges Reliable

We say that the network is ${\text{UP}}$ if each pair of terminals is connected by a path of non-erased elements. Let node 2 is ${\text{up}}$, and nodes 3, 4, 5 are in the ${\text{down}}$ state. Then the network is ${\text{UP}}$, because the node 2 connects terminals 1 and 6. Let now nodes 2 and 4 are ${\text{down}}$, and nodes 3 and 5—${\text{up}}$. Then the network is DOWN.

Terminal Connectivity Criterion. Edges Unreliable, Nodes Reliable

Suppose that edges (1,2), (2,5) and (5,6) are ${\text{up}}$, and all other edges are ${\text{down}}$. The network is ${\text{UP}}$. Let now the edges (1,2) and (1,4) be ${\text{down}}$, and all other edges are up. The network is ${\text{DOWN}}$.

Max Component and Max Cluster Criteria. Nodes Unreliable

For this example, we need the definition of a component. A subset $V_{1} \subset V$ is called an isolated component of N if all nodes of $V_{1}$ are connected to each other and there are no edges of type $e = \left( {a,b} \right)$, where $a \in V_{1}$ and $b \in V - V_{1}$. An isolated node is considered as an isolated component. The size of a component is the number of nodes in it.

We say that the network is in UP state if the maximal component has at least $x$ nodes, where $x$ is some given number. Suppose that $x = 3$. Let the nodes 3 and 5 are ${\text{up}}$, and the rest of the nodes—${\text{down}}$. Then the maximal component consisting of nodes 3, 5, 6 and edges (3,6), and (5,6) is of size 3, and therefore $N$ is ${\text{UP}}$. Let now nodes 3 and 4 are ${\text{up}}$, and nodes 2, 5 are ${\text{down}}$. Obviously N is ${\text{DOWN}}$.

By the definition, an isolated component of N is called a cluster if it contains at least one terminal node. We say that the network is UP if it contains a cluster of size at least $x$, where $x$ is some given number. Let x = 4. If the nodes 2 and 5 are ${\text{up}}$ and 3, 4 are down, then we have a cluster of size 4, and N is ${\text{UP}}$. If only nodes 3 and 5 are ${\text{up}}$ then we have maximal cluster of size 3, and N is ${\text{DOWN}}$. (Recall that the terminals are always ${\text{up}}$.)

Further we will use the notions ${\text{cut}}$ and min-cut. Appropriate definition follows.

Definition 1

A subset of network unreliable elements $\left( {c_{1} ,c_{2} , \ldots ,c_{k} } \right)$ is called a cut if the following condition is satisfied:

If all these elements are in state ${\text{down}}$, then the network is also in state ${\text{DOWN}}$.

A cut is called minimal (min-cut) if after removing any element, the new subset is no more a cut.

Consider for example, the network in Fig. 10.1 for the case when the nodes are unreliable. The subset of nodes (2, 3, 5) is cut, but not a min-cut. Indeed, if node 3 is removed, the remaining subset (2, 5) is still a cut. It is obvious that (2,5) is min-cut.

10.2 Destruction Spectrum and Network Reliability

10.2.1 D-Spectrum and CD-Spectrum

Definition 2

Let $\pi = e_{{i_{1} }} ,e_{{i_{2} }} , \ldots ,e_{{i_{n} }}$ be a permutation of all unreliable elements (edges or nodes). Start with a network with all elements being up and ‘erase’ the elements in the order they appear in $\pi$, from left to right. Stop at the first element $e_{{i_{r} }}$ when the network becomes DOWN. The ordinal number $r$ of this element is called the ${\text{anchor}}$ of permutation $\pi$ and denoted $r\left( \pi \right)$.

Remark 1

Note that the anchor value for given $\pi$ depends only on the network structure and its DOWN definition. It is completely separated from the stochastic mechanism that governs the node or edge failures in a real network destruction process.

Example 1

Consider the network shown in Fig. 10.1. In this network with two terminals 1 and 6, the edges are reliable and nodes 2, 3, 4, 5 are unreliable. Consider an arbitrary permutation $\pi$ of node numbers, e.g. $\pi = \left( {3,5,2,4} \right)$. We start the destruction process with all nodes in the $up$ state. Erase one node after another in the order prescribed by $\pi$, from the left to right. The network becomes DOWN after erasing the third node, i.e. node 2. So we have $r\left( \pi \right) = 3$.

Definition 3

Let $x_{i}$ be the number of permutations such that their anchor equals $i$. The set

$$D = \left\{ {d_{1} = \frac{{x_{1} }}{n!}, \ldots ,d_{n} = \frac{{x_{n} }}{n!}} \right\}$$

(10.1)

is called the D-spectrum of the network.

Remark 2

‘D’ in Definition 1 refers to the ‘destruction’ process of erasing network elements from left to right in the permutation $\pi$. $D$-spectrum is distribution of the anchor value, and obviously $\sum\nolimits_{i = 1}^{n} {d_{i} = 1}$. Numerically, the $D$-spectrum coincides with the so-called ${\text{Signature}}$ introduced first in (Samaniego 1985, see [2]). It was proved there that if system elements fail independently and their lifetimes $X_{i}$ have identical continuous distribution function $F\left( t \right)$, then the system lifetime distribution $F_{S} (T) = \sum\nolimits_{{i = 1}}^{n} {d_{i} } \cdot F_{{i:n}} \left( t \right)$ where $F_{i:n} \left( t \right)$ is the cumulative distribution function of the $i$ th order statistics in random sample $X_{1} ,X_{2} , \ldots ,X_{n}$.

Example 1

(continued) Table 10.1 shows all 24 permutations of the nodes. The nodes destruction of which caused the failure of the network are marked by asterisk. Directly from this table we get $x_{1} = 0,x_{2} = 8,x_{3} = 10,x_{4} = 6$, and $D$-spectrum of the network equals $\left( {d_{1} = 0,d_{2} = 1/3,d_{3} = 5/12,d_{4} = 1/4} \right)$.

Table 10.1 All permutations of nodes

Definition 4

Let $y_{b} = \mathop \sum \limits_{i = 1}^{b} d_{i} ,b = 1,2, \ldots ,n.$ Then the set $\left( {y_{1} ,y_{2} , \ldots ,y_{n} } \right)$ is called the Cumulative D-spectrum (${\text{CD}}$-spectrum).

Remark 3

Like an anchor, both spectra ($D$ and CD) depend only on the network structure and the definition of network DOWN state. That is, they are ${\text{invariant}}$ with respect to the ${\text{up/down}}$ probabilities of the elements.

The following theorem establishes an important combinatorial property of the ${\text{CD}}$-spectrum.

Theorem 1

Let $C\left( i \right)$ be the number of cut sets of size $i$ in the network. Then

$$C\left( i \right) = y_{i} \cdot \frac{n!}{{i!\left( {n - i} \right)!}}$$

(10.2)

The proof of Theorem 1 can be found in the textbook [3].

Example 1

(continued)

We get the following CD-spectrum of our network: $(y_{1} = 0,y_{2} = 1/3,$ $y_{3} = 3/4,y_{4} = 1)$.

Using formula (10.2), we get: $C\left( 1 \right) = 0,C\left( 2 \right) = 2,C\left( 3 \right) = 3,C\left( 4 \right) = 1$.

10.2.2 Network Reliability and ${\text{CD}}$-Spectrum Monte Carlo

The following theorem gives an expression of network reliability using ${\text{CD - spectrum}}$.

Theorem 2

If all $p_{i} = p$ , then network static reliability $R\left( N \right)$ can be expressed in the following form:

$$R\left( N \right) = 1 - \sum\limits_{i = 1}^{n} {y_{i} \cdot \frac{{n!q^{i} p^{n - i} }}{{i!\left( {n - i} \right)!}}}$$

(10.3)

It is clear that even for relatively small networks, the exact calculation of network CD-spectrum is extremely difficult. Below we present Monte Carlo algorithm for estimating the CD spectrum.

Algorithm 1: Evaluation of CD-spectrum

• 1. Initialize all $a_{i}$ to be zero, $i = 1, \ldots ,n$.

• 2. Simulate permutation $\pi$ of all elements.

• 3. Find out the anchor $r\left( \pi \right)$.

• 4. Put $a_{r} = a_{r} + 1.$

• 5. Put $r = r + 1$. If $r \le n$ GOTO 4.

• 6. Repeat 2–5 $M$ times.

• 7. Estimate $y_{i}$ via $\hat{y}_{i} = \frac{{a_{i} }}{M}$.

Figure 10.2 shows a network with 32 unreliable nodes and 60 reliable edges. Nodes 4, 13, 27, 30 are terminals. Table 10.2 shows CD-spectrum for grid network with unreliable nodes and for terminal connectivity criterion. Table 10.3 shows CD-spectrum for the same network, but with unreliable edges and maximal cluster criterion ($x$ = 25). Both spectra were obtained using algorithm 1 with M = 10,000.

Fig. 10.2

Grid network with 32 unreliable nodes and 60 reliable edges. Nodes 4, 13, 27, 30 are terminals

Table 10.2 Grid CD-spectrum. Nodes unreliable. Terminals T = (4, 13, 27, 30) terminal connectivity criterion

Table 10.3 Grid CD-spectrum. Edges unreliable. Terminals T = (4, 13, 27, 30). Maximal cluster criterion, x = 25

Remark 4

Using CD-Monte Carlo for calculating network reliability has several advantages over other methods, including the following two.

• 1. Since CD-spectrum is an invariant, once estimated it, we can calculate network reliability for any values of $p$.

• 2. Using this method, we avoid the so-called rare event phenomenon [3].

10.2.3 Two Alternative Methods for Evaluating Network Reliability

Method 1: Crude Monte Carlo

A common method for evaluating network reliability is the Crude Monte Carlo (CMC) method. We present below the corresponding algorithm.

Algorithm 2: CMC

• 1. Set $Y = 0$

• 2. For each element $i$, Simulate its state with probability $p_{i}$

• 3. Check the network state in accordance with given criterion

• 4. If the network state is UP Then $Y: = Y + 1$

• 5. Repeat steps 2, 3, 4 $M$ times.

• 6. Estimate $\hat{R}$ as $\hat{R} = \frac{Y}{M}$

In many cases, using CMC gives good results, but unlike the CD-Monte Carlo, it has some drawbacks, including the following two.

• 1. For each $p$ value, it is necessary to restart the simulation process.

• 2. The main disadvantage of CMC is the presence of a rare event phenomenon. That is, if $p \to 1$, then the relative error $r.e.\left( {\text{CMC}} \right) \to \infty$. Therefore CMC is not suitable for evaluating very reliable networks, which is actually an important practical case.

Method 2: Burtin–Pittel Approximation

Burtin–Pittel approximation provides rather accurate network reliability estimates for the case of a highly reliable network and independent and equal element unreliability $q_{i} = q$.

Assume that $q \to 0$, that is the network is highly reliable. Let the number of min-cuts of a minimal size $r$ is equal to $s$.

Then by Burtin-Pittel approximation

$$Q\left( N \right) = 1 - R\left( N \right) \approx s \cdot q^{r} .$$

(10.4)

Note that this approximation was first suggested in a more general form by Burtin and Pittel (see [4]).

We explain this approximation using the example of the network in Fig. 10.1. As we have seen in the above example, the unreliability of this network is $Q\left( N \right) = 1 - R\left( N \right) = 2q^{2} p^{2} + 3q^{3} p + q^{4}$. The main term here (when $q \to 0$) is $2q^{2} p^{2}$, where $2$ is the number of min-cuts of minimal size. Clearly that $2q^{2} p^{2}$ = $2q^{2} \left( {1 + o\left( 1 \right)} \right)$ as $q \to 0$.

Consider now the grid network in Fig. 10.2. Obviously, the minimal size of the min-cuts is 3. All min-cuts of size 3 are as follows: (3,5,10), (7,14,19), (24,29,36), (24,29,34), (24,29,35). So in this case, we get $1 - R\left( N \right) \approx 5 \cdot q^{3}$.

Table 10.4 presents grid network reliability for different values of $p$, calculated using CMC, Destruction Monte Carlo (DMC), both with M = 10,000, and also Burtin-Pittel approximation (B-P). Comparing CMC and DMC we see a good correspondence up to $p = 0.95$. However, starting from $p = 0.99$ reliability values obtained using CMC with M = 10,000 will be 1.

Table 10.4 Grid network reliability by CMC, Destruction Monte Carlo (DMC) and Burtin–Pittel approximation (B–P)

Note that here we see the rare event phenomenon.

For example, we want to estimate the reliability of the order of 0.99999 with relative error at least 10%. (Note that rel.arr. (CMC) = $\frac{\sqrt R }{{\sqrt {M \cdot \left( {1 - R} \right)} }}$.) Then we get M = 10,000,000.

A more detailed comparison of these methods can be found in [5].

As for B-P method, we see that it gives good approximation starting from $p = 0.9$.

10.3 Network Resilience

One of the important concepts in the analysis of the network behaviour under random attack on its elements is network resilience.

Definition 5

Probabilistic resilience [6] Assume that network element failures appear in random order, i.e. all $n!$ orderings are equally probable.

Let N be a network with $n$ elements. The probabilistic resilience ${\text{res}}_{\text{pr}} \left( {N;\beta } \right)$ is the largest number of element failures such that N is still UP with probability $1 - \beta$. Formally,

$${\text{res}}_{\text{pr}} \left( {N,\beta } \right) = \hbox{max} \left\{ {I:\mathop \sum \limits_{i = 1}^{I} P\left( {N,i} \right) \le \beta } \right\}.\#$$

The concepts of resilience and CD-spectrum are closely related. From the CD-spectrum, we can get the network resilience for any $\beta$.

Consider, for example, CD-spectrum shown in Table 10.2, and let $\beta$ = 0.01, 0.05, 0.1, 0.3, 0.5. Then we get:

$$\begin{aligned} & {\text{res}}_{\text{pr2}} \left( {N,0.01} \right) = 2,{\text{res}}_{\text{pr}} \left( {N,0.05} \right) = 6, \\ & {\text{res}}_{\text{pr}} \left( {N,0.1} \right) = 7,{\text{res}}_{\text{pr}} \left( {N,0.3} \right) = 9, \\ & {\text{res}}_{\text{pr}} \left( {N,0.5} \right) = 11. \\ \end{aligned}$$

Consider now CD-spectrum shown in Table 10.3. We get:

$$\begin{aligned} & {\text{res}}_{\text{pr2}} \left( {N,0.01} \right) = 17,{\text{res}}_{\text{pr}} \left( {N,0.05} \right) = 20, \\ & {\text{res}}_{\text{pr}} \left( {N,0.1} \right) = 22,{\text{res}}_{\text{pr}} \left( {N,0.3} \right) = 25, \\ & {\text{res}}_{\text{pr}} \left( {N,0.5} \right) = 27. \\ \end{aligned}$$

Note that resilience is also an invariant of the network, since it depends solely on the network topology and criterion ${\text{UP/DOWN}}$.

10.4 Birnbaum Importance Measure (BIM) and BIM-Spectrum

In this section, we introduce the Birnbaum Importance Measure (BIM) [3, 7] of network element $j$, $j = 1,2, \ldots ,k$. Let network reliability $R\left( {p_{1} ,p_{2} , \ldots ,p_{k} } \right)$ be a function of element reliability $p_{i}$. Then BIM of element $j$ is defined as

$$\begin{aligned} {\text{BIM}}_{j} & = \frac{{\partial R\left( {p_{1} ,p_{2} , \ldots ,p_{n} } \right)}}{{\partial p_{j} }} = R\left( {p_{1} ,p_{2} , \ldots ,1_{j} , \ldots ,p_{n} } \right) \\ & \quad - R\left( {p_{1} ,p_{2} , \ldots ,0_{j} , \ldots ,p_{n} } \right) \\ \end{aligned}$$

(10.5)

BIM has a transparent probabilistic meaning: it is the gain in network reliability received from replacing a down element $j$ by an absolutely reliable one. ${\text{BIM}}_{j}$ gives the approximation to the network reliability $\delta R$ resulted from element $j$ reliability increment by $\delta p_{j}$.

The use of BIM in practice is limited since usually the reliability function $R\left( {p_{1} ,p_{2} , \ldots ,p_{k} } \right)$ is not available in explicit form. However the BIM-spectrum that we define below allows to estimate the element BIM’s without knowing the analytic form of the reliability function [3].

Definition 6

Denote by $Z_{ij}$ the number of permutations satisfying the following two conditions:

• (1) If the first $i$ elements in the permutation are down, then the network is DOWN.

• (2) Element $j$ is among the first $i$ elements of the permutation.

The collection of $z_{ij} = Z_{ij} /k!$ values, $i = 1, \ldots ,k$; $j = 1, \ldots ,k$, is called BIM-spectrum of the network. The set of $z_{ij}$ values for fixed $j$ and $i = 1, \ldots ,k$ is called ${\text{BIM}}_{j}$-spectrum, or the importance spectrum of element $j$.

Example 2

Let us return to the network in Fig. 10.1, and using Table 10.1 calculate one of the $Z_{ij}$ values, say $Z_{42}$. The permutations that satisfy the condition of the above definition are the following: (2,4,3,5), (2,4,5,3), (4,2,3,5), (4,3,5,3). Table 10.5 presents the BIM-spectrum for our network.

Table 10.5 BIM-spectrum for network in Fig. 10.1

The columns in this table are the ${\text{BIM}}_{j}$ spectra.

The following theorem [3] demonstrates how ${\text{BIM}}_{j}$ can be calculated without using the reliability function.

Theorem 3

${\text{BIM}}_{j}$, $j = 1, \ldots ,k,$ equals,

$${\text{BIM}}_{j} = \mathop \sum \limits_{i = 1}^{n} \frac{{n!(z_{i,j} \cdot q^{i - 1} p^{n - i} - \left( {y_{i} - z_{i,j} } \right)q^{i} p^{n - i - 1} }}{{i!\left( {n - i} \right)!}}$$

(10.6)

Note that $y_{k} - z_{kj} = 0$, which means that in the second term of the numerator of (10.6) one can assume that index i changes from 1 to $k - 1$.

Remark 5

BIM-spectrum depends only on the network structure and the definition of network DOWN state. That is, this is ${\text{invariant}}$ with respect to the ${\text{up/down}}$ probabilities of the elements.

The exact calculation of BIM-spectra is a formidable task, but we can estimate the spectra using Monte Carlo approach. An appropriate algorithm [3, 5] simultaneously estimates the CD-spectrum and the BIM-spectra for all network elements.

Sometimes in the problems of analysis and design of networks, we do not need to know the values of the importance of the elements. We want to know how the elements are ranked by importance. The following theorem [3, 5] allows us to compare elements without calculating their BIM’s.

Theorem 4

Suppose the BIM’s for the network are given. Let us fix two indices $\alpha$ and $\beta$, $\alpha \ne \beta$, and the corresponding $Z_{i,\alpha }$ and $Z_{i,\beta }$ values. Then if for all $i,i = 1, \ldots ,k$, $Z_{i,\alpha } \ge Z_{i,\beta }$, then ${\text{BIM}}_{\alpha } \ge {\text{BIM}}_{\beta }$ for all $p$ values.

For the network in Fig. 10.1, comparing the columns in Table 10.5 we get:

$${\text{BIM}}_{2} > {\text{BIM}}_{4} = {\text{BIM}}_{5} > {\text{BIM}}_{3}$$

Additional information on BIM’s can be found in [8].

10.5 Border States

10.5.1 Border States and Reliability Gradient

In this section, we introduce the so-called network border states that are closely related to the reliability gradient.

Definition 7

Reliability gradient vector $\nabla R$ is defined as,

$$\nabla R = \left[ {\frac{\partial R}{{\partial p_{1} }}, \ldots ,\frac{\partial R}{{\partial p_{k} }}} \right]$$

(10.7)

In words: component $i$ of $\nabla R$ is ${\text{BIM}}_{i}$.

For the following definition, it is more convenient for us to determine the state of the network as a vector of element indicator variables, i.e. state ${\mathbf{x}}$ = $\left( {x_{1} , \ldots ,x_{k} } \right)$, where $x_{i} = 1$, if element $i$ is up, and $x_{i} = 0$ otherwise.

Definition 8

Network state ${\mathbf{x}} = \left( {x_{1} , \ldots ,x_{k} } \right) \in {\text{DOWN}}$ is called the ${\text{neighbour}}$ of the state ${\mathbf{y}} = \left( {y_{1} , \ldots ,y_{k} } \right)$ if x differs from y in exactly one position. If ${\mathbf{y}} \in UP$ then we call the x border state. The set of all border states is called the border set and denoted as ${\text{DN}}^{*}$.

Remark 6

It is clear from the definition 8 that the border state and also the border set are network invariants.

Example 3

Consider the network in Fig. 10.1. Its state is determined by the vector of nodes indicators $\left( {x_{2} ,x_{3} ,x_{4} ,x_{5} } \right)$. (Recall that nodes 1 and 6 are terminals.) For example $\left( {x_{2} = 0,x_{3} = 0,x_{4} = 1,x_{5} = 0} \right) \in {\text{DOWN}}$ is the neighbour of $\left( {x_{2} = 1,x_{3} = 0,x_{4} = 1,x_{5} = 0} \right) \in {\text{UP}}$ (and also the neighbour of $\left( {x_{2} = 0,x_{3} = 0,x_{4} = 1,x_{5} = 1} \right) \in {\text{UP}}$). So $x$ is a border state. The border set for our network is

$$\begin{aligned} {\text{DN}}^{*} = & \left\{ {v_{1} = \left( {0,0,0,0} \right),v_{2} = \left( {0,1,0,0} \right),v_{3} = \left( {0,0,1,0} \right),} \right. \\ & \left. {\quad v_{4} = \left( {0,0,0,1} \right),v_{5} = \left( {0,1,1,0} \right),v_{6} = \left( {0,1,0,1} \right).} \right\} \\ \end{aligned}$$

To clarify the connection between border states and gradient, we introduce an artificial evolution process [3, 9] on network elements.

Assume that at $t = 0$ each element is down. Element $i$ is born after random time $\tau_{i} \sim \exp \left( {\mu_{i} } \right)$. After the ‘birth’, the element remains up ‘forever’. Note that for fixed time $t_{0}$, $P(\tau_{i} > t_{0} )$ = $q_{i}$ = ${\text{e}}^{{ - \mu_{i} t_{0} }}$.

The following theorem [3, 9] opens the way to calculating the reliability gradient.

Theorem 5

Let $P\left( {v;t} \right)$ be the probability that the network is in state $v$ at time $t$ . Denote by $\Gamma \left( v \right)$ the sum of $\mu_{i}$ over all set of indices $i$ such that $v + \left( {0, \ldots 1_{i} ,0, \ldots 0} \right) \in {\text{UP}}$ . Formally

$$\varGamma \left( v \right) = \mathop \sum \limits_{{v \in DN^{*} ,v + \left( {0, \ldots ,1_{i} ,0, \ldots ,0} \right) \in {\text{UP}}}} \mu_{i}$$

(10.8)

Then the following equation holds:

$$\nabla R \bullet \left\{ {q_{1} \mu_{1} , \ldots ,q_{k} \mu_{k} } \right\} = \sum\limits_{{v \in DN^{ *} }} {P\left( {v;t} \right)\Gamma \left( v \right)} ,$$

(10.9)

where by $\bullet$ denoted scalar profuct.

We see from the last equation, that knowing the probabilities of border states, we can calculate the reliability gradient. In most cases, the explicit expression of these probabilities is not available. However, formula 10.9 makes possible using the well-known Lomonosov’s algorithm [3, 9] for estimating $P\left( {v;t} \right)$ and $\nabla R$.

Here we restrict ourselves to a brief description of the idea of the Monte Carlo algorithm of estimation the gradient.

First of all, we introduce an evolutionary process on network elements, as described above. We recall that for fixed time $t_{0}$ element $i$ is in the state up with probability $p_{i}$. Now consider a sequence in an evolution process. This sequence starts from a zero state $w_{0}$. Let $\pi = \left( {i_{1} ,i_{2} , \ldots ,i_{k} } \right)$ be some permutation of the network elements, so that $i_{1}$ has a minimum birth time, $i_{2}$ was born the second, and so on. We associate with this permutation a sequence of network states: a state $w_{1}$ in which only $i_{1}$ is up, a state $w_{2}$ with two elements in up, and so on, up to the first state UP. This sequence of states we call the ${\text{trajectory}}$ $w$ = $\left( {w_{0} ,w_{1} , \ldots ,w_{s} } \right)$. Consider, for example, the network with unreliable nodes is shown in Fig. 10.1. Suppose node 4 is born first, node 5 is born next and node 3 is born third. Then we get the following trajectory:

$$w = \{ w_{0} = \left( {x_{2} = 0,x_{3} = 0,x_{4} = 0,x_{5} = 0} \right),$$

$$w_{1} = \left( {x_{2} = 0,x_{3} = 0,x_{4} = 1,x_{5} = 0} \right),$$

$$w_{2} = \left( {x_{2} = 0,x_{3} = 0,x_{4} = 1,x_{5} = 1} \right),$$

$$w_{3} = \left( {x_{2} = 0,x_{3} = 1,x_{4} = 1,x_{5} = 1} \right) \in UP\}$$

Note that $w_{2}$ is one of the border states.

The following is a simplified algorithm for estimating the gradient.

Algorithm 3: Evaluation of Gradient

• 1. Put $\frac{\partial R}{{\partial p_{1} }} = 0$, $i = 1, \ldots ,n$.

• 2. Generate trajectory $w = \left( {w_{0} ,w_{1} , \ldots ,w_{s} } \right)$.

• 3. Find the first $j$ so that $w_{j}$ is a border state.

• 4. Calculate convolution ${\text{Conv}} = P\left( {\tau \left( {w_{j} } \right) \le t_{0} } \right) - P\left( {\tau \left( {w_{j + 1} } \right) \le t_{0} } \right)$,

  where $\tau \left( {w_{j} } \right)$ and $\tau \left( {w_{j + 1} } \right)$ are the birth time of $w_{j}$ and $w_{j + 1}$, respectively.

  For each $x_{i} \in\Gamma \left( {w_{j} } \right)$ calculate $\frac{\partial R}{{\partial p_{1} }}$ = $\frac{\partial R}{{\partial p_{1} }}$ + Conv.

• 5. Put $j = j + 1$. If $j < s$ Goto 4.

• 6. Repeat 2–5 $M$ times.

• 7. For each $i = 1, \ldots ,n$ put $\frac{\partial R}{{\partial p_{i} }}$ = $\frac{\partial R}{{\partial p_{i} }}/M \cdot q_{i}$.

Detailed explanation of the algorithm as well as an analytical expression for calculating the convolution of exponentials are given in [3].

10.5.2 Border States and Availability

Let us now consider the following dynamic model. Each network element, independently of others, alternates between two states: up and down. When element $i$ is up, it has failure rate $\lambda_{i}$. if it is down, it has repair rate $\mu_{i}$. In ${\text{equilibrium}}$ element $i$ is up with probability $p_{i} = \mu_{i} /\left( {\mu_{i} + \lambda_{i} } \right)$. Let $T_{U}$ and $T_{D}$ be the average UP and DOWN periods of the network in equilibrium. Our goal is to find these periods.

It is known [4] that the network availability $Av\left( N \right)$ can be expressed as follows:

$$Av\left( N \right) = R\left( {p_{1} ,p_{2} , \ldots ,p_{k} } \right) = \frac{{T_{U} }}{{T_{U} + T_{D} }}$$

(10.10)

The value $\rho = \frac{1}{{T_{U} + T_{D} }}$ is called network ${\text{DOWN}} \to {\text{UP}}$ transition rate. The following theorem shows the relationship between the transition rate and the border states.

Theorem 6

It can be shown in [3, 9],

$$\rho = \sum\limits_{{v \in DN^{*} }} {P\left( v \right)\Gamma \left( v \right)}$$

(10.11)

Example 4

Consider the network in Fig. 10.1. Assume that node $i$ has failure rate $\lambda_{i}$ and repair rate $\mu_{i}$. Rewrite the network border set obtained above.

$$\begin{aligned} DN^{ *} & = \{ v_{1} = \left( {0,0,0,0} \right),v_{2} = \left( {0,1,0,0} \right),v_{3} = \left( {0,0,1,0} \right), \\ & v_{4} = \left( {0,0,0,1} \right),v_{5} = \left( {0,1,1,0} \right),v_{6} = \left( {0,1,0,1} \right)\} . \\ \end{aligned}$$

Now by (10.11) we get:

$$\begin{aligned} \rho & = P\left( {v_{1} } \right)\mu_{2} + P\left( {v_{2} } \right)\mu_{2} + P\left( {v_{3} } \right)\left( {\mu_{2} + \mu_{5} } \right) \\ & \quad + P\left( {v_{4} } \right)\left( {\mu_{2} + \mu_{4} } \right) + P\left( {v_{5} } \right)\left( {\mu_{2} + \mu_{5} } \right) + P\left( {v_{6} } \right)\left( {\mu_{2} + \mu_{4} } \right). \\ \end{aligned}$$

For convenience, let $\mu_{i} = \mu ,\lambda_{i} = \lambda$, for all $i = 2,3,4,5$. Suppose that $\mu = 4$, $\lambda = 1$. Then $p = 0.8$, $q = 0.2$. Using a little arithmetics, we get $\rho$ = $\mu \left( {q^{4} + 5pq^{3} + 4p^{2} q^{2} } \right)$ = 0.544. Now, easy to get $R\left( N \right) = p + p^{2} - p^{3}$ = 0.928. Finally using (10.10) and (10.11), we obtain: $T_{U} = 1.706$, $T_{D} = 0.132$.

In the case of a large network, the Lomonosov’s algorithm adapted for this purpose is used.

Let $\Omega$ be the set of all trajectories. We can rewrite (10.11) in the following form:

$$\rho = \mathop \sum \limits_{{w \in\Omega }} \left( w \right)P(v|w)\Gamma \left( v \right),$$

where $Pr\left( w \right)$ is the probability of the trajectory $w$ (see [3], Chap. 9), and $v$ is the border state determined by the trajectory $w$. Now, simulating the trajectories and using the corresponding variant of the Lomonosov’s algorithm we obtain the availability estimate.

Remark 7

An extremely efficient Lomonosov’s algorithm is based on ingenious graph-theoretic construction known as an evolution process on so-called Lomonosov’s ‘turnip’ [3], Chap. 9. This algorithm has a number of useful properties. Let us mention some of them.

• 1. The algorithm is a highly effective tool for calculating the reliability of monotone systems, for any criteria UP, and for arbitrary (not necessarily equal) element probabilities up.

• 2. The algorithm avoids the occurrence of a rare event phenomenon. Indeed, a distinctive feature of a rare event is that the relative error in estimating the probability of this event tends to infinity. In the Lomonosov’s algorithm, the random choice of the trajectories does not depend on the probabilities of the elements and this explains the absence of this phenomenon.

• 3. It can be used to evaluate the mean stationary UP and DOWN periods.

• 4. It can be used to evaluate reliability gradient $\nabla R$.

Detailed description of the algorithm and its applications can be found in the book [3], Chap. 9.

10.6 Examples

In this section, we present several examples of using the network invariants described above.

10.6.1 Network Reliability Improvement

Consider the network with unreliable nodes in Fig. 10.2. Assume that all nodes are in state up with probability $p = 0.7$. The network reliability (see Table 10.4) equals then $R = 0.6786$. Our goal is to increase network reliability to $R^{ *} = 0.8$. Suppose it is possible to replace several nodes with more reliable ones, say with up probability $p^{ *} = 0.9$, and we are interested in doing minimal number of such replacements. A good heuristic approach to solve this problem is the following.

First, rank all the nodes in descending order of their BIM’s. Next, successively replace the nodes with more reliable ones until we get the required reliability.

The calculations performed show that all the nodes can be divided into several groups according to their importance. In particular, the first group consists of one node—29, the second group consists of four nodes: 10, 14, 24 and 28. We write it for clarity as follows:

$${\text{BIM}}_{29} > \left( {{\text{BIM}}_{10} = {\text{BIM}}_{14} = {\text{BIM}}_{24} = {\text{BIM}}_{28} } \right)$$

This conclusion is based on the analysis of the network BIM-spectra.

Further, replacing the nodes 29, 10, 14, 24 with more reliable ones, we achieve the desired reliability $R^{ *} = 0.8169$.

Partially, the BIM-spectrum data for the nodes 1, 10, 14, 24, 28, 29 are presented in Table 10.6.

Table 10.6 Grid Network BIM-spectrum. Nodes unreliable. Terminals T = (4,13,27,30)

Spectrum values in the range of 20–32 are not shown. These values are almost the same, since the probability of network failure starting from step 20 is very close to 1, and at step 23 is already equal to 1. From the table, we see that the BIM spectrum values of node 29 are greater than those of the other nodes. Spectrum values for nodes 10, 14, 24, 28 are close and intertwined. Node 1 does not belong to the first two groups.

Remark 8

It should be noted that the problem described above can also be solved taking into account the cost of replacing elements. More information on network analysis and optimal network design can be found in [3, 6].

10.6.2 Resilience of Flow Network

In this section, we consider the flow network. These networks are important in many applications. By the definition, flow network is a directed network, where each edge $\left( {a,b} \right)$ has a flow capacity $c\left( {a,b} \right)$. The flow delivered from $a$ to $b$ cannot exceed $c\left( {a,b} \right)$. Denote by $s$ and $t$ the source and sink nodes of the network. Denote by Maxflow the maximal flow from $s$ to $t$ when all edges are up. We say that the network is in DOWN state if its maximal flow is below some fixed level $\Phi$. (Note that there exists an extensive literature with several fast algorithms for finding the maximum flow in networks.)

Let us consider now the network shown in Fig. 10.3. It has 16 reliable nodes and 30 unreliable and directed edges. The nodes 1 and 16 are the source and sink, respectively. The corresponding capacities are given in Table 10.7. The calculated value of ${\text{Maxflow}}$ equals 26.

Fig. 10.3

Flow network with 16 reliable nodes and 30 unreliable edges

Table 10.7 Edge capacities

Table 10.8 presents 14 values of the network spectra for $\Phi = 10$ and $\Phi = 15$. Based on these spectra, we can obtain the network resilience for different values of $\Phi$. $\Phi = 10$ and $\Phi = 15$. Table 10.9 shows resilience for $\Phi = 10$ and $\Phi = 15$, for some values of $\alpha$.

Table 10.8 Flow network CD-spectrum for $\Phi = 10$ and $\Phi = 15$

Table 10.9 Comparing resilience of flow network for $\Phi = 10$ and $\Phi = 15$

Remark 9

More detailed information on resilience of flow networks can be found in [10]. Note also that in [5] an example of comparing the resilience of networks with the same number of nodes and edges but with different topological structures is given.

10.7 Concluding Remarks

Analysing the text above and the example section, we see that network sustainability analysis involves two types of information. Type A information is of non-stochastic nature and is based on network graph description, node, edge, terminal definitions and UP/DOWN definition of network states.

Four structural invariants have been defined in this paper (Signatures or Internal Distributions), CD-spectrum, BIM -spectrum and Border States) representing type A information.

All further analysis of network performance is done by combining structural invariants with information on the stochastic behaviour of network components subject to failure (edges or nodes), in static or dynamic situations. This information we call of type B. A typical example of combining A and B types of information is given in Sect. 10.6.1 on network reliability improvement.

A special ‘artificial’ variant of B-type information was an assumption that network components subject to failure fail in random and equiprobable manner imitating an external ‘shock’ situation. This shock model allows defining network resilience parameter and compares networks resilience for various versions of their structure.

In conclusion, let us note that this chapter is based on ‘binary’ approach to network structure. The book [11] goes further and introduces networks with several DOWN states. This leads to multi-dimensional invariants. Moreover, also the binary nature of failing edges or nodes can also be generalised, see [11] where in addition to up and down states of failed components, an intermediate third ‘mid’ state has been added.