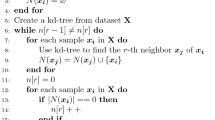Fast Backward Iterative Laplacian Score for Unsupervised Feature Selection

Abstract

Iterative Laplacian Score (IterativeLS), an extension of Laplacian score (LS) for unsupervised feature selection, iteratively updates the nearest neighborhood graph for evaluating the importance of a feature by its local preserving ability. However, LS and IterativeLS separately measure the importance of each feature and do not consider the association of features. To remedy it, this paper proposes an enhanced version of IterativeLS, called fast backward iterative Laplacian score (FBILS). The goal of FBILS is to fast remove some unimportant features by taking into account the association of features. The proposed FBILS evaluates the feature importance according to the joint local preserving ability that reflects the association of features. In addition, FBILS deletes more than one feature in an iteration, which would speed up the process of feature selection. Extensive experiments are conducted on UCI and microarray gene datasets. Experimental results confirm that FBILS can achieve a good performance.

Supported by the Natural Science Foundation of the Jiangsu Higher Education Institutions of China under Grant No. 19KJA550002, the Six Talent Peak Project of Jiangsu Province of China under Grant No. XYDXX-054, and the Priority Academic Program Development of Jiangsu Higher Education Institutions.

1 Introduction

With the development of technology and storage, the dimensionality of data could be very high in many applications, such as image annotation [1], object tracking [5] and image classification [15]. Usually, data may contain irrelevant and redundant information, which would have a negative effect on learning algorithms owing to the curse of dimensionality. As a technique of dimensionality reduction, feature selection has attracted a lot of attention in pattern recognition, machine learning and data mining. Feature selection can eliminate irrelevant and redundant features, which promotes the computational efficiency and keeps the interpretation of reduced description [13, 15].

According to the situations of data labels, feature selection methods can be divided into three types: supervised, unsupervised and semi-supervised ones [2]. Both supervised and semi-supervised methods for feature selection, to some extent, depend on the label information to guide the feature evaluation by encoding features’ discriminative information contained in labels [10]. For unsupervised methods, feature importance is assessed by the ability to maintain specific attributes of data, such as the variance value [4], and Laplacian score (LS) [9]. LS was proposed based on the spectral graph theory and uses a neighborhood graph to determine optimal features. Zhu et al. [17] proposed an iterative Laplacian score (IterativeLS), which progressively changes the neighborhood graph by discarding the least important features in each iteration and assesses the importance of the feature by its Laplacian score value. In each iteration, IterativeLS would reconstruct a neighborhood graph using the rest features. In doing so, higher time complexity is required for IterativeLS. Moreover, both LS and IterativeLS separately measure the importance of each feature and ignore the association of features.

To enhance both LS and IterativeLS, this paper presents a fast backward iterative Laplacian score (FBILS) method for unsupervised feature selection. Inspired by IterativeLS, FBILS also adopts a recursive scheme to select features. FBILS differs from IterativeLS in that it deletes more than one feature at each iteration, greatly reducing the number of iterations. The criterion of evaluating the feature importance in FBILS is to calculate the joint local preserving ability of features, which is totally different from those in both LS and IterativeLS. In summary, FBILS could speed up the process of iterative feature selection and take into account the association of features. The validity and stability of FBILS is confirmed by experimental results.

The remainder of this paper is organized as follows. In Sect. 2, we review two unsupervised methods for feature selection. Section 3 proposes the FBILS method and discusses its properties. In Sect. 4, we conduct experiments on UCI and gene datasets to compare the proposed method with the existing unsupervised methods. This paper is summarized in Sect. 5.

2 Related Methods

This section briefly reviews two unsupervised feature selection methods: LS and IterativeLS, which are very related to our work.

Assume that there is a set of unlabeled data $X=\{\mathbf {x}_{1},\cdots ,\mathbf {x}_{u}\}$, where $\mathbf{x} _i\in \mathbb {R}^{n}$, n is the number of features, and u is the number of samples. Let $F=\{f_1, \cdots , f_n\}$ be the feature set with features $f_k$, $k=1,\cdots ,n$ and $\mathbf {X}\in \mathbb {R}^{u \times n}$ be the sample matrix with row sample vectors $\mathbf {x}_i$, $i=1,\cdots ,u$.

2.1 LS

He et al. [9] proposed LS based on manifold learning. The goal of LS is to select features which can keep the local structure of the original data. That is to say that LS concerns the local structure rather than the global structure of data.

For the given X, LS first constructs the neighborhood graph that can be represented by a weight matrix $\mathbf {S}$:

$$\begin{aligned} S_{ij}={\left\{ \begin{array}{ll} \exp \left\{ -\gamma \Vert \mathbf {x}_i-\mathbf {x}_j\Vert ^2\right\} , &{}\quad if~\left( \mathbf {x}_i \in KNN(\mathbf {x}_j)~\vee ~ \mathbf {x}_j\in KNN(\mathbf {x}_i)\right) \\ 0, &{}\quad otherwise \end{array}\right. } \end{aligned}$$

(1)

where $\gamma >0$ is a constant to be tuned, and $KNN(\mathbf {x}_i)$ denotes the set of K nearest neighbors of $\mathbf {x}_i$.

LS measures the importance of feature $f_k$ by calculating its Laplacian score:

$$\begin{aligned} J_{LS}(f_k)= \frac{\sum _{i=1}^u\sum _{j=1}^u (x_{ik}-x_{jk})^2S_{ij}}{\sum _{i=1}^u (x_{ik}-\mu _k)^2D_{ii}} \end{aligned}$$

(2)

where $x_{ik}$ denotes the kth feature of the ith sample, $\mu _k=\frac{1}{u}\sum _{i=1}^{u} x_{ik}$ is the mean of all samples on feature $f_k$, and $\mathbf {D}$ is a diagonal matrix with $D_{ii}=\sum _j S_{ij}$.

The smaller the score $J_{LS}(f_k)$ is, the more important the kth feature is for keeping the local structure of data. The computational complexity of constructing $\mathbf {S}$ is O$(nu^2)$, and the computational complexity of calculating scores for n features is $O(nu^2)$. Hence, the overall computational complexity of LS is $O(nu^2)$.

2.2 IterativeLS

IterativeLS was presented by introducing the iterative idea into LS [17]. Experimental results in [17] indicated that IterativeLS outperforms LS on both classification and clustering tasks.

The key idea of IterativeLS is to gradually improve the neighborhood graph based on the remaining features. In each iteration, IterativeLS discards the least relevant feature with the greatest score among the remaining features. Similar to LS, IterativeLS evaluates the importance of a feature by its Laplacian score that is calculated according to (2).

Assume that A is the remaining feature subset in the current iteration. Let $|A|=n'$. In the current iteration, the computational complexity of constructing $\mathbf {S}$ is O$(n'u^2)$, and computational complexity of calculating scores for $n'$ features is $O(n'u^2)$. Note that $n' < n$. Hence, the overall computational complexity of IterativeLS is $O(n^2u^2)$ for n iterations.

3 Fast Backward Iterative Laplacian Score

This section presents the novel method for unsupervised feature selection: FBILS, which is an extension of LS. Both LS and IterativeLS measure the importance of features separately using the ability to maintain the local structure that is measured by the Laplacian score. Similar to both LS and IterativeLS, FBILS also considers maintaining the local structure. However, FBILS measures the importance of feature $f_k$ by considering its joint local preserving ability. Similar to IterativeLS, FBILS adopts a recursive scheme. The difference is that IterativeLS discards the least relevant feature with the greatest Laplacian score in each iteration, and FBILS uses a new criterion to remove more than one feature in each iteration. Therefore, FBILS greatly reduces the running time with less iterations.

3.1 Criterion

FBILS iteratively removes features according to a novel criterion, the joint local preserving ability. We first discuss how to measure the joint Laplacian score for feature subsets before we introduce the criterion to measure the importance of feature $f_k$.

Both LS and IterativeLS calculate the Laplacian score of only single feature. Because we want to consider the association between features, we have to calculate the Laplacian score of feature subsets, or joint Laplacian score that is defined as follows.

Definition 1

Given the weight matrix $\mathbf {S}$, the centered sample matrix $\widetilde{\mathbf {X}}_{A}$ and its corresponding feature subset A, the joint Laplacian score of A is defined as

$$\begin{aligned} J(A) =\frac{trace\left( \widetilde{\mathbf {X}}_A^T\mathbf {L}\widetilde{\mathbf {X}}_A\right) }{trace\left( \widetilde{\mathbf {X}}_A^T\mathbf {D}\widetilde{\mathbf {X}}_A\right) } \end{aligned}$$

(3)

where $trace(\cdot )$ is the sum of the diagonal elements of a matrix, $\mathbf {L}=\mathbf {D}-\mathbf {S}$ is the Laplacian matrix, and $\mathbf {D}$ is a diagonal matrix with $D_{ii}=\sum _{j}S_{ij}$.

According to Definition 1, we need to construct the weight matrix $\mathbf {S}$ to represent the neighborhood graph. For the given subset of data $X_A$ that is a part of X and consists of features in A, we need to make it centered, which results in a new set with zero mean. Given these conditions, we can calculate the joint Laplacian score of A by (3). A smaller joint Laplacian score of A means that the local structure can be maintained better by using this feature subset, or A is more important. On the basis of Definition 1, we can describe the novel criterion as follows.

Definition 2

Given the feature set F, a feature subset $A \subseteq F$, and any feature $f_k\in A$, the joint local preserving ability of $f_k$ under A is defined as

$$\begin{aligned} L(f_k|A) = J\left( A-\{f_k\}\right) -J(A) \end{aligned}$$

(4)

where $A-\{f_k\}$ denotes that feature $f_k$ is removed from A, and $J(A-\{f_k\})$ and J(A) are the joint Laplacian scores of feature subsets $(A-\{f_k\})$ and A, respectively.

Definition 2 implies that the joint local preserving ability of feature $f_k$ is related to two joint Laplacian scores. One is J(A) that is the same for all $f_k\in A$. The other is $J(A-\{f_k\})$, the joint Laplacian score of the candidate subset $A-\{f_k\}$. We discuss two cases: $L(f_k|A)>0$ and $L(f_k|A)\le 0$.

• When $L(f_k|A) \le 0$, $J(A-\{f_k\})$ is smaller than or equal to J(A). In other words, the joint Laplacian score does not change or becomes small when feature $f_k$ is removed from A. Note that LS-like algorithms prefer features with small Laplacian scores. In this case, we much prefer the feature subset $A-\{f_k\}$ to the one A. That is, $f_k$ is less important.

• When $L(f_k|A) > 0$, $J(A-\{f_k\})$ is greater than J(A). In this case, it is unwise to remove feature $f_k$ from A.

In summary, the greater the value $L(f_k|A)$ is, the stronger the joint local preserving ability of $f_k$ under A is. Thus, what we need to do is to remove these features with a weak joint local preserving ability. We could follow the way of IterativeLS, or deleting the weakest feature in each iteration. However, it is time-consuming if just one bad feature is removed in an iteration.

One goal of FBILS is to speed up the iterative procedure, which can be implemented by using the following deletion rule:

$$\begin{aligned} \forall f_k\in A, f_k~~ is~~ delected~~ from ~~A, if~~L(f_k|A) \le 0 \end{aligned}$$

(5)

The deletion rule allows us to remove all possible bad features from the current feature subset in one time. The feasibility and reasonability of this rule is discussed later in Subsect. 3.3.

3.2 Algorithm Description

The detail algorithm description of FBILS is shown in Algorithm 1. Quite simply, FBILS requires constructing a neighborhood graph and calculating joint Laplacian scores of feature subsets in each iteration, which is repeated until all features are ranked.

The inputs of FBILS include the given dataset and the parameter K that is required for the neighborhood graph. In the first step, the subset of remaining features A is initialized to be a complete set, or the whole feature set. $\bar{A}$ is the ordered set and $\bar{A}=\emptyset$. Step 3 computes the weight matrix $\mathbf {S}_A$ using the dataset $X_A$ in the current iteration. Step 4 computes the joint Laplacian score of the feature subset A by (3). Steps 5–8 get the joint local preserving ability for all features in A. Step 10 finds out the unimportant features in A with $L(f_k|A) \le 0$ and forms a temporary feature subset B. If B is empty, then FBILS would come to an end. In this case, features in A would be ranked according to the value of $L(f_k|A)$. If B is non-empty, then features in B would be ranked according to their joint local preserving ability. Then the ranked features are inserted in the list $\bar{A}$. Note that the smaller the value $L(f_k|A)$ is, the later is the insertion of the corresponding feature $f_k$ in the list. If B is non-empty, features in B should be removed from A. Repeat Steps 3–18 until A is empty.

Finally, Algorithm 1 greturns the ranking of all features. Assume that the number of features required by a given task is provided in advance, say r. There are two ways to get r features using FBILS. One way is that we can only pick up the r top features in $\bar{A}$ after we perform Algorithm 1. The other way is to change the termination condition in Step 2 as $|A|>r$ and return the remaining feature subset A instead of $\bar{A}$. In Step 20, if $|A|<r$, we would get the $r-|A|$ top features in $\bar{A}$ and put them into A.

3.3 Properties Analysis

This part concerns about the properties of FBILS. We give a lemma and a theorem, and do not prove them for limitation of space.

Lemma 1

For a non-empty feature subset A, its joint Laplacian score is positive, or

$$\begin{aligned} J(A)\ge 0. \end{aligned}$$

(6)

Lemma 1 indicates that the joint Laplacian score of feature subsets are greater than zero. The following theorem is related to our deletion rule (5).

Theorem 1

Let A be the feature subset. For $f_k\in A$, given the joint Laplacian score J(A), the joint local preserving ability $L(f_k|A)$ and the Laplacian score $J_{LS}(f_k)$, the following relationships hold true:

• If $L(f_k|A) > 0$, then $J_{LS}(f_{k}) < J(A)$;

• If $L(f_k|A) \le 0$, then $J_{LS}(f_{k}) \ge J(A)$.

Theorem 1 implies the relationship between the Laplacian score of feature $f_k$ and the joint Laplacian score of the feature subset A containing $f_k$ when $L(f_k|A) \le 0$ or $L(f_k|A) > 0$. When $L(f_k|A) \le 0$, the Laplacian score of $f_k$ is greater than or equal to the joint Laplacian score of A. The deletion rule states that those features with $L(f_k|A) \le 0$ would be removed from the current feature subset. In other words, we would delete all $f_k\in A$ with $J_{LS}(f_{k}) \ge J(A)$, where J(A) is taken as a threshold to make us select more than one feature in one iteration. According to the view of both LS and IterationLS, the greater $J_{LS}(f_{k})$ is, the less important feature $f_k$ is. Thus, our deletion rule is reasonable because it consists with the view.

Now, we analyze the computational complexity of FBILS. Without loss in generality, let A be the remaining feature subset in the current iteration. Let $|A|=n'$. Similar to IterativeLS, the computational complexity of constructing $\mathbf {S}_A$ is O$(n'u^2)$. If we directly compute joint Laplacian scores, which has a computational complexity of $O(n'^2u^2)$, FBILS would be slow. Fortunately, we could speed up this procedure. According to the proof of Theorem 1, the calculation of $J(A-\{f_k\})$ can be reduced. For limitations of space, we do not discuss it any more. Thus, the computational complexity of computing joint Laplacian scores is reduced to be O$(n'u^2)$. Then the overall time complexity of FBILS is between $O(nu^2)$ and $O(n^2u^2)$, which is related to the iteration number. Assume that the iteration number is T, then the complexity is $O(Tnu^2)$.

4 Experimental Analysis

In order to verify the feasibility and effectiveness of FBILS, simulation experiments were carried out on several UCI datasets [7] and microarray gene expression datasets [11]. We compared FBILS with both LS and IterativeLS and used the nearest neighbor classifier to measure the discriminant ability of selected features.

All experiments were performed in MATLAB 2015b and run in a hardware environment with an Intel Core i5 CPU at 2.60 GHz and with 8 GB RAM.

4.1 UCI Dataset

We considered 8 UCI datasets here and compared FBILS with Variance, LS and IterativeLS algorithms. The related information of 8 UCI datasets, including Australian, Glass, Heart, Ionosphere, Segment, soybeanLarge, Vehicle and Wdbc, is shown in Table 1. For these UCI datasets, the original features were normalized to the interval [0, 1]. To validate the ability to select features, we added n noise features to the original data before normalization, where n is the number of features. In the ranked feature list, we only considered the first n features. We thought that a good method for feature selection should rank these noise features towards the end of the list.

In order to obtain more convincing comparison results and eliminate accidental errors, we used 10-fold cross-validation. That is to say, the original dataset was randomly divided into ten equal-sized subsets. Then 9 subsets were used as the training set and the rest one was used as the test set. The 10 subsets were used as test sets in turn, and then the average of 10 times was calculated as the final result of classification. In addition, all compared algorithms require the parameter K for constructing the neighborhood graph. Let it vary in the set $\{1,2,\cdots ,9\}$.

Table 2 shows the highest average accuracy with the corresponding standard deviation and optimal feature number of all compared algorithms, where the best values among compared methods are in bold. We can see that FBILS is superior to Variance, LS and IterativeLS on all datasets. For example, FBILS achieves the accuracy 92.00% on the SoybeanLarge dataset, followed by IterativeLS 90.80%. In a nutshell, FBILS can effectively rank features and make good ones at the top of feature list. Table 3 shows the running time and iteration numbers of FBILS and IterativeLS on the UCI datasets. Owing to the small number of features in UCI datasets, the time required for LS and variance is very small. Thus, we did not list them here. It can be clearly seen that the number of iterations of FBILS is much smaller than IterativeLS, and the running time of FBILS is also less.

Table 1. Description of UCI datasets

Table 2. Average accuracy and standard deviation of different methods on UCI datasets

Table 3. Running time (sec.) and iteration numbers of FBILS and IterativeLS on UCI datasets

Table 4. Description of microarray gene datasets

4.2 Microarray Gene Datasets

In experiments, FBILS was applied to microarray gene datasets, including Leukemia [8], Novartis [6], St. Jude Leukemia (SJ-Leukemia) [16], Lungcancer [3] and the central nervous system (CNS) [12]. It is well-known that the number of features is much greater than the number of samples in the gene datasets. The gene expression datasets we used have been processed as described in [11]. Further biological details about these datasets can be found in the referenced papers. Most data were processed on the Human Genome U95 Affymetrix ©microarrays. The leukemia dataset was from the previous-generation Human Genome HU6800 Affymetrix ©microarray. The relevant information of these datasets is summaries in Table 4.

Here, we also compared FBILS with the unsupervised methods: Variance, LS and IterativeLS. In order to obtain convincing comparison results and eliminate accidental errors, as in the previous section, we used cross-validation. Because the number of samples in datasets is small, three-fold cross-validation was applied. In each trail, we randomly selected 2/3 of the samples as the training set, and the remaining 1/3 of samples as the test set. The experimental results were reported on the well-defined test sets. According to the statement in [14], we can know that we need 400 genes at most to complete the classification task of microarray gene data. Therefore, we analyze on the first 400 top features.

Figure 1 gives the classification accuracy vs. feature number on five microarray gene datasets. From Fig. 1, we can see that FBILS is obviously superior to other three methods on CNS, Lungcancer and Novartis datasets. In addition, FBILS can quickly achieve a better classification performance. We summarized the highest accuracy of compared methods in Table 5 according to Fig. 1, where bold numbers are the best results among compared methods. FBILS algorithm achieves better accuracies on all five gene datasets. On the Leukemia datasets, FBILS has the same accuracy as LS and IterativeLS. On the Lungcancer dataset, the accuracy of FBILS is 1.5% higher than LS. Table 6 shows the running time of the four methods on the gene dataset. The Variance and LS methods are fast without iteration. Two iterative methods, FBILS and IterativeLS take more time. However, it can be clearly seen that FBILS runs many times faster than IterativeLS.

Table 5. Average accuracy and standard deviation comparison on five microarray gene datasets

Table 6. Running time (sec.) of different methods on five microarray gene datasets

Fig. 1.

Accuracy vs. feature number on five gene datasets

5 Conclusion

This paper concentrates on unsupervised feature selection and proposes an algorithm called FBILS. FBILS aims to speed up the iterative process and maintains the local manifold structure. Different from existing LS-like methods, FBILS evaluates the joint locality preserving ability of features instead of Laplacian score, and picks up more than one features in one time. On eight UCI and five microarray gene datasets, a series of experiments were conducted for evaluating the proposed method. FBILS retains the highest classification accuracy on most datasets. From the running time of the UCI and gene dataset, we know that FBILS is much faster than of IterativeLS.