An Inverse Kinematic Code for Cable-Driven Parallel Robots Considering Cable Sagging and Pulleys

Abstract

A key advantage of cable-driven parallel robots, compared to other robot types, is their large workspace. Despite this fact, experiments in previous works have shown that cable-driven parallel robots often cannot fully realize their theoretically estimated workspace in practice.

To remedy this shortcoming, a new inverse kinematic code is developed which considers the previously neglected effects of both cable sagging and pulleys. For a realistic exemplary robot, the new kinematic code yields a $19.5\%$ larger wrench-feasible workspace volume for the catenary-pulley model than previous codes. This result shows that the effects of cable sagging and pulleys should be considered in the kinematic codes, especially for large cable-driven parallel robots.

1 Introduction

Many works in the field of cable-driven parallel robots (CDPR) study their workspace as its large size distinguishes them from other types of robots [8, 11]. The kinematic codes used to control CDPR are commonly based on the standard geometric model [8, section 3.2], which assumes that their cables are straight lines and neglects the effects of their weight and pulleys. Research by Kraus [4, p. 91] and Riehl et al. [10] shows that in practice these simplifications decrease the workspace volume and positioning accuracy of CDPR. To improve these qualities, Kozak et al. [3] apply the catenary model to the cables of CDPR and Goutfarde et al. [1] analyze its combination with a pulley model. Merlet [5] presents an algorithm for finding all solutions of the inverse kinematic problem for the catenary model.

To apply these models on a CDPR in practice, this work introduces a new inverse kinematic code for redundantly constrained CDPR based on a combined catenary-pulley model. This code computes feasible and continuous cable lengths that can be used by a future CDPR controller.

The structure of this work is as follows: Sect. 2 introduces the necessary definitions and assumptions. The catenary-pulley model is derived in Sect. 3.

Based on this model, Sect. 4 develops a new inverse kinematic code. Section 5 evaluates the new code for an exemplary CDPR and compares it to a state-of-the-art one. Finally, Sect. 6 provides the conclusion and outlook.

2 Definitions and Assumptions

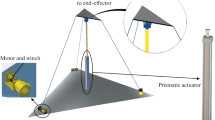
A CDPR consists of $m\in \mathbb {N}$ cables which are used to manipulate the pose $\left( \mathbf{r},\mathbf{R}\right) \in \text {SE}_{3}$ of its platform. Each cable $i\in \left\{ 1,...,m\right\}$ originates from a winch at a fixed point $\mathbf{a}_{i}$ and is wound around a pulley of radius r, with a panning axis $\mathbf{e}_{i}$. The weight of the cable segment on the pulley is neglected. It is assumed that the pulley is statically balanced around its panning axis $\mathbf{e}_{i}$ and that there is no friction in this axis or between the cable and the pulley. The other end of each cable i is connected to the platform at the distal endpoint $\mathbf{b}_{i}$ in the platform coordinate frame $\mathscr {K}_\text {p}$. Its location $\mathbf{r}+\mathbf{Rb}_{i}$ in the world coordinate frame $\mathscr {K}_{0}$ depends on the platform’s position $\mathbf{r}\in \mathbb {R}^3$ and orientation $\mathbf{R}\in \text {SO}_{3}$. The suspended cable between the pulley and the platform is modeled according to Irvine’s catenary model [2] with the parameters: weight force density $\varvec{\mu } g$, Young’s modulus E, and cross-section area A.

Figure 1 illustrates the catenary-pulley model for a cable of a CDPR. All symbols and force vectors associated with this model are highlighted in blue and, for better readability, the cable’s index i is omitted from them.

Fig. 1.

Illustration of the catenary-pulley model for cable i

An unstretched cable length $l_0$ is considered feasible for a given platform pose $\left( \mathbf{r},\mathbf{R}\right)$ if the resulting cable force $\left\| \mathbf {F}_\mathbf {c}\right\| _{}$ in the first section of the cable, at the pulley, lies within the feasible interval $\left\| \mathbf {F}_\mathbf {c}\right\| _{}\in \left[ f_{\min }, f_{\max } \right]$. This condition is imposed on the cable’s force near the winch $\mathbf {F}_\mathbf {c}$ instead of at the platform $\mathbf {F}_\text {p}$, since in practice the maximal cable force $f_{\max }$ of a CDPR is usually constrained by its winches or motors and not the cables themselves.

3 The Catenary-Pulley Model

The catenary-pulley model determines the location of the distal endpoint $\mathbf {d}_i\left( \mathbf {F}_\mathbf {c},l_0\right)$ of a cable i, which is attached to the platform, in $\mathscr {K}_{0}$ as a function of its force $\mathbf {F}_\mathbf {c}$ and unstretched cable length $l_0$. Two sections of the cable are distinguished, which contain the unstretched cable lengths and with .

The first section is wound on the pulley between the points $\mathbf{a}_{i}$ and $\mathbf {c}$, as shown in Fig. 1. The force vector $\mathbf {F}_\mathbf {c}$ defines the direction in which the cable tangentially leaves the pulley at the point $\mathbf {c}$ and its norm $\left\| \mathbf {F}_\mathbf {c}\right\| _{}$ represents the force in the cable at this point. The plane in which the pulley lies is spanned by its panning axis $\mathbf{e}_{i}$ and the orthogonalized direction $\mathbf {e}_{\mathbf {c}}^\perp =\frac{\mathbf {F}_{\mathbf {c}}-\left\langle {\mathbf {F}_{\mathbf {c}},\mathbf {e}_{i}}\right\rangle _{}\mathbf {e}_{i}}{\left\| \mathbf {F}_{\mathbf {c}}-\left\langle {\mathbf {F}_{\mathbf {c}},\mathbf {e}_{i}}\right\rangle _{}\mathbf {e}_{i}\right\| _{}}$ of the cable force $\mathbf {F}_\mathbf {c}$.

Using these axes, the location of $\mathbf {c}$ can be expressed in $\mathscr {K}_{0}$ as

$$\begin{aligned} \mathbf {c}=\mathbf{a}_{i}+r\mathbf {e}_{\mathbf {c}}^\perp +\frac{r}{\left\| \mathbf {F}_{\mathbf {c}}\right\| _{}} \left( \left\langle {\mathbf {F}_{\mathbf {c}},\mathbf {e}^\perp _{\mathbf {c}}}\right\rangle _{}\mathbf {e}_{i} - \left\langle {\mathbf {F}_{\mathbf {c}},\mathbf {e}_{i}}\right\rangle _{}\mathbf {e}^\perp _{\mathbf {c}} \right) \;. \end{aligned}$$

(1)

The wrapping angle $\beta$ of the cable around the pulley from $\mathbf{a}_{i}$ to $\mathbf {c}$ is given by

$$\begin{aligned} \beta =\text {atan2}\left( \left\langle {\mathbf {F}_{\mathbf {c}},\mathbf {e}^\perp _{\mathbf {c}}}\right\rangle _{},\left\langle {\mathbf {F}_{\mathbf {c}},\mathbf {e}_{i}}\right\rangle _{}\right) \;. \end{aligned}$$

(2)

Due to the assumption of no friction between the pulley and the cable, the force $\left\| \mathbf {F}_\mathbf {c}\right\| _{}$ in the cable on the pulley is constant. The unstretched cable lengths of the first and second cable sections are calculated as

(3)

The vertical component of the cable force vector at the platform accounts for the weight of the cable in the second section, i.e. the catenary.

The horizontal cable force components are denoted as $\mathbf {F}_{x,y}=\begin{bmatrix} \left\langle {\mathbf {F}_{\mathbf {c}},\mathbf {e}_x}\right\rangle _{}&\left\langle {\mathbf {F}_{\mathbf {c}},\mathbf {e}_y}\right\rangle _{}&0 \end{bmatrix}^\mathsf {T}$. Hereby, $\mathbf {e}_x$, $\mathbf {e}_y$ and $\mathbf {e}_z$ denote the axes of $\mathscr {K}_{0}$. Finally, the location of the distal endpoint $\mathbf {d}_i\left( \mathbf {F}_\mathbf {c},l_0\right)$ can be calculated in $\mathscr {K}_{0}$, using Irvine’s catenary model [2], as

(4)

With this expression, the loop closure equation of the catenary-pulley model for cable i is formulated as

$$\begin{aligned} \mathbf {d}_i\left( \mathbf {F}_\mathbf {c},l_0\right) -\left( \mathbf{r}+\mathbf{Rb}_{i}\right) =\mathbf {0}\in \mathbb {R}^3 \;. \end{aligned}$$

(5)

The new inverse kinematic code, which is introduced in the next section, requires this equation system to be solved for a feasible unstretched cable length $l_0$ and direction $\left( \theta ,\varphi \right)$ of the cable force $\mathbf {F}_\mathbf {c}$, while its norm $\left\| \mathbf {F}_\mathbf {c}\right\| _{}$ is fixed. For this purpose, the cable force is expressed in spherical coordinates $\mathbf {F}_\mathbf {c} = \begin{bmatrix} \left\| \mathbf {F}_\mathbf {c}\right\| _{}&\theta&\varphi \end{bmatrix}^\mathsf {T}$.

Equation (5) can then be solved for $\left( l_0,\theta ,\varphi \right)$ using numerical methods like Newton-Raphson. Once a solution is found, it is necessary to calculate how the cable forces at the pulley $\mathbf {F}_\mathbf {c}$ and the platform $\mathbf {F}_\text {p}$ change when the unstretched cable length $l_0$ is modified by the winch. These relationships are captured by the partial derivatives $\frac{\partial \mathbf {F}_\text {p}}{\partial l_0}$ and $\frac{\partial \mathbf {F}_\mathbf {c}}{\partial l_0}$. They are derived by taking the derivative $\frac{\text {d}}{\text {d}l_0}$ of the loop closure equation with the constrain that the platform pose $\left( \mathbf{r},\mathbf{R}\right)$ remains constant:

$$\begin{aligned} \mathbf {0}=\frac{\text {d}}{\text {d}l_0}\left( \mathbf {d}_i\left( \mathbf {F}_\mathbf {c},l_0\right) -\left( \mathbf{r}+\mathbf{Rb}_{i}\right) \right) =\frac{\text {d}}{\text {d}l_0}\mathbf {d}_i\left( \mathbf {F}_\mathbf {c},l_0\right) \;. \end{aligned}$$

(6)

This can be reformulated in terms of partial derivatives of $\mathbf {d}_i\left( \mathbf {F}_\mathbf {c},l_0\right)$

(7)

With the relationship obtained from Eq. (3), the partial derivatives of the cable forces can be expressed as

(8)

In the following section, these expressions are used to linearize the catenary-pulley model.

4 An Inverse Kinematic Code for the Catenary-Pulley Model

Inverse kinematic codes for CDPR compute feasible cable lengths $\mathbf {l}_0$ for a given platform pose $\left( \mathbf{r},\mathbf{R}\right)$ and external wrench $\mathbf {w}_{\text {ext}}$. The inverse kinematic code developed in this section is based on the definition of feasible cable lengths from Sect. 2.

It is aimed at redundantly constrained CDPR and inspired by Pott’s force distribution method [7], which uses the least squares solution of the wrench equilibrium equation for the standard geometric model [8, Eq. 5.9 on p. 167] of CDPR as a starting point to calculate feasible cable forces. In contrast to the setting of the standard geometric model, the wrench equilibrium equation for the catenary-pulley model is nonlinear in the cable forces. Therefore, this kinematic code linearizes the cable wrench $\mathbf {w}_{i}$ of each cable i around the unstretched cable lengths $l_0^i$, that are obtained by solving the catenary-pulley model as described in Sect. 3 for the fixed cable force norm $\left\| \mathbf {F}_\mathbf {c}\right\| _{}=\frac{1}{2}\left( f_{\min }+f_{\max }\right)$ in the middle of the feasible interval $\left[ f_{\min }, f_{\max } \right]$. The resulting wrench equilibrium equation is linear in the additional cable length parameters $\varDelta l_0^i$:

$$\begin{aligned} \mathbf {0} = \mathbf {w}_{\text {p}}+\mathbf {w}_{\text {ext}} + \sum _{i=1}^{m}\mathbf {w}_{i} + \sum _{i=1}^{m} \frac{\partial \mathbf {w}_{i}}{\partial l_0}\varDelta l_0^i \;. \end{aligned}$$

(9)

Hereby, $\mathbf {w}_{\text {ext}}$ and $\mathbf {w}_{\text {p}}$ denote the wrenches on the platform due to external influences and the platform mass $m_{\text {p}}$, respectively. The wrench of each cable i and its derivative are given by

$$\begin{aligned} \mathbf {w}_{i} = - \begin{bmatrix} \mathbf {F}_{\text {p}} \\ \mathbf{Rb}_{i}\times \mathbf {F}_{\text {p}} \end{bmatrix} \quad \text {and} \quad \frac{\partial \mathbf {w}_i}{\partial l_0} = - \begin{bmatrix} \frac{\partial \mathbf {F}_\text {p}}{\partial l_0} \\ \mathbf{Rb}_{i}\times \frac{\partial \mathbf {F}_\text {p}}{\partial l_0} \end{bmatrix} \;. \end{aligned}$$

(10)

The vectors $\mathbf {F}_{\text {p}}$ and $\frac{\partial \mathbf {F}_\text {p}}{\partial l_0}$ are calculated from the solution of the catenary-pulley model as described in Sect. 3. The parameters $\varDelta l_0^i$ are determined as the least squares solution of Eq. (9).

Similarly, as in [7], the cable lengths $l_0^i+\varDelta l_0^i$ are further modified to comply with the force limits $f_{\min }$ and $f_{\max }$. It is checked whether for all cables $i\in \left\{ 1,...,m\right\}$, the cable force at the pulley lies within the feasible interval

$$\begin{aligned} \left\| \mathbf {F}_\mathbf {c}+\frac{\partial \mathbf {F}_\mathbf {c}}{\partial l_0}\varDelta l_0^i\right\| _{} \in \left[ f_{\min }, f_{\max } \right] \;. \end{aligned}$$

(11)

If this is not true for all cables $i\in \left\{ 1,...,m\right\}$, the cable j whose force is the furthest outside of the feasible interval is selected. Its force is reset to the limit which it previously violated, e.g. $f_{\max }$, by recalculating $\varDelta l_0^j$ as a root of the quadratic equation

$$\begin{aligned} f_{\max }^2= \left\| \mathbf {F}_\mathbf {c}+\frac{\partial \mathbf {F}_\mathbf {c}}{\partial l_0}\varDelta l_0^j\right\| _{}^2 = \left\| \frac{\partial \mathbf {F}_\mathbf {c}}{\partial l_0}\right\| _{}^2 \left( \varDelta l_0^j\right) ^2 +2\left\langle {\mathbf {F}_\mathbf {c},\frac{\partial \mathbf {F}_\mathbf {c}}{\partial l_0}}\right\rangle _{}\varDelta l_0^j +\left\| \mathbf {F}_\mathbf {c}\right\| _{}^2 \;. \end{aligned}$$

(12)

Since the cable force previously violated the force limit, this quadratic equation must have two distinct, real roots. Regardless of which limit was violated, $\varDelta l_0^j$ is set to be the larger or smaller root of Eq. (12) depending on whether the sign of $\left\langle {\mathbf {F}_\mathbf {c},\frac{\partial \mathbf {F}_\mathbf {c}}{\partial l_0}}\right\rangle _{}$ is positive or negative. Based on this new value of $\varDelta l_0^j$, the wrench $\mathbf {w}_j$ in Eq. (9) is updated according to Eq. (10) with the new cable force at platform $\mathbf {F}_\text {p}+\frac{\partial \mathbf {F}_\text {p}}{\partial l_0}\varDelta l_0^j$. The term containing $\varDelta l_0^j$ is subsequently removed from Eq. (9) as the length and force of cable j are now fixed. A new least squares solution for the remaining parameters $\varDelta l_0^i$ with $i\in \left\{ 1,...,m\right\} \setminus \left\{ j \right\}$ is calculated.

This procedure of updating $\mathbf {w}_j$ for the cable j that violates the condition from Eq. (11) the most, removing the corresponding term $\varDelta l_0^j$ from Eq. (9) and computing a new least squares solution of the wrench equilibrium for the remaining cable parameters $\varDelta l_0^i$, is repeated until either Eq. (11) is satisfied for all cables, or the solution for the remaining six parameters $\varDelta l_0^i$ is infeasible.

To reduce the error due to the linearization of the catenary-pulley model, the steps, which are described until here, are repeated a second time for the remaining parameters $\varDelta l_0^i$. Hereby the catenary-pulley model of each such cable i is recalculated for the fixed cable force norm of either $\left\| \mathbf {F}_{\text {c}}+\frac{\partial \mathbf {F}_\mathbf {c}}{\partial l_0}\varDelta l_0^i\right\| _{}$ or a limit of the feasible interval $\left[ f_{\min }, f_{\max } \right]$ if it was violated.

If Eq. (11) is now satisfied for all cables, the inverse kinematic code has found feasible cable lengths $l_0^i+\varDelta l_0^i$ for the pose $\left( \mathbf{r},\mathbf{R}\right)$ and external wrench $\mathbf {w}_{\text {ext}}$.

Otherwise, it failed and considers the given pose unfeasible.

5 Comparison to a State-of-the-Art Inverse Kinematic Code

In this section, the new inverse kinematic code is compared to a state-of-the-art code in terms of the resulting workspaces and cable forces for an exemplary CDPR.

The state-of-the-art inverse kinematic code is a combination of the force distribution method from [7] and the pulley kinematics from [6].

The workspace of the CDPR is calculated by composing the new or the state-of-the-art inverse kinematics with a forward kinematics of the catenary-pulley model.

A platform pose $\left( \mathbf{r},\mathbf{R}\right)$ is within the workspace if, for the given external wrench $\mathbf {w}_{\text {ext}}$, the resulting cable forces are feasible according to the definition from Sect. 2.

As part of this work, all kinematic codes and the following comparison are implemented in WireX [9], an open source analysis and design software for CDPR.

The exemplary CDPR consists of $m=8$ cables described by the catenary-pulley model with parameters resembling steel cables: $\mu g=6\,\frac{{\text {N}}}{{\text {m}}}$, $EA=7\cdot 10^{6} \,\text {N}$, $r=0.25 \,\text {m}$. The geometry of the cable robot $\left\{ \mathbf{a}_{i},\mathbf{b}_{i}\right\} _{i=1}^m$ is given by all sign combinations of the vectors $\mathbf{a}_{i}=\begin{bmatrix} \pm 5.0\,\text {m}&\pm 6.0\,\text {m}&\pm 2.5\,\text {m} \end{bmatrix}^\mathsf {T}$ and $\mathbf{b}_{i}=\begin{bmatrix} \pm 0.5\,\text {m}&\pm 0.3\,\text {m}&\mp 0.4\,\text {m} \end{bmatrix}^\mathsf {T}$. The panning axes of the pulleys are $\mathbf{e}_{i}=\begin{bmatrix} 1&0&0 \end{bmatrix}^\mathsf {T}$ for $i \in \left\{ 1,2,5,6\right\}$ and $\mathbf{e}_{i}=\begin{bmatrix} -1&0&0 \end{bmatrix}^\mathsf {T}$ for $i \in \left\{ 3,4,7,8\right\}$. The cable force limits are $f_{\min }=1000\,\text {N}$ and $f_{\max }=10000\,\text {N}$. The external wrench $\mathbf {w}_{\text {ext}}$ is set to be zero. The wrench induced by the platform’s weight force $m_{\text {p}}g=8000\,\text {N}$ is $\mathbf {w}_{\text {p}} = \begin{bmatrix} 0&0&-m_{\text {p}}g&0&0&0 \end{bmatrix}^\mathsf {T}$, since its center of mass is at the origin of $\mathscr {K}_\text {p}$.

The workspace of the new inverse kinematics code for this CDPR has a volume of $157.2\,\text {m}^3$ and fully contains the one of the state-of-the-art code, which has a volume of $131.6\,\text {m}^3$. This $19.5\%$ increase can be attributed to the consideration of the nonlinear effects of cable sagging and pulleys.

Figure 2 shows a slice of the workspaces of the new (yellow) and the state-of-the-art code (green) in the XY-plane.

Fig. 2.

Workspace comparison in the XY-plane

Along the black line, which starts at the center of the robot geometry and lies within the plane, the cable forces of the new and the state-of-the-art code are visualized in Fig. 3 in yellow and green, respectively.

Fig. 3.

Evolution of cable forces along a straight line

It can be observed that the new inverse kinematic code produces continuous cable lengths and forces. From the start until the $2.4\,\text {m}$ mark, its forces are similar to those of the state-of-the-art code From that point on, one cable force of the new code is set to the force limit $f_{\max }$. At $3.2\,\text {m}$, the forces of the state-of-the-art code become unfeasible while the new code continues to find feasible cable lengths until a distance of $4.6\,\text {m}$ from the center.

The averaged computation time for one evaluation of the workspace criterion is $5.7\cdot 10^{-3}\,\text {s}$ for the new code and $4.0\cdot 10^{-3}\,\text {s}$ for the state-of-the-art code, as measured on a laptop with an Intel^® Core™ i5-7440HQ CPU running at 2.80 GHz.

The new code is slower because it requires solving the nonlinear catenary-pulley model for each cable as described in Sect. 3.

6 Conclusion and Outlook

This work presents a new inverse kinematic code for redundantly constrained CDPR that considers the effects of cable sagging and pulleys. For an exemplary CDPR, the new code yields continuous cable forces and a $19.5\%$ larger workspace volume than a state-of-the-art code. This shows that considering the catenary-pulley model in the kinematic codes of CDPR can substantially increase the size of their workspace.

Future research could prove that the new code is indeed continuous as observed in this work. Furthermore, it should be implemented on a CDPR to evaluate its performance in practice.