Abstract
Peirce’s \(\beta \) variant of Existential Graphs (EGs) is a diagrammatic formalism, equivalent in expressive power to classical first-order logic. We show that the syntax of EGs can be presented as the arrows of a free symmetric monoidal category. The advantages of this approach are (i) that the associated string diagrams share the visual features of EGs while (ii) enabling a rigorous distinction between “free” and “bound” variables. Indeed, this diagrammatic language leads to a compositional relationship of the syntax with the semantics of logic: we obtain models as structure-preserving monoidal functors to the category of relations.
In addition to a diagrammatic syntax for formulas, Peirce developed a sound and complete system of diagrammatic reasoning that arose out of his study of the algebra of relations. Translated to string diagrams we show the implied algebraic structure of EGs sans negation is that of cartesian bicategories of relations: for example, lines of identity obey the laws of special Frobenius algebras. We also show how the algebra of negation can be presented, thus capturing Peirce’s full calculus.
This research was supported by the ESF funded Estonian IT Academy research measure (project 2014-2020.4.05.19-0001).
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
1 Introduction
Peirce’s Existential Graphs (EGs) arose out of his continued study and development of the algebra of relations. As a diagrammatic calculus, EGs use lines to represent identity, conjunction and existence and nested circles (Peirce’s notion of the “cut”Footnote 1) to capture negation. These graphical elements are drawn on the sheet of assertion: the blank page upon which a graph is scribed. Our focus is on the algebra of the \(\beta \) variant of EGs, which we treat as string diagrams. The resulting language, which we call \(\mathsf {D\beta }\), shares the same visual features of EGs.
We argue that Peirce’s \(\beta \) is closely related to the algebraic structure of cartesian bicategories of relations [7]. Indeed, lines of identity, as string diagrams, obey the laws of special Frobenius algebras, while derivations in the negation-free fragment are the 2-cells of free cartesian bicategories. We identify the additional rules needed to handle negation, which are adapted from Peirce’s calculus of diagrammatic reasoning. Throughout, we argue that Peirce’s seminal studies led him to intuitions that suggest that he—at least implicitly—identified the very same algebraic structures.
While \(\mathsf {D\beta }\) is visually similar—we joke that a diagram in \(\mathsf {D\beta }\) looks like an EG if you squint—it is important to highlight some differences. Making the Frobenius structure explicit in \(\mathsf {D\beta }\) imposes more rigour on lines of identity. Relations in \(\mathsf {D\beta }\) have left and right wires corresponding to arity/co-arities of the relations. This may actually help the presentation of graphs in EGs as Peirce sometimes imposes an order on relations that is not directly read off the ligatures. An explicit Frobenius structure gives the flexibility of rearranging wires as needed, so expressivity is not lost, but also allows us to have a definite ordering, which is useful in many examples. This amendment, maintaining the visual features while being more definite/exact, may very well be a welcome addition.
Perhaps more significantly, in order to achieve compositionality, the string diagrammatic account forces us to keep track of bound and free variables in a more precise way than in Peirce’s original EGs. Indeed the existential in the name of EGs means that scribing a graph on the sheet of assertion is to assert the existence (i.e. the quantification) of the respective predicate/variable. EGs have, as Zeman has put it, “implicit quantification” [19]. Treatment of free and bound variables in modified versions of EG (see [4, 10]) equip EGs with additional structure. The string diagrammatic language \(\mathsf {D\beta }\) makes this treatment quite natural—the result is less cumbersome than the technology of variable management (e.g. \(\alpha \)-conversion, capture-avoiding substitution) often waved through at the start of many traditional courses on predicate logic.
Brady and Trimble have previously developed a string diagrammatic account of EGs [2, 3], relying as we do on monoidal categories and in particular, the poset-enriched monoidal category of relations as a semantic universe for logic. However, their string diagrams are geometric/topological entities. Instead, we emphasize their syntactic nature, which allows, e.g. to define the notion of model as simple inductive procedure, not unlike Tarski’s compositional semantics for predicate logic. Moreover, we work in the framework of (poset enriched) props [11], which emphasizes the algebraic structure borne by the underlying monoidal category.
In the discussion below we assume some familiarity with the reading and transformation (i.e. inference) rules of EGs. For a lengthier introduction to Peirce’s EGs, and one that includes a description of Peirce’s transformation rules, see [17]. Further accounts can be found in [4, 9, 18], and the introduction in [15]. For an introduction to Peirce’s compositional/valental account of relations, see [17, p. 113–118]. A contemporary presentation can be found in [5].
Structure of the Paper. In Sect. 2 we introduce \(\mathsf {D\beta }\) and show how to translate it to and from traditional syntax. In Sect. 3 we introduce the structure of cartesian bicategories, which informs the notion of model of the logic, introduced in Sect. 4. We identify iteration laws of this structure with the cut in Sect. 5 and conclude with a worked example of diagrammatic reasoning in Sect. 6.
2 String Diagrams as Syntax
We start with Peirce’s valental theory of relations, inspired by the theory of valence in chemistry, where elements have open bonds that act as attachment points from which more complex compounds and molecules can be built. Relations are thus seen as having analogous open bonds that can be filled and combined with other relations to form more complex relations.
Consider the ‘loves’ relation, which in usual FOL syntax is written \(\mathsf {loves}(x,y)\). The relation remains indefinite insofar as the objects/subjects of the relation are unspecified, i.e. the variables x and y remain free. Peirce adds “blanks” or “hooks” as graphical placeholders to represent the unspecified objects/subjects, which when filled, “complete the relation”. In our example ‘loves’ is a dyadic relation, and we represent hooks as “dangling” wires, arriving at
 . Filling in the hooks/connecting the wires in the diagrammatic notation is an analogous operation to passing from free to bound variables in the usual FOL syntax.
. Filling in the hooks/connecting the wires in the diagrammatic notation is an analogous operation to passing from free to bound variables in the usual FOL syntax.
Specific relations are combined by joining free hooks together with what Peirce calls a line of identity. A line of identity asserts the identity of each object/subject at its endpoints. We represent lines of identity with the generators  of a monoid-comonoid pair. Consider the diagrams below.
of a monoid-comonoid pair. Consider the diagrams below.

Reading from left to right, the first diagram is the conjunction of the \(\mathsf {is\ a\ pear}\) and \(\mathsf {is\ ripe}\) relations where the hooks are unfilled/wires are dangling. In usual FOL syntax, \(\mathsf {is\ a\ pear}(x)\wedge \mathsf {is\ ripe}(y)\). In the second diagram the hooks are filled/wires are capped off with a unit generator. In usual FOL syntax, \(\exists x.\;\mathsf {is\ a\ pear}(x)\wedge \exists y.\;\mathsf {is\ ripe}(y)\). In the third, using the comultiplication generator the two wires have been equated but there is a dangling wire to the left; \(\mathsf {is\ a\ pear}(x)\wedge \mathsf {is\ ripe}(x)\). In the final diagram the wire has been capped off: \(\exists x.\; \mathsf {is\ a\ pear}(x)\wedge \mathsf {is\ ripe}(x)\).
The syntax of \(\mathsf {D\beta }\) below follows Peircean considerations. Let \(\varSigma \) be a monoidal signature: symbols R each with an arity \(ar(R)\in \mathbb {N}\) and coarity \(coar(R)\in \mathbb {N}\).
Example 1
The signature for our running example is
with \(ar(\mathsf {adores})=coar(\mathsf {adores})=1\), \(ar(\mathsf {is\;a\;woman})=ar(\mathsf {is\;a\;catholic})=1\), \(coar(\mathsf {is\;a\;woman})=coar(\mathsf {is\;a\;catholic})=0\). The diagrammatic convention for an element \(R\in \varSigma \) is to draw it as a box, with \(ar(R)\) wires, ordered from top to bottom, “dangling” on the left and, similarly, \(coar(R)\) wires on the right. Thus:

Below we define our recursively defined syntax using BNF notation. These are the basic syntactical elements from which terms in \(\mathsf {D\beta }_\varSigma \) are constructed.Footnote 2



At this point, the diagrammatic elements of the syntax in (1) and (2) ought to be considered as mere symbols that denote constants. The operations are given in (3): two binary operations ‘\(\mathrel {;}\)’, ‘\(\oplus \)’ and one unary operation \({\bullet }^-\). These have their own diagrammatic convention: \(c \mathrel {;}c'\) is drawn
 , \(c \oplus c'\) is drawn
, \(c \oplus c'\) is drawn
 , and \({c}^-\) is drawn
, and \({c}^-\) is drawn
 . Roughly the operations here can again be seen in terms of our relational story from above. ‘\(\oplus \)’ allows us to scribe relations adjacent to each other (i.e. in parallel) on the sheet, ‘\(\mathrel {;}\)’ allows us to wire relations together in series (similar to connecting relations via lines of identity), and placing a relation inside a cut expresses its negation/complement.
. Roughly the operations here can again be seen in terms of our relational story from above. ‘\(\oplus \)’ allows us to scribe relations adjacent to each other (i.e. in parallel) on the sheet, ‘\(\mathrel {;}\)’ allows us to wire relations together in series (similar to connecting relations via lines of identity), and placing a relation inside a cut expresses its negation/complement.
As opposed to the usual syntax of FOL, ours (1) (2) (3) does not have variables, nor variable binding. The price is an inductive discipline, given in Fig. 1. Intuitively, it keeps track of “dangling” wires—terms are associated with a sort, a pair of natural numbers \((n,\,m)\) that counts the wires on the left and on the right—and ensures that for a term \(c\mathrel {;}c'\), c and \(c'\) have the right number of wires on their corresponding boundaries so that ‘\(\mathrel {;}\)’ as “connecting wires” to make sense. It is easy to prove that if a term has a sort, it is unique.
Example 2
The term  has no sort and no diagrammatic depiction. On the other hand
has no sort and no diagrammatic depiction. On the other hand  . Given the signature of Example 1, consider the term
. Given the signature of Example 1, consider the term  with sort \((0,\,0)\). Using the diagrammatic conventions yields the following, where the dotted-line boxes play the role of the parentheses.
with sort \((0,\,0)\). Using the diagrammatic conventions yields the following, where the dotted-line boxes play the role of the parentheses.

It is not difficult to see that sorted terms are in 1-1 correspondence with such diagrams, provided that enough dotted-line boxes are inserted to disambiguate the associativity of ‘\(\mathrel {;}\)’ and ‘\(\oplus \)’ and the priority between them.
2.1 Translating to and from Traditional Syntax
The (traditional) syntax below is expressive enough to capture first order logic, containing equality, relation symbols, existential quantification and negation.

To ease the translation between the diagrammatic and the traditional, we introduce a half-way formalism that constraints the syntax FOL with explicit free-variable management. This is a mild extension of a similar calculus in [1, Sec. 2] where an analogous translation is given, albeit without the presence of negation.



The idea is that a judgment \(n\vdash \varPhi \) expresses the fact that \(\varPhi \) is a formula with free variables from the set \(\{x_0,x_1,\dots ,x_{n-1}\}\). Indeed, we have the following:
Proposition 1
A formula \(\varPhi \) with free variables in \(\{x_0,x_1,\dots ,x_{n-1}\}\) is derivable from (FOL) if and only if \(n\vdash \varPhi \).
Using the above, we can present a translation \(\Theta \) from (FOL) to \(\mathsf {D\beta }\) by induction on the derivation of \(n\vdash \varPhi \). The rules are given in Fig. 2. A similar translation can be given from \(\mathsf {D\beta }\) to (FOL). Another important fact is that the translations respect the underlying semantics of the logics—due to space restrictions we are not able to show this here. We shall introduce the semantics of \(\mathsf {D\beta }\) in Sect. 4.
Example 3
Referring to Example 2, the formula expressed by the diagram is
2.2 String Diagrams
In order not to clutter diagrams with dotted-line boxes, we will not consider raw terms, but terms quotiented by the laws of symmetric strict monoidal categories [11, 12] of a particularly simple nature: the set of objects is the natural numbers and \(m \oplus n {\mathop {=}\limits ^{\mathrm {def}}}m + n\). Such categories are called props. Some care has to be taken with the \({\bullet }^-\) operation, which is not standard: we introduce a simple extension to the usual definition below.
Definition 1
A prop \(\mathbb {X}\) with a unary operation on homsets (uoh-prop) is a prop with a family of operations \({}^-_{m,n}:\mathbb {X}[m,n]\rightarrow \mathbb {X}[m,n]\), where \(m,n\in \mathbb {N}\).
We are ready to define the notion of syntax we will use throughout the paper.
Definition 2
(Syntax). Let \(\mathsf {D\beta }\) be the uoh-prop where arrows \(m\rightarrow n\) are (m, n)-sorted terms, modulo the laws of symmetric monoidal categories. The additional unary operation on homsets is given by \({\bullet }^-\).
While Definition 2 emphasises the construction of terms from the grammar, \(\mathsf {D\beta }\) has an extremely concise mathematical description: it is the free uoh-prop on \(\varSigma \). The characterisation of \(\mathsf {D\beta }\) as a free algebraic structure is important: first, it means that our string diagrams are a bona fide notion of syntax, not unlike usual syntax trees. Second, just as syntax admits elegant inductive definitions (not unlike, for instance, Tarski’s semantics of first order logic), in order to define a structure preserving translation (homomorphism of uoh-props) from \(\mathsf {D\beta }\) to some target semantic universe (some uoh-prop), it suffices to define the target of the constants (1). We shall use this for the concept of model in Sect. 4.
Example 4
For the category-theory uninitiated reader, let us give an intuitive summary of the algebraic structure given by Definition 1, used in Definition 2.
-
the two composition operations are strictly associative, e.g.

This means the result is the same irrespective of the order we compose, i.e. whether we start with the adored woman or the adoring catholic.
-
the two composition operations are compatible, e.g.

-
the first two constants of (2) are identities; the first the identity on 0, the second the identity on 1. This means, e.g.

The combination of identity laws and the compatibility of ‘\(\mathrel {;}\)’ with ‘\(\oplus \)’ means that unconnected components can be “slid” past each other, e.g.
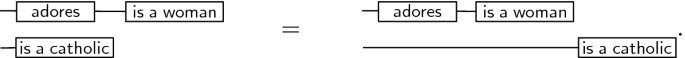
In Peirce’s EGs these features are built directly into the conventions of the sheet of assertion. The identities follow from the properties of composition with a blank sheet or with a line of identity. In regards to composition and associativity on the sheet itself, Peirce writes: “If two propositions are written, detached from one another, on the sheet of assertion, both are asserted, regardless of whether one is to the right, to the left, at the top, or at the bottom of the other...If three or more propositions are all written, detached from one another, on the sheet of assertions, the logical relation of any pair of them is the same as that of any other pair” [16, p. 488].
-
the last constant of (3) is a symmetry. This means that diagrams constructed from it and the identity “behave” as permutations, e.g.

and arbitrary diagrams can “slide” across symmetriesFootnote 3, e.g.

3 The Algebra of Lines of Identity
In this section we identify some of the algebraic structure of \(\mathsf {D\beta }\) that will, in Sect. 5, result in a calculus for diagrammatic reasoning. In addition, the structure introduced here will allow us to specify the correct concept of model in Sect. 4.
Figure 3 depicts the laws of cartesian bicategories (of relations)
[7]. Equations (coas), (coco), (counl) say that  is a cocommutative comonoid, while (as), (co), (unl) say that
is a cocommutative comonoid, while (as), (co), (unl) say that  is a commutative monoid.
is a commutative monoid.
The three equations (fr) are the Frobenius equations. While any two of the three can be used to derive the others, all three are useful in diagrammatic reasoning. The equation (sp) is the so-called “special” law. The equations thus far define what is usually referred to as a (commutative) special Frobenius bimonoid.
It is worth reflecting on how these laws are captured in Peirce’s EGs. As mentioned previously, associativity and commutativity are built into the conventions of the sheet of assertion, where the order of composition of relations on the sheet is immaterial. Each of the other rules can be seen as following from the combination of monadic, dyadic, triadic identity elements. (unl) and (counl) are equivalent to being able to add a branch to any line of identity. Peirce called this triadic identity element, where a branch forms a point with three extending wires, the teridentity relation. Peirce’s interpretation of this rule in EGs, given in a letter to Lady Welby, is worth quoting: “every line of identity ought to be considered as bristling with microscopic points of teridentity” [14].Footnote 4
The (fr) and (sp) equations can be seen as observations about the composition of teridentity relations. Two teridentity relations brought together by connecting two of each of the three wires is equivalent to a single (dyadic) line of identity. This yields the (sp) equation. Similarly, the various combinations of two teridentity relations connected through one wire likewise yield the (fr) equalities. Peirce is explicit about the interpretation of this rule in his EGs. He writes: “Quateridentity [Peirce’s term for a point with four extending wires] is obviously composed of two teridentities; i.e. This
 is
is
 or
or
 or
or
 [14]. Clearly, Peirce had the topological intuitions conveyed by the Frobenius structure.Footnote 5
[14]. Clearly, Peirce had the topological intuitions conveyed by the Frobenius structure.Footnote 5
Notice that (wh1) and (wh2) are not equalities and as such, in subsequent diagrammatic reasoning, derivations can only use them left-to-right. Moreover, they use the diagrammatic convention where a wire with a natural number label m stands for m wires stacked on top of each other. The inequations (wh1) and (wh2) specify that all arrows are weakly homomorphic w.r.t. the comonoid structure. In cartesian bicategories, moreover, the monoid structure is required to be right adjoint to the comonoid structure. This means the following inequalities:


In the context of Frobenius bimonoids that satisfy (wh1) and (wh2), all of (ra1)-(ra4) are redundant. As we will see, (wh1) and (wh2) (along with the redundant (ra1)-(ra4)) give rise to Peirce’s transformation rules in EGs. Peirce’s assertion, for example, that any graph scribed on the sheet itself (i.e. that is not scribed within a cut) can be erased can be proved as follows.
Lemma 1

Proof

Remark 1
It is well-known that the Frobenius equations induce a self-dual compact closed structure. Roughly speaking, this allows us to “rewire” diagrams, moving wires between the boundaries. We have used this already in the first diagrams of Example 4, on the \(\mathsf {is\ a\ catholic}\) relation.
4 Models
Recal uoh-props, introduced in Definition 1. Below we identify an important class of uoh-props, which together serve as the semantic universe for \(\mathsf {D\beta }\).
Definition 3
Let X be a set. The uoh-prop \({\mathsf {Rel}}_{\scriptscriptstyle X}\) has, as arrows \(m\rightarrow n\), relations \(X^m \rightarrow X^n\) (subsets of \(X^m\times X^n\)), where \(X^m\) is the m-fold cartesian product of X. Given a relation \(R\mathrel {:}X^m \rightarrow X^n\), \({R}^-\) is the (set-theoretical) complement of R as a subset of \(X^m\times X^n\).
Composition in \({\mathsf {Rel}}_{\scriptscriptstyle X}\) is relational composition: given \(R\mathrel {:}m\rightarrow k\) and \(S\mathrel {:}k\rightarrow n\), \(R\mathrel {;}S = \{\;(\mathbf {x},\mathbf {y})\;|\;\exists \mathbf {z}\in X^k.\; (\mathbf {x},\mathbf {z})\in R \wedge (\mathbf {z},\mathbf {y})\in S\;\}\subseteq X^m\times X^n\). The monoidal product is cartesian product of relations.
It is well-known that \({\mathsf {Rel}}_{\scriptscriptstyle X}\) is a cartesian bicategory of relations, that is, it satisfies all of the equations of Fig. 3. In the setting of \({\mathsf {Rel}}_{\scriptscriptstyle X}\),  is the diagonal relation \(\{(x, \left( {\begin{array}{c}x\\ x\end{array}}\right) )\;|\;x\in X\}\) while
is the diagonal relation \(\{(x, \left( {\begin{array}{c}x\\ x\end{array}}\right) )\;|\;x\in X\}\) while  is the relation \(\{(x,\star )\;|\;x\in X\}\), where \(\star \) is the unique element of the singleton set \(X^0\). The relations denoted by
is the relation \(\{(x,\star )\;|\;x\in X\}\), where \(\star \) is the unique element of the singleton set \(X^0\). The relations denoted by  and
and  are, respectively, the opposite relations. Henceforward we will call these four relations the canonical Frobenius structure of \({\mathsf {Rel}}_{\scriptscriptstyle X}\).
are, respectively, the opposite relations. Henceforward we will call these four relations the canonical Frobenius structure of \({\mathsf {Rel}}_{\scriptscriptstyle X}\).
The following is the central definition of this section.
Definition 4
A model for \(\mathsf {D\beta }\) consists of a set X and a morphism of uoh-props
that maps  to the canonical Frobenius structure of \({\mathsf {Rel}}_{\scriptscriptstyle X}\).
to the canonical Frobenius structure of \({\mathsf {Rel}}_{\scriptscriptstyle X}\).
Referring back to the syntax definition (1), to give such a morphism is to give, for each \(\sigma \mathrel {:}(m,\,n) \in \varSigma \), a relation \([\![\sigma ]\!]\subseteq X^m\times X^n\). The rest of the mapping is induced compositionally.
Remark 2
Note that closed diagrams, that is those of sort \((0,\,0)\) map to relations of type \(0\rightarrow 0\), that is, subsets of \(X^0\times X^0\). Since \(X^0\) is a singleton, there are precisely two such relations – the empty (\(\varnothing \)) and the full (\(\{(\star ,\star )\}\)). We identify these with truth values – \(\varnothing \) with \(\bot \) (false) and \(\{(\star ,\star )\}\) with \(\top \) (true).
Example 5
Take the signature of Example 1. Let \(X=\{m, w\}\). To define \([\![- ]\!]\mathrel {:}\mathsf {D\beta }\rightarrow {\mathsf {Rel}}_{\scriptscriptstyle X}\) we need only choose valuations of
 ,
,
 , and
, and
 as relations. Let
as relations. Let
 \(\subseteq X^1\times X^0 =\{(w,\star )\}\). Similarly, let
\(\subseteq X^1\times X^0 =\{(w,\star )\}\). Similarly, let
 \(=\{(m,\star )\}\). If we set
\(=\{(m,\star )\}\). If we set
 \(\subseteq X^1 \times X^1 = \{(m,w)\}\)
\(\subseteq X^1 \times X^1 = \{(m,w)\}\)
On the other hand, if we assign
 \(= \{(m,m)\}\) then
\(= \{(m,m)\}\) then


Having established the notion of model, we introduce the notions of soundness, completeness and logical equivalence. Two terms t, u of \(\mathsf {D\beta }\) are said to be logically equivalent if they have the same semantics in all models, \([\![t ]\!]=[\![u ]\!]\). An equation is sound if it preserves logical equivalence. A calculus is complete if it equates all logically equivalent terms. Note that the fact that \({\mathsf {Rel}}_{\scriptscriptstyle X}\) is a cartesian bicategory of relations means that all of the laws introduced in Sect. 3 are sound.
5 The Algebra of Cut
In Sect. 3 we began the process of axiomatising logical equivalence. Thus far, negation has not played a significant role in our exposition. In Fig. 4 we identify a calculus that is sound, and—taken in conjunction with the laws of Fig. 3—we conjecture to be complete. The equations of Fig. 4 describe the interactions between the algebraic structure of Fig. 3 and Peirce’s cut (negation). First, we explain the jagged-line notation, which emphasizes the local nature of the interactions. It is shorthand for an arbitrary context inside the cut. For example, (frcut) stands for

for arbitrary R, S and T. Thus with (frcut) we can, roughly speaking, “rewire” a cut to move wires between its left and right boundaries. Indeed (frcut) is a kind of Frobenius law for cuts. In short, the combination of (symcut) and (frcut) means that the cut boundary is permeable to “wiring” and the permutation structure.
(dcut) is a diagrammatic representation of Peirce’s rule for adding or erasing a double cut around any partial graph. Of course, this is a non-constructive rule; in this paper we only consider classical logic. Some progress has been made recently [13] in the study of how EGs can be used as an intuitionistic logic and we plan to investigate this in our framework in future work.
The (ctrpos) judgement single-handedly captures much of the behavior of the transformation rules within the cut. Peirce explains it as follows: “Of whatever transformation is permissible on the sheet of assertion, the reverse transformation is permissible within a single cut.” [16, p. 353]. While our presentation of (ctrpos) represents this point with respect to a single cut, it is worth noting that the reversal continues within subsequent nested cuts. The result is that the same transformation rules that apply on the sheet itself (i.e. to graphs that are not within a cut) also apply to graphs within an even number of cuts.Footnote 6 As a rule the principle of contraposition has been markedly absent from other presentations of Peirce’s transformation rules in the literature. The latter point is all the more significant in that Peirce often emphasizes the principle at the beginning of his presentations of EGs and often motivates the other transformation rules from it.Footnote 7 Our presentation situates the principle in its position of primary importance.
Intuitively, the principle of contraposition captures the symmetry between the valid twin inference rules of modus ponens and modus tollens. If we can infer the transformation from R to S then we can likewise infer from the denial of S the denial of R. In terms of \(\mathsf {D\beta }\) and Peirce’s EGs, and as stated above, the principle of contraposition allows us to perform the reverse transformations when working within a cut. Our previous proof of the erasure rule, which states that any graph written on the sheet itself (i.e. in an even area) can be erased, can be reversed using (ctrpos) to yield Peirce’s insertion rule. Likewise, Peirce’s rule that a line of identity can be broken on the sheet itself (ra3) can be reversed using (ctrpos) to yield his rule that a line of identity can be joined in an odd area.Footnote 8
The rule (it-deit) is a statement of Peirce’s principle of iteration/deiteration. In Peirce’s own words the rule is stated as follows: “...any partial graph, detached or attached, may be iterated within the same or additional cuts provided every line or hook of the iterated graph be attached in the new replica to identically the same ligatures as in the primitive replica; and if a partial graph be already so iterated it can be deiterated by the erasure of one of the replicas which must be within every cut that the replica left standing is within” [16, p. 358]. This rule applies in the same area as the partial graph—i.e. the same rule holds in the case where no cut is present. For us, it is useful to separate the two ideas conceptually, since the latter is implied by the algebraic structure in Sect. 3.
It is worth noting that our (it-deit) rule is similar to Burch’s presentation of “Dopplegänger pairs” that form when a line of identity crosses a cut (or two lines of identity abut each other at a cut) [6]. Our rule is more general, as it applies not simply to lines of identity but to relations and partial graphs. Each case is unified under the same rule here.
While the soundness of the other rules in Fig. 4 is straightforward, (it-deit) is more involved and less intuitive.
Lemma 2
(it-deit) is sound.
Proof
Since we can “rewire” any cut so that it only has wires on its left boundary, without loss of generality it suffices to show that:
is sound for all possible valuations of R and S. Using traditional syntax, and simplifying somewhat, this is to show the following logical equivalence:
Instead of dealing with the complicated formulas above, we instead directly use the definition of model introduced in Sect. 4. Suppose for some model, \(\left( \begin{array}{c}x_1 \\ x_2 \end{array}\right) \) is on the LHS. This happens exactly when there is some \(y_2\) s.t. \(x_2Ry_2\) and \(\left( \begin{array}{c}x_1 \\ x_2 \end{array}\right) \notin S\).
Suppose now that \(\left( \begin{array}{c}x_1 \\ x_2 \end{array}\right) \in \) RHS. This happens exactly when there is some \(y_2\) s.t. \(x_2Ry_2\) and \(\left( \begin{array}{c}x_1 \\ x_2 \\ y_2 \end{array}\right) \notin \)
 . This non-inclusion happens exactly when it is not the case that \(x_2Ry_2\) or \(\left( \begin{array}{c}x_1 \\ x_2 \end{array}\right) \notin S\). Since \(x_2 R y_2\) by assumption, it happens precisely when \(x_2Ry_2\) and \(\left( \begin{array}{c}x_1 \\ x_2 \end{array}\right) \notin S\).
. This non-inclusion happens exactly when it is not the case that \(x_2Ry_2\) or \(\left( \begin{array}{c}x_1 \\ x_2 \end{array}\right) \notin S\). Since \(x_2 R y_2\) by assumption, it happens precisely when \(x_2Ry_2\) and \(\left( \begin{array}{c}x_1 \\ x_2 \end{array}\right) \notin S\).
It follows that LHS and RHS denote the same relation in all models. \(\square \)

We can use (it-deit) to obtain two similar laws that are useful in diagrammatic proofs. We omit proofs for space reasons but note that Peirce can be seen using an instance of (ii) in his 1903 Lowell Lectures [16, p. 358-9].
Lemma 3
(i)

(ii)

We can also use (it-deit) to extend a line of identity into a cut. Note that Lemma 4 follows from (it-deit2) when S is the counit.
Lemma 4

Both Lemma 3 and Lemma 4 show how (it-deit) captures both iteration for a line of identity and for a relation/partial graph.
6 Diagrammatic Reasoning in Action
Example 6
We return to our running example and conclude with a complete diagrammatic derivation of the judgement
In the derivation we use the triangle notationFootnote 9 to denote a constant symbol of the logic, that is, a relation that is guaranteed to have singleton models. This (and similarly function symbols) are easily encoded in the graphical formalism and do not add expressivity; it suffices to assert that:
We proceed with the derivation below:


7 Conclusion
Peirce’s EGs arose out of his continued study of the algebra of relations and his concern for developing an efficient graphical notation. Seen through contemporary string diagrams, Peirce’s lines of identity obey the rules of special Frobenius algebras, while Peirce’s inference rules for lines of identity are the axioms of cartesian bicategories of relations. Moreover, diagrammatic reasoning can be extended to cover negation in a straightforward manner.
The category theoretic account of EGs presented here yields a diagrammatic calculus that is as expressive as first-order logic. We summarize the specific benefits of the graphical logical language when we say that it is compositional. The syntax is string diagrams, the semantics is \({\mathsf {Rel}}_{\scriptscriptstyle X}\), and models structure-preserving maps. In particular sub-formulas (sub-diagrams) have their own meaning as relations, with the meaning of the entire formula (diagram) obtained by composing these. In these respects our approach follows Peirce’s original intentions.
In regards to Peirce scholarship, our presentation suggests new means of interpreting the transformation rules in EGs. Following Peirce, this presentation showcases contraposition as the governing duality between positive and negative contexts on the sheet. We also clarify the rule of iteration. Robert’s presentation [17, pp. 57-8] includes important but fairly ad hoc clauses to the Beta rules of iteration. These clauses, as well as Burch’s more recent developments in [6], are unified here with a single principle of iteration. Finally, situating Peirce’s EGs in contemporary category theory [2, 3] allows for further study and comparisons.
Notes
- 1.
In this paper, we use “cut” in the Peircean sense to mean negation, not the standard notion of cut from proof theory.
- 2.
Henceforward we will not write the subscript \(\varSigma \), assuming a fixed ambient monoidal signature.
- 3.
These equations are examples of naturality of the symmetry.
- 4.
See, also, [CP 4:583]: “the line of identity...must be understood quite differently. We must hereafter understand it to be potentially the graph of teridentity by which means there will virtually be at least one loose end in every graph”.
- 5.
Elsewhere Peirce writes: “There is no need of a point from which four lines of identity proceed; for two triple points answer the same purpose
 [16, p. 357].
[16, p. 357]. - 6.
Following the passage quoted above, Peirce writes: “In short, whatever transformation is permissible on the sheet of assertion is permissible on the sheet of assertion within any even number of cuts while the reverse transformation is permissible within any odd number of cuts” [16, p. 353] Or alternatively: “All illative processes are subject to the apagogical principle, or principle of contraposition, which, as applied to graphs, is as follows: If any illative process is valid within an even number of enclosures, its reverse is valid within an odd number, and vice versa” [15, p. 94]. See also [16, p. 257-8, p. 478-9, & p. 539].
- 7.
See, for example, the passages in the previous footnote.
- 8.
In Peirce’s words: “...it is to be noted that a line of identity may be broken within an even number of cuts or on the sheet of assertion, while two lines may be joined within an odd number of cuts” [16, p. 358].
- 9.
Borrowed from the notation for states in categorical quantum mechanics [8].
References
Bonchi, F., Seeber, J., Sobociński, P.: Graphical conjunctive queries. In: Computer Science Logic 2018 (CSL 2018) (2018)
Brady, G., Trimble, T.: A categorical interpretation of C. S. Peirce’s propositional logic alpha. J. Pure Appl. Algebra 149, 213–239 (2000)
Brady, G., Trimble, T.: A string diagram calculus for predicate logic and C. S. Peirce’s system beta (2000)
Burch, R.W.: A Peircean Reduction Thesis. Texas Tech University Press, Lubbock (1991)
Burch, R.W.: Valental aspects of peircean algebraic logic. Comput. Math. Appl. 23(6), 665–677 (1992). https://doi.org/10.1016/0898-1221(92)90128-5. http://www.sciencedirect.com/science/article/pii/0898122192901285
Burch, R.W.: The fine structure of Peircean ligatures and lines of identity. Semiotica 186, 21 (2020–01-22T12:56:46313+01:00 2011). https://doi.org/10.1515/semi.2011.045. https://www.degruyter.com/view/j/semi.2011.2011.issue-186/semi.2011.045/semi.2011.045.xml
Carboni, A., Walters, R.F.C.: Cartesian bicategories I. J. Pure Appl. Algebra 49, 11–32 (1987)
Coecke, B., Kissinger, A.: Picturing Quantum Processes - A First Course in Quantum Theory and Diagrammatic Reasoning. Cambridge University Press, Cambridge (2017)
Dau, F.: Mathematical logic with diagrams based on the Existential Graphs of Peirce (2005)
Hereth Correia, J., Pöschel, R.: The power of peircean algebraic logic (PAL). In: Eklund, P. (ed.) ICFCA 2004. LNCS (LNAI), vol. 2961, pp. 337–351. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-24651-0_29
Lack, S.: Composing PROPs. Theor. Appl. Categories 13(9), 147–163 (2004)
Mac Lane, S.: Categorical algebra. Bull. Am. Math. Soc. 71, 40–106 (1965)
Minghui, M., Pietarinen, A.: A graphical deep inference system for intuitionistic logic. Logique et Analyse 245, 73–114 (2019). https://doi.org/10.2143/LEA.245.0.3285706
Peirce, C.S.: Letters to Lady Welby. MS [R] L463, from the Commens Bibliography. http://www.commens.org/bibliography/manuscript/peirce-charles-s-nd-letters-lady-welby-ms-r-l463
Pietarinen, A.V.: The Logic of the Future, vol. 1. De Gruyter, Berlin (2019)
Pietarinen, A.V.: The Logic of the Future, vol. 2 & 3. De Gruyter, Berlin (forthcoming) (cited page numbers are from a previous draft copy)
Roberts, D.D.: The Existential Graphs of Charles S. Peirce. Mouton, The Hague (1973)
Shin, S.: The Iconic Logic of Peirce’s Graphs. MIT Press, Cambridge (2002)
Zeman, J.J.: A system of implicit quantification. J. Symb. Logic 32(4), 480–504 (1967). http://www.jstor.org/stable/2270176
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 Springer Nature Switzerland AG
About this paper
Cite this paper
Haydon, N., Sobociński, P. (2020). Compositional Diagrammatic First-Order Logic. In: Pietarinen, AV., Chapman, P., Bosveld-de Smet, L., Giardino, V., Corter, J., Linker, S. (eds) Diagrammatic Representation and Inference. Diagrams 2020. Lecture Notes in Computer Science(), vol 12169. Springer, Cham. https://doi.org/10.1007/978-3-030-54249-8_32
Download citation
DOI: https://doi.org/10.1007/978-3-030-54249-8_32
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-54248-1
Online ISBN: 978-3-030-54249-8
eBook Packages: Computer ScienceComputer Science (R0)









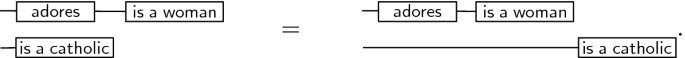



 [
[