Keywords

1 Introduction

Mathematical optimization is an important topic of operations researches and is widely used in making good decisions. Including fuzzy concepts in mathematical models the researchers extended even more its applicability. In this study we analyze possible solutions to linear programming problems with both fuzzy coefficients and decision variables. Such problems arise when a real life system is modeled as an optimization problem under a certain kind of uncertainty. Li et al. [12] described a method able to transform heterogeneous information into trapezoidal fuzzy numbers, and Morente-Molinera et al. [15] used the sentiment analysis and fuzzy linguistic modeling procedures to organize the unstructured information to properly work with it.

Highlighting the limits and achievements of fuzzy approaches from the literature and comparing the use of quantitative and qualitative scales in measuring the decisions, Dubois [7] provided critical overview of the role of fuzzy sets in the field of decision analysis. One of the open questions formulated in [7] is related to developing a methodology able to validate the fuzzy decision analysis approaches.

Ghanbari et al. [10] surveyed the models and solutions provided in the literature to fuzzy linear programming problems. One section was devoted to solving full fuzzy linear programming problems, including full fuzzy transportation problems. Their survey presented the practical applications of this class of problems and discussed some limitations of the existing solving methods.

Baykasoglu and Subulan [1] carried out a research on fuzzy efficient solutions to full fuzzy reverse logistics network design problem with fuzzy decision variables. Their study took into consideration different levels of uncertainty and the risk-averse attitude of the decision maker. Later on, Baykasoglu and Subulan [2] proposed a constrained fuzzy arithmetic approach for solving a wide variety of fuzzy transportation problems. They compared their solution approach with the state of the art approaches from the literature.

Pérez-Cañedo and Concepción-Morales [16] proposed a solution approach to derive a unique optimal fuzzy value to a full fuzzy linear programming problem with inequality constraints containing unrestricted LR fuzzy parameters and decision variables. Later on, in [17] they used the lexicographic optimization to rank LR-type intuitionistic fuzzy numbers and introduced a method to derive solutions to full intuitionistic fuzzy linear programming problems with unique optimal values.

Stanojević et al. [19] applied the interval expectation to trapezoidal fuzzy numbers and used it to transform the fuzzy linear programming problem into an interval optimization problem. An order relation was employed to rank the obtained intervals; and a parametric model was used to handle the acceptance degree of the violated fuzzy constraints. Finally, the Pareto optimal solutions to the parametric bi-objective linear programming problem were analyzed.

There are many studies in the recent literature announcing the usefulness of fuzzy linear programming models in their fields, and the possibility to use them to replace the classic linear models. For instance, Zhang et al. [22] proposed soft consensus cost models for group decision making, and discussed their economic interpretations. Emphasizing that fuzzy information is widely used to describe the uncertain preferences of the decision-makers when crisp values fail to represent the real viewpoints, the authors planed to include interval preferences in their linear models.

Liu and Kao [14] proposed a solution approach to a fuzzy transportation problem with crisp decision variables based on the extension principle. In order to simplify their approach they imposed a restrictive constraint of total supply less or equal to the total demand, thus loosing its generality. However, their approach is significant and can be extended to a more general one, namely to solve a full fuzzy linear programming problem. Liu [13] solved a fractional transportation problem with fuzzy parameters using the same solution concept based on the extension principle.

Ezzati et al. [9] applied fuzzy arithmetic and derived the triangular fuzzy value of the objective function with respect to the triangular fuzzy values of the decision variables and parameters. Then, he constructed a 3-objective crisp problem and solved it by a lexicographic method. We include one of the examples solved in [9] in our experiments; compare their solution to the empirical solution obtained by our Monte Carlo simulation; and draw some conclusions.

Bhardwaj and Kumar [4] pointed out a shortcoming that arose in [9] when fuzzy inequality constraints were transformed into equalities.

Kumar et al. [11] employed a ranking function (for the fuzzy number values of the objective function) and a component-wise comparison of the left and right hand sides of the constraints to transform the full fuzzy problem into a deterministic one. They finally solved one single objective linear programming problem deriving optimal values for all components of all decision variables.

Das et al. [6] introduced a new method to solve fully fuzzy linear programming problem with trapezoidal fuzzy numbers. Their method was based on solving a mathematical model derived from the multiple objective linear programming problem and lexicographic ordering method. They illustrated the applicability of their approach by solving real life problems as production planning and diet problems.

The main contribution of this paper is three-fold: (i) we define the membership functions of the fuzzy set solution components to a full fuzzy linear program; (ii) using a Monte Carlo simulation we compare the empirical solutions based on the new introduced definition to the analytical solutions provided in the literature; and (iii) we propose a model able to numerically describe the membership function of the fuzzy set of the feasible objective values.

Our presentation further includes: Sect. 2 that presents notation and terminology; Sec. 3 that introduces our advances in fuzzy linear optimization through the extension principle, and the new optimization model to depict the feasible objective values; Sect. 4 that reports our numerical results, and Sect. 5 that contains our concluding remarks.

2 Preliminaries

Zadeh [20] introduced the fuzzy sets as collection of elements with certain membership degrees. With respect to a universe X, a fuzzy subset \(\tilde{A}\) in X is generally defined by \(\widetilde{A}=\left\{ \left( x,\mu _{\widetilde{A}}(x)\right) |x\in X\right\} \), where \(\mu _{\widetilde{A}}\) is the membership function of \(\widetilde{A}\), \(\mu _{\widetilde{A}}(x)\) represents the membership degree of x in \(\widetilde{A}\), \(\mu _{\widetilde{A}}(x)\in [0,1]\).

The set of elements of the universe X whose membership degree in \(\widetilde{A}\) is greater than \(\alpha \), \(\alpha \in \left[ 0,1\right] \), is called the \(\alpha \)-level set (or \(\alpha \)-cut) of the fuzzy subset \(\widetilde{A}\). It is formalized by

$$ \left[ \widetilde{A}\right] _{\alpha }=\left\{ x\in R|\mu _{\widetilde{A}}\left( x\right) \ge \alpha \right\} . $$

The set \(\left\{ x\in R|\mu _{\widetilde{A}}\left( x\right) >0\right\} \) is called the support of the fuzzy subset \(\widetilde{A}\).

The special fuzzy subsets of the real numbers universe \(\mathbb {R}\) that are convex and normalized, and whose membership function is upper semi-continuous and has the functional value 1 at least at one element are called fuzzy numbers. They were introduced in [21] together with their elementary arithmetic operations. Any classic arithmetic operator between real numbers can be extend to a fuzzy operator between fuzzy numbers with the help of the extension principle.

A triangular fuzzy number \(\widetilde{A}=\left( a^{1},a^{2},a^{3}\right) \), with \(a^{1}\le a^{2}\le a^{3}\) is an especial fuzzy set with the membership function defined as follows:

$$ \begin{array}{c} \mu _{\widetilde{A}}\left( x\right) =\left\{ \begin{array}{ll} {\displaystyle \left( x-a^{1}\right) /\left( a^{2}-a^{1}\right) ,} &{} a^{1}\le x<a^{2},\\ {\displaystyle \left( a^{3}-x\right) /\left( a^{3}-a^{2}\right) ,} &{} a^{2}\le x\le a^{3},\\ 0, &{} \text {otherwise}. \end{array}\right. \end{array} $$

For each \(\alpha \in \left( 0,1\right] \) the \(\alpha \)-cut of a triangular fuzzy number \(\widetilde{A}=\left( a^{1},a^{2},a^{3}\right) \) is the interval

$$\begin{aligned} \left[ \widetilde{A}\right] _{\alpha }=\left[ \alpha a^{2}+\left( 1-\alpha \right) a^{1},\alpha a^{2}+\left( 1-\alpha \right) a^{3}\right] . \end{aligned}$$
(1)

An LR flat fuzzy number [8] is a quadruple \(\left( m,n,\alpha ,\beta \right) _{LR}\), \(\alpha ,\beta >0\) whose components define its corresponding membership function as follows:

$$ \begin{array}{c} \mu _{\tilde{A}}\left( x\right) =\left\{ \begin{array}{rl} {\displaystyle L\left( \left( m-x\right) /\alpha \right) ,} &{} x\le m,\\ 1, &{} m<x<n,\\ {\displaystyle R\left( \left( x-n\right) /\beta \right) ,} &{} n\le x,\\ 0, &{} \text {otherwise}, \end{array}\right. \end{array} $$

where L and R are reference non-increasing functions defined on the interval \(\left[ 0,\infty \right) \), taking values from the interval \(\left[ 0,1\right] \), and fulfilling the double equality \(L\left( 0\right) =R\left( 0\right) =1\).

Bellman and Zadeh [3] formulated the extension principle widely used to aggregate the fuzzy subsets. Applying the extension principle, the fuzzy subset \(\widetilde{B}\) of the universe Y that is intended to be the aggregation of the fuzzy subsets \(\widetilde{A}_{1},\widetilde{A}_{2},\dots ,\widetilde{A}_{r}\) over their universes \(X_{1},X_{2},\dots ,X_{r}\) through the function f that is a mapping of the Cartesian product \(X_{1}\times X_{2}\times \dots \times X_{r}\) to the universe Y is defined through its membership function as

$$ \mu _{\widetilde{B}}(y)=\left\{ \begin{array}{ll} {\displaystyle \sup _{\left( x_{1},\dots ,x_{r}\right) \in f^{-1}\left( y\right) }}\left( \min \left\{ \mu _{\widetilde{A}_{1}}\left( x_{1}\right) ,\dots ,\mu _{\widetilde{A}_{r}}\left( x_{r}\right) \right\} \right) , &{} f^{-1}\left( y\right) \ne \varnothing ,\\ 0, &{} \text {otherwise.} \end{array}\right. $$

In Sect. 3 we apply the extension principle to define a solution to full fuzzy linear programming (FF-LP) problems. Zimmermann [23] and [24] has already formulated solutions to fuzzy mathematical programming problems based on the extension principle. However, he solved another class of problems, namely vector optimization problems involving fuzzy goals and fuzzy constraints.

The extension principle was also used to define the elementary arithmetic operations over the set of fuzzy numbers. We recall the definitions for addition, subtraction and multiplication of triangular fuzzy numbers since we use them in the sequel.

Given two triangular fuzzy numbers \(\widetilde{A}=(a_{1},a_{2},a_{3})\) and \(\widetilde{B}=(b_{1},b_{2},b_{3})\), the basic arithmetic operations are defined as follows:

  • addition: \(\widetilde{A}+\widetilde{B}=(a_{1}+b_{1},a_{2}+b_{2},a_{3}+b_{3})\);

  • subtraction: \(\widetilde{A}-\widetilde{B}=(a_{1}-b_{3},a_{2}-b_{2},a_{3}-b_{1})\);

  • multiplication: the exact result of \(\widetilde{A}\cdot \widetilde{B}\) is commonly approximated by the triangular fuzzy number \((c_{1},c_{2},c_{3})\), where \(c_{2}= a_{2}b_{2}\) and

    $$ c_{1}=\min \left\{ a_{1}b_{1},a_{1}b_{3},a_{3}b_{1},a_{3}b_{3}\right\} ,c_{3}=\max \left\{ a_{1}b_{1},a_{1}b_{3},a_{3}b_{1},a_{3}b_{3}\right\} . $$

3 The Optimization via the Extension Principle

Without loss of generality an optimization problem consists in finding maximum of a real valued objective function f over a feasible set X. A formalized model is given by

$$\begin{aligned} \begin{array}{ll} \max &{} f\left( x\right) ,\\ \text {subject to} &{} \\ &{} x\in X, \end{array} \end{aligned}$$
(2)

where, x is the vector decision variable and \(f:X\rightarrow R\).

In a full fuzzy linear programming problem the objective function is linear; the feasible set is defined with the help of linear constraints; and uses fuzzy numbers for the both coefficients and decision variables. For a maximization problem, a formalized model is given below.

$$\begin{aligned} \begin{array}{lll} \max &{} \,\widetilde{f}\left( \widetilde{x}\right) ={\displaystyle \sum _{j=1}^{n}\widetilde{c}_j\widetilde{x}_j,}\\ \text {subject to} &{} \\ &{} {\displaystyle \sum _{j=\overline{1,n}}}\widetilde{a}_{ij}\widetilde{x}_{j}\preceq \widetilde{b}_{i}, &{} i=\overline{1,m},\\ &{} \widetilde{x}_{j}\succeq 0, &{} j=\overline{1,n}. \end{array} \end{aligned}$$
(3)

In order to define an optimal solution to Problem (3), we employ the crisp linear programming problem

$$\begin{aligned} \begin{array}{lll} \max &{} {\displaystyle \sum _{j=1}^{n}{c}_j {x}_j,}\\ \text {subject to} &{} \\ &{} {\displaystyle \sum _{j=\overline{1,n}}}a_{ij}x_{j}\le b_{i}, &{} i=\overline{1,m},\\ &{} x_{j}\ge 0, &{} j=\overline{1,n}, \end{array} \end{aligned}$$
(4)

where the real numbers \(a_{ij}\), \(b_i\), \(c_j\) and \(x_j\), \(i=1,\dots ,m\), \(j=1,\dots ,n\) belong to the supports of the fuzzy numbers \(\widetilde{a}_{ij}\), \(\widetilde{b_i}\), \(\widetilde{c_j}\) and \(\widetilde{x_j}\) respectively.

3.1 The Membership Functions of the Fuzzy Set Solution

Let us denote by \(X_{a,b}\) the feasible set of Problem (4). Let \(P_{\left( \widetilde{a},\widetilde{b},\widetilde{c}\right) }\left( a,b,c\right) \) denote the aggregated membership level of all parameters,

$$\begin{aligned} P_{\left( \widetilde{a},\widetilde{b},\widetilde{c}\right) }\left( a,b,c\right) =\min \left\{ \mu _{\widetilde{a}}\left( a\right) ,\mu _{\widetilde{b}}\left( b\right) ,\mu _{\widetilde{c}}\left( c\right) \right\} , \end{aligned}$$
(5)

where

$$ \begin{array}{l} \mu _{\widetilde{a}}\left( a\right) =\min \left\{ \mu _{\widetilde{a}_{ij}}\left( a_{ij}\right) |i=\overline{1,m},j=\overline{1,n}\right\} ,\\ \mu _{\widetilde{b}}\left( b\right) =\min \left\{ \mu _{\widetilde{b}_{i}}\left( b_{i}\right) |i=\overline{1,m},\right\} ,\\ \mu _{\widetilde{c}}\left( c\right) =\min \left\{ \mu _{\widetilde{c}_{j}}\left( c_{j}\right) |j=\overline{1,n}\right\} . \end{array} $$

We follow Liu [13], and apply the extension principle to define the membership function of the fuzzy optimal value

$$ \mu _{\widetilde{f}}\left( z\right) =\left\{ \begin{array}{ll} {\displaystyle \max _{\left( a,b,c\right) |z={\displaystyle \max _{x\in X_{a,b}}c^{T}x}}}\left( P_{\left( \widetilde{a},\widetilde{b},\widetilde{c}\right) }\left( a,b,c\right) \right) , &{} \exists a,b,c|z={\displaystyle \max _{x\in X_{a,b}}c^{T}x},\\ 0, &{} \text {otherwise.} \end{array}\right. $$

Liu [13] used such membership function to describe the fuzzy solution value to a transportation problem with fuzzy numbers and crisp decision variables. In addition, we use the extension principle to define each fuzzy optimal solution component as seen in Formula (6).

$$\begin{aligned} \mu _{\widetilde{x}}\left( x\right) =\left\{ \begin{array}{ll} {\displaystyle \max _{\left( a,b,c\right) |c^{T}x={\displaystyle \max _{y\in X_{a,b}}c^{T}y}}}\left( P_{\left( \widetilde{a},\widetilde{b},\widetilde{c}\right) }\left( a,b,c\right) \right) , &{} \exists a,b,c|c^{T}x={\displaystyle \max _{y\in X_{a,b}}c^{T}y},\\ 0, &{} \text {otherwise.} \end{array}\right. \end{aligned}$$
(6)

3.2 The Mathematical Model

Keeping in mind above definitions we now introduce the mathematical model (7) that computes the membership degree of each feasible objective value z. It is clear that the decreasing piece of the so determined membership function describes the fuzzy set solution to a maximization problem (3). Model (7)

$$\begin{aligned} \begin{array}{llll} \max &{} \alpha \\ \text {subject to} &{} \\ &{} \mu _{\widetilde{a}_{ij}}\left( a_{ij}\right) \ge \alpha , &{} i=\overline{1,m}, &{} j=\overline{1,n}\\ &{} \mu _{\widetilde{b}_{i}}\left( b_{i}\right) \ge \alpha , &{} i=\overline{1,m},\\ &{} \mu _{\widetilde{c}_{j}}\left( c_{j}\right) \ge \alpha , &{} j=\overline{1,n},\\ &{} c^{T}x=z,\\ &{} x\in X_{a.b}, \end{array} \end{aligned}$$
(7)

is non-linear and maximizes \(\alpha \) with respect to variables x, a, b, c and \(\alpha \).

Model (7) consists in maximizing \(P_{\left( \widetilde{a},\widetilde{b},\widetilde{c}\right) }\left( a,b,c\right) \) over the feasible combinations of the parameters \(\left( a,b,c\right) \) able to derive a vector \(x\in X_{a.b}\) such that \(c^{T}x=z\), separately for fixed values z of the objective function. Indeed, for a value \(\alpha =P_{\left( \widetilde{a},\widetilde{b},\widetilde{c}\right) }\left( a,b,c\right) \) we have

$$ \begin{array}{lll} \mu _{\widetilde{a}}\left( a\right) \ge \alpha ,&\mu _{\widetilde{b}}\left( b\right) \ge \alpha ,&\mu _{\widetilde{c}}\left( c\right) \ge \alpha ,\end{array} $$

with at least one equality among the inequalities. Therefore, the maximization of \(\alpha \) determines the highest level of membership for the given crisp value z.

Considering that all parameters are expressed by triangular fuzzy numbers we use the definition of \(\alpha \)-cut intervals (1) to rewrite the constraint system of (7). Since

$$ \begin{array}{ll} \mu _{\widetilde{a}_{ij}}\left( a_{ij}\right) \ge \alpha \Leftrightarrow a_{ij}\in \left[ \widetilde{a}_{ij}\right] _{\alpha }, &{} i=\overline{1,m},j=\overline{1,n}\\ \mu _{\widetilde{b}_{i}}\left( b_{i}\right) \ge \alpha \Leftrightarrow b_{i}\in \left[ \widetilde{b}_{i}\right] _{\alpha }, &{} i=\overline{1,m},\\ \mu _{\widetilde{c}_{j}}\left( c_{j}\right) \ge \alpha \Leftrightarrow c_{j}\in \left[ \widetilde{c}_{j}\right] _{\alpha }, &{} j=\overline{1,n}, \end{array} $$

we derive the specific Model (8) whose first three sets of constraints are linear.

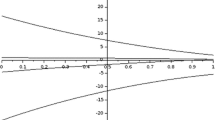
$$\begin{aligned} \begin{array}{lll} \max &{} \alpha \\ \text {subject to}\\ &{} \alpha a_{ij}^{2}+\left( 1-\alpha \right) a_{ij}^{1}\le a_{ij}\le \alpha a_{ij}^{2}+\left( 1-\alpha \right) a_{ij}^{3}, &{} i=\overline{1,m},j=\overline{1,n}\\ &{} \alpha b_{i}^{2}+\left( 1-\alpha \right) b_{i}^{1}\le b_{i}\le \alpha b_{i}^{2}+\left( 1-\alpha \right) b_{i}^{3}, &{} i=\overline{1,m},\\ &{} \alpha c_{j}^{2}+\left( 1-\alpha \right) c_{j}^{1}\le c_{j}\le \alpha c_{j}^{2}+\left( 1-\alpha \right) c_{j}^{3}, &{} j=\overline{1,n},\\ &{} c^{T}x=z,\\ &{} x\in X_{a.b}. \end{array} \end{aligned}$$
(8)

Figure 1 shows a fuzzy set of the feasible objective values obtained by solving Model (8). The envelope of optimal objective values obtained by a dual optimization as suggested in Liu [13] can be also seen in Fig. 1.

3.3 The Monte Carlo Simulation

Monte Carlo algorithms are widely used to provide numerical results by a random sampling of certain parameters. Buckley and Jowers’s book [5] on Monte Carlo methods in fuzzy optimization focused exclusively on generating random fuzzy numbers to be used in evaluating the objective functions. Our approach generates random crisp values for the parameters, finds crisp optimal values, and uses them in constructing the fuzzy set solution value to the original full fuzzy linear problem.

The definitions of the membership functions given in Sect. 3.1 are difficult to be directly used in practice. An analytical definition would be the most convenient, but such a definition is also hard (if not impossible) to be obtained. Model (7) introduced in Sect. 3.2 provides the upper bounds on the maximal values of the objective function with respect to their membership degrees, but lower bounds on those maximal values are still unknown.

Fig. 1.
figure 1

Fuzzy set of feasible objective values obtained by solving Model (8); and the results of a Monte Carlo simulation that describe the fuzzy set of optimal solution values

Full size image
figure a

Under additional assumptions, Liu and Kao [14] described the lower bound on the maximal values of the objective function of a full fuzzy transportation problem. They made use of the dual of the crisp transportation problem to transform a two level min-max model to a two level max-max problem that was finally solved as an one-level max problem.

We aim to disclose the shapes of the membership functions of the fuzzy sets solution to Problem (3) by a Monte Carlo simulation which generates random values for the coefficients needed in obtaining optimal solutions to Problem (4). In order to obtain more accurate shapes, for fixed values of \(\alpha \in \left[ 0,1\right] \), the values of the coefficients are randomly chosen from the \(\alpha \)-cut interval of their corresponding fuzzy numbers.

Algorithm 1 describes the steps needed for the simulation.

The third component of the triple

$$ l_{k}=\left( x^{k},z^{k},P_{\left( \widetilde{a},\widetilde{b},\widetilde{c}\right) }\left( a,b,c\right) \right) , $$

which is an element of the output list L of Algorithm 1, namely \(P_{\left( \widetilde{a},\widetilde{b},\widetilde{c}\right) }\left( a,b,c\right) \), represents a minorant of the membership degree of both \(x^{k}\) and \(z^{k}\).

After running the algorithm we group the elements \(l_{k}\in L\) with respect to their second component as follows: we split the interval \(\left[ {\displaystyle \min _{l_{k}\in L}z^{k},\max _{l_{k}\in L}z^{k}}\right] \) in q sub-intervals \(I_{1}\), \(I_{2},\) \(\dots \), \(I_{q}\) of the same length \({ \frac{1}{q}}\left( {\displaystyle \max _{l_{k}\in L}z^{k}-\min _{l_{k}\in L}z^{k}}\right) \), and compute the values

$$ f_{j}={\displaystyle M\left( \left\{ z^{k}|l_{k}\in L,z^{k}\in I_{j}\right\} \right) },j=1,\dots ,q, $$

where \(M\left( S\right) \) represents the mean value of the elements belonging to the set S. The membership degree of the value \(f_{j}\) is obtained as maximum of the values of the third component of those elements \(l_{k}\in L\) that have the second component in \(I_{j}\). In a similar way, grouping the elements of L in q sub-intervals of the same length, with respect to the values of the components of the vector \(x^{k}\), we compute the membership values that correspond to the mean values of the components belonging to the same sub-interval.

This simulation provides an empirical computation for the membership functions of the solution and solution value to Problem (3) when solving Model (7) fails to obtain a correct solution due to its non-linearity. Model (7) is replaced by the quadratic Model (8) when triangular fuzzy numbers are used to describe the components of the parameters \(\left( a,b,c\right) \). In this case, and also in the case of the trapezoidal fuzzy numbers used to describe the parameters, the non-linearity appears in last two constraints \(c^{T}x=z\) and \(x\in X(a,b)\), and it is very likely one to be able to solve the model correctly. On the other side, if LR flat fuzzy numbers [8] are used to describe the parameters of Problem (3), the non-linearity appears in all constraints, and may create difficulties in finding a global optimal solution.

4 Numerical Example

We recall the following example from the literature ([9, 11]).

$$\begin{aligned} \begin{array}{ll} \max &{} {\displaystyle \widetilde{c}^{T}\widetilde{x},}\\ \text {subject to} &{} \\ &{} \widetilde{a}\widetilde{x}=\widetilde{b},\\ &{} \widetilde{x}\succeq 0, \end{array} \end{aligned}$$
(9)

where the fuzzy number values of the coefficients are

$$\begin{aligned} \widetilde{a}=\left[ \begin{array}{rrrr} \left( 8;10;13\right) &{} \left( 10;11;13\right) &{} \left( 9;12;13\right) &{} \left( 11;15;17\right) \\ \left( 12;14;16\right) &{} \left( 14;18;19\right) &{} \left( 14;17;20\right) &{} \left( 13;14;18\right) \end{array}\right] , \end{aligned}$$
(10)
$$\begin{aligned} \begin{array}{cc} \begin{array}{cc} \widetilde{b}= &{} \left[ \begin{array}{c} \left( 271.75;411.75;573.75\right) \\ \left( 385.5;539.5;759.5\right) \end{array}\right] \end{array}, &{} \widetilde{c}=\left[ \begin{array}{c} \left( 10;15;17\right) \\ \left( 10;16;20\right) \\ \left( 10;14;17\right) \\ \left( 10;12;14\right) \end{array}\right] .\end{array} \end{aligned}$$
(11)
Fig. 2.
figure 2

The results of several Monte Carlo simulations with different number of iterations; and the envelope’s approximation obtained via the optimization model

Full size image
Fig. 3.
figure 3

Fuzzy set of optimal objective values to Problem (9) defined with the values of the parameters given in (10) and (11)

Full size image

In short, the solution approach proposed in Kumar et al. [11] used a ranking function to transform the fuzzy number values of the objective function into crisp values; and a component-wise comparison of the left and right hand sides of the fuzzy constraints to transform them into deterministic ones. The obtained crisp linear problem was solved, and the optimal values for all components of all decision variables were derived. The fuzzy number value of the objective function was finally computed using the fuzzy number values of the decision variables and parameters.

The solution approach proposed in Ezzati et al. [9] first formally computed the components of the triangular fuzzy value of the objective function with respect to the triangular fuzzy values of the decision variables and parameters. Second, it constructed a three-objective crisp problem and solved it by a lexicographic method.

The component-wise method (described in Stanojević et al. [18] for solving full fuzzy linear fractional programming problems, but applied here to the linear case) was based on solving two crisp linear programming problems for several fixed \(\alpha \) levels. The parameters for these crisp problems were the left and right endpoints respectively of the \(\alpha \)-cut intervals. Their optimal solutions were used to construct the membership functions of the fuzzy numbers representing the final solution.

Fig. 4.
figure 4

Fuzzy sets of optimal values of the decision variables to Problem (9) defined with the values of the parameters given in (10) and (11)

Full size image

Figures 3 and 4 show our empirical results obtained by a Monte Carlo simulation compared to the results found in the literature. Increasing the number of iterations, the simulation provides more accurate results (Fig. 2).

Aiming to find the maximal values that the objective function can reach we must pay attention to the right sides of the fuzzy numbers. It is clearly shown in Fig. 3 that both solutions from the literature are far from the desired values no matter how the membership degree is chosen.

Table 1. Components of the fuzzy sets representing the optimal values of the objective function
Full size table
Table 2. Components of the fuzzy sets representing the optimal values of the decision variables
Full size table

Tables 1 and 2 report the same solutions by their components as triangular fuzzy numbers. For the Monte Carlo simulation we approximate the results providing the extreme values, i.e. the minimum, the value with maximal amplitude and the maximum. For our analysis and graphic representations we run the component-wise method and reported the obtained solution, but used the numerical values reported in Ezzati et al. [9] for other two methods [9] and [11].

5 Conclusion

In this study we addressed the full fuzzy linear programming, and formalized the definition of the optimal solution via Zadeh’s extension principle. We conducted a Monte Carlo simulation, and compared the solution derived in this way to the solutions yielded by approaches proposed in the literature. Concluding that there is a wide gap between our empirical results and the results provided by the solution approaches from the literature, we proposed a model that is able to describe numerically the membership function of the fuzzy set of feasible objective values that follows the extension principle. Our goal was to provide decision-makers with more relevant information on the extreme values that the objective function can reach under uncertain given constraints.

In our future research we will conduct more experiments on a wider class of mathematical programming problems (e.g. full fuzzy linear fractional programming problems) aiming to prove that the simulation we proposed can be used as a basic method to test the validity of any solution approach to full fuzzy programming problems.