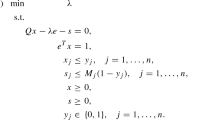Keywords

1 Introduction

Coordinate-wise minimization, or coordinate descent, is an iterative optimization method, which in every iteration optimizes only over a single chosen variable while keeping the remaining variables fixed. Due its simplicity, this method is popular among practitioners in large-scale optimization in areas such as machine learning or computer vision, see e.g.  [32]. A natural extension of the method is block-coordinate minimization, where every iteration minimizes the objective over a block of variables. In this paper, we focus on coordinate minimization with exact updates, where in each iteration a global minimum over the chosen variable is found, applied to convex optimization problems.

For general convex optimization problems, the method need not converge and/or its fixed points need not be global minima. A simple example is the unconstrained minimization of the function \(f(x,y)=\max \{x-2y,y-2x\}\), which is unbounded but any point with \(x=y\) is a coordinate-wise local minimum. Despite this drawback, (block-)coordinate minimization can be very successful for some large-scale convex non-differentiable problems. The prominent example is the class of convergent message passing methods for solving dual linear programming (LP) relaxation of maximum a posteriori (MAP) inference in graphical models, which can be seen as various forms of (block-)coordinate descent applied to various forms of the dual. In the typical case, the dual LP relaxation boils down to the unconstrained minimization of a convex piece-wise affine (hence non-differentiable) function. These methods include max-sum diffusion [21, 26, 29], TRW-S  [18], MPLP  [12], and SRMP  [19]. They do not guarantee global optimality but for large sparse instances from computer vision the achieved coordinate-wise local optima are very good and TRW-S is significantly faster than competing methods  [16, 27], including popular first-order primal-dual methods such as ADMM  [5] or  [8].

This is a motivation to look for other classes of convex optimization problems for which (block-)coordinate descent would work well or, alternatively, to extend convergent message passing methods to a wider class of convex problems than the dual LP relaxation of MAP inference. A step in this direction is the work  [31], where it was observed that if the minimizer of the problem over the current variable block is not unique, one should choose a minimizer that lies in the relative interior of the set of block-optimizers. It is shown that any update satisfying this rule is, in a precise sense, not worse than any other exact update. Message-passing methods such as max-sum diffusion and TRW-S satisfy this rule. If max-sum diffusion is modified to violate the relative interior rule, it can quickly get stuck in a very poor coordinate-wise local minimum.

To be precise, suppose we minimize a convex function \(f{:}\ X\rightarrow \mathbb {R}\) on a closed convex set \(X\subseteq \mathbb {R}^n\). We assume that f is bounded from below on X. For brevity of formulation, we rephrase this as the minimization of the extended-valued function \(\bar{f}{:}\ \mathbb {R}^n\rightarrow \mathbb {R}\cup \{\infty \}\) such that \(\bar{f}(x)=f(x)\) for \(x\in X\) and \(\bar{f}(x)=\infty \) for \(x\notin X\). One iteration of coordinate minimization with the relative interior rule  [31] chooses a variable index \(i\in [n]=\{1,\ldots ,n\}\) and replaces an estimate \(x^k=(x_1^k,\ldots ,x_n^k)\in X\) with a new estimate \(x^{k+1}=(x^{k+1}_1,\ldots ,x^{k+1}_n)\in X\) such thatFootnote 1

$$\begin{aligned} x_i^{k+1}&\in \mathop {\mathrm {ri}}\mathop {\mathrm {argmin}}_{y\in \mathbb {R}} \bar{f}(x^k_1,\ldots ,x^k_{i-1},y,x^k_{i+1},\ldots ,x^k_n) ,\\ x_j^{k+1}&= x_j^k \quad \forall j\ne i , \end{aligned}$$

where \(\mathop {\mathrm {ri}}Y\) denotes the relative interior of a convex set Y. As this is a univariate convex problem, the set \(Y=\mathop {\mathrm {argmin}}_{y\in \mathbb {R}} \bar{f}(x^k_1,\ldots ,x^k_{i-1},y,x^k_{i+1},\ldots ,x^k_n)\) is either a singleton or an interval. In the latter case, the relative interior rule requires that we choose \(x_i^{k+1}\) from the interior of this interval. A point \(x=(x_1,\ldots ,x_n)\in X\) that satisfies

$$ x_i \in \mathop {\mathrm {ri}}\mathop {\mathrm {argmin}}_{y\in \mathbb {R}} \bar{f}(x_1,\ldots ,x_{i-1},y,x_{i+1},\ldots ,x_n) $$

for all \(i\in [n]\) is called a (coordinate-wise) interior local minimum of function f on set X.

Some classes of convex problems are solved by coordinate-wise minimization exactly. E.g., for unconstrained minimization of a differentiable convex function, it is easy to see that any fixed point of the method is a global minimum; moreover, it has been proved that if the function has unique univariate minima, then any limit point is a global minimum [4, §2.7]. The same properties hold for convex functions whose non-differentiable part is separable  [28]. Note that these classical results need not assume the relative interior rule  [31].

Therefore, it is natural to ask if the relative interior rule can widen the class of convex optimization problems that are exactly solved by coordinate-wise minimization. Leaving convergence asideFootnote 2, more precisely we can ask for which problems interior local minima are global minima. A succinct characterization of this class is currently out of reach. Two subclasses of this class are known [18, 26, 29]: the dual LP relaxation of MAP inference with pairwise potential functions and two labels, or with submodular potential functions.

In this paper, we restrict ourselves to linear programs (where f is linear and X is a convex polyhedron) and present a new class of linear programs with this property. We show that dual LP relaxations of a number of combinatorial optimization problems belong to this class and coordinate-wise minimization converges in reasonable time on large practical instances. Unfortunately, the practical impact of this result is limited because there exist more efficient algorithms for solving these LP relaxations, such as reduction to max-flow. It is open whether there exist some useful classes of convex problems that are exactly solvable by (block-)coordinate descent but not solvable by more efficient methods. There is a possibility that our result and the proof technique will pave the way to such results.

2 Reformulations of Problems

Before presenting our main result, we make an important remark: while a convex optimization problem can be reformulated in many ways to an ‘equivalent’ problem which has the same global minima, not all of these transformations are equivalent with respect to coordinate-wise minimization, in particular, not all preserve interior local minima.

Example 1

One example is dualization. If coordinate-wise minimization achieves good local (or even global) minima on a convex problem, it can get stuck in very poor local minima if applied to its dual. Indeed, trying to apply (block-) coordinate minimization to the primal LP relaxation of MAP inference (linear optimization over the local marginal polytope) has been futile so far.

Example 2

Consider the linear program \(\min \{ x_1 + x_2 \mid x_1, x_2 \ge 0\}\), which has one interior local minimum with respect to individual coordinates that also corresponds to the unique global optimum. But if one adds a redundant constraint, namely \(x_1 = x_2\), then any feasible point will become an interior local minimum w.r.t. individual coordinates, because the redundant constraint blocks changing the variable \(x_i\) without changing \(x_{3-i}\) for both \(i \in \{1,2\}\).

Example 3

Consider the linear program

$$\begin{aligned} \min&\, \sum _{j = 1}^m z_j \end{aligned}$$
(1a)
$$\begin{aligned} z_j&\ge a_{ij}^Tx + b_{ij}&\forall i&\in [n], j \in [m] \end{aligned}$$
(1b)
$$\begin{aligned} z&\in \mathbb {R}^m, x \in \mathbb {R}^p\end{aligned}$$
(1c)

which can be also formulated as

$$\begin{aligned} \min&\, \sum _{j = 1}^m \max _{i =1}^n (a_{ij}^Tx + b_{ij})\end{aligned}$$
(2a)
$$\begin{aligned} x&\in \mathbb {R}^p. \end{aligned}$$
(2b)

Optimizing over the individual variables by coordinate-wise minimization in (1) does not yield the same interior local optima as in (2). For instance, assume that \(m = 3\), \(n = p = 1\) and the problem (2) is given as

$$\begin{aligned} \min \, \left( \max \{x,0 \} + \max \{-x,-1 \} + \max \{-x,-2 \} \right) , \end{aligned}$$
(3)

where \(x \in \mathbb {R}\). Then, when optimizing directly in form (3), one can see that all the interior local optima are global optimizers.

However, when one introduces the variables \(z \in \mathbb {R}^3\) and applies coordinate-wise minimization on the corresponding problem (1), then there are interior local optima that are not global optimizers, for example \(x = z_1 = z_2 = z_3 = 0\), which is an interior local optimum, but is not a global optimum.

On the other hand, optimizing over blocks of variables \(\{z_1, \dots , z_{m}, x_i\}\) for each \(i \in [p]\) in case (1) is equivalent to optimization over individual \(x_i\) in formulation (2).

3 Main Result

The optimization problem with which we are going to deal is in its most general form defined as

$$\begin{aligned} \min \; \;&\Bigl (\sum _{i = 1}^m \max \{w_i-\varphi _i, 0\} + a^T\varphi + b^T\lambda + \sum _{j = 1}^p \max \{v_j + A_{:j}^T\varphi + B_{:j}^T\lambda ,0\} \Bigr ) \end{aligned}$$
(4a)
$$\begin{aligned}&\underline{\varphi }_i \le \varphi _i \le \overline{\varphi }_i \;\;\forall i \in [m] \end{aligned}$$
(4b)
$$\begin{aligned}&\underline{\lambda }_i \le \lambda _i \le \overline{\lambda }_i \;\;\forall i \in [n], \end{aligned}$$
(4c)

where \(A \in \mathbb {R}^{m \times p}, B \in \mathbb {R}^{n \times p}\), \(a \in \mathbb {R}^{m}\), \(b \in \mathbb {R}^{n}\), \(w \in \mathbb {R}^m\), \(v \in \mathbb {R}^p\), \(\underline{\varphi }\in (\mathbb {R} \cup \{-\infty \})^m\), \(\overline{\varphi }\in (\mathbb {R} \cup \{\infty \})^m\), \(\underline{\lambda }\in (\mathbb {R} \cup \{-\infty \})^n\), \(\overline{\lambda }\in (\mathbb {R} \cup \{\infty \})^n\) (assuming \(\underline{\varphi }< \overline{\varphi }\) and \(\underline{\lambda }< \overline{\lambda }\)). We optimize over variables \(\varphi \in \mathbb {R}^m\) and \(\lambda \in \mathbb {R}^n\). \(A_{:j}\) and \(A_{i:}\) denotes the j-th column and i-th row of A, respectively.

Applying coordinate-wise minimization with relative-interior rule on the problem (4) corresponds to cyclic updates of variables, where each update corresponds to finding the region of optima of a convex piecewise-affine function of one variable on an interval. If the set of optimizers is a singleton, then the update is straightforward. If the set of optimizers is a bounded interval [a, b], the variable is assigned the middle value from this interval, i.e. \((a+b)/2\). If the set of optima is unbounded, i.e. \([a,\infty )\), then we set the variable to the value \(a+\varDelta \), where \(\varDelta > 0\) is a fixed constant. In case of \((-\infty ,a]\), the variable is updated to \(a-\varDelta \). The details for the update in this setting are in Appendix A in [10].

Theorem 1

Any interior local optimum of (4) w.r.t. individual coordinates is its global optimum if

  • matrices A, B contain only values from the set \(\{-1,0,1\}\) and contain at most two non-zero elements per row

  • vector a contains only elements from the set \((-\infty ,-2] \cup \{-1,0,1,2\} \cup [3, \infty )\)

  • vector b contains only elements from the set \((-\infty ,-2] \cup \{-1,0,1\} \cup [2, \infty )\).

In order to prove Theorem 1, we formulate problem (4) as a linear program by introducing additional variables \(\alpha \in \mathbb {R}^m\) and \(\beta \in \mathbb {R}^p\) and construct its dual. The proof of optimality is then obtained (see Theorem 2) by constructing a dual feasible solution that satisfies complementary slackness.

The primal linear program (with corresponding dual variables and constraints on the same lines) reads

$$\begin{aligned} \min \sum _{i \in [m]} \alpha _i + \sum _{i \in [p]}&\beta _i + a^T\varphi + b^T\lambda&\max \, f(z,y,s,r,&q,x)&\end{aligned}$$
(5a)
$$\begin{aligned} \beta _j - A_{:j}^T\varphi - B_{:j}^T\lambda&\ge v_j&x_j&\ge 0&\forall j&\in [p] \end{aligned}$$
(5b)
$$\begin{aligned} \alpha _i + \varphi _i&\ge w_i&s_i&\ge 0&\forall i&\in [m] \end{aligned}$$
(5c)
$$\begin{aligned} \varphi _i&\ge \underline{\varphi }_i&y_i&\ge 0&\forall i&\in [m] \end{aligned}$$
(5d)
$$\begin{aligned} \varphi _i&\le \overline{\varphi }_i&z_i&\le 0&\forall i&\in [m] \end{aligned}$$
(5e)
$$\begin{aligned} \lambda _i&\ge \underline{\lambda }_i&q_i&\ge 0&\forall i&\in [n] \end{aligned}$$
(5f)
$$\begin{aligned} \lambda _i&\le \overline{\lambda }_i&r_i&\le 0&\forall i&\in [n] \end{aligned}$$
(5g)
$$\begin{aligned} \varphi _i&\in \mathbb {R}&s_i + z_i + y_i - A_{i:}^Tx&= a_i&\forall i&\in [m] \end{aligned}$$
(5h)
$$\begin{aligned} \lambda _i&\in \mathbb {R}&r_i + q_i - B_{i:}^Tx&= b_i&\forall i&\in [n] \end{aligned}$$
(5i)
$$\begin{aligned} \beta _j&\ge 0&x_j&\le 1&\forall j&\in [p] \end{aligned}$$
(5j)
$$\begin{aligned} \alpha _i&\ge 0&s_i&\le 1&\forall i&\in [m], \end{aligned}$$
(5k)

where the dual criterion is

$$\begin{aligned} f(z,y,s,r,q,x) = {\overline{\varphi }}^Tz+{\underline{\varphi }}^Ty+w^Ts+{\overline{\lambda }}^Tr+{\underline{\lambda }}^Tq+v^Tx \end{aligned}$$
(6)

and clearly, at optimum of the primal, we have

$$\begin{aligned} \alpha _i&= \max \{w_i-\varphi _i,0\}&\forall i \in [m] \end{aligned}$$
(7a)
$$\begin{aligned} \beta _j&= \max \{v_j + A_{:j}^T\varphi + B_{:j}^T\lambda ,0\}&\forall j \in [p]. \end{aligned}$$
(7b)

The variables \(\alpha ,\beta \) were eliminated from the primal formulation (5) to obtain (4) due to similar reasoning as in Example 3. We also remark that setting \(\overline{\varphi }_i = \infty \) (resp. \(\underline{\varphi }_i = -\infty \), \(\overline{\lambda }_i = \infty \), \(\underline{\lambda }_i = -\infty \)) results in \(z_i = 0\) (resp. \(y_i = 0\), \(r_i = 0\), \(q_i = 0\)).

Even though the primal-dual pair (5) might seem overcomplicated, such general description is in fact necessary because as described in Sect. 2, equivalent reformulations may not preserve the structure of interior local minima and we would like to describe as general class, where optimality is guaranteed, as possible.

Example 4

To give the reader better insight into the problems (5), we present a simplification based on omitting the matrix A (i.e. \(m = 0\)) and setting \(\underline{\lambda }= 0\), \(\overline{\lambda }= \infty \), which results in \(r_i = 0\) and variables \(q_i\) become slack variables in (5i). The primal-dual pair in this case then simplifies to

$$\begin{aligned} \min \sum _{i \in [p]}&\beta _i + b^T\lambda&\max \,&v^Tx&\end{aligned}$$
(8a)
$$\begin{aligned} \beta _j - B_{:j}^T\lambda&\ge v_j&x_j&\ge 0&\forall j&\in [p] \end{aligned}$$
(8b)
$$\begin{aligned} \beta _j&\ge 0&x_j&\le 1&\forall j&\in [p] \end{aligned}$$
(8c)
$$\begin{aligned} \lambda _i&\ge 0&- B_{i:}^Tx&\le b_i&\forall i&\in [n]. \end{aligned}$$
(8d)

Theorem 2

For a problem (4) satisfying conditions of Theorem 1 and a given interior local minimum \((\varphi , \lambda )\), the valuesFootnote 3

$$\begin{aligned} x_j&= {\left\{ \begin{array}{ll} 0 &{} \text {if } A_{:j}^T\varphi + B_{:j}^T\lambda + v_j< 0 \\ \frac{1}{2} &{} \text {if } A_{:j}^T\varphi + B_{:j}^T\lambda + v_j = 0 \\ 1 &{} \text {if } A_{:j}^T\varphi + B_{:j}^T\lambda + v_j> 0 \end{array}\right. }&s_i&= {\left\{ \begin{array}{ll} 1 &{} \text {if } w_i>\varphi _i \\ 0 &{} \text {if } w_i<\varphi _i \\ h_{[0,1]}(a_i+A_{i:}^Tx) &{} \text {if } w_i=\varphi _i \end{array}\right. } \\ r_i&= {\left\{ \begin{array}{ll} 0 &{} \text {if } \lambda _i< \overline{\lambda }_i \\ h_{\mathbb {R}^-_0}(b_i + B_{i:}^Tx) &{} \text {if } \lambda _i = \overline{\lambda }_c \end{array}\right. }&z_i&= {\left\{ \begin{array}{ll} 0 &{} \text {if } \varphi _i < \overline{\varphi }_i \\ h_{\mathbb {R}^-_0}(a_i + A_{i:}^Tx - s_i) &{} \text {if } \varphi _i = \overline{\varphi }_i \end{array}\right. } \\ q_i&= {\left\{ \begin{array}{ll} 0 &{} \text {if } \lambda _i> \underline{\lambda }_i \\ h_{\mathbb {R}^+_0}(b_i + B_{i:}^Tx) &{} \text {if } \lambda _i = \underline{\lambda }_i \end{array}\right. }&y_i&= {\left\{ \begin{array}{ll} 0 &{} \text {if } \varphi _i > \underline{\varphi }_i \\ h_{\mathbb {R}^+_0}(a_i + A_{i:}^Tx - s_i) &{} \text {if } \varphi _i = \underline{\varphi }_i \end{array}\right. } \end{aligned}$$

are feasible for the dual (5) and satisfy complementary slackness with primal (5), where the remaining variables of the primal are given by (7).

It can be immediately seen that all the constraints of dual (5) are satisfied except for (5h) and (5i), which require a more involved analysis. The complete proof of Theorem 2 is technical (based on verifying many different cases) and given in Appendix B in [10].

4 Applications

Here we show that several LP relaxations of combinatorial problems correspond to the form (4) or to the dual (5) and discuss which additional constraints correspond to the assumptions of Theorem 1.

4.1 Weighted Partial Max-SAT

In weighted partial Max-SAT, one is given two sets of clauses, soft and hard. Each soft clause is assigned a positive weight. The task is to find values of binary variables \(x_i \in \{0,1\}\), \(i\in [p]\) such that all the hard clauses are satisfied and the sum of weights of the satisfied soft clauses is maximized.

We organize the m soft clauses into a matrix \(S\in \{-1,0,1\}^{m\times p}\) defined as

$$\begin{aligned} S_{ci} = {\left\{ \begin{array}{ll} 1 &{} \text {if literal } x_i \text { is present in soft clause } c\\ -1 &{} \text {if literal } \lnot x_i \text { is present in soft clause } c\\ 0 &{} \text {otherwise } \end{array}\right. }, \end{aligned}$$

In addition, we denote \(n^S_c=\sum _i [\![S_{ci} < 0]\!]\) to be the number of negated variables in clause c. These numbers are stacked in a vector \(n^S\in \mathbb {Z}^m\). The h hard clauses are organized in a matrix \(H\in \{-1,0,1\}^{h\times p}\) and a vector \(n^H\in \mathbb {Z}^h\) in the same manner.

The LP relaxation of this problem reads

$$\begin{aligned} \max&\sum _{c \in [m]} w_c s_c \end{aligned}$$
(10a)
$$\begin{aligned} s_c&\le S_{c:}^Tx + n^S_c&\forall c&\in [m] \end{aligned}$$
(10b)
$$\begin{aligned} H_{c:}^Tx + n^H_c&\ge 1&\forall c&\in [h] \end{aligned}$$
(10c)
$$\begin{aligned} x_i&\in [0,1]&\forall i&\in [p] \end{aligned}$$
(10d)
$$\begin{aligned} s_c&\in [0,1]&\forall c&\in [m], \end{aligned}$$
(10e)

where \(w_c \in \mathbb {R}^+_0\) are the weights of the soft clauses \(c \in [m]\). This is a sub-class of the dual (5), where \(A = S\), \(B = -H\), \(a = n^S\), \(b = 1-n^H\), \(\underline{\varphi }= 0\) (\(y \ge 0\) are therefore slack variables for the dual constraint (5h) that correspond to (10b)), \(\overline{\varphi }= \infty \) (therefore \(z = 0\)), \(\underline{\lambda }= -\infty \) (therefore \(q = 0\)), \(\overline{\lambda }= 0\) (\(r \le 0\) are slack variables for the dual constraint (5i) that correspond to (10c)), \(v = 0\).

Formulation (10) satisfies the conditions of Theorem 1 if each of the clauses has length at most 2. In other words, optimality is guaranteed for weighted partial Max-2SAT.

Also notice that if we omitted the soft clauses (10b) and instead set \(v = -1\), we would obtain an instance of Min-Ones SAT, which could be generalized to weighted Min-Ones SAT. This relaxation would still satisfy the requirements of Theorem 1 if all the present hard clauses have length at most 2.

Results. We tested the method on 800 smallestFootnote 4 instances that appeared in Max-SAT Evaluations [2] in years 2017 [1] and 2018 [3]. The results on the instances are divided into groups in Table 1 based on the minimal and maximal length of present clauses. We have also tested this approach on 60 instances of weighted Max-2SAT from Ke Xu  [33]. The highest number of logical variables in an instance was 19034 and the highest overall number of clauses in an instance was 31450. It was important to separate the instances without unit clauses (i.e. clauses of length 1), because in such cases the LP relaxation (10) has a trivial optimal solution with \(x_i = \frac{1}{2}\) for all \(i \in V\).

Coordinate-wise minimization was stopped when the criterion did not improve by at least \(\epsilon = 10^{-7}\) after a whole cycle of updates for all variables. We report the quality of the solution as the median and mean relative difference between the optimal criterion and the criterion reached by coordinate-wise minimization before termination.

Table 1 reports not only instances of weighted partial Max-2SAT but also instances with longer clauses, where optimality is no longer guaranteed. Nevertheless, the relative differences on instances with longer clauses still seem not too large and could be usable as bounds in a branch-and-bound scheme.

Table 1. Experimental comparison of coordinate-wise minimization and exact solutions for LP relaxation on instances from [2] (first 4 rows) and  [33] (last row).
Full size table

4.2 Weighted Vertex Cover

Dual (8) also subsumesFootnote 5 the LP relaxation of weighted vertex cover, which reads

$$\begin{aligned} \min \, \Big \{ \sum _{i \in V} v_i x_i \Bigm \vert x_i + x_j \ge 1 \; \forall \{i,j\} \in E, x_i \in [0,1] \; \forall i \in V \Big \} \end{aligned}$$
(11)

where V is the set of nodes and E is the set of edges of an undirected graph. This problem also satisfies the conditions of Theorem 1 and therefore the corresponding primal (4) will have no non-optimal interior local minima.

On the other hand, notice that formulation (11), which corresponds to dual (5) can have non-optimal interior local minima even with respect to all subsets of variables of size \(|V|-1\), an example is given in Appendix C in [10].

We reported the experiments on weighted vertex cover in [30] where the optimality was not proven yet. In addition, the update designed in [30] ad hoc becomes just a special case of our general update here.

4.3 Minimum st-Cut, Maximum Flow

Recall from [11] the usual formulation of max-flow problem between nodes \(s \in V\) and \(t \in V\) on a directed graph with vertex set V, edge set E and positive edge weights \(w_{ij} \in \mathbb {R}^+_0\) for each \((i,j) \in E\), which reads

$$\begin{aligned} \max \sum _{(s,i) \in E}&f_{si} \end{aligned}$$
(12a)
$$\begin{aligned} 0 \le f_{ij}&\le w_{ij}&\forall (i,j)&\in E \end{aligned}$$
(12b)
$$\begin{aligned} \sum _{(u,i) \in E} f_{ui} - \sum _{(j,u) \in E} f_{ju}&= 0&\forall u&\in V-\{s,t\}. \end{aligned}$$
(12c)

Assume that there is no edge (s, t), there are no ingoing edges to s and no outgoing edges from t, then any feasible value of f in (12) is an interior local optimum w.r.t. individual coordinates by the same reasoning as in Example 2 due to the flow conservation constraint (12c), which limits each individual variable to a single value. We are going to propose a formulation which has no non-globally optimal interior local optima.

The dual problem to (12) is the minimum st-cut problem, which can be formulated as

$$\begin{aligned} \max \,&\sum _{(i,j) \in E} w_{ij} y_{ij} \end{aligned}$$
(13a)
$$\begin{aligned} y_{ij}&\le 1-x_i+x_j&\forall (i,j)&\in E, i \ne s, j\ne t \end{aligned}$$
(13b)
$$\begin{aligned} y_{sj}&\le x_j&\forall (s,j)&\in E \end{aligned}$$
(13c)
$$\begin{aligned} y_{it}&\le 1-x_i&\forall (i,t)&\in E \end{aligned}$$
(13d)
$$\begin{aligned} y_{ij}&\in [0,1]&\forall (i,j)&\in E, \end{aligned}$$
(13e)
$$\begin{aligned} x_i&\in [0,1]&\forall i&\in V-\{s,t\}, \end{aligned}$$
(13f)

where \(y_{ij} = 0\) if edge (i, j) is in the cut and \(y_{ij} = 1\) if edge (i, j) is not in the cut. The cut should separate s and t, so the set of nodes connected to s after the cut will be denoted by S and \(T = V - S\) is the set of nodes connected to t. Using this notation, \(x_i = [\![i \in S]\!]\). Formulation (13) is different from the usual formulation by replacing the variables \(y_{ij}\) by \(1-y_{ij}\), therefore we also maximize the weight of the not cut edges instead of minimizing the weight of the cut edges, therefore if the optimal value of (13) is O, then the value of the minimum st-cut equals \(\sum _{(i,j)\in E}w_{ij} - O\).

Formulation (13) is subsumed by the dual (5) by setting \(\underline{\varphi }= 0\), \(\overline{\varphi }= \infty \) and omitting the B matrix. Also notice that each \(y_{ij}\) variable occurs in at most one constraint. The problem (13) therefore satisfies the conditions of Theorem 1 and the corresponding primal (4) is a formulation of the maximum flow problem, in which one can search for the maximum flow by coordinate-wise minimization. The corresponding formulation (4) reads

$$\begin{aligned} \min&\Bigl (\sum _{(i,j) \in E} \max \{w_{ij}-\varphi _{ij}, 0\} + \sum _{(i,j) \in E, i \ne s}\varphi _{ij} +\nonumber \\&+ \sum _{i \in V - \{s,t\}}\max \Bigl \{\sum _{(j,i) \in E} \varphi _{ji} - \sum _{(i,j) \in E} \varphi _{ij},0\Bigr \}\Bigr ) \end{aligned}$$
(14a)
$$\begin{aligned}&\varphi _{ij} \ge 0 \;\;\forall (i,j) \in E. \end{aligned}$$
(14b)

Results. We have tested our formulation for coordinate-wise minimization on max-flow instancesFootnote 6 from computer vision. We report the same statistics as with Max-SAT in Table 2, the instances corresponded to stereo problems, multiview reconstruction instances and shape fitting problems.

For multiview reconstruction and shape fitting, we were able to run our algorithm only on small instances, which have approximately between \(8 \cdot 10^5\) and \(1.2 \cdot 10^6\) nodes and between \(5 \cdot 10^6\) and \(6 \cdot 10^6\) edges. On these instances, the algorithm terminated with the reported precision in 13 to 34 min on a laptop.

Table 2. Experimental comparison of coordinate-wise minimization on max-flow instances, the references are the original sources of the data and/or to the authors that reformulated these problems as maximum flow. The first 6 rows correspond to stereo problems, the 2 following rows are multiview reconstruction instances, the last row is a shape fitting problem.
Full size table

4.4 MAP Inference with Potts Potentials

Coordinate-wise minimization for the dual LP relaxation of MAP inference was intensively studied, see e.g. the review [29]. One of the formulations is

$$\begin{aligned} \min \sum _{i \in V} \max _{k \in K} \theta ^\delta _i(k) +\sum _{\{i,j\} \in E} \max _{k,l \in K} \theta ^\delta _{ij}(k,l)\end{aligned}$$
(15a)
$$\begin{aligned} \delta _{ij}(k) \in \mathbb {R} \;\;\forall \{i,j\} \in E, k \in K, \end{aligned}$$
(15b)

where K is the set of labels, V is the set of nodes and E is the set of unoriented edges and

$$\begin{aligned} \theta _i^\delta (k)&= \theta _i(k) - \sum _{j \in N_i}\delta _{ij}(k) \end{aligned}$$
(16a)
$$\begin{aligned} \theta _{ij}^\delta (k,l)&= \theta _{ij}(k,l) + \delta _{ij}(k) + \delta _{ji}(l) \end{aligned}$$
(16b)

are equivalent transformations of the potentials. Notice that there are \(2 \cdot |E| \cdot |K|\) variables, i.e. two for each direction of an edge. In [24], it is mentioned that in case of Potts interactions, which are given as \(\theta _{ij}(k,l) = -[\![k \ne l]\!]\), one can add constraints

$$\begin{aligned} \delta _{ij}(k) + \delta _{ji}(k)&= 0&\forall \{i,j\}&\in E, k \in K \end{aligned}$$
(17a)
$$\begin{aligned} -\tfrac{1}{2} \le \delta _{ij}(k)&\le \tfrac{1}{2}&\forall \{i,j\}&\in E, k \in K \end{aligned}$$
(17b)

to (15) without changing the optimal objective. One can therefore use constraint (17a) to reduce the overall amount of variables by defining

$$\begin{aligned} \lambda _{ij}(k) = -\delta _{ij}(k) = \delta _{ji}(k) \end{aligned}$$
(18)

subject to \(\tfrac{1}{2} \le \lambda _{ij}(k) \le \tfrac{1}{2}\). The decision of whether \(\delta _{ij}(k)\) or \(\delta _{ji}(k)\) should have the inverted sign depends on the chosen orientation \(E'\) of the originally undirected edges E and is arbitrary. Also, given values \(\delta \) satisfying (17), it holds for any edge \(\{i,j\} \in E\) and pair of labels \(k,l \in K\) that \(\max \limits _{k,l \in K}\theta _{ij}^\delta (k,l) = 0\), which can be seen from the properties of the Potts interactions.

Therefore, one can reformulate (15) into

$$\begin{aligned} \min \sum _{i \in V}&\max _{k \in K} \, \theta ^\lambda _i(k)\end{aligned}$$
(19a)
$$\begin{aligned} - \tfrac{1}{2} \le \lambda _{ij}(k)&\le \tfrac{1}{2} \;\;\forall (i,j) \in E', k \in K, \end{aligned}$$
(19b)

where the equivalent transformation in \(\lambda \) variables is given by

$$\begin{aligned} \theta _i^\lambda (k) = \theta _i(k) + \sum _{(i,j) \in E'} \lambda _{ij}(k) - \sum _{(j,i) \in E'} \lambda _{ji}(k) \end{aligned}$$
(20)

and we optimize over \(|E'|\cdot |K|\) variables \(\lambda \), the graph \((V,E')\) is the same as graph (V, E) except that each edge becomes oriented (in arbitrary direction). The way of obtaining an optimal solution to (15) from an optimal solution of (19) is given by (18) and depends on the chosen orientation of the edges in \(E'\). Also observe that \(\theta _i^\delta (k) = \theta _i^\lambda (k)\) for any node \(i \in V\) and label \(k \in K\) and therefore the optimal values will be equal. This reformulation therefore maps global optima of (19) to global optima of (15). However, it does not map interior local minima of (19) to interior local minima of (15) when \(|K| \ge 3\), an example of such case is shown in Appendix D in [10].

In problems with two labels (\(K = \{1,2\}\)), problem (19) is subsumed by (4) and satisfies the conditions imposed by Theorem 1 because one can rewrite the criterion by observing that

$$\begin{aligned} \max _{k\in \{1,2\}} \theta ^\lambda _i(k) = \max \{\theta ^\lambda _i(1)-\theta ^\lambda _i(2),0\}+\theta ^\lambda _i(2) \end{aligned}$$
(21)

and each \(\lambda _{ij}(k)\) is present only in \(\theta _i^\lambda (k)\) and \(\theta _j^\lambda (k)\). Thus, \(\lambda _{ij}(k)\) will have non-zero coefficient in the matrix B only on columns i and j. The coefficients of the variables in the criterion are only \(\{-1,0,1\}\) and the other conditions are straightforward.

We reported the experiments on the Potts problem in  [30] where the optimality was not proven yet. In addition, the update designed in [30] ad hoc becomes just a special case of our general update here.

4.5 Binarized Monotone Linear Programs

In [13], integer linear programs with at most two variables per constraint were discussed. It was also allowed to have 3 variables in some constraints if one of the variables occurred only in this constraint and in the objective function. Although the objective function in [13] was allowed to be more general, we will restrict ourselves to linear criterion function. It was also shown that such problems can be transformed into binarized monotone constraints over binary variables by introducing additional variables whose amount is defined by the bounds of the original variables, such optimization problem reads

$$\begin{aligned} \min \, {w}^Tx&+{e}^Tz \end{aligned}$$
(22a)
$$\begin{aligned} Ax - Iz&\le 0\end{aligned}$$
(22b)
$$\begin{aligned} Cx&\le 0 \end{aligned}$$
(22c)
$$\begin{aligned} x&\in \{0,1\}^{n_1}\end{aligned}$$
(22d)
$$\begin{aligned} z&\in \{0,1\}^{n_2}, \end{aligned}$$
(22e)

where A, C contain exactly one \(-1\) per row and exactly one 1 per row and all other entries are zero, I is the identity matrix. We refer the reader to [13] for details, where it is also explained that the LP relaxation of (22) can be solved by min-st-cut on an associated graph. We can notice that the LP relaxation of (22) is subsumed by the dual (5), because one can change the minimization into maximization by changing the signs in w, e. Also, the relaxation satisfies the conditions given by Theorem 1.

In the paper [13], there are listed many problems which are transformable to (22) and are also directly (without any complicated transformation) subsumed by the dual (5) and satisfy Theorem 1, for example, minimizing the sum of weighted completion times of precedence-constrained jobs (ISLO formulation in [9]), generalized independent set (forest harvesting problem in [14]), generalized vertex cover [15], clique problem [15], Min-SAT (introduced in [17], LP formulation in [13]).

For each of these problems, it is easy to verify the conditions of Theorem 1, because they contain at most two variables per constraint and if a constraint contains a third variable, then it is the only occurrence of this variable and the coefficients of the variables in the constraints are from the set \(\{-1,0,1\}\).

The transformation presented in [13] can be applied to partial Max-SAT and vertex cover to obtain a problem in the form (22) and solve its LP relaxation. But this step is unnecessary when applying the presented coordinate-wise minimization approach.

5 Concluding Remarks

We have presented a new class of linear programs that are exactly solved by coordinate-wise minimization. We have shown that dual LP relaxations of several well-known combinatorial optimization problems (partial Max-2SAT, vertex cover, minimum st-cut, MAP inference with Potts potentials and two labels, and other problems) belong, possibly after a reformulation, to this class. We have shown experimentally (in this paper and in [30]) that the resulting methods are reasonably efficient for large-scale instances of these problems. When the assumptions of Theorem 1 are relaxed (e.g., general Max-SAT instead of Max-2SAT, or the Potts problem with any number of labels), the method experimentally still provides good local (though not global in general) minima.

We must admit, though, that the practical impact of Theorem 1 is limited because the presented dual LP relaxations satisfying its assumptions can be efficiently solved also by other approaches. Thus, max-flow/min-st-cut can be solved (besides well-known combinatorial algorithms such as Ford-Fulkerson) by message-passing methods such as TRW-S. Similarly, the Potts problem with two labels is tractable and can be reduced to max-flow. In general, all considered LP relaxations can be reduced to max-flow, as noted in Sect. 4.5. Note, however, that this does not make our result trivial because (as noted in Sect. 2) equivalent reformulations of problems may not preserve interior local minima and thus message-passing methods are not equivalent in any obvious way to our method.

It is open whether there are practically interesting classes of linear programs that are solved exactly (or at least with constant approximation ratio) by (block-) coordinate minimization and are not solvable by known combinatorial algorithms such as max-flow. Another interesting question is which reformulations in general preserve interior local minima and which do not.

Our approach can pave the way to new efficient large-scale optimization methods in the future. Certain features of our results give us hope here. For instance, our approach has an important novel feature over message-passing methods: it applies to a constrained convex problem (the box constraints (4b) and (4c)). This can open the way to a new class of applications. Furthermore, updates along large variable blocks (which we have not explored) can speed algorithms considerably, e.g., TRW-S uses updates along subtrees of a graphical model, while max-sum diffusion uses updates along single variables.