Polynomial Scheduling Algorithm for Parallel Applications on Hybrid Platforms

Abstract

This work addresses the problem of scheduling parallel applications into hybrid platforms composed of two different types of resources. We focus on finding a generic approach to schedule applications represented by directed acyclic graphs that minimises makespan with performance guarantee. A three-phase algorithm is proposed; the first two phases consist in solving linear formulations to find the type of processor assigned to execute each task. In the third phase, we compute the start execution time of each task to generate a feasible schedule. Finally, we test our algorithm on a large number of instances. These tests demonstrate that the proposed algorithm achieves a close-to-optimal performance.

1 Introduction

Nowadays, High Performance Computers (HPC) are popular and powerful commercial platform due to the increasing demand for developing efficient computing resources to execute large parallel applications. In order to increase the computing power of these platforms while keeping a reasonable level of energy consumption, the heterogeneous platforms have appeared. It is possible to integrate several types of material resources such that each one is specialised for certain types of calculations. Thus we have to take into account that the execution time for any task of the application depends on the type of resource used to execute it. However, using these platforms efficiently became very challenging. Consequently, more and more attention has been focused on scheduling techniques for solving the problem of optimizing the execution of parallel applications on heterogeneous computing systems [1, 2].

This work addresses the problem of scheduling parallel applications onto a particular case of HPC composed of two different types of resources: CPU (Central Processing Unit) and GPU (Graphics Processing Unit). These platforms are often called hybrid platform. The number of platforms of the TOP500¹ equipped with accelerators has significantly increased during the last years. TGCC Curie supercomputer² is an example of these platforms.

We focus here in finding a generic approach to schedule applications presented by DAG (Directed Acyclic Graph) into a hybrid platform that minimises the completion time of the application by considering communication delays. An algorithm with three phases has been proposed; the first phase consists in solving a mathematical formulation $(P')$ and then define a new formulation using the solution obtained. The second phase solves an assignment problem to find the type of processor affected to execute the tasks (processing element type 1 or 2) using a linear formulation. In the last phase, we compute the starting execution time of each task to generate a feasible schedule. Our algorithm has been experimented on a large number of instances and evaluated compared to the exact solution.

The rest of the paper is organised as follows: Sect. 2 gives a quick overview of previous research in scheduling strategies on hybrid platforms. Section 3 presents the detailed problem with mathematical formulation. In Sect. 4, we describe the proposed algorithm for our problem and the approximation ratio we obtain for the scheduling problem. Section 5 shows some preliminary numerical results. Finally, we conclude and provide insights for future work in Sect. 6.

2 Related Work

The problem of scheduling tasks on hybrid parallel platforms has attracted a lot of attention. In the case where all processors have the same processing power and there is a cost for any communication ($P|prec,com|C_{max}$), the problem has been shown to be NP-hard [3].

Several works have studied the problem of scheduling independent tasks on $\ell$ (resp. k) processors of type $\mathcal {A}$ (resp. $\mathcal {B}$) which is represented by $(P\ell ,Pk)||C_{max}$. Imreh  [4] proves that the greedy algorithm provides a solution with a performance guarantee of $(2+\frac{\ell -1}{k})$, where $k\leqslant \ell$. Recently, a 2-approximation algorithm has been proposed in  [5]. For the same problem, Kedad-Sidhoum et al. [6] proposed two families of approximation algorithms that can achieve an approximation ratio smaller than $(\frac{3}{2}+\epsilon )$. By considering precedence constraints without communication delays $(P\ell ,Pk)|prec|C_{max}$, Kedad-Sidhoum et al. [7] developed a tight 6-approximation algorithm for general structure graphs on hybrid parallel multi-core machines. This work was later revisited in [8] who showed that by separating the allocation phase and the scheduling phase, they could obtain algorithms with a similar approximation ratio but that performs significantly better in practice.

In term of heuristic strategies, the most famous one is Heterogeneous Earliest Finish Time algorithm (HEFT)  [9], which is developed for the problem of DAG scheduling on heterogeneous platforms considering communication delays ($Rm|prec,com|C_{max}$). It could also be applied for hybrid platforms. It has no performance guarantee, but performs particularly well. Other heuristics for this problem can be roughly partitioned into two classes: clustering and list scheduling algorithms.

Clustering algorithms  [10, 11] usually provide good solutions for communication-intensive graphs by scheduling heavily communicating tasks onto the same processor. After grouping tasks into a set of clusters using different clustering policies. Clusters are mapped onto processors using communication sensitive or insensitive heuristics.

List scheduling algorithms  [12] are often used to handle a limited number of processors. Most of them  [13, 14] can be decomposed in two main phases. The first one assigns priorities based on certain task properties, typically run time and/or communication delays. The second phase assigns tasks to processors following a priority list. Experimentally, a comparison of different list scheduling algorithms can be found in the work of Kushwaha and Kumar  [14].

Our problem was first treated in  [15], a non polynomial-time two-phase approach was proposed with a performance guarantee of 6. Numerical evaluations demonstrate that the proposed algorithm achieves a close-to-optimal performance. However, the running time of this method can be important for large instances. We focus here in finding a polynomial-time approach which is able to maintain an interesting performance with reasonable complexity.

3 Problem Definition

We consider in this work a hybrid platform composed of 2 unrelated Processing elements $Pe_{1}$ and $Pe_{2}$ (1 CPU and 1 GPU, or 2 different GPUs or CPUs, ...).

An application A of n tasks is represented by a Directed Acyclic Graph (DAG) oriented G(V, E), each vertex represents a task $t_{i}$. Each arc $e =(t_{i},t_{j})$ represents a precedence constraint between two tasks $t_{i}$ and $t_{j}$. We associate it with the value $ct_{i,j}$ which represents the communication delay between $t_{i}$ and $t_{j}$ if they are executed on two different resource types. The exact formula to evaluate $ct_{i, j}$ which takes into consideration latencies and available bandwidth between processors is provided in  [16]. We denote by $\varGamma ^{-}(i)$ (resp. $\varGamma ^{+}(i)$) the sets of the predecessors (resp. successors) of task $t_{i}$. Any task $t_{i}$ can be executed by both processing elements. Executing the task $t_{i}$ on $Pe_{1}$ (resp. $Pe_{2}$) generates an execution time equal to $w _{i,0}$ (resp. $w _{i,1}$). A task $t_{i}$ can be executed only after the complete execution of its predecessors $\varGamma ^{-}(i)$. We do not allow duplication of tasks and preemption. We denote by $C_{max}$ the completion time of the application A (makespan). The aim is to minimise $C_{max}$.

Our problem can be modelled by a Mixed Integer formulation (Opt). Let $x_ {i}$ be the decision variable which is equal to 1 if the task $t_{i}$ is assigned to a $Pe_{1}$ and 0 otherwise. Let $C_{i}$ be the finish time of the task $t_{i}$. To manage overlapping tasks on the same processing element, we add an intermediary variable $o_{i,j}$ for each two different tasks $t_{i}$ and $t_{j}$. If $t_{i}$ and $t_{j}$ are executed in the same processing element and $t_{j}$ is executed after the finish execution time of $t_{i}$, then $o_{i,j}=1$, otherwise $o_{i,j}=0$. Finally, for each two successive tasks $(t_{i},t_{k})\in E$, we add an intermediary variable $\zeta _{i,k}$ to manage communication delays.

$$ (Opt)\left\{ \begin{array}{ll} C_{i}+x_{j}w _{j,0}+(1-x_{j})w _{j,1}+\zeta _{i,j}ct_{i,j}\leqslant C_{j} \text { }\forall (t_{i},t_{j}) \in E&{}(1)\\ x_{i}-x_{j}\leqslant \zeta _{i,j}, \text { }\forall (t_{i},t_{j}) \in E&{}(2)\\ x_{j}-x_{i}\leqslant \zeta _{i,j}, \text { }\forall (t_{i},t_{j}) \in E&{}(3)\\ x_{i}w _{i,0}+(1-x_{i})w _{i,1}\leqslant C_{i}, \forall i\in \{1,\ldots ,n\}, \varGamma ^{-}{(i)}=\emptyset &{} (4)\\ 0\leqslant C_{i}\leqslant C_{max}, \forall i\in \{1,\ldots ,n\}, \varGamma ^{+}{(i)}=\emptyset &{} (5)\\ C_{i}+x_{j}w _{j,0}\leqslant C_{j}+B\times (3-x_{i}-x_{j}-o_{i,j})\text { }\forall t_{i}\ne t_{j} &{} (6)\\ C_{j}+x_{i}w _{i,0}\leqslant C_{i}+B\times (2-x_{i}-x_{j}+o_{i,j})\text { }\forall t_{i}\ne t_{j} &{}(7)\\ C_{i}+(1-x_{j})w _{j,1}\leqslant C_{j}+B\times (1+x_{i}+x_{j}-o_{i,j})\text { }\forall t_{i}\ne t_{j} &{} (8)\\ C_{j}+(1-x_{i})w _{i,1}\leqslant C_{i}+B\times (x_{i}+x_{j}+o_{i,j})\text { }\forall t_{i}\ne t_{j} &{}(9)\\ x_{i},\text { } \zeta _{i,j},\text { } o_{i,j}\in \{0,1\}, \ \forall i\in \{1,\ldots ,n\}, \text { } B=Cte&{} \\ Z(min) = C_{max}&{}\\ \end{array} \right. $$

Constraints (1 to 3) describe the critical path, such as if task $t_{i}$ precedes $t_{j}$, and these two tasks are assigned to two different processors, we obtain two cases: either $x_{i}=1$ and $x_{j}=0$ or $x_{i}=0$ and $x_{j}=1$. In the two cases, we obtain $\zeta _{i,j}\geqslant 1$. If tasks $t_{i}$ and $t_{j}$ are assigned to the same processor, $x_{i}=0$ and $x_{j}=0$ or $x_{i}=1$ and $x_{j}=1$. In the two cases, $\zeta _{i,j}\geqslant 0$. Since it is a minimisation problem and without loss of generality, $\zeta _{i,j}$ should take the smallest possible value. Tasks without predecessors (respectively successors) are considered in the constraint (4) (resp. (5)). Overlapping tasks on $Pe_{1}$ (resp. $Pe_{2}$) is avoided by constraints (6) and (7) (resp. (8) and (9)) by using a large constant B (upper bound for example), such that if two tasks $t_{i}$ and $t_{j}$ are executed on the same processor, then either $t_{i}$ starts after the completion time of the task $t_{j}$ or $t_{j}$ starts after the completion time of the task $t_{i}$. We have two cases:

• 1. $t_{i}$ and $t_{j}$ are executed on $Pe_{1}$, then $x_{i}=1$ and $x_{j}=1$:

  

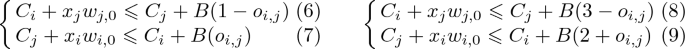
  If $o_{i,j}=1$ (resp. $o_{i,j}=0$), only constraint (6) (resp. (7)) becomes relevant, with $C_{i}+x_{j}w _{j,0}\leqslant C_{j}$ (resp. $C_{j}+x_{i}w _{i,0}\leqslant C_{i}$), then $t_{j}$ (resp. $t_{i}$) starts after the finish execution time of task $t_{i}$ (resp. $t_{j}$). Other constraints will remain valid no matter the execution order of $t_{i}$ and $t_{j}$.

• 2. $t_{i}$ and $t_{j}$ are executed on $Pe_{2}$, then $x_{i}=0$ and $x_{j}=0$:

  

  If $o_{i,j}=1$ (resp. $o_{i,j}=0$), only constraint (8) (resp. (9)) becomes relevant, with $C_{i}+(1-x_{j})w _{j,1}\leqslant C_{j}$ (resp. $C_{j}+(1-x_{i})w _{i,1}\leqslant C_{i}$), then $t_{j}$ (resp. $t_{i}$) starts after the finish execution time of task $t_{i}$ (resp. $t_{j}$). Other constraints will remain valid no matter the execution order of $t_{i}$ and $t_{j}$.

The formulation (Opt) can be used to obtain an optimal solution for only small instances with limited number of tasks using solvers like CPLEX [17]. To solve larger instances, a polynomial method is proposed in the following.

4 Solution Method

In this section, we develop a three-phase algorithm. In Phase 1, we start by proposing a new formulation (P) then we solve its relaxation $(P^{'})$. After that, we use in Phase 2 the solution obtained by this formulation to define another formulation (P1). Finally, after rounding the fractional solution of the formulation (P1) to obtain a feasible assignment of the tasks, in Phase 3 we use a list scheduling algorithm to find a feasible schedule. Details of each phase are described in the following.

4.1 Phase 1: Formulation (P) and Its Relaxation $(P^{'})$

We solve here a linear formulation with continuous variables. From the formulation (Opt), we define a more simplified formulation (P) which is more useful for the next phase. The first 5 constraints of (Opt) are thus taken up again, but the non-overlapping constraints (6) and (7) are replaced by two workload constraints. Thus, (P) is defined as follow, where Constraint (6) (resp. (7)) simply expresses that the makespan should be be larger than the average $Pe_{1}$ (resp. $Pe_{2}$) workload. The aim is to minimise $C_{maxp}$.

$$ (P)\left\{ \begin{array}{ll} C_{i}+x_{j}w _{j,0}+(1-x_{j})w _{j,1}+\zeta _{i,j}ct_{ i, j}\leqslant C_{j}, \text { }\forall (t_{i},t_{j}) \in E &{}(1)\\ x_{i}-x_{j}\leqslant \zeta _{i,j}, \text { }\forall (t_{i},t_{j}) \in E&{}(2)\\ x_{j}-x_{i}\leqslant \zeta _{i,j}, \text { }\forall (t_{i},t_{j}) \in E&{}(3)\\ x_{i}w _{i,0}+(1-x_{i})w _{i,1}\leqslant C_{i}, \forall i\in \{1,\ldots ,n\}, \varGamma ^{-}{(i)}=\emptyset &{} (4)\\ 0\leqslant C_{i}\leqslant C_{maxp}, \forall i\in \{1,\ldots ,n\}, \varGamma ^{+}{(i)}=\emptyset &{} (5)\\ \sum \nolimits _{i=1}^{n}x_{i}w _{i,0}\leqslant C_{maxp}&{} (6)\\ \sum \nolimits _{i=1}^{n}(1-x_{i})w _{i,1}\leqslant C_{maxp}&{}(7)\\ x_{i}, \zeta _{i,j}\in \{0,1\}, \ \forall i\in \{1,\ldots ,n\}&{} \\ Z(min) = C_{maxp}&{}\\ \end{array} \right. $$

Remark 1

The optimal solution $C_{maxp}^{\star }$ of this formulation does not take into account non-overlapping constraints, so it represents a lower bound for our problem, $C_{maxp}^{\star }\leqslant C_{max}^{\star }$.

Lemma 1

For each two successive tasks $(t_{i},t_{j}) \in E$, constraints (2) and (3) can be written as $max (x_{i},x_{j})-min (x_{i},x_{j}) \leqslant \zeta _{i,j}$. Furthermore, $max (x_{i},x_{j})-min (x_{i},x_{j})= (1-min(x_{i},x_{j})) +(max (x_{i},x_{j})-1)=max (1-x_{i},1-x_{j})-min(1-x_{i},1-x_{j})$. Thus, constraints (2) and (3) can also be written as $max(1-x_{i},1-x_{j})-min (1-x_{i},1-x_{j}) \leqslant \zeta _{i,j}$.

Remark 2

In each feasible solution of (P), for each couple of tasks $(t_{i},t_{j}) \in E$, we have always $max (x_{i},x_{j})=1$ or $max (1-x_{i},1-x_{j})=1$ (or both), $\forall (x_{i},x_{j})\in \{0,1\}\times \{0,1\}$.

Lemma 2

In the optimal solution of (P), for each couple of tasks $(t_{i},t_{j}) \in E$, from Lemma 1 we have at least $max (x_{i},x_{j})=1$ or $max (1-x_{i},1-x_{j})=1$, such that:

• If $max (x_{i},x_{j})=1$, then constraints (2) and (3) can be represented by $\widetilde{Con}_{i,j}^{1}:1-min (x_{i},x_{j}) \leqslant \zeta _{i,j}$.

• If $max (1-x_{i},1-x_{j})=1$, then constraints (2) and (3) can be represented by $\widetilde{Con}_{i,j}^{2}:1-min (1-x_{i},1-x_{j}) \leqslant \zeta _{i,j}$.

The optimal solution obtained by the formulation (P) without constraints (6) and (7) represents the optimal solution of the scheduling problem on platforms with unlimited resources. This problem has been proven to be NP-hard  [18]. Thus, the problem of finding the optimal mapping using (P) is also NP-complete. In order to simplify the problem, we relax the integer variables $x_{i}$ for $i\in \{1,\ldots ,n\}$ and we obtain the relaxed formulation $(P^{'})$. We denote by $\widetilde{x}_{i}^{'}\in [0,1]$, the value of $x_{i}$ in the optimal solution of the formulation $(P^{'})$.

4.2 Phase 2: Formulation (P1)

Based on Lemma 1 and using the solution of $(P^{'})$, we define another formulation (P1). The decision variables are $x_{i}^{'}$, and an intermediary variable $y_{i,j}^{'} \in [0,1]$, with $i\in \{1,\ldots ,n\}$ and $j\in \{1,\ldots ,n\}$. For all $(t_{i},t_{j}) \in E$, we define the constraint $Con_{i,j}$ as follows:

• If min$\{\widetilde{x}_{i}^{'},\widetilde{x}_{j}^{'}\}>$min$\{1-\widetilde{x}_{i}^{'},1-\widetilde{x}_{j}^{'}\}$, then $Con_{i,j}= \left\{ \begin{array}{ll} y_{i,j}^{'}\leqslant x_{i}^{'}&{}(1)\\ y_{i,j}^{'}\leqslant x_{j}^{'}&{}(2)\\ \zeta _{i,j}^{'}=(1-y_{i,j}^{'})&{}(3) \end{array} \right.$ From $Con_{i,j}$, we have $y_{i,j}^{'}\leqslant min\{x_{i}^{'},x_{j}^{'}\}$. Then, $\zeta _{i,j}^{'}=1-y_{i,j}^{'}\geqslant (1-min\{x_{i}^{'},x_{j}^{'}\})$, which is equivalent to constraint $\widetilde{Con}_{i,j}^{1}$. Since it is a minimisation problem, we can set $\zeta _{i,j}^{'}=(1-min\{x_{i}^{'},x_{j}^{'}\})$.

• If min$\{\widetilde{x}_{i}^{'},\widetilde{x}_{j}^{'}\}\leqslant$min$\{1-\widetilde{x}_{i}^{'},1-\widetilde{x}_{j}^{'}\}$ then $Con_{i,j}= \left\{ \begin{array}{ll} y_{i,j}^{'}\leqslant 1- x_{i}^{'}&{}(1)\\ y_{i,j}^{'}\leqslant 1-x_{j}^{'}&{}(2)\\ \zeta _{i,j}^{'}=(1-y_{i,j}^{'})&{}(3) \end{array} \right.$ From $Con_{i,j}$, we have $y_{i,j}^{'}\leqslant min\{1-x_{i}^{'},1-x_{j}^{'}\}$. Then, $\zeta _{i,j}^{'}=1-y_{i,j}^{'}\geqslant (1-min\{1-x_{i}^{'},1-x_{j}^{'}\})$, which is equivalent to constraint $\widetilde{Con}_{i,j}^{2}$. Since it is a minimisation problem, we can set $\zeta _{i,j}^{'}=(1-min\{1-x_{i}^{'},1-x_{j}^{'}\})$.

The formulation (P1) is then given by:

$$ (P1)\left\{ \begin{array}{ll} C_{i}^{'}+x_{j}^{'}w _{j,0}+ (1-x_{j}^{'})w _{j,1}+\zeta _{i,j}^{'}ct_{ i, j}\leqslant C_{j}^{'}, \forall (t_{i},t_{j}) \in E&{}(1)\\ Con_{i,j}, \forall (t_{i},t_{j}) \in E &{}(2)\\ x_{i}^{'}w_{i,0}+(1-x_{i}^{'})w_{i,0}\leqslant C_{i}^{'}, \forall i\in \{1,\ldots ,n\}, \varGamma ^{-}{(i)}=\emptyset &{} (3)\\ 0\leqslant C_{i}^{'}\leqslant C_{max1'}, \forall i\in \{1,\ldots ,n\}, \varGamma ^{+}{(i)}=\emptyset &{} (4)\\ \sum \nolimits _{i=1}^{n}x_{i}^{'}w_{i,0}\leqslant C_{max1'}&{}(5)\\ \sum \nolimits _{i=1}^{n}(1-x_{i}^{'})w_{i,0}\leqslant C_{max1'}&{}(6)\\ x_{i}^{'}, y_{i,j}^{'},\zeta _{i,j}^{'} \in [0,1], \ \forall i\in \{1,\ldots ,n\}, j\in \{1,\ldots ,n\}&{} \\ Z(min) = C_{max1'}&{}\\ \end{array} \right. $$

We can notice that constraints (1, 3, 4, 5, 6) of the formulation (P1) are equivalent to constraints (1, 4, 5, 6, 7) of the formulation $(P^{'})$. We denote by $C_{max1'}^{\star }$ the optimal solution of the formulation (P1) and $C_{maxp'}^{\star }$ the optimal solution of $(P^{'})$.

Theorem 1

If the optimal solution $\widetilde{x}_{i}^{\star }$ obtained by $(P^{'})$ is an integer for all $i \in \{1,\ldots ,n\}$, then $C_{max1'}^{\star }=C_{maxp'}^{\star }$.

Proof

By setting the value of ${x}_{i}^{'}=\widetilde{x}_{i}^{\star }$, for all $i \in \{1,\ldots ,n\}$, then for each two successive tasks $(t_{i},t_{j})\in E$, we have two cases:

• 1. min$\{\widetilde{x}_{i}^{\star },\widetilde{x}_{j}^{\star }\}>$min$\{1-\widetilde{x}_{i}^{\star },1-\widetilde{x}_{j}^{\star }\}$, then $Con_{i,j}= \left\{ \begin{array}{ll} y_{i,j}^{'}\leqslant {x}_{i}^{'}&{}(1)\\ y_{i,j}^{'}\leqslant x_{j}^{'}&{}(2)\\ \zeta _{i,j}^{'}=(1-y_{i,j}^{'})&{}(3) \end{array} \right.$ Furthermore, min$\{\widetilde{x}_{i}^{\star },\widetilde{x}_{j}^{\star }\}=1$, then $\widetilde{x}_{i}^{\star }=1$ and $\widetilde{x}_{j}^{\star }=1$, follows $\widetilde{x}_{i}^{\star }-\widetilde{x}_{j}^{\star }=0\leqslant \widetilde{\zeta }_{i,j}^{\star }$ ($\widetilde{\zeta }_{i,j}^{\star }=0$ since it is a minimisation problem). Furthermore, $\zeta _{i,j}^{'}=(1-min\{{x}_{i}^{'},x_{j}^{'}\})=1-1=0$, then $\zeta _{i,j}^{'} =\widetilde{\zeta }_{i,j}^{\star }$.

• 2. min$\{\widetilde{x}_{i}^{\star },\widetilde{x}_{j}^{\star }\}\leqslant$min$\{1-\widetilde{x}_{i}^{\star },1-\widetilde{x}_{j}^{\star }\}$, then $Con_{i,j}= \left\{ \begin{array}{ll} y_{i,j}^{'}\leqslant 1-x_{i}^{'}&{}(1)\\ y_{i,j}^{'}\leqslant 1-x_{j}^{'}&{}(2)\\ \zeta _{i,j}^{'}=(1-y_{i,j}^{'})&{}(3) \end{array} \right.$

  • if min$\{1-\widetilde{x}_{i}^{\star },1-\widetilde{x}_{j}^{\star }\}=1$, then $1-\widetilde{x}_{i}^{\star }=1$ and $1-\widetilde{x}_{j}^{\star }=1$, follows $\widetilde{x}_{i}^{\star }-\widetilde{x}_{j}^{\star }=0\leqslant \widetilde{\zeta }_{i,j}^{\star }$ with $\widetilde{x}_{i}^{\star }=0$ and $\widetilde{x}_{j}^{\star }=0$. Furthermore, $\zeta _{i,j}^{'}=(1-min\{1-x_{i}^{'},1-x_{j}^{'}\})=1-1=0$.

  • if min$\{1-\widetilde{x}_{i}^{\star },1-\widetilde{x}_{j}^{\star }\}=0$, then we suppose that $\widetilde{x}_{i}^{\star }=1$ and $\widetilde{x}_{j}^{\star }=0$, follows $\widetilde{x}_{i}^{\star }-\widetilde{x}_{j}^{\star }=1\leqslant \widetilde{\zeta }_{i,j}^{\star }$. Furthermore, $\zeta _{i,j}^{'}=(1-min\{1-x_{i}^{'},1-x_{j}^{'}\})=1-0=1$. In both cases, we have $\zeta _{i,j}^{'} =\widetilde{\zeta }_{i,j}^{\star }$.

Thus, the finish execution time of each task in the formulation $(P^{'})$ is the same in (P1). Furthermore, since $\sum _{i=1}^{n}x_{i}^{'}w _{i,0}=\sum _{i=1}^{n}x_{i}^{\star }w _{i,0}$ and $\sum _{i=1}^{n}(1-x_{i}^{'})w _{i,1}=\sum _{i=1}^{n}(1-x_{i}^{\star })w _{i,1}$, then constraints (5) and (6) of the formulation $(P^{'})$ are the same in (P1). Finally, $C_{max1'}^{\star }=C_{maxp'}^{\star }$.

However, finding the ratio between $C_{max1'}^{\star }$ and $C_{maxp'}^{\star }$ for the general case is difficult. In the following, we suppose that $C_{max1'}^{\star }\leqslant \alpha C_{maxp'}^{\star }$, with $\alpha \in \mathbb {R}^{+}$.

Table 1 shows the standard deviation between $C_{max1'}^{\star }$ and $C_{maxp'}^{\star }$ for 20 randomly generated instances of different sizes (DAG graphs). For each instance $I_{i}$, we compute $\alpha _{i}=\frac{C_{max1'}^{\star } (I_{i})}{C_{maxp'}^{\star }(I_{i})}$. Then, we calculate Average GAP$=\frac{\sum _{i=1}^{20}\alpha _{i}}{20}$ and Standard deviation$=\sqrt{\frac{\sum _{i=1}^{20}\alpha _{i}^{2}}{20}}$.

From table 1, we can notice that the value of $\alpha$ tends towards 1 when we increase the size of the instances. What can be said, is that the solution of $C_{max1'}^{\star }$ is very close to the solution of $C_{maxp'}^{\star }$ in the general case.

Lemma 3

The ratio between the optimal solution $C_{max1'}^{\star }$ of the formulation (P1) and the optimal scheduling solution $C_{max}^{\star }$ of our main problem is given by $C_{max1'}^{\star } \leqslant \alpha C_{max}^{\star }$.

Proof

From Remark 1, we have $C_{maxp}^{\star }\leqslant C_{max}^{\star }$. Then, $C_{max1'}^{\star } \leqslant \alpha C_{maxp'}^{\star }\leqslant \alpha C_{maxp}^{\star }\leqslant \alpha C_{max}^{\star }$.

Table 1. GAP and standard deviation

Rounding strategy: If $x_{i}^{'}$ is integer for $i \in \{1,\ldots ,n\}$, the solution obtained is feasible and optimal for (P1), otherwise the fractional values are rounded. We denote by $x_{i}^{r}$ the rounded value of the fractional value of the assignment variable of task $t_{i}$ in the optimal solution of (P1). We set $x_{i}^{r}=0$ if $x_{i}^{'}<\frac{1}{2}$, $x_{i}^{r}=1$ otherwise.

Let $\theta _{1}$ be the mapping obtained by this rounding. Each task $t_{i}$ is mapped in either $Pe_{1}$ or $Pe_{2}$. Thus, $\theta _{1}(t_{i})\longrightarrow \{Pe_{1},Pe_{2}\}$.

4.3 Phase 3: Scheduling Algorithm

Using the mapping $\theta _{1}$, the following algorithm determines for a task order given by a priority list L, the corresponding scheduling by executing the first task ready of the list as long as there are free processing elements.

The priority list L can be defined in different ways. To achieve good scheduling, the most important and influential tasks must be executed first. For this purpose, the following list is particularly interesting for this problem because it takes into account the critical path of the graph. First, we start by defining graph $G'(V,E)$, with $V=\{t_{1},t_{2},...,t_{n}\}$ and E represents the set of graph edges. The vertices are labelled by the execution time of each task according to their assignments. The edges are labelled by the communication costs if $t_{i}$ precedes $t_{j}$ and $x_{i}^{r}\ne x_{j}^{r}$, 0 otherwise. Then, we can calculate the longest path $LP(t_{i})$ from each task $t_{i}$ to its last successor. The list LLP is given by $LLP=\{t_{1},t_{2},...,t_{n}\}$, such that $LP(t_{1})\geqslant LP(t_{2})\geqslant ...\geqslant LP(t_{n})$. The following algorithm executes task by task, executing first the task $t_{i}$ with the highest $LP(t_{i})$ from ready tasks. It uses an insertion policy that tries to insert a task at the earliest idle time between two already scheduled tasks on the processing element, if the slot is large enough to execute the task.

The three steps of PLS (Polynomial List Scheduling) algorithm can be summarized as follows. Solve the relaxed formulation $(P^{'})$ then us its solution to define another formulation (P1), then solve (P1). Finally, After rounding the solutions obtained by (P1), use Algorithm 1 with the obtained mapping $\theta _{1}$ and the priority list LLP.

Complexity: Mapping $\theta _{1}$ is based on solving two linear formulations ($(P^{'})$ and (P1)) with continuous variables, which are two polynomial problems. This gives polynomial-time solving methods for the first two phases of PLS algorithm. In the last phase, ready-list is calculated with $\mathcal{O}(n^{2})$ time complexity. The insertion policy is verified on a processing element by checking the non-overlapping with at most $(n-1)$ tasks. This makes a complexity of $\mathcal{O}(n^{2})$ for the last phase. Thus, the complexity time of PLS algorithm is polynomial.

Algorithm Analysis: In the following, we study the performance of PLS algorithm in the worst case compared to the optimal solution. We look for the ratio between the solution $\widehat{C}_{max}$ obtained by PLS algorithm and the optimal scheduling solution $C_{max}^{\star }$ of our main problem.

Lemma 4

The rounding $\theta _{1}$ previously defined satisfies the following inequalities: $x_{i}^{r}\leqslant 2x_{i}^{'}$ and $(1-x_{i}^{r})\leqslant 2(1-x_{i}^{'}).$

Proof

If $0\leqslant x_{i}^{'}<\frac{1}{2}$, then $x_{i}^{r}=0\leqslant 2x_{i}^{'}$. Furthermore, $2x_{i}^{'}\leqslant 1$, then $0\leqslant 1-2x_{i}^{'}$, follows $-x_{i}^{r}=0\leqslant 1-2x_{i}^{'}$, then $1-x_{i}^{r}\leqslant 2(1-x_{i}^{'})$. If $\frac{1}{2}\leqslant x_{i}^{'}$ then $1\leqslant 2x_{i}^{'}$, follows $x_{i}^{r}=1\leqslant 2x_{i}^{'}$. Furthermore, $x_{i}^{'}\leqslant 1$ then $-2x_{i}^{'}\geqslant -2$, follows $1-2x_{i}^{'}\geqslant -1$, then $-x_{i}^{r}=-1\leqslant 1-2x_{i}^{'}$, then $1-x_{i}^{r}\leqslant 2(1-x_{i}^{'}).$

Let $w_i^{r}$ be the execution time of the task $t_{i}$ by considering the rounding $\theta _{1}$, where $w_i^{r}=w _{i,0}$ if $x_{i}^{r}=1$, $w_i^{r}=w _{i,1}$ otherwise. Let $w_i^{'}$ be the execution time of the task $t_{i}$ by considering the solution of (P1), where $w_i^{'}=x_{i}^{'}w _{i,0}+(1-x_{i}^{'})w _{i,1}$.

Proposition 1

The relation between $w_i^{r}$ and $w_i^{'}$ of each task $t_{i}$ is given by $w_i^{r}\leqslant 2w_i^{'}$, $i\in \{1,\ldots ,n\}$.

Proof

From Lemma 4, $2w_i^{'}=2x_{i}^{'}w _{i,0}+2(1-x_{i}^{'})w _{i,1}\geqslant x_{i}^{r}w _{i,0}+(1-x_{i}^{r})w _{i,1}= w_i^{r}$.

Lemma 5

For two successive tasks $(t_{i},t_{j})\in E$, if $t_{i}$ and $t_{j}$ are executed by two different processing elements, then $\zeta _{i,j}^{'}>\frac{1}{2}$.

Proof

We have two cases:

• 1. If min$\{\widetilde{x}_{i}^{'},\widetilde{x}_{j}^{'}\}>$min$\{1-\widetilde{x}_{i}^{'},1-\widetilde{x}_{j}^{'}\}$, then from $Con_{i,j}$ constraint, we have $\zeta _{i,j}^{'}=(1-min\{x_{i}^{'},x_{j}^{'}\})$:

  • a. If $x_{i}^{'}<\frac{1}{2}$ and $x_{j}^{'}\geqslant \frac{1}{2}$, then $\zeta _{i,j}^{'}=(1-x_{i}^{'})>\frac{1}{2}$.

  • b. If $x_{i}^{'}\geqslant \frac{1}{2}$ and $x_{j}^{'}<\frac{1}{2}$, then $\zeta _{i,j}^{'}=(1-x_{j}^{'})>\frac{1}{2}$.

• 2. If min$\{\widetilde{x}_{i}^{'},\widetilde{x}_{j}^{'}\}\leqslant$min$\{1-\widetilde{x}_{i}^{'},1-\widetilde{x}_{j}^{'}\}$, then from $Con_{i,j}$ constraint, we have $\zeta _{i,j}^{'}=(1-min\{1-x_{i}^{'},1-x_{j}^{'}\})$:

  • a. If $1-x_{i}^{'}<\frac{1}{2}$ and $1-x_{j}^{'}\geqslant \frac{1}{2}$, then $\zeta _{i,j}^{'}=x_{i}^{'}>\frac{1}{2}$.

  • b. If $1-x_{i}^{'}\geqslant \frac{1}{2}$ and $1-x_{j}^{'}<\frac{1}{2}$, then $\zeta _{i,j}^{'}=x_{j}^{'}>\frac{1}{2}$.

For each couple of tasks $(t_{i},t_{j})\in E$, we denote by $Cost_{i,j}^{r}$ the value given by $Cost_{i,j}^{r}=0$ if $x_{i}^{r}=x_{j}^{r}$, $Cost_{i,j}^{r}=ct_{ i, j}$ otherwise. Let $Cost_{i,j}^{'}$ be the value given by $Cost_{i,j}^{'}=\zeta _{i,j}^{'}ct_{ i, j}$.

Proposition 2

For each couple of tasks $(t_{i},t_{j})\in E$, the relation between $Cost _{i,j}^{r}$ and $Cost _{i,j}^{'}$ is given by $Cost _{i,j}^{r}< 2Cost _{i,j}^{'}.$

Proof

If $t_{j}$ and $t_{j}$ are executed by the same processing element, $Cost _{i,j}^{r}=0\leqslant 2\zeta _{i,j}^{'}ct_{ i, j}$, because $\zeta _{i,j}^{'}\geqslant 0$. If $t_{j}$ and $t_{j}$ are executed by two different processing elements, then $Cost _{i,j}^{r}=ct_{i,j}$. Then, from Lemma 5, $\zeta _{i,j}^{'}>\frac{1}{2}$, then $2\zeta _{i,j}^{'}> 1$, follows $Cost _{i,j}^{r}=ct_{i,j}\leqslant 2\zeta _{i,j}^{'}ct_{i,j}=2Cost _{i,j}^{'}$.

Proposition 3

For each two successive tasks $(t_{i},t_{j})\in E$, let be $l_{i,j}^{r}=w_{i}^{r}+Cost _{i,j}^{r}+w_{j}^{r}$ (resp. $l_{i,j}^{'}=w_{i}^{'}+Cost _{i,j}^{'}+w_{j}^{'}$) the length of $(t_{i},t_{j})$ in PLS solution (resp. (P1) solution). Then, we have $l_{i,j}^{r}<2l_{i,j}^{'}$.

Proof

From Proposition 1 and Proposition 2, $l_{i,j}^{r}=w_{i}^{r}+Cost _{i,j}^{r}+w_{j}^{r}< 2w_{i}^{'}+2Cost _{i,j}^{'}+2w_{j}^{'} =2l_{i,j}^{'}$. Thus, $l_{i,j}^{r}<2l_{i,j}^{'}$.

Theorem 2

Let $\widehat{C}_{max}$ be the solution obtained by using PLS algorithm, then $\widehat{C}_{max}< 6C_{max1'}^{\star }$.

Proof

From Proposition 3, the length of each path L from G(V, E) is given by $length(L)^{r}=\sum _{(t_{i},t_{i+1})\in L}^{}l_{i,i+1}^{r}\leqslant 2 \sum _{(t_{i},t_{i+1})\in L}^{}l_{i,i+1}^{'}=2length(L)^{'}$, where $length(L)^{r}$ (resp. $length(L)^{'}$) is the length of L in PLS solution (resp. (P1) solution). Furthermore, the workload of the tasks assigned to $Pe_{1}$ (resp. $Pe_{2}$) is given by $\sum _{i=1}^{n} x_{i}^{r}w _{i,0}=2 \sum _{i=1}^{n} x_{i}^{'}w _{i,0}$ (resp. $\sum _{i=1}^{n} (1-x_{i}^{r})w _{i,0}=2\sum _{i=1}^{n} (1-x_{i}^{'})w _{i,0}$). Thus, the value of the critical path and the workloads on $Pe_{1}$ and $Pe_{2}$ will be at most doubled compared to the lower bounds. Finally, the interaction between the longest paths and the workload on each processing element has been studied in  [15], such that if we have these properties, then $\widehat{C}_{max}< 6C_{max1'}^{\star }$.

Theorem 3

The ratio between the solution $\widehat{C}_{max}$ obtained by PLS algorithm and the optimal scheduling solution $C_{max}^{\star }$ is given by $\dfrac{\widehat{C}_{max}}{C_{max}^{\star }}< 6\alpha$.

Proof

From Lemma 3, we have $C_{max1'}^{\star } \leqslant \alpha C_{max}^{\star }$. Then, $\dfrac{\widehat{C}_{max}}{C_{max}^{\star }}< \dfrac{6C_{max1'}^{\star }}{C_{max}^{\star }} \leqslant \dfrac{6\alpha C_{max}^{\star }}{C_{max}^{\star }} \leqslant 6\alpha$.

5 Numerical Results

We compare here the performance of PLS (Polynomial List Scheduling) algorithm to HEFT (Heterogeneous Earliest Finish Time) and LS (List Scheduling) algorithm using benchmarks generated by Turbine [19].

The benchmark is composed of ten parallel DAG applications. We denote by $test\_i$ instance number i. We generate 10 different applications for each $test\_i$ with $i\in \{1,\ldots ,10\}$. The execution times of the tasks are generated randomly over an interval [$w_{min},w_{max}$], $w_{min}$ has been fixed at 5 and $w_{max}$ at 70. The number of successors of each task is generated randomly over an interval [$d_{min},d_{max}$], $d_{min}$ has been fixed at 1 and $d_{max}$ at 10. The communication rate for each arc was generated on an interval [$ct_{min},ct_{max}$], we set $ct_{min}$ to 35 and $ct_{max}$ to 80.

To study the performance of our method, we compared the ratio between each makespan value obtained by PLS algorithm with HEFT and LS algorithm, the optimal solution obtained by CPLEX and the lower bound $C_{max1'}$ obtained by (P1). Table 2 shows the average results obtained on 10 instances given in column Inst of each application size given in the second column using CPLEX, HEFT, PLS and LS algorithms. We show the average time that was needed to CPLEX to provide the optimal solution using (Opt). We only have the result for the first two instances due to the large running time for instances with more than 60 tasks ($>4h$). Then, we show the results obtained by HEFT, PLS and LS algorithm. GAP columns give the average ratio between the makespan obtained by each method compared to $C_{max1'}$ using the following formula: $GAP = \frac{\text {method makespan} - C_{max1'}}{C_{max1'}} \times 100.$ Time columns show the average time that was needed for each method to provide a solution. Best columns present the number of instances where each algorithm provides better or the same solution than other methods. A line Average is added at the end of each table which represents the average of the values each column.

Table 2. CPLEX, HEFT, LS and PLS algorithms results.

For the running time, HEFT algorithm requires less time than PLS and LS algorithms to provide a solution. PLS algorithm is the most efficient method with a gap of $9.76\%$ and $69\%$ of better solutions compared to other methods. Its average running time is 1.72 s, which is slightly higher than the running time of LS algorithm.

6 Conclusion and Perspectives

This paper presents an efficient algorithm to solve the problem of scheduling parallel applications on hybrid platforms with communication delays. The objective is to minimise the total execution time (makespan).

After modelling the problem, we proposed a three-phase algorithm; the first two phases consist in solving linear formulations to find the type of processor assigned to execute each task. In the third phase, we compute the start execution time of each task to generate a feasible schedule. Tests on large instances close to reality demonstrated the efficiency of our method comparing to other methods and shows the limits of solving the problem with a solver such as CPLEX.

A proof of the performance guarantee for PLS algorithm was initiated. In future works, we will focus on finding the value of $\alpha$ to have a fixed bound on the ratio between $\widehat{C}_{max}$ and $C_{max}^{\star }$. Tests on real applications and an extension to more general heterogeneous platforms is also planned.