Design and Performance Analysis of Super-Twisting Algorithm Control for Direct-Drive PMSG Wind Turbine Feeding a Water Pumping System

Abstract

This paper deals with the nonlinear control of a direct-drive PMSG wind turbines using the super-twisting algorithm. The studied system is assumed supplying a water pumping system for the use in isolated sites and areas. The aim of the proposed control strategy is tracking the wind turbine maximum power point. The designed controllers are based on one of the high-order sliding mode controller (HOSM) versions, which is the super-twisting algorithm. This latter possess many attractive features as the chattering-free behavior, finite time convergence, less information demand, simplicity, stability and robustness against external disturbances. The performance of the whole system in closed-loop mode is assessed through computer simulations.

1 Introduction

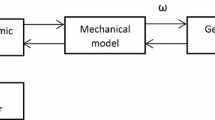
In recent decades, wind energy has received a lot of attention as one of the clean alternative energy sources [1]. In general, renewable energies aim to reduce the negative impact of conventional electricity sources on the environment and also supplying remote areas and isolated sites where access to the classical energy is difficult. Water pumping is one of the principal renewable energy application; photovoltaic energy is the most used and preferred for water supply. In some cases and for some locations, solar energy cannot be the best solution. Wind energy has recently been adopted as a solution for regions with good wind potential. In literature, many wind electric water pumping configurations and control strategies have been proposed and studied [2,3,4]. The main goal of the existed studies is ensuring an optimal and a maximum efficiency of the water pumping system operation. The studied configuration in this paper is shown in Fig. 1. It consists of permanent-magnet synchronous generator, a controlled AC/DC converter connected to a permanent-magnet DC motor driving a centrifugal pump (nonlinear load).

Fig. 1.

Studied Wind Electric Water Pumping System.

The permanent-magnet synchronous generator (PMSG) is one of the most preferred choice for standalone systems due to its high efficiency, self-excitation features, reliability and also for allowing a direct-drive systems avoiding by that the use of a gearbox [5]. The major drawbacks of wind energy conversion systems (WECS) is the highly nonlinear behavior [1]. Figure 2.b represent the power coefficient $\left( {C_{p} } \right)$ as function of the pitch angle $\left( \beta \right)$ and the specific speed ($\lambda$), and Fig. 2.a shows the mechanical power as a function of rotor speed of the turbine for different values of wind speed. Maximizing the captured wind energy power is the main objective, many control strategies can be found in literature as well as controllers improvements in order to overcome the drawbacks of the conventional controllers. In [1], an adaptive fuzzy-PI control is considered to replace the conventional constant gains PI controller for PMSG vector control. A sliding mode control strategy is proposed in [6] and [7] for a PMSG controlled by vector control. In [8] a hybrid fuzzy sliding mode controller is proposed for controlling the permanent magnet synchronous generator speed. In [9], a general regression neural network (GRNN) controller is proposed for induction generator (IG) speed drive. A fuzzy neural network controller is proposed in [10] for the same generator kind. In [11], a hybrid intelligent PMSG control based on sliding mode controller combined with fuzzy inference mechanism and adaptive algorithm is proposed.

Fig. 2.

a. Wind generator power curves at various wind speed, b. Characteristics $C_{p}$ vs $\lambda$ for different values of the pitch angle $\beta$.

This paper presents the control of a direct-drive permanent-magnet synchronous generator wind turbine used in an autonomous water pumping system. The proposed optimal control of the PMSG wind turbine is based on super-twisting algorithm. The overall control functions of the wind electric water pumping system are developed including the maximization of the captured power. The presented control strategy allows an efficient operation of the system in a wide range of winds and aims to make the turbine operating on the curve corresponding to the maximum power point. Computer simulations are presented in order to validate and evaluated the performance of the adopted control strategy on the studied system.

2 Modeling of Wind Electric Water Pumping System

2.1 Modeling of the Wind Turbine

The model of the turbine is modeled from the following system equations [1, 5, 7]:

$$ p_{v} = \frac{{\left( {\rho .A.v_{w}^{3} } \right)}}{2} $$

(1)

$$ p_{m} = \frac{1}{2}C_{p} \left( {\lambda ,\beta } \right).\rho .A.v_{w}^{3} $$

(2)

$$ \lambda = \frac{{\Omega _{m}^{G} R}}{{v_{w} }} $$

(3)

$$ \begin{aligned} \left\{ {\begin{array}{*{20}c} {C_{p} \left( {\lambda ,\beta } \right) = C_{1} \left( {\frac{{C_{2} }}{\gamma } - C_{3} .\beta - C_{4} } \right)e^{{\frac{{ - C_{5} }}{\gamma }}} + C_{6} .\lambda } \\ {\frac{1}{\gamma } = \frac{1}{\lambda + 0.08\beta } - \frac{0.035}{{\beta^{3} + 1}}} \\ \end{array} } \right. \hfill \\ C_{1} = 0.5176, C_{2} = 116, C_{3} = 0.4, C_{4} = 5, C_{5} = 21 \hfill \\ \end{aligned} $$

(4)

$$ T_{m}^{G} = \frac{{p_{m} }}{{\Omega _{m}^{G} }} = \frac{1}{{2.\Omega _{m}^{G} }}C_{p} \left( {\lambda ,\beta } \right).\rho .A.v_{w}^{3} $$

(5)

$$ \left\{ {\begin{array}{*{20}c} {T_{m}^{G} = J^{G} {\dot{\varOmega }}_{m}^{G} + f.\Omega _{m}^{G} + T_{em}^{G} } \\ {J^{G} = J_{turbine}^{G} + J_{g}^{G} } \\ \end{array} } \right. $$

(6)

Where $p_{v}$ is the wind power, $\rho$ is the air density, $A$ is the circular area, $v_{w}$ is the wind speed, $p_{m}$ is the mechanical power, $C_{p}$ is the power coefficient, $\beta$ is the pitch angle, $\lambda$ is the tip speed ratio, $\Omega _{m}^{G}$ is the turbine rotor speed, $R$ is the turbine radius, $T_{m}^{G}$ is the mechanical torque, $T_{em}^{G}$ is the electromagnetic torque produced by the generator, $f$ is the friction coefficient and $J^{G}$ is the total moment of inertia of the rotating parts.

2.2 Permanent Magnet Synchronous Generator (PMSG) Model

The d-q stator voltage equations of this generator are given by the following expressions [12, 18, 19]:

$$ \left\{ {\begin{array}{*{20}c} {V_{ds} = R_{s} I_{ds} + L_{d} \dot{I}_{ds} -\upomega_{r} \psi_{qs} } \\ {V_{qs} = R_{s} I_{qs} + L_{q} \dot{I}_{qs} +\upomega_{r} \psi_{ds} } \\ {\psi_{ds} = L_{d} I_{ds} + \psi_{0} } \\ {\psi_{qs} = L_{q} I_{qs} } \\ \end{array} } \right. $$

(7)

The differential equations of the PMSG can be obtained as follow:

$$ \left\{ {\begin{array}{*{20}c} {L_{d} \dot{I}_{ds} = V_{ds} - R_{s} I_{ds} +\upomega_{r} L_{q} I_{qs} } \\ {L_{q} \dot{I}_{qs} = V_{qs} - R_{s} I_{qs} -\upomega_{r} L_{d} I_{ds} - \psi_{0}\upomega_{r} } \\ \end{array} } \right. $$

(8)

The electromagnetic torque is represented by:

$$ T_{em}^{G} = \frac{3}{2}p\left[ {\left( {L_{d} - L_{q} } \right)I_{ds} I_{qs} + \psi_{0} I_{qs} } \right] $$

(9)

The PMSG is assumed to be wound-rotor, then $L_{d} = L_{q}$, and the expression of the electromagnetic torque in the rotor can be described as follow:

$$ T_{em}^{G} = \frac{3}{2}p\psi_{0} I_{qs} $$

(10)

Where $L_{d}$, $L_{q}$ are the inductances of the generator on the q and d axis, $R_{s}$ is the stator resistance, $\psi_{0}$ is the permanent magnetic flux, $\upomega_{r}$ is the electrical rotating speed of the PMSG which is given by $\upomega_{r} = p.\Omega _{m}^{G}$ and $p$ is the number of pole pairs.

2.3 Permanent-Magnet DC Motor (PMDC) and Centrifugal Pump Model

The model of the PMDC motor is represented by the following equations [3]:

$$ \left\{ {\begin{array}{*{20}c} {V_{aM} = R_{aM} I_{aM} + L_{aM} \dot{I}_{aM} + e} \\ {T_{e}^{M} = K_{t} I_{aM} } \\ {e = K_{e}\Omega _{m}^{M} } \\ {T_{e}^{M} - T_{L}^{M} = J^{M} {\dot{\varOmega }}_{m}^{M} + B_{m} .\Omega _{m}^{M} + T_{f}^{M} } \\ \end{array} } \right. $$

(11)

The load torque of the centrifugal pump is given by the following expression:

$$ T_{L}^{M} = a.\Omega _{m}^{{M^{n} }} + b $$

(12)

Where $R_{aM}$ is the armature winding resistance, $L_{aM}$ is the armature self-inductance, $I_{aM}$ is the motor armature current, $V_{aM}$ is the applied voltage, $e$ is the back e.m.f of the PMDC motor, $K_{e}$ is the voltage constant, $\Omega _{m}^{M}$ is the angular speed, $K_{t}$ is the torque constant, $J^{M}$ is the moment of inertia, $B_{m}$ is the viscous torque constant, $T_{f}^{M}$ is the torque constant for rotational losses, $T_{e}^{M}$, $T_{L}^{M}$ are the electromagnetic torque and load torque respectively, and $a$, $b$ are the constants of the pump.

3 PMSG Side Converter Control

In order to control the generator speed, a vector control strategy is applied to the AC/DC converter (Fig. 3). The generator speed $\Omega _{m}^{G}$ can be controlled by adjusting the electromagnetic torque ($T_{em}^{G}$) to its reference ($T_{em}^{{G^{*} }} )$. That can be done by acting on the q-axis current ($I_{qs}$) using the equation $I_{qs}^{*} = \frac{2}{{3p\psi_{0} }}T_{em}^{{G^{*} }}$. The d-axis stator current ($I_{ds}$) component is forced to zero to achieve the maximum torque of the generator [12, 18]. The optimal reference rotational speed is calculated using $\Omega _{mopt }^{G} = \frac{{\lambda^{*} .v_{w} }}{R}$ where $\lambda^{*}$ represents the optimum tip-speed ratio.

Fig. 3.

Applied super-twisting algorithm based MPPT control

• Super Twisting Algorithm (STA)

The major known drawback associated with variable structure control implementation is the chattering phenomenon [13]. The most used technique to avoid this problem is the approach known as high-order sliding mode (HOSM). This latter is very well known in their stability and robustness against external disturbances and uncertainty. The increasing information demand is the main problem of the high-order sliding mode controllers; the implementation of the rth-order controller requires the knowledge of $\upsigma, \dot{\sigma }, \ddot{\sigma }, \ldots ,\sigma^{{\left( {r - 1} \right)}}$ ($\sigma$ is the sliding surface). The super-twisting algorithm is the exception, it has two main advantages. The first one is that the ST algorithm can be applied to any system having a relative degree equal to 1 with respect to sliding variable, and the second and the important advantage is that the ST algorithm does not require any information on the time derivative of the sliding variable and maintains all the distinctive robust features of the SMC [14, 15].

• Outer STA Generator Speed Controller

The sliding surface for the STA speed controller is given as follows:

$$ \sigma_{{\Omega _{m}^{G} }} =\Omega _{mopt }^{G} -\Omega _{m}^{G} $$

(13)

It follows that

$$ \left\{ {\begin{array}{*{20}c} {\dot{\sigma }_{{\Omega _{m}^{G} }} = {\dot{\varOmega }}_{mopt }^{G} - {\dot{\varOmega }}_{m}^{G} = {\dot{\varOmega }}_{mopt }^{G} - \frac{{T_{m}^{G} - f.\Omega _{m}^{G} - T_{em}^{G} }}{{J^{G} }}} \\ {\ddot{\sigma }_{{\Omega _{m}^{G} }} = {\varrho }_{1} \left( {t,x} \right) + \varUpsilon_{1} \left( {t,x} \right)\dot{T}_{em}^{{G^{*} }} } \\ \end{array} } \right. $$

(14)

Where ${\varrho }_{1} \left( {t,x} \right)$ and $\varUpsilon_{1} \left( {t,x} \right)$ are uncertain bounded functions that satisfy

$$ {\varrho }_{1} \left( {t,x} \right) > 0,\left| {{\varrho }_{1} \left( {t,x} \right)} \right| > \varPhi_{1} ,0 <\Gamma _{m1} < \varUpsilon_{1} <\Gamma _{M1} $$

(15)

The proposed second-order sliding mode control has been designed using the super twisting algorithm. The control law contains two parts, one is the continuous function of the sliding surface ($\sigma_{{\Omega _{m}^{G} }} )$ and, the other, is the integral of a discontinuous control action [20]:

$$ T_{em}^{{G^{*} }} = \upsilon_{1} + \upsilon_{2} $$

(16)

Where:

$$ \left\{ {\begin{array}{*{20}c} {\dot{\upsilon }_{1} = - \alpha_{1} sign\left( {\sigma_{{\Omega _{m}^{G} }} } \right)} \\ {\upsilon_{2} = - \beta_{1} \left| {\sigma_{{\Omega _{m}^{G} }} } \right|^{\rho } sign\left( {\sigma_{{\Omega _{m}^{G} }} } \right)} \\ \end{array} } \right. $$

(17)

Using the Eqs. (10) and (16), the final STA speed controller is given as follows:

$$ I_{qs}^{*} = \frac{2}{{3p\psi_{0} }}\left( { - \beta_{1} \left| {\sigma_{{\varOmega_{m}^{G} }} } \right|^{\rho } sign\left( {\sigma_{{\Omega _{m}^{G} }} } \right) - \smallint \alpha_{1} sign\left( {\sigma_{{\Omega _{m}^{G} }} } \right)dt} \right) $$

(18)

Where $\alpha_{1} , \beta_{1} {\text{and}} \rho$ are design parameters. To ensure the sliding manifolds convergence to zero in finite time, the gains can be chosen as follows [16]:

$$ \left\{ {\begin{array}{*{20}c} {\alpha_{1} > \frac{{\varPhi_{1} }}{{\Gamma _{m1} }}} \\ {\beta_{1}^{2} \ge \frac{{4\varPhi_{1} }}{{\Gamma _{m1}^{2} }}\frac{{\Gamma _{M1} \left( {\alpha_{1} + \varPhi_{1} } \right)}}{{\Gamma _{m1} \left( {\alpha_{1} - \varPhi_{1} } \right)}}} \\ {0 < \rho \le 0.5} \\ \end{array} } \right. $$

(19)

• Inner STA Current Controllers

In order to regulate currents components $I_{qs}$ and $I_{ds}$ to their references ($I_{ds}^{*}$ and $I_{qs}^{*}$), the sliding surfaces were chosen as follow:

$$ \left\{ {\begin{array}{*{20}c} {\sigma_{{I_{ds} }} = I_{ds}^{*} - I_{ds} } \\ {\sigma_{{I_{qs} }} = I_{qs}^{*} - I_{qs} } \\ \end{array} } \right. $$

(20)

It follows that

$$ \left\{ {\begin{array}{*{20}c} {\dot{\sigma }_{{I_{ds} }} = \dot{I}_{ds}^{*} - \dot{I}_{ds} } \\ {\ddot{\sigma }_{{I_{ds} }} = \varrho_{2} \left( {t,x} \right) + \varUpsilon_{2} \left( {t,x} \right)\dot{V}_{ds}^{*} } \\ \end{array} } \right.\,and\,\left\{ {\begin{array}{*{20}c} {\dot{\sigma }_{{I_{qs} }} = \dot{I}_{ds}^{*} - \dot{I}_{qs} } \\ {\ddot{\sigma }_{{I_{qs} }} = \varrho_{3} \left( {t,x} \right) + \varUpsilon_{3} \left( {t,x} \right)\dot{V}_{qs}^{*} } \\ \end{array} } \right. $$

(21)

Where $\varrho_{2} \left( {t,x} \right)$, $\varrho_{3} \left( {t,x} \right)$, $\varUpsilon_{2} \left( {t,x} \right)$ and $\varUpsilon_{3} \left( {t,x} \right)$ are uncertain bounded functions that satisfy

$$ \left\{ {\begin{array}{*{20}c} {\varrho_{2} \left( {t,x} \right) > 0, \left| {\varrho_{2} \left( {t,x} \right)} \right| > \varPhi_{2} ,0 < \varGamma _{m2} < \varUpsilon_{2} < \varGamma_{M2} } \\ {\varrho_{3} \left( {t,x} \right) > 0, \left| {\varrho_{3} \left( {t,x} \right)} \right| > \varPhi_{3} ,0 < \varGamma _{m3} < \varUpsilon_{3} < \varGamma_{M3} } \\ \end{array} } \right. $$

(22)

The proposed second-order sliding mode control has been designed using the super twisting algorithm. The control voltages of q and d axis are defined as follow:

$$ \left\{ {\begin{array}{*{20}c} {V_{ds}^{*} = \mu_{1} + \mu_{2} - Fem_{d} } \\ {V_{qs}^{*} = w_{1} + w_{2} + Fem_{q} } \\ \end{array} } \right. $$

(23)

Where:

$$ \left\{ {\begin{array}{*{20}c} {\dot{\mu }_{1} = - \alpha_{2} sign\left( {\sigma_{{I_{ds} }} } \right)} \\ {\mu_{2} = - \beta_{2} \left| {\sigma_{{I_{ds} }} } \right|^{\rho } sign\left( {\sigma_{{I_{ds} }} } \right)} \\ {Fem_{d} = p\Omega _{m}^{G} L_{q} I_{qs} } \\ \end{array} } \right.and\left\{ {\begin{array}{*{20}c} {\dot{w}_{1} = - \alpha_{3} sign\left( {\sigma_{{I_{qs} }} } \right)} \\ {w_{2} = - \beta_{3} \left| {\sigma_{{I_{qs} }} } \right|^{\rho } sign\left( {\sigma_{{I_{qs} }} } \right)} \\ {Fem_{q} = p\varOmega_{m}^{G} \left( {L_{d} I_{ds} + \psi_{0} } \right)} \\ \end{array} } \right. $$

(24)

$Fem_{d}$ and $Fem_{q}$ are the compensation terms.

The final inner STA current controllers are given as follow:

$$ \left\{ {\begin{array}{*{20}c} {V_{ds}^{*} = - \beta_{2} \left| {\sigma_{{I_{ds} }} } \right|^{\rho } sign\left( {\sigma_{{I_{ds} }} } \right) - \smallint \alpha_{2} sign\left( {\sigma_{{I_{ds} }} } \right)dt - p\Omega _{m}^{G} L_{q} I_{qs} } \\ {V_{ds}^{*} = - \beta_{3} \left| {\sigma_{{I_{qs} }} } \right|^{\rho } sign\left( {\sigma_{{I_{qs} }} } \right) - \smallint \alpha_{3} sign\left( {\sigma_{{I_{qs} }} } \right)dt + p\Omega _{m}^{G} \left( {L_{d} I_{ds} + \psi_{0} } \right)} \\ \end{array} } \right. $$

(25)

Where $\alpha_{i} , \beta_{i} \,{\text{and}}\, \rho$ ($i = 2,3$) are design parameters. To ensure the sliding manifolds convergence to zero in finite time, the gains can be chosen as follows [16]:

$$ \left\{ {\begin{array}{*{20}c} {\alpha_{i} > \frac{{\varPhi_{i} }}{{\Gamma _{mi} }}} \\ {\beta_{i}^{2} \ge \frac{{4\varPhi_{i} }}{{\Gamma _{mi}^{2} }}\frac{{\Gamma _{Mi} \left( {\alpha_{i} + \varPhi_{i} } \right)}}{{\Gamma _{mi} \left( {\alpha_{i} - \varPhi_{i} } \right)}}} \\ {0 < \rho \le 0.5} \\ \end{array} } \right. , \left( {i = 2,3} \right). $$

(26)

4 Results and Discussion

The following results were obtained for the studied wind electric water-pumping system described in Fig. 1 using Matlab/Simulink software. The control strategy was performed under variable wind speed profile. The wind speed was modeled as a sum of deterministic several harmonics [17].

$$ v_{w} \left( t \right) = 7 + 0.2\sin \left( {0.1047t} \right) + 2\sin \left( {0.2665t} \right) + \sin \left( {1.2930t} \right) + 0.2\sin \left( {3.6645t} \right) $$

(27)

The applied wind speed profile is shown in Fig. 4. The used waveforms contains two regions, the high wind speed range and the low one. Figure 5 illustrate the variation of the turbine mechanical power and the electrical absorbed power by the motor-pump group. The obtained results shows a good tracking performance of the maximum mechanical power. The dynamic difference between the mechanical turbine power and the electrical absorbed power is due to system inertia, friction and losses at converter and generator level. It is observed also on Fig. 8 that the power coefficient $\left( {C_{p} } \right)$ has been kept at its maximum value $0.48$ even under random wind speed profile.

Fig. 4.

Applied wind speed profile.

Fig. 5.

Variation of the turbine mechanical power and the electrical absorbed power by the motor-pump.

Fig. 6.

d-q axis stator currents components.

Fig. 7.

Zoom of d-q axis stator currents components.

Fig. 8.

Power coefficient and its optimal reference

The PMSG vector control can be verified by observing the d and q current axis. Figures 6 and 7 show a good pursuit of the reference q current axis $(I_{qs}^{*} )$ generated by the outer super twisting algorithm controller, similarly to the d current component $( I_{ds} )$, it can been seen on the same figures that the $I_{ds}$ remains around its reference (zero). Figure 9 shows that generator currents are sinusoidal, no harmonics or perturbations are observed at generator level, the thing that will increase the system efficiency. Figure 10 shows a good tracking performance of the speed rotor to the reference (optimal) speed with a very small error.

Fig. 9.

abc axis current evolution.

Fig. 10.

Actual rotor speed and its reference (optimal).

Figure 11 illustrates the motor-pump performances; it shows the evolution of the permanent-magnet DC motor speed, the electrical torque produced by the dc motor and the load torque opposed by the centrifugal pump.

Fig. 11.

Motor-pump performances.

5 Conclusion

In this paper, a wind electric water pumping system based on direct-drive PMSG wind turbine and PMDC motor connected to a centrifugal pump is studied and presented. A vector control strategy based on super-twisting algorithm controllers has been designed and evaluated under varying wind conditions. The obtained results proved the effectiveness and the robustness of the proposed control strategy on the studied system. The selected super-twisting algorithm has shown a good stability without chattering effects. The main advantage of the presented control strategy is that the ST algorithm requires only knowledge of the sign of the sliding variable, which means an easier implementation and good performances with less information demand. The proposed control strategy can be improved by replacing the mechanical sensors with observers state in order to reduce the overall system cost.