Keywords

1 Introduction

In MRI an inherent mismatch exists between the scale at which water diffusion occurs and the scale at which measurements are taken. This mismatch makes the interpretation of changes in tissue microstructure challenging which is further complicated by water diffusion in a hindered and restricted tissue micro-environment. In this paper, we attempt to address this issue by studying the potential role of anomalous diffusion models (a subset of non-Gaussian diffusion models) in linking tissue microstructure differences with changes in anomalous diffusion model parameters. Our investigations are performed in the context of glioblastoma, a grade IV glioma in the brain, as increasing evidence suggests that proper mapping of the tissue micro-environment in this disease can lead to improved treatment planning [8], better surgical intervention with positive outcomes [19] and the development of drugs targeting specific tissue micro-environment features such as angiogenesis [27].

Studies in diffusion-weighted MRI (DWI) involve a parameter called the b-value (units of s/mm\(^2\)) which is a function of diffusion gradient amplitude and its duration, and the amount of time water is allowed to diffuse in tissue. It is widely observed that the DWI signal decay at high b-values (>1000 s/mm\(^2\)) does not follow the classical mono-exponential model which assumes diffusing spins are undergoing Brownian motion in tissue [26], and hence a simple ADC value obtained from the mono-exponential model may not be able to adequately capture tissue heterogeneity. Due to the limitation of ADC, several research groups have developed a number of more sophisticated diffusion models to extract structure tissue information beyond what ADC can provide (eg. [7, 14,15,16,17,18, 20]). In this study, we focus on several anomalous diffusion models developed using theory in fractional calculus. These models incorporate a broad and continuous distribution of diffusion compartments, and describe water molecule transport processes influenced by the multiple length and time scales through a heterogeneous medium at sub-voxel resolution [5, 24]. Anomalous diffusion models considered in this study include

  • stretched exponential model (also known as super-diffusion model) which allows for deviation from mono-exponential decay by assuming diffusing spins are more likely to take long jumps, ie. undergoing Lévy walks rather than Brownian motion [3, 9, 10];

  • sub-diffusion model which assumes the waiting times between jumps for diffusing spins follow a long-tailed probability distribution (ie. long waiting times) [5, 9] ;

  • continuous time random walk model which incorporates assumptions for both super- and sub-diffusions, i.e. diffusing spins are more likely to take long jumps and have long waiting times between jumps [9, 12, 13]; and

  • fractional Bloch-Torrey equation which generalises the Bloch-Torrey equation through fractional order differential operators [20];

Each of these models yields a new set of parameters to describe the anomalous diffusion in complex biological tissue, which provide useful information not only on the diffusion coefficient (D) but also on the tissue structures (\(\alpha \) and/or \(\upbeta \)) through which water molecules diffuse. For example, researchers used anomalous diffusion models to differentiate low- and high- grade pediatric brain tumours [13, 14, 25], to characterise white matter tissue microstructure [28, 29], to study healthy fixed rat brain tissue [12], and to characterise myocardial microstructure in cardiac tissue [5].

Previous studies [21, 22] reported that there are often three concentric layers observed in the glioma tumour mass (core/necrotic, intermediate layer and peripheral/hyper-vascularised layer). The formation of such layered structure is driven by the extent of hypoxia within the tumour region. The goal of this study is to investigate the utility of anomalous diffusion model parameters in differentiating the three tumour layers in a mouse model of glioma.

2 Methods

2.1 Anomalous Diffusion Models in MRI

Based on the Bloch-Torrey equation for the magnetisation of water protons and in conjunction with the Stejskal-Tanner diffusion protocol, the amplitude of the acquired diffusion weighted signal follows a mono-exponential decay

$$\begin{aligned} S/S_0 = \exp (-bD), \end{aligned}$$
(1)

where \(S_0\) is the baseline signal intensity, D is the diffusion coefficient of water in tissue (typically, \(2\times 10^{-3}\)  mm\(^2/s\) for water at room temperature), \(b = (\gamma G \delta )^2(\Delta -\delta /3)\) is the degree of sensitisation to diffusion of the MRI pulse sequence, \(\gamma \) is the gyromagnetic ratio (42.58 MHz/T for protons) and the diffusion-weighting is applied with a pair of unipolar gradient waveforms of duration \(\delta \), separation \(\Delta \), and amplitude G. As a generalisation of this mono-exponential decay, a stretched exponential model

$$\begin{aligned} S/S_0 = \exp \left( -(bD)^\alpha \right) ,~~~ 0<\alpha \le 1, \end{aligned}$$
(2)

has been proposed in a few previous studies [2, 3, 10], which becomes (1) when \(\alpha = 1\). The model parameter \(\alpha \) is the so-called heterogeneity index and can be used to infer microscopic tissue structure [3].

Alternatively, the mono-exponential model can be generalised to a sub-diffusion model [5, 9]

$$\begin{aligned} S/S_0 = E_\upbeta (-bD), ~~~ 0<\upbeta \le 1 \end{aligned}$$
(3)

where \(E_\upbeta (z) = \sum _{k=0}^{\infty } \frac{z^k}{\Gamma (1+\upbeta k)}\) and \(\Gamma (\cdot )\) are the Mittag-Leffler and Gamma functions, respectively [23]. When \(\upbeta =1\), \(\Gamma (1+k) = k!\), and \(E_1(z)\) by definition is the exponential function.

A further generalisation of the stretched exponential model (2) and the sub-diffusion model (3) gives the continuous-time random walk (CTRW) model (demonstrated on healthy fixed rat ventricles [5], healthy fixed rat brain tissue [12] and paediatric brain tumours [13])

$$\begin{aligned} S/S_0 = E_\upbeta (-(bD)^\alpha ), ~~~ 0<\alpha ,\upbeta \le 1. \end{aligned}$$
(4)

Finally, using first principles and by adopting the fractional calculus in the derivation, a solution to the fractional Bloch-Torrey equation (FBTE) [20] is obtained,

$$\begin{aligned} S/S_0 = \exp \left[ -D\mu ^{2(\alpha -1)}(\gamma G \delta )^{2\alpha }\left( \Delta - \frac{2\alpha -1}{2\alpha +1}\delta \right) \right] , \end{aligned}$$
(5)

where \(\mu ^{2(\alpha -1)}\) is fractional order space constant needed to preserve units.

2.2 Mouse Preparation and Data Acquisition

All animal experiments were approved by the University of Queensland animal ethics committee. To form intracranial tumours, \(1\times 10^5\) U87 cells were injected into the right striatum of six-week old NOD/SCID mice, +0.6 mm anterior-posterior, +1.2 mm mediolateral from bregma and at a depth of 3 mm from the dural surface using a stereotactic device. MR images were acquired at 7, 14, 19 and 21 days post injection. The MRI examination included T2-weighted and multiple b-value DWI data acquisitions using a Bruker Biospin 9.4 T large bore MRI animal scanner. T2-weighted images were acquired using the fast spin echo MRI sequence with TR/TE \(=\) 2500/33 ms, echo train length \(=\) 8, matrix size \(=\) 256 by 256, field of view (FOV) \(=\) 2 cm by 2 cm, spatial resolution \(=\) 78.125 \(\upmu \)m by 78.125 \(\upmu \)m, slice thickness \(=\) 0.7 mm. The multiple b-value DWI data was acquired using an echo planar imaging (EPI) sequence with b-values \(=\) 0, 500, 1000, 1500, 2000, 2500, 3000, 3500, 4000 s/mm\(^2\). Three \(b = 0\) images were acquired. At each nonzero b-value, trace-weighted images were generated from the 30 direction Stejskal-Tanner DWI data. The key data acquisition parameters were: TR/TE \(=\) 5000/30 ms, separation between the Stejskal-Tanner gradient lobes \(\Delta \) \(=\) 20 ms, diffusion gradient duration \(\delta \) \(=\) 3 ms, matrix size \(=\) 108 by 96, field of view (FOV) \(=\) 2.16 cm by 1.92 cm, spatial resolution \(=\) 0.2 mm by 0.2 mm, slice thickness \(=\) 0.2 mm. The acquisition time was approximately 10 min per mouse. Following the final MRI acquisition, mice were euthanised and the brain drop fixed in 4% paraformaldehyde. Paraffin-embedded brains were sectioned by microtome at room temperature using a section thickness of 12 \(\upmu \)m and hematoxylin and eosin (H&E) staining was performed. Slides were scanned using an Aperio CS2 digital slide scanner and the images were processed using ImageScope.

2.3 Image Analysis

Multi b-value diffusion images were fitted to the anomalous diffusion models (2)–(5) on a voxel-by-voxel basis. Firstly, D was calculated using the mono-exponential decay model (1) for the subset of acquired data up to b \(=\) 1000 s/mm\(^2\). Secondly, the full range of b-values was used to fit the parameters using the trust-region-reflective algorithm [4, 6] with prescribed tolerance of \(10^{-6}\). Parameter bounds were taken as \(0<\alpha ,\upbeta \le 1\), with initial guesses \(\alpha =1\) and \(\upbeta =1\), representative of the case of diffusion governed by the mono-exponential model. Parameter fittings were implemented in MATLAB. Evaluation of the Mittag-Leffler function was performed using Garrappa’s optimal parabolic contour algorithm, which is available in MATLAB central (file exchange number 48154). We found fitting results to be insensitive to the choice of initial values.

Regions of interest (ROIs) were carefully selected, guided by the histological sections (H&E), to represent each layer of tumour tissue (core, intermediate and peripheral) and the contralateral normal-appearing tissue. The ROIs were placed on the diffusion images first and then propagated to the corresponding model parameters for statistical analysis: (D, \(\alpha \)) for the stretched exponential model, (D, \(\upbeta \)) for the sub-diffusion model, (D, \(\alpha \), \(\upbeta \)) for the CTRW model and (D, \(\alpha \), \(\mu \)) for the FBTE model.

2.4 Statistical Analysis

For each anomalous diffusion model, mean values and standard deviations of model parameters were calculated from the tumour and the normal-appearing ROIs. A two-sided Wilcoxon rank sum test with significance set at \(p<0.05\) was performed for comparing parameter values in each pair of ROIs, i.e., core-versus-intermediate, core-versus-peripheral, core-versus-normal, intermediate-versus-peripheral, intermediate-versus-normal, and peripheral-versus-normal.

Since anomalous diffusion models have at least two parameters, multinomial logistic regression was used in two ways: (i) to determine the significance of each model parameter and (ii) to evaluate the set of model parameters in differentiating three tumour regions as well as normal brain tissue region. In statistics or machine learning, this is called a multi-class classification problem. Quality of the overall classification is assessed by precision, recall(also known as sensitivity) and F1-score in the macro-averaging sense. Precision-recall curves were also generated to assess the performance of the set of parameters from each anomalous diffusion model. All statistical analyses were carried out in MATLAB.

3 Results

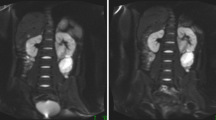
Figure 1 presents the progression of gliomas in the right hemisphere of mouse brains as observed in longitudinal T2-weighted MRI scans. These images show the level of temporal and spatial heterogeneity in tumour development.

Fig. 1
figure 1

T2-weighted MRI scans at 7, 14, 19 and 21 days showing glioblastoma progression in three different mice. Tumour cells were injected on day 0, and mouse 3 was euthanised after the day 19 imaging session. All other mice were euthanised after the day 21 imaging session

Full size image

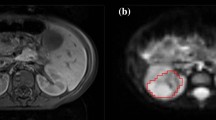
To capture additional information on tumour structure apart from water diffusivity D, the anomalous diffusion models (2)–(5) were fitted to the acquired diffusion data to yield a new set of parameters. Representative spatially resolved maps of the diffusion coefficient (D), the anomalous diffusion parameters and the relative fitting errors for each model are shown in Fig. 2. The D map was computed using the mono-exponential model with lower b values (\(\le 1000\) s/mm\(^2\)) as outlined in the methods section, and it is not model dependent. This parameter was also comparable to the ADC value, which is typically obtained with \(b=0\) and \(b=1000\) s/mm\(^2\). The relative fitting error was calculated by \(\text {norm}(\text {signal values}-\text {fitted values})/\text {norm}(\text {signal values})\). The relative error maps corresponding to each model fit have a level of similarity between them, whilst the contrast of the spatially resolved parameter maps varies with method.

Fig. 2
figure 2

Representative parameter maps and errors from fitting anomalous diffusion models. A D and \(\alpha \) maps for stretched exponential model; B D and \(\upbeta \) maps for sub-diffusion model c \(\alpha \) and \(\upbeta \) maps for continuous time random walk model (CTRW); D D and \(\mu \) maps for fractional Bloch-Torrey equation (FBTE). Note D map is obtained from fitting the mono-exponential model for \(b \le 1000\) s/mm\(^2\) and remains the same for the anomalous diffusion models

Full size image
Fig. 3
figure 3

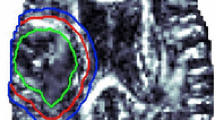
Behaviour of model parameters for representative specific regions of interest inside and around the tumour. Shown are A selected regions of interest marked on the diffusion image; B Histological section (H&E staining) of the right hemisphere of a mouse brain; C–F notched box plots of parameters based on the stretched exponential, sub-diffusion, CTRW and FBTE models, respectively. Note, if the notches \((> <)\) of the two box plots do not overlap, it indicates that the medians of two regions are significantly different at the 95% confidence level

Full size image

Our key observations from these images are: (i) \(\alpha \) from the stretched exponential model (Fig. 2A), \(\upbeta \) from the sub-diffusion model (Fig. 2B) and \(\upbeta \) from CTRW (Fig. 2C) provide a clear delineation of the three layers of tumour tissue; (ii) Both \(\alpha \)s from the CTRW (Fig. 2C) and FBTE (Fig. 2D) show a darker core layer of the tumour, but they cannot differentiate the intermediate and peripheral layers of tumour; (iii) \(\mu \) values from the FBTE (Fig. 2D) seem very similar across the whole brain region and hence not very sensitive to brain and tumour tissue structure. Since \(\mu \) is used to preserve units, so its interpretation may not be meaningful.

These observations were further confirmed by the box plots analysis in Fig. 3. Regions of interest (Fig. 3A) have been selected based on H&E section of the tumour-bearing right hemisphere of mouse brain (Fig. 3B). In Fig. 3C–F, separation of notches \((> <)\) implies the medians are significantly different across ROIs at the 95% confidence level. This hypothesis was confirmed by the Wilcoxon rank sum test as described in the methods section. A statistical summary of the parameter values for each ROI is presented in Table 1.

Table 1 Statistics of the anomalous diffusion parameters in tumour and normal tissue ROIs
Full size table
Fig. 4
figure 4

Precision-Recall curves and F1-scores (shown in brackets) for evaluating the performance of model parameters on differentiating different tumour tissue layers and normal tissue

Full size image

Multivariate logistic regression analysis showed that all the anomalous diffusion model parameters were significant with \(p<0.01\). Figure 4 shows the precision-recall curves and F1-scores (in brackets) for each set of model parameters to differentiate three tumour layers and normal tissue. The curves for anomalous diffusion models behaved similarly, bowing towards the corner (1, 1), and well above the curve for mono-exponential model. F1-scores for each anomalous model were very similar (around 0.8), and again outperformed the mono-exponential model with F1-score 0.55. These metrics indicate that anomalous diffusion models preformed very well in differentiating tumour layers and normal tissue.

4 Discussion

We set out to investigate the role of anomalous diffusion models in the characterisation of the tissue microenvironment in a mouse model of glioblastoma, a grade IV brain cancer. We acquired 9.4T DWI mouse brain data with multiple b-values at fixed diffusion time over four time points. Whilst several other anomalous diffusion models have been described in the literature (e.g.  [7, 14,15,16,17,18, 20]), only a subset of them are applicable in the fixed diffusion time regime considered herein. Moreover, different models behave differently based on the diffusion time set in the experiment. With this in mind, we investigated the utility of four anomalous diffusion models in characterising the tumour tissue layers through spatial variations in model parameters (see Figs. 2 and 3). After applying the stretched exponential, sub-diffusion, continuous time random walk and fractional Bloch-Torrey equation models to the data, we found the anomalous diffusion model parameters are very sensitive to tissue changes in the presence of a tumour. In particular, \(\alpha \) from the stretched exponential model (Fig. 2A), \(\upbeta \) from the sub-diffusion model (Fig. 2B) and \(\upbeta \) from CTRW (Fig. 2C) provide a clear delineation of the three layers (core, intermediate layer and peripheral/hyper-vascularised layer) of tumour tissue.

We found the three-parameter models (CTRW and FBTE) to marginally better fit and classify the data than the two-parameter models (stretched exponential and sub-diffusion models) in terms of relative fitting errors and F1-scores from the multinomial logistic regression and multi-class classification analysis. However, both \(\alpha \)s of the CTRW and FBTE models were not able to differentiate regions within the tissue micro-environment to the same extent as \(\alpha \) and \(\upbeta \) from the stretched exponential and sub-diffusion models. We may attribute this finding with a potential of data over-fitting using the three-parameter models. For example, the AIC (Akaike Information Criteria) for model selection involves a term representative of fitting error which is penalised by an increase in models parameters [1]. Since our relative fitting errors are somewhat similar across the different models (see Figs. 2 and 3), we may argue that insufficient gain in fitting quality is achieved through an increase in the degrees of freedom within the model. As such, a change in one parameter can counteract a change in another parameter, which make the underlying effects on the model parameters less distinguishable (comparing Fig. 3E, F with Fig. 3C, D).

In the box plots for \(\alpha \) from the stretched exponential model (Fig. 3C) and \(\upbeta \) from the sub-diffusion model (Fig. 3C), the notches on selected regions of interest inside tumour do not overlap, which means the medians of any regions are significantly different at the 95% confidence level. Hence, the anomalous diffusion parameters from the stretched exponential model and the sub-diffusion model have the ability to differentiate tissue types in tumour, whereas such detailed information on tumour structure can not be observed in vivo usually [11]. In addition, the \(\alpha \) and \(\upbeta \) values are higher in the normal-appearing brain tissue and lower in the tumour tissue region. This can be explained through fractional calculus theory; i.e. if \(\alpha \) is closer to 1 then the diffusion process is closer to Gaussian diffusion (free diffusion) and if less than 1 then the diffusion process is more anomalous and indicating the diffusion medium is more heterogeneous and complex (such as tumour tissue) [2, 20].

Moreover, multinomial logistic regression and multi-class classification analysis revealed that the combination of D and anomalous diffusion parameter (\(\alpha \) and/or \(\upbeta \)) greatly improved the classification power in terms of F1-scores compared with the current approach in clinics, in which the diffusion coefficient D is used alone.

With these results, our mouse brain glioma study demonstrates the ability of using anomalous diffusion models to differentiate tumour layers and normal brain tissue. Future work will be to apply such analysis to patient data.