Approximate Bilevel Optimization with Population-Based Evolutionary Algorithms

Abstract

Population-based optimization algorithms, such as evolutionary algorithms, have enjoyed a lot of attention in the past three decades in solving challenging search and optimization problems. In this chapter, we discuss recent population-based evolutionary algorithms for solving different types of bilevel optimization problems, as they pose numerous challenges to an optimization algorithm. Evolutionary bilevel optimization (EBO) algorithms are gaining attention due to their flexibility, implicit parallelism, and ability to customize for specific problem solving tasks. Starting with surrogate-based single-objective bilevel optimization problems, we discuss how EBO methods are designed for solving multi-objective bilevel problems. They show promise for handling various practicalities associated with bilevel problem solving. The chapter concludes with results on an agro-economic bilevel problem. The chapter also presents a number of challenging single and multi-objective bilevel optimization test problems, which should encourage further development of more efficient bilevel optimization algorithms.

1 Introduction

Bilevel and multi-level optimization problems are omni-present in practice. This is because in many practical problems there is a hierarchy of two or more problems involving different variables, objectives and constraints, arising mainly from the involvement of different hierarchical stakeholders to the overall problem. Consider an agro-economic problem for which clearly there are at least two sets of stakeholders: policy makers and farmers. Although the overall goal is to maximize food production, minimize cost of cultivation, minimize water usage, minimize environmental impact, maximum sustainable use of the land and others, clearly, the overall solution to the problem involves an optimal design on the following variables which must be settled by using an optimization algorithm: crops to be grown, amount of irrigation water and fertilizers to be used, selling price of crops, fertilizer taxes to be imposed, and others. Constraints associated with the problem are restricted run-off of harmful chemicals, availability of limited budget for agriculture, restricted use of land and other resources, and others. One can attempt to formulate the overall problem as a multi-objective optimization problem involving all the above-mentioned variables, objectives, and constraints agreeable to both stake-holders in a single level. Such a solution procedure has at least two difficulties. First, the number of variables, objectives, and constraints of the resulting problem often becomes large, thereby making the solution of the problem difficult to achieve to any acceptable accuracy. Second, such a single-level process is certainly not followed in practice, simply from an easier managerial point of view. In reality, policy-makers come up with fertilizer taxes and agro-economic regulations so that harmful environmental affects are minimal, crop production is sustainable for generations to come, and revenue generation is adequate for meeting the operational costs. On the other hand, once a set of tax and regulation policies are announced, farmers consider them to decide on the crops to be grown, amount and type of fertilizers to be used, and irrigated water to be utilized to obtain maximum production with minimum cultivation cost. Clearly, policy-makers are at the upper level in this overall agro-economic problem solving task and farmers are at the lower level. However, upper level problem solvers must consider how a solution (tax and regulation policies) must be utilized optimally by the lower level problem solvers (farmers, in this case). Also, it is obvious that the optimal strategy of the lower level problem solvers directly depends on the tax and regulation policies declared by the upper level problem solvers. The two levels of problems are intricately linked in such bilevel problems, but, interestingly, the problem is not symmetric between upper and lower levels; instead the upper level’s objectives and constraints control the final optimal solution more than that of the lower level problem.

When both upper and lower level involve a single objective each, the resulting bilevel problem is called a single-objective bilevel problem. The optimal solution in this case is usually a single solution describing both upper and lower level optimal variable values. In many practical problems, each level independently or both levels may involve more than one conflicting objectives. Such problems are termed here as multi-objective bilevel problems. These problems usually have more than one bilevel solution. For implementation purposes, a single bilevel solution must be chosen using the preference information of both upper and lower level problem solvers. Without any coordinated effort by upper level decision makers with lower level decision-makers, a clear choice of the overall bilevel solution is uncertain, which provides another dimension of difficulty to solve multi-objective bilevel problems.

It is clear from the above discussion that bilevel problems are reality in practice, however their practice is uncommon, simply due to the fact that the nested nature of two optimization problems makes the solution procedure computationally expensive. The solution of such problems calls for flexible yet efficient optimization methods, which can handle different practicalities and are capable of finding approximate optimal solutions in a quick computational manner. Recently, evolutionary optimization methods have been shown to be applicable to such problems because of ease of customization that helps in finding near-optimal solution, mainly due to their population approach, use of a direct optimization approach instead of using any gradient, presence of an implicit parallelism mechanism constituting a parallel search of multiple regions simultaneously, and their ability to find multiple optimal solutions in a single application.

In this chapter, we first provide a brief description of metaheuristics in Sect. 13.2 followed by a step-by-step procedure of an evolutionary optimization algorithm as a representative of various approaches belonging to this class of algorithms. Thereafter, in Sect. 13.3, we discuss the bilevel formulation and difficulties involved in solving a bilevel optimization problem. Then, we provide the past studies on population-based methods for solving bilevel problems in Sect. 13.4. Thereafter, we discuss in detail some of the recent efforts in evolutionary bilevel optimization in Sect. 13.5. In Sect. 13.6, we present two surrogate-assisted single-objective evolutionary bilevel optimization (EBO) algorithms—BLEAQ and BLEAQ2. Simulation results of these two algorithms are presented next on a number of challenging standard and scalable test problems provided in the Appendix. Bilevel evolutionary multi-objective optimization (BL-EMO) algorithms are described next in Sect. 13.7. The ideas of optimistic and pessimistic bilevel Pareto-optimal solution sets are differentiated and an overview of research developments on multi-objective bilevel optimization is provided. Thereafter, in Sect. 13.8, a multi-objective agro-economic bilevel problem is described and results using the proposed multi-objective EBO algorithm are presented. Finally, conclusions of this extensive chapter is drawn in Sect. 13.9.

2 Metaheuristics Algorithms for Optimization

Heuristics refers to relevant guiding principles, or effective rules, or partial problem information related to the problem class being addressed. When higher level heuristics are utilized in the process of creating new solutions in a search or optimization methodology for solving a larger class of problems, the resulting methodology is called a metaheuristic. The use of partial problem information may also be used in metaheuristics to speed up the search process in arriving at a near-optimal solution, but an exact convergence to the optimal solution is usually not guaranteed. For many practical purposes, metaheuristics based optimization algorithms are more pragmatic approaches [13]. These methods are in rise due to the well-known no-free-lunch (NFL) theorem.

Theorem 13.2.1

No single optimization algorithm is most computationally effective for solving all problems.△

Although somewhat intuitive, a proof of a more specific and formal version of the above theorem was provided in [66]. A corollary to the NFL theorem is that for solving a specific problem class, there exists a customized algorithm which would perform the best; however the same algorithm may not work so well on another problem class.

It is then important to ask a very important question: ‘How does one develop a customized optimization algorithm for a specific problem class?’. The search and optimization literature does not provide a ready-made answer to the above question for every possible problem class, but the literature is full of different application problems and the respective developed customized algorithms for solving the problem class. Most of these algorithms use relevant heuristics derived from the description of the problem class.

We argue here that in order to utilize problem heuristics in an optimization algorithm, the basic structure of the algorithm must allow heuristics to be integrated easily. For example, the well-known steepest-descent optimization method cannot be customized much with available heuristics, as the main search must always take place along the negative of the gradient of the objective functions to allow an improvement or non-deterioration in the objective value from one iteration to the next. In this section, we discuss EAs that are population-based methods belonging to the class of metaheuristics. There exist other population-based metaheuristic methods which have also been used for solving bilevel problems, which we do not elaborate here, but provide a brief description below:

• Differential Evolution (DE) [ 59]: DE is a steady-state optimization procedure which uses three population members to create a “mutated” point. It is then compared with the best population member and a recombination of variable exchanges is made to create the final offspring point. An optional selection between offspring and the best population member is used. DE cannot force its population members to stay within specified variable bounds and special operators are needed to handle them as well as other constraints. DE is often considered as a special version of an evolutionary algorithm, described later.

• Particle Swarm Optimization (PSO) [ 28, 31]: PSO is a generational optimization procedure which creates one new offspring point for each parent population member by making a vector operation with parent’s previous point, its best point since the start of a run and the best-ever population point. Like DE, PSO cannot also force its population members to stay within specified variable bounds and special operators are needed to handle them and other constraints.

• Other Metaheuristics [ 5, 22]: There exists more than 100 other metaheuristics-based approaches, which use different natural and physical phenomenon. Variable bounds and constraints are often handled using penalty functions or by using special operators.

These algorithms, along with evolutionary optimization algorithms described below, allow flexibility for customizing the solution procedure by enabling any heuristics or rules to be embedded in their operators.

Evolutionary algorithms (EAs) are mostly synonymous to metaheuristics based optimization methods. EAs work with multiple points (called a population) at each iteration (called a generation). Here are the usual steps of a generational EA:

• 1. An initial population P ₀ of size N (population size) is created, usually at random within the supplied variable bounds. Every population member is evaluated (objective functions and constraints) and a combined fitness or a selection function is evaluated for each population member. Set the generation counter t = 0.

• 2. A termination condition is checked. If not satisfied, continue with Step 3, else report the best point and stop.

• 3. Select better population members of P _t by comparing them using the fitness function and store them in mating pool M _t.

• 4. Take pairs of points from M _t at a time and recombine them using a recombination operator to create one or more new points.

• 5. Newly created points are then locally perturbed by using a mutation operator. The mutated point is then stored in an offspring population Q _t. Steps 4 and 5 are continued until Q _t grows to a size of N.

• 6. Two populations P _t and Q _t are combined and N best members are saved in the new parent population P _t+1. The generation counter is incremented by one and the algorithm moves to Step 2.

The recombination operator is unique in EAs and is responsible for recombining two different population members to create new solutions. The selection and recombination operators applied on a population constitutes an implicitly parallel search, providing their power. In the above generational EA, $NT_{\max }$ is the total number of evaluations, where $T_{\max }$ is the number of generations needed to terminate the algorithm. Besides the above generational EA, steady-state EAs exist, in which the offspring population Q _t consists of a single new mutated point. In the steady-state EA, the number of generations $T_{\max }$ needed to terminate would be more than that needed for a generational EA, but the overall number of solution evaluations needed for the steady-state EA may be less, depending on the problem being solved.

Each of the steps in the above algorithm description—initialization (Step 1), termination condition (Step 2), selection (Step 3), recombination (Step 4), mutation (Step 5) and survival (Step 6)—can be changed or embedded with problem information to make the overall algorithm customized for a problem class.

3 Bilevel Formulation and Challenges

Bilevel optimization problems have two optimization problems staged in a hierarchical manner [55]. The outer problem is often referred to as the upper level problem or the leader’s problem, and the inner problem is often referred to as the lower level problem or the follower’s problem. Objective and constraint functions of both levels can be functions of all variables of the problem. However, a part of the variable vector, called the upper level variable vector, remains fixed for the lower level optimization problem. For a given upper level variable vector, an accompanying lower level variable set which is optimal to the lower level optimization problem becomes a candidate feasible solution for the upper level optimization problem, subject to satisfaction of other upper level variable bounds and constraint functions. Thus, in such nested problems, the lower level variable vector depends on the upper level variable vector, thereby causing a strong variable linkage between the two variable vectors. Moreover, the upper level problem is usually sensitive to the quality of lower level optimal solution, which makes solving the lower level optimization problem to a high level of accuracy important.

The main challenge in solving bilevel problems is the computational effort needed in solving nested optimization problems, in which for every upper level variable vector, the lower level optimization problem must be solved to a reasonable accuracy. One silver lining is that depending on the complexities involved in two levels, two different optimization algorithms can be utilized, one for upper level and one for lower level, respectively, instead of using the same optimization method for both levels. However, such a nested approach may also be computationally expensive for large scale problems. All these difficulties provide challenges to optimization algorithms while solving a bilevel optimization problem with a reasonable computational complexity.

There can also be situations where the lower level optimization in a bilevel problem has multiple optimal solutions for a given upper level vector. Therefore, it becomes necessary to define, which solution among the multiple optimal solutions at the lower level should be considered. In such cases, one assumes either of the two positions: the optimistic position or the pessimistic position. In the optimistic position, the follower is assumed to favorable to the leader and chooses the solution that is best for the leader from the set of multiple lower level optimal solutions. In the pessimistic position, it is assumed that the follower may not be favorable to the leader (in fact, the follower is antagonistic to leader’s objectives) and may choose the solution that is worst for the leader from the set of multiple lower level optimal solutions. Intermediate positions are also possible and are more pragmatic, which can be defined with the help of selection functions. Most of the literature on bilevel optimization usually focuses on solving optimistic bilevel problems. A general formulation for the bilevel optimization problem is provided below.

Definition 13.3.1

For the upper level objective function $F:\mathbb {R}^n\times \mathbb {R}^m \to \mathbb {R}$ and lower level objective function $f:\mathbb {R}^n\times \mathbb {R}^m \to \mathbb {R}$, the bilevel optimization problem is given by

$$\displaystyle \begin{aligned} \begin{array}{rcl} \mathop{\mathrm{min}}\limits_{{\mathbf{x}}_u, {\mathbf{x}}_l} &\displaystyle &\displaystyle F({\mathbf{x}}_u, {\mathbf{x}}_l), \end{array} \end{aligned} $$

(13.3.1)

$$\displaystyle \begin{aligned} \begin{array}{rcl} \mathop{\mbox{subject}\ \mbox{to}} &\displaystyle &\displaystyle {\mathbf{x}}_l \in \mathop{\mathrm{argmin}}\limits_{{\mathbf{x}}_l} \lbrace f({\mathbf{x}}_u, {\mathbf{x}}_l) : g_j({\mathbf{x}}_u, {\mathbf{x}}_l)\leq 0, \quad j=1,\ldots,J \rbrace, \end{array} \end{aligned} $$

(13.3.2)

$$\displaystyle \begin{aligned} \begin{array}{rcl} &\displaystyle &\displaystyle \qquad \quad G_k({\mathbf{x}}_u, {\mathbf{x}}_l)\leq 0, \quad k=1,\ldots,K, \end{array} \end{aligned} $$

(13.3.3)

where $G_k:\mathbb {R}^n\times \mathbb {R}^m \to \mathbb {R}$, k = 1, …, K denotes the upper level constraints, and $g_j:\mathbb {R}^n\times \mathbb {R}^m \to \mathbb {R}$, j = 1, …, J represents the lower level constraints, respectively. Variables x _u and x _l are n and m dimensional vectors, respectively. It is important to specify the position one is taking while solving the above formulation.△

4 Non-surrogate-Based EBO Approaches

A few early EBO algorithms were primarily either nested approaches or used the KKT conditions of the lower level optimization problem to reduce the bilevel problem to a single level and then a standard algorithm was applied. In this section, we provide a review of such approaches. It is important to note that the implicit parallel search of EAs described before still plays a role in constituting an efficient search within both the upper and lower level optimization tasks.

4.1 Nested Methods

Nested EAs are a popular approach to handle bilevel problems, where lower level optimization problem is solved corresponding to each and every upper level member [36, 41, 47]. Though effective, nested strategies are computationally very expensive and not viable for large scale bilevel problems. Nested methods in the area of EAs have been used in primarily two ways. The first approach has been to use an EA at the upper level and a classical algorithm at the lower level, while the second approach has been to utilize EAs at both levels. Of course, the choice between two approaches is determined by the complexity of the lower level optimization problem.

One of the first EAs for solving bilevel optimization problems was proposed in the early 1990s. Mathieu et al. [35] used a nested approach with genetic algorithm at the upper level, and linear programming at the lower level. Another nested approach was proposed in [69], where the upper level was an EA and the lower level was solved using Frank–Wolfe algorithm (reduced gradient method) for every upper level member. The authors demonstrated that the idea can be effectively utilized to solve non-convex bilevel optimization problems. Nested PSO was used in [31] to solve bilevel optimization problems. The effectiveness of the technique was shown on a number of standard test problems with small number of variables, but the computational expense of the nested procedure was not reported. A hybrid approach was proposed in [30], where simplex-based crossover strategy was used at the upper level, and the lower level was solved using one of the classical approaches. The authors report the generations and population sizes required by the algorithm that can be used to compute the upper level function evaluations, but they do not explicitly report the total number of lower level function evaluations, which presumably is high.

DE based approaches have also been used, for instance, in [72], authors used DE at the upper level and relied on the interior point algorithm at the lower level; similarly, in [3] authors have used DE at both levels. Authors have also combined two different specialized EAs to handle the two levels, for example, in [2] authors use an ant colony optimization to handle the upper level and DE to handle the lower level in a transportation routing problem. Another nested approach utilizing ant colony algorithm for solving a bilevel model for production-distribution planning is [9]. Scatter search algorithms have also been employed for solving production-distribution planning problems, for instance [10].

Through a number of approaches involving EAs at one or both levels, the authors have demonstrated the ability of their methods in solving problems that might otherwise be difficult to handle using classical bilevel approaches. However, as already stated, most of these approaches are practically non-scalable. With increasing number of upper level variables, the number of lower level optimization tasks required to be solved increases exponentially. Moreover, if the lower level optimization problem itself is difficult to solve, numerous instances of such a problem cannot be solved, as required by these methods.

4.2 Single-Level Reduction Using Lower Level KKT Conditions

Similar to the studies in the area of classical optimization, many studies in the area of evolutionary computation have also used the KKT conditions of the lower level to reduce the bilevel problem into a single-level problem. Most often, such an approach is able to solve problems that adhere to certain regularity conditions at the lower level because of the requirement of the KKT conditions. However, as the reduced single-level problem is solved with an EA, usually the upper level objective function and constraints can be more general and not adhering to such regularities. For instance, one of the earliest papers using such an approach is by Hejazi et al. [24], who reduced the linear bilevel problem to single-level and then used a genetic algorithm, where chromosomes emulate the vertex points, to solve the problem. Another study [8] also proposed a single level reduction for linear bilevel problems. Wang et al. [62] reduced the bilevel problem into a single-level optimization problem using KKT conditions, and then utilized a constraint handling scheme to successfully solve a number of standard test problems. Their algorithm was able to handle non-differentiability at the upper level objective function, but not elsewhere. Later on, Wang et al. [64] introduced an improved algorithm that was able to handle non-convex lower level problem and performed better than the previous approach [62]. However, the number of function evaluations in both approaches remained quite high (requiring function evaluations to the tune of 100,000 for 2–5 variable bilevel problems). In [63], the authors used a simplex-based genetic algorithm to solve linear-quadratic bilevel problems after reducing it to a single level task. Later, Jiang et al. [27] reduced the bilevel optimization problem into a non-linear optimization problem with complementarity constraints, which is sequentially smoothed and solved with a PSO algorithm. Along similar lines of using lower level optimality conditions, Li [29] solved a fractional bilevel optimization problem by utilizing optimality results of the linear fractional lower level problem. In [60], the authors embed the chaos search technique in PSO to solve single-level reduced problem. The search region represented by the KKT conditions can be highly constrained that poses challenges for any optimization algorithm. To address this concern, in a recent study [57], the authors have used approximate KKT-conditions for the lower level problem. One of the theoretical concerns of using the KKT conditions to replace lower level problem directly is that the associated constraint qualification conditions must also be satisfied for every lower level solution.

5 Surrogate-Based EBO Approaches

The earlier approaches suffered with some drawbacks like high computational requirements, or reliance on the KKT conditions of the lower level problem. To overcome this, recent research has focused on surrogate-based methods for bilevel problems. Researchers have used surrogates in different ways for solving bilevel problems that we discuss in this section.

Surrogate-based solution methods are commonly used for optimization problems [61], where actual function evaluations are expensive. A meta-model or surrogate model is an approximation of the actual model that is relatively quicker to evaluate. Based on a small sample from the actual model, a surrogate model can be trained and used subsequently for optimization. Given that, for complex problems, it is hard to approximate the entire model with a small set of sample points, researchers often resort to iterative meta modeling techniques, where the actual model is approximated locally during iterations.

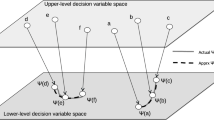
Bilevel optimization problems contain an inherent complexity that leads to a requirement of large number of evaluations to solve the problem. Metamodeling of the lower level optimization problem, when used with population-based algorithms, offers a viable means to handle bilevel optimization problems. With good lower level solutions being supplied at the upper level, EA’s implicit parallel search power constructs new and good upper level solutions, making the overall search efficient. In this subsection, we discuss three ways in which metamodeling can be applied to bilevel optimization. There are two important mappings in bilevel optimization, referred to as the rational reaction set and lower level optimal value function. We refer the readers to Fig. 13.1, which provides an understanding of these two mappings graphically for a hypothetical bilevel problem.

Fig. 13.1

Graphical representation of rational reaction set (Ψ) and lower level optimal value function (φ)

5.1 Reaction Set Mapping

One of the approaches to solve bilevel optimization problems using EAs would be through iterative approximation of the reaction set mapping Ψ. The bilevel formulation in terms of the Ψ-mapping can be written as below.

$$\displaystyle \begin{aligned} \begin{array}{rcl} \mathop{\mathrm{min}}\limits_{{\mathbf{x}}_u, {\mathbf{x}}_l} &\displaystyle &\displaystyle F({\mathbf{x}}_u,{\mathbf{x}}_l), \end{array} \end{aligned} $$

(13.5.4)

$$\displaystyle \begin{aligned} \begin{array}{rcl} \mathop{\mbox{subject}\ \mbox{to}} &\displaystyle &\displaystyle {\mathbf{x}}_l \in \Psi({\mathbf{x}}_u), \end{array} \end{aligned} $$

(13.5.5)

$$\displaystyle \begin{aligned} \begin{array}{rcl} &\displaystyle &\displaystyle G_k({\mathbf{x}}_u,{\mathbf{x}}_l)\leq 0,\quad k=1,\dots,K. \end{array} \end{aligned} $$

(13.5.6)

If the Ψ-mapping in a bilevel optimization problem is known, it effectively reduces the problem to single level optimization. However, this mapping is seldom available; therefore, the approach could be to solve the lower level problem for a few upper level members and then utilize the lower level optimal solutions and corresponding upper level members to generate an approximate mapping $\hat {\Psi }$. It is noteworthy that approximating a set-valued Ψ-mapping offers its own challenges and is not a straightforward task. Assuming that an approximate mapping, $\hat {\Psi }$, can be generated, the following single level optimization problem can be solved for a few generations of the algorithm before deciding to further refine the reaction set.

$$\displaystyle \begin{aligned} \begin{array}{rcl} \mathop{\mathrm{min}}\limits_{{\mathbf{x}}_u, {\mathbf{x}}_l} &\displaystyle &\displaystyle F({\mathbf{x}}_u,{\mathbf{x}}_l), \\ \mathop{\mbox{subject}\ \mbox{to}} &\displaystyle &\displaystyle {\mathbf{x}}_l \in \hat{\Psi}({\mathbf{x}}_u), \\ &\displaystyle &\displaystyle G_k({\mathbf{x}}_u,{\mathbf{x}}_l)\leq 0, \quad k=1,\dots,K. \end{array} \end{aligned} $$

EAs that rely on this idea to solve bilevel optimization problems are [4, 44, 45, 50]. In some of these studies, authors have used quadratic approximation to approximate the local reaction set. This helps in saving lower level optimization calls when the approximation for the local reaction set is good. In case the approximations generated by the algorithm are not acceptable, the method defaults to a nested approach. It is noteworthy that a bilevel algorithm that uses a surrogate model for reaction set mapping may need not be limited to quadratic models but other models can also be used.

5.2 Optimal Lower Level Value Function

Another way to use metamodeling is through the approximation of the optimal value function φ. If the φ-mapping is known, the bilevel problem can once again be reduced to single level optimization problem as follows [68],

$$\displaystyle \begin{aligned} \begin{array}{rcl} \mathop{\mathrm{min}}\limits_{{\mathbf{x}}_u, {\mathbf{x}}_l} &\displaystyle &\displaystyle F({\mathbf{x}}_u,{\mathbf{x}}_l), \\ \mathop{\mbox{subject}\ \mbox{to}} &\displaystyle &\displaystyle f({\mathbf{x}}_u,{\mathbf{x}}_l) \le \varphi({\mathbf{x}}_u), \\ &\displaystyle &\displaystyle g_j({\mathbf{x}}_u,{\mathbf{x}}_l)\leq 0, \quad j=1,\dots,J,\\ &\displaystyle &\displaystyle G_k({\mathbf{x}}_u,{\mathbf{x}}_l)\leq 0, \quad k=1,\dots,K. \end{array} \end{aligned} $$

However, since the value function is seldom known, one can attempt to approximate this function using metamodeling techniques. The optimal value function is a single-valued mapping; therefore, approximating this function avoids the complexities associated with set-valued mapping. As described previously, an approximate mapping $\hat {\varphi }$, can be generated with the population members of an EA and the following modification in the first constraint: $f({\mathbf {x}}_u,{\mathbf {x}}_l) \le \hat {\varphi }({\mathbf {x}}_u).$ Evolutionary optimization approaches that rely on this idea can be found in [51, 56, 58].

5.3 Bypassing Lower Level Problem

Another way to use a meta-model in bilevel optimization would be to completely by-pass the lower level problem, as follows:

$$\displaystyle \begin{aligned} \begin{array}{rcl} \mathop{\mathrm{min}}\limits_{{\mathbf{x}}_u} &\displaystyle &\displaystyle \hat{F}({\mathbf{x}}_u), \\ \mathop{\mbox{subject}\ \mbox{to}} &\displaystyle &\displaystyle \hat{G}_k({\mathbf{x}}_u)\leq 0, \quad k=1,\ldots,K. \end{array} \end{aligned} $$

Given that the optimal x _l are essentially a function of x _u, it is possible to construct a single level approximation of the bilevel problem by ignoring x _l completely and writing the objective function and constraints for the resulting single level problem as a function of only x _u. However, the landscape for such a single level problem can be highly non-convex, disconnected, and non-differentiable. Advanced metamodeling techniques might be required to use this approach, which may be beneficial for certain classes of bilevel problems. A training set for the metamodel can be constructed by solving a few lower level problems for different x _u. Both upper level objective F and constraint set (G _k) can then be meta-modeled using x _u alone. Given the complex structure of such a single-level problem, it might be sensible to create such an approximation locally.

5.4 Limitations and Assumptions of Surrogate-Based Approaches

The idea of using function approximations within EAs makes them considerably more powerful than simple random search. However, these algorithms are still constrained by certain background assumptions, and are not applicable to arbitrary problems. In order for the approximations to work, we generally need to impose some constraining assumptions on the bilevel problem to even ensure the existence of the underlying mappings that the algorithms are trying to approximate numerically.

For example, when using function approximations for the reaction set mapping in single objective problems, we need to assume that the lower level problem is convex with respect to the lower level variables. If the lower level problem is not convex, the function could be composed by global as well as local optimal solutions, and if we consider only global optimal solutions in the lower level problem, the respective function could become discontinuous. This challenge can be avoided by imposing the convexity assumption. Furthermore, we generally need to require that the lower level objective function as well as the constraints are twice continuously differentiable. For more insights, we refer to [50], where the assumptions are discussed in greater detail in case of both polyhedral and nonlinear constraints. When these assumptions are not met, there are also no guarantees that the approximation based algorithms can be expected to work any better than a nested search.

In the next section, we describe recent surrogate-based EBO algorithms, but would like to highlight that they are not exempt from the above convexity and differentiability assumptions.

6 Single-Objective Surrogate-Based EBO Algorithms

In this section, we discuss the working of two surrogate-based EBO algorithms—BLEAQ and BLEAQ2—that rely on the approximation of the Ψ- and φ-mappings. In a single-objective bilevel problems, both upper and lower level problems have a single objective function: F(x _u, x _l) and f(x _u, x _l). There can be multiple constraints at each level. We describe these algorithms in the next two subsections.

6.1 Ψ-Approach and BLEAQ Algorithm

In the Ψ-approach, the optimal value of each lower level variable is approximated using a surrogate model of the upper level variable set. Thus, a total of m = |x _l| number of metamodels must be constructed from a few exact lower level optimization results.

After the lower level problem is optimized for a few upper level variable sets, the optimal lower level variable can be modeled using a quadratic function of upper level variables: $x^{\ast }_{l,i} = q_i({\mathbf {x}}_u)$. In fact, the algorithm creates various local quadratic models, but for simplicity we skip the details here. Thereafter, upper level objective and constraint functions can be expressed in terms of the upper level variables only in an implicit manner, as follows:

$$\displaystyle \begin{aligned} \begin{array}{rcl} \mathop{\mathrm{min}}\limits_{{\mathbf{x}}_u} &\displaystyle &\displaystyle F\left({\mathbf{x}}_u,\mathbf{q}({\mathbf{x}}_u)\right), \\ \mathop{\mbox{subject}\ \mbox{to}} &\displaystyle &\displaystyle G_k\left({\mathbf{x}}_u,\mathbf{q}({\mathbf{x}}_u)\right) \leq 0, \quad k=1,2,\ldots, K. \end{array} \end{aligned} $$

Note that q(x _u) represents the quadratic approximation for the lower level vector. The dataset for creating the surrogate q(x _u), is constructed by identifying the optimal lower level vectors corresponding to various upper level vectors by solving the following problem:

$$\displaystyle \begin{aligned} {\mathbf{x}}^{\ast}_{l} = \mathrm{argmin}\left\{f({\mathbf{x}}_u,{\mathbf{x}}_l)\big| g_j({\mathbf{x}}_u,{\mathbf{x}}_l)\leq 0, \quad j=1,2,\ldots,J\right\}. \end{aligned}$$

The validity of the quadratic approximation is checked after a few iterations. If the existing quadratic model does not provide an accurate approximation, new points are introduced to form a new quadratic model. We call this method BLEAQ [45, 50]. Note that this method will suffer whenever the lower level has multiple optimal solutions at the lower level, and also it requires multiple models q _i(x _u), ∀ i ∈{1, …, m}, to be created.

6.2 φ-Approach and BLEAQ2 Algorithm

Next, we discuss the φ-approach that overcomes the various drawbacks of the Ψ-approach. In the φ-approach, an approximation of the optimal lower level objective function value φ(x _u) as a function of x _u is constructed that we refer to as $\hat {\varphi }({\mathbf {x}}_u)$. Thereafter, the following single-level problem is solved:

$$\displaystyle \begin{aligned} \begin{array}{rl} \mbox{Minimize} & F\left({\mathbf{x}}_u,{\mathbf{x}}_l\right), \\ \mbox{subject to} & f({\mathbf{x}}_u,{\mathbf{x}}_l) \leq \hat{\varphi}({\mathbf{x}}_u), \\ & G_k\left({\mathbf{x}}_u,{\mathbf{x}}_l\right) \leq 0, \quad k=1,2,\ldots, K. \end{array} \end{aligned} $$

(13.6.7)

The above formulation allows a single surrogate model to be constructed and the solution of the above problem provides optimal x _u and x _l vectors.

In the modified version of BLEAQ, that we called BLEAQ2 [58], both Ψ and φ-approaches are implemented with a check. The model that has higher level of accuracy is used to choose the lower level solution for any given upper level vector. Both Ψ and φ models are approximated locally and updated iteratively.

6.3 Experiments and Results

Next, we assess the performance of three algorithms, the nested approach, BLEAQ, and BLEAQ2 on a set of bilevel test problems. We perform 31 runs for each test instance. For each run, the upper and lower level function evaluations required until termination are recorded separately. Information about the various parameters and their settings can be found in [50, 58].

6.3.1 Results on Non-scalable Test Problems

We first present the empirical results on eight non-scalable test problems selected from the literature (referred to as TP1–TP8). The description for these test problems is provided in the Appendix. Table 13.1 contains the median upper level (UL) function evaluations, lower level (LL) function evaluations and BLEAQ2’s overall function evaluation savings as compared to other approaches from 31 runs of the algorithms. The overall function evaluations for any algorithm is simply the sum of upper and lower level function evaluations. For instance, for the median run with TP1, BLEAQ2 requires 63% less overall function evaluations as compared to BLEAQ, and 98% less overall function evaluations as compared to the nested approach.

Table 13.1 Median function evaluations on non-scalable test problems TP1–TP8

All these test problems are bilevel problems with small number of variables, and all the three algorithms were able to solve the eight test instances successfully. A significant computational saving can be observed for both BLEAQ2 and BLEAQ, as compared to the nested approach, as shown in the ‘Savings’ column of Table 13.1. The performance gain going from BLEAQ to BLEAQ2 is quite significant for these test problems even though none of them leads to multiple lower level optimal solutions. Detailed comparison between BLEAQ and BLEAQ2 in terms of upper and lower level function evaluations is provided through Figs. 13.2 and 13.3, respectively. It can be observed that BLEAQ2 requires comparatively much less number of lower level function evaluations than BLEAQ algorithm, while there is no conclusive argument can be made for the number of upper level function evaluations. However, since the lower level problem is solved more often, as shown Table 13.1, BLEAQ2 requires significantly less number of overall function evaluations to all eight problems.

Fig. 13.2

Variation of upper level function evaluations required by BLEAQ and BLEAQ2 algorithms in 31 runs applied to TP1–TP8

Fig. 13.3

Variation of lower level function evaluations required by BLEAQ and BLEAQ2 algorithms in 31 runs applied to TP1–TP8

6.3.2 Results on Scalable Test Problems

Next, we compare the performance of the three algorithms on the scalable SMD test suite (presented in the Appendix) which contains 12 test problems [46]. The test suite was later extend to 14 test problems by adding two additional scalable test problems. First we analyze the performance of the algorithms on five variables, and then we provide the comparison results on 10-variable instances of the SMD test problems. For the five-variable version of the SMD test problems, we use p = 1, q = 2 and r = 1 for all SMD problems except SMD6 and SMD14. For the five-variable version of SMD6 and SMD14, we use p = 1, q = 0, r = 1 and s = 2. For the 10-variable version of the SMD test problems, we use p = 3, q = 3 and r = 2 for all SMD problems except SMD6 and SMD14. For the 10-variable version of SMD6 and SMD14, we use p = 3, q = 1, r = 2 and s = 2. In their five-variable versions, there are two variables at the upper level and three variables at the lower level. They also offer a variety of tunable complexities to any algorithm. For instance, the test set contains problems which are multi-modal at the upper and the lower levels, contain multiple optimal solutions at the lower level, contain constraints at the upper and/or lower levels, etc.

Table 13.2 provides the median function evaluations and overall savings for the three algorithms on all 14 five-variable SMD problems. The table indicates that BLEAQ2 is able to solve the entire set of 14 SMD test problems, while BLEAQ fails on two test problems. The overall savings with BLEAQ2 is larger as compared to BLEAQ for all problems. Test problems SMD6 and SMD14 which contain multiple lower level solutions, BLEAQ is unable to handle them. Further details about the required overall function evaluations from 31 runs are provided in Fig. 13.4.

Fig. 13.4

Overall function evaluations needed by BLEAQ and BLEAQ2 for solving five-dimensional SMD1–SMD14 problems

Table 13.2 Median function evaluations on five-variable SMD test problems

Results for the 10-variable SMD test problems are presented in Table 13.3. BLEAQ2 leads to much higher savings as compared to BLEAQ. BLEAQ is found to fail again on SMD6 and also on SMD7 and SMD8. Both methods outperform the nested method on most of the test problems. We do not provide results for SMD9–SMD14 as none of the algorithms are able to handle these problems. It is noteworthy that SMD9–SMD14 offer difficulties with multi-modalities and having highly constrained search space, which none of the algorithms are able to handle with the parameter setting used here. Details for the 31 runs on each of these test problems are presented in Fig. 13.5.

Fig. 13.5

Overall function evaluations needed by BLEAQ and BLEAQ2 for solving 10-dimensional SMD1–SMD14 problems

Table 13.3 Median function evaluations on 10-variable SMD test problems

The advantage of BLEAQ2 algorithm comes from the use of both Ψ and φ-mapping based surrogate approaches. We pick two SMD problems—SMD1 and SMD13—to show that one of the two surrogate approaches perform better depending on their suitability on the function landscape. Figure 13.6 shows that in SMD1 problem, φ-approximation performs better and Fig. 13.7 shows that Ψ-approximation is better on SMD13. In these figures, the variation of the Euclidean distance of lower level solution from exact optimal solution with generations is shown. While both approaches reduce the distance in a noisy manner, BLEAQ2 does it better by using the best of both approaches than BLEAQ which uses only the Ψ-approximation. The two figures show the adaptive nature of the BLEAQ2 algorithm in choosing the right approximation strategy based on the difficulties involved in a bilevel optimization problem.

Fig. 13.6

Approximation error (in terms of Euclidean distance) of a predicted lower level optimal solution when using localized Ψ and φ-mapping during the BLEAQ2 algorithm on the five-variable SMD1 test problem

Fig. 13.7

Approximation error (in terms of Euclidean distance) of a predicted lower level optimal solution when using localized Ψ and φ-mapping during the BLEAQ2 algorithm on the five-variable SMD13 test problem

6.4 Other Single-Objective EBO Studies

Most often, uncertainties arise from unavoidable variations in implementing an optimized solution. Thus, the issue of uncertainty handling is of great practical significance. Material properties, measurement errors, manufacturing tolerances, interdependence of parameters, environmental conditions, etc. are all sources of uncertainties, which, if not considered during the optimization process, may lead to an optimistic solution without any practical relevance. A recent work [34] introduces the concept of robustness and reliability in bilevel optimization problems arising from uncertainties in both lower and upper level decision variables and parameters. The effect of uncertainties on the final robust/reliable bilevel solution was clearly demonstrated in the study using simple, easy-to-understand test problems, followed by a couple of application problems. The topic of uncertainty handling in bilevel problems is highly practical and timely with the overall growth in research in bilevel methods and in uncertainty handling methods.

Bilevel methods may also be used for achieving an adaptive parameter tuning for optimization algorithms, for instance [48]. The upper level problem considers the algorithmic parameters as variables and the lower level problem uses the actual problem variables. The lower level problem is solved using the algorithmic parameters described by the upper level multiple times and the resulting performance of the algorithm is then used as an objective of the upper level problem. The whole process is able to find optimized parameter values along with the solution of the a number of single-objective test problems.

In certain scenarios, bilevel optimization solution procedures can also be applied to solve single level optimization problems in a more efficient way. For example, the optimal solution of a single-level primal problem can be obtained by solving a dual problem constructed from the Lagranrian function of dual variables. The dual problem formulation is a bilevel (min-max) problem with respect to two sets of variables: upper level involves Lagrangian multipliers or dual variables and lower level involves problem variables or primal variables. A study used evolutionary optimization method to solve the (bilevel) dual problem using a co-evolutionary approach [18]. For zero duality gap problems, the proposed bilevel approach not only finds the optimal solution to the problem, but also produces the Lagrangian multipliers corresponding to the constraints.

7 Multi-Objective Bilevel Optimization

Quite often, a decision maker in a practical optimization problem is interested in optimizing multiple conflicting objectives simultaneously. This leads us to the growing literature on multi-objective optimization problem solving [11, 12]. Multiple objectives can also be realized in the context of bilevel problems, where either a leader, or follower, or both might be facing multiple objectives in their own levels [1, 25, 32, 70]. This gives rise to multi-objective bilevel optimization problems that is defined below.

Definition 13.7.1

For the upper level objective function $F:\mathbb {R}^n\times \mathbb {R}^m \to \mathbb {R}^p$ and lower level objective function $f:\mathbb {R}^n\times \mathbb {R}^m \to \mathbb {R}^q$, the multi-objective bilevel problem is given by

where $G_k:\mathbb {R}^n\times \mathbb {R}^m \to \mathbb {R}$, k = 1, …, K denotes the upper level constraints, and $g_j:\mathbb {R}^n\times \mathbb {R}^m \to \mathbb {R}$ represents the lower level constraints, respectively.△

Bilevel problems with multiple objectives at lower level are expected to be considerably more complicated than the single-objective case. Surrogate based methods can once again be used, but even verification of the conditions, for instance, when the use of approximations for the reaction set mapping are applicable, is a challenge and requires quite many tools from variational analysis literature. Some of these conditions are discussed in [53]. As remarked in [52], bilevel optimal solution may not exist for all problems. Therefore, additional regularity and compactness conditions are needed to ensure existence of a solution. This is currently an active area of research. Results have been presented by [21], who established necessary optimality conditions for optimistic multi-objective bilevel problems with the help of Hiriart-Urruty scalarization function.

7.1 Optimistic Versus Pessimistic Solutions in Multi-Objective Bilevel Optimization

The optimistic or pessimistic position becomes more prominent in multi-objective bilevel optimization. In the presence of multiple objectives at the lower level, the set-valued mapping Ψ(x _u) normally represents a set of Pareto-optimal solutions corresponding to any given x _u, which we refer as follower’s Pareto-optimal frontier. A solution to the overall problem (with optimistic or pessimistic position) is expected to produce a trade-off frontier for the leader that we refer as the leader’s Pareto-optimal frontier. In these problems, the lower level problem produces its own Pareto-optimal set and hence the upper level optimal set depends on which solutions from the lower level would be chosen by the lower level decision-makers. The optimistic and pessimistic fronts at the upper level mark the best and worst possible scenarios at the upper level, given that the lower level solutions are always Pareto-optimal.

Though optimistic position have commonly been studied in classical [20] and evolutionary [17] literature in the context of multi-objective bilevel optimization, it is far from realism to expect that the follower will cooperate (knowingly or unknowingly) to an extent that she chooses any point from her Pareto-optimal frontier that is most suitable for the leader. This relies on the assumption that the follower is indifferent to the entire set of optimal solutions, and therefore decides to cooperate. The situation was entirely different in the single-objective case, where, in case of multiple optimal solutions, all the solutions offered an equal value to the follower. However, this can not be assumed in the multi-objective case. Solution to the optimistic formulation in multi-objective bilevel optimization leads to the best possible Pareto-optimal frontier that can be achieved by the leader. Similarly, solution to the pessimistic formulation leads to the worst possible Pareto-optimal frontier at the upper level.

If the value function or the choice function of the follower is known to the leader, it provides an information as to what kind of trade-off is preferred by the follower. A knowledge of such a function effectively, casually speaking, reduces the lower level optimization problem into a single-objective optimization task, where the value function may be directly optimized. The leader’s Pareto-optimal frontier for such intermediate positions lies between the optimistic and the pessimistic frontiers. Figure 13.8 shows the optimistic and pessimistic frontiers for a hypothetical multi-objective bilevel problem with two objectives at upper and lower levels. Follower’s frontier corresponding to ${\mathbf {x}}_{u}^{(1)}$, ${\mathbf {x}}_{u}^{(2)}$ and ${\mathbf {x}}_{u}^{(3)}$, and her decisions A _l, B _l and C _l are shown in the insets. The corresponding representations of the follower’s frontier and decisions (A _u, B _u and C _u) in the leader’s space are also shown.

Fig. 13.8

Leader’s Pareto-optimal (PO) frontiers for optimistic and pessimistic positions. Few follower’s Pareto-optimal (PO) frontiers are shown (in insets) along with their representations in the leader’s objective space. Taken from [55]

7.2 Bilevel Evolutionary Multi-Objective Optimization Algorithms

There exists a significant amount of work on single objective bilevel optimization; however, little has been done on bilevel multi-objective optimization primarily because of the computational and decision making complexities that these problems offer. For results on optimality conditions in multi-objective bilevel optimization, the readers may refer to [21, 67]. On the methodology side, Eichfelder [19, 20] solved simple multi-objective bilevel problems using a classical approach. The lower level problems in these studies have been solved using a numerical optimization technique, and the upper level problem is handled using an adaptive exhaustive search method. This makes the solution procedure computationally demanding and non-scalable to large-scale problems. In another study, Shi and Xia [40] used 𝜖-constraint method at both levels of multi-objective bilevel problem to convert the problem into an 𝜖-constraint bilevel problem. The 𝜖-parameter is elicited from the decision maker, and the problem is solved by replacing the lower level constrained optimization problem with its KKT conditions.

One of the first studies, utilizing an evolutionary approach for multi-objective bilevel optimization was by Yin [69]. The study involved multiple objectives at the upper lever, and a single objective at the lower level. The study suggested a nested genetic algorithm, and applied it on a transportation planning and management problem. Multi-objective linear bilevel programming algorithms were suggested elsewhere [7]. Halter and Mostaghim [23] used a PSO based nested strategy to solve a multi-component chemical system. The lower level problem in their application was linear for which they used a specialized linear multi-objective PSO approach. A hybrid bilevel evolutionary multi-objective optimization algorithm coupled with local search was proposed in [17] (For earlier versions, refer [14,15,16, 43]). In the paper, the authors handled non-linear as well as discrete bilevel problems with relatively larger number of variables. The study also provided a suite of test problems for bilevel multi-objective optimization.

There has been some work done on decision making aspects at upper and lower levels. For example, in [42] an optimistic version of multi-objective bilevel optimization, involving interaction with the upper level decision maker, has been solved. The approach leads to the most preferred point at the upper level instead of the entire Pareto-frontier. Since multi-objective bilevel optimization is computationally expensive, such an approach was justified as it led to enormous savings in computational expense. Studies that have considered decision making at the lower level include [49, 52]. In [49], the authors have replaced the lower level with a value function that effectively reduces the lower level problem to single-objective optimization task. In [52], the follower’s value function is known with uncertainty, and the authors propose a strategy to handle such problems. Other work related to bilevel multi-objective optimization can be found in [33, 37,38,39, 71].

7.3 BL-EMO for Decision-Making Uncertainty

In most of the practical applications, a departure from the assumption of an indifferent lower level decision maker is necessary [52]. Instead of giving all decision-making power to the leader, the follower is likely to act according to her own interests and choose the most preferred lower level solution herself. As a result, lower level decision making has a substantial impact on the formulation of multi-objective bilevel optimization problems. First, the lower level problem is not a simple constraint that depends only on lower level objectives. Rather, it is more like a selection function that maps a given upper level decision to a corresponding Pareto-optimal lower level solution that it is most preferred by the follower. Second, while solving the bilevel problem, the upper level decision maker now needs to model the follower’s behavior by anticipating her preferences towards different objectives. The following formulation of the problem is adapted from [52].

Definition 13.7.2

Let ξ ∈ Ξ denote a vector of parameters describing the follower’s preferences. If the upper level decision maker has complete knowledge of the follower’s preferences, the follower’s actions can then be modeled via selection mapping

$$\displaystyle \begin{aligned} \sigma: {\mathbf{x}}_u\times \Xi \to {\mathbf{x}}_l, \quad \sigma({\mathbf{x}}_u,\xi)\in\Psi({\mathbf{x}}_u), \end{aligned} $$

(13.7.8)

where Ψ is the set-valued mapping defined earlier. The resulting bilevel problem can be rewritten as follows:

$$\displaystyle \begin{aligned} \mathop{\mathrm{min}}\limits_{{\mathbf{x}}_u}\quad & F({\mathbf{x}}_u,{\mathbf{x}}_l)=(F_1({\mathbf{x}}_u,{\mathbf{x}}_l),\ldots, F_p({\mathbf{x}}_u,{\mathbf{x}}_l)) \\ \mathop{\mbox{subject}\ \mbox{to}}\quad & {\mathbf{x}}_l=\sigma({\mathbf{x}}_u,\xi) \in \Psi({\mathbf{x}}_u) \\ & G_k({\mathbf{x}}_u,{\mathbf{x}}_l)\leq 0, \quad k=1,\dots,K \end{aligned} $$

△

To model the follower’s behavior, one approach is to consider the classical value function framework [52]. We can assume that the follower’s preferences are characterized by a function $V:\mathbb {R}^q \times \Xi \to \mathbb {R}$ that is parameterized by the preference vector ξ. This allows us to write σ as a selection mapping for a value function optimization problem with x _u and ξ as parameters:

$$\displaystyle \begin{aligned} \sigma({\mathbf{x}}_u,\xi) \in \mathop{\mathrm{argmin}}\limits_{{\mathbf{x}}_l}\{V(f({\mathbf{x}}_u,{\mathbf{x}}_l),\xi) : \ g_j({\mathbf{x}}_u,{\mathbf{x}}_l)\leq 0, \quad j=1,\dots,J\}. \end{aligned} $$

(13.7.9)

When the solution is unique, the above inclusion can be treated as an equality that allows considering σ as a solution mapping for the problem. For most purposes, it is sufficient to assume that V  is a linear form where ξ acts as a stochastic weight vector for the different lower level objectives:

$$\displaystyle \begin{aligned} V(f({\mathbf{x}}_u,{\mathbf{x}}_l),\xi)&=\sum_{i=1}^q f_i({\mathbf{x}}_u,{\mathbf{x}}_l)\xi_i. \end{aligned} $$

(13.7.10)

The use of linear value functions to approximate preferences is generally found to be quite effective and works also in situations where the number of objectives is large.

Usually, we have to assume that the follower’s preferences are uncertain, i.e. $\xi ~\sim \mathcal {D}_{\xi }$, the value function parameterized by ξ is itself a random mapping. To address such problems, the leader can consider the following two-step approach [52]: (1) First, the leader can use her expectation of follower’s preferences to obtain information about the location of the Pareto optimal front by solving the bilevel problem with fixed parameters and value function V . (2) In the second step, the leader can examine the extent of uncertainty by estimating a confidence region around the Pareto optimal frontier corresponding to the expected value function (POF-EVF). Based on the joint evaluation of the expected solutions and the uncertainty observed at different parts of the frontier, the leader can make a better trade-off between her objectives while being aware of the probability of realizing a desired solution. Given the computational complexity of bilevel problems, carrying out these steps requires careful design. One implementation of such algorithm is discussed in detail in [52].

7.3.1 An Example

Consider an example which has two objectives at both the levels and the problem is scalable in terms of lower level variables; see Table 13.4. Choosing m = 14 will result in a 15 variable bilevel problem with 1 upper level variable and 14 lower level variables. Assume the follower’s preferences to follow a linear value function with a bi-variate normal distribution for the weights.

Table 13.4 Two-objective bilevel example problem

For any x _u, the Pareto-optimal solutions of the lower level optimization problem are given by

$$\displaystyle \begin{aligned} \Psi(x_u)=\{ {\mathbf{x}}_l \in \mathbb{R}^m \ | \ x_{l,1}\in [0,x_u], \ x_{l,i}=0 \text{ for } i=2,\dots,m \}. \end{aligned} $$

The best possible frontier at the upper level may be obtained when the lower level decision maker does not have any real decision-making power; see Fig. 13.9.

Fig. 13.9

Upper level pareto-optimal front (without lower level decision making) and few representative lower level pareto-optimal fronts in upper level objective space

Now let us consider the example with a lower level decision-maker, whose preferences are assumed to follow V (f ₁, f ₂) = ξ ₁f ₁ + ξ ₂f ₂. The upper level front corresponding to the expected value function is obtained by solving identifying the Pareto optimal front corresponding to the expected value function (POF-EVF). The outcome is shown in Fig. 13.10, where the follower’s influence on the bilevel solution is shown as shift of the expected frontier away from the leader’s optimal frontier. The extent of decision uncertainty is described using the bold lines around the POF-EVF front. Each line corresponds to the leader’s confidence region C _α(x _u) with α = 0.01 at different x _u. When examining the confidence regions at different parts of the frontier, substantial variations can be observed.

Fig. 13.10

Expected pareto-optimal front at upper level and lower level decision uncertainty

8 Application Studies of EBO

We consider an agri-environmental policy targeting problem for the Raccoon River Watershed, which covers roughly 9400 km² in West-Central Iowa. Agriculture accounts for the majority of land use in the study area, with 75.3% of land in crop land, 16.3% in grassland, 4.4% in forests and just 4% in urban use [26]. The watershed also serves as the main source of drinking water for more than 500,000 people in Central Iowa. However, due to its high concentration of nitrate pollution from intensive fertilizer and livestock manure application, nitrate concentrations routinely exceed Federal limits, with citations dating back to the late 1980s.

Given the above issues, one of the objectives the policy maker faces is to reduce the extent of pollution caused by agricultural activities by controlling the amount of fertilizer used [65]. However, at the same time the policy maker does not intend to hamper agricultural activities to an extent of causing significant economic distress for the farmers.

Consider a producer (follower) i ∈{1, …, I} trying to maximize her profits from agricultural production through N inputs ${\mathbf {x}}^i = \{x^{i}_{1},\ldots ,x^{i}_{N}\}$ and M outputs ${\mathbf {y}}^{i} = \{y^{i}_{1},\ldots , y^{i}_{M}\}$. Out of the N inputs, $x_{N}^{i}$ denotes the nitrogen fertilizer input for each farm. The policy maker must choose the optimal spatial allocation of taxes, τ = {τ ¹, …, τ ^I} for each farm corresponding to the nitrogen fertilizer usage ${\mathbf {x}}_{N}=\{x^{1}_{N}, \ldots , x_{N}^{I}\}$ so as to control the use of fertilizers. Tax vector τ = {τ ¹, …, τ ^I} denotes the tax policy for I producers that is expressed as a multiplier on the total cost of fertilizers. Note that the taxes can be applied as a constant for the entire basin, or they can be spatially targeted at semi-aggregated levels or individually at the farm-level. For generality, in our model we have assumed a different tax policy for each producer. The objectives of the upper level are to jointly maximize environmental benefits, B(x _N)—which consists of the total reduction of non-point source emissions of nitrogen runoff from agricultural land—while also maximizing the total basin’s profit Π(τ, x _N). The optimization problem that the policy maker needs to solve in order to identify a Pareto set of efficient policies is given as follows:

$$\displaystyle \begin{aligned} \underset{\mbox{{${\boldsymbol \tau}$}},\mathbf{x}}{\mathrm{max}}\; \;& F(\mbox{{${\boldsymbol \tau}$}}, \mathbf{x}) =\big(\Pi(\mbox{{${\boldsymbol \tau}$}}, {\mathbf{x}}_{N} ),\,B({\mathbf{x}}_{N})\big) {}\\ \mathrm{s.t.}\; \; & x_{N}^{i} \in \underset{{\mathbf{x}}^{i}}{\mathrm{argmax}} \{ \pi^{i}(\tau^{i},x_{N}^{i}): (\tau^{i},\,{\mathbf{x}}^{i}) \in \Omega^{i} \} \\ & x^{i}_{n}\ge 0,\, \forall \; i \in \{1, \ldots, I\}, \ n \in \{1, \ldots, N\}, \\ & y^{i}_{m}\ge 0,\, \forall \; i \in \{1, \ldots, I\}, \ m \in \{1, \ldots, M\}, \\ & \tau^{i} \ge 1,\, \forall \; i \in \{1, \ldots, I\}, \end{aligned} $$

(13.8.11)

The fertilizer tax, τ, serves as a multiplier on the total cost of fertilizer, so τ ⁱ ≥ 1. The environmental benefit is the negative of pollution and therefore can be written as the negative of the total pollution caused by the producers, i.e. $B({\mathbf {x}}_N)=-\sum _{i=1}^{I}p(x^{i}_N)$. Similarly the total basin profit can be written as the sum total of individual producer’s profit, i.e. $\Pi (\mbox{{${\boldsymbol \tau }$}}, {\mathbf {x}}_{N})=\sum _{i=1}^{I}\pi (\tau ^i,x_N^i)$. The lower level optimization problem for each agricultural producer can be written as:

$$\displaystyle \begin{aligned} \underset{x_{N}^{i}}{\mathrm{max}} & \quad \pi^{i} (\tau^{i},x_N^i) = p^{i}y^{i} - \overset{N-1}{\underset{n=1}{\sum}} w_{n}x_{n}^{i} - \tau^i w_{N} x_{N}^{i}, \\ \mathrm{s.t.} & \quad y^{i} \le P^k(x^{i}), \end{aligned} $$

(13.8.12)

where w and p are the costs and prices of the fertilizer inputs x and crop yields y, respectively. P ⁱ(x ⁱ) denotes the production frontier for producer i. Heterogeneity across producers, due primarily to differences in soil type, may prevent the use of a common production function that would simplify the solution of (13.8.11). Likewise, the environmental benefits of reduced fertilizer use vary across producers, due to location and hydrologic processes within the basin. This also makes the solution of (13.8.11) more complex.

The simulation results [6] considering all 1175 farms in the Raccoon River Watershed are shown in Fig. 13.11. The Pareto-optimal frontiers trading off the environmental footprints and economic benefits are compared among the three algorithms.

Fig. 13.11

The obtained pareto-optimal frontiers from various methods. The lower level reaction set mapping is analytically defined in this problem. We directly supply the lower level optimal solutions in case of single-level optimization algorithm like NSGA-II and SPEA2 and compare the performance. Taken from [6]

9 Conclusions

Bilevel optimization problems are omnipresent in practice. However, these problems are often posed as single-level optimization problems due to the relative ease and availability of single-level optimization algorithms. While this book presents various theoretical and practical aspects of bilevel optimization, this chapter has presented a few viable EAs for solving bilevel problems.

Bilevel problems involve two optimization problems which are nested in nature. Hence, they are computationally expensive to solve to optimality. In this chapter, we have discussed surrogate modeling based approaches for approximating the lower level optimum by a surrogate to speed up the overall computations. Moreover, we have presented multi-objective bilevel algorithms, leading to a number of research and application opportunities. We have also provided a set of systematic, scalable, challenging, single-objective and multi-objective unconstrained and constrained bilevel problems for the bilevel optimization community to develop more efficient algorithms.

Research on bilevel optimization by the evolutionary computation researchers has received a lukewarm interest so far, but hopefully this chapter has provided an overview of some of the existing efforts in the area of evolutionary computation toward solving bilevel optimization problems, so that more efforts are devoted in the near future.

Appendix: Bilevel Test Problems

1.1 Non-scalable Single-Objective Test Problems from Literature

In this section, we provide some of the standard bilevel test problems used in the evolutionary bilevel optimization studies. Most of these test problems involve only a few fixed number of variables at both upper and lower levels. The test problems (TPs) involve a single objective function at each level. Formulation of the problems are provided in Table 13.5.

Table 13.5 Standard test problems TP1–TP8

Table 6 Table 13.5 Continued.

1.2 Scalable Single-Objective Bilevel Test Problems

Sinha-Malo-Deb (SMD) test problems [46] are a set of 14 scalable single-objective bilevel test problems that offer a variety of controllable difficulties to an algorithm. The SMD test problem suite was originally proposed with eight unconstrained and four constrained problems [46], it was later extended with two additional unconstrained test problems (SMD13 and SMD14) in [54]. Both these problems contain a difficult φ-mapping, among other difficulties. The upper and lower level functions follow the following structure to induce difficulties due to convergence, interaction, and function dependence between the two levels. The vectors x _u = x and x _l = y are further divided into two sub-vectors. The φ-mapping is defined by the function f ₁. Formulation of SMD test problems are provided in Table 13.6.

$$\displaystyle \begin{aligned} \begin{array}{l} F(\mathbf{x}, \mathbf{y}) = F_1({\mathbf{x}}^{1}) + F_2({\mathbf{y}}^{1}) + F_3({\mathbf{x}}^{2}, {\mathbf{y}}^{2}), \\ f(\mathbf{x}, \mathbf{y}) = f_1({\mathbf{x}}^{1}, {\mathbf{x}}^{2}) + f_2({\mathbf{y}}^{1}) + f_3({\mathbf{x}}^{2}, {\mathbf{y}}^{2}), \end{array} \end{aligned} $$

(13.10.13)

where, x = (x ¹, x ²) and y = (y ¹, y ²).

Table 13.6 SMD test problems 1–14

Table 8 Table 13.6 Continued.

Table 9 Table 13.6 Continued.

1.3 Bi-objective Bilevel Test Problems

The Deb-Sinha (DS) test suite contains five test problems with two objectives at each level. All problems are scalable with respect to variable dimensions at both levels. Note that x _u = x and x _l = y. The location and shape of respective upper and lower level Pareto-optimal fronts can be found at the original paper [14].

1.3.1 DS 1

Minimize:

$$\displaystyle \begin{aligned} \begin{cases} F_1(\mathbf{x}, \mathbf{y}) = 1 + r - \cos{}(\alpha\pi x_1)) + \sum_{j=2}^{K}(x_j - \frac{j-1}{2})^2 + \tau\sum_{i=2}^{K}(y_i - x_i)^2 - r~\cos\Big(\gamma\frac{pi}{2}\frac{y_1}{x_1}\Big)\\ F_2(\mathbf{x}, \mathbf{y}) = 1 + r - \sin{}(\alpha\pi x_1)) + \sum_{j=2}^{K}(x_j - \frac{j-1}{2})^2 + \tau\sum_{i=2}^{K}(y_i - x_i)^2 - r~\sin\Big(\gamma\frac{pi}{2}\frac{y_1}{x_1}\Big)\\ \end{cases} \end{aligned}$$

subject to:

$$\displaystyle \begin{aligned} \mathbf{y}\in \mathop{\mathrm{argmin}}\limits_{\mathbf{y}} \begin{cases} f_1(\mathbf{x}, \mathbf{y}) = & y_1^2 + \sum_{i=2}^{K}(y_i - x_i)^2 + \sum_{i=2}^{K}10(1 - \cos{}(\frac{\pi}{K}(y_i - x_i))) \\ f_2(\mathbf{x}, \mathbf{y}) = & \sum_{i=1}^{K}(y_i - x_i)^2 + \sum_{i=2}^{K}10|\sin{}(\frac{\pi}{K}(y_i - x_i))| \end{cases} \end{aligned}$$

$$\displaystyle \begin{aligned}y_i \in [-K,K], ~i = 1,\ldots,K, ~x_1 \in [1,4], ~x_j \in [-K,K], ~j=2,\ldots,K.\end{aligned}$$

Recommended parameter setting for this problem, K = 10 (overall 20 variables), r = 0.1, α = 1, γ = 1, τ = 1. This problem results in a convex upper level Pareto-optimal front in which one specific solution from each lower level Pareto-optimal front gets associated with each upper level Pareto-optimal solution.

1.3.2 DS 2

Minimize:

subject to:

$$\displaystyle \begin{aligned} \mathbf{y}\in \mathop{\mathrm{argmin}}\limits_{\mathbf{y}} \begin{cases} f_1(\mathbf{x}, \mathbf{y}) = & y_1^2 + \sum_{i=2}^{K}(y_i - x_i)^2 \\ f_2(\mathbf{x}, \mathbf{y}) = & \sum_{i=1}^{K}i(y_i - x_i)^2 \end{cases} \end{aligned}$$

$$\displaystyle \begin{aligned}y_i \in [-K,K], ~i = 1,\ldots,K, ~x_1 \in [0.001,K], ~x_j \in [-K,K], ~j=2,\ldots,K.\end{aligned}$$

Recommended parameter setting for this problem, K = 10 (overall 20 variables), r = 0.25. Due to the use of periodic terms in v ₁ and v ₂ functions, the upper level Pareto front corresponds to only six discrete values of y ₁ = [0.001, 0.2, 0.4, 0.6, 0.8, 1]. Setting τ = −1 will introduces a conflict between upper and lower level problems. For this problem, a number of contiguous lower level Pareto-optimal solutions are Pareto-optimal at the upper level for each upper level Pareto-optimal variable vector.

1.3.3 DS 3

Minimize:

$$\displaystyle \begin{aligned} \begin{array}{l} \begin{cases} F_1(\mathbf{x}, \mathbf{y}) = x_1 + \sum_{j=3}^{K}(x_j - j/2)^2 + \tau\sum_{i=3}^{K}(y_i-x_i)^2 - R(x_1)\cos\big(4\tan^{-1}(\frac{x_2-y_2}{x_1-y_1})\big),\\ F_2(\mathbf{x}, \mathbf{y}) = x_2 + \sum_{j=3}^{K}(x_j - j/2)^2 + \tau\sum_{i=3}^{K}(y_i-x_i)^2 - R(x_1)\sin\big(4\tan^{-1}(\frac{x_2-y_2}{x_1-y_1})\big),\\ \end{cases} \end{array} \end{aligned}$$

subject to:

$$\displaystyle \begin{aligned} \begin{array}{l} \mathbf{y}\in \mathop{\mathrm{argmin}}\limits_{\mathbf{y}} \begin{cases} f_1(\mathbf{x}, \mathbf{y}) = y_1 + \sum_{i=3}^{K}(y_i - x_i)^2, \\ f_2(\mathbf{x}, \mathbf{y}) = y_2 + \sum_{i=3}^{K}(y_i - x_i)^2,\\ \mathop{\mbox{subject}\ \mbox{to}}: \quad g_1(y) = (y_1 - x_1)^2 + (y_2 - x_2)^2 \leq r^2, \end{cases}\\ G(\mathbf{x}) = x_2 - (1 - x_1^2) \geq 0, \\ y_i \in [-K,K], ~i = 1,\ldots,K, ~x_j \in [0,K], ~j = 1,\ldots,K, ~x_1 \mbox{ is a multiple of } 0.1. \end{array} \end{aligned}$$

In this test problem, the variable x ₁ is considered to be discrete, thereby causing only a few x ₁ values to represent the upper level Pareto front. Recommended parameter setting for this problem: $R(x_1)=0.1+0.15|\sin {}(2\pi (x_1 - 0.1)|$ and use r = 0.2, τ = 1, and K = 10. Like in DS2, in this problem, parts of lower level Pareto-optimal front become upper level Pareto-optimal.

1.3.4 DS 4

Minimize:

$$\displaystyle \begin{aligned} \begin{array}{l} \begin{cases} F_1(\mathbf{x}, \mathbf{y}) = (1 - y_1)(1 + \sum_{j=2}^{K} y_j^2)x_1, \\ F_2(\mathbf{x}, \mathbf{y}) = y_1(1 + \sum_{j=2}^K y_j^2)x_1, \\ \end{cases} \mathop{\mbox{subject}\ \mbox{to}}: \\ \mathbf{y}\in \mathop{\mathrm{argmin}}\limits_{\mathbf{y}} \begin{cases} f_1(\mathbf{x}, \mathbf{y}) = (1 - y_1)(1 + \sum_{j=K+1}^{K+L} y_j^2)x_1, \\ f_2(\mathbf{x}, \mathbf{y}) = y_1(1 + \sum_{j=K+1}^{K+L} y_j^2)x_1, \\ \end{cases}\\ G(\mathbf{x}) = (1-y_1)x_1 + \frac{1}{2} x_1 y_1 - 1 \geq 0, \\ 1 \leq x_1 \leq 2, \quad -1 \leq y_1 \leq 1, \quad -(K + L) \leq y_i \leq (K + L), \ i = 2, \ldots, (K + L). \end{array}\end{aligned}$$

For this problem, there are a total of K + L + 1 variables. The original study recommended K = 5 and L = 4. This problem has a linear upper level Pareto-optimal front in which a single lower level solution from a linear Pareto-optimal front gets associated with the respective upper level variable vector.

1.3.5 DS 5

This problem exactly the same as DS4, except

$$\displaystyle \begin{aligned}G(\mathbf{x}) = (1-y_1)x_1 + \frac{1}{2} x_1 y_1 - 2 + \frac{1}{5}\left[5(1-y_1)x_1+ 0.2\right] \geq 0.\end{aligned}$$

This makes a number of lower level Pareto-optimal solutions to be Pareto-optimal at the upper level for each upper level variable vector.