On the Elliptic Kashiwara–Vergne Lie Algebra

Abstract

We recall the definitions of two independently defined elliptic versions of the Kashiwara–Vergne Lie algebra ${\mathfrak {krv}}$, namely the Lie algebra ${\mathfrak {krv}}^{(1,1)}$ constructed by Alekseev, Kawazumi, Kuno and Naef arising from the study of graded formality isomorphisms associated to topological fundamental groups of surfaces, and the Lie algebra ${\mathfrak {krv}}_{ell}$ defined using mould theoretic techniques arising from multiple zeta theory by Raphael and Schneps, and show that they coincide.

Both authors gratefully acknowledge support from the Simons Center for Geometry and Physics, Stony Brook University, at which some of the research for this paper was performed.

1 Introduction

From its inception in Grothendieck’s Esquisse d’un Programme [9], Grothendieck–Teichmüller theory was intended to study the automorphism groups of the profinite mapping class groups—the fundamental groups of moduli spaces of Riemann surfaces of all genera and any number of marked points—with the goal of discovering new properties of the absolute Galois group $\mathrm{Gal}(\overline{\mathbb {Q}}/{\mathbb {Q}})$. However, due to the ease of study of the genus zero mapping class groups, which are essentially braid groups, the genus zero case garnered most of the attention, starting from the definition of the Grothendieck–Teichmüller group $\widehat{GT}$ by  Drinfel’d [5] and the simultaneous construction by  Ihara of the Grothendieck–Teichmüller Lie algebra ${\mathfrak {grt}}$ [12, 13] in 1991. The extension of the definition to a Grothendieck–Teichmüller group acting on the profinite mapping class groups in all genera was subsequently given in 2000 by  Hatcher,  Lochak,  Schneps and  Nakamura (cf.  [11, 14]). The higher genus profinite Grothendieck–Teichmüller group satisfies the two-level principle articulated by Grothendieck, which states that the subgroup of $\widehat{GT}$ consisting of automorphisms that extend to the genus one mapping class groups with one or two marked points will automatically extend to automorphisms of the higher mapping class groups.

It has proven much more difficult to extend the Lie algebra Grothendieck–Teichmüller construction to higher genus. Indeed, while the genus zero mapping class groups have a natural Lie algebra analog in the form of the braid Lie algebras, there is no good Lie algebra analog of the higher genus mapping class groups. The only possible approach for the moment seems to be to replace the higher genus mapping class groups by their higher genus braid subgroups, which do have good Lie algebra analogs.¹ An early piece of work due to Tsunogai [19] in 2003 computed the relations that must be satisfied by a derivation acting on the genus one 1-strand braid Lie algebra ${\mathfrak {lie}}^{(1,1)}$ (which is free on two generators) to ensure that it extends to a derivation on the genus one 2-strand braid Lie algebra, in analogy with the derivations in ${\mathfrak {grt}}$, shown by Ihara to be exactly those that act on the genus zero 4-strand braid Lie algebra (also a free Lie algebra on two generators) and extend to derivations of the 5-strand braid Lie algebra.

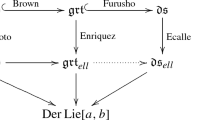
After this, the next real breakthrough in the higher genus Lie algebra situation came with the work of  Enriquez ([7], 2014) based on his previous joint work with  Calaque and Etingof ([4], 2009). In particular, using the same approach as Tsunogai of replacing the higher genus mapping class groups with their higher genus braid subgroups, Enriquez in [7] was able to extend the definition of ${\mathfrak {grt}}$ to an elliptic version ${\mathfrak {grt}}_{ell}$, which he identified with an explicit Lie subalgebra of the algebra of derivations of the algebra of the genus one 1-strand braid Lie algebra ${\mathfrak {lie}}^{(1,1)}$ that extend to derivations of the 2-strand genus one braid Lie algebra. He showed in particular that there is a canonical surjection ${\mathfrak {grt}}_{ell}\rightarrow \!\!\!\!\rightarrow {\mathfrak {grt}}$, and a canonical section of this surjection, $\gamma :{\mathfrak {grt}}\hookrightarrow {\mathfrak {grt}}_{ell}$.

The Grothendieck–Teichmüller Lie algebra is closely related to two other Lie algebras, the double shuffle Lie algebra that arises from the theory of multiple zeta values and the Kashiwara–Vergne Lie algebra that arises from solutions to the (linearized) Kashiwara–Vergne problem. Indeed, there exist injective Lie algebra morphisms

$$ {\mathfrak {grt}}\hookrightarrow {\mathfrak {ds}}\hookrightarrow {\mathfrak {krv}}, $$

by work of Furusho [8] for the first injection,  Écalle and  Schneps [6, 16] for the second and Alekseev and  Torossian [3] for a direct proof that ${\mathfrak {grt}}$ maps into ${\mathfrak {krv}}$. In fact, these three algebras are conjectured to be isomorphic, a conjecture that is supported by computation of the graded parts up to weight about 20. Thus it was a natural consequence of the work of Enriquez to consider the possibility of extending also these other Lie algebras from genus zero to genus one. An answer was proposed for the double shuffle Lie algebra in [18], which proposes a definition of an elliptic double shuffle Lie algebra ${\mathfrak {ds}}_{ell}$ based on mould theory and an elliptic interpretation of a major theorem of Écalle (cf.  [6, 17, 18]). This elliptic double shuffle Lie algebra admits a section $\gamma :{\mathfrak {ds}}\hookrightarrow {\mathfrak {ds}}_{ell}$ which extends Enriquez’s section in the sense that the following diagram commutes;

One interesting aspect of the mould theoretic approach is that it reveals a close relationship between the elliptic double shuffle Lie algebra and the associated graded of the usual double shuffle Lie algebra for the depth filtration. In the article [15], the authors of this paper showed that an analogous approach works to construct an elliptic version of ${\mathfrak {krv}}$, denoted ${\mathfrak {krv}}_{ell}$, which is given by two defining mould theoretic properties, and again has the key features of

• being naturally identified with a Lie subalgebra of the derivation algebra of the free Lie algebra on two generators;

• being equipped with an injective Lie algebra morphism $\gamma :{\mathfrak {krv}}\hookrightarrow {\mathfrak {krv}}_{ell}$ which extends the Grothendieck–Teichmüller and double shuffle sections;

• having a structure closely related to that of the associated graded of ${\mathfrak {krv}}$ for the depth filtration.

In independent work, Alekseev et al.  [1, 2] took a different approach to the construction of higher genus Kashiwara–Vergne Lie algebras ${\mathfrak {krv}}^{(g,n)}$ for all $g,n\ge 1$, following the classical approach to the Kashiwara–Vergne problem which focuses on determining graded formality isomorphisms between prounipotent fundamental groups of surfaces and their graded counterparts (i.e. the exponentials of the associated gradeds of their associated Lie algebras).

More precisely, if $\Sigma$ denotes a compact oriented surface of genus g with $n + 1$ boundary components, the space $g(\Sigma )$ spanned by free homotopy classes of loops in $\Sigma$ carries the structure of a Lie bialgebra equipped with the Goldman bracket and the Turaev cobracket. The Goldman–Turaev formality problem is the construction of a Lie bialgebra homomorphism $\theta$ from $g(\Sigma )$ to its associated graded $\mathrm{gr}\,g(\Sigma )$ such that $\mathrm{gr}\,\theta = \mathrm{id}$. In order to solve this problem, Alekseev et al. defined a family $KV(g, n + 1)$ of Kashiwara–Vergne problems. In the particular situation where $(g,n)=(1,0)$, the surface $\Sigma$ is of genus 1 with one boundary component, and its fundamental group is free on two generators A, B, with the boundary loop being given by $C=(A,B)$. The associated prounipotent fundamental group is then free on two generators $e^a$, $e^b$ with a boundary element $e^c$ satisfying $e^c=(e^a,e^b)=e^ae^be^{-a}e^{-b}$. The associated Lie algebra is free on generators a, b. Since we have $c=\log (e^ae^be^{-a}e^{-b})$, the explicit formula for c in the Lie algebra is

$$ c=CH\Bigl (CH\bigl (CH(a,b),-a\bigr ),-b\Bigr )=[a,b]+\mathrm{higher\ order\ terms}, $$

where CH denotes the Campbell-Hausdorff law on ${\mathfrak {lie}}^{(1,1)}\simeq \mathrm{Lie}[a,b]$. To define the genus one Kashiwara–Vergne Lie algebra ${\mathfrak {krv}}^{(1,1)}$, Alekseev et al. first defined the space of derivations d of $\mathrm{Lie}[a,b]$ that annihilate the element c and further satisfy a certain non-commutative divergence condition (see Sect. 2 for more detail), and then took ${\mathfrak {krv}}^{(1,1)}$ to be the associated graded of the above space. In fact this essentially comes down to using the same defining conditions but replacing c by its lowest graded component [a, b]. They showed that the resulting space is a Lie algebra under the bracket of derivations, and also that, like ${\mathfrak {krv}}_{ell}$, it is equipped with an injective Lie algebra morphism ${\mathfrak {krv}}\hookrightarrow {\mathfrak {krv}}^{(1,1)}$ that extends the Enriquez section $\gamma :{\mathfrak {grt}}\hookrightarrow {\mathfrak {grt}}_{ell}$.

The main result of this article is the equivalence of these two definitions of the elliptic Kashiwara–Vergne Lie algebra.

Main Theorem

There is a canonical isomorphism ${\mathfrak {krv}}^{(1,1)}\simeq {\mathfrak {krv}}_{ell}.$

It is an easy consequence of known results that the first defining property of ${\mathfrak {krv}}_{ell}$ corresponds to the annihilation of [a, b]. The proof of the theorem thus consists essentially in comparing the second defining properties of the two algebras. The article is organised as follows. In Sect. 2, we recall the definition of ${\mathfrak {krv}}^{(1,1)}$, in particular the divergence property, and in Sect. 3, we give a new reformulation of the divergence property. In Sect. 4 we recall the definition of ${\mathfrak {krv}}_{ell}$ and show that translating its second mould theoretic defining property back to a property of derivations on ${\mathfrak {lie}}^{(1,1)}$, it coincides with the reformulated version of the divergence property of ${\mathfrak {krv}}^{(1,1)}$ given in Sect. 3, which completes the proof.

2 The Elliptic Kashiwara–Vergne Lie Algebra from [AKKN]

Let ${\mathfrak {lie}}^{(1,1)}$ be the free Lie algebra on two generators $\mathrm{Lie}[a,b]$, to be thought of as the Lie algebra associated to the fundamental group of the once-punctured torus. Let ${\mathfrak {lie}}_n^{(1,1)}$ denote the weight n part of ${\mathfrak {lie}}^{(1,1)}$, where the weight is the total degree in a and b, and let ${\mathfrak {lie}}_{n,r}^{(1,1)}$ denote the weight n, depth r part of ${\mathfrak {lie}}^{(1,1)}$, where the depth is the b-degree. From this point on, we use the notation $c:=[a,b]$ in ${\mathfrak {lie}}^{(1,1)}$ (this comes down to replacing the previous c by its minimal weight part in the associated graded).

Let ${\mathfrak {der}}^{(1,1)}$ denote the Lie subalgebra of $\mathrm{Der}\,{\mathfrak {lie}}^{(1,1)}$ of derivations d such that $d(c)=0$. Let ${\mathfrak {der}}_n^{(1,1)}$ denote the subspace of ${\mathfrak {der}}^{(1,1)}$ of derivations d such that $d(a),d(b)\in {\mathfrak {lie}}_n^{(1,1)}$.

We define the push-operator on ${\mathfrak {lie}}^{(1,1)}$ as follows. We can write any monomial in the form $a^{i_0}b\cdots ba^{i_r}$, where the $i_j\ge 0$. The push-operator acts on monomials by

$$\begin{aligned} push(a^{i_0}ba^{i_1}b\cdots ba^{i_r})=a^{i_r}ba^{i_0}b\cdots ba^{i_{r-1}}, \end{aligned}$$

(1)

i.e. by cyclically permuting the powers of a between the b’s. The operator extends to polynomials by linearity. We say that an element $f\in {\mathfrak {lie}}^{(1,1)}$ is push-invariant if $push(f)=f$.

Let $f\in {\mathfrak {lie}}_n^{(1,1)}$ for $n>1$. It is shown in Theorem 21 of [16] that there exists an element $g\in {\mathfrak {lie}}_n^{(1,1)}$ satisfying $[a,g]+[b,f]=0$ if and only if f is push-invariant, and if this is the case then g is unique. This condition is equivalent to the existence of a g such that the derivation determined by $a\mapsto f$, $b\mapsto -g$ annihilates the bracket [a, b]. Thus, f is the value on a of a derivation $d\in {\mathfrak {der}}_n^{(1,1)}$ if and only if f is push-invariant, in which case d(b) is uniquely defined.

Any element $f\in {\mathfrak {lie}}^{(1,1)}$ can be decomposed uniquely as

$$\begin{aligned} f=f_aa+f_bb=af^a+bf^b=af^a_aa+af^a_bb+bf^b_aa+bf^b_bb \end{aligned}$$

(2)

with $f_a,f_b,f^a,f^b,f^a_a,f^a_b,f^b_a,f^b_b\in {\mathbb {Q}}\langle a,b\rangle$. Let $Tr_2$ be the quotient of the free associative algebra ${\mathbb {Q}}\langle a,b\rangle$ (identified with the universal enveloping algebra of ${\mathfrak {lie}}^{(1,1)}\simeq \mathrm{Lie}[a,b]$) by the equivalence relation: two words w and $w'$ are equivalent if one can be obtained from the other by cyclic permutation of the letters. We write $tr:{\mathbb {Q}}\langle a,b\rangle \rightarrow Tr_2$ for this quotient map, called the trace map.

The elliptic divergence map $\textit{div}:{\mathfrak {der}}^{(1,1)}\rightarrow Tr_2$ is defined in [AKKN] by

$$ \textit{div}(u)=tr(f_a+g_b) $$

where $d\in {\mathfrak {der}}^{(1,1)}$ satisfies $d(a)=f$ $d(b)=g$. Since $d([a,b])=[a,g]+[f,b]=0$, we have

$$ ag_aa+ag_bb-ag^aa-bg^ba=bf_aa-af^ab-bf^bb+bf_bb. $$

Comparing the terms on both sides that start with a and end with b shows that $g_b=-f^a$. Thus we can write the divergence condition as a function of just f:

$$ \textit{div}(d)=tr(f_a-f^a). $$

In fact, using the decomposition (2), we have

$$ tr(f_a-f^a)=tr(af^a_a+bf^b_a-f^a_aa-f^a_bb)=tr\bigl ((f^b_a-f^a_b)b\bigr ), $$

so

$$ \textit{div}(d)=tr\bigl ((f^b_a-f^a_b)b\bigr ). $$

Definition

The elliptic Kashiwara–Vergne Lie algebra ${{\mathfrak {krv}}}^{(1,1)}$ defined in [AKKN] is the ${\mathbb {Q}}$-vector space spanned by the derivations $d\in {\mathfrak {der}}_n^{(1,1)}$, $n\ge 3$ having the property that there exists $K\in {\mathbb {Q}}$ such that

$$\begin{aligned} \textit{div}(d)= {\left\{ \begin{array}{ll}K\,tr\bigl ([a,b]^{{n-1}\over {2}}\bigr ) &{}\mathrm{if}\, n\, \mathrm{is~odd}\\ 0&{}\mathrm{if}\, n\, \mathrm{is~even}. \end{array}\right. } \end{aligned}$$

(3)

It is closed under the bracket of derivations.

3 A Reformulation of the $\textit{div}$ Condition

The $\textit{div}$ condition is related in a natural way to the push-operator defined in (1). For any word w, let C(w) denote its trace class in $Tr_2$, i.e. the set of words obtained from w by cyclically permuting its letters. We also write $C^b(w)$ (resp. $C_b(w)$) for the subset of C(w) of words starting (resp. ending) with b. For any word $u=a^{i_0}b\cdots ba^{i_{r-1}}$ of depth $r-1$, set

$$P(u)=\{push^i(u)\,\bigl |\,0\le i\le r-1\}.$$

Note that we have $C_b(ub)=\{push^i(u)b\,\bigl |\,0\le i\le r-1\}$, i.e. $C_b(ub)=P(u)\cdot b$, and $|P(u)|=|C_b(ub)|$. The fact that |P(u)| can be less than r is due to the possible symmetries in the word u with respect to the push-operator. For example, if $u=abbab$, we have $r=4$ but $P(u)=\{abbab,babba\}$, $C_b(ub)=\{abbabb,babbab\}$.

Set

$$ pushsym(u)=\sum _{v\in P(u)} w. $$

We extend the operator pushsym to all of ${\mathbb {Q}}\langle a,b\rangle$ by linearity.

Let (f|w) denote the coefficient of a word w in the polynomial f. We also write $\bigl (tr(f)|C(w)\bigr )$ for the coefficient of the trace class C(w) in $tr(f)\in Tr_2$.

Let $f\in {\mathbb {Q}}\langle a,b\rangle$.  Then for any word u in a, b, setting $w=ub$, we have the equality

(4)

Since $w=ub$, we have $C(w)=C(ub)=C(bu)$. Indeed, the first equality holds because since the polynomial $(f^b_a-f^a_b)b$ ends in b, we only need to consider the coefficients of words in C(w) ending in b; the second holds because the subset of words in $C(w)=C(ub)$ ending in b is equal to $C_b(ub)$, and the third holds because $C_b(ub)=P(u)\cdot b$ as noted above.

Equation (4) allows us to rewrite the divergence condition (3) on an element $f\in {\mathfrak {lie}}_n^{(1,1)}$ as the following condition: there exists $K\in {\mathbb {Q}}$ such that for every word u of weight $n-2$ and depth $r-1$, we have

(5)

This is the version of the divergence condition that we will use for comparison with the Lie algebra ${\mathfrak {krv}}_{ell}$.

4 The Mould Theoretic ${\mathfrak {krv}}_{ell}$ from [15]

Recall that a mould is a family $A=(A_r)_{r\ge 0}$ where $A_r(u_1,\ldots ,u_r)$ is a function of r commutative variables. We restrict our attention here to rational-function moulds with coefficients in ${\mathbb {Q}}$. These form a ${\mathbb {Q}}$-vector space under componentwise addition and multiplication by scalars. When the number of variables is specified, we drop the subscript r, for instance we write $A(u_1,\ldots ,u_r)=A_r(u_1,\ldots ,u_r)$.

A mould is said to be alternal if $A(\emptyset )=0$ and

$$ \sum _{w\in sh\bigl ((u_1,\ldots ,u_k),(u_{k+1},\ldots ,u_r)\bigr )} A_r(w)=0 $$

for $r\ge 2$ and $1\le k\le r-1$.

Let us define a few mould operators. The swap, push, circ and $\Delta$-operators on moulds are given by

$$\begin{aligned} swap(A)(v_1,\ldots ,v_r)&=A(v_r,v_{r-1}-v_r,\ldots ,v_1-v_2)\\ push(A)(u_1,\ldots ,u_r)&=A(u_2,\ldots ,u_r,-u_1-\cdots -u_r)\\ circ(A)(v_1,\ldots ,v_r)&=A(v_r,v_1,\ldots ,v_{r-1})\\ \Delta (A)(u_1,\ldots ,u_r)&=(u_1+\cdots +u_r)u_1\cdots u_r\, A(u_1,\ldots ,u_r). \end{aligned}$$

There is no difference between the use of the commutative variables $u_i$ or $v_i$, however the $v_i$’s are traditionally used for operators and relations concerning the swap of a mould.

There is a direct connection between power series in a, b (having no constant term in a) and polynomial-valued moulds. Let $c_i=ad(a)^{i-1}(b)$ for $i\ge 1$, and consider Lie algebra $Lie[c_1,c_2,\ldots ]$ inside the polynomial algebra ${\mathbb {Q}}\langle c_1,c_2,\ldots \rangle$. By Lazard elimination, these algebras are free and all polynomials in ${\mathfrak {lie}}^{(1,1)}$ having no linear term in a can be written as Lie polynomials in the $c_i$.

There is a bijection between the space of polynomials in the $c_i$ and the space of polynomial-valued moulds, coming from linearly extending the map

$$\begin{aligned} c_{a_1}\cdots c_{a_r}\rightarrow (-1)^{n+r}u_1^{a_1-1}\cdots u_r^{a_r-1}, \end{aligned}$$

(6)

where $n=a_1+\cdots +a_r$. It is well-known that under this map, the subspace $\mathrm{Lie}[c_1,c_2,\ldots ]$ of ${\mathfrak {lie}}^{(1,1)}$, which consists of all Lie polynomials having no linear term in a, maps bijectively onto the space of alternal polynomial-valued moulds. In other words, when speaking of polynomial moulds, alternality corresponds precisely to the condition that the associated polynomial in a, b should be primitive for the standard coproduct $\Delta (a)=a\otimes 1+1\otimes a$ $\Delta (b)=b\otimes 1+1\otimes b$, i.e. should be a Lie polynomial.

Writing $f\in {\mathfrak {lie}}_m^{(1,1)}$ as

$$f=\sum _{\underline{k}} c_{\underline{k}}\,a^{k_0}b\cdots ba^{k_r}$$

and F for the corresponding mould, then swap(F) is explicitly given by

$$\begin{aligned} swap(F)(v_1,\ldots ,v_r)=(-1)^{m-1}\sum _{\underline{k}\ \mathrm{s.t.}\ k_r=0} c_{\underline{k}}\,v_1^{k_0}\cdots v_r^{k_{r-1}} \end{aligned}$$

(7)

(cf. [[17], §3]).

A mould A is said to be push-invariant if $push(A)=A$, and circ-neutral if for all $r\ge 2$, we have

$$ \sum _{i=0}^{r-1} circ^i(A)(v_1,\ldots ,v_r)=0. $$

We say that A is circ$^*$-neutral if it is becomes circ-neutral after adding on a constant-valued mould.

Definition

The mould version of ${\mathfrak {krv}}_{ell}$ consists of all polynomial-valued moulds F that are alternal and push-invariant and such that $swap\bigl (\Delta ^{-1}(F)\bigr )$ is circ$^*$-neutral.

The space ${\mathfrak {krv}}_{ell}$ is bigraded for the depth and the degree. Let $F\in {\mathfrak {krv}}_{ell}$ be a mould of depth r and degree d, so that it corresponds under the bijection (6) to a polynomial $f\in {\mathfrak {lie}}_{n,r}^{(1,1)}$ with $n=d+r$. The mould push-invariance property of a polynomial-valued mould F is equivalent to the polynomial push-invariance $push(f)=f$ (cf. [[15], Prop. 12]). In turn, the polynomial push-invariance of f implies that there exists a unique polynomial $g\in {\mathfrak {lie}}_{n,r+1}^{(1,1)}$ such that setting $d(a)=f$, $d(b)=g$, we obtain a derivation $d\in {\mathfrak {der}}_n^{(1,1)}$. The Lie bracket on ${\mathfrak {krv}}_{ell}$ corresponds to the Lie bracket on ${\mathfrak {krv}}^{(1,1)}$, namely bracketing of the derivations d. Thus, in order to prove that ${\mathfrak {krv}}_{ell}$ is in bijection with ${\mathfrak {krv}}^{(1,1)}$, it remains only to prove that the circ$^*$-neutrality condition on $swap\bigl (\Delta ^{-1}(F)\bigr )$ is equivalent to the divergence condition (5) on f.

Since

$$\Delta ^{-1}(F)(u_1,\ldots ,u_r)={{1}\over {(u_1+\cdots +u_r)u_1\cdots u_r}} F(u_1,\ldots ,u_r),$$

we have

$$swap\bigl (\Delta ^{-1}(F)\bigr )(v_1,\ldots ,v_r)={{1}\over {v_1(v_1-v_2)\cdots (v_{r-1}-v_r)v_r}}swap(F)(v_1,\ldots ,v_r),$$

so the circ$^*$-neutrality condition is given explicitly as the existence of a constant $K\in {\mathbb {Q}}$ such that

$$\begin{aligned}&\dfrac{{swap(F)(v_1,\dots ,v_r)}}{{v_1(v_1-v_2)\cdots (v_{r-1}-v_r)v_r}} + \dfrac{{swap(F)(v_2,\dots ,v_1)}}{{v_2(v_2-v_3)\cdots (v_r-v_1)v_1}}+\cdots +\nonumber \\&+\dfrac{{swap(F)(v_r,\dots ,v_{r-1})}}{{v_r(v_r-v_1)\cdots (v_{r-2}-v_{r-1})v_{r-1}}} = {\left\{ \begin{array}{ll} 0&{}n\ne 2r+1\\ (-1)^rKr&{}n=2r+1. \end{array}\right. } \end{aligned}$$

(8)

Indeed, we note that the only possibility for the sum to be equal to a constant is when the degrees of the numerator and denominator are equal, which can only happen when the degree $n-r$ of the mould $F=ma(f)$ in depth r is equal to the degree $r+1$ of the $\Delta$-denominator in depth r, i.e. when $n=2r+1$. We write $(-1)^rKr$ for the constant rather than simply K, in order for the value of K in this formula to correspond to the value in the definition of the divergence condition given in (5) when we prove that the two conditions are equal.

Putting the left-hand side of (8) over a common denominator and multiplying both sides by that denominator gives the equivalent equality

$$ swap(F)(v_1,v_2,\dots ,v_r) v_2\dots v_{r-1} (v_r-v_1) +swap(F)(v_2,\ldots ,v_r,v_1)v_3\cdots v_r(v_1-v_2)+\cdots $$

$$ \ \ \ \ \ \ \ \ \ \ \ + swap(F)(v_r,\dots ,v_{r-1}) v_1\dots v_{r-2} (v_{r-1}-v_r) = (-1)^rKr\, v_1\cdots v_r(v_1-v_2)\cdots (v_r -v_1), $$

where $K=0$ unless $n=2r+1$. The left-hand side of this expands to

$$\begin{aligned}&v_2\dots v_{r-1}v_r \,swap(F)(v_1,\dots ,v_r)-v_1v_2\dots v_{r-1}\,swap(F)(v_1,\dots ,v_r) \nonumber \\&\ \ \ +v_1v_3\dots v_r\;swap(F)(v_2,\dots ,v_r,v_1) -v_2v_3..v_r \,swap(F)(v_2,..,v_r,v_1)+\cdots \nonumber \\&\ \ \ \ \ \ +v_1\dots v_{r-1}\; swap(F)(v_r,\dots ,v_{r-1}) - v_1\dots v_{r-2}v_r\; swap(F)(v_r,\ldots v_{r-1}). \end{aligned}$$

(9)

Fix a monomial $v_1^{i_1+1}v_2^{i_2+1}\dots v_r^{i_r+1}$. Calculating its coefficient in (9) yields

$$\begin{aligned}&\bigl (swap(F)(v_1,\dots ,v_r) | v_1^{i_1+1}v_2^{i_2}\dots v_r^{i_r}\bigr ) - \bigl (swap(F)(v_1,\dots ,v_r) | v_1^{i_1}v_2^{i_2}\dots v_r^{i_r+1}\bigr ) \\&\ \ \ +\bigl (swap(F)(v_2,\dots ,v_r,v_1) | v_1^{i_1}v_2^{i_2+1}\dots v_r^{i_r}\bigr ) - \bigl (swap(F)(v_2,\dots ,v_r,v_1) | v_1^{i_1+1}v_2^{i_2}\dots v_r^{i_r}\bigr )+\cdots \\&\ \ \ \ \ \ \ +\bigl (swap(F)(v_r,v_1,\dots ,v_{r-1}) | v_1^{i_1}\dots v_r^{i_r+1}\bigr )-\bigl (swap(F)(v_r,v_1,\dots ,v_{r-1}) | v_1^{i_1}\dots v_{r-1}^{i_{r-1}+1} v_r^{i_r}\bigr )\\&=\bigl (swap(F)(v_1,\dots ,v_r) | v_1^{i_1+1}v_2^{i_2}\dots v_r^{i_r}\bigr ) - \bigl (swap(F)(v_1,\dots ,v_r) | v_1^{i_1}v_2^{i_2}\dots v_r^{i_r+1}\bigr ) \\&\ \ \ +\bigl (swap(F)(v_1,\dots ,v_r) | v_1^{i_2+1}v_2^{i_3}\dots v_r^{i_1}\bigr ) - \bigl (swap(F)(v_1,\dots ,v_r) | v_1^{i_2}v_2^{i_3}\dots v_r^{i_1+1}\bigr )+\cdots \\&\ \ \ \ \ \ +\bigl (swap(F)(v_1,\dots ,v_r) | v_1^{i_r+1}\dots v_r^{i_{r-1}}\bigr )- \bigl (swap(F)(v_1,\dots ,v_r) | v_1^{i_r}\dots v_r^{i_{r-1}+1}\bigr ), \end{aligned}$$

where the equality is obtained by bringing every term back to a coefficient of a word in $swap(F)(v_1,\ldots ,v_r)$.

The circ$^*$-neutrality condition on $swap\bigl (\Delta ^{-1}(F)\bigr )$ can thus be expressed by the family of relations for every tuple $(i_1,\ldots ,i_r)$:

$$\begin{aligned}&\bigl (swap(F)(v_1,\dots ,v_r) | v_1^{i_1+1}v_2^{i_2}\dots v_r^{i_r}\bigr ) - \bigl (swap(F)(v_1,\dots ,v_r) | v_1^{i_1}v_2^{i_2}\dots v_r^{i_r+1}\bigr ) \nonumber \\&\ \ \ +\bigl (swap(F)(v_1,\dots ,v_r) | v_1^{i_2+1}v_2^{i_3}\dots v_r^{i_1}\bigr ) - \bigl (swap(F)(v_1,\dots ,v_r) | v_1^{i_2}v_2^{i_3}\dots v_r^{i_1+1}\bigr )+\cdots \nonumber \\&\ \ \ \ \ \ +\bigl (swap(F)(v_1,\dots ,v_r) | v_1^{i_r+1}\dots v_r^{i_{r-1}}\bigr )- \bigl (swap(F)(v_1,\dots ,v_r) | v_1^{i_r}\dots v_r^{i_{r-1}+1}\bigr )\nonumber \\&=(-1)^rKr\,\bigl ((v_1-v_2)\dots (v_r-v_1)\,|\,v_1^{i_1}\dots v_r^{i_r}\bigr )\nonumber \\&=(-1)^rKr\,\bigl ((v_1-v_2)\dots (v_{r-1}-v_r)v_r\,|\,v_1^{i_1}\dots v_r^{i_r}\bigr ) -(-1)^rKr\,\bigl (v_1(v_1-v_2)\dots (v_{r-1}-v_r)\,|\,v_1^{i_1}\dots v_r^{i_r}\bigr )\nonumber \\&=(-1)^rKr\,\bigl ((v_1-v_2)\dots (v_{r-1}-v_r)v_r\,|\,v_1^{i_1}\dots v_r^{i_r}\bigr ) +Kr\,\bigl ((v_1-v_2)\dots (v_{r-1}-v_r)v_r\,|\,v_1^{i_r}v_2^{i_{r-1}}\dots v_r^{i_1}\bigr ). \end{aligned}$$

(10)

We now translate this equality back into polynomial terms. We start with the right-hand side. The right-hand side is zero unless $n=2r+1$, so let us compute it in the case $n=2r+1$. We have $[a,b]=ad(a)(b)=c_2$, so $[a,b]^r=c_2^r$, and by formula (6), the polynomial-valued mould corresponding to $[a,b]^r$ is thus given by

$$\begin{aligned} A(u_1,\ldots ,u_r)=(-1)^ru_1\cdots u_r. \end{aligned}$$

(11)

The swap of this mould is given by

$$swap(A)(v_1,\ldots ,v_r)=(-1)^r(v_1-v_2)\cdots (v_{r-1}-v_r)v_r.$$

The moulds A and swap(A) are concentrated in degree r in depth r. Thus the right-hand side of (10) is zero unless $i_1+\cdots +i_r=r$, in which case it can be written as

$$\begin{aligned} Kr\Bigl (swap(A)(v_1,\ldots ,v_r)\,\bigl |\,v_1^{i_1}v_2^{i_2}\cdots v_r^{i_r}\Bigr ) +(-1)^rKr\Bigl (swap(A)(v_1,\ldots ,v_r)\,\bigl |\,v_1^{i_r}v_2^{i_{r-1}}\cdots v_r^{i_1}\Bigr ). \end{aligned}$$

(12)

So by (7), this expression translates back to polynomials as

$$\begin{aligned} -Kr\,\Bigl ([a,b]^r\,|\,a^{i_1}b\cdots a^{i_r}b\Bigr ) +(-1)^{r-1}Kr\,\Bigl ([a,b]^r\,|\,a^{i_r}b\cdots a^{i_1}b\Bigr ), \end{aligned}$$

(13)

since here $m=2r$ is the degree of $[a,b]^r$.

Using (7) to directly translate the left-hand side of (10) in terms of the polynomial f, we thus obtain the following expression equivalent to the circ-neutrality property (10):

$$\begin{aligned}&\bigl (f\,|\,a^{i_1+1}ba^{i_2}b\cdots ba^{i_r}b\bigr )- \bigl (f\,|\,a^{i_1}ba^{i_2}b\cdots ba^{i_r+1}b\bigr ) \nonumber \\&\ \ \ +\bigl (f\,|\,a^{i_2+1}ba^{i_3}b\cdots ba^{i_1}b\bigr )- \bigl (f\,|\,a^{i_2}ba^{i_3}b\cdots ba^{i_1+1}b\bigr )+\cdots \nonumber \\&\ \ \ \ \ \ +\bigl (f\,|\,a^{i_r+1}ba^{i_1}b\cdots ba^{i_{r-1}}b\bigr )- \bigl (f\,|\,a^{i_r}ba^{i_1}b\cdots ba^{i_{r-1}+1}b\bigr )\nonumber \\&=-Kr\,\Bigl ([a,b]^r\,|\,a^{i_1}b\cdots a^{i_r}b\Bigr )- (-1)^rKr\,\Bigl ([a,b]^r\,|\,a^{i_r}b\cdots a^{i_1}b\Bigr ). \end{aligned}$$

(14)

Since f is push-invariant, we have $(f|ub)=(f|bu)$ for every word u, so we can modify the negative terms in (14):

$$\begin{aligned}&\bigl (f\,|\,a^{i_1+1}ba^{i_2}b\cdots ba^{i_r}b\bigr )- \bigl (f\,|\,ba^{i_1}ba^{i_2}b\cdots ba^{i_r+1}\bigr ) \nonumber \\&\ \ \ +\bigl (f\,|\,a^{i_2+1}ba^{i_3}b\cdots ba^{i_1}b\bigr )- \bigl (f\,|\,ba^{i_2}ba^{i_3}b\cdots ba^{i_1+1}\bigr )+\cdots \nonumber \\&\ \ \ \ \ \ +\bigl (f\,|\,a^{i_r+1}ba^{i_1}b\cdots ba^{i_{r-1}}b\bigr )- \bigl (f\,|\,ba^{i_r}ba^{i_1}b\cdots ba^{i_{r-1}+1}\bigr )\nonumber \\&=-Kr\,\Bigl ([a,b]^r\,|\,a^{i_1}b\cdots a^{i_r}b\Bigr )- (-1)^rKr\,\Bigl ([a,b]^r\,|\,a^{i_r}b\cdots a^{i_1}b\Bigr ). \end{aligned}$$

(15)

Now all words in the positive terms start in a and end in b, and all words in the negative terms start in b and end in a, so we can remove these letters and write

$$\begin{aligned}&\bigl (f^a_b\,|\,a^{i_1}ba^{i_2}b\cdots ba^{i_r}\bigr )- \bigl (f^b_a\,|\,a^{i_1}ba^{i_2}b\cdots ba^{i_r}\bigr ) \nonumber \\&\ \ \ +\bigl (f^a_b\,|\,a^{i_2}ba^{i_3}b\cdots ba^{i_1}\bigr )- \bigl (f^b_a\,|\,a^{i_2}ba^{i_3}b\cdots ba^{i_1}\bigr )+\cdots \nonumber \\&\ \ \ \ \ \ +\bigl (f^a_b\,|\,a^{i_r}ba^{i_1}b\cdots ba^{i_{r-1}}\bigr )- \bigl (f^b_a\,|\,a^{i_r}ba^{i_1}b\cdots ba^{i_{r-1}}\bigr )\nonumber \\&=-Kr\,\Bigl ([a,b]^r\,|\,a^{i_1}b\cdots a^{i_r}b\Bigr ) -(-1)^rKr\,\Bigl ([a,b]^r\,|\,a^{i_r}b\cdots a^{i_1}b\Bigr ). \end{aligned}$$

(16)

Consider now a word $u=a^{i_1}ba^{i_2}b\cdots ba^{i_r}$ of degree (weight) $n-2$ and depth $r-1$, and let $u'$ denote u written backwards. Using the previous notation m for the degree of $ub=a^{i_1}b\cdots a^{i_r}b$, we have $n-2=m-1$, i.e. $m=n-1$. The left-hand side of (16) is equal to

$$\sum _{i=0}^{r-1} \Bigl ((f^a_b-f^b_a)\,\bigl |\,push^i(u)\Bigr ) ={{r}\over {|P(u)|}}\Bigl (pushsym(f^a_b-f^b_a)\,\bigl |\,u\Bigr ).$$

Changing the sign of both sides of (16) in order to compare with (5), it becomes

$$\begin{aligned} {{1}\over {|P(u)|}}\Bigl (pushsym(f^b_a-f^a_b)\,\bigl |\,u\Bigr ) ={\left\{ \begin{array}{ll} 0&{}n\ne 2r+1\\ K\,\Bigl ([a,b]^r\,|\,ub\Bigr )+(-1)^rK\,\Bigl ([a,b]^r\,|\,u'b\Bigr ) &{}n=2r+1. \end{array}\right. } \end{aligned}$$

(17)

Since the left-hand sides of (5) and (17) are identical, in order to prove that they give the same condition, we only need to check that the two right-hand sides are equal. Cancelling the factor Kr from each, this reduces to the following lemma.

Lemma

Let u be a word of depth $r-1$ and weight $n=2r-1$, let $u'$ be u written backwards, and let C(ub) denote the set of cyclic permutations of ub. Then

$$\begin{aligned} \sum _{v\in C(ub)} \bigl ([a,b]^r\,|\,v\bigr )= |P(u)|\bigl ([a,b]^r\,|\,ub\bigr ) +(-1)^r|P(u)|\bigl ([a,b]^r\,|\,u'b\bigr ). \end{aligned}$$

(18)

Proof

Observe that if $([a,b]^r|ub)\ne 0$, then ub must satisfy the parity property that, writing $ub=u_1\cdots u_{2r}$ where each $u_i$ is letter a or b, the pair $u_{2i-1}u_{2i}$ must be either ab or ba for $0\le i\le r$. The coefficient of the word ub in $[a,b]^r$ is equal to $(-1)^j$ where j is the number of pairs $u_{2i-1}u_{2i}$ in ub that are equal to ba. In other words, if a word w appears with non-zero coefficient in $[a,b]^r$, then letting $U=ba$ and $V=ab$, we must be able to write w as a word in U, V, and the coefficient of w in $[a,b]^r$ is $(-1)^m$ where m denotes the number of times the letter U occurs.

If $w=ub=V^r=(ab)^r$, then $u'b=ub$. The coefficient of $V^r$ in $[a,b]^r$ is equal to 1, so the right-hand side of (18) is equal to 2 if r is even and 0 if r is odd. For the left-hand side, $C(ub)=\{V^r,U^r\}$ and $C_b(ub)=\{V^r\}$, so $|C_b(ub)|=1$. The coefficient of $U^r$ in $[a,b]^r$ is equal to $(-1)^r$, so the left-hand side is again equal to 2 if r is even and 0 if r is odd. Since $|C_b(ub)|=|P(u)|$, this proves (18) in the case $ub=V^r$.

Suppose now that $ub\ne V^r$ but that it satisfies the parity property. Write $ub=U^{a_1}V^{b_1}\cdots U^{a_s}V^{b_s}$ in which all the $a_i,b_i\ge 1$ except for $a_1$, which may be 0. Then $u'b$ is equal to $aU^{b_s-1}V^{a_s}\cdots U^{b_1}V^{a_1}b$. If $b_s>1$, then the pair $u_{2(b_s-1)+1}u_{2(b_s-1)+2}$ is aa, so $([a,b]^r|u'b)=0$. If $b_s=1$, then the word $u'b$ begins with aa and thus does not have the parity property, so again $([a,b]^r|u'b)=0$. This shows that if $([a,b]^r|ub)\ne 0$ then $([a,b]^r|u'b)=0$ and vice versa.

This leaves us with three possibilities for $ub\ne V^r$.

Case 1: $([a,b]^r|ub)\ne 0$. Then ub has the parity property, so we write $ub=U^{a_1}V^{b_1}\cdots U^{a_s}V^{a_s}$ as above. The right-hand side of (18) is then equal to $(-1)^j$ where $j=a_1+\cdots +a_s$. For the left-hand side, we note that the only words in the cyclic permutation class C(ub) that have the parity property are the cyclic shifts of ub by an even number of letters, otherwise a pair aa or bb necessarily occurs as above. These are the same as the cyclic permutations of the word ub written in the letters U, V. All these cyclic permutations obviously have the same number of occurrences j of the letter U. Thus, the words in C(ub) for which $[a,b]^r$ has a non-zero coefficient are the cyclic permutations of the word ub in the letters U, V, and the coefficient is always equal to $(-1)^j$. These words are exactly half of the all the words in C(ub), so the sum in the left-hand side is equal to $(-1)^j|C(ub)|/2$. But $|C_b(ub)|=|P(u)|=|C(ub)|/2$, so the left-hand side is equal to $(-1)^j$, which proves (18) for words ub having the parity property.

Case 2: $([a,b]^r|u'b)\ne 0$. In this case it is $u'b$ that has the parity property, and the right-hand side of (18) is equal to $(-1)^{r+j'}$ where $j'$ is the number of occurrences of U in the word $u'b=U^{a_1}V^{b_1}\cdots U^{a_s}V^{b_s}$, i.e. $j'=a_1+\cdots +a_s$. We have $ub=aU^{b_s-1}V^{a_s}\cdots U^{b_1}V^{b_1}b$. The word $w=U^{b_s-1}V^{a_s}\cdots U^{b_1}V^{b_1}U$ then occurs in C(ub), and the number of occurrences of the letter U in ub is equal to $j=b_1+\cdots +b_{s-1}+b_s$. Since $a_1+b_1+\cdots +a_s+b_s=r$, we have $j+j'=r$ so $j'=r-j$ and the right-hand side of (18) is equal to $(-1)^j$. The number of words in C(ub) that have non-zero coefficient in $[a,b]^r$ is $|C(ub)|/2=|C_b(ub)|=|P(u)|$ as above, these words being exactly the cyclic permutations of w written in U, V, and the coefficient is always equal to $(-1)^j$. So the left-hand side of (18) is equal to $(-1)^j$, which proves (18) in the case where $u'b$ has the parity property.

Case 3: $([a,b]^r|ub)=([a,b]^r|u'b)=0$. The right-hand side of (18) is zero. For the left-hand side, consider the words in C(ub). If there are no words in C(ub) whose coefficient in $[a,b]^r$ is non-zero, then the left-hand side of (18) is also zero and (18) holds. Suppose instead that there is a word $w\in C(ub)$ whose coefficient in $[a,b]^r$ is non-zero. Then as we saw above, w is a cyclic shift of ub by an odd number of letters, and since all cyclic shifts of w by an even number of letters then have the same coefficient in $[a,b]^r$ as w, we may assume that w is the cyclic shift of ub by one letter, i.e. taking the final b and putting it at the beginning. Since w has non-zero coefficient in $[a,b]^r$, we can write $w=U^{a_1}V^{b_1}\cdots U^{a_s} V^{b_s}$, where $a_1>0$ since w now starts with b, but $b_s$ may be equal to 0 since w may end with a. Then $ub=aU^{a_1-1}V^{b_1}\cdots U^{a_s}V^{b_s}b$, so we can write $u'b=U^{b_s}V^{a_s}\cdots U^{b_1}V^{a_1-1}ab=U^{b_s}V^{a_s} \cdots U^{v_1}V^{a_1}$. But then $u'b$ satisfies the parity property, so its coefficient in $[a,b]^r$ is non-zero, contradicting our assumption. Thus under the assumption, all words in C(ub) have coefficient zero in $[a,b]^r$, which completes the proof of the Lemma. $\diamondsuit$