Seismic Analysis of Pine Flat Concrete Dam

Abstract

Seismic safety of Pine Flat gravity dam is reevaluated by conducting a dam-reservoir-foundation interaction analysis. Contrary to conventional procedures, a foundation with mass is assumed and to avoid unrealistic detrimental effects of wave reflection at truncated boundaries of model, resort is made to non-reflecting boundary conditions. Plane strain 2D model with different element types are prepared. Solid elements are used to model dam and foundation. Compressible fluid elements is utilized in reservoir. Solid and fluid elements are tied (coupled) together on wet interfaces. To simulate elastic wave propagation in a uniform half-space and non-reflecting conditions at boundaries of truncated FE model, infinite elements along with appropriate free-field boundary conditions are incorporated. Efficiency of adopted numerical model is verified by imposing the foundation block to high and low frequency shear traction impulses applied at the base and calculating resulting velocity responses. Loading consists of self-weight, hydrostatic pressure, harmonic nodal force and base excitations due to earthquake records. Since, the FE model is a foundation with mass, thus the deconvolved acceleration records or the equivalent shear traction records are imposed at the base of foundation. Linear and nonlinear material properties are assumed for concrete. Nonlinearity is consistent with concrete damage plasticity model. In compression, uniaxial stress-strain relation as proposed by Saenz and in tension, stress-crack opening displacement relation as suggested by Hordijk are adopted. Analysis works consist of eigenvalue solution, displacement, acceleration and hydrodynamic pressure time histories for a few selected points. In addition, extent of damage suffered in dam when exposed to earthquake records of Taft and Endurance Time Acceleration Function is estimated.

1 Introduction

The intention of the ICOLD 15th Numerical Benchmark Workshop is to perform a seismic analysis of Pine Flat dam. The main scope of workshop is to investigate uncertainties in finite element analysis of concrete dams in a systematic and comparative approach. US Army Corps of Engineers constructed the Pine Flat dam located on King’s River, California in 1954. It is a straight gravity dam consisting of thirty-six monoliths. Dam crest length is about 561 m. Its thickness at base and crest elevations are 95.8 and 9.75 m, respectively. Theme A includes an analysis of the highest non-overflow monolith No. 16 of the dam. The height of monolith is 121.91 m and its width is 15.24 m.

2 Studied Cases

Case studies introduced by Benchmark Formulators are designated as Case A to Case F. In the present study, results of a limited list of Cases are submitted.

Case A includes an eigen value analysis and a simulation of eccentric-mass vibration generator (EMVG) test performed in 1971. Case B investigates foundation size effect and efficiency of adopted non-reflecting and free-field boundary conditions in seismic events. High and low frequency shear impulses are applied at foundation base. Employed numerical model is a rectangular block with a fine mesh.

Case D investigates the effect of reservoir water level in an interaction analysis of dam-reservoir-foundation exposed to Taft earthquake. In Cases A and D, concrete is treated as a linear material.

Case E is again a seismic interaction analysis conducted for both records of Taft and ETAF (Endurance Time Acceleration Function) but with nonlinear behavior of concrete. Numerical models of Cases A, D and E are similar except in reservoir region where separate models are generated for different water levels.

3 Loads

Applied individual loads consist of self-weight, hydrostatic pressure, harmonic nodal force, impulsive shear traction and earthquake induced excitations in form of base shear tractions.

3.1 Self-weight

It is applied only over concrete dam. No gravity effect is considered for reservoir or foundation.

3.2 Hydrostatic Load

It is applied only over wet part of the dam water face. Three reservoir levels are considered corresponding to winter at 268.21, summer at 278.57 and normal condition at 290.0 masl. No hydrostatic pressure is imposed over bottom part of reservoir at interface of rock foundation.

3.3 EMVG Harmonic Force

As is shown in Fig. 1, it is a harmonic nodal force time history applied in the middle of dam crest width and simulates an Eccentric Mass Vibration Generator (EMVG). Sine wave has a duration of 10 s, frequency of 3.47 Hz and an amplitude of 35.4 kN. In 2D plane strain case, the EMVG force is scaled by dividing it to the width (15.24 m) of the monolith No. 16.

Fig. 1

EMVG harmonic force, high and low frequency shear impulses

3.4 Impulsive Shear Tractions

Efficiency of adopted numerical model in simulating non-reflecting boundary conditions is verified by imposing high and low frequency shear traction impulses at the base of foundation. Initially, it is a generated free-surface velocity (pulse) time history (v_x) where its frequency content depends on foundation model depth (H = 122 m), maximum element size (h = 1.5 m) and shear wave velocity (v_s= 1939 m/s).

As is shown in Fig. 1, velocity pulse is then scaled to shear traction by $\tau_{xy} \left( t \right) = \rho v_{s} v_{x} \left( t \right)$ and applied at foundation base in horizontal (X) direction. Both shear impulses have an amplitude of 48.15 kPa and an initial quiet period of 10 points.

3.5 Seismic Excitations

Taft earthquake in form of shear traction is applied as input at the base of foundation. Shear traction is found by multiplying Taft free-surface velocity time history (v_x) by rock foundation density (ρ) and shear wave velocity (v_s). Taft base shear traction (TBST) is shown in Fig. 2.

Fig. 2

Taft base shear traction, ETAF record and response spectra

Endurance Time Acceleration Function (ETAF) is an artificially generated intensifying acceleration record, where its response spectra linearly increase with record duration (RDT). Seismic performance of structure is determined by the extent of time it can endure the dynamic input. The ETAF record and its response spectra is shown in Fig. 2.

4 Material Properties

Linear elastic and isotropic material properties are assumed for concrete and rock. The elastic properties are taken to be homogeneous. Reservoir water is assumed inviscid and irrotational. Linear properties are utilized in Cases A and D. Basic properties are summarized in Table 1.

Table 1 Basic properties

In Case E, concrete in treated as a nonlinear material and its behavior is described by Concrete Damage Plasticity Model (CDPM). In uniaxial compression (σ_c), Eq. (1) defines its stress-strain relation. This relation was proposed by Saenz (1964) [1].

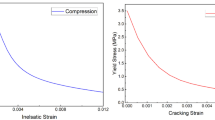
Initial compressive yield stress of concrete is taken equal to $f'_{c0} = 0.45f'_{c}$ as per ACI 350 M-06, clause R8.5.1 [2]. In Fig. 3, variation of (σ_c) beyond initial yield stress $\left( {f'_{c0} } \right)$ is shown. Compressive damage variable (d_c) is defined as a function of inelastic strain (εⁱⁿ) by Eq. (2). The ratio of ε^pl/εⁱⁿ is taken constant [3]. This ratio is found by experimental tests and in compression is assumed equal to b_c= 0.7.

Fig. 3

Uniaxial stress-strain and damage variable in compression

$$ \sigma_{c} = \frac{{E_{c} \varepsilon }}{{1 + \left( {\frac{{E_{c} \varepsilon_{c} }}{{f^{\prime}_{c} }} - 2} \right)\left( {\frac{\varepsilon }{{\varepsilon_{c} }}} \right) + \left( {\frac{\varepsilon }{{\varepsilon_{c} }}} \right)^{2} }} $$

(1)

$$ d_{c} = 1 - \frac{{{{\sigma_{c} } \mathord{\left/ {\vphantom {{\sigma_{c} } {E_{c} }}} \right. \kern-0pt} {E_{c} }}}}{{\varepsilon^{in} \left( {1 - b_{c} } \right) + {{\sigma_{c} } \mathord{\left/ {\vphantom {{\sigma_{c} } {E_{c} }}} \right. \kern-0pt} {E_{c} }}}}, \, b_{c} = \frac{{\varepsilon^{pl} }}{{\varepsilon^{in} }}, \, \varepsilon^{in} = \varepsilon - {{\sigma_{c} } \mathord{\left/ {\vphantom {{\sigma_{c} } {E_{c} }}} \right. \kern-0pt} {E_{c} }} $$

(2)

The stress-strain relation (σ_t) for tensile loading consists of a linear part up to the tensile strength $\left( {f'_{t} } \right)$ and a nonlinearly descending (softening) part that depends on the specimen geometry. In the tensile softening branch, stress is defined as a function of crack opening (w) as is shown in Fig. 4.

Fig. 4

Uniaxial stress-strain and damage variable in tension

This relation is proposed by Hordijk (1992) and is presented by Eq. (3). Critical crack opening (w_cr) is defined as a function of tensile fracture energy (G_F). Tensile damage variable (d_t) is defined as a function of inelastic strain (εⁱⁿ) as given by Eq. (4) but with εⁱⁿ= w/L_t. The average element length (L_t) is fixed to 1.5 m. Again, the ratio of ε^pl/εⁱⁿ is taken constant and in tension is assumed equal to b_t= 0.1.

$$ \begin{aligned} \frac{{\sigma_{t} }}{{f^{\prime}_{t} }} =& \left[ {1 + \left( {c_{1} \frac{w}{{w_{cr} }}} \right)^{3} } \right]e^{{ - c_{2} \frac{w}{{w_{cr} }}}} - \frac{w}{{w_{cr} }}\left( {1 + c_{1}^{3} } \right)e^{{ - c_{2} }} , \, c_{1} = 3.0, \\ & c_{2} = 6.93, \, w_{cr} = 5.14\frac{{G_{F} }}{{f^{\prime}_{t} }} \end{aligned} $$

(3)

$$ d_{t} = 1 - \frac{{{{\sigma_{t} } \mathord{\left/ {\vphantom {{\sigma_{t} } {E_{c} }}} \right. \kern-0pt} {E_{c} }}}}{{\varepsilon^{in} \left( {1 - b_{t} } \right) + {{\sigma_{t} } \mathord{\left/ {\vphantom {{\sigma_{t} } {E_{c} }}} \right. \kern-0pt} {E_{c} }}}}, \, b_{t} = \frac{{\varepsilon^{pl} }}{{\varepsilon^{in} }}, \, \varepsilon^{in} = \frac{w}{{L_{t} }} $$

(4)

This value fits well with experimental results of concrete cyclic tests [3]. It is worth to mention that the crack opening (w) is equal to crack displacement (u_ck) as per ABAQUS designation [4]. In order to avoid numerical ill conditioning, the values of tensile stress (σ_t) is limited to $0.01f'_{t}$.

In Table 2, parameters related to concrete multiaxial loading, i.e., yield surface and plastic potential function that is assumed a Drucker-Prager hyperbolic function are included.

Table 2 Multiaxial loading parameters

5 Numerical Model

First order plane strain solid elements of type CPE4 are used to discretized dam and foundation. To model far-field region, infinite elements of type CINPE4 are utilized.

This type of element is capable of absorbing impinging compression and shear waves (Fig. 5). Nodes along the edge of CINPE4 elements that point in the infinite direction are positioned at about twice as far from dam as nodes on the boundary between finite and infinite elements. Material properties of infinite elements are taken identical to neighboring rock.

Fig. 5

Solid, fluid and infinite elements in FE model

In reservoir, 4-noded acoustic fluid elements of type AC2D4 are employed. Solid and fluid elements are tied together on wet interfaces. Effect of gravity waves was neglected by prescribing zero pressure (p = 0) at reservoir free surface. At reservoir far end, nonreflecting boundaries corresponding to that of normal incidence plane waves are prescribed [4].

6 Free-Field Effects

In order to find Effective Earthquake Forces (EEF) on the lateral vertical boundaries of the model, it is necessary to calculate free-field motions, i.e., displacement ($u_{x}$) and velocity ($\dot{u}_{x}$) responses at each nodal point located along vertical sides of the model [5]. Since, in the present study only a vertically propagating shear S-wave is taken into account, other components of the motion ($u_{y} , \dot{u}_{y}$) are equal to zero. With P-waves in seismic field, both components are involved.

As is shown in Fig. 6, analysis of this system reduces to a single column of the foundation-rock with absorbing infinite elements only at its base. The mesh density of the rock-column is taken identical to main FE model of foundation. For Cases D and E, Taft earthquake record in form of uniform Base Shear Traction (TBST) is applied at the base of rock-column. Prior to imposition of seismic load, displacement of pair of nodes positioned on both sides of rock-column model are constrained (using ABAQUS keyword: *MPC-Multi-point Constraints). Coupling (tying) is defined for both components.

Fig. 6

Rock-column with infinite element at base and tied lateral nodes

Knowing Lamé constants ($\lambda , G$) and mass density (ρ) of rock foundation, the effective earthquake forces ($P^{n}$) applied at nodes (n and n + 1) of an element of length (h) located on vertical side are calculated by Eq. (5):

$$ \begin{aligned} P_{x}^{n} = 0.5\left[ {h\rho c_{p} \dot{u}_{x}^{n} + l_{x} \lambda \left( {u_{y}^{n + 1} - u_{y}^{n} } \right)} \right], \, P_{x}^{n + 1} = 0.5\left[ {h\rho c_{p} \dot{u}_{x}^{n + 1} + l_{x} \lambda \left( {u_{y}^{n + 1} - u_{y}^{n} } \right)} \right] \hfill \\ P_{y}^{n} = 0.5\left[ {h\rho c_{s} \dot{u}_{y}^{n} + l_{x} G\left( {u_{x}^{n + 1} - u_{x}^{n} } \right)} \right], \, P_{y}^{n + 1} = 0.5\left[ {h\rho c_{s} \dot{u}_{y}^{n + 1} + l_{x} G\left( {u_{x}^{n + 1} - u_{x}^{n} } \right)} \right] \hfill \\ G = {{0.5E} \mathord{\left/ {\vphantom {{0.5E} {\left( {1 + \nu } \right)}}} \right. \kern-0pt} {\left( {1 + \nu } \right)}}, \, \lambda = {{2G\nu } \mathord{\left/ {\vphantom {{2G\nu } {(1 - 2\nu }}} \right. \kern-0pt} {(1 - 2\nu }}), \, c_{p} = \sqrt {{{(\lambda + 2G)} \mathord{\left/ {\vphantom {{(\lambda + 2G)} \rho }} \right. \kern-0pt} \rho }} , \, c_{s} = \sqrt {{G \mathord{\left/ {\vphantom {G \rho }} \right. \kern-0pt} \rho }} \hfill \\ \end{aligned} $$

(5)

where ($c_{p}$) designates P-wave and ($c_{s}$) S-wave velocities in foundation domain. For left side boundary, the coefficient ($l_{x} = - 1)$ is taken and on right side ($l_{x} = 1$) [6]. Nodal force calculation must be carried out for both vertical lateral boundaries, separately. With Shear Traction (TBST) imposed at the rock-column base, evidently $u_{y} = \dot{u}_{y} = 0$. Therefore, at each time increment the calculated $P_{x}^{n}$ on both sides are identical and pointing in same direction. The same governs for $P_{y}^{n}$, but forces are in opposite directions. In Fig. 6, time history of resulting forces at node No. 31 (Main model 685) located on free surface (elevation 173.73) is shown.

For verification and check of results, infinite elements are added on vertical sides of the rock-column model and free-field forces are applied within a dynamic step together with TBST loading. Coefficients of Rayleigh damping are taken α = 0.75 s⁻¹ and β = 0.0005 s. Excellent agreement is achieved with Taft free-surface records.

In Case B, resort is made to another method known as tied lateral boundaries [7]. Procedure of tying (constraining) is quite similar to that used in rock-column model. In Case A, considering nature of its loading, no Free-Field Boundary (FFB) effect is deemed necessary to be imposed.

7 Analysis Results

7.1 Cases A-1 and A-2

The eigen value analysis is performed in order to find out the first six natural frequencies and vibration mode shapes of undamped free vibration of the dam-reservoir-foundation system. Two reservoir water levels are considered at 268.21 and 278.57 corresponding to winter and summer, respectively. No infinite elements are included in the FE model. Fully restrained boundary conditions are imposed at foundation base. On sides of foundation model, only horizontal displacement is restrained.

Normalized mode shapes and eigen frequencies are presented in Fig. 7.

Fig. 7

Eigen frequencies and normalized mode shapes

7.2 Cases A-3 and A-4

A harmonic nodal force time history in the upstream-downstream d(5)irection is applied in the middle of dam crest width. It simulates an Eccentric Mass Vibration Generator (EMVG) and is equivalent to actual loading applied during a test performed in 1971. In addition, self-weight of concrete dam and hydrostatic pressure (only) on dam water face are imposed.

Rayleigh viscous damping with coefficients α = 0.75 s⁻¹ and β = 0.0005 s is utilized (refer to Fig. 11). This leads to a damping ratio of 3–2% in frequency range of 2–10 Hz. Integration time increment is taken equal to Δt = 0.005 s. No free-field boundary condition is considered due to nature of loading.

Relative horizontal displacement ($\Delta u_{x}$) results for two specific points (A, C) located on dam upstream face at heel and crest elevations are illustrated in Fig. 8. Position of points is shown in Fig. 11. Acceleration responses ($\ddot{u}_{x}$) are also given. As is evident, shape of imposed harmonic force is quite similar to acceleration time histories at crest point (C).

Fig. 8

Relative displacement/acceleration responses

7.3 Cases B-1 and B-2

This is actually a wave propagation analysis in foundation domain. High and low frequency shear traction impulses are applied at the base. As is shown in Fig. 9, base shear impulses should reproduce the assumed free-surface velocity time history at the top of the model if it provides a good representation of the semi-infinite domain.

Fig. 9

Free-surface velocity pulses

The characteristic frequency ($f_{N}$) of impulses are chosen by $f_{N} = 4Nf_{0}$ with N_high = 2.5, N_low= 0.25 and for shear S-waves $f_{0} = \frac{{v_{s} }}{4H}$. Assuming a quarter-wavelength approximation and shear S-wave velocity in rock v_s = 1939 m/s, the lowest resolving frequency is found $f_{0} = 4$ Hz. Dimensions of model are taken L = 700 by H = 122 m. Element size is confined to 1.5 m. Structural loading and viscous damping effect are excluded.

In Case B to include free-field effect, infinite non-reflecting elements located on left and right sides of the model are excluded. The infinite elements idealize a viscous boundary that could only absorb radiating waves. Instead, free-field boundary conditions are imposed to account for the effective seismic forces on vertical sides of the model. Imposition of free-field boundary conditions has a significant effect on analysis results of the nodes that are located nearby to side boundaries.

Resort is made to an approach known as tied lateral boundaries [7]. In this method, displacement of pair of nodal points positioned on lateral boundaries are constrained together. Coupling (tying) is defined for both displacement components. This leads to identical displacements of pair of nodes. For flat sites and horizontal layers, it provides an exact solution.

In Fig. 10, position of a few specific nodal points and corresponding extreme values of calculated velocities are tabulated. In addition, time history of horizontal velocity ($\dot{u}_{x}$) responses are shown. As is evident, responses of all top points are identical. Same behavior governs at base points. Pulse amplitude at base points are halved. Physical expectation confirms the results.

Fig. 10

Nodal velocity response histories

7.4 Cases D

In Case D, the effect of reservoir water level (RWL) in a dam-reservoir-foundation interaction analysis when exposed to the Taft seismic event is investigated. Reservoir water levels are given in Table 3. A separate numerical model is prepared for each level. Static loading consists of self-weight of concrete dam plus hydrostatic pressure on dam water face. Taft excitation is imposed in form of uniform shear traction (TBST) at the base of foundation (refer to Fig. 2).

Table 3 Summary of results

Effective earthquake forces on the vertical lateral boundaries are calculated and superimposed in dynamic analysis step. These forces are extracted from a single rock-column in free-field condition.

Concrete is treated as a linear material. Rayleigh viscous damping with coefficients α = 0.75 s⁻¹ and β = 0.0005 s is utilized. Integration time increment is taken equal to Δt = 0.01 s. Identical time interval is used for result output. In Fig. 11, position of nodal points (A, C) and corresponding total displacement ($u_{x}$), hydrodynamic pressure (p) and acceleration ($\ddot{u}_{x}$) responses are shown. Extreme values are summarized in Table 3.

Fig. 11

Displacement, acceleration and hydrodynamic pressure responses

Following results are evident:

• 1. Displacement at heel point (A) almost matches free-surface displacement of the Taft record

• 2. Acceleration at heel point (A) nearly fits free-surface acceleration of the Taft record

• 3. Crest displacement is increasing with rising up of reservoir water level

• 4. Calculated acceleration at crest point (C) is about 10 times of heel point (A)

It would be of interest to compare displacement results obtained at Point-A with and without inclusion of effective earthquake forces (EEF). In Fig. 12, the results are summarized. Without EEF, maximum response difference at A and Taft free-surface record is about 33%. Whilst, with EEF included, displacement ($u_{x}$) at heel point (A) almost fits free-surface displacement of the Taft record. Same scenario also governs for $\dot{u}_{x}$ and $\ddot{u}_{x}$ responses. It is worth to remind that, on both graphs of Fig. 12 the initial displacement due to static loading is excluded for proper comparison.

Fig. 12

EEF effects on displacement response (left: included, right: excluded)

7.5 Cases E-1

In Case E-1, a nonlinear dynamic interaction analysis is performed by applying Taft excitation in form of uniform shear traction (TBST) at the base of foundation. Static loading consists of dam self-weight plus hydrostatic pressure on dam water face with RWL at 268.21. Applied effective earthquake forces on the vertical lateral boundaries is taken identical to Case D. Rayleigh viscous damping is same as Case D. Concrete is treated as a nonlinear material and its behavior is described by Concrete Damage Plasticity Model (CDPM). Automatic Time Incrementation (ATI) scheme is used.

Output interval of results is fixed at 0.01 s. Damage Index (DI) at concrete-rock interface is defined as the ratio of the damaged length to the total length of dam base (95.8 m). In Fig. 13, total displacement ($u_{x}$), hydrodynamic pressure (p) and acceleration ($\ddot{u}_{x}$) responses for the nodal points that are positioned on dam heel and crest (A, C) are displayed. For comparison, Taft free-surface displacement record is also added. In addition, stress history for an element at top cracking zone is given. Remarkable outcomes are:

Fig. 13

Displacement, acceleration and hydrodynamic pressure responses

• 1. Displacement at heel point (A) almost matches free-surface displacement of Taft

• 2. Acceleration at heel point (A) nearly fits free-surface acceleration of Taft

• 3. No local failure occurs within dam wall specially near its top narrow neck

• 4. Damage index along dam-foundation interface is found zero with no base failure

• 5. Magnitude of maximum principal stress (p1) is found about 1.72 MPa near dam top at t = 8.10 s.

7.6 Cases E-2

In Case E-2, a nonlinear dynamic interaction analysis is performed by applying record of Endurance Time Acceleration Function (ETAF) at the base of foundation. It is an artificially generated intensifying acceleration record (refer to Fig. 2).

Static loadings, nonlinear properties of concrete, Rayleigh damping and integration scheme are identical to Case E-1. Seismic performance of structure is determined by the extent of time it can endure ETAF dynamic input. The damage index is defined as the ratio of sum of individual areas of local damages to total cross sectional area of dam (5710.86 m²). At each integration time step, elements with overall value of tensile damage variable (D_t) greater than 0.25 are marked as the damaged ones.

In Fig. 14, percentage of damage index, pressure response at node A and relative displacement history of nodes A and C are displayed. A snapshot of in-plane principal stresses at time t = 1.86 s prior to failure is also given. In addition, four snapshots showing evolution of damage in dam wall are included. Time of the first one is at the beginning of damage (t = 1.4 s) and the last one at the end of calculation (t = 1.865 s).

Fig. 14

Failure modes, damage index and displacement/pressure responses

Following comments are relevant:

• 1. Dam fails in tension as the calculated compression damage variable (D_c) is not noticeable

• 2. Local damages start form dam air face and propagates toward water face

• 3. There is a numerically ill-condition with no further convergence at failure time 1.865 s

• 4. Maximum (total) crest displacement at C is found −10.53 cm at time 1.865 s.

8 Conclusions

Seismic safety of Pine Flat gravity dam is reevaluated. A foundation with mass is assumed but with non-reflecting boundaries. To simulate elastic wave propagation in a uniform half-space, infinite elements are placed along foundation base and sides. Free-field effects are included in the model either by constraining pair of nodes on lateral boundaries or by direct calculation of effective seismic forces by rock-column approach.

A 2D plane strain fluid-structure interaction analysis is carried out. Both linear and nonlinear material behaviors are considered for concrete. Nonlinearity is described by concrete damage plasticity model. Elements with tensile damage variable (D_t) greater than 0.25 are marked as the damaged ones. Damage index (DI) is defined as the ratio of sum of local damaged areas to total dam cross sectional area. Notable conclusions are:

• Considering outcomes of wave propagation analysis (Case B), application of infinite elements are justifiable to idealize non-reflecting boundaries. Imposition of free-field boundary conditions by an approach known as nodal constraining (tying) of lateral boundaries leads to exact correspondence with analytical solutions

• Inclusion of free-field effect is essential and computation of effective earthquake forces by general approach of rock-column is straightforward

• With Taft shear traction imposed at the base of foundation (Case E), no local damages are detected not only within dam wall but also at the concrete-rock interface

• Results for ETAF record are different. Local damages initiate near top narrow neck of the dam. Development of cracks starts from air face and extends towards water face. Halt of numerical solution corresponding to dam failure is at time t = 1.865 s

• Results of nonlinear solutions are quite susceptible to input parameters of the material model that describes concrete nonlinear behavior.