Abstract
We consider several macroscopic models, based on systems of conservation laws, for the study of crowd dynamics. All the systems considered here contain nonlocal terms, usually obtained through convolutions with smooth functions, used to reproduce the visual horizon of each individual. We classify the various models according to the physical domain (the whole space \({\mathbb {R}}^N\) or a bounded subset), to the terms affected by the nonlocal operators, and to the number of different populations we aim to describe. For all these systems, we present the basic well posedness and stability results.
Access provided by Autonomous University of Puebla. Download chapter PDF
Similar content being viewed by others
1 Introduction
From a macroscopic point of view, a crowd can be described through a density function ρ, i.e., a time and space dependent quantity measuring the fraction of space occupied by individuals. It is then natural to ground macroscopic crowd dynamics models on Conservation Laws, which are partial differential equations of the form
where Ω, typically a subset of \({\mathbb {R}}^2\), is the domain available to crowd’s movements. A key role is played by the speed law v, a map assigning to each (t, x) ∈ Ω the velocity vector describing the movement of the individual at position x at time t.
Equation (1.1), also known as the continuity equation, is used in a variety of modeling frameworks, ranging from fluid dynamics to vehicular traffic. Specific features of crowd motion are its being not isotropic and the fact that each “particle” moves according to what he/she sees within his/her own visual horizon. These features are present in the speed law: in particular, in the models presented in the sequel, v depends on ρ or on its space gradient ∇xρ through spatial averages, usually obtained through convolutions ρ ∗ η, or ∇x(ρ ∗ η), with an averaging kernel η, i.e., \(\eta \in {\mathbf {C}}^{1} ({\mathbb {R}}^2;{\mathbb {R}}^+)\) and \(\int _{{\mathbb {R}}^2}\eta = 1\). The geometry of the support of η, in particular its diameter, describes the visual horizon of the individuals in the crowd.
Moreover, again differently from fluid particles, individuals in a crowd may well have different destinations, behaviors or reactions. Within the framework provided by (1.1), this variety can be described through the introduction of different populations, replacing (1.1) with a system, say
where members of the same populations, that is, counted within the same density ρ i, have somewhat homogeneous behaviors, for instance, sharing the same destination. Otherwise, when a few single individuals play a leading role in directing the crowd motion, we use equations of the type (1.1) or (1.2) coupled with ordinary differential equations describing the leaders’ movements.
A natural question arising from the results below is the relation between nonlocal and local models, the latter referring to situations where v depends on ρ(x), i.e., on ρ evaluated at a single point x. Since, as is well known, ρ ∗ η → ρ as η → δ, δ being Dirac’s delta, one might expect similar convergence results ensuring the convergence of nonlocal models to local ones as the visual horizon vanishes, see [3]. This question motivated various results yielding negative answers [35,36,37,38] as well as positive results, see [18].
Crowd dynamics is currently described also through other analytic tools: from systems of partial differential equations motivated through fluid dynamics [59], to cellular automata [4], to measure valued partial differential equations [55, 56], to kinetic models [2, 6], to discrete or microscopic models [5, 24, 51]. Also the level of the related works is very diverse, ranging from purely analytic investigations [39], to numerically oriented results [14], to data analysis [54]. For more information on mixed systems and relations among the different descriptions, refer for instance to [7, 8, 43] and to the references therein.
It is worth mentioning also the modeling of crowd dynamics through conservation laws that mimic fluid dynamics, developed, for instance, in [41, 45].
On the other hand, nonlocal conservation laws are currently used also in the modeling of vehicular traffic [9, 21,22,23], in that of supply chains [40, 58], in predator prey dynamics [27], in the modeling of laser beams cutting steel [25, 53] as well as in the modeling of biological pest control [31]. Other strictly analytical investigations on nonlocal conservation or balance laws are, for instance, [42].
Hoping that this work might serve as a reference, all statements are placed in \({\mathbb {R}}^N\) wherever this generality does not require any extra effort.
Throughout, I is a fixed time interval, say I = [0, T] for a positive T, or \(I = {\mathbb {R}}^+\). The notation used for function spaces and differential operators is standard and collected in section “List of Symbols” in Appendix.
The next section is devoted to the analytic results that serve as a basis for the later sections. In Sect. 3 we describe models for one or more populations defined on all of \({\mathbb {R}}^N\), so that the geometric constraints to crowd movements are encoded in the speed law v. The case of Initial Boundary Value Problems (IBVP) is treated in Sect. 5 while mixed systems consisting of coupled ordinary and partial differential equations are deferred to Sect. 6.
2 Stability and Well Posedness in MultiD Conservation Laws
This section provides the basic well posedness and stability results on the Cauchy Problem for a scalar multiD balance law of the type
The definitions and theorems in this section serve both as a tool and as a model for the subjects developed in later sections. Several monographs cover the basic theory of conservation, or balance, laws. We refer, for instance, to [16, 44, 47].
Definition 2.1 ([47, Chapter 1])
Fix an initial datum \(\rho _o \in {{\mathbf {L}}^\infty } ({\mathbb {R}}^N; {\mathbb {R}})\). A function \(\rho \in {{\mathbf {L}}^\infty } \big (I; \rho _o + {{\mathbf {L}}^1}( {\mathbb {R}}^N; {\mathbb {R}})\big )\) is a weak solution to (2.1) if limt→0+ρ(t) = ρ
o in L
1 and for any test function 
Even in the case of a (nonlinear) Riemann Problem [16, Chapter 5] in one space dimension, such as
the above definition does not single out a unique solution, since both the maps
solve (2.2) in the sense of Definition 2.1.
It is the next, classical, definition that under suitable assumptions singles out a unique solution to (2.1) and is used throughout the next sections.
Definition 2.2 ([49, Definition 1], [47, § 2.1])
Fix an initial datum \(\rho _o \in {{\mathbf {L}}^\infty } ({\mathbb {R}}^N; {\mathbb {R}})\). A function \(\rho \in {{\mathbf {L}}^\infty } \big (I; \rho _o + {{\mathbf {L}}^1}( {\mathbb {R}}^N; {\mathbb {R}})\big )\) is a Kružkov solution to (2.1) if limt→0+ρ(t) = ρ
o in L
1 and for any constant \(k \in {\mathbb {R}}\) and for any test function 
Both choices \(k > {\left \|\rho \right \|}_{{{\mathbf {L}}^\infty }(I \times {\mathbb {R}}^N; {\mathbb {R}})}\) and \(k < -{\left \|\rho \right \|}_{{{\mathbf {L}}^\infty }(I \times {\mathbb {R}}^N; {\mathbb {R}})}\) show that a Kružkov solution is also a weak solution.
The results collected below ensure that Definition 2.2 is the correct tool to establish a well posedness theory for the Cauchy Problem (2.1).
2.1 The Linear Case
We consider first the case where f in (2.1) is linear in ρ and F is affine in ρ, i.e.:
In the study of (2.3), the characteristic equation \(\dot x = v (t,x)\) plays a key role. Therefore, with reference to (2.3), introduce the notation
We collect here a few results about the map X above.
Lemma 2.3
Assume that
Then, the map X defined in (2.4) is well defined and, for a.e. t, t o ∈ I, \(x \in {\mathbb {R}}^N\) and \(\delta _o \in {\mathbb {R}}^N\)
The proof relies on classical ordinary differential equations techniques; see for instance [17, § 2.3] and [33, § 5.1].
A careful mixing of [33, Lemma 5.1, Lemma 5.2] and [27, Proposition 2.8], see also [29], yields the following result.
Theorem 2.4
Consider the Cauchy Problem
where v satisfies (2.5) and
Then, for all \(\rho _o \in ({{\mathbf {L}}^1} \cap {{\mathbf {L}}^\infty }) ({\mathbb {R}}^N; {\mathbb {R}})\) , the map
solves (2.6) in the sense of Definition 2.2 (Kružkov solution). Moreover, any solution to (2.6) in the sense of Definition 2.1 (weak solution) coincides with ρ as given by (2.7).
The explicit expression (2.7) allows to prove a variety of estimates, see [27, 29, 33].
2.2 The General Case
The classical work by Kružkov [49] ensures the existence of a solution to (2.1), its uniqueness and its continuous dependence on the initial datum with respect to the L 1 norm.
The stability of solutions with respect to the flow f and source F is more recent. The case of a conservation law, i.e. F = 0, was initially addressed assuming that the flow depends only on the unknown variable, i.e. f = f(ρ). A first result in this direction is in [52], inspired by numerics, and an improvement was then obtained in [15], while the case of systems in one space dimension was solved in [10].
An x dependent flow was then considered in [20] where the necessity of a priori bounds on the total variation in space of the solution is evident.
The stability of the solutions to the general balance law (2.1) with respect to variations in the time and space dependent flow and source was first addressed in [32], with further improvements being provided in [50].
Introduce the following assumptions on (2.1):
-
(H.1)
\(f \in {\mathbf {C}}^{0} (I \times {\mathbb {R}}^N \times {\mathbb {R}}; {\mathbb {R}}^N)\), the derivatives \(\partial _\rho f, \partial _\rho \nabla _x f, \nabla _x^2 f\) exist and are continuous and for all R > 0, \(\partial _\rho f \in {{\mathbf {L}}^\infty } (I \times {\mathbb {R}}^N \times [-R, R]; {\mathbb {R}}^N)\).
\(F \in {\mathbf {C}}^{0} (I \times {\mathbb {R}}^N \times {\mathbb {R}}; {\mathbb {R}})\) and the derivatives ∂ ρF, ∇xF exist and are continuous.
For all R > 0, \((F - \mathop {\mathrm {div}_{\mathrm {x}}} \nolimits f), \, \partial _\rho (F- \mathop {\mathrm {div}_{\mathrm {x}}} \nolimits f) \in {{\mathbf {L}}^\infty } (I \times {\mathbb {R}}^N \times [-R, R]; {\mathbb {R}})\).
-
(H.2)
For all R > 0, \(\partial _\rho \nabla _x f \in {{\mathbf {L}}^\infty } (I \times {\mathbb {R}}^N \times [-R, R]; {\mathbb {R}}^{N \times N})\), \(\partial _\rho F \in {{\mathbf {L}}^\infty } (I \times {\mathbb {R}}^N \times [-R, R]; {\mathbb {R}})\) and \(\int _I \int _{{\mathbb {R}}^N} {\left \|\nabla _x (F - \mathop {\mathrm {div}_{\mathrm {x}}} \nolimits f) (t, x, \cdot )\right \|}_{{{\mathbf {L}}^\infty } ([-R, R]; {\mathbb {R}})} \mathrm{d} {x} \mathrm{d} {t} < + \infty \).
-
(H.3)
For all R > 0, \(\partial _\rho f \in {{\mathbf {L}}^\infty } (I \times {\mathbb {R}}^N \times [-R, R]; {\mathbb {R}}^{N \times N})\), \(\partial _\rho F \in {{\mathbf {L}}^\infty } (I \times {\mathbb {R}}^N \times [-R, R]; {\mathbb {R}})\) and \(\int _I \int _{{\mathbb {R}}^N} {\left \|(F - \mathop {\mathrm {div}_{\mathrm {x}}} \nolimits f) (t, x, \cdot )\right \|}_{{{\mathbf {L}}^\infty } ([-R, R]; {\mathbb {R}})} \mathrm{d} {x} \mathrm{d} {t} < + \infty \).
First, we recall the key well posedness result by Kružkov.
Theorem 2.5 ([49, Theorem 1])
Let f, F satisfy (H.1) and fix \(\rho _o \in {{\mathbf {L}}^\infty } ({\mathbb {R}}^N; {\mathbb {R}})\). Then, the Cauchy Problem (2.1) admits a unique Kružkov solution ρ defined on all I and L 1-continuous in time from the right.
The following total variation estimate is a necessary step towards the stability estimate on the dependence of the solution to (2.1) on flow and source.
Theorem 2.6 ([50, Theorem 2.2])
Let (H.1) and (H.2) hold. Fix an initial datum \(\rho _o \in ({{\mathbf {L}}^1} \cap {{\mathbf {L}}^\infty } \cap \mathbf {BV}) ({\mathbb {R}}^N; {\mathbb {R}})\). Then, the Kružkov solution ρ to (2.1) satisfies \(\rho (t) \in \mathbf {BV} ({\mathbb {R}}^N; {\mathbb {R}})\) for all t ∈ I.
Define
Then, for all t ∈ I, setting \(W_N = \int _0^{\pi /2} (\cos \theta )^N \mathrm{d} \theta \),
Remark that when (2.1) reduces to the usual case \(\partial _t \rho + \mathop {\mathrm {div}_{\mathrm {x}}} \nolimits f (\rho ) = 0\), the above estimate reduces to the well known property that solutions to conservation law have a nonincreasing total variation in space.
Moreover, setting f = 0 and F = F(t, ρ), (2.1) reduces to a Cauchy Problem for an ordinary differential equation and, coherently, the estimate provided by Theorem 2.6 reduces to the standard ODE estimate resulting from the application of Gronwall Lemma.
The continuous dependence of the solutions to (2.1) on time directly follows from Theorem 2.6.
Corollary 2.7 ([50, Corollary 2.4])
Let (H.1) – (H.3) hold. Fix an initial datum \(\rho _o \in ({{\mathbf {L}}^1} \cap {{\mathbf {L}}^\infty } \cap \mathbf {BV}) ({\mathbb {R}}^N; {\mathbb {R}})\). Then, the Kružkov solution ρ to (2.1) satisfies \(\rho \in {\mathbf {C}}^{0}\big (I; \rho _o + {{\mathbf {L}}^1} ({\mathbb {R}}^N; {\mathbb {R}})\big )\) and moreover for any t 1, t 2 ∈ I, with the notation (2.8),
Moreover, under the stronger condition
we have \(\rho \in {\mathbf {C}}^{0,1} \big (I; \rho _o + {{\mathbf {L}}^1} ({\mathbb {R}}^N; {\mathbb {R}})\big )\).
We are now ready to tackle the stability of the solutions to (2.1) with respect to variations in the flow f and in the source F. To this aim, we consider the two Cauchy Problems
Theorem 2.8 ([50, Theorem 2.5])
Let both pairs \((\hat {f}, \hat {F})\) and \((\check {f}, \check {F})\) satisfy (H.1) , \((\hat {f}, \hat {F})\) satisfy (H.2) and \((\hat {f} - \check {f}, \hat {F}-\check {F})\) satisfy (H.3) . Fix initial data \(\hat {\rho }_o\), \(\check {\rho }_o\) in \(({{\mathbf {L}}^1} \cap {{\mathbf {L}}^\infty } \cap \mathbf {BV}) ({\mathbb {R}}^N)\) and call \(\hat {\rho }, \check {\rho }\) the corresponding solutions. Besides the quantities defined in (2.8), introduce also
Then, for any positive r and for any x o in \({\mathbb {R}}^N\), the solutions \(\hat {\rho }\) and \(\check {\rho }\) to (2.9) satisfy:
The above estimate can be easily extended to bound the L 1 distance between solutions over all of \({\mathbb {R}}^N\).
As a side remark, we observe that the recurrent appearance of the term \(F - \mathop {\mathrm {div}_{\mathrm {x}}} \nolimits f\) is to be expected, for it reflects the obvious nonuniqueness of the distinction between flow and source. Indeed, for instance, in the case n = N = 1, the two flow–source pairs
define the same balance law and, clearly, \(\check F - \mathop {\mathrm {div}_{\mathrm {x}}} \nolimits \check f = \hat F - \mathop {\mathrm {div}_{\mathrm {x}}} \nolimits \hat f\).
3 A Single Population in \({\mathbb {R}}^N\)
While moving in a crowd, each individual is affected by what happens within his/her visual horizon. It is then natural to choose the speed law v in the general model (1.1) so that its value at time t and position x depends on the density ρ as a function, not only on the value ρ(t, x) attained by ρ at (t, x). In other words, the term nonlocal means that the flux function may depend in a nonlocal way on the density. More precisely, we consider the Cauchy Problem
where ρ is the crowd density, V is the velocity vector field, and \(\mathcal I\) is a nonlocal operator. A typical choice for the operator \(\mathcal {I}\) is a convolution operator, such as
As soon as η is sufficiently regular, nonnegative and with integral 1, the quantity \(\left (\mathcal {I} \big (\rho (t)\big )\right ) (x)\) above yields a weighted average of the values attained by ρ at time t around x.
Below, we addressed the basic well posedness and stability issues related to (3.1). In doing this, we distinguish two different nonlocalities in V i, namely the one where the speed modulus is given by a nonlocal operator, and that where it is (also) the velocity direction which is a nonlocal operator.
A numerical procedure to integrate (3.1) is detailed in [3].
3.1 A NonLocal Speed Modulus
As a first example of (3.1) we assume that the pedestrians’ trajectories are assigned, but their speed depends on the local average of the crowd density. Hence, we consider a speed law of the form
where \(\mathcal {I} (\rho ) = \rho * \eta \), the convolution kernel η being smooth, nonnegative and with \(\int _{{\mathbb {R}}^N} \eta (x) \mathrm{d} {x} = 1\), so that (ρ(t) ∗ η)(x) results in the local average of the density ρ(t) in \(x + \mathop {\mathrm {spt}}\eta \). The scalar nonnegative function v is nonincreasing, meaning that at higher densities the speed is lower. The unit vector v(x) describes the direction typically followed by the individual at x.
Definition 3.1 ([33, Definition 2.1])
Fix \(\rho _0 \in {{\mathbf {L}}^\infty }({\mathbb {R}}^N;{\mathbb {R}})\). A weak entropy solution to(3.1)–(3.2) on I is a bounded measurable map \(\rho \in {\mathbf {C}}^{0} \big ( I; {{\mathbf {L}}_{loc}^{1}}({\mathbb {R}}^N;{\mathbb {R}}) \big )\) which is a Kružkov solution to
The basic well posedness and stability result for (3.1)–(3.2) is as follows.
Theorem 3.2 ([33, Theorem 2.2 and Proposition 4.1])
Consider the conservation law (3.1) with speed law (3.2). Assume that
-
v \(\in {\mathbf {C}}^{2} ({\mathbb {R}}; {\mathbb {R}})\)
-
\(\mathbf {v}\in ({\mathbf {C}}^{2} \cap {{\mathbf {W}}^{2,1}}) ({\mathbb {R}}^N; {\mathbb {R}}^N)\) with \(\sup _{{\mathbb {R}}^N} {\left \|\mathbf {v} (s)\right \|} \leq 1\),
-
η \(\in {\mathbf {C}}_c^{2} ({\mathbb {R}}^N; {\mathbb {R}}^+)\) is such that \( \mathop {\mathrm {spt}} \eta \subseteq \overline {B (0,1)}\) and \({\left \|\eta \right \|}_{{{\mathbf {L}}^1} ({\mathbb {R}}^N; {\mathbb {R}})} = 1\).
Then, for all α, β > 0 with β > α, there exists a time T(α, β) > 0 such that for all \(\rho _0 \in ({{\mathbf {L}}^1} \cap \mathbf {BV}) ({\mathbb {R}}^N; [0,\alpha ])\), problem (3.1)–(3.2) admits a unique weak entropy solution \(\rho \in {\mathbf {C}}^{0} \big ( [0, T(\alpha ,\beta )]; ({{\mathbf {L}}^1} \cap \mathbf {BV}) ({\mathbb {R}}^N; [0,\beta ] \big )\) in the sense of Definition 3.1. Moreover,
-
1.
\({\left \|\rho (t)\right \|}_{{{\mathbf {L}}^\infty } ({\mathbb {R}}^N; {\mathbb {R}})} \leq \beta \) for all t ∈ [0, T(α, β)] .
-
2.
There exists a function \(L \in {\mathbf {C}}^{0} ({\mathbb {R}}^+;{\mathbb {R}}^+)\) such that for all ρ 0,1, ρ 0,2 in \(({{\mathbf {L}}^1} \cap \mathbf {BV}) ({\mathbb {R}}^N; [0,\alpha ]\), the corresponding solutions satisfy, for all t ∈ [0, T(α, β)],
$$\displaystyle \begin{aligned} {\left\|\rho_1(t) - \rho_2(t)\right\|}_{{{\mathbf{L}}^1} ({\mathbb{R}}^N; {\mathbb{R}})} \leq L(t) \, {\left\|\rho_{0,1} - \rho_{0,2}\right\|}_{{{\mathbf{L}}^1} ({\mathbb{R}}^N; {\mathbb{R}})} \,. \end{aligned}$$ -
3.
There exists a constant \(\mathcal {L} = \mathcal {L}(\beta )\) such that for all \(\rho _0 \in ({{\mathbf {L}}^1} \cap \mathbf {BV}) ({\mathbb {R}}^N; [0,\alpha ])\), the corresponding solution satisfies for all t ∈ [0, T(α, β)]
$$\displaystyle \begin{aligned} \begin{array}{rcl} \mathinner{\mathrm{TV}}\left(\rho(t) \right) &\displaystyle \leq &\displaystyle \left( \mathinner{\mathrm{TV}}(\rho_0) + \mathcal{L} \, t \, {\left\|\rho_0\right\|}_{{{\mathbf{L}}^\infty} ({\mathbb{R}}^N; {\mathbb{R}})} \right) \mathrm{e}^{\mathcal{L} t} \\ {\left\|\rho(t)\right\|}_{{{\mathbf{L}}^\infty} ({\mathbb{R}}^N; {\mathbb{R}})} &\displaystyle \leq &\displaystyle {\left\|\rho_0\right\|}_{{{\mathbf{L}}^\infty} ({\mathbb{R}}^N; {\mathbb{R}})} \; \mathrm{e}^{\mathcal{L} t} \,. \end{array} \end{aligned} $$
The above result can be easily extended to ensure the existence of global in time solutions, see Sect. 4.1 below and [33].
On the basis of Theorem 3.2, a few control problems can be addressed, leading to the corresponding optimality conditions, see [33, § 2.2 and § 2.3].
3.2 A NonLocal Velocity Direction
Now, we consider a single nonlocal conservation law in all of \({\mathbb {R}}^N\), i.e. n = 1, where the unknown ρ = ρ(t, x) is defined for t ≥ 0 and \(x \in \Omega = {\mathbb {R}}^N\). More precisely, we study the following Cauchy problem:
Here the velocity function \(V\left (t, x, \rho , \mathcal I\right )\) in (4.1) is equal to \(v (\rho ) \, \left (\sigma (x) + \mathcal {I} (\rho )\right )\), where the scalar function ρ↦v(ρ) describes the pedestrians’ speed, independently of geometrical considerations, the vector \(\sigma (x) \in {\mathbb {R}}^N\) is the preferred direction of the pedestrian at x, while the nonlocal term \(\mathcal {I}(\rho ) (x)\) describes how the pedestrian at x deviates from the preferred direction, due to the crowd distribution. Roughly speaking, an individual at position \(x \in {\mathbb {R}}^2\) moves at the speed \(v\left (\rho (t,x)\right )\) depending only on the density ρ(t, x). Moreover the individual at position x and time t is assumed to move along the direction \(\sigma (x) + \left ( \mathcal {I} \big ( \rho (t) \big ) \right ) (x)\).
On the functions defining (3.3), we introduce the following hypotheses:
-
(v)
\(v \in {\mathbf {C}}^{2} ({\mathbb {R}}; {\mathbb {R}})\) is nonincreasing, v(0) = V and v(R) = 0 for fixed V, R > 0.
-
(σ)
\(\sigma \in ({\mathbf {C}}^{2} \cap {{\mathbf {W}}^{1,\infty }}) ({\mathbb {R}}^N; {\mathbb {R}}^N)\) is such that \( \mathop {\mathrm {div}_{\mathrm {x}}} \nolimits \sigma \in ({{\mathbf {W}}^{1,1}} \cap {{\mathbf {W}}^{1,\infty }}) ({\mathbb {R}}^N; {\mathbb {R}})\).
-
(I)
\(\mathcal {I} \in {\mathbf {C}}^{0} \big ( {{\mathbf {L}}^1}({\mathbb {R}}^N; [0,R]); {\mathbf {C}}^{2} ({\mathbb {R}}^N; {\mathbb {R}}^N) \big )\) satisfies the following estimates:
-
(I.1)
There exists an increasing \(C_I \in {{\mathbf {L}}_{loc}^{\infty }}({\mathbb {R}}^+; {\mathbb {R}}^+)\) such that, for all \(r \in {{\mathbf {L}}^1}({\mathbb {R}}^N;[0,R])\),
$$\displaystyle \begin{aligned} \begin{array}{rcl} {\left\|\mathcal{I}(r)\right\|}_{{{\mathbf{W}}^{1,\infty}} ({\mathbb{R}}^N; {\mathbb{R}}^N)} &\displaystyle \leq &\displaystyle C_I({\left\|r\right\|}_{{{\mathbf{L}}^1} ({\mathbb{R}}^N; {\mathbb{R}})}) \quad \mbox{ and } \quad \\ {\left\|\mathop{\mathrm{div}_{\mathrm{x}}}\nolimits \mathcal{I}(r)\right\|}_{{{\mathbf{L}}^1}({\mathbb{R}}^N; {\mathbb{R}})} &\displaystyle \leq &\displaystyle C_I({\left\|r\right\|}_{{{\mathbf{L}}^1}({\mathbb{R}}^N; {\mathbb{R}})})\,. \end{array} \end{aligned} $$ -
(I.2)
There exists an increasing \(C_I \in {{\mathbf {L}}_{loc}^{\infty }}({\mathbb {R}}^+; {\mathbb {R}}^+)\) such that, for all \(r \in {{\mathbf {L}}^1}({\mathbb {R}}^N;[0,R])\),
$$\displaystyle \begin{aligned} {\left\|\nabla_x \mathop{\mathrm{div}_{\mathrm{x}}}\nolimits \mathcal{I}(r)\right\|}_{{{\mathbf{L}}^1}({\mathbb{R}}^N; {\mathbb{R}}^N)} \leq C_I({\left\|r\right\|}_{{{\mathbf{L}}^1}({\mathbb{R}}^N; {\mathbb{R}})})\,. \end{aligned}$$ -
(I.3)
There exists a constant K I such that for all \(r_1, r_2\in {{\mathbf {L}}^1}({\mathbb {R}}^N; [0,R])\),
$$\displaystyle \begin{aligned} \begin{array}{rcl} {\left\|\mathcal{I}(r_1) - \mathcal{I}(r_2)\right\|}_{{{\mathbf{L}}^\infty} ({\mathbb{R}}^N; {\mathbb{R}}^N)} &\displaystyle \leq &\displaystyle K_I \cdot {\left\|r_1-r_2\right\|}_{{{\mathbf{L}}^1} ({\mathbb{R}}^N;{\mathbb{R}})} \\ {\left\|\mathcal{I}(r_1) - \mathcal{I}(r_2)\right\|}_{{{\mathbf{L}}^1} ({\mathbb{R}}^N;{\mathbb{R}}^N)} &\displaystyle \leq &\displaystyle K_I \cdot {\left\|r_1-r_2\right\|}_{{{\mathbf{L}}^1} ({\mathbb{R}}^N;{\mathbb{R}})} \\ {\left\|\mathop{\mathrm{div}_{\mathrm{x}}}\nolimits\big(\mathcal{I}(r_1 ) - \mathcal{I}(r_2)\big)\right\|}_{{{\mathbf{L}}^1}({\mathbb{R}}^N;{\mathbb{R}})} &\displaystyle \leq &\displaystyle K_I \cdot {\left\|r_1-r_2\right\|}_{{{\mathbf{L}}^1} ({\mathbb{R}}^N;{\mathbb{R}})}\,. \end{array} \end{aligned} $$
-
(I.1)
Following Definition 2.2, we introduce the notion of solution for (3.3).
Definition 3.3 ([34, Definition 2.1])
Fix a positive T and an initial datum \(\rho _o \in {{\mathbf {L}}^1} ({\mathbb {R}}^N;[0,R])\). A function \(\rho \in {\mathbf {C}}^{0} \big (I; {{\mathbf {L}}^1} ({\mathbb {R}}^N;{\mathbb {R}})\big )\) is a weak entropy solution to(3.3) if it is a Kružkov solution (see Definition 2.2) to the Cauchy problem
Note that Definitions 2.2 and 3.3 imply that for all \(k \in {\mathbb {R}}\) and for all \(\varphi \in {\mathbf {C}}_c^{\infty } (\left ]-\infty ,T \right ] \times {\mathbb {R}}^N; {\mathbb {R}}^+)\),
where \(w(t,x) = \sigma (x) + \left (\mathcal {I} \big ( \rho (t) \big ) \right ) (x)\).
The following existence and uniqueness result for (3.3) holds.
Theorem 3.4 ([34, Theorem 2.1])
Let (v) , (σ), and (I) hold. Fix \(\rho _o \in ({{\mathbf {L}}^1} \cap \mathbf {BV}) ({\mathbb {R}}^N;[0,R])\). Then, there exists a unique weak entropy solution
to (3.3) in the sense of Definition 3.3. Moreover, ρ conserves the L 1 norm, i.e. for a.e. \(t\in {\mathbb {R}}^+\),
and, for a.e. \(t \in {\mathbb {R}}^+\) , satisfies the total variation inequality
where
The proof relies on a careful application of Banach Fixed Point Theorem. Moreover the following theorem contains stability results for (3.3).
Theorem 3.5 ([34, Theorem 2.2])
Let (v) , (σ), and (I) be satisfied by both systems
where q 1(ρ) = ρ v 1(ρ) and q 2(ρ) = ρ v 2(ρ) and \(\rho _{0,1},\rho _{0,2} \in ({{\mathbf {L}}^1} \cap \mathbf {BV}) ({\mathbb {R}}^N;[0,R])\). Then, for a.e. \(t \in {\mathbb {R}}^+\), the two solutions ρ 1 and ρ 2 satisfy
where
and the map \(C \in {\mathbf {C}}^{0} ({\mathbb {R}}^+; {\mathbb {R}}^+)\) vanishes at t = 0 and depends on TV(ρ 0,1), \({\left \|\rho _{0,1}\right \|}_{{{\mathbf {L}}^1}}\), \({\left \|\sigma _1\right \|}_{{{\mathbf {L}}^\infty }}\), \({\left \| \mathop {\mathrm {div}_{\mathrm {x}}} \nolimits \sigma _1\right \|}_{{{\mathbf {W}}^{1,1}}}\), \({\left \|\rho _1 v_1\left (\rho _1\right )\right \|}_{{{\mathbf {W}}^{1,\infty }}}\), \({\left \|\rho _2 v_2\left (\rho _2\right )\right \|}_{{{\mathbf {W}}^{1,\infty }}}\).
Theorems 3.4 and 3.5 allow to consider various realistic situations and control problems, among which we recall the important problem of evacuation of a room in minimum time; see [34, § 4] for more detailed discussions.
4 Several Populations in \({\mathbb {R}}^N\)
In this part we consider a system of conservation laws, i.e. n > 1, in the whole domain \({\mathbb {R}}^N\), where the unknowns ρ i = ρ 1(t, x) are defined for t ≥ 0 and \(x \in \Omega = {\mathbb {R}}^N\).
More precisely, we consider the system
where ρ = (ρ 1, ⋯ , ρ n) is the vector of conserved quantities, \(n \in {\mathbb {N}} \setminus \{0\}\) denotes the number of equations, t > 0 is time, \(x \in {\mathbb {R}}^2\) is the space variable, V = (V 1, ⋯ , V n) is the velocity vector field, and \(\mathcal I = (\mathcal I^1, \cdots , \mathcal I^n)\) is a nonlocal operator, which depends on the whole vector ρ of the densities.
Remarkably, couplings among the different equations in (4.1) motivated by the description of moving crowds allow to prove the well posedness and stability of systems of nonlocal conservation laws in several space dimensions. As is well known, general results of this type for local conservation laws are currently unavailable.
For the description of a numerical procedure to tackle (4.1) we refer to [1].
4.1 A NonLocal Speed Modulus
In this part, we consider system (4.1) where the nonlocal operator acts only on the modulus of the speed, but not on the direction. More precisely, we study the following Cauchy problem:

Here the velocity functions \(V^i(t, x, \rho ^i, \mathcal I^i)\) in (4.1) are given by
where the functions v i(r) describe the pedestrians’ speed of the i-th population, independently of geometrical considerations, the vectors \(\sigma ^i (x) \in {\mathbb {R}}^N\) represent the direction of the pedestrian of the i-th class at x, while \(\mathcal {I}^i(\rho )\) are nonlocal functions of the overall total density. More precisely, we assume that \(\mathcal I^i \colon {{\mathbf {L}}^1} ({\mathbb {R}}^d; {\mathbb {R}}^n) \to {\mathbf {C}}^{0} ({\mathbb {R}}^d; {\mathbb {R}}^n)\) are given by
where η j are suitable mollifiers functions.
Definition 4.1 ([26, Definition 2.1])
Fix a positive T and an initial datum \(\rho _o \in {{\mathbf {L}}^1} ({\mathbb {R}}^N; {\mathbb {R}}^n)\). A function \(\rho \in {\mathbf {C}}^{0} \big (I; {{\mathbf {L}}^1} ({\mathbb {R}}^N;{\mathbb {R}}^n)\big )\) is a weak entropy solution to (4.2) if, for every i ∈{1, ⋯ , n}, the i-th component ρ i is a Kružkov solution (see Definition 2.2) to the Cauchy problem
The following well posedness result holds.
Theorem 4.2 ([26, Theorem 2.2])
Assume that for every i ∈{1, ⋯ , n}
-
1.
\(v^i \in \big ({\mathbf {C}}^{2} \cap {{\mathbf {W}}^{2,\infty }}\big ) ({\mathbb {R}}; {\mathbb {R}})\);
-
2.
\(\sigma ^i \in \big ({\mathbf {C}}^{2} \cap {{\mathbf {W}}^{2,1}}\big ) ({\mathbb {R}}^N; {\mathbb {R}}^N)\) satisfies \({\left \|\sigma ^i(x)\right \|} \leq 1\) for every \(x \in {\mathbb {R}}^N\);
-
3.
\(\eta ^i \in ({\mathbf {C}}^{2} \cap {{\mathbf {W}}^{2,\infty }}) ({\mathbb {R}}^N; [0, 1])\) and \({\left \|\eta ^i\right \|}_{{{\mathbf {L}}^1}\left ({\mathbb {R}}^N; {\mathbb {R}}\right )} = 1\).
Then, there exists a semigroup
such that the following conditions hold.
-
1.
For every initial datum \(\rho _o \in ({{\mathbf {L}}^1} \cap {{\mathbf {L}}^\infty } \cap \mathbf {BV}) ({\mathbb {R}}^N; {\mathbb {R}}^n)\), for every t ≥ 0, the orbit t↦S tρ o is the unique solution to (4.2), in the sense of Definition 4.1. Furthermore, the map t↦S tρ o belongs to \({\mathbf {C}}^{0} \big ({\mathbb {R}}^+; {{\mathbf {L}}^1} ({\mathbb {R}}^N; {\mathbb {R}}^n) \big )\).
-
2.
For every \(\rho _o \in ({{\mathbf {L}}^1} \cap {{\mathbf {L}}^\infty } \cap \mathbf {BV}) ({\mathbb {R}}^N; ({\mathbb {R}}^+)^n)\), we have that (S tρ o)i ≥ 0 for all t > 0 and i ∈{1, ⋯ , n}.
-
3.
There exists a constant \(\mathcal L\) such that, for all \(\rho _o \in ({{\mathbf {L}}^1} \cap {{\mathbf {L}}^\infty } \cap \mathbf {BV}) ({\mathbb {R}}^N; {\mathbb {R}}^n)\) and \(t \in {\mathbb {R}}^+\),
$$\displaystyle \begin{aligned} \mathinner{\mathrm{TV}}\big(S_t (\rho_o)\big) \le \left(\mathinner{\mathrm{TV}} (\rho_o) + \mathcal L \, t \, {\left\|\rho_o\right\|}_{{{\mathbf{L}}^\infty}({\mathbb{R}}^N; {\mathbb{R}}^n)}\right) \mathrm{e}^{\mathcal L t} \end{aligned}$$and
$$\displaystyle \begin{aligned} {\left\|S_t(\rho)\right\|}_{{{\mathbf{L}}^\infty}({\mathbb{R}}^N; {\mathbb{R}}^n)} \le {\left\|\rho_o\right\|}_{{{\mathbf{L}}^\infty}({\mathbb{R}}^N; {\mathbb{R}}^n)}. \end{aligned}$$ -
4.
There exists a function \(\mathcal L \in {\mathbf {C}}^{0}({\mathbb {R}}^+; {\mathbb {R}}^+)\) such that,
$$\displaystyle \begin{aligned} {\left\|S_t (\rho_o^{\prime}) - S_t (\rho_o^{\prime\prime})\right\|}_{{{\mathbf{L}}^1}({\mathbb{R}}^N; {\mathbb{R}}^n)} \le \big(1 + t \, \mathcal L(t)\big) \; {\left\|\rho_o^{\prime} - \rho_o^{\prime\prime}\right\|}_{{{\mathbf{L}}^1}({\mathbb{R}}^N; {\mathbb{R}}^n)} \end{aligned}$$for all \(\rho _o^{\prime }, \rho _o^{\prime \prime } \in ({{\mathbf {L}}^1} \cap {{\mathbf {L}}^\infty } \cap \mathbf {BV}) ({\mathbb {R}}^N; {\mathbb {R}}^n)\) and \(t \in {\mathbb {R}}^+\).
-
5.
If \(\rho _o \in {{\mathbf {W}}^{1,1}} ({\mathbb {R}}^N; {\mathbb {R}}^n)\), then \(S_t(\rho _o) \in {{\mathbf {W}}^{1,1}} ({\mathbb {R}}^N; {\mathbb {R}}^n)\) for all t > 0. Moreover there exists a positive constant C such that, for t > 0,
$$\displaystyle \begin{aligned} {\left\|S_t(\rho)\right\|}_{{{\mathbf{W}}^{1,1}} ({\mathbb{R}}^N; {\mathbb{R}}^n)} \le (1 + C \, t) \, \mathrm{e}^{Ct} \, {\left\|\rho_o\right\|}_{{{\mathbf{W}}^{1,1}} ({\mathbb{R}}^N; {\mathbb{R}}^n)}. \end{aligned}$$ -
6.
If \(\rho _o \in {{\mathbf {W}}^{1,\infty }} ({\mathbb {R}}^N; {\mathbb {R}}^n)\), then \(S_t(\rho _o) \in {{\mathbf {W}}^{1,\infty }} ({\mathbb {R}}^N; {\mathbb {R}}^n)\) for all t > 0. Moreover, there exists a positive constant C such that, for t > 0,
$$\displaystyle \begin{aligned} {\left\|S_t(\rho)\right\|}_{{{\mathbf{W}}^{1,\infty}} ({\mathbb{R}}^N; {\mathbb{R}}^n)} \le (1 + C \, t) \, \mathrm{e}^{Ct} \, {\left\|\rho_o\right\|}_{{{\mathbf{W}}^{1,\infty}} ({\mathbb{R}}^N; {\mathbb{R}}^n)}. \end{aligned}$$ -
7.
If \(v \in {\mathbf {C}}^{4} ({\mathbb {R}}; {\mathbb {R}}^n)\), then, for every initial datum \(\rho _o \in ({{\mathbf {W}}^{2,\infty }} \cap {{\mathbf {W}}^{2,1}}) ({\mathbb {R}}^N; {\mathbb {R}}^n)\), \(\sigma _o \in ({{\mathbf {W}}^{1,1}} \cap {{\mathbf {L}}^\infty }) ({\mathbb {R}}^N; {\mathbb {R}}^n)\) and for all time t > 0, the semigroup S is strongly L 1 Gâteaux differentiable in the direction σ o. The derivative D S t(ρ o)(σ o) of S t at the point ρ o in the direction σ o is \(\Sigma ^{\rho _o}_t(\sigma _o)\), where \(\Sigma ^{\rho _o}\) is the linear semigroup whose orbits are the Kružkov solutions to
$$\displaystyle \begin{aligned} \left\{ \begin{array}{l} \partial_t \sigma^i + \mathop{\mathrm{div}_{\mathrm{x}}}\nolimits \left( \sigma^i \, V^i \big(S_t(\rho_o)\big) + \big(S_t(\rho_o)\big)^i \, DV^i\big(S_t(\rho_o)\big)(\sigma) \right) = 0 \\ \sigma^i(0, x) = \sigma^i_o(x) \,, \end{array} \right. \end{aligned}$$where V i is defined in (4.3).
The Cauchy problem (4.2) is also stable with respect to variations of the functions η i, v i, and σ i. More precisely, consider the Cauchy problems

where
Denote by \(\hat {\rho }\) and \(\check {\rho }\) the respective solutions.
Theorem 4.3 ([26, Theorem 2.2])
Fix a positive constant M. Then, there exists a function \(\mathcal L \in {\mathbf {C}}^{0}({\mathbb {R}}^+; {\mathbb {R}}^+)\) such that
for every initial data \(\hat \rho _o, \check \rho _o \in {{\mathbf {L}}^1}({\mathbb {R}}^N; {\mathbb {R}}^n)\), for every velocity functions \(\hat v, \check v \in ({\mathbf {C}}^{2} \cap {{\mathbf {W}}^{2,\infty }}) ({\mathbb {R}}; {\mathbb {R}}^n)\), for every directions \(\hat \sigma , \check \sigma \in ({\mathbf {C}}^{2} \cap {{\mathbf {W}}^{2,1}}) \big ({\mathbb {R}}^N; {\mathbb {R}}^{Nn}\big )\), and for every mollifier \(\hat \eta , \check \eta \in ({\mathbf {C}}^{2} \cap {{\mathbf {W}}^{2,\infty }}) ({\mathbb {R}}^N; [0, 1]^n)\) with \({\left \|\hat \eta ^i\right \|}_{{{\mathbf {L}}^1}({\mathbb {R}}^N; {\mathbb {R}})} = {\left \|\check \eta ^i\right \|}_{{{\mathbf {L}}^1}({\mathbb {R}}^N; {\mathbb {R}})} = 1\) for i ∈{1, ⋯ , n}.
4.2 A NonLocal Velocity Direction
In this part, we consider system (4.1) where the nonlocal operator influences the geometric direction of the velocity. More precisely, we study the following Cauchy problem:

Here the velocity functions \(V^i(t, x, \rho ^i, \mathcal I^i)\) in (4.1), for \(i \in \left \{1, \cdots , n\right \}\), are given by
More precisely, the velocity V i of the i-th population is the product of a scalar crowding factor v i(ρ i) with a vector \({{\mathbf {v}}^i}(x) + \mathcal {I}^i(\rho ^1, \ldots , \rho ^n)\), which is the sum of a preferred direction v i(x) and a deviation \(\mathcal {I}^i (\rho ^1, \ldots , \rho ^n)\). The scalar v i(ρ i) approximately gives the modulus of the speed. A possible choice for the preferred direction v i is, for instance, the tangent vector at x to the geodesic that the individuals in the i-th population follow to reach their destination, if unaffected by any other individual. Instead, the term \(\mathcal {I}^i(\rho ^1, \ldots , \rho ^n)\) describes how the i-th population deviates from its preferred trajectory due to the interaction among individuals, both of the same and of different populations. It is a nonlocal functional, since its value at any position x depends on the population densities averaged over a neighborhood of x.
Definition 4.4 ([26, Definition 3.1])
Fix a positive T and, for every \(i \in \left \{1, \cdots , n\right \}\), the initial datum \(\rho ^i_{o} \in ({{\mathbf {L}}^1} \cap {{\mathbf {L}}^\infty }) ({\mathbb {R}}^N; {\mathbb {R}}^n)\). A map \(\rho \in {\mathbf {C}}^{0} \left ( [0,T]; {{\mathbf {L}}^1}({\mathbb {R}}^N; {\mathbb {R}}^n) \right )\) is a weak entropy solution to (4.4) if, for i = 1, ⋯ , n, ρ i is a Kružkov solution to the Cauchy problem
where \(V^i(t,x) = {{\mathbf {v}}^i} (x) + \mathcal {I}^i \left ( \rho _1(t), \cdots , \rho _n(t) \right ) (x)\).
The following well posedness result holds.
Theorem 4.5 ([26, Theorem 3.2])
Assume that for every \(i \in \left \{1, \cdots , n\right \}\),
-
1.
\(v^i\in {\mathbf {C}}^{2}({\mathbb {R}}; {\mathbb {R}}^+)\) satisfies v i(R) = 0 for a suitable R > 0;
-
2.
\({{\mathbf {v}}^i}\in ({\mathbf {C}}^{2} \cap {{\mathbf {W}}^{1,\infty }}) ({\mathbb {R}}^N; {\mathbb {R}}^N)\) and \( \mathop {\mathrm {div}_{\mathrm {x}}} \nolimits {{\mathbf {v}}^i} \in {{\mathbf {W}}^{1,1}} ({\mathbb {R}}^N; {\mathbb {R}}^{N\times N})\);
-
3.
there exists a constant C I > 0 such that \(\mathcal {I}^i \colon {{\mathbf {L}}^1}({\mathbb {R}}^N; {\mathbb {R}}^n) \to {\mathbf {C}}^{2} ({\mathbb {R}}^N; {\mathbb {R}}^N)\) satisfies, for every \(\rho , \rho ' \in {{\mathbf {L}}^1}({\mathbb {R}}^N; [0,R]^n)\),
$$\displaystyle \begin{aligned} {\left\|\nabla_x\mathcal{I}^i(\rho)\right\|}_{{{\mathbf{L}}^\infty}({\mathbb{R}}^N; {\mathbb{R}}^N)} & \le C_I \, {\left\|\rho\right\|}_{{{\mathbf{L}}^1}({\mathbb{R}}^N; {\mathbb{R}}^n)} , \\ {\left\|\nabla_x \mathop{\mathrm{div}_{\mathrm{x}}}\nolimits \left(\mathcal{I}^i (\rho)\right)\right\|}_{{{\mathbf{L}}^1}({\mathbb{R}}^N; {\mathbb{R}}^{N\times N})} & \le C_I \, {\left\|\rho\right\|}_{{{\mathbf{L}}^1}({\mathbb{R}}^N; {\mathbb{R}}^n)} , \\ {\left\| \mathcal{I}^i(\rho) - \mathcal{I}^i(\rho')\right\|}_{{{\mathbf{L}}^\infty}({\mathbb{R}}^N; {\mathbb{R}}^N)} & \le C_I \, {\left\|\rho-\rho'\right\|}_{{{\mathbf{L}}^1}({\mathbb{R}}^N; {\mathbb{R}}^n)} , \\ {\left\| \mathop{\mathrm{div}_{\mathrm{x}}}\nolimits \left( \mathcal{I}^i(\rho) - \mathcal{I}^i(\rho') \right)\right\|}_{{{\mathbf{L}}^1}({\mathbb{R}}^N; {\mathbb{R}})} & \le C_I \, {\left\|\rho-\rho'\right\|}_{{{\mathbf{L}}^1}({\mathbb{R}}^N; {\mathbb{R}}^n)} . \end{aligned} $$
Then, there exists a semigroup
such that the following conditions hold.
-
1.
For all \(\rho _o \in ({{\mathbf {L}}^1} \cap \mathbf {BV}) ({\mathbb {R}}^N; [0,R]^n)\), the orbit t↦S tρ o is the unique solution to (4.4) in the sense of Definition 4.4.
-
2.
For all \(\rho _o \in ({{\mathbf {L}}^1} \cap \mathbf {BV}) ({\mathbb {R}}^N; [0,R]^n)\) and t > 0
$$\displaystyle \begin{aligned} \mathinner{\mathrm{TV}} (S_t \rho_o) \leq \mathinner{\mathrm{TV}}(\rho_o) \, \mathrm{e}^{\kappa_o t} + N \, K\, W_N \, \mathrm{e}^{\kappa_o t} \left(C_I + {\left\|\mathop{\mathrm{div}_{\mathrm{x}}}\nolimits \mathbf v\right\|} _{{{\mathbf{L}}^\infty}\left({\mathbb{R}}^N; {\mathbb{R}}\right)}\right) \, t \,, \end{aligned}$$where \(W_N = \int _0^{\pi /2} \cos ^N(\theta ) \mathrm{d} \theta \), K > 0, and κ o > 0.
-
3.
For M > 0, there exist \(b \in {\mathbf {C}}^{0} ({\mathbb {R}}^+; {\mathbb {R}}^+)\) such that for all \(\rho _{o,1}, \rho _{o,2} \in {{\mathbf {L}}^1} ({\mathbb {R}}^N; [0,R]^n)\) with TV(ρ o,i) ≤ M and for all \(t \in {\mathbb {R}}^+\)
$$\displaystyle \begin{aligned} {\left\|S_t\rho_{o,1} - S_t \rho_{o,2}\right\|}_{{{\mathbf{L}}^1}\left({\mathbb{R}}^N; {\mathbb{R}}^n\right)} \le \left(1 + t \, \mathrm{e}^{t\, b (t)}\right) {\left\|\rho_{o,1} - \rho_{o,2}\right\|}_{{{\mathbf{L}}^1}\left({\mathbb{R}}^N; {\mathbb{R}}^n\right)}. \end{aligned}$$
The Cauchy problem (4.4) is also stable with respect to variations of the functions v i and v i.
Theorem 4.6 ([26, Theorem 3.2])
There exists a function \(\mathcal L \in {\mathbf {C}}^{0}({\mathbb {R}}^+; {\mathbb {R}}^+)\) such that
for every initial data \(\hat \rho _o, \check \rho _o \in {{\mathbf {L}}^1}({\mathbb {R}}^N; {\mathbb {R}}^n)\), for every velocity functions \(\hat v, \check v \in ({\mathbf {C}}^{2} \cap {{\mathbf {W}}^{2,\infty }}) ({\mathbb {R}}^N; {\mathbb {R}}^n)\), for every directions \(\hat {\mathbf v}, \check {\mathbf v} \in ({\mathbf {C}}^{2} \cap {{\mathbf {W}}^{2,1}}) \big ({\mathbb {R}}^N; {\mathbb {R}}^{Nn}\big )\), where \(\hat \rho \) (resp. \(\check \rho \)) denotes the solutions for \(\hat \rho _o\), \(\hat v\), and \(\hat {\mathbf v}\) (resp. for \(\check \rho _o\), \(\check v\), and \(\check {\mathbf v}\)).
5 NonLocal Conservation Laws in Bounded Domains
In this part we consider a system of conservation laws, i.e. n > 1, in an open, connected, and bounded domain Ω of \({\mathbb {R}}^N\) with boundary of class C 2. More precisely, we study the initial boundary value problem for system (4.1), i.e. the problem
where ρ denotes the vector (ρ 1, ⋯ , ρ n). For numerical examples; see [30].
The presence of a boundary has two different effects. First, boundary conditions need to be carefully considered. Indeed, as is well known, the data imposed by boundary conditions need not be strictly assumed, see [57] and the references therein. Second, nonlocal terms have to be evaluated exclusively inside the domain of reference. Indeed, the presence, or absence, of people behind a wall cannot influence the pedestrians’ speed choices, see the discussion in [30].
Definition 5.1 ([30, Definition 4.1])
Fix a positive T and an initial datum \(\rho _o \in {{\mathbf {L}}^1} (\Omega ; {\mathbb {R}}^n)\). A function \(\rho \in {\mathbf {C}}^{0} \big (I; {{\mathbf {L}}^1} (\Omega ; {\mathbb {R}}^n)\big )\) is a solution to (5.1) if, for every i ∈{1, ⋯ , n}, the i-th component ρ i is a regular entropy solution, in the sense of Definition A.2, to

In the following well posedness result, the key assumptions require relations (bounds) on the nonlocal operator. Remark that these bounds all depend exclusively on values of the various functions inside the domain Ω. In other words, we substitute the usual convolution
where \(\bar \rho \) is the null extension of ρ from Ω to all of \({\mathbb {R}}^N\):
This choice is coherent with the above remark about letting each individual react exclusively to what is within his/her horizon and inside Ω.
Theorem 5.2 ([28, Theorem 2.2])
Assume the following hypotheses hold.
-
1.
For every i ∈{1, ⋯ , n},
 .
. -
2.
There exists M > 0 such that for every i ∈{1, ⋯ , n} and
 , \(V^i(t) \in {\mathbf {C}}^{2} (\Omega \times {\mathbb {R}}^m; {\mathbb {R}}^N)\) and \({\left \|V^i(t)\right \|}_{{\mathbf {C}}^{2} (\Omega \times {\mathbb {R}}^m; {\mathbb {R}}^N)} \le M\).
, \(V^i(t) \in {\mathbf {C}}^{2} (\Omega \times {\mathbb {R}}^m; {\mathbb {R}}^N)\) and \({\left \|V^i(t)\right \|}_{{\mathbf {C}}^{2} (\Omega \times {\mathbb {R}}^m; {\mathbb {R}}^N)} \le M\). -
3.
For every i ∈{1, ⋯ , n}, \(\mathcal {I}^i : {{\mathbf {L}}^1} (\Omega ;{\mathbb {R}}^n) \to {\mathbf {C}}^{2} (\Omega ; {\mathbb {R}}^m)\) is such that there exists a positive K and a nondecreasing map \(\mathcal {K} \in {{\mathbf {L}}_{loc}^{\infty }} ({\mathbb {R}}^+; {\mathbb {R}}^+)\) such that:
-
a.
for all \(r \in {{\mathbf {L}}^1} (\Omega ;{\mathbb {R}}^n)\),
$$\displaystyle \begin{aligned} {\left\|\mathcal{I}^i (r)\right\|}_{{{\mathbf{L}}^\infty} (\Omega;{\mathbb{R}}^m)} \le & K \, {\left\|r\right\|}_{{{\mathbf{L}}^1} (\Omega;{\mathbb{R}}^n)} \, , \\ {\left\|\nabla_x \mathcal{I}^i (r)\right\|}_{{{\mathbf{L}}^\infty} (\Omega;{\mathbb{R}}^{m\times N})} \le & K \, {\left\|r\right\|}_{{{\mathbf{L}}^1} (\Omega;{\mathbb{R}}^n)} \, , \\ {\left\|\nabla_x^2 \mathcal{I}^i (r)\right\|}_{{{\mathbf{L}}^\infty} (\Omega;{\mathbb{R}}^{m\times N \times N})} \le & \mathcal{K}\left({\left\|r\right\|}_{{{\mathbf{L}}^1} (\Omega;{\mathbb{R}}^n)}\right) \; {\left\|r\right\|}_{{{\mathbf{L}}^1} (\Omega;{\mathbb{R}}^n)} \, ; \end{aligned} $$ -
b.
for all \(r_1, \, r_2 \in {{\mathbf {L}}^1} (\Omega ;{\mathbb {R}}^n)\)
$$\displaystyle \begin{aligned} {\left\|\mathcal{I}^i (r_1) - \mathcal{I}^i (r_2)\right\|}_{{{\mathbf{L}}^\infty} (\Omega;{\mathbb{R}}^m)} \le & K \; {\left\|r_1 - r_2\right\|}_{{{\mathbf{L}}^1} (\Omega;{\mathbb{R}}^n)} \, , \\ {\left\| \nabla_x \big(\mathcal{I}^i (r_1) - \mathcal{I}^i (r_2)\big) \right\|}_{{{\mathbf{L}}^\infty} (\Omega;{\mathbb{R}}^{m \times N})} \le & \mathcal{K} \left({\left\|r_1\right\|}_{{{\mathbf{L}}^1} (\Omega;{\mathbb{R}}^n)}\right) \; {\left\|r_1 - r_2\right\|}_{{{\mathbf{L}}^1} (\Omega;{\mathbb{R}}^n)} \, . \end{aligned} $$
-
a.
Then:
-
1.
For every \(\rho _o \in ({{\mathbf {L}}^\infty } \cap \mathbf {BV}) (\Omega ; {\mathbb {R}}^n)\), there exists a unique
 solving (5.1) in the sense of Definition 5.1.
solving (5.1) in the sense of Definition 5.1. -
2.
For every \(\rho _o \in ({{\mathbf {L}}^\infty } \cap \mathbf {BV}) (\Omega ; {\mathbb {R}}^n)\) and for every
 , $$\displaystyle \begin{aligned} {\left\|\rho (t)\right\|}_{{{\mathbf{L}}^1} (\Omega;{\mathbb{R}}^n)} & \le {\left\|\rho_o\right\|}_{{{\mathbf{L}}^1} (\Omega;{\mathbb{R}}^n)} \,, \\ {\left\|\rho (t)\right\|}_{{{\mathbf{L}}^{\infty}} (\Omega;{\mathbb{R}}^n)} & \le {\left\|\rho_o\right\|}_{{{\mathbf{L}}^{\infty}} (\Omega;{\mathbb{R}}^n)} \exp \left( t \, M (1 + K \, {\left\|\rho_o\right\|}_{{{\mathbf{L}}^1} (\Omega;{\mathbb{R}}^n)}) \right) \,, \\ \mathinner{\mathrm{TV}} \big(\rho (t)\big) & \le \exp\left( t \, M (1 + K \, {\left\|\rho_o\right\|}_{{{\mathbf{L}}^1} (\Omega;{\mathbb{R}}^n)}) \right) \\ & \,\times \bigg[ \mathcal{O} (1) \, n \, {\left\|\rho_o\right\|}_{{{\mathbf{L}}^\infty} (\Omega;{\mathbb{R}}^n)} + \mathinner{\mathrm{TV}}(\rho_o) + n \, t \, {\left\|\rho_o\right\|}_{{{\mathbf{L}}^1} (\Omega;{\mathbb{R}}^n)} \, M \\ &\, \times\! \left(\! 1 {+} {\left\|\rho_o\right\|}_{{{\mathbf{L}}^1} (\Omega;{\mathbb{R}}^n)}\! \left(\! K {+} K^2 {\left\|\rho_o\right\|}_{{{\mathbf{L}}^1} (\Omega;{\mathbb{R}}^n)} {+} \mathcal{K} \big( {\left\|\rho_o\right\|}_{{{\mathbf{L}}^1} (\Omega;{\mathbb{R}}^n)}\big)\! \right)\! \right)\! \bigg] . \end{aligned} $$
, $$\displaystyle \begin{aligned} {\left\|\rho (t)\right\|}_{{{\mathbf{L}}^1} (\Omega;{\mathbb{R}}^n)} & \le {\left\|\rho_o\right\|}_{{{\mathbf{L}}^1} (\Omega;{\mathbb{R}}^n)} \,, \\ {\left\|\rho (t)\right\|}_{{{\mathbf{L}}^{\infty}} (\Omega;{\mathbb{R}}^n)} & \le {\left\|\rho_o\right\|}_{{{\mathbf{L}}^{\infty}} (\Omega;{\mathbb{R}}^n)} \exp \left( t \, M (1 + K \, {\left\|\rho_o\right\|}_{{{\mathbf{L}}^1} (\Omega;{\mathbb{R}}^n)}) \right) \,, \\ \mathinner{\mathrm{TV}} \big(\rho (t)\big) & \le \exp\left( t \, M (1 + K \, {\left\|\rho_o\right\|}_{{{\mathbf{L}}^1} (\Omega;{\mathbb{R}}^n)}) \right) \\ & \,\times \bigg[ \mathcal{O} (1) \, n \, {\left\|\rho_o\right\|}_{{{\mathbf{L}}^\infty} (\Omega;{\mathbb{R}}^n)} + \mathinner{\mathrm{TV}}(\rho_o) + n \, t \, {\left\|\rho_o\right\|}_{{{\mathbf{L}}^1} (\Omega;{\mathbb{R}}^n)} \, M \\ &\, \times\! \left(\! 1 {+} {\left\|\rho_o\right\|}_{{{\mathbf{L}}^1} (\Omega;{\mathbb{R}}^n)}\! \left(\! K {+} K^2 {\left\|\rho_o\right\|}_{{{\mathbf{L}}^1} (\Omega;{\mathbb{R}}^n)} {+} \mathcal{K} \big( {\left\|\rho_o\right\|}_{{{\mathbf{L}}^1} (\Omega;{\mathbb{R}}^n)}\big)\! \right)\! \right)\! \bigg] . \end{aligned} $$ -
3.
For every \(\rho _o \in ({{\mathbf {L}}^\infty } \cap \mathbf {BV}) (\Omega ; {\mathbb {R}}^n)\) and for any
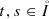 , $$\displaystyle \begin{aligned} {\left\|\rho (t) - \rho (s)\right\|}_{{{\mathbf{L}}^1} (\Omega;{\mathbb{R}}^n)} \le \mathinner{\mathrm{TV}} \left( \rho(\max \{t,s\}) \right) \, {\left|t-s\right|}. \end{aligned}$$
, $$\displaystyle \begin{aligned} {\left\|\rho (t) - \rho (s)\right\|}_{{{\mathbf{L}}^1} (\Omega;{\mathbb{R}}^n)} \le \mathinner{\mathrm{TV}} \left( \rho(\max \{t,s\}) \right) \, {\left|t-s\right|}. \end{aligned}$$ -
4.
For every initial data \(\rho _o, \tilde \rho _o \in ({{\mathbf {L}}^\infty } \cap \mathbf {BV}) (\Omega ; {\mathbb {R}}^n)\) and for any
 , calling ρ and \(\tilde \rho \) the corresponding solutions to (5.1), $$\displaystyle \begin{aligned} {\left\|\rho (t) - \tilde\rho (t)\right\|}_{{{\mathbf{L}}^1} (\Omega;{\mathbb{R}}^n)} \le \mathrm{e}^{\mathcal{L}(t)} \, {\left\|\rho_o - \tilde \rho_o\right\|}_{{{\mathbf{L}}^1} (\Omega;{\mathbb{R}}^n)}, \end{aligned}$$
, calling ρ and \(\tilde \rho \) the corresponding solutions to (5.1), $$\displaystyle \begin{aligned} {\left\|\rho (t) - \tilde\rho (t)\right\|}_{{{\mathbf{L}}^1} (\Omega;{\mathbb{R}}^n)} \le \mathrm{e}^{\mathcal{L}(t)} \, {\left\|\rho_o - \tilde \rho_o\right\|}_{{{\mathbf{L}}^1} (\Omega;{\mathbb{R}}^n)}, \end{aligned}$$where \(\mathcal {L}(t)>0\) depends on Ω, V i, \(\mathcal {I}^i\), \({\left \|\rho _o\right \|}_{{{\mathbf {L}}^1} (\Omega ;{\mathbb {R}}^n)}\), \({\left \|\tilde \rho _o\right \|}_{{{\mathbf {L}}^1} (\Omega ;{\mathbb {R}}^n)}\), \({\left \|\rho _o\right \|}_{{{\mathbf {L}}^\infty } (\Omega ;{\mathbb {R}}^n)}\), \({\left \|\tilde \rho _o\right \|}_{{{\mathbf {L}}^\infty } (\Omega ;{\mathbb {R}}^n)}\), TV(ρ o), and on \(\mathinner {\mathrm {TV}} (\tilde \rho _o)\).
-
5.
Fix \(\rho _o \in ({{\mathbf {L}}^\infty } \cap \mathbf {BV}) (\Omega ; {\mathbb {R}}^n)\). Let \(\tilde V^i\) satisfies the same assumptions of V i. Call ρ and \(\tilde \rho \) the solutions to problem (5.1) corresponding, respectively, to the choices V and \(\tilde V\). Then, for every
 , $$\displaystyle \begin{aligned} {\left\|\rho (t) - \tilde\rho (t)\right\|}_{{{\mathbf{L}}^1} (\Omega;{\mathbb{R}}^n)} \le \mathcal{C} (t) \int_0^t {\left\|V (s) - \tilde V (s)\right\|}_{{\mathbf{C}}^{1}(\Omega \times {\mathbb{R}}^m; {\mathbb{R}}^{nN})} \, \mathrm{d}{s}, \end{aligned}$$
, $$\displaystyle \begin{aligned} {\left\|\rho (t) - \tilde\rho (t)\right\|}_{{{\mathbf{L}}^1} (\Omega;{\mathbb{R}}^n)} \le \mathcal{C} (t) \int_0^t {\left\|V (s) - \tilde V (s)\right\|}_{{\mathbf{C}}^{1}(\Omega \times {\mathbb{R}}^m; {\mathbb{R}}^{nN})} \, \mathrm{d}{s}, \end{aligned}$$where \(\mathcal {C}\) depends on Ω, V i, \(\tilde V^i\), \(\mathcal I^i\), and on the initial datum.
-
6.
For i ∈{1, ⋯ , n}, if \(\rho ^i_o \ge 0\) a.e. in Ω, then ρ i(t) ≥ 0 a.e. in Ω for all
 .
.
We conclude this section noting that the extension of Theorem 5.2 to the case of several interacting populations in a bounded domain is, at present, apparently still to be considered.
6 Mixed Micro–Macro Models in \({\mathbb {R}}^N\)
Here we consider the case of a system similar to (4.1) coupled with ordinary differential equations. In typical situations, the system of conservation laws is used to describe the evolution of several populations through their macroscopic densities, while the ordinary differential equations model the microscopic dynamics of few agents.
For i ∈{1, ⋯ , n}, we consider the system
where q(ρ) = ρ v(ρ), t > 0, \(x \in \Omega = {\mathbb {R}}^N\), ρ = (ρ 1, ⋯ , ρ n) is the vector of the macroscopic densities, \(p \in {\mathbb {R}}^m\) describes the positions and possibly the velocity of \(d \in {\mathbb {N}}\) agents, so that m = Nd or m = 2Nd. Moreover \(\mathcal {I}^i\) and \(\mathcal {J}\) are nonlocal operators, reflecting the fact that the behavior of the members of the population as well as of the agents depends on suitable spatial averages. System (6.1) is supplemented with the initial conditions
with \(\rho _o \in {{\mathbf {L}}^1}({\mathbb {R}}^N; {\mathbb {R}}^n)\) and \(p_o \in {\mathbb {R}}^m\).
Definition 6.1 ([13, Definition 2.6])
Fix \(\rho _o \in ({{\mathbf {L}}^1} \cap \mathbf {BV}) ({\mathbb {R}}^N; {\mathbb {R}}^n)\) and \(p_{o} \in {\mathbb {R}}^m\). A couple \(\left (\rho , p\right )\) with
is a solution to (6.1)–(6.2) if the following conditions are satisfied:
-
1.
For every i ∈{1, ⋯ , n}, the map ρ i is a Kružkov solution, in the sense of Definition 2.2, to the scalar conservation law
$$\displaystyle \begin{aligned} \partial_t \rho^i + \mathop{\mathrm{div}_{\mathrm{x}}}\nolimits \big[ q^i(\rho^i)\, V (t,x) \big] = 0 \,, \quad \end{aligned}$$where \(V (t,x) = V^i \big ( t, x, \mathcal {I}^i \left (\rho (t)\right ) (x), p (t) \big )\).
-
2.
The map p is a Carathéodory solution to the ordinary differential equation
$$\displaystyle \begin{aligned} \dot p = \mathcal{F} (t, p) \quad \mbox{ where } \quad \mathcal{F} (t,p) = F \big(t, p, \mathcal{J} \big(\rho (t)\big) (p)\big)\,. \end{aligned}$$ -
3.
ρ(0, x) = ρ o(x) for a.e. \(x \in {\mathbb {R}}^N\).
-
4.
p(0) = p o.
The following well posedness and stability result holds; for a proof see [13, Theorem 2.2 and Section 4.1].
Theorem 6.2 ([13, Theorem 2.2])
Assume the following hypotheses.
-
1.
For every i ∈{1, ⋯ , n}, \(q^i \in {\mathbf {C}}^{2}({\mathbb {R}}^+; {\mathbb {R}}^+)\) satisfies q i(0) = 0 and q i(R) = 0, for some R > 0.
-
2.
For every i ∈{1, ⋯ , n}, \(V^i \in ({\mathbf {C}}^{2} \cap {{\mathbf {L}}^\infty }) ({\mathbb {R}}^+ \times {\mathbb {R}}^N \times {\mathbb {R}}^{N} \times {\mathbb {R}}^m; {\mathbb {R}}^N)\).
-
3.
The map \(F \in {\mathbf {C}}^{0}({\mathbb {R}}^+ \times {\mathbb {R}}^m \times {\mathbb {R}}^\ell ; {\mathbb {R}}^m)\) is such that
-
a.
For all compact subset K of \({\mathbb {R}}^m\), there exists a constant L F > 0 such that, for every \(t \in {\mathbb {R}}^+\), p 1, p 2 ∈ K and \(b_1, b_2 \in {\mathbb {R}}^\ell \),
$$\displaystyle \begin{aligned} {\left\|F(t,p_1,b_1) - F(t,p_2,b_2)\right\|}_{{\mathbb{R}}^m} \le L_F \, \left( {\left\|p_1 - p_2\right\|}_{{\mathbb{R}}^m} + {\left\|b_1 - b_2\right\|}_{{\mathbb{R}}^\ell} \right) \,. \end{aligned}$$ -
b.
There exists a map \(C_F \in {{\mathbf {L}}_{loc}^{1}}({\mathbb {R}}^+; {\mathbb {R}}^+)\) such that for all t > 0, \(b \in {\mathbb {R}}^\ell \), and \(p \in {\mathbb {R}}^m\)
$$\displaystyle \begin{aligned} {\left\|F(t,p,b)\right\|}_{{\mathbb{R}}^m} \le C_F(t) \, \left(1 + {{\left\|p\right\|}}_{{\mathbb{R}}^m} + {\left\|b\right\|}_{{\mathbb{R}}^\ell}\right) \,. \end{aligned}$$
-
a.
-
4.
For every i ∈{1, ⋯ , n}, the maps \(\mathcal {I}^i: {{\mathbf {L}}^1}({\mathbb {R}}^N; {\mathbb {R}}^n) \to ({\mathbf {C}}^{2} \cap {{\mathbf {W}}^{2,1}}) ({\mathbb {R}}^N; {\mathbb {R}}^N)\) are Lipschitz continuous and satisfy \(\mathcal {I}^i (0) = 0\). In particular there exists a positive constant \(L_{\mathcal I} > 0\) such that, for every \(\rho _1, \rho _2 \in {{\mathbf {L}}^1}({\mathbb {R}}^N; [0,R]^n)\),
$$\displaystyle \begin{aligned} & \quad {\left\|\mathcal{I}^i (\rho_1) - \mathcal{I}^i (\rho_2)\right\|} _{{{\mathbf{W}}^{2,1}}\left({\mathbb{R}}^N; {\mathbb{R}}^N\right)} + {\left\|\mathcal{I}^i (\rho_1) - \mathcal{I}^i (\rho_2)\right\|} _{{\mathbf{C}}^{2}\left({\mathbb{R}}^N; {\mathbb{R}}^N\right)} \\ & \le L_{\mathcal I} \; {\left\|\rho_1 - \rho_2\right\|}_{{{\mathbf{L}}^1}({\mathbb{R}}^N; {\mathbb{R}}^n)}. \end{aligned} $$ -
5.
The map \(\mathcal {J}\colon {{\mathbf {L}}^1}({\mathbb {R}}^N; {\mathbb {R}}^n) \to {{\mathbf {W}}^{1,\infty }}({\mathbb {R}}^m; {\mathbb {R}}^\ell )\) is Lipschitz continuous and satisfies \(\mathcal J(0) = 0\). In particular, there exists a positive constant \(L_{\mathcal J} > 0\) such that, for every \(\rho _1, \rho _2 \in {{\mathbf {L}}^1}({\mathbb {R}}^N; [0,R]^n)\),
$$\displaystyle \begin{aligned} {\left\| \mathcal{J} (\rho_1) - \mathcal{J} (\rho_2) \right\|}_{{{\mathbf{W}}^{1,\infty}}\left({\mathbb{R}}^m; {\mathbb{R}}^\ell\right)} \le L_{\mathcal J} \; {\left\|\rho_1 - \rho_2\right\|}_{{{\mathbf{L}}^1}({\mathbb{R}}^N; {\mathbb{R}}^n)}. \end{aligned}$$
Then, given the sets
there exists a process \(\mathcal {P}:\, \mathcal T \times \mathcal {R} \times {\mathbb {R}}^m \to \mathcal {R} \times {\mathbb {R}}^m\) such that:
-
1.
for every \(t \in {\mathbb {R}}^+\), \(\mathcal {P}_{t, t}\) is the identity map;
-
2.
for all \(t_1,t_2,t_3 \in {\mathbb {R}}^+\) with t 3 ≥ t 2 ≥ t 1, \(\mathcal {P}_{t_2, t_3} \circ \mathcal {P}_{t_1, t_2} = \mathcal {P}_{t_1, t_3}\);
-
3.
for all \((\rho _o, p_o) \in \mathcal {R} \times {\mathbb {R}}^m\) and \(t_o \in {\mathbb {R}}^+\), the map \(t \mapsto \mathcal {P}_{t_o,t} (\rho _o, p_o)\) is continuous, defined for t ≥ t o, and the unique solution to (6.1) in the sense of Definition 6.1 with initial datum (ρ o, p o) assigned at time t o;
-
4.
for every \((\rho _o^1,p_o^1), (\rho _o^2,p_o^2) \in \mathcal {R} \times {\mathbb {R}}^m\), there exists a function \(\mathcal {L} \in {\mathbf {C}}^{0} ({\mathbb {R}}^+; {\mathbb {R}}^+)\) such that \(\mathcal {L} (0) = 0\) and, setting \((\rho _i,p_i) (t) = \mathcal {P}_{0,t} (\rho _o^i,p_o^i)\),
$$\displaystyle \begin{aligned} {\left\|\rho_1 (t) {-} \rho_2 (t)\right\|}_{{{\mathbf{L}}^1}({\mathbb{R}}^N; {\mathbb{R}}^n)} & \le \! \big(1{+}\mathcal{L} (t)\big) \, {\left\|\rho_o^1{-}\rho_o^2\right\|}_{{{\mathbf{L}}^1}({\mathbb{R}}^N; {\mathbb{R}}^n)} \!\!\! {+} \mathcal{L} (t) \, {\left\|p_o^1{-}p_o^2\right\|}_{{\mathbb{R}}^m} , \\ {\left\|p_1 (t) {-} p_2 (t)\right\|}_{{\mathbb{R}}^m} & \le \! \mathcal{L} (t) \, {\left\|\rho_o^1{-}\rho_o^2\right\|} _{{{\mathbf{L}}^1}({\mathbb{R}}^N; {\mathbb{R}}^n)} \!\!\! {+} \big(1{+}\mathcal{L} (t)\big)\, {\left\|p_o^1{-}p_o^2\right\|}_{{\mathbb{R}}^m} ; \end{aligned} $$ -
5.
for all \((\rho _o, p_o) \in \mathcal {R} \times {\mathbb {R}}^m\), if q 1, q 2, V 1, V 2, and F 1, F 2 satisfy the same assumptions as q, V , and F, then there exists a function \(\mathcal {K} \in {\mathbf {C}}^{0} ({\mathbb {R}}^+; {\mathbb {R}}^+)\) such that \(\mathcal {K} (0)=0\) and, calling (ρ i, p i) the corresponding solutions, for t > 0,
$$\displaystyle \begin{aligned} & \quad {\left\|\rho_1 (t) - \rho_2 (t)\right\|}_{{{\mathbf{L}}^1}({\mathbb{R}}^N; {\mathbb{R}}^n)} + {\left\|p_1 (t) - p_2 (t)\right\|}_{{\mathbb{R}}^m} \\ & \le \mathcal{K} (t) \left( {\left\|q_1 - q_2\right\|}_{{{\mathbf{W}}^{1,\infty}}({\mathbb{R}}^+; {\mathbb{R}}^+)} + {\left\|V_1 - V_2\right\|}_{{{\mathbf{W}}^{1,\infty}}\left({\mathbb{R}}^+ \times {\mathbb{R}}^N \times {\mathbb{R}}^{N} \times {\mathbb{R}}^m; {\mathbb{R}}^N\right)} \right) \\ & \quad + \mathcal{K} (t)\, {\left\|F_1 - F_2\right\|}_{{{\mathbf{L}}^\infty}\left({\mathbb{R}}^+ \times {\mathbb{R}}^m \times {\mathbb{R}}^\ell; {\mathbb{R}}^m\right)}\, . \end{aligned} $$
For further models based on the coupling of conservation laws with ordinary differential equations, see [11, 12].
7 Conclusions
Above, we collected various results that, together, allow a rigorous study of several macroscopic crowd dynamics models based on conservation laws. On these bases, several research directions naturally open.
From a strictly analytic point of view, a natural question is the relation between the models above and the so-called microscopic ones. It is apparently still unknown if a nonlocal conservation law model can be rigorously proved to be the limit as n → +∞ of a microscopic model for n individuals, typically based on ordinary differential equations. A few results in this direction, currently limited to a single space dimension, are, for instance, in [46, 48].
From a control theoretic point of view, the modeling frameworks introduced above allow to state many optimization problems. In particular, we stress the relevance of shape optimization problems: is there an optimal shape for an exit, so that emergency evacuations are as quick as possible? Preliminary results in this direction are, for instance, in [34]. Note that, in this connection, both necessary and sufficient conditions for optimality are nowadays apparently unknown.
From a numerical point of view, the introduction of efficient algorithms would definitely foster the development and the spread of these models. Indeed, nonlocal terms impose the computation of (possibly several) convolution integrals at each time step. A detailed numerical study aimed at optimizing the choices of the meshes used in the PDE integration and in the convolution integrals might have dramatic effects on the integration times. Preliminary numerical studies in this direction are, for instance, in [1, 3, 19].
References
A. Aggarwal, R.M. Colombo, P. Goatin, Nonlocal systems of conservation laws in several space dimensions. SIAM J. Numer. Anal. 53(2), 963–983 (2015)
J.P. Agnelli, F. Colasuonno, D. Knopoff, A kinetic theory approach to the dynamics of crowd evacuation from bounded domains. Math. Models Methods Appl. Sci. 25(1), 109–129 (2015)
P. Amorim, R.M. Colombo, A. Teixeira, On the numerical integration of scalar nonlocal conservation laws. ESAIM Math. Model. Numer. Anal. 49(1), 19–37 (2015)
F. Bagarello, F. Gargano, F. Oliveri, A phenomenological operator description of dynamics of crowds: escape strategies. Appl. Math. Model. 39(8), 2276–2294 (2015)
R. Bailo, J.A. Carrillo, P. Degond, Pedestrian models based on rational behaviour, in Modeling and Simulation in Science, Engineering and Technology (Birkhäuser, New York, 2018), pp. 259–292
N. Bellomo, A. Bellouquid, On multiscale models of pedestrian crowds from mesoscopic to macroscopic. Commun. Math. Sci. 13(7), 1649–1664 (2015)
N. Bellomo, S. Berrone, L. Gibelli, A.B. Pieri, Macroscopic first order models of multicomponent human crowds with behavioral dynamics, in Advances in Computational Fluid-Structure Interaction and Flow Simulation. Modeling and Simulation in Science, Engineering and Technology (Birkhäuser/Springer, Cham, 2016), pp. 295–306
N. Bellomo, L. Gibelli, N. Outada, On the interplay between behavioral dynamics and social interactions in human crowds. Kinet. Relat. Models 12(2), 397–409 (2019)
F. Berthelin, P. Goatin, Regularity results for the solutions of a non-local model of traffic flow. Discrete Contin. Dyn. Syst. 39(6), 3197–3213 (2019)
S. Bianchini, R.M. Colombo, On the stability of the standard Riemann semigroup. Proc. Am. Math. Soc. 130(7), 1961–1973 (2002)
R. Borsche, R.M. Colombo, M. Garavello, On the coupling of systems of hyperbolic conservation laws with ordinary differential equations. Nonlinearity 23(11), 2749–2770 (2010)
R. Borsche, R.M. Colombo, M. Garavello, Mixed systems: ODEs - balance laws. J. Differ. Equ. 252(3), 2311–2338 (2012)
R. Borsche, R.M. Colombo, M. Garavello, A. Meurer, Differential equations modeling crowd interactions. J. Nonlinear Sci. 25(4), 827–859 (2015)
R. Borsche, A. Klar, F. Schneider, Numerical methods for mean-field and moment models for pedestrian flow, in Crowd Dynamics. Vol. 1. Modeling and Simulation in Science, Engineering and Technology (Birkhäuser/Springer, Cham, 2018), pp. 167–209
F. Bouchut, B. Perthame, Kružkov’s estimates for scalar conservation laws revisited. Trans. Am. Math. Soc. 350(7), 2847–2870 (1998)
A. Bressan, Hyperbolic Systems of Conservation Laws. Oxford Lecture Series in Mathematics and Its Applications, vol. 20 (Oxford University Press, Oxford, 2000). The one-dimensional Cauchy problem
A. Bressan, B. Piccoli, Introduction to the Mathematical Theory of Control. AIMS Series on Applied Mathematics, vol. 2 (American Institute of Mathematical Sciences, Springfield, 2007)
A. Bressan, W. Shen, On traffic flow with nonlocal flux: a relaxation representation (2019). arXiv: 1911.03636
C. Chalons, P. Goatin, L.M. Villada, High-order numerical schemes for one-dimensional nonlocal conservation laws. SIAM J. Sci. Comput. 40(1), A288–A305 (2018)
G.-Q. Chen, K.H. Karlsen, Quasilinear anisotropic degenerate parabolic equations with time-space dependent diffusion coefficients. Commun. Pure Appl. Anal. 4(2), 241–266 (2005)
F.A. Chiarello, P. Goatin, Global entropy weak solutions for general non-local traffic flow models with anisotropic kernel. ESAIM Math. Model. Numer. Anal. 52(1), 163–180 (2018)
F.A. Chiarello, P. Goatin, Non-local multi-class traffic flow models. Netw. Heterog. Media 14(2), 371–387 (2019)
F.A. Chiarello, P. Goatin, E. Rossi, Stability estimates for non-local scalar conservation laws. Nonlinear Anal. Real World Appl. 45, 668–687 (2019)
A. Colombi, M. Scianna, A. Alaia, A discrete mathematical model for the dynamics of a crowd of gazing pedestrians with and without an evolving environmental awareness. Comput. Appl. Math. 36(2), 1113–1141 (2017)
R.M. Colombo, F. Marcellini, Nonlocal systems of balance laws in several space dimensions with applications to laser technology. J. Differ. Equ. 259(11), 6749–6773 (2015)
R.M. Colombo, L.-M. Mercier, Nonlocal crowd dynamics models for several populations. Acta Math. Sci. 32(1), 177–196 (2012)
R.M. Colombo, E. Rossi, Hyperbolic predators vs. parabolic prey. Commun. Math. Sci. 13(2), 369–400 (2015)
R.M. Colombo, E. Rossi, Nonlocal conservation laws in bounded domains. SIAM J. Math. Anal. 50(4), 4041–4065 (2018)
R.M. Colombo, E. Rossi, Control in a mixed hyperbolic-parabolic predator prey model (2019, in preparation)
R.M. Colombo, E. Rossi, Modelling crowd movements in domains with boundaries. IMA J. Appl. Math. 84(5), 833–853 (2019)
R.M. Colombo, E. Rossi, A modeling framework for biological pest control. Math. Biosci. Eng. 17(mbe-17-02-072), 1413 (2020)
R.M. Colombo, M. Mercier, M.D. Rosini, Stability and total variation estimates on general scalar balance laws. Commun. Math. Sci. 7(1), 37–65 (2009)
R.M. Colombo, M. Herty, M. Mercier, Control of the continuity equation with a non local flow. ESAIM Control Optim. Calc. Var. 17(2), 353–379 (2011)
R.M. Colombo, M. Garavello, M. Lécureux-Mercier, A class of nonlocal models for pedestrian traffic. Math. Models Methods Appl. Sci. 22(4), 1150023, 34 (2012)
M. Colombo, G. Crippa, L.V. Spinolo. Blow-up of the total variation in the local limit of a nonlocal traffic model (2018)
M. Colombo, G. Crippa, M. Graff, L.V. Spinolo. On the role of numerical viscosity in the study of the local limit of nonlocal conservation laws (2019)
M. Colombo, G. Crippa, M. Graff, L.V. Spinolo. Recent results on the singular local limit for nonlocal conservation laws (2019)
M. Colombo, G. Crippa, L.V. Spinolo, On the singular local limit for conservation laws with nonlocal fluxes. Arch. Ration. Mech. Anal. 233(3), 1131–1167 (2019)
A. Corli, L. Malaguti, Viscous profiles in models of collective movement with negative diffusivity. Z. Angew. Math. Phys. 70(2), Art. 47, 22 (2019)
J.-M. Coron, M. Kawski, Z. Wang, Analysis of a conservation law modeling a highly re-entrant manufacturing system. Discrete Contin. Dyn. Syst. Ser. B 14(4), 1337–1359 (2010)
V. Coscia, C. Canavesio, First-order macroscopic modelling of human crowd dynamics. Math. Models Methods Appl. Sci. 18(Suppl.), 1217–1247 (2008)
G. Crippa, M. Lécureux-Mercier, Existence and uniqueness of measure solutions for a system of continuity equations with non-local flow. Nonlinear Differ. Equ. Appl. 20(3), 523–537 (2013)
E. Cristiani, B. Piccoli, A. Tosin, Multiscale Modeling of Pedestrian Dynamics. MS&A. Modeling, Simulation and Applications, vol. 12 (Springer, Cham, 2014)
C.M. Dafermos, Hyperbolic Conservation Laws in Continuum Physics. Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], vol. 325, 4th edn. (Springer, Berlin, 2016)
E. De Angelis, Nonlinear hydrodynamic models of traffic flow modelling and mathematical problems. Math. Comput. Model. 29(7), 83–95 (1999)
M. Di Francesco, M.D. Rosini, Rigorous derivation of nonlinear scalar conservation laws from follow-the-leader type models via many particle limit. Arch. Ration. Mech. Anal. 217(3), 831–871 (2015)
H. Holden, N.H. Risebro, Front Tracking for Hyperbolic Conservation Laws. Applied Mathematical Sciences, vol. 152, 2nd edn. (Springer, Heidelberg, 2015)
H. Holden, N.H. Risebro, The continuum limit of Follow-the-Leader models—a short proof. Discrete Contin. Dyn. Syst. 38(2), 715–722 (2018)
S.N. Kružhkov, First order quasilinear equations with several independent variables. Mat. Sb. (N.S.) 81(123), 228–255 (1970)
M. Lécureux-Mercier, Improved stability estimates for general scalar conservation laws. J. Hyperbolic Differ. Equ. 8(4), 727–757 (2011). See also the revised version at http://math.univ-lyon1.fr/~mercier
R. Loehner, On the modeling of pedestrian motion. Appl. Math. Model. 34(2), 366–382 (2010)
B.J. Lucier, A moving mesh numerical method for hyperbolic conservation laws. Math. Comput. 46(173), 59–69 (1986)
F. Marcellini, On the stability of a model for the cutting of metal plates by means of laser beams. Appl. Math. Lett. 68, 143–149 (2017)
S. Motsch, M. Moussaïd, E.G. Guillot, M. Moreau, J. Pettré, G. Theraulaz, C. Appert-Rolland, P. Degond, Modeling crowd dynamics through coarse-grained data analysis. Math. Biosci. Eng. 15(6), 1271–1290 (2018)
B. Piccoli, F. Rossi, Measure-theoretic models for crowd dynamics, in Crowd Dynamics. Vol. 1. Modeling and Simulation in Science, Engineering and Technology (Birkhäuser/Springer, Cham, 2018), pp. 137–165
B. Piccoli, A. Tosin, Time-evolving measures and macroscopic modeling of pedestrian flow. Arch. Ration. Mech. Anal. 199(3), 707–738 (2011)
E. Rossi, Definitions of solutions to the IBVP for multi-dimensional scalar balance laws. J. Hyperbolic Differ. Equ. 15(2), 349–374 (2018)
E. Rossi, V. Schleper, Convergence of numerical scheme for a mixed hyperbolic-parabolic system in two space dimensions. ESAIM Math. Model. Numer. Anal. 50(2), 475–497 (2016)
M. Twarogowska, P. Goatin, R. Duvigneau, Macroscopic modeling and simulations of room evacuation. Appl. Math. Model. 38(24), 5781–5795 (2014)
J. Vovelle, Convergence of finite volume monotone schemes for scalar conservation laws on bounded domains. Numer. Math. 90(3), 563–596 (2002)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendices
Appendices
1.1 Regular Entropy Solutions for IBVP Problems
In this appendix we briefly recall the concept of regular entropy solutions for an initial boundary value problem. To this aim, fix T > 0, an open and bounded subset Ω of \({\mathbb {R}}^N\), and let us consider the system

where  satisfies, for every
satisfies, for every  , \(u(t) \in {\mathbf {C}}^{2} ( \Omega ; {\mathbb {R}}^N)\) and \({\left \|u(t)\right \|}_{{\mathbf {C}}^{2}\left (\Omega ; {\mathbb {R}}^N\right )} \le M\) for a suitable positive constant M. The definition of a boundary entropy–entropy flux pair is as follows.
, \(u(t) \in {\mathbf {C}}^{2} ( \Omega ; {\mathbb {R}}^N)\) and \({\left \|u(t)\right \|}_{{\mathbf {C}}^{2}\left (\Omega ; {\mathbb {R}}^N\right )} \le M\) for a suitable positive constant M. The definition of a boundary entropy–entropy flux pair is as follows.
Definition A.1 ([28, Definition 4.1], [60, Definition 2])
The pair of functions  is said a boundary entropy–entropy flux pair for (7.1) if:
is said a boundary entropy–entropy flux pair for (7.1) if:
-
1.
the function z↦H(z, w) is convex for every \(w \in {\mathbb {R}}\);
-
2.
the equality \(\partial _z Q\left (t, x, z, w\right ) = \left (\partial _z H\left (z, w\right )\right ) u\left (t, x\right )\) holds for every
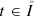 , \(x \in \overline \Omega \), and \(z, w \in {\mathbb {R}}\);
, \(x \in \overline \Omega \), and \(z, w \in {\mathbb {R}}\); -
3.
the equalities \(H\left (w, w\right ) = 0\), \(Q\left (t, x, w, w\right ) = 0\), and \(\partial _z H\left (w, w\right ) = 0\) hold for every
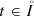 , \(x \in \overline \Omega \), and \(w \in {\mathbb {R}}\).
, \(x \in \overline \Omega \), and \(w \in {\mathbb {R}}\).
It is now possible to state the definition of regular entropy solution.
Definition A.2 ([57, Definition 3.3])
A regular entropy solution to (7.1) is a function  such that, for every boundary entropy–entropy flux pair \(\left (H, Q\right )\), in the sense of Definition A.1, for every \(k \in {\mathbb {R}}\) and for every \(\varphi \in {\mathbf {C}}_c^{1} ({\mathbb {R}} \times {\mathbb {R}}^N; {\mathbb {R}}^+)\), it holds
such that, for every boundary entropy–entropy flux pair \(\left (H, Q\right )\), in the sense of Definition A.1, for every \(k \in {\mathbb {R}}\) and for every \(\varphi \in {\mathbf {C}}_c^{1} ({\mathbb {R}} \times {\mathbb {R}}^N; {\mathbb {R}}^+)\), it holds

where \({\mathcal {H}}^{N-1}\) denotes the Hausdorff measure of dimension N − 1.
1.2 List of Symbols
- C 0, 1(A; B):
-
with A and B subsets of normed vector spaces, is the set of functions defined on A, with values in B, that are Lipschitz continuous on A.
- C k(A; B):
-
with A and B subsets of normed vector spaces, is the set of functions defined on A, with values in B, whose k-derivatives are continuous on A.
- \({\mathbf {C}}_c^{k} (A;B)\) :
-
with A and B subsets of normed vector spaces, is the set of compactly supported functions defined on A, with values in B whose k-derivatives are continuous on A.
- \(\overline {I}\) :
-
is the closure of the set I.
-
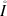 :
: -
is the interior of the set I.
- L p(A; B):
-
with p ≥ 1, \(A \subseteq {\mathbb {R}}^n\) and \(B \subseteq {\mathbb {R}}^m\), is the set of measurable functions f defined on A, with values in B, such that \({\left |f\right |}^p\) is Lebesgue integrable on A.
- L ∞(A; B):
-
with \(A \subseteq {\mathbb {R}}^n\) and \(B \subseteq {\mathbb {R}}^m\), is the set of measurable functions f defined on A, with values in B, essentially bounded.
- \({\mathbb {R}}^+\) :
-
is the set \(\left [0, +\infty \right [\) of 0 and all positive real numbers.
-
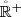 :
: -
is the set \(\left ]0, +\infty \right [\) of all strictly positive real numbers.
- \(\mathbb S^{N-1}\) :
-
is the unit sphere in \({\mathbb {R}}^N\).
- \( \mathop {\mathrm {spt}} \rho \) :
-
is the support of the function ρ.
- W 1, p(A; B):
-
with 1 ≤ p ≤∞, \(A \subseteq {\mathbb {R}}^n\) and \(B \subseteq {\mathbb {R}}^m\), is the Sobolev space of functions defined in A with values in B whose first weak derivative is in L p.
Rights and permissions
Copyright information
© 2020 Springer Nature Switzerland AG
About this chapter
Cite this chapter
Colombo, R.M., Lecureux-Mercier, M., Garavello, M. (2020). Crowd Dynamics Through Conservation Laws. In: Gibelli, L. (eds) Crowd Dynamics, Volume 2. Modeling and Simulation in Science, Engineering and Technology. Birkhäuser, Cham. https://doi.org/10.1007/978-3-030-50450-2_5
Download citation
DOI: https://doi.org/10.1007/978-3-030-50450-2_5
Published:
Publisher Name: Birkhäuser, Cham
Print ISBN: 978-3-030-50449-6
Online ISBN: 978-3-030-50450-2
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)





 .
. ,
,  solving (
solving ( ,
, 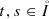 ,
,  , calling ρ and
, calling ρ and  ,
,  .
.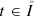 ,
, 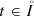 ,
, 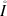 :
: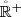 :
: