Development and Application of the Statistically Similar Representative Volume Element for Numerical Modelling of Multiphase Materials

Abstract

Modern aerospace, automotive and construction industries rely on materials with non-homogeneous properties like composites or multiphase structures. Such materials offer a lot of advantages, but they also require application of advanced numerical models of exploitation condition, which are of high importance for designers, architects and engineers. However, computational cost is one of the most important problems in this approach, being very high and sometimes unacceptable. In this paper we propose approach based on Statistically Similar Representative Volume Element (SSRVE), which is generated by combination of isogeometric analysis and optimization methods. The proposed solution significantly decreases computational cost of complex multiscale simulations and simultaneously maintains high reliability of solvers. At first, the motivation of the work is described in introduction, which is followed by general idea of the SSRVE as a modelling technique. Afterwards, examples of generated SSRVEs based on two different cases are given and passed further to numerical simulations of exploitation conditions. The results obtained from these calculations are used in the model predicting gradients of material properties, which are crucial results for discussion on uniqueness of the proposed solution. Additionally, some aspects of computational cost reduction are discussed, as well.

1 Introduction

In recent years it was observed that heterogeneous materials benefit from the best features due to the mix of phases they are made of. Taking an advantage of heterogeneity is the main strengthening mechanism for multiphase steels, which are developed today. On the other hand, steep gradients of properties between various phases in these steels may lead to low local fracture resistance [1, 2]. Thus, searching for a compromise between strengthening by multiphase microstructure and tendency to local fracture due to steep gradients of properties became an important field of research in materials engineering [3]. This research requires multiscale material models, which explicitly account for the microstructure. Thus, a detailed description of the microstructure features of the Complex Phase (CP) steels is required to investigate the correlation between the multiphase structure and exploitation properties. Smoothing of gradients of properties can be reached by control of such phenomena as segregation of elements, evolution of the morphology of hard phases, evolution of dislocation populations in the soft phase and precipitation. Modelling of these phenomena requires advanced models. Large spectrum of material models with various complexity and various predictive capabilities are available now [4]. However, mean field models, which predict only average parameters of the microstructure, are not applicable. Multiscale models, which use representative volume element (RVE) have to be used. Since computing costs are an important criterion in the model selection, designers intensively search for methods of model reduction, see discussion in [4]. Application of the statistically similar representative volume element (SSRVE), which was proposed in [5], is one of the possibilities.

The basic idea of the SSRVE is to replace a RVE with an arbitrary complex inclusion morphology by a periodic one composed of optimal unit cells [5]. To reach this goal, the parameters describing fraction of different phases and their geometrical characteristics are determined for a considered microstructure. Following this, optimization methods are used to design morphology of hard inclusions in the SSRVE. Authors have already applied SSRVE to modelling deformation of Dual Phase (DP) steels with the microstructure composed of hard martensite islands in soft ferrite matrix [6]. In publication [7] four shape coefficients were considered to describe multiphase microstructure. Seven more parameters, which are used in the image analysis, were added and described in the paper [6]. Since a large number of parameters can be used to describe multiphase microstructure, uniqueness of the solution is always questionable.

The objectives of the present paper were formulated with the above comments in mind. Computational aspects of the SSRVE design for the microstructures were discussed and accuracy as well as uniqueness of the solution were evaluated. Beyond this, as it has been mentioned above, complex phase steels microstructures, which allow to obtain smoother gradients of properties, are of particular interest now. Thus, an attempt to design SSRVE for multiphase microstructures composed of various constituents and phases was the main objective of the work.

2 Statistically Similar Representative Volume Element

2.1 General Idea

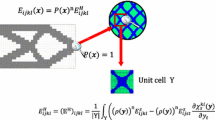
In the micro-macro modelling approach an RVE representing the underlying microscale domain is usually attached at each Gauss point of the macroscopic solution [8]. The constitutive law describing material behaviour in the macroscale is obtained by averaging the first Piola-Kirchoff stresses with respect to the RVE. The theoretical basis of the micro-macro modelling is well described in the scientific literature (e.g. [5]) and it is not repeated here. In the SSRVE application to DP steel, already mentioned in introduction [6], the focus was on development of the simplest SSRVE, which allows to decrease the computing costs and will make micro-macro modelling approach more efficient. The basic idea was to replace an RVE with an arbitrary complex inclusion morphology by a periodic one composed of optimal unit cells, as shown in Fig. 1.

Fig. 1.

Illustration of the basic concept of the SSRVE, a) RVE, b) periodically arranged SSRVE.

This idea is applied in the present work to the analysis of the more sophisticated steels microstructures composed of more than two phases like CP or TRIP steels with Transformation Induced Plasticity effect. Both of these materials are difficult to analyse and model, while various phases are characterized by different properties and morphologies. This fact highly influences computational complexity of both creation and application of SSRVE models for such materials in practice.

2.2 Design of the SSRVE

The process of SSRVE creation consists of the following steps (Fig. 2):

Fig. 2.

Procedure of SSRVE creation

• image analysis aiming at conversion of set of original micrographs from optical microscope to RVE containing separated phases and grains inside of them,

• qualitative and quantitative analysis leading to obtain information on shape coefficients based on grains/phases shapes, which allows to apply sensitivity analysis and indicate the most important coefficients characterizing microstructure,

• construction of a cost function for optimization procedures, implementation of a proper optimization procedure and selection of the most suitable results.

The procedure of SSRVE creation starts with an analysis of original micrographs, which aims at creation of binary (segmented) images with separated phases or inclusions. The algorithms for processing of various micrographs are presented in details in [9]. Then, in the case of 2D SSRVE, the shape coefficients of inclusions in original images are estimated directly from the segmented pictures. In the case of 3D procedure, the reconstruction of 3D microstructure on the basis of 2D images has to be performed [10]. Afterwards, the shape coefficients of 3D inclusions are estimated. Ohser and Muecklich [7] proposed four basic parameters for statistical shape description. Few more parameters, which are used in the image analysis, were added and described by Authors in [6]. In consequence, the following parameters describing shape of inclusions were considered: volume fraction, area/volume, roundness, ellipsoid fit, contour to center ratio, border index, mean curvature, total curvature, Malinowska coefficient, Blair-Bliss coefficient, Danielsson coefficient and Haralick coefficient. Not all of these parameters can be adapted from 2D to 3D. Thus, some of the coefficients are used only for 2D SSRVE.

Additionally, statistical and rheological coefficients are calculated to obtain full set of reference coefficients, which describe all aspects of material properties and which are used further in optimization procedure. Brandts et al. [11] introduced the higher order statistical measures for microstructures: n-point probability functions, spectral density and lineal-path function. The latter parameter is crucial in description of anisotropic microstructures, while it describes the probability that a complete line segment a = $\overrightarrow {{{\mathbf{a}}_{1} {\mathbf{a}}_{2} }}$ is located in specific direction in the same phase, where a₁ = {x₁, y₁} and a₂ = {x₂, y₂} are coordinates of the ends of the line segment. Lu and Torquato [12] gave a general mathematical description of this measure for multi-phase anisotropic materials. Simplified approach, which is applicable to DP microstructures represented in form digital images composed of a set of pixels, can be defined by the following equation:

$$ \zeta_{LP} \left( {m,k} \right) = \frac{1}{{N_{x} N_{y} }}\sum\limits_{p = 1}^{{N_{x} }} {\sum\limits_{q = 1}^{{N_{y} }} {\chi \left( {\overrightarrow {{{\mathbf{a}}_{1} {\mathbf{a}}_{2} }} } \right)} } $$

(1)

where m and k are the length of vector $\overrightarrow {{\varvec{a}_{1} \varvec{a}_{2} }}$ in x and y directions respectively, N_x, N_y are the dimensions of micrograph in pixels, and $\chi^{(i)} \left( {\overrightarrow {{{\mathbf{a}}_{1} {\mathbf{a}}_{2} }} } \right)$ is modified indicator function defined for phase $D^{(i)}$ as:

$$ \chi^{(i)} \left( {\overrightarrow {{{\mathbf{a}}_{1} {\mathbf{a}}_{2} }} } \right) = \left\{ {\begin{array}{*{20}c} {1\,\,\,\text{if} \,\,\,\overrightarrow {{{\mathbf{a}}_{1} {\mathbf{a}}_{2} }} \in D^{(i)} } \\ {0\,\,\,\text{otherwise} \,\,\,\,\,\,\,\,} \\ \end{array} } \right. $$

(2)

The estimated shape coefficients as well as statistical measures are the main elements of optimization function aiming at SSRVE creation. Optimization procedure is based on approach proposed in [6]. Originally, a method for the construction of simple periodic structures for the special case of randomly distributed circular inclusions with constant equal diameters was proposed by Povirk [13]. In that work the positions of circular inclusions with given diameter were found by minimizing the objective function, which was defined as a square root error between spectral density of the periodic RVE and non-periodic real microstructure. In our work this function was adapted to the following form:

$$ \Upphi = \sqrt {\sum\limits_{i = 1}^{n} {\left[ {w_{i} \left( {\frac{{\varsigma_{i} - \varsigma {}_{iSSRVE}}}{{\varsigma_{i} }}} \right)} \right]} } $$

(3)

where: w_i – normalized weights, n – number of coefficients, ζ_i – i^th reference coefficient obtained from original microstructure, ζ_iSSRVE – i^th coefficient obtained from SSRVE. The coefficients include all mentioned parameters describing shape, rheology and statistics. The current implementation of optimization procedure is based on genetic algorithm (GA), where chromosome is composed of m elements representing coordinates of control points determining SSRVE shape. These points are connected with spline functions forming smooth shape of SSRVE inclusion. Calculations of the objective function are performed iteratively for each proposition of new SSRVE shape. The optimization loop is preceded by sensitivity analysis (SA), which allows to determine the most influential parameters of the optimization or to determine the weights used in the objective function (3).

2.3 Optimization Procedure

On the basis of results obtained from sensitivity analysis the reference coefficients, their values and weights were established. A set of these parameters was used further in optimization procedure as $\varsigma_{i}$ in (3). Multi-iterative genetic algorithm [14] was applied as an optimization procedure. The procedure is composed of the following steps:

• Generation of initial population – random generation of n specimens containing information about coordinates of control points and their weights. Size of the specimen depends strongly on a number of control points describing inclusions in the SSRVE. At the beginning of calculations the control points form m random shapes, where m is a number of inclusions.

• Estimation of the objective function value – the procedure calculates values of $\varsigma_{iSSRVE}$ on the basis of shapes of inclusions in subsequently generated SSRVEs. Shapes of these inclusions are described by Non-uniform Relational B-Splines (NURBS). These parametric curves are controlled by basic interpolation functions and a set of mentioned control points. The weight of each control point influences the position of curve near the particular control point. The shapes of inclusions influence also rheological properties and statistical description of microstructure. Rheological model of SSRVE is determined by processing of this element in virtual uniaxial compression, tensile and shear deformation tests. Obtained stress-strain relations allow to calculate equivalent tensile stress, which describes material rheology. The main statistical measure is lineal-path function, calculated directly from pixels or voxels values of SSRVE.

• Stop conditions – two fundamental conditions are implemented i.e. number of iterations and mean square error between expected and actual objective function.

• Application of genetic operators – crossing and mutation operators were implemented in the presented approach. The former operator is responsible for exchange of random number of genes between two specimens (Fig. 3).

  Fig. 3.

  

  Illustration of crossing operator for 2D specimens.

The first of mutation operators (Fig. 4) changes positions of control points regarding centre of gravity of the shape. The operator determines random set of control points, which will be mutated, and then the new position is calculated also on the basis of randomized operations. The second mutation operator changes the positions of control points in X or Y axis direction by using random values of coordinates in the vector of translation.

Fig. 4.

Illustration of mutation operator for 2D specimens.

• Generation of a new population – the specimens obtained after operations of crossing and mutation are included in the new population. In each subsequent iteration, each specimen is validated. On the basis of validation the worst specimens are removed from population, some of the best specimens go further without changes and the rest is passed again to crossing and mutation operators.

In the case of 3D calculations shape of inclusion is composed of 2D layers, which are used in reconstruction algorithm mentioned at the beginning of this section. Thus, the specimen in 3D contains additional Z coordinates, which influence all the algorithms inside optimization procedure. Therefore, the crossing operator is based on exchange of a set of whole layers between two specimens instead of a set of single control points. The first mutation operator behaves similarly by translating of whole layers in Z axis direction, while the second mutation operator chooses two layers randomly and replaces them inside one SSRVE.

3 SSRVE for Complex Phase Steel

Verification of the SSRVE concept for more than two phases inside material microstructure was performed on micrographs obtained for CP steels. This group of steels is a part of Advanced High Strength Steels (AHSSs), widely used by modern industry and characterized by elevated mechanical properties [15]. High strength of CP steels is gained through extremely fine grain size and microstructure containing small amounts of martensite, pearlite and retained austenite embedded in a ferrite-bainite matrix. Therefore, from numerical simulations point of view such material is very difficult to be modelled, especially meshing of computational domain and coverage of larger scale with full field micro model. Example of CP micrograph is presented in Fig. 5.

Fig. 5.

Microstructure of CP steel composed of bainite (1^st phase in blue), martensite (2^nd phase in green), ferrite matrix (yellow), small inclusions of retained austenite (light yellow). (Color figure online)

A set of fundamental input data is composed of series of images, like in Fig. 5, obtained from optical microscope or EBSD, which marks various phases and inclusions in different colours. Such set of images is passed to image analysis procedures to divide original micrographs into subsets dedicated to different phases (Fig. 6).

Fig. 6.

Separated phases of microstructure: (a) bainite – 40% of volume fraction, (b) martensite – 2%.

3.1 SSRVE Generation

For validation purposes and SSRVE generation two CP steels were analysed with different volume fraction of phases: I – 40% of bainite and 7% of martensite, II – 30% of bainite and 15% of martensite. Both steels contained 50% of ferrite. Optimization procedure responsible for generation of SSRVEs was performed several times for both cases assuming random initial generation of SSRVE in the first iteration. The set of images for each steel contained six micrographs taken in various places in material. This assumption allowed to evaluate whether obtained elements will result in the same material response as far as gradient of properties is considered (Sect. 4.2). The results of SSRVE calculations are presented in Fig. 7.

Fig. 7.

Three selected results of SSRVE generation for CP steel variant I (a-c) and variant II (d-f)

3.2 Computing Cost Analysis

Computing cost mostly depends on selected shape coefficients. Preliminary sensitivity analysis allowed for the identification of representative geometric coefficients for each phase. In the case of bainite grains: volume fraction of phases ξ₁, mean curvature ξ₈, ratio between maximum distance in inclusion phase and its circumference Lp2, ratio between maximum and minimum distance in inclusion phase Lp3, compactness factor R_c were selected. In the case of martensite grains: volume fraction of phases ξ₁, ellipsoid fit ξ₅, mean curvature ξ₈ were used. The details of each coefficient are broadly described in [6, 16]. Satisfactory results were obtained after about 300 iteration for each attempt. Minimal improvements in the objective functions were observed in further analysis. Full calculations (1000 iterations) took about 10 h on a typical, 8 cores, desktop computer, but a satisfactory threshold was reached after just 2 h. Examples of the changes of the Root Mean Square Error (RMSE) in the optimization procedure are shown in Fig. 8.

Fig. 8.

Root Mean Square Error minimization during SSRVE generation procedure.

4 Solution Uniqueness Analysis

As it has been mentioned in the introduction, depending on their microstructure multiphase steels show differing damage mechanisms. In general global formability and local formability is distinguished [2]. The former is an ability of a material to undergo plastic deformation without formation of a localized neck respectively to distribute strains uniformly. The latter is an ability of a material to undergo plastic deformation in a local area without fracture. These two features can be characterized experimentally as described in [2]. In the present work, however an attempt of the numerical approach to this problem is described. An assumption was made that by evaluation of gradients of properties in the microstructure, local formability can be predicted.

4.1 Simulation of Deformation of Complex Phase Steels

Distribution of the properties in complex phase steels depends on several phenomena, which are mentioned in the introduction. In the present paper the focus is on calculation of gradients of properties, and therefore, properties of each phase were described by the work-hardening curve. The curves were taken from the literature [17] without an analysis of phenomena responsible for the hardening. Typical CP microstructure was analysed and SSRVE was created, as described in Sect. 3.1. To reveal different behaviour of hard and soft constituents, that SSRVE was subjected to small plastic deformation of 5%. The calculations were performed using Finite Element Method (FEM) and results are presented in Fig. 9.

Fig. 9.

Results of uniaxial compression tests for SSRVE with distribution of the flow stress for variant I (a-c) and variant II (d-f).

4.2 Gradients of Properties

As it was shown in [3], gradients of mechanical properties in the microstructure can be considered as a measure of the local formability. The local flow stress of the material was selected as a measure of these properties in the present work. It was assumed that description of the gradients can be based on the local and global sensitivity analysis (SA) methods [18]. Considered physical phenomenon during material manufacturing or processing can be described as a non-stationary system y(t, p, x), where p is a vector of process parameters including model coefficients, x is a position vector in the computation domain, t is time. To predict gradient distributions in the whole material volume, the first order sensitivity indices were applied and expressed through a Taylor series expansion with respect to a position vector x. Thus, locally, sensitivity matrix can be computed as:

$$ {\mathbf{S}} = \left\{ {s_{ij} } \right\} = \left\{ {\partial y_{i} /\partial x_{j} } \right\} $$

(4)

where y_i - model outputs, x_i - components of a position vector x.

On the other hand, the screening sensitivity analysis method, called Morris Design (MD) [15], allows to estimate a global measure of the sensitivity. In this algorithm elementary effects (ξ_i) are defined:

$$ \xi_{j} ({\bar{\mathbf{x}}}): = \frac{{{\mathbf{y}}(\bar{x}_{1} , \ldots ,\bar{x}_{j - 1} ,\bar{x}_{j} + \Delta_{j} ,\bar{x}_{j + 1} , \ldots ,\bar{x}_{k} ) - {\mathbf{y}}({\bar{\mathbf{x}}})}}{{\Delta_{j} }} $$

(5)

where: y - model output, ${\bar{\mathbf{x}}}$ ∈ Ω ⊂ Ρ^k – k - dimensional vector of model inputs x_j, Δ_j - an increment of the model input $\bar{x}_{j}$.

Sampling $\bar{x}_{j}$ in the space Ω gives a finite distribution of elementary effects ξ_j calculated for the j^th component of an input vector ${\bar{\mathbf{x}}}$. Based on this distribution expected value μ_j for j^th model input can be estimated through the classic estimators for independent random samples.

For estimation material gradient properties let ${\bar{\mathbf{x}}}$ from MD algorithm be a position vector x in the equation describing a process. Thus, the elementary effects (5), for Δ_j → 0, correspond to derivatives in the sensitivity matrix (4). In the present work only one model output was considered (i = 1). The matrix S is a vector calculated for one model input ${\bar{\mathbf{x}}}$ and for gradient estimation $\left\| {\mathbf{S}} \right\|$ was taken. The distribution of $\left\| {\mathbf{S}} \right\|$ was obtained by sampling ${\bar{\mathbf{x}}}$ over the whole computation domain. Next, based on the MD method assumptions, two sensitivity indices were estimated: expected values μ of all $\left\| {\mathbf{S}} \right\|$ as a global measure of properties gradient and μ_0.05 as expected values of the gradient properties for 5% of maximum values. The last measure was introduced to evaluate maximum gradients in the microstructure. However, since a single maximum value of gradient could be a result of a numerical error, a mean of 5% of maximum values was calculated.

One of the main assumptions of the gradients estimation algorithm is that the data for which gradients are estimated may be either experimental or derived from numerical simulations. In general, the data is defined as a points cloud form. The efficient management of this cloud required the introduction of a specific data structure for a flexible search of single points and their neighbours. For this, a quadtree structure [19] was developed and adopted for gradients estimation requirements.

To approximate value v for point of coordinates (x₁, x₂), based on N points of known values v_i, i = 1,…, N, Shepard’s method and the inverse distance weighting were applied [20]:

$$ \begin{aligned} v(x_{1} ,x_{2} ) = \left\{ {\begin{array}{*{20}l} {v_{i} } & {\exists i:x_{1} = x_{1}^{i} \wedge x_{2} = x_{2}^{i} } \\ {\frac{{\sum\nolimits_{i = 1}^{N} {w_{i} (x_{1} ,x_{2} )v_{i} } }}{{\sum\nolimits_{i = 1}^{N} {w_{i} (x_{1} ,x_{2} )} }}} & {otherwise} \\ \end{array} } \right. \hfill \\ w_{i} (x_{1} ,x_{2} ) = \left( {\sqrt {(x_{1} - x_{1}^{i} )^{2} + (x_{2} - x_{2}^{i} )^{2} } } \right)^{ - 2} \hfill \\ \end{aligned} $$

(6)

Gradients of the flow stress in the SSRVE were calculated in an analytical way for the approximation given by Eq. (6) and using the finite difference method. Finally, expected values μ and μ_0.5 were computed as global measures of gradients of properties. The gradient distributions for two variants of SSRVE are presented in Fig. 10 and the quantities of μ were as follows: 55.2 MPa/μm, 53.4 MPa/μm and 502.5 MPa/μm for variant I and plots (a-c), and 62.6 MPa/μm, 36.8 MPa/μm, 110.4 MPa/μm for variant II and plots (d-f), respectively. For the measure μ_0.5 the results were: 412.0 MPa/μm, 277.6 MPa/μm and 17508.7 MPa/μm for variant I (plots (a-c) Fig. 10), and 524.8 MPa/μm, 179.7 MPa/μm, 1802.9 MPa/μm for variant II (plots (d-f) Fig. 10).

Fig. 10.

Gradient distributions for SSRVE: variant I (a-c), variant II (d-f).

4.3 Discussion of Results

SSRVE elements were generated with the goal function based on the selected geometric coefficients and a proper description of a microstructure morphology was obtained. Optimization based on the genetic algorithms was efficient and satisfactory results were obtained after about 300 iteration for each attempt. On the other hand, although the geometrical effect was correct, subsequent runs of the optimization procedure yielded the properties of material, which were not unique and different values of gradients were obtained for the same phase composition. In the present work the SSRVEs were selected and analysis was performed to highlight those differences.

Analysis of the results of global measures of material gradient properties showed that the differences are significant and they can reach an order of magnitude in extreme examples. Keeping in mind the results of calculations performed so far, a suggestion was made that the goal function for SSRVE generation cannot be based solely on the geometrical parameters and it should include also the data of maximum strains or stresses for each of the material phase. Further investigations over these problems will be carried out.

5 Conclusions

Methodology of design of the SSRVE for complex phase steel composed of three phases and application of this SSRVE to evaluation of gradients of properties is described in the paper. The following conclusions were drawn:

• Application of the SSRVE allowed significant decrease of the computing costs comparing to classical RVE solution in terms of element dimension. Following this, it is possible to apply more SSRV elements in a multiscale simulation than when RV elements are with the same computation cost.

• Good convergence of the optimization was observed during SSRVE generation. Satisfactory results were obtained after about 300 iteration for each attempt.

• Design of the SSRVE based on the geometrical features only does not guarantee uniqueness of the solution. Different gradients were obtained for one phase composition and several optimization runs. It leads to a conclusion that additional parameters based on maximum strains and stresses in various phases should be introduced in the objective function. This will be subject of the future works.

• The methodology based on the sensitivity analysis proved to be efficient for evaluation of gradients of materials properties when they are defined as a cloud of points.