Open Boundary Modeling in Molecular Dynamics with Machine Learning

Abstract

Molecular-continuum flow simulations combine molecular dynamics (MD) and computational fluid dynamics for multiscale considerations. A specific challenge in these simulations arises due to the “open MD boundaries” at the molecular-continuum interface: particles close to these boundaries do not feel any forces from outside which results in unphysical behavior and incorrect thermodynamic pressures. In this contribution, we apply neural networks to generate approximate boundary forces that reduce these artefacts. We train our neural network with force-distance pair values from periodic MD simulations and use this network to later predict boundary force contributions in non-periodic MD systems. We study different training strategies in terms of MD sampling and training for various thermodynamic state points and report on accuracy of the arising MD system. We further discuss computational efficiency of our approach in comparison to existing boundary force models.

P. Neumann and N. Wittmer thank the Scientific Computing Group, University of Hamburg, for providing computational resources.

1 Introduction

1.1 Molecular Dynamics

Molecular dynamics (MD) enables investigations of fluids, suspensions and materials at the nanoscale. For this purpose, the considered system is modeled in terms of molecules or atoms that are characterized through positions $\mathbf{x} _i$ and velocities $\mathbf{v} _i$, as well as through forces $\mathbf{F} _i$, with the latter typically arising from pairwise inter-molecular interactions in terms of pair potentials [13]. The interplay of these variables is described by Newton’s equations of motion

$$\begin{aligned} \begin{array}{l} \frac{d\mathbf{x} _i}{dt} = \mathbf{v} _i,\\ \frac{d\mathbf{v} _i}{dt} = \frac{1}{m_i}{} \mathbf{F} _i. \end{array} \end{aligned}$$

(1)

We will restrict considerations in the following to short-range single-site Lennard-Jones NVT systems, that is two spherical particles i, j interact via forces

$$\begin{aligned} {} \mathbf{F} _{ij}=\frac{48\epsilon }{\sigma ^2}\left[ \left( \frac{\sigma }{r_{ij}}\right) ^{14}-\frac{1}{2}\left( \frac{\sigma }{r_{ij}}\right) ^8\right] \mathbf{r} _{ij} \end{aligned}$$

(2)

with $\mathbf{r} _{ij}:=\mathbf{x} _i-\mathbf{x} _j$, $r_{ij}:=\Vert \mathbf{r} _{ij}\Vert$, as long as the particles lie within a cut-off distance $r_{ij}\le r_c$; the total force on a particle arises as $\mathbf{F} _i=\sum \limits _{i\ne j} \mathbf{F} _{ij}$. The parameters $\epsilon ,~\sigma$ are material-dependent parameters. Temperature is controlled via a thermostat. Despite its simplicity, this model is used in a great variety of applications and implemented in basically all popular MD packages; we made use of the package LAMMPS for all our tests [12].

1.2 The Challenge: Modeling Open Boundaries

MD for fluid systems is often used in combination with periodic boundary conditions. This approach naturally extends the molecular interaction potential across the actual boundaries of the considered system. However, modeling open boundaries for non-periodic domains—which are relevant for actual flow scenarios in engineering applications or, in particular, in multiscale flow simulation such as molecular-continuum coupling [3, 9, 14]—poses a grand challenge, especially for dense particle systems: as no particle interactions exist between near-boundary particles and the fluid domain beyond the boundary, particles would be pushed out of the domain. This results in invalid thermodynamic conditions and pressure distributions as well as in unphysical particle fluxes. Consequently, an open boundary force model is required to counteract this behavior and ties back into the MD system via an additional forcing term $\mathbf{F} _i^{ext}$, i.e. $\mathbf{F} _i=\sum \limits _{i\ne j}{} \mathbf{F} _{ij}+\mathbf{F} _i^{ext}$ for particles close to the open boundary.

1.3 Open Boundary Force Modeling: State-of-the-Art

The goal of an open boundary force model is typically (i) to impose the correct average hydrodynamic pressure on the MD system, (ii) to take into account the molecular information of the system, (iii) to yield the correct molecular structure close to the boundary, i.e. the model shall add as little physical perturbations to the particle system as possible, and (iv) to perform at acceptable computational cost, that is particle updates close to the boundary must not be inhibitively more expensive than particle updates in the inner part of the computational domain.

The first developed open boundary force models were based on analytical formulae, incorporating the pressure, particle density and, potentially, weighting functions to take into account the distance of a particle from the boundary [3, 4, 11]. These approaches, however, lack molecular information (ii) and resulted in rather severe density perturbations in proximity of the open boundary (iii). A significant reduction of perturbations could be achieved through the use of radial distribution functions (RDFs) [14], which impose the average hydrodynamic pressure (i) and—through the RDFs—incorporate molecular information (ii). Although accurate density profiles near the boundary were obtained for several particle systems, stronger oscillations were observed in case of very dense particle systems (iii). Besides, the creation of the actual force model from the measured RDFs required an additional interpolation/integration step. An extension of this approach to multi-site molecules was presented in [10].

A purely density-driven approach was presented in [7]: the particle density is measured close to the boundary, and its trend is captured over time via noise filters and gradient approximations. Based on this trend, the boundary force is adopted to yield a flat density profile at the boundary. While this algorithm also naturally extends towards multi-site molecules [6], easily extends towards non-stationary flows (i.e. adopting boundary forces to varying flow velocities) and can be automatically employed for arbitrary MD systems, it misses molecular information (ii); to the authors’ knowledge, no molecular structure investigations have been provided for this method (iii), except for molecular orientation measurements in case of multi-site molecules [6]. Besides, an amplification factor for the force relaxation needs to be prescribed which is not necessarily known a priori.

Finally, a parameter space exploration was carried out in [15, 16] for single-site Lennard-Jones systems and a regression formula for a boundary force in dependence of a particle’s distance from the open boundary was derived over a wide range of temperature and density values. While this formula is highly valuable for many systems and provides accurate forcing (i), (ii), no molecular investigations were reported so far (iii). Besides, entire parameter space explorations are computationally very expensive.

All derived methods were found to perform at acceptable cost (iv) in molecular-continuum simulations with open boundaries, with some limitations of the approach presented in [10].

1.4 Outline and Objective

In the following, we describe a methodology that uses neural networks to estimate open boundary forces from existing MD data (ii) via regression. We demonstrate that the neural network-based approach

• provides accurate open boundary force predictions that are in good agreement with and partly outperform the model by Zhou et al. [15, 16] (i),

• retains the molecular structure rather well, even in very close proximity of the open boundary (iii); this is also shown for the Zhou model in this context,

• performs at acceptable computational cost (iv).

MD data is very noisy and there are several variants available to improve neural networks for these cases. For the sake of simplicity and facilitated applicability of our method, we make use of standard neural network formulations and we further implemented the algorithm using the freely available open source software TensorFlow.

We describe the design and discuss the choice of our ML-based approach in Sect. 2. The sensitivity of our ML-based approach with regard to sampling methodology and used parameters as well as of the Zhou model are studied in Sect. 3.1; more in-depth comparison of the molecular structure close to the open boundary for the Zhou model and the best ML-based approximation is given in Sect. 3.2. Estimates on sampling numbers and training epochs are provided in Sect. 3.3. To underpin the generality of the method, various MD state points are examined in Sect. 3.4, followed by a discussion of run times of the open boundary force-augmented MD systems in Sect. 3.5. We close with a summary and give an outlook to future work in Sect. 4.

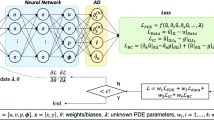
2 Machine-Learning Approach to Boundary Forcing

We use TensorFlow [1, 2] to develop a neural network model for nonlinear regression of boundary forces in non-periodic boundary conditions. Our initial model contains one hidden layer with five neurons. This number results from a reasonable estimate to approximate the average force and its gradient sufficiently well, given, for example, the interpolating representation described by Zhou et al. [15, 16]. The commonly used sigmoid function tanh [8] serves as activation function within the hidden layer whereas on the output layer a linear activation function is used.

For optimization of the parameters, we apply the ADAM [5] optimizer in combination with the mean-squared-error (MSE) function. ADAM is an extension of the standard stochastic gradient descent which claims to be computationally efficient, especially in terms of memory usage; MSE is a default choice for the error function. Due to rotational symmetry of single-site particles, we use solely the distance of particles from the open boundary as input feature and the boundary force perpendicular to the respective boundary as output feature. Both input and output features are obtained from periodic MD simulations in which we assume a virtual wall inside the domain: we determine corresponding distances of the particles from the virtual wall as well as forces that act onto the particles from beyond the virtual wall. The network thus only contains one input and one output neuron. Input data are normalized to lie within the unit interval [0, 1]. Since MD systems are typically equilibrated initially in periodic settings, the equilibration phase can be immediately used to generate these values for both training and validation of the network.

The learning rate was set so 0.001 in all of our scenarios which is the default for the ADAM optimizer, and the network was trained with a number of epochs between 1000 and 30,000.

Fig. 1.

Predicted boundary forces compared to Zhou force. (a) Force predictions and actual, measured samples. (b) Close-up of predicted force profiles.

3 Results

For our initial tests, we set up a short-range single-site Lennard-Jones-based system with reduced parameters $\sigma \,=\,\epsilon \,=\,m\,=\,k_B\,=\,1$, where $k_B$ denotes the Boltzmann constant. The Lennard-Jones potential has a cut-off distance $r_c\,=\,2.5\sigma$. We simulate a box of size $30\times 30\times 30$ with a mass density $\rho \,=\,0.81$, resulting in $21,952$ particles homogeneously distributed within the simulation box. Temperature was set to 1.1. The time step size $\varDelta t$ was set to $0.002$.

MD equilibration was performed over 20,000 time steps employing periodic boundary conditions on all sides of the simulation box. This results in a random distribution of the molecules with a fluctuating density profile with the same mean value $\rho$; every corresponding MD simulation with open boundaries should feature the same mean value and, optimally, no or only small deviations from it. We used this state to generate training samples for the neural network from a subsequent period of 110,000 time steps. Afterwards, the left and the right boundary were changed into reflecting boundaries to hinder particles from escaping. Besides, the force model was activated.

The system was then equilibrated for another 5,000 time steps. From this point on, each simulation was run over a period of 20,000 time steps. Sampling of all quantities reported in this work was performed within this last part of the simulations.

3.1 Sensitivity of Machine Learning-Based Algorithm

For first investigations, we generated 200,000 samples from the periodic simulation. As a base setup for training, we randomly chose 80,000 of these samples (we refer to this strategy as regular sampling in the following) for training over 30,000 epochs.

In Fig. 1(a), the resulting boundary forcing estimate is displayed together with the Zhou profile, and actual force contributions used to train the model. Both our ML model and Zhou’s method perform a regression upon the Lennard-Jones force model; Fig. 1(b) shows a close-up of the arising force profiles. Apparently, the trained ML model diverges from the Zhou profile in close proximity of the boundary. The minimum of the force profile is approximately the same for both models, yet it is slightly shifted towards the right in the ML approach.

The remaining parameters are the same as in Sect. 2. The following analyses have been computed by sampling periodic and, especially, open boundary simulations over 20,000 timesteps.

Fig. 2.

(a) Density profile of a simulation using a model trained with 80,000 samples, compared to the density profile of a simulation using Zhou forcing. (b) RDF of the same simulation computed over a strip close to the boundary with thickness $r_c$. Dashed: Density and RDF as result of applying the Zhou force at the boundaries. Continuous: Resulting quantities when using our predicted force model in the simulation. Dotted: Periodic RDF

Figure 2(a) shows the density profile of our simulation using this setup in comparison to a simulation using Zhou boundary forcing. The quality of the neural network’s force computation reaches basically the same accuracy as the Zhou method: the maximum density deviation of our ML-based simulation is 12.9% compared to 11.4% in the Zhou model. Note that our sampling is carried out in small bins of size 0.1 to capture fine-scale structures in the different quantities in very close proximity of the boundary, which explains the actual visibility of these deviations. This is done for a detailed comparison of the methods; very good accuracy was already shown for the Zhou model in [15]. In a distance of one cut-off region ($2.5\sigma$), the density profiles of periodic and open boundary simulation are basically indistinguishable.

Fig. 3.

Distribution of x-velocities for particles using Zhou model and ML-based model within a boundary distance $r_c$. Gray: Distribution resulting from a simulation using (a) the Zhou boundary force and (b) our predicted boundary force

The RDF in Fig. 2(b) has been computed over the boundary region within a boundary strip of thickness $r_c$. Due to non-periodicity of our domain, we scaled the distribution by a volumetric factor per particle depending on the distance from the open boundary to account for the correspondingly missing particle pairs across the open boundary. The RDF of our simulated model near the boundary exhibits the same contour as the RDF obtained from a fully periodic and a Zhou-based open boundary simulation. We further checked the distribution of x-velocities (i.e., the velocity component of the molecules perpendicular to the open boundary) within the same boundary strip. Figure 3 demonstrates that the expected normal distribution is captured well.

In order to increase the efficiency of the training, we reduced the number of samples needed to train the model. For this purpose, we organized the boundary region in bins and evenly distributed the training samples over these bins.

Fig. 4.

(a) Density profile of a simulation trained with binned sampling approach. (b) Density profile for run with regular sampling using 10,000 epochs for training

Figure 4(a) shows the results for training with binned samples, using 100 bins with 512 samples in each bin to discretize the boundary strip $r_c$. The resulting density exhibits only slight fluctuations similar to the Zhou model and the original ML-based regular sampling model, i.e. the density deviates by less than 10.8%; yet, through the binning and corresponding homogeneous distribution of samples, we require 36% less samples than in the regular sampling case.

We further investigated the influence of the number of epochs used in the training. A resulting density profile for a reduced number of 10,000 epochs is shown in Fig. 4(b). The deviations are higher, amounting to approx. 16% in this case.

Using the ML-based approach, we were able to even outperform the Zhou model in terms of particle density approximation. One of the results is shown in Figs. 5(a) and (b). This run used 19,000 randomly selected samples and training was carried out over 30,000 epochs. The force estimate behaves similarly compared to the force estimate from Fig. 1(b) but the gradient is smoother within the range [0, 0.5] and there seems to be little more emphasis on attracting forces.

Fig. 5.

Force and density profiles of best case scenario using 19,000 samples over 30,000 epochs

The density in this run deviates by 8.4%, which is ca. 3% less than the deviations in the Zhou-based forcing scenario.

We further studied the influence of the size of the ML-based model’s hidden layer, e.g. changing from five to three hidden neurons. Two of the resulting density profiles are shown in Fig. 6. Figure 6(a) shows the best run using regular sampling during training, Fig. 6(b) shows the best result using binned sampling. Using binning results in a density deviation of 9.8%, whereas the regular sampling method reaches 11.5%. As we were not able to produce better results in most configurations that could compare to the other models, we decided to stay with the initial five neurons. We further experimented with different learning rates. This approach did not significantly improve the quality of the trained models, but could possibly be employed for optimizing the performance of the training phase.

Fig. 6.

Two examples from running simulations using models which were trained with three instead of five neurons

3.2 Best Case Properties

In the previous section we have demonstrated the general applicability of our approach to a Lennard-Jones fluid. Next, we examine the best run so far more closely and compare its results with those of the Zhou simulation.

Figure 7 shows the RDF profiles sampled from the simulation in significantly thinner boundary strips. Both RDFs from Zhou and ML-based model slightly underestimate the maximum peak of the expected RDF (obtained from the periodic case).

Fig. 7.

RDF profile sampled over boundary strip of thickness (a) $1.25\sigma$ and (b) $0.3125\sigma$

We sampled the distribution of x-velocities in the same boundary strips, cf. Fig. 8. While the estimation in the strip of thickness $1.25\sigma$ resembles the normal distribution, (very) slight fluctuations are visible for the $0.3125\sigma$-thick strip.

Fig. 8.

Distribution of x-velocities sampled over boundary strip of thickness (a) $1.25\sigma$ and (b) $0.3125\sigma$

3.3 Estimating the Sampling Properties

We further aimed at an estimate for how many samples are needed to obtain accurate force profiles for the subsequent simulation. We therefore ran tests with training sample sizes ranging from 1000 to 150,000 samples. We ran theses tests with 10,000, 20,000, and 30,000 epochs and extracted the maximum density deviation per simulation.

The results of these experiments are shown in Fig. 9. Obviously, less than 10,000 samples is not enough to generate a valid model.

Fig. 9.

Maximum density deviations for varying sample size using different numbers of epochs

Fig. 10.

Density and RDF for setup ${\rho =0.5}$ using boundary force prediction

3.4 Varying State Points

We further validated our method in simulations of varying densities. For this purpose, we set up two more simulations, using density values ${\rho =0.5}$ and $\rho =0.3$. In both cases, temperature was set to ${T=1.1}$. Simulation time was scaled up linearly according to the base setup of ${\rho =0.81}$ to provide comparable sampling quality and, thus, to enable comparison with the results reported in prior sections. We did not compare the resulting models to the Zhou model, since this model’s underlying parameter space exploration does not capture these state points.

Fig. 11.

Distribution of x-velocities for ${\rho =0.5}$, boundary strip thickness ${0.3125\sigma }$

Figure 10(a) displays the resulting density profile of one simulation for the case of ${\rho =0.5}$. The periodic density profile deviates from the expected density by 6.5%, the ML profile deviates by 5.9%. Close to the boundaries, we can still observe slightly higher fluctuations within the ML profile. Figure 10(b) shows the RDF estimate from the boundary strip of thickness ${0.3125\sigma }$. The estimated RDF fits the expected radial distribution nearly perfectly.

The estimated velocity distribution is shown in Fig. 11. Similar to the default case $\rho =0.81$, the normal distribution is basically perfectly matched.

We made similar observations for the test case with density ${\rho \,=\,0.3}$. In this case, the density in the periodic simulation deviates by 6.7% whereas the shown ML model deviates by 8.2% (cf. Fig. 12(a)). The estimated velocity distribution is again captured well near the boundary, (cf. Fig. 12(b)).

Fig. 12.

Density and distribution of x-velocities for ${\rho \,=\,0.3}$ using boundary force prediction

Fig. 13.

(a) Training times of different sampling setups. (b) Run times of different setups, running periodic simulations or open boundary simulations with the Zhou or ML-based models

3.5 Run Time Considerations

Performance tests were conducted on a small cluster at the Scientific Computing Group, University of Hamburg. The utilized nodes contain two CPUs of type Intel Xeon X5650 with six cores each. The size of the memory per node is 12 GB. All tests were performed in sequential mode.

Regarding the training step of our method, the number of samples plays a considerable role. The higher the size of our sample set, the longer the training takes to complete. Furthermore, the complexity of the model affects its run time during training as well as during a simulation.

Figure 13(a) shows the times needed for training of some of the ML models considered in this work. Using the binning method, the training completes ca. nine times faster. Due to the number of samples, not only the run time of one epoch is lower, but also the overall number could be reduced while retaining the quality of the density profile or even improving it.

Figure 13(b) contains the measured run times of the different setups. The Zhou model is slightly faster than a purely periodic simulation. The ML-based runs are not as efficient as Zhou and yield higher run times than the periodic version. The force computation during a simulation employing the ML model is conducted in bulk mode. That is, at each time step the force and distance values of each particle in the boundary regions are collected and passed at once to the neural network. As Tensorflow is optimized for parallel computation, there is quite some overhead expected when the tool is used in sequential mode.

4 Conclusion and Outlook

We have introduced a novel ML-based model to predict open boundary forcing. The model is built from molecular data from a prior equilibration and thus reflects the molecular structure of the fluid well. It further yields accurate forcings at acceptable computational performance, which has been demonstrated in various tests, including a detailed comparison with the parameter space exploration-based Zhou model. It shall be remarked that relying on a prior equilibration is only necessary for the startup phase: in case of molecular systems, that change dynamically over time, the ML model could be adjusted “on-the-fly” by simply using more molecular data from the inner part of the MD domain where valid MD information should be available. This should in principal work well, since our analysis showed that potential perturbations in the molecular systems are very marginal and have only been observed in close proximity of the open boundary. Yet, enough samples need to be found in this case in a sufficiently short time frame. This appears a promising route that shall be investigated in the future.

We have discussed various aspects of parametrization of our ML-based model and also provided estimates on how many samples and training epochs are required to generate valid open boundary force models, cf. Sect. 3.3. Yet, improved explainability of the arising network weights in relation to, e.g., the impact of thermal fluctuations or the RDFs of the fluid would be desirable.

Further research to optimize the overall neural network and improve its outputs, e.g. by optimizing the learning rate as briefly discussed in Sect. 3.1 would be desirable. Employing ensemble strategies is another possibility to improve the quality of ML-based boundary forcing. Both aspects were, however, beyond the scope of this work.

The actual power of machine learning lies in the prediction of highly complex systems, e.g. deducing information from higher-dimensional inputs. With the method presented in this contribution delivering very good results, an extension towards multi-site molecules or dynamic systems with locally varying densities as well as further computational performance improvements would therefore be logical next steps in our analysis and are, partly, work in progress. Since the ML-based model can potentially be used in conjunction with arbitrary MD solvers and is not restricted to LAMMPS that has been used in our studies, we further plan to incorporate the model into MaMiCo, a coupling tool for hybrid molecular-continuum simulations [9]. This would thus provide the functionality and make it re-usable for different combinations of MD solvers and molecular-continuum coupling algorithms in the future.

In terms of performance, we observed, besides the slight overheads of the ML approach compared to periodic simulations, that modifications of the learning rate could reduce the number of epochs needed for training in some of our test scenarios. Optimization of the learning rate would, thus, be also helpful in our case, similar to many other ML systems.