Keywords

1 Introduction

Physics-informed machine learning incorporates physical knowledge as inductive biases [1], providing significant advantages in terms of generalization and data efficiency when contrasted with pure machine learning systems (ML) applied to physical domains [8, 15]. Moreover, inductive biases often help ML models play down their “technical debt” [16], reducing model complexity while improving model explainability. Several recently proposed approaches augment neural networks with physical knowledge [5, 9, 10, 17, 18]. But these models do neither allow including or structurally capturing explicitly defined physical equations, nor do they generalize to unseen initial and boundary conditions [15]. The recently introduced finite volume neural network (FINN) [7, 14] accounts for both: it combines the learning abilities of artificial neural networks with physical and structural knowledge from numerical simulations by modeling partial differential equations (PDEs) in a mathematically compositional manner. So far, FINN is the only physics-aware neural network that can handle boundary conditions that were not considered during training.

Nonetheless, the boundary conditions (BCs) need to be known and presented to all these networks explicitly. To date, not even FINN can predict processes, where the boundary conditions are completely unknown. In realistic application scenarios, however, a quantity of interest is measured for a specific, limited region only. The amount of the quantity that flows into the observed volumes through boundaries are notoriously unknown and impossible to predict. One example is weather forecasting: a prediction system observes e.g. precipitation or cloud density for a limited area. Incoming weather dynamics from outside of the observed region that strongly control the processes inside the domain cannot be incorporated, turning into one of the main error sources in the numerical simulations.

Here, we present an approach to infer the explicitly modeled BC values of FINN on-the-fly, while observing a particular spatiotemporal process. The approach is based on a retrospective inference principle [2, 13], which applies a prediction error-induced gradient signal to adapt the BC values of a trained FINN model. Only very few data points are required to find boundary conditions that best explain the recently observed process dynamics and, moreover, to predict the process henceforth with high accuracy in closed-loop. We compare the quality of the inferred boundary conditions and the prediction error of FINN with two state-of-the-art architectures, namely, DISTANA [6] and PhyDNet [5]. Our results indicate that FINN is the only architecture that reliably infers BC values and outperforms all competitors on predicting non-linear advection-diffusion-reaction processes when the BC values are unknown.

2 Finite Volume Neural Network

The finite volume neural network (FINN) introduced in [7, 14] is a physics-aware neural network model that combines the well-established finite volume method (FVM) [11] as an inductive bias with the learning abilities of deep neural networks. FVM discretizes a continuous partial differential equation (PDE) spatially into algebraic equations over a finite number of control volumes. These volumes have states and exchange fluxes via a clear mathematical structure. The enforced physical processing within the FVM structure constrains FINN to implement (partially) known physical-laws, resulting in an interpretable, well generalizing, and robust method.

2.1 Architecture

FINN solves PDEs that express non-linear spatiotemporal advection-diffusion-reaction processes, such as formulated in [7] as

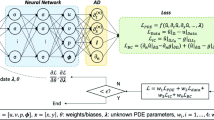
$$\begin{aligned} \frac{\partial u}{\partial t} = D(u) \frac{\partial ^2 u}{\partial x^2} - v(u)\frac{\partial u}{\partial x} + q(u), \end{aligned}$$
(1)

where u is the state or the unknown function of time t and spatial coordinate x. The objective of a PDE solver (if the PDE was fully known) is to find the value of u in all time steps and spatial locations. However, Eq. 1 is composed by three, often unknown functions of u, i.e. D, v, and q. D is the diffusion coefficient, which controls the equilibration between high and low concentrations, v is the advection velocity, which represents the movement of concentration due to the bulk motion of a fluid, and q is the source/sink term, which increases or decreases the quantity of u locally. These unknown functions are approximated by neural network modules, which imitate the structure of Eq. 1 applying it to a set of spatially discretized control volumes. Figure 1 and Eq. 2 illustrate how FINN models the PDE for a single control volume i. The first- and second-order spatial derivatives \(\smash {\left( \frac{\partial u}{\partial x}, \smash {\frac{\partial ^2 u}{\partial x^2}}\right) }\), for example, can be approximated with a linear layer, \(\varphi _{\mathcal {N}}\), aiming to learn the FVM stencil, i.e. the exchange terms between adjacent volumes. Furthermore, and in order to account for the structure of Eq. 1, FINN introduces two kernels that are applied on each control volume with index i—similar to how convolution kernels are shifted over an input image. First, the flux kernel \(\mathcal {F} = f_{-}+f_{+}\) models both the diffusive \(D(u) \smash {\frac{\partial ^2 u}{\partial x^2}}\) and the advective flux \(v(u)\frac{\partial u}{\partial x}\), respectively, via the feedforward network modules \(\varphi _{\mathcal {D}}\) and \(\varphi _{\mathcal {A}}\). Second, the state kernel \(\mathcal {S}\) models the source/sink term q for each volume. All modules’ outputs are summed up to conclude in \(\smash {\frac{\partial u}{\partial t}}\), which results in a system of ODEs with respect to time that is solved by NODE [3]. Accordingly, FINN predicts u in time step \((t + 1)\), that is \(\hat{u}^{(t+1)}\), and the error is computed via \(\mathcal {L}(\hat{u}^{(t+1)}_i, u^{(t+1)}_i)\), where i corresponds to the discretized spatial control volume index and \(\mathcal {L}\) is the mean squared error. FINN operates entirely in a closed-loop manner, i.e. only \(u^{(t=0)}\) is fed into the model to unroll a prediction \(\hat{u}^{(1:T)}\) into the future, with sequence length T. The connection scheme of the different kernels and modules ensures compliance with fundamental physical rules, such that advection can spatially propagate exclusively to the left or to the right. Note that we only consider one-dimensional problems in this work, although FINN can also be applied to higher-dimensional equations. The reader is referred to [7] and [14] for an in-depth depiction of the model.

Fig. 1.
figure 1

The composition of the modules to represent and learn different parts of an advection-diffusion equation. Figure from [7].

Full size image
(2)

2.2 Boundary Condition Inference

The specification of boundary conditions (BCs) is required to obtain a unique solution of a PDE. Common BCs are Dirichlet (fixed values for u), periodic (quantity leaving the field on the left enters on the right side), or Neumann (the derivative of u is specified at the boundary). In contrast to state-of-the-art physics-aware neural networks [5, 10, 15, 19], FINN allows the explicit formulation of a desired BC. Thus, FINN can deal with not only simple boundary conditions (Dirichlet or periodic) but also more complicated ones (e.g. Neumann) [7]. This study applies constant Dirichlet BCs, while we leave the in-depth exploration of other BCs for future research.

FINN uses the boundary conditions strictly. The solid implementation of a BC type (Dirichlet, periodic, Neumann) paves the way for the model to read out an unknown/unseen BC value of a given dataset. So far, however, it was unfeasible not to use an explicit BC for solving a PDE. However, novel ML models reinforced by inductive biases can extract essential information from data. FINN is an ML model that is predestined for this purpose, as it is tailored to conveniently implement various BC types and values for different PDEs. Accordingly, it is able to learn which BC values best describe a specific dataset—during both training and prediction. Here we show that it is possible to infer BC values in a much larger range via retrospective inference.

From a broader perspective, the need for BCs is often a modeling artifact for real-world problems—simply because we do not have the means to simulate an entire system but need to restrict ourselves to a bounded subdomain. Even if these boundaries do not exist in the original system, our resulting model needs to identify their conditions for accurate forecasting. Our aim is to infer appropriate BCs and their values quickly, accurately, and reliably. Technically, a BC value is inferred by setting it as a learnable parameter and projecting the prediction error over a defined temporal horizon onto this parameter. Intuitively, the determination of the BC values can thus be described as an optimization problem where the BC value instead of the network weights are subject for optimization.

3 Equations

We performed experiments on two different PDEs and will first introduce these equations to later report the respective experiments and results.

3.1 Burgers’ Equation

Burgers’ equation is frequently used in different research fields to model e.g. fluid dynamics, nonlinear acoustics, or gas dynamics [4, 12], and is a practical toy example formulated as a 1D equation in this work as

$$\begin{aligned} \frac{\partial u}{\partial t} = - v(u)\frac{\partial u}{\partial x} + D\frac{\partial ^2 u}{\partial x^2}, \end{aligned}$$
(3)

where u is the unknown function and v(u) is the advective velocity, which is defined as an identity function \(v(u) = u\). The diffusion coefficient D is set to \(0.01 / \pi \) in data generation. During training, Burgers’ equation has constant values on the left and right boundaries defined as \(u(-1,t) = u(1,t) = 0\). However, these were modified to take different symmetric values at inference in order to assess the ability of the different models to cope with such variations. The initial condition is defined as \(u(x,0) = -\sin (\pi x)\).

3.2 Allen-Cahn Equation

Allen-Cahn is chosen and also defined as a 1D equation that could have periodic or constant boundary conditions. It is typically applied to model phase-separation in multi-component alloy systems and has also been used in [15] to analyse the performance of their physics-informed neural network (PINN). The equation is defined as

$$\begin{aligned} \frac{\partial u}{\partial t} = D \frac{\partial ^2 u}{\partial x^2} + R(u), \end{aligned}$$
(4)

where the reaction term takes the form \(R(u) = 5u - 5u^3\). The diffusion coefficient is set to \(D=0.05\), which is significantly higher than in [7] where it was set to \(D = 10^{-4}\). The reason for this decision is to scale up the diffusion relative to the reaction, such that a stronger effect of the BCs is more apparent.

4 Experiments

We have conducted two different experiments. First, the ability to learn BC values during training is studied in Sect. 4.1. Afterwards, we analyze the ability of the pre-trained models to infer unknown BC values in Sect. 4.2. Data was generated with numerical simulation using the Finite Volume Method, similarly to [7].

4.1 Learning with Fixed Unknown Boundary Conditions

This experiment is conducted in order to discover whether it is possible for the model to approximate the boundary conditions of the given dataset. It can be utmost useful in real-world-datasets to determine the unknown BC values simultaneously while training the model.

The learnt BC values shown in Table 1 suggest that it is not even slightly possible for DISTANA and PhyDNet to infer reasonable BC values. Also for FINN, the problem is non-trivial. The complex nature of the equations combined with large-range BC values yield a challenging optimization problem, in which gradient-based approaches can easily end-up in local minima. Additionally, the fact that FINN uses NODE [3] to integrate the ODE, may, for example, lead to the convergence into a stiff system. In preliminary experiments, we have realized that the usage of shorter sequences actually helped identifying the correct BC values. Moreover, a sufficiently large learning rate was advantageous. The shape of the generated training data was (256, 49), where \(N_x = 49\) specifies the discretized spatial locations and \(N_t = 256\) the number of simulation steps. To train FINN, we only used the first 30 time steps of a sequence. As a result, FINN identifies the correct BCs and—although this was not necessarily the goal—even yields a lower test error for the entire 256 time steps of the sequence, even though it was trained on only the first 30. Neither PhyDNet nor DISTANA offer the option to meaningfully implement boundary conditions. Accordingly, they are simply fed into the model on the edges of the simulation domain. The missing inductive bias of how to use these BC values prevent the models to determine the correct BC values (c.f. Table 1). Nevertheless, both PhyDNet and DISTANA can approximate the equation fairly correct (albeit not reaching FINN’s accuracy), even when the determined BC values deviate from the true values. The learnt BC values by the two models do not converge to any point and persist around the initial values which are \([0.5, -0.5]\) for Burgers’ and \([-0.5, 0.5]\) for Allen-Cahn. Similarly, they remain around 0 when we set the initial BC values to 0. This suggests that PhyDNet and DISTANA did not consider the BC values at all. On the other hand, FINN appears to benefit from the structural knowledge about BCs when determining their values. The BC values in Table 1 converged from \([4.0, -4.0]\) to \([1.0,-1.0]\), well-maintaining them for the rest of the training (see first row of Fig. 2). As it can be seen on the second row of Fig. 2, FINN also manages to infer BC values for Allen-Cahn in a larger range. In Fig. 2, FINN shows its ability to neither overshoot nor undershoot. As we used synthetic data in this study, we knew what the true BC values were. However, it would be possible to trust FINN, even when the BC values are unknown to the researcher—as the correct BC values are learnt, the gradients of the boundary conditions converge to 0, maintaining the accurate BC well (see the right plots of Fig. 2).

Table 1. Comparison of the training errors and the learnt BC values of all models. For each trial the average results over 5 repeats are presented. Burgers’ dataset BC \(= [1.0,-1.0]\) and Allen-Cahn dataset BC \(= [-1.0, 1.0]\).
Full size table
Fig. 2.
figure 2

Convergence of the boundary conditions and their gradients during training in FINN. The dataset \({\text {BC}} = [1.0,-1.0]\) for Burgers’ on the first row. On the second row for Allen-Cahn with \({\text {BC}} = [-6.0, 6.0].\)

Full size image

4.2 Boundary Condition Inference with Trained Models

The main purpose of this experiment is to investigate the possibility to infer an unknown BC value after having trained a model on a particular BC value. In accordance with this purpose, we examined two different training algorithms, while applying the identical inference process when evaluating the BC inference ability of the trained models.

Table 2. Comparison of multi-batch training and prediction errors along with the inferred BC values by the corresponding models. The experiments were repeated 5 times for each trial and the average results are presented. Burgers’ dataset BC \(= [3.0,-3.0]\) and Allen-Cahn dataset BC \(= [-1.0, 1.0]\).
Full size table

Multi-batch Training and Inference. Ten different sequences with randomly sampled BC values from the ranges \([-1,1]\) for Burgers’ and \([-0.3,0.3]\) for Allen-Cahn equation were used as training data. Thus, the models have the opportunity to learn the effect of different BC values, allowing the weights to be adjusted accordingly.

During inference, the models had to infer BC values outside of the respective ranges when observing 30 simulation steps. The rest of the dataset, that is, the remaining 98 time steps, was used for simulating the dynamics in closed-loop. As can be seen in Table 2, FINN is superior in this task compared to DISTANA and PhyDNet. All three models have small training errors, but DISTANA and PhyDNet mainly fail to infer the correct BC values as well as to predict the equations accurately. FINN, however, manages to find the correct BC values with high precision and significantly small deviations. After finding the correct BC values, FINN manages to predict the equations correctly. Figure 3 shows how the prediction error changes in different models as the BC range drifts away from the BC range of the training set. On the other hand, Fig. 4 depicts the predictions of the multi-batch trained models after inference presenting once again the precision of FINN.

Fig. 3.
figure 3

Average prediction errors of 5 multi-batch trained models for Allen-Cahn-Equation. Standard deviations of FINN’s averaged errors range from \(4\times 10^{-6}\) to \(1\times 10^{-3}\). Hence it is not possible to see them in the plot.

Full size image
Table 3. Comparison of one-batch training and prediction errors after inference along with the BCs inferred by the corresponding models. The experiments were repeated 5 times for each trial and the average results are presented. Burgers’ dataset BC \(= [3.0,-3.0]\) and Allen-Cahn dataset BC \(= [-1.0, 1.0]\).
Full size table

One-Batch Training and Inference. In this experiment, the models receive only one sequence with \(t = [0,2]\), \(N_t = 256\) and \(N_x = 49\). The BC values of the dataset are constant and set to [0.0, 0.0]. Hence the models do not see how the equations behave under different BC values. This is substantially harder compared to the previous experiment and the results clearly exhibit this (see Table 3). Despite low training errors, DISTANA and PhyDNet fail to infer correct BC values. The prediction errors when testing in closed-loop after BC inference also indicate that these models have difficulties solving the task. FINN manages to infer the correct BC values, but also its prediction error increases significantly when compared to the training error. Nonetheless, FINN still infers the correct BC values and produces the lowest test error. These results demonstrate that the networks largely benefit from sequences with various BC values, enabling them to infer and predict the same equations over a larger range of novel BCs. While we only report the results of one set of boundary conditions for each experiment, due to space constraints, we have conducted these experiments with several other BC values, which all show the same result pattern.

Fig. 4.
figure 4

The predictions of the Allen-Cahn dynamics after inference. First row shows the models’ predictions over space and time. The respective white columns on the left side of the model predictions are the 15 simulation steps that were used for inference and subtracted before the prediction. Second row shows the predictions over x and \(u(x,t=1)\), i.e. u in the last simulation step. Best models were used for the plots.

Full size image

5 Discussion

The aim of our first experiment (see Sect. 4.1) was to assess whether FINN, DISTANA, and PhyDNet are able to learn the fixed and unknown Dirichlet BC values of data generated by Burgers’ and Allen-Cahn equations. This was achieved by setting the value of the BC as a learnable parameter to optimize it along with the models’ weights during training. The results, as detailed in Table 1, suggest two conclusions: First, all models can satisfactorily approximate the equations by achieving error rates far below \(10^{-1}\). Second, only FINN can infer the BC values underlying the data accurately. Although DISTANA and PhyDNet simulate the process with high accuracy, they apparently do not exhibit an explainable and interpretable behavior. Instead, they treat the BC values in a way that does not reflect their true values and physical meaning. This is different in FINN, where the inferred BC value can be extracted and interpreted directly from the model. This is of great value for real-world applications, where data are given with an unknown BC, such as in weather forecasting or traffic forecasting in a restricted simulation domain.

In the second experiment (see Sect. 4.2), we addressed the question of whether the three models can infer an unknown BC value when they have already been trained on a (set of) known BC values. Technically, this is a traditional test for generalization. The results in Table 2 suggest that both DISTANA and PhyDNet decently learn the effect of the different BC values on the data when being trained on a range of BC values. Once the models are trained on one single BC value only (c.f. Table 3), however, the inferred BC values of DISTANA and PhyDNet are far off the true values. This is different for FINN: although the test error on Burgers’ could still be improved, FINN still determines the underlying BC values in both cases accurately, even when trained on one single BC value only.

Our main aim was to infer physically plausible and interpretable BC values. Although FINN is a well tested model and it has been compared with several models such as ConvLSTM, TCN, and CNN-NODE in [7], we applied FINN to 1D equations in this work. However, since the same principles underly higher dimensional equations, we anticipate the applicability of the proposed method to higher dimensional problems.

6 Conclusion

In a series of experiments, we found that the physics-aware finite volume neural network (FINN) is the only model—among DISTANA (a pure spatiotemporal processing ML approach) and PhyDNet (another physics-aware model)—that can determine an unknown boundary condition value of data generated with two different PDEs with high accuracy. Once the correct BC values are found, it can predict the equation depending on them with high precision. So far, the universal pure ML models stay too general to solve the problem studied in this work. State-of-the-art physics-aware networks (e.g. in [5, 8]) are likewise not specific enough. Instead, this work suggests that a physically structured model that can be considered as an application-specific inductive bias is indispensable and should be paired with the learning abilities of neural networks. FINN integrates these two aspects by implementing multiple feedforward modules and mathematically composing them to satisfy physical constraints. This structure allows FINN to determine unknown boundary condition values both during training and inference, which, to the best of our knowledge, is a unique property under physics-aware ML models.

In future work, we will investigate how different BC types (Dirichlet, periodic, Neumann, etc.)—and not only their values—can be inferred from data. Moreover, an adaptive and online inference scheme that can deal with dynamically changing BC types and values is an exciting direction to further advance the applicability of FINN to real-world problems. Finally, the further evaluation of FINN on real-world data is imminent.